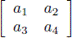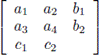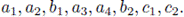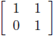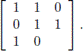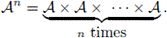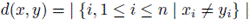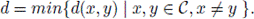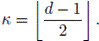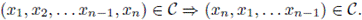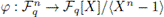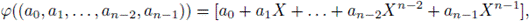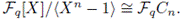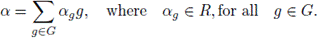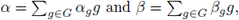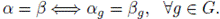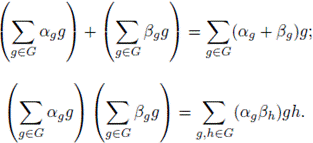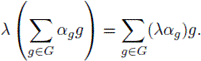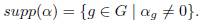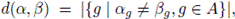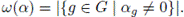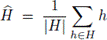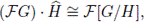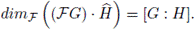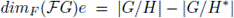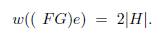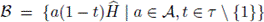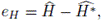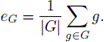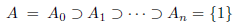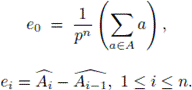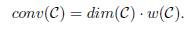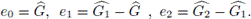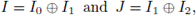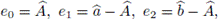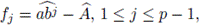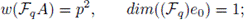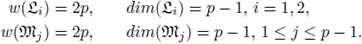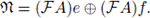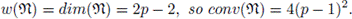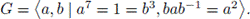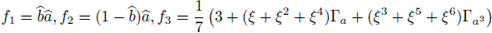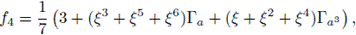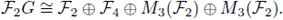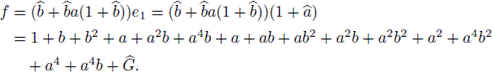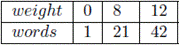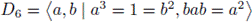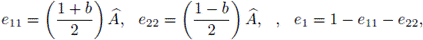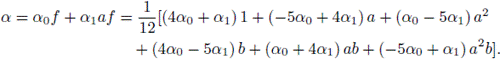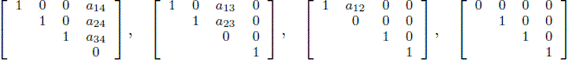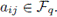1. Introduction
Group algebras play a very large role in the theory of error-correcting codes. In this very short survey we cover only one aspect of this role: we focus on the relationship between weight and dimension of group codes. This type of codes have recently been the object of active research (see [2], [6], [7], [8], [9], [10], [11], [12], [13], [19], [20], [24], [27]).
We start from the most basic definitions to render the paper accessible to the general mathematical reader. It should be noted that some important concepts of the theory, such as encoding and decoding, are not treated here since they are of no direct interest to our objectives
2. A brief history
Already at the early days of computing, a method was devised to prevent a computer from working with wrong data.
Each "word" of information sent to the computer was composed of a series of digits equal to either 0 or 1 (or bits, as they are called in this context). One such word could be, for example 10011001. Then, an extra digit was added at the end of each word, called the parity-check digit which would be equal to 0 or 1 depending on whether the number of bits equal to 1 in the given word were even or odd, In the case of our example, the parity check would be 0 and the extended word would be 100110010.
In this way, every extended word sent to the computer would now have nine digits and an even number of bits equal to 1.
On receiving each word, the computer would check the number of digits equal to 1, and in case this number were odd it would know that there was a mistake in this word and stop the task.
Of course this method has some inconveniences. First, if two mistakes were committed the error would not be detected. Also, even if the existence of a mistake is detected, it is not possible to determine which is the wrong bit in the word.
This was the method used in 1947 at the Bell Telephone Laboratories, where the engineer Richard W. Hammming worked. In those days computers were much slower than nowadays and their time was disputed among the users of the machine. Hamming's priority was rather low, so he had to submit his "jobs" to stand in a queue over the weekend to be processed when possible. The computer would work on each job and if an error was detected it, would just stop and proceed to the next job.
In an interview [18], Hamming recalls how the idea of error correcting codes came to him:
Two weekends in a row I came and found that all my stuff had been dumped and nothing was done. I was really aroused and annoyed and I wanted those answers and two weekends had been lost. And so I said, "Damn it, if the machine can detect an error, why can't it locate the position of the error and correct it?"1
He started to work on this question and his idea was to add to each word not just one parity-check digit but more digits that he called redundancy which would allow to locate the error and hence correct it. Still in 1947, in an internal memorandum of the Bell Telephone Company he developed a code in which the information to be transmitted was composed of words of four bits and contained another four bits of redundancy.
Let a 1 a 2 a 3 a 4 be a word to be transmitted. First, write it as a matrix of size 2 x 2 :
Then extend it to a matrix of size 3 x 3 (but without the entry corresponding to position 3, 3) in such a way that each row and each column has an even number of digits equal to 1:
Then the matrix can be written as a 'word' taking it by rows:
For example, if the initial word is 1101 we dispose it as
and extend it to the matrix
Then, the word to be sent to the computer would be 11001110. The computer would then reproduce the 3 x 3 matrix, check parity of rows and columns and it is an easy exercise to verify that if one error is committed, then it is possible to detect the existence of the error and also its position, so it can be corrected.
In this same memorandum, Hamming asks if it would be possible to correct an error in a word containing four original digits of information, using only three digits of redundancy. His results could not be published in a journal for a general audience because the company applied for the corresponding patents and Hamming had to wait for the end of this process, until 1950 Quoted in T. Thompson, [30, p.17], where the reader can find more information on this story. [17].
A positive answer to Hamming's question appeared in a paper by his colleague at the company Claude Shannon Quoted in T. Thompson, [30, p.17], where the reader can find more information on this story. [29] in 1948. This long work by Shannon is considered today as a paper giving birth to two mathematical theories: the Theory of Error-Correcting Codes and Mathematical Information Theory.
Shortly afterwords, Marcel Golay, inspired by the work of Shannon, published a paper, one page long, in which he gives two of the most used codes in use to this day. E.R. Berlekamp [3, p. 4] described this paper as the "best page ever published" in Coding Theory.
3. Basic facts
A code is essentially a language devised to communicate with a machine or for communication among machines.
The fundamental elements to produce a code are:
A finite set A which we call an alphabet; its elements are frequently called letters. We denote by q = |A| the number of elements in A and say that the code is q-ary.
Finite sequences of elements of A are called words. The number of letters in a word is called its length. We shall assume that all the words in the codes considered here have the same length.
A q-ary code C of length n is then a set (of our choice) of words of length n; i.e., a code C is a subset of
This set is sometimes called the ambient space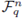 of the code.
of the code.
Definition 3.1. Given two words x = (x
1
, x2,..., x
n
) and y = (y
1
, y2,..., yn) in a code
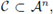 the Hamming distance from x to y is the number of coordinates in which these elements differ; i.e.:
the Hamming distance from x to y is the number of coordinates in which these elements differ; i.e.:
Given a code
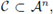 the minimal distance of C is the number
the minimal distance of C is the number
For a rational number α we denote by
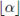 the greatest integer m such that m ≤ α. The first important result in coding theory is the following.
the greatest integer m such that m ≤ α. The first important result in coding theory is the following.
Theorem 3.2. Let C be a code with minimal distance d and set
Then, it is possible to detect up to d - 1 errors and correct up to K errors.
The number k above is called the error-correcting capacity of the code. A q-ary code of length n containing M words and having minimal distance d is called an (n, M, d)-code.
A natural goal, when designing a code is to look for efficiency (in the sense that it contains a large number of words, so it can transmit enough information) and also a large minimum distance, so that it can correct a big number of errors.
Unfortunately, these goals conflict with each other, since the ambient space AN is finite. The problem of maximizing one of the parameters (n, M, d) when the other two are given is known as the main problem of Coding Theory.
A most important class of codes are the so-called linear codes which are constructed as follows.
We take, as an alphabet, a finite field
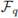 with q elements (where q is now a power of a prime
with q elements (where q is now a power of a prime
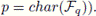 The ambient space
The ambient space
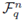 is then a vector space of dimension n over
is then a vector space of dimension n over
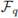 .
.
A linear code C of length n over
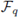 is a proper linear subspace of
is a proper linear subspace of
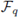 . If dim(C) = m, then m < n.
. If dim(C) = m, then m < n.
It is easy to see that, in this case, the number of words in C is qm, so we refer to one such code, for briefness, as an (n, m, d)-code.
A special class of linear codes was introduced in 1957 by E. Prange [25]. Originally these codes were introduced because they allowed for efficient implementation, but they also have a rich algebraic structure and can be used in many different ways. Many practical codes actually in use are of this kind.
Given a word
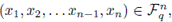 , its right shift is the word
, its right shift is the word
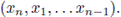 A linear code C is cyclic if, for every word in the code its right shift is also in the code; i.e., if
A linear code C is cyclic if, for every word in the code its right shift is also in the code; i.e., if
Notice that this implies that if a given word (x1,x2,... xn-i,xn) is in the code, then all its circular permutations are in the code.
where [f] denotes the class of the polynomial f ∈ 𝔽q [X] in Rn, is a linear isomorphism, and it is easy to see that a linear subspace C in
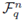 is a cyclic code if and only if φ(C) is an ideal of
is a cyclic code if and only if φ(C) is an ideal of
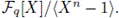 Hence, the study of cyclic codes of length n over
Hence, the study of cyclic codes of length n over
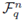 is the same as the study of ideals in the quotient ring
is the same as the study of ideals in the quotient ring
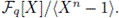
On the other hand, if Cn denotes the cyclic group of order n and
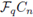 its group algebra over
its group algebra over
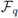 , it is well-known that
, it is well-known that
Hence, the study of cyclic codes of length n over the field
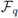 can also be regarded as the study of ideals in the group ring
can also be regarded as the study of ideals in the group ring
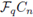 .
.
4. Group Codes
The concept of codes as ideals in group algebras of cyclic groups can be extended naturally to other classes of groups. This was first done in 1967 by S.D. Berman ([4], (5]) and independently by F.J. MacWilliams [21] in 1970.
Recall that the group algebra of a finite group G over a field R is the set of all formal linear combinations:
We define:
For λ in R we define
The set RG, with the operations above, is called the group algebra of G over R.
The elements of the group G form a basis of the group algebra RG over R. So if we enumerate them in any given order G = {g1, g2,..., gn}, we can think of a word (x1, x2,..., xn) in a space
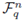 as corresponding to the element
as corresponding to the element
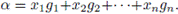
With this correspondence in mind, we define:
Let G be a finite group and
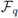 a finite field. A group code or, more precisely, a G-code over
a finite field. A group code or, more precisely, a G-code over
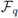 is an ideal of the group algebra
is an ideal of the group algebra
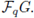
We recall that the support of an element
 in the group 𝔽qG of a group G over a field 𝔽q is the set
in the group 𝔽qG of a group G over a field 𝔽q is the set
The Hamming distance between two elements
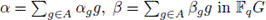 is
is
and the weight of an element α is w(α) = d(α, 0) = |supp(α)|; then,
Notice that, for linear codes, it is easy to see that the minimum distance of a code coincides with its minimum weight.
Given an ideal I ⊂ 𝔽qG, the weight distribution of I is the map which assigns, to each possible weight t, the number of elements of I having weight t.
It is well-known that, due to Maschke's Theorem (see [23, Corollary 3.2.8]), the structure of the group algebra
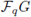 changes dramatically, depending on weather q and |G| are, or not, relatively prime.
changes dramatically, depending on weather q and |G| are, or not, relatively prime.
We shall always assume, throughout, that gcd(q, |G|) = 1. In this case the group algebra FqG is semisimple, meaning that every ideal (right, left or two-sided) is a direct summand and is thus a principal ideal, generated by an idempotent element.
Morover, it can be shown that:
(i) 𝔽qG is a direct sum of a finite number of two-sided ideals {Ai}1≤i≤r, called the simple components of 𝔽qG. Each Ai is a simple algebra.
(ii) Any two-sided ideal of 𝔽qG is a direct sum of some of the members of the family {Bi}1≤i≤r.
(iii) Each simple component Ai is isomorphic to a full matrix ring of the form Mni (
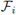 ), where
), where
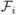 is a field containing an isomorphic copy of 𝔽q in its center.
is a field containing an isomorphic copy of 𝔽q in its center.
Since every simple component is generated by an idempotent element, the results above can be translated as follows:
Let G be a finite group, and let 𝔽q be a field such that
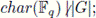 and let
and let
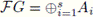 be the decomposition of the group algebra as a direct sum of minimal two-sided ideals. Then, there exists a family {e1,..., es} of elements of FG such that:
be the decomposition of the group algebra as a direct sum of minimal two-sided ideals. Then, there exists a family {e1,..., es} of elements of FG such that:
(i) ei ≠ 0 is a central idempotent, 1 ≤ i ≤ t.
(ii) If i ≠ j, then eiej = 0.
(iii) 1 = e1 + … + e t .
(iv) ei cannot be written as
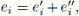 where
where
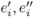 are central idempotents such that both
are central idempotents such that both
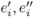 ≠ 0 and
≠ 0 and
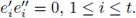
(v) Ai = Ae i , 1 ≤ i ≤ s.
The idempotents above are called the primitive central idempotents of 𝔽qG.
There is a rather standard way of constructing idempotents in group algebras. If H is a subgroup of G, then
is an idempotent of FG, and
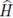 is central if and only if H is normal in G. It is well-known that [23, Proposition 3.6.7]
is central if and only if H is normal in G. It is well-known that [23, Proposition 3.6.7]
so,
Also, it is easy to see that if τ is a transversal of H in G, i.e., a complete set of representatives of cosets of H in G, then
Unfortunately, an element in such an ideal is of the form
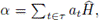 which means that, when written in the basis G of FG, it has the same coefficient along all the elements of the form th for a fixed t ∈ Τ and any h ∈ H. Thus, this kind of ideals defines repetition codes, which are not particularly interesting.
which means that, when written in the basis G of FG, it has the same coefficient along all the elements of the form th for a fixed t ∈ Τ and any h ∈ H. Thus, this kind of ideals defines repetition codes, which are not particularly interesting.
There is another kind of idempotents that will define more significant codes.
Theorem 4.1 ([13]). Let G be a finite group and
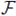 a field such that
a field such that
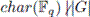 . Let H and H* be normal subgroups of G such that H ⊂ H*, and set
. Let H and H* be normal subgroups of G such that H ⊂ H*, and set
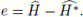 Then,
Then,
and
Let
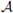 be a transversal of H* in G and τ a transversal of H in H* containing 1. Then,
be a transversal of H* in G and τ a transversal of H in H* containing 1. Then,
In the case when G is an abelian group, it is possible to decide when all primitive central idempotents can be obtained in this way.
Let A be an abelian p-group. For each subgroup H of A such that A/H ≠ {1} is cyclic, we shall construct an idempotent of
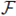 A. Since A/H is a cyclic subgroup of order a power of p, there exists a unique subgroup H* of A, containing H, such that |H* /H| = p.
A. Since A/H is a cyclic subgroup of order a power of p, there exists a unique subgroup H* of A, containing H, such that |H* /H| = p.
We set
and also
Theorem 4.2 ([13]). Let p be an odd prime and let A be an abelian p-group of exponent p
r
. Then, the set of idemponts above is the set of primitive idempotents of
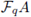 if and only if one of the following holds:
if and only if one of the following holds:
(i) pr = 2, and q is odd.
(ii) pr =4 and q = 3 (mod 4).
(iii) o(q) = φ(p
n
) in
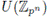 (where ip denotes Euler's Totient function).
(where ip denotes Euler's Totient function).
In the particular case when G is a cyclic group of order pn, with gcd(p,q) = 1, the theorem above gives the following
Corollary 4.3 ([13], [26]). Let
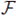 be a field with q elements and A a cyclic group of order pn
such that o(q) = φ(p
n
) in
be a field with q elements and A a cyclic group of order pn
such that o(q) = φ(p
n
) in
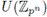 . Let
. Let
be the descending chain of all subgroups of A. Then, the set of primitive idempotents of FA is given by
A similar result holds for cyclic groups of order 2pn (see [1], [13]).
Since the introduction of abelian codes by Berman and MacWiliams, untill recent times there were no evidence that they would produce better codes than the cyclic ones. This was mainly due to the fact that most of the codes that were constructed were defined from minimal ideals and, as we shall see, these are not the ones that should be taken into account for this purpose.
Let G
1 and G
2 denote two finite groups of the same order,
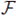 a field, and let γ : G
1
→ G
2 be a bijection. Denote by
a field, and let γ : G
1
→ G
2 be a bijection. Denote by
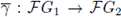 its linear extension to the corresponding group algebras.
its linear extension to the corresponding group algebras.
Clearly,
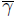 is a Hamming isometry; i.e., elements corresponding under this map have the same Hamming weight. Ideals I
1 ⊂
is a Hamming isometry; i.e., elements corresponding under this map have the same Hamming weight. Ideals I
1 ⊂
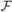 G
1 and I
2 C
G
1 and I
2 C
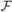 G
2 such that
G
2 such that
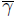 (I
1) = I
2 are thus equivalent, in the sense that they have the same dimension and the same weight distribution. In this case, the codes I
1 and I
2 are said to be permutation equivalent and were called combinatorially equivalent in [28]. We have the following
(I
1) = I
2 are thus equivalent, in the sense that they have the same dimension and the same weight distribution. In this case, the codes I
1 and I
2 are said to be permutation equivalent and were called combinatorially equivalent in [28]. We have the following
Theorem 4.4 ([7]). Every minimal ideal in the semisimple group algebra
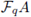 of a finite abelian group A is permutation equivalent to a minimal ideal in the group algebra
of a finite abelian group A is permutation equivalent to a minimal ideal in the group algebra
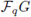 of a cyclic group C of the same order.
of a cyclic group C of the same order.
However, when working with non-minimal ideals, the situation is quite different.
As mentioned in the previous section, when we stated the Main Problem of Coding Theory, we wish to build codes with a good error correcting capacity and dimension as big as possible. Since one of this numbers decreases as the other increases, to compare efficiency of codes with different weights and dimensions, it seems rather natural to make the following
Definition 4.5. For a code C, we call convenience of C the number
Notice that this notion makes sense if one wishes to compare codes with dimensions or weights that are somehow close. However one might have a code with a high convenience where one of the parameter is quite big and the other rather small. Certainly, this would not be a useful code.
Set G =< a >, with a
p2 = 1, a cyclic code of order p2 and let
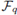 be any field as in the hypotheses of the Theorem above. Then, from the Corollary, there exist in
be any field as in the hypotheses of the Theorem above. Then, from the Corollary, there exist in
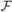 G only three principal idempotents:
G only three principal idempotents:
So the maximal ideals are:
with dim(I) = p, w(I) = p and dim(J) = p 2 - 1, w(J) = 2, and thus conv(I) = p 2 and conv(J) = 2(p 2 - 1).
On the other hand, also from the Theorem above, it can be shown that if we set A = C
p
x C
p
, then the principal idempotents of
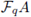 are
are
and
where a and b denote the respective generators of both direct factors.
We have that
and for the other minimal ideals 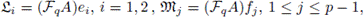 we have:
we have:
If H =< h > and K =< k > are two subgroups of order p of C
p x C
p
, the corresponding idempotents are
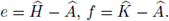 Set
Set
Then, we have the following
Proposition 4.6 ([22]). The weight and dimension of
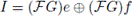 are
are
Hence, if p > 3, we have that conv
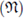 is greater than conv(I) for all proper ideal I of
is greater than conv(I) for all proper ideal I of
5. Non Abelian groups
Codes in group algebras of non-abelian groups have been considered for quite some time. Lomonaco and Sabin [28] studied metacyclic groups and showed that central idempotents generate codes that are combinatorially equivalent to abelian codes.
More recently, C. García Pillado, S. González, C. Martínez, V. Markov, and A. Nechaev, [15] showed that this is also the case for groups G that can be written as G = AB, where both A and B are abelian.
Hence, one should focus on ideals generated by non-central idempotents. We offer a couple of examples in this direction taken from [2].
It can be shown that the central primitive idempotents of
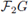 are
are
and
where ξ is a primitive 7th root of unity.
It can be shown also that
Take
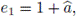 which is not a central primitive idempotent, and compute
which is not a central primitive idempotent, and compute
The weight of f is w(f) = 12, and it can be shown that the weight distribution of this ideal is
This is a [21,6,8]-code, which has the same weight of the best known [21,6]-code (see [16]).
Example 5.2. Let
be the dihedral group of order 6, and let
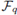 be a finite field with q elements such that
be a finite field with q elements such that
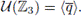 By [11, Theorem 3.3]), the central primitive idempotents of
By [11, Theorem 3.3]), the central primitive idempotents of
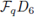 are
are
and we can write f = e11 - e12 and set I =
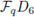 · f. Since dim[I] = 2, the set {f,af} is a basis over
· f. Since dim[I] = 2, the set {f,af} is a basis over
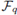 , and an element
, and an element
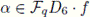 can be written as
can be written as
If q = 11, a direct computation show us that w(I) = 5, the weight of the best known [6,2]-code according to [16]. This is also the case for any field of characteristic different from 2, 3, 5 and 7.
5.1. Idempotents and left ideals in matrix algebras
Since the building blocks of finite semisimple group algebras are matrix algebras over finite fields, it is natural to try to determine all non-central idempotents defining left ideals in this kind of rings. These can be obtained as follows.
Let E(n, k) denote the set of all matrices A = (aij) such that there exist k rows, at positions denoted i1, i2,..., ik, verifying:
(i) Every row of A, except these, is a row of zeros.
(ii)
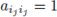 and
and
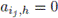 if h < i
j, 1 ≤ j ≤ k.
if h < i
j, 1 ≤ j ≤ k.
(iii)
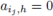 for h = is, j + 1 ≤ s ≤ k.
for h = is, j + 1 ≤ s ≤ k.
The set of numbers i1, i2,..., ik will be called the pivotal positions of A.
For example, E(4, 3) is the set of all matrices of the form:
Theorem 5.3 ([14]). The elements of the set E(n,k) are idempotent generators of the different left ideals of rank k of
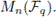 Moreover, each left ideal of rank k has q
(n-k)k
different idempotent generators.
Moreover, each left ideal of rank k has q
(n-k)k
different idempotent generators.