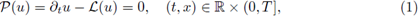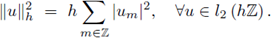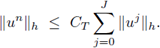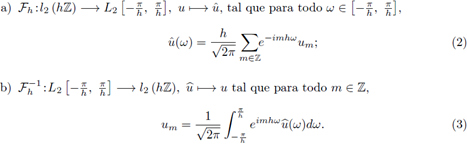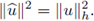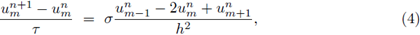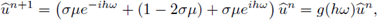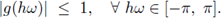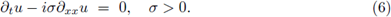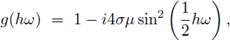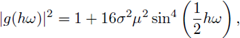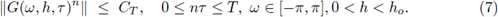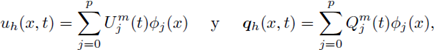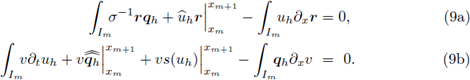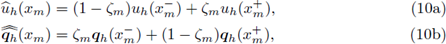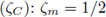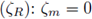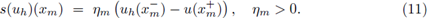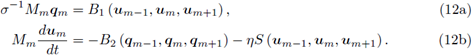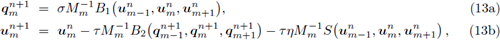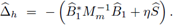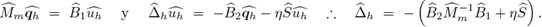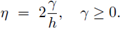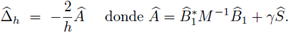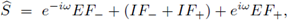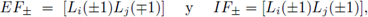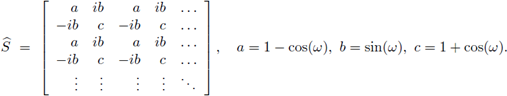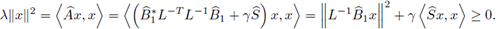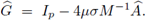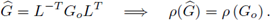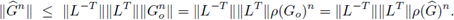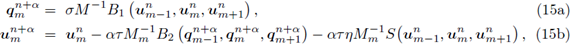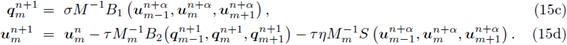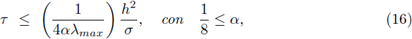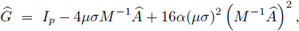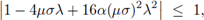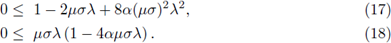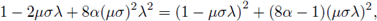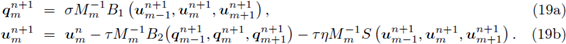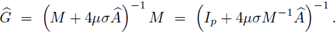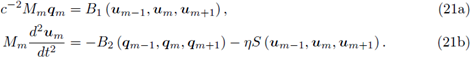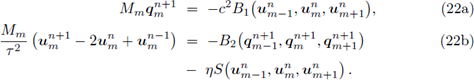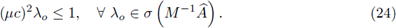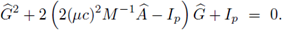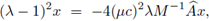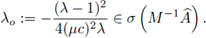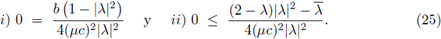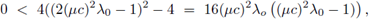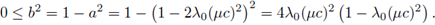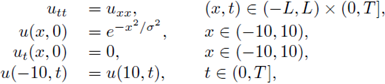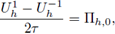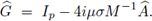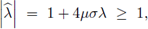Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
1. Introducción
Uno de los conceptos fundamentales en la simulación de problemas transitorios es el de estabilidad numérica. En términos simples, este establece la relación que debe ocurrir entre la resolución temporal y la espacial de un esquema numérico a fin de que la aproximación no presente oscilaciones, las cuales podrían crecer sin control, degradando completamente la calidad de la aproximación. Esta noción es de gran interés, en particular al aplicar discretizaciones temporales explícitas.
En las últimas décadas los métodos de elemento finito de Galerkin discontinuos han sido ampliamente utilizados en una extensa variedad de ecuaciones. A diferencia del método de elemento finito clásico (continuo), los métodos discontinuos se caracterizan fundamentalmente por imponer continuidad en forma débil, por lo que la aproximación no requiere continuidad entre celdas. Esto posibilita su formulación variacional, de manera natural, en mallas suficientemente arbitrarias, como por ejemplo aquellas que poseen nodos colgantes. Además, permite el uso de aproximaciones polinomiales de grado arbitrario, pero no necesariamente uniforme, lo cual es ideal para la versión hp del método de elemento finito. Aquí se considerará uno de estos métodos, conocido en inglés como Local Discontinuous Galerkin (LDG), el cual fue propuesto y analizado por Cockburn y Shu en [8], para problemas transitorios de difusión y convección no lineal.
Este artículo tiene como objetivo derivar algunas condiciones necesarias y suficientes para la estabilidad numérica del método LDG, aplicado a ecuaciones clásicas basadas en el operador laplaciano, en combinación con esquemas explícitos en tiempo. Si bien es cierto que para problemas de difusión el uso de discretizaciones temporales implícitas es lo más recomendable, algunos investigadores prefieren, por su sencillez en la programación, el uso de métodos explícitos en tiempo, los cuales no requieren resolver sistemas lineales o no lineales. Por lo que es importante hacer un análisis de las condiciones de estabilidad; o de la constante de estabilidad CFL (Courant-Friedrichs-Lewy), en función de los parámetros característicos del método y del grado de aproximación. Con este objetivo en mente, se repasa brevemente el concepto de estabilidad numérica y se introduce una de las herramientas teóricas esenciales: el análisis de estabilidad de Von Neumann, también conocido como análisis de estabilidad de Fourier. Aunque nuestro análisis se restringe al caso unidimensional, el uso de dicha herramienta para el estudio de la constante CFL en un método Galerkin discontinuo no es del todo trivial, ya que su aplicación a una sola ecuación es similar a la de analizar la condición CFL para un sistema de ecuaciones.
El estudio de la CFL para discretizaciones espaciales de tipo Galerkin discontinuo ha sido considerado mayormente en el caso de problemas hiperbólicos, donde las discretizaciones temporales explícitas son preferiblemente utilizadas. Por ejemplo, Kubatko, Westering y Dawson [11] presentaron un estudio numérico de la condición CFL para una clase de métodos de Runge Kutta explícitos, aplicada a un problema de advección lineal unidimensional; y posteriormente, dicho estudio fue extendido, por los mismos autores, a mallas triangulares en [10], y por Toulorge y Desmet en [14]. Recientemente, Castillo y Gómez [4] estudiaron la condición CFL del método LDG aplicado a la ecuación fraccionaria nolineal de Schrödinger, utilizando el método "pídola" (conocido en inglés como Leapfrog) como esquema de avance de tiempo. En dicho estudio se concluye que el uso de métodos explícitos puede ser una muy buena alternativa cuando el orden de la difusión fraccionaria es cercano a 1.
La organización de este artículo es la siguiente. En la Sección 2 se introduce el concepto de estabilidad numérica. Aunque este ha sido mayormente utilizado en el contexto de discretizaciones basadas en diferencias finitas, también puede ser aplicado al método de elemento finito clásico en mallas cartesianas uniformes; y por consiguiente, también para los métodos de tipo Galerkin discontinuo, que son los de nuestro interés. En la Sección 3 se presenta la idea general de la discretización del operador laplaciano por medio del método LDG, utilizando como ecuación modelo la de calor en una dimensión. En la Sección 4, utilizando el análisis de estabilidad de von Neumann de la Sección 2.1, se analizan las condiciones de estabilidad numérica del método LDG aplicado a algunas ecuaciones clásicas, como la ecuación de calor, la ecuación lineal de Schrödinger y la de onda, para varias discretizaciones en tiempo.
2. Estabilidad numérica
Considérese el siguiente problema de valores iniciales: u(x, 0) = u 0(x) para todo x ∈ ℝ,
donde
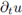denota la derivada parcial con respecto a
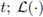es un operador diferencial lineal en la variable espacial x. Se denotan por h, τ ∈ ℝ+ los parámetros característicos de la discretización en espacio y tiempo, respectivamente; y por
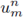la aproximación de u(mh,nτ) para cualesquiera m ∈ ℤ y n ∈ ℕ. La noción de estabilidad numérica sintetiza la idea de que en cualquier tiempo, t
n = nτ < T, la norma de la aproximación en ese tiempo está acotada uniformemente con respecto a τ y h a medida que estos tienden a cero. Este concepto se formaliza de la siguiente manera: sea l
2 (hℤ) el espacio de las sucesiones de valor complejo
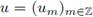tales que
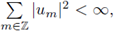dotado, por
conveniencia, de la norma, dependiente de h, definida por
Se considera la siguiente definición de estabilidad numérica utilizada en los libros de Strickwerda [13] y Gustafsson, Kreiss y Oliger [9]:
Definición 2.1 (Estabilidad numérica). Se dice que un esquema
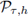para el problema
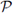es estable en una región Γ, si existe un entero J tal que para todo tiempo T > 0 existe una constante C
T tal que para todo 0 ≤ nτ ≤ T con (h, τ) ∈ Γ se verifique
Nótese que la cota superior solamente depende de la norma de un número fijo, J, de aproximaciones iniciales; y que la constante C T depende del tiempo final, pero no de los tiempos intermedios ni de los parámetros τ y h.
2.1. Análisis de von Neumann
Por lo general, la aplicación de la Definición 2.1 a esquemas numéricos de alta precisión requiere cálculos muy engorrosos. En [5], haciendo uso de la transformada discreta de Fourier, Charney, Fjörtoft y von Neumann desarrollaron, rigurosamente, una herramienta para determinar las condiciones de estabilidad de un esquema numérico, la cual se conoce como análisis de estabilidad de von Neumann o análisis de estabilidad local de Fourier. La idea fundamental es motivada por i) la igualdad de Parseval, (ver más adelante la Proposición 2.3), la cual establece que la transformada discreta de Fourier es una isometría y, ii) el hecho de que en el espacio de frecuencias la norma de la aproximación en el tiempo t n+1 se puede expresar como la norma de la aproximación en el tiempo anterior, t n, multiplicada por un factor de amplificación. Es importante mencionar que esta herramienta posee la limitación de restringirse a problemas lineales con coeficientes constantes, condiciones periódicas o en un dominio infinito y discretizaciones en mallas uniformes. No obstante, a pesar de dichas restricciones, se puede obtener una idea sobre la estabilidad de un esquema en el caso de problemas nolineales, al aplicar este análisis a una linearización del problema original.
Sea
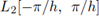el espacio de funciones medibles,
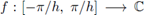tal que
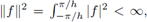donde la integración se realiza en el sentido de Lebesgue. La transformada de Fourier y su inversa se definen como sigue:
Definición 2.2. La transformada discreta de Fourier, F
h
, y su inversa,
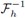, son operadores lineales definidos por
El uso de esta transformada discreta es motivado por la igualdad de Parseval, la cual permite expresar la Definición 2.1 en el espacio de frecuencia, preservando las normas.
Proposición 2.3 (Igualdad de Parseval). Para todo u ∈ l
2 (hℤ), sea
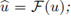entonces se tiene
Como breve repaso, a continuación, se ilustra el uso de la transformada discreta de Fourier (análisis de von Neumann) para el análisis de las condiciones de estabilidad numérica del siguiente esquema explícito, conocido como FTCS, por sus siglas en inglés (Forward in Time Central in Space):
el cual aproxima la solución de la ecuación del calor,
Este esquema se deriva considerando en (x m , t n ) = (mh,nτ) la aproximación por diferencias hacia adelante para la derivada temporal, y la central, para la derivada espacial. Aplicando la inversa de la transformada discreta de Fourier, a cada término del esquema (4), y por la unicidad de la transformada, se deduce la relación
donde
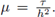Esta ecuación indica que en el espacio de frecuencias
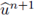se obtiene multiplicando
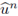por el factor de amplificación o símbolo
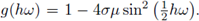Charney y col. [5] observaron que la estabilidad de un esquema se reduce al estudio de este factor. Para este ejemplo una condición necesaria y suficiente para garantizar la estabilidad del esquema numérico es
De manera análoga se puede considerar el método explícito de Euler (4) para la ecuación lineal de Schrödinger
Aplicando el análisis de estabilidad de von Neumann se obtiene el factor de amplificación
del cual se deduce que, para todo hw ∈ [-π, π],
por lo que este esquema es incondicionalmente inestable.
La transformada discreta de Fourier también puede definirse en el espacio de sucesiones
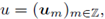donde
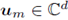para cualesquiera
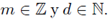Lo cual permite extender el análisis de von Neumann a esquemas numéricos aplicados a sistemas de ecuaciones. En este caso las condiciones de estabilidad son más delicadas de obtener, ya que el factor de amplificación es una matriz, G(w, h, τ). El criterio de estabilidad análogo a la definición 2.1, en el espacio de frecuencias, se traduce de la siguiente manera: para todo T > 0 existe una constante C
T
(la cual solamente depende de T), para la cual
En algunos casos, el análisis de estabilidad se reduce al estudio de la relación entre h y T de tal forma que se verifique la llamada Condición de von Neumann
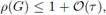o su versión más estricta p(G) ≤ 1. Sin embargo, puesto que para toda matriz
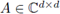y para todo n ∈ ℕ se tiene la desigualdad
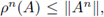la cual puede ser estricta, la condición de von Neumann es una condición de estabilidad necesaria pero no suficiente. Algunos resultados que garantizan que la condición de von Neumann es además suficiente se demuestran en [9,13] y sus referencias.
3. Método LDG
La formulación variacional del método LDG aplicado a un operador diferencial de segundo orden se ilustra a continuación, utilizando como modelo la ecuación de calor escrita como un sistema de ecuaciones de primer orden:
Sea
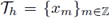una partición uniforme de
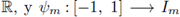el mapa local de la celda Im = [x
m
, xm+1], para todo m ∈ ℤ. Se denota por
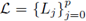la familia de polinomios ortogonales de Legendre, la cual forma una base en el espacio ℙ
p
([-1, 1]) de polinomios de grado menor o igual a p, restringidos a la celda de referencia [-1, 1]; entonces, para todo m ∈ ℤ, la familia
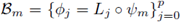es una base polinomial del espacio de elemento finito ℙ
p
(I
m
). En cada paso de tiempo t ∈ (0, T], y para cada celda Im, m ∈ ℤ, el método LDG busca una aproximación de la forma
tales que las siguientes ecuaciones se cumplan, para todo
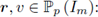
Los flujos numéricos
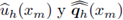son aproximaciones de u y q, respectivamente, en cada nodo xm de la malla, y se definen como combinaciones convexas de los valores de uh y q
h por ambos lados del nodo:
donde
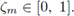Esta definición particular preserva la simetría de la discretización del operador diferencial de segundo orden,
(para más detalles, ver [2]). En este trabajo se consideran tres casos particulares de flujos:
1) Izquierdo
para todo m;
2) Central
para todo m;
3) Derecho
para todo m.
La selección de los flujos influye únicamente en la densidad del operador discreto, pero no en el orden de convergencia del método. En [1] Castillo propuso algunas heurísticas para reducir el código de plantilla del operador discreto para problemas en 2D y 3D. En problemas unidimensionales, los flujos direccionales (izquierdo y derecho) producen un código compacto, mientras que el central produce uno de mayor tamaño.
En [2] se presentó, por primera vez, un análisis de error para la versión mixta del método en el régimen estacionario y dominios en 2D. Se demostró que las variables u
h y q
h convergen, para cualquier flujo numérico, con orden
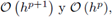respectivamente. Perugia y Schötzau [12] realizaron un análisis de error para la variable primaria uh y la versión hp. En ambos análisis, la existencia y unicidad de la solución del problema discreto se garantiza utilizando el término de estabilización s(uh) de la ec. (9b), definido por
Sin embargo, Cockburn y Dong [7], utilizando flujos direccionales, mostraron estabilidad del método aun cuando η = 0 en todas las aristas interiores. Para diferenciar esta nueva versión de la clásica o estabilizada (η > 0), esta se conoce como LDG de disipación mínima (md-LDG). El análisis del método en dominios unidimensionales y problemas lineales transitorios de convección y difusión fue presentada en [3] para la versión hp, donde además se obtuvo convergencia para aproximaciones constantes, es decir p = 0. El caso multidimensional fue analizado por Cockburn y Dawson en [6].
Sean
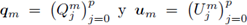los vectores de coeficientes que representan qh y uh, respectivamente, en la base local B
m de la celda I
m. Suponiendo constante el parámetro de estabilidad η, la formulación semi-discreta (ecuaciones (9a) y (9b)) se escribe localmente como un sistema de ecuaciones diferenciales ordinarias de la siguiente forma:
4. Análisis de estabilidad.
Contrariamente al método de diferencias finitas, la aplicación del análisis de von Neumann para discretizaciones espaciales discontinuas es, por lo general, más complicada, en particular para aproximaciones de alto orden, es decir, para 1 ≤ p. Esto se debe a que el factor de amplificación es una matriz. El caso p = 0, aproximaciones constantes por celda, corresponde al método de volumen finito; su análisis es similar al de un esquema de diferencias finitas y el factor de amplificación es un escalar. Las condiciones de estabilidad necesarias, y en algunos casos suficientes, para el método LDG aplicado a un problema escalar, se obtienen del análisis de estabilidad de von Neumann en su versión de sistemas, mencionado en la Sección 2.1. Para poder llevar a cabo el análisis de estabilidad, se asume de aquí en adelante que el dominio está dividido en celdas de igual longitud h.
4.1. Ecuación de calor
Como primer ejemplo se analiza la condición CFL de la discretización espacial LDG aplicada a la ecuación de calor, ecuación (5), utilizando el método de Euler explícito para la discretización en tiempo. El método completamente discretizado, FT-LDG, toma la siguiente forma en la celda I m:
donde el superíndice n + 1 se refiere al tiempo discreto t n+1 = t n + τ y Mm es la matriz de masa local en la celda I m.
Sean
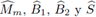los símbolos de los operadores
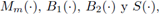respectivamente, los cuales pueden depender de h, w y τ.
Proposición 4.1. El símbolo del operador laplaciano discreto, Δh(·); generado por el método LDG es
Demostración. Aplicando la transformada discreta de Fourier, en su versión de sistemas, a la ecuación (12a) y al término de la derecha de la ecuación (12b), se obtiene
El resultado se obtiene observando que, por la definición de los flujos numéricos (10a) y (10b), se tiene la relación
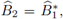donde í denota el operador adjunto (conjugada compleja de una matriz), y que
Por conveniencia para el análisis, el parámetro de estabilización η se escribirá de la siguiente forma
Nótese que el valor γ = 0 se refiere al método de disipación mínima, md-LDG. De esta forma se incluyen todas las variantes del método LDG. Sea M la matriz de masa en la celda de referencia [-1,1]; para cualquier celda I
m
se tiene
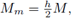luego
Las propiedades del método se reducen al estudio del espectro de
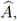el cual no depende del incremento en tiempo τ, pero sí del tamaño de la partición h, de la frecuencia w y del grado del polinomio de aproximación.
Proposición 4.2. El símbolo
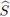del operador de estabilización S(·) es una matriz hermítica no negativa para toda aproximación de grado p.
Demostración. De acuerdo a la definición del término de estabilización de la ecuación (11) se tiene
con
donde
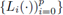es una base de polinomios en la celda de referencia [-1,1]. Utilizando por ejemplo los polinomios de Legendre, el símbolo se reduce a
Claramente
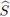es hermítica, y por la relación ac = b2 se deduce que además es de rango 1 para todo w ∈ [-π, π], por lo que
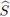posee dos valores propios: 0 de multiplicidad p y otro de multiplicidad 1, y se puede verificar sin mayor dificultad que es positivo.
Proposición 4.3. Para todo γ ≥ 0, los autovalores de la matriz
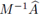son no negativos.
Demostración. Siendo M la matriz de masa, esta es simétrica positiva definida. Considerando su descomposición de Cholesky, M = LL
T, se deduce que para todo eigenpar (λ, x) de
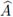se tiene
Por la Proposición 4.2 y el hecho de que γ ≥ 0, se concluye que
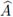es hermítica no negativa; y a su vez, la matriz
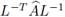también lo es. El resultado se obtiene notando que las matrices
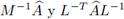poseen el mismo espectro.
Proposición 4.4. Una condición necesaria y suficiente de estabilidad para el método FT-LDG, aplicado a la ecuación del calor, es
donde λmax
es el autovalor de
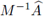de mayor magnitud.
Demostración. Sean I
p
la matriz identidad de orden p + 1, y μ = τ/h
2
. Escribiendo esta vez el parámetro de estabilidad en la forma
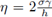con γ ≥ 0 constante, y aplicando la transformada discreta de Fourier, en su versión de sistemas, a las ecuaciones (13a) y (13b), el símbolo
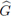del esquema FT-LDG se reduce a
Por la no negatividad del espectro de
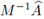, Proposición 4.3, y como todo autovalor
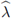de G es de la forma 1 - 4μσλ con λ autovalor de
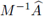, la hipótesis, desigualdad (14), equivale a tener p(
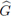) ≤ 1 (condición estricta de von Neumann).
La condición de von Neumann es además suficiente. Nótese que la matriz
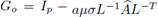es hermítica, por lo que
además, se tiene
Luego, para todo n ∈ ℕ se cumple
Claramente, si la condición de von Neumann se cumple se tiene estabilidad, ecuación (7), con
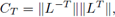esta constante no depende w, h y τ. 0
En el Cuadro 1 se muestra el autovalor λmax de mayor magnitud de la matriz
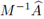, para el método de disipación mínima, utilizando el flujo izquierdo. Ese valor fue obtenido numéricamente en MATLAB. Se observa un comportamiento asintótico de orden
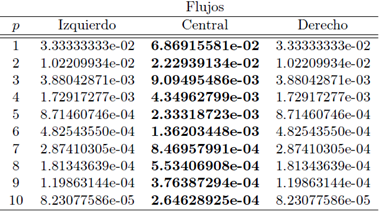
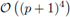para aproximaciones de grado p. Nótese que la condición de estabilidad para p = 0 es la misma que la del método de diferencias finitas. Además se incluyó la constante CFL(p) = 1/ (2λmax). Para el flujo derecho se obtuvo el mismo comportamiento, así como la misma condición CFL.
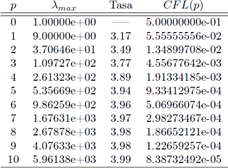
Cuadro 1 Comportamiento de λmax y condición CFL como función del grado de aproximación para el método md-LDG.
Obsérvese que la constante CFL (Courant-Friedrichs-Lewy) 1/(2λmax), para aproximaciones constantes, es decir p = 0, es igual a la del esquema clásico de diferencias finitas. Por lo general se desea que esta constante sea lo más grande posible. Sin embargo, nótese que la condición de estabilidad es más restrictiva para aproximaciones de alto orden.
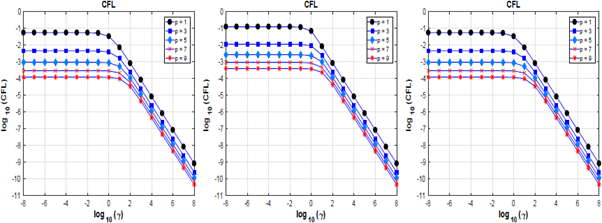
En la Figura 1 se muestra el comportamiento de la condición CFL con respecto al término de estabilización γ para el método LDG estabilizado. Se observa un comportamiento muy similar para los tres tipos de flujos y cualquier grado de aproximación. Para valores pequeños de γ la CFL se comporta como la del método de disipación mínima, mientras que para valores grandes de γ se observa una condición de estabilidad más severa.
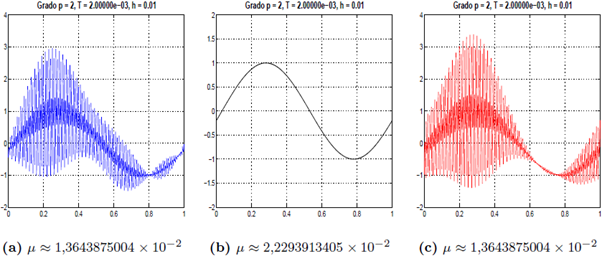
En el Cuadro 2 se presenta la condición CFL para el término de estabilización γ = 1 y los tres flujos considerados en este artículo. El valor elevado de la constante CFL para el flujo central muestra una leve ventaja de este en comparación con los flujos izquierdo y derecho. Esta se ilustra concretamente en la Figura 2, donde se muestra la aproximación obtenida para los flujos izquierdo y derecho, para un valor de μ más grande que el requerido por el criterio de estabilidad del Cuadro 2 para aproximaciones cuadráticas. Para obtener una aproximación correcta en el tiempo final T = 0,002 estos flujos requieren 1957 pasos de tiempo, mientras que para el flujo central solamente se necesitaron 897. Para este cálculo se consideró γ = 1.
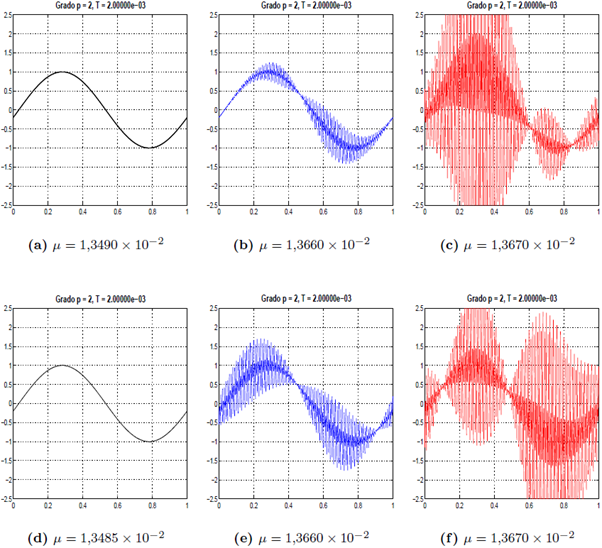
En la Figura 3 se comparan las aproximaciones obtenidas por el método md-LDG con polinomios cuadráticos y distintos valores de μ para el flujo izquierdo (subfiguras 3a-3c) y para el flujo derecho (subfiguras 3d-3f). Para este experimento σ = 1, y el dominio [0, 1] se discretizó con una partición uniforme de tamaño h = 0,01. Nótese la aparición de oscilaciones en las subfiguras 3b, 3c, 3e y 3f, debida a que los valores de μ utilizados no cumplen con la condición de estabilidad, CFL(2) ≈ 1,34899708 x 10-2 del Cuadro 1.
Con el propósito de mejorar la estabilización del método anterior, es decir, aumentar la constante CFL, se considera la siguiente modificación denotada por a-FT-LDG, la cual consiste en utilizar la aproximación uh n+α en el tiempo intermedio t n+α = t n + ατ:
= aM- 1 B 1 «-1, «m, , (15a)
<+" = «m - a.rM m 1 B2 (C-i, 9m+a, C+i) - arnMm 1S(«m-i, «m, <+0, (15b)
Proposición 4.5. Una condición necesaria y suficiente de estabilidad para el esquema explícito α-FT-LDG, aplicado a la ecuación del calor, es
donde λ
max
es el mayor autovalor de la matriz
.
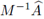Demostración. El símbolo
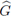del método se escribe de la forma
y los autovalores de
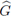son de la forma 1 - 4/μσλ + 16α(μσ)2λ2, donde λ es un autovalor de
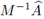. La estabilidad del método se obtiene satisfaciendo la desigualdad
lo cual equivale a satisfacer simultáneamente y para todo autovalor λ de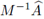 
las desigualdades
Observando que
la desigualdad (17) se verifica siempre que 8α - 1 ≥ 0. Por otro lado, de acuerdo con la Proposición 4.3, los autovalores λ son no negativos; y por la desigualdad (18) se tiene la condición
0 ≤ 1 - 4αμσλ,
de suerte que se obtiene la condición estricta de von Neumann. Aplicando el mismo tipo de argumentos que en la prueba del método FT-LDG, se deduce que la condición es también suficiente.
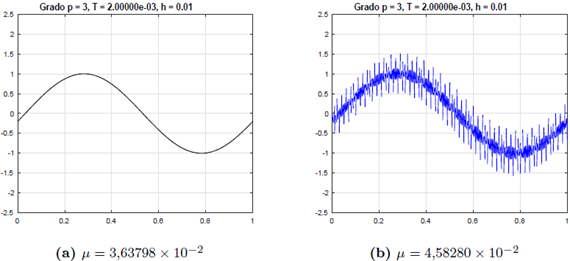
Obsérvese que para α = 1/8 la constante CFL del esquema alcanza su valor máximo, el cual es cuatro veces mayor que el del esquema FT-LDG. Esta superioridad se ilustra en la Figura 4, donde se muestran las aproximaciones cúbicas obtenidas por este método, utilizando el flujo central con γ = 1 y
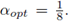Para la Figura 4a se utilizó el valor obtenido en la Proposición 4.5, μ = 4 x CFL(3) ≈ 3,6379819 x 10-2, donde CFL(3) corresponde al valor de CFL para aproximaciones cúbicas del Cuadro 2. Como era de esperar, la solución no presenta ningún tipo de oscilaciones, mientras que en la Figura 4b el cálculo se realizó con un valor de μ mayor.
El uso de métodos explícitos, como los analizados anteriormente, se ve limitado debido a la severa restricción impuesta por la condición CFL. En la práctica es más conveniente el uso de métodos implícitos para problemas altamente difusivos y aproximaciones de alto orden. A continuación se analiza el método implícito denotado por BT-LDG aplicado a la ecuación de calor (ecuación (5)), el cual se expresa en la celda I m de la siguiente forma:
Proposición 4.6. El método implícito BT-LDG es incondicionalmente estable para cualquier grado de aproximación.
Demostración. Realizando cálculos similares a los realizados en los esquemas anteriores se deduce que el símbolo del esquema implícito BT-LDG es
El resultado se obtiene observando que los autovalores
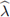de
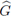son de la forma (1 + 4μσλ)-1, con λ como autovalor de
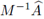; de acuerdo con la Proposición 4.3, λ ≥ 0, por lo que
independientemente del valor de μ.
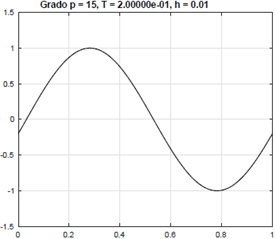
La estabilidad incondicional del método implícito BT-LDG se ilustra en la Figura 5, donde se muestra la aproximación con polinomios de grado 15 en el tiempo final T = 0,2, para un incremento de tiempo τ = 105 τ15, donde τ15 corresponde al incremento en tiempo requerido por la condición CFL del método FT-LDG para aproximaciones de grado 15 y h = 0,01, τ15 ≈ 6,4455 x 10-9. Nótese que la aproximación obtenida no muestra oscilaciones y es cualitativamente correcta, a pesar de solo haber realizado 311 pasos de tiempo.
4.2. Ecuación de onda
Otra de las ecuaciones fundamentales de la física es la ecuación de onda, la cual, por conveniencia, se escribirá de la siguiente manera:
donde c > 0. Asumiendo el parámetro de estabilidad η constante, la formulación semi-discreta obtenida al aplicar la discretización espacial LDG puede escribirse localmente, en la celda I m, como un sistema de ecuaciones diferenciales ordinarias:
Considerando la fórmula de diferenciación central para la segunda derivada en tiempo, se obtiene el método completamente discreto CT-LDG el cual se escribe en forma compacta como
A diferencia de la ecuación de calor, el operador de segundo orden en tiempo no permite una expresión explícita del símbolo, por lo que solamente se presentará una relación entre τ y h que garantice la condición estricta de von Neumann.
Proposición 4.7. Sea
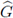el símbolo del método CT-LDG aplicado a la ecuación de onda, ecuación (20); entonces la relación
donde λ
max
es el autovalor de
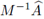de mayor magnitud, garantiza la condición estricta de von Neumann, es decir
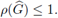
Demostración. A diferencia de la ecuación del calor, ahora se espera una relación lineal entre τ y h. Sea μ = τ/h, y considérese el parámetro de estabilidad de la forma
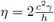con γ ≥ 0 constante. Por la hipótesis, se deduce que
Nótese que el símbolo
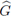del esquema CT-LDG no se obtiene de manera explícita, pero satisface la ecuación matricial
Por lo que, si (λ, x) es un eigenpar de
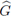, entonces satisface la igualdad
de modo que
Escribiendo λ = a + ib, de acuerdo con la Proposición 4.3, los autovalores de
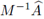son no negativos, por lo que se tiene
Si
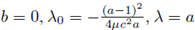es una solución real de la ecuación cuadrática de coeficientes reales
Nótese que esta ecuación admite dos soluciones reales si, y solamente si,
lo cual contradice la desigualdad de la hipótesis (24). Para el caso límite, (μc)2λ0 = 1, no hay problema, ya que λ = -1, (|λ| = 1). Por lo tanto, para todo
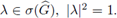Además,
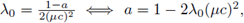de donde
Por la hipótesis, esta desigualdad se cumple para todo λo.
Comentario 1. Del cuadro 1 tenemos que λmax(0) = 1 para el método md-LDG; en este caso, la condición CFL del método CT-LDG coincide con la del método de diferencias finitas,
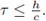
Comentario 2. La ecuación (26) posee dos soluciones reales cuando 1 < (μc)2λ0. Nótese que en este caso una de las soluciones,
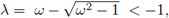donde w = 1 - (μc)2λ0, por lo que el método sería inestable. En el siguiente ejemplo se ilustra la inestabilidad del método al violar la condición (23). Para ello se considera el siguiente problema:
cuya solución exacta está dada por
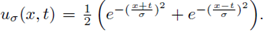El primer paso del método CT-LDG se realiza de forma análoga que para el método de diferencias finitas, denotando por 
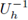un paso auxiliar:
donde Πh,0 es la proyección L2 de la condición inicial ut(x, 0); luego, utilizando esta aproximación de
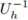, se aplica el método CT-LDG para encontrar
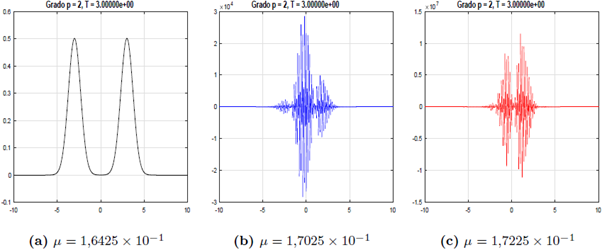
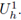En la Figura 6 se muestran las aproximaciones obtenidas por el método md-LDG con polinomios cuadráticos y distintos valores de μ, para el flujo derecho. El dominio se discretizó con una partición uniforme de tamaño h = 0,2. Nótese la aparición de oscilaciones en las figuras 6b, 6c, debida a que los valores de μ utilizados no cumplen con la condición de estabilidad, CFL(2) ≈ 1,64255720 x 10-1.
4.3. Ecuación lineal de Schrödinger
Realizando un procedimiento análogo al de la Proposición (4.4) se puede demostrar, sin mayor dificultad, que el símbolo
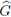del esquema FT-LDG aplicado a la ecuación lineal de Schrödinger, ecuación (6), es
Por lo tanto, el método FT-LDG aplicado a dicha ecuación corre la misma suerte que el de la discretización espacial basada en diferencias finitas, es decir, se tiene el siguiente resultado:
Proposición 4.8. El método explícito FT-LDG aplicado a la ecuación lineal de Schrödinger es incondicionalmente inestable para cualquier grado de aproximación.
Demostración. Nótese que todo autovalor
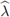de
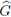es de la forma 1 - 4iμσλ, con λ como autovalor de
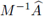. Por la no negatividad del espectro de
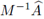, Proposición (4.3), se tiene
por lo que el método FT-LDG aplicado a la ecuación lineal de Schrödinger es inestable.
En [4] Castillo y Gómez presentaron un análisis de estabilidad y un estudio numérico de la condición CFL para el esquema explícito "pídola" en combinación con la discretización espacial LDG aplicado a la ecuación lineal de Schrödinger fraccionaria. En dicha ecuación se consideró la derivada fraccionaria de Riesz, de orden 1 < α ≤ 2, como operador diferencial.
5. Conclusiones
En este trabajo se ha ilustrado el uso del análisis de estabilidad de von Neumann para obtener condiciones suficientes y necesarias de estabilidad numérica para varias discretizaciones explícitas en tiempo, en combinación con la discretización espacial LDG para el operador de difusión. Se mostró, numéricamente, que el comportamiento asintótico de la constante CFL en función del grado de aproximación p decrece de orden
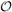((p + 1)-4) para la ecuación del calor, y de orden
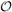((p + 1)-2) para la ecuación de onda. El uso de una discretización temporal explícita para problemas difusivos, en combinación con la discretización espacial LDG, se ve muy limitado debido a la severa restricción en el incremento en tiempo de orden
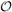h2 . La superioridad de discretizaciones temporales implícitas se ilustró mediante un ejemplo en el cual se permite un paso de tiempo mucho más grande que el de una explícita. Sin embargo, el estudio de la CFL es relevante para aquellos investigadores que prefieren el uso de técnicas explícitas en tiempo.
En general, el análisis muestra un comportamiento similar al de discretizaciones espaciales basadas en diferencias finitas, tanto para la ecuación de calor como para la ecuación de onda y la de Schrödinger.
