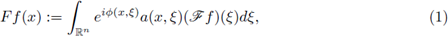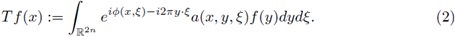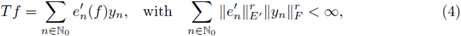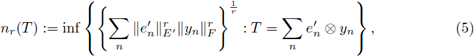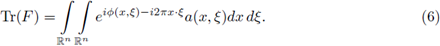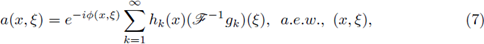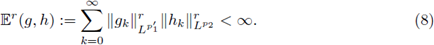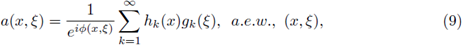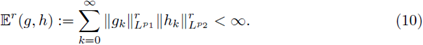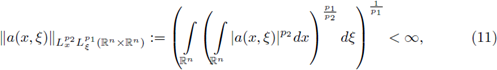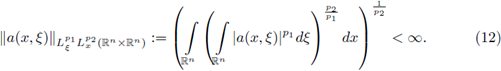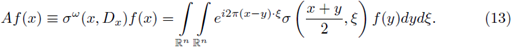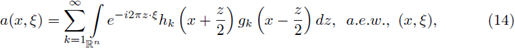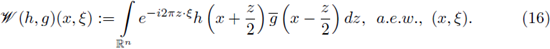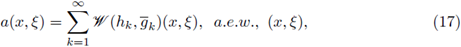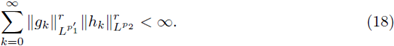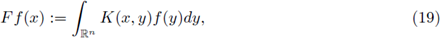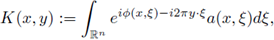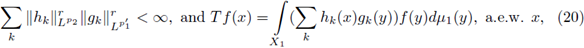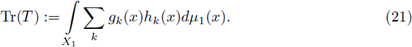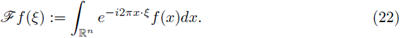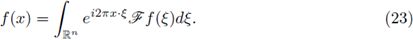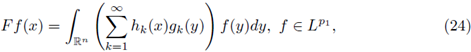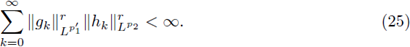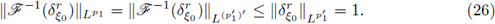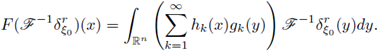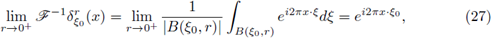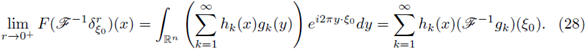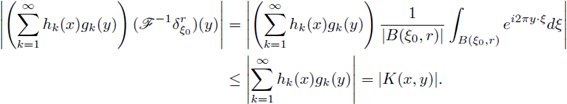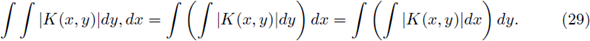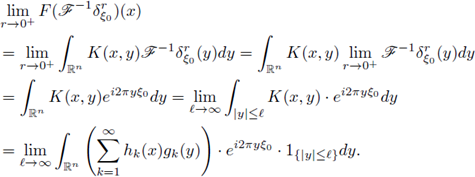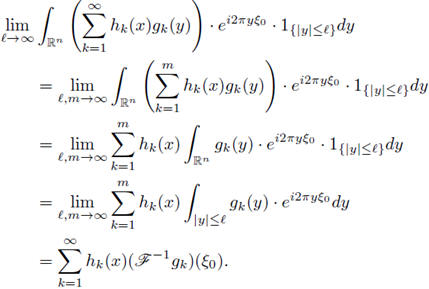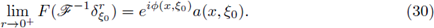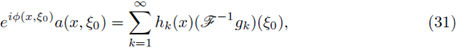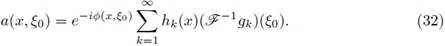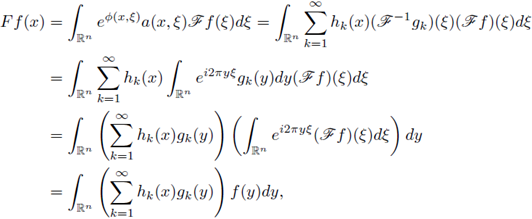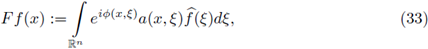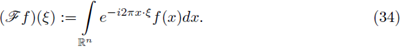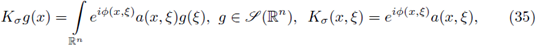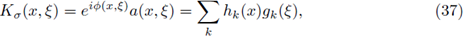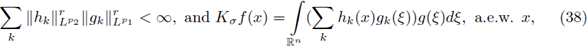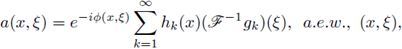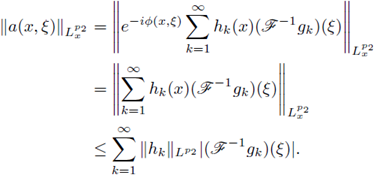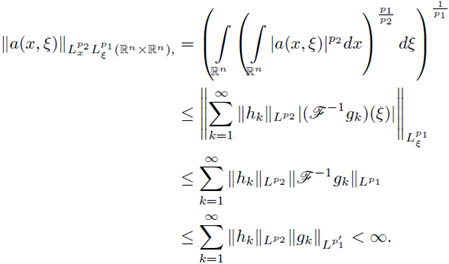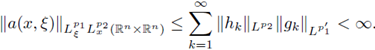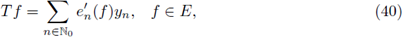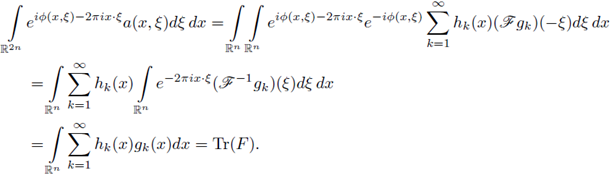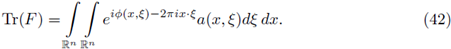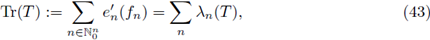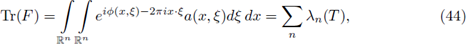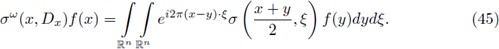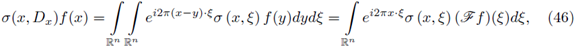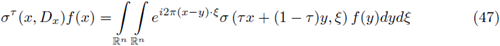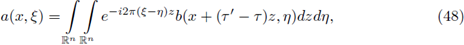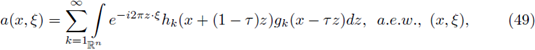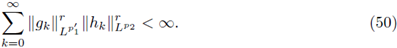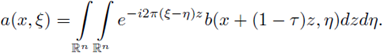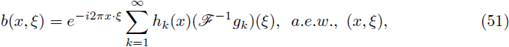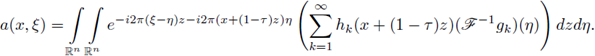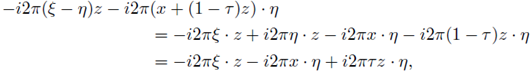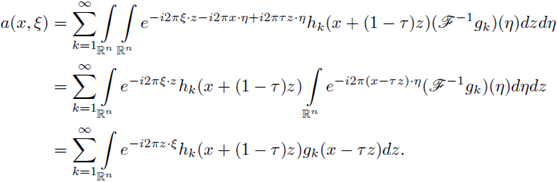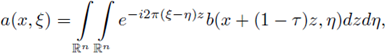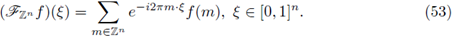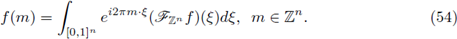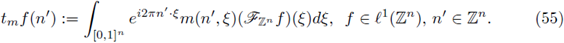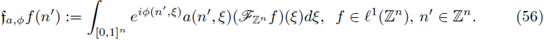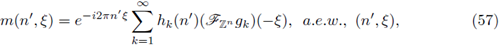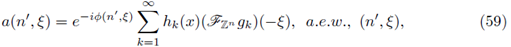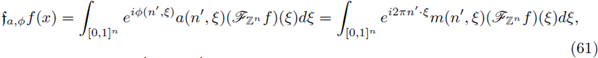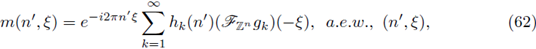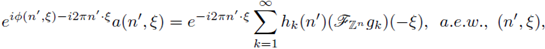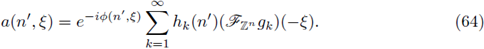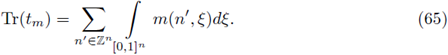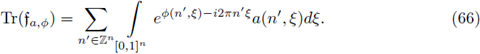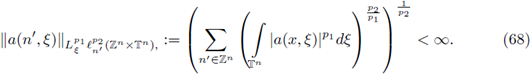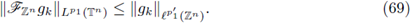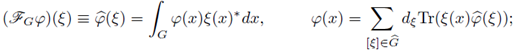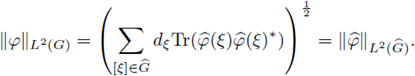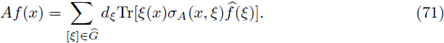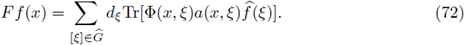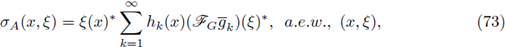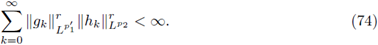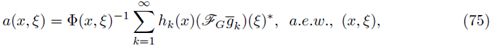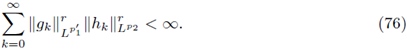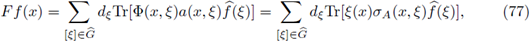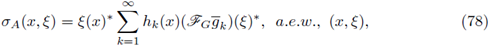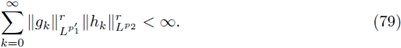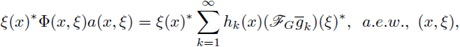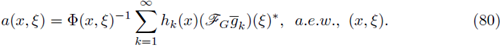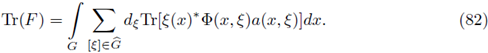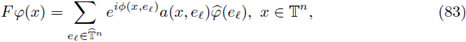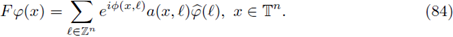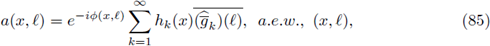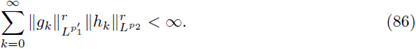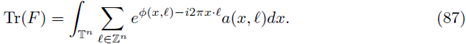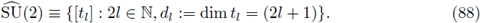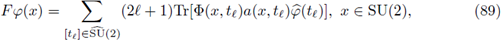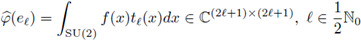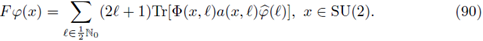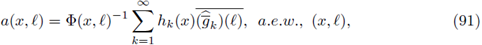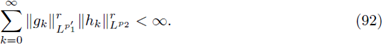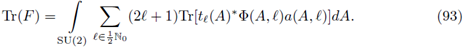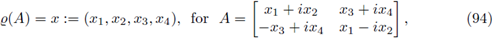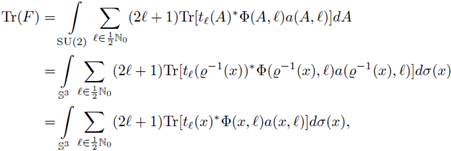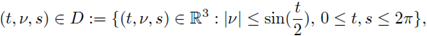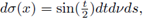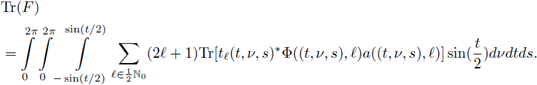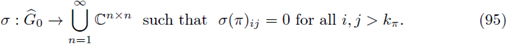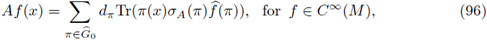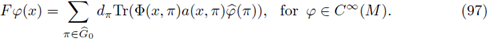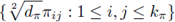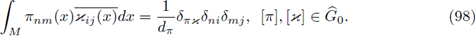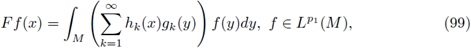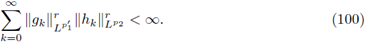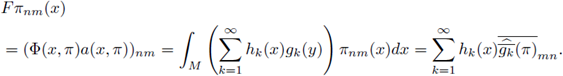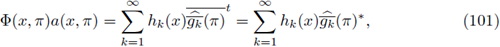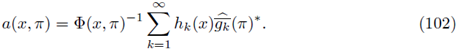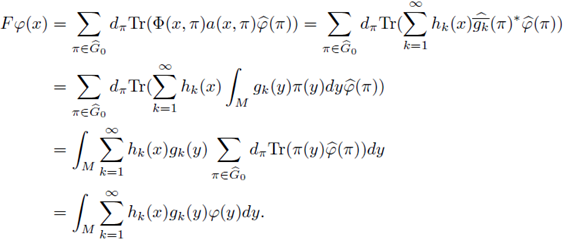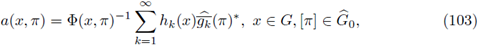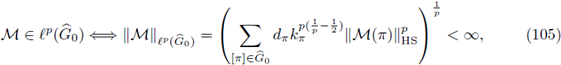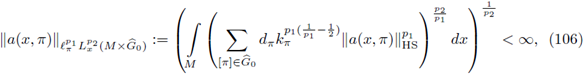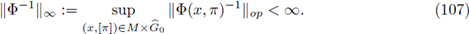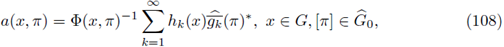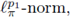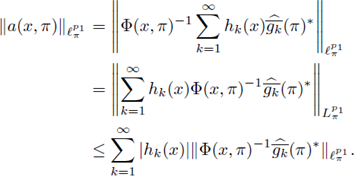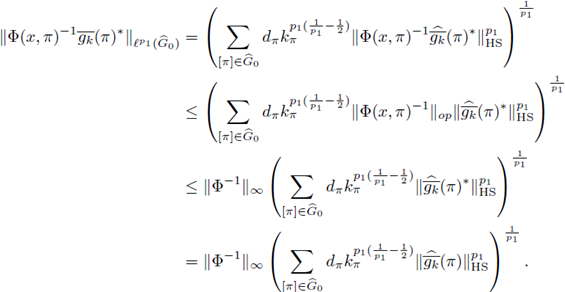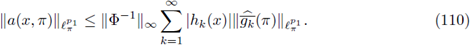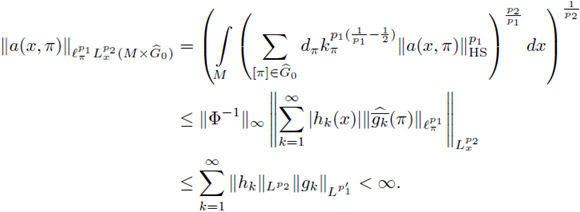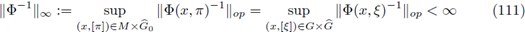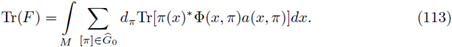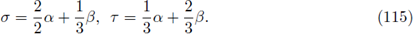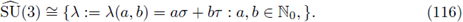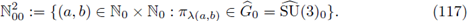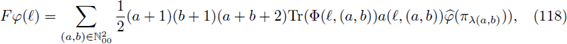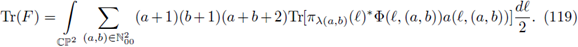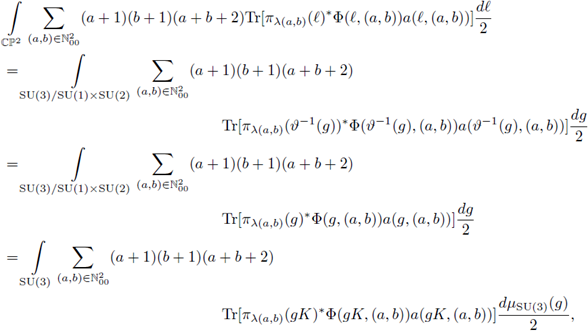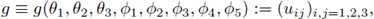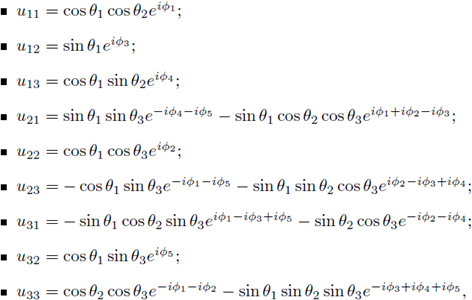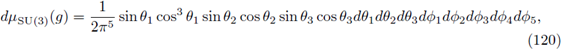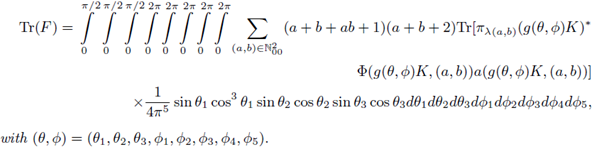1. Introduction
In this paper we characterise the r-nuclearity of Fourier integral operators on Lebesgue spaces. Fourier integral operators will be considered in ℝn, the discrete group ℤn, the n-dimensional torus and symmetric spaces (compact homogeneous manifolds). We also give formulae for the nuclear trace of these operators. Explicit examples will be given on ℤn, the torus 𝕋n, the special unitary group SU(2), and the projective complex plane ℂℙ2. Our main theorems will be applied to the characterization of r-nuclear pseudo-differential operators defined by the Weyl quantization procedure.
1.1. Outline of the paper
Let us recall that the Fourier integral operators (FIOs) on ℝn, are integral operators of the form
where
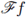 is the Fourier transform of f, or in a more general setting, linear integral operators formally defined by
is the Fourier transform of f, or in a more general setting, linear integral operators formally defined by
As it is well known, FIOs are used to express solutions to Cauchy problems of hyperbolic equations as well as for obtaining asymptotic formulas for the Weyl eigenvalue function associated to geometric operators (see Hörmander [32], [33], [34], and Duistermaat and Hörmander [25]).
According to the theory of FIOs developed by Hörmander [32], the phase functions ϕ are positively homogeneous of order 1 and they are considered smooth at ξ ≠ 0, while the symbols are considered satisfying estimates of the form
for every compact subset K of ℝ2n. Let us observe that L p-properties for FIOs can be found in the references Hörmander [32], Eskin [26], Seeger, Sogge and Stein [51], Tao [52], Miyachi [37], Peral [39], Asada and Fujiwara [2], Fujiwara [28], Kumano-go [35], Coriasco and Ruzhansky [10], [11], Ruzhansky and Sugimoto [44], [45], [46], [47], Ruzhansky [50], and Ruzhansky and Wirth [49].
A fundamental problem in the theory of Fourier integral operators is that of classifying the interplay between the properties of a symbol and the properties of its associated Fourier integral operator.
In this paper our main goal is to give, in terms of symbol criteria and with simple proofs, characterizations for the r-nuclearity of Fourier integral operators on Lebesgue spaces. Let us mention that this problem has been considered in the case of pseudo-differential operators by several authors. However, the obtained results belong to one of two possible approaches. The first ones are sufficient conditions on the symbol trough of summability conditions with the attempt of studying the distribution of the spectrum for the corresponding pseudo-differential operators. The second ones provide, roughly speaking, a decomposition for the symbols associated to nuclear operators, in terms of the Fourier transform, where the spatial variables and the momentum variables can be analyzed separately. Nevertheless, in both cases the results can be applied to obtain Grothendieck-Lidskii's formulae on the summability of eigenvalues when the operators are considered acting in L p spaces.
Necessary conditions for the r-nuclearity of pseudo-differential operators in the compact setting can be summarized as follows. The nuclearity and the 2/3-nuclearity of pseudo-differential operators on the circle 𝕊1 and on the lattice ℤ can be found in Delgado and Wong [14]. Later, the r-nuclearity of pseudo-differential operators was extensively developed on arbitrary compact Lie groups and on (closed) compact manifolds by Delgado and Ruzhansky in the works [16], [17], [18], [19], [21], and by the author in [9]; other conditions can be found in the works [20], [22], [23]. Finally, the subject was treated for compact manifolds with boundary by Delgado, Ruzhansky, and Tokmagambetov in [24].
On the other hand, characterizations for nuclear operators in terms of decomposition of the symbol trough of the Fourier transform were investigated by Ghaemi, Jamalpour Birgani, and Wong in [29], [30], [36] for 𝕊1, ℤ, and also for arbitrary compact and Hausdorff groups. Finally the subject has been considered for pseudo-multipliers associated to the harmonic oscillator (which can be qualified as pseudo-differential operators according to the Ruzhansky-Tokmagambetov calculus when the reference operators is the quantum harmonic oscillator) in the works of the author [3], [7], [8].
1.2. Nuclear Fourier integral operators
In order to present our main result we recall the notion of nuclear operators. By following the classical reference Grothendieck [31], we recall that a densely defined linear operator T : D(T) ⊂ E → F (where D(T) is the domain of T, and E, F are choose to be Banach spaces) extends to a r-nuclear operator from E into F, if there exist sequences
 in E’ (the dual space of E) and
in E’ (the dual space of E) and
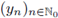 in F such that, the discrete representation
in F such that, the discrete representation
holds true for all f ∈ D(T). The class of r-nuclear operators is usually endowed with the natural semi-norm
and, if r =1, n 1(·) is a norm and we obtain the ideal of nuclear operators. In addition, when E = F is a Hilbert space and r = 1 the definition above agrees with that of trace class operators. For the case of Hilbert spaces H, the set of r-nuclear operators agrees with the Schatten-von Neumann class of order r (see Pietsch [40], [41]). In order to characterize the r-nuclearity of Fourier integral operators on ℝn, we will use (same as in the references mentioned above) Delgado's characterization (see [15]), for nuclear integral operators on Lebesgue spaces defined in σ-finite measure spaces, which in this case will be applied to L P(ℝn)-spaces. Consequently, we will prove that r-nuclear Fourier integral operators defined as in (1) have a nuclear trace given by
In this paper our main results are the following theorems.
Theorem 1.1. Let 0 < r ≤ 1. Let a(·, ·) be a symbol such that
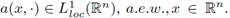 Let 2 ≤ p
i < ∞, 1 ≤ p
2 < ∞, and let F be the Fourier integral operator associated to a(·, ·). Then, F : L
P1 (ℝn) → L
P2 (ℝn) is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition of the form
Let 2 ≤ p
i < ∞, 1 ≤ p
2 < ∞, and let F be the Fourier integral operator associated to a(·, ·). Then, F : L
P1 (ℝn) → L
P2 (ℝn) is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition of the form
where
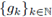 and
and
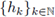 are sequences of functions satisfying
are sequences of functions satisfying
Theorem 1.2. Let 0 < r ≤ 1, and let us consider a measurable function a(·, ·) on ℝ2n . Let 1 < p 1 ≤ 2, 1 ≤ p 2 < ∞, and F be the Fourier integral operator associated to a(·, ·). Then, F : L P1 (ℝn) → L P2 (ℝn) is r-nuclear if the symbol a(·, ·) admits a decomposition of the form
where
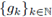 and
and
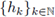 are sequences of functions satisfying
are sequences of functions satisfying
This theorem is sharp in the sense that the previous condition is a necessary and sufficient condition for the r-nuclearity of F when p 1 = 2.
The previous results are analogues of the main results proved in Ghaemi, Jamalpour Birgani, and Wong [29], [30], Jamalpour Birgani [36], and Cardona and Barraza [3]. Theorem 1.1, can be used for understanding the properties of the corresponding symbols in Lebesgue spaces. Moreover, we obtain the following result as a consequence of Theorem 1.1.
Theorem 1.3. Let a(·, ·) be a symbol such that
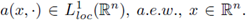 Let 2 ≤ p
1
< ∞, 1 ≤ p
2
< ∞, and let F be the Fourier integral operator associated to a(·, ·). If F : L
p1 (ℝn) → L
P2 (ℝn) is nuclear, then
Let 2 ≤ p
1
< ∞, 1 ≤ p
2
< ∞, and let F be the Fourier integral operator associated to a(·, ·). If F : L
p1 (ℝn) → L
P2 (ℝn) is nuclear, then
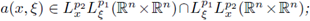 this means that
this means that
and
Sufficient conditions in order that pseudo-differential operators in L2(ℝn) can be extended to (trace class) nuclear operators are well known. Let us recall that the Weyl-quantization of a distribution
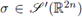 is the pseudo-differential operator defined by
is the pseudo-differential operator defined by
As it is well known σ = σ
A (·, ·) ∈ L1(ℝ2n), implies that A : L
2
→ L
2 is class trace, and A : L2
→ L2 is Hilbert-Schmidt if, and only if, σ
A ∈ L2(ℝ2n). In the framework of the Weyl-Hörmander calculus of operators A associated to symbols σ in the S(m, g)-classes (see [34]), there exist two remarkable results. The first one, due to Lars Hörmander, which asserts that σ
A ∈ S(m,g) and a σ ∈ L1(ℝ2n), implies that A : L2
→ L2 is a trace class operator. The second one, due to L. Rodino and F. Nicola, expresses that σ
A ∈ S(m, g) and
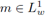 (the weak-L1 space), and implies that A : L2
→ L2 is Dixmier traceable [43]. Moreover, an open conjecture by Rodino and Nicola (see [43]) says that
(the weak-L1 space), and implies that A : L2
→ L2 is Dixmier traceable [43]. Moreover, an open conjecture by Rodino and Nicola (see [43]) says that
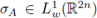 gives an operator A with finite Dixmier trace. General properties for pseudo-differential operators on Schatten-von Neumann classes can be found in Buzano and Toft [6].
gives an operator A with finite Dixmier trace. General properties for pseudo-differential operators on Schatten-von Neumann classes can be found in Buzano and Toft [6].
As an application of Theorem 1.1 to the Weyl quantization we present the following theorem.
Theorem 1.4. Let 0 < r ≤ 1. Let a(·, ·) be a differentiable symbol. Let 2 ≤ p 1 < ∞, 1 ≤ p 2 < ∞, and let a w(x, D x) be the Weyl quantization of the symbol a(·, ·). Then, a w (x, Dx) : L P1 (ℝn) → L P2 (ℝn) is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition of the form
where
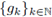 and
and
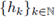 are sequences of functions satisfying
are sequences of functions satisfying
Remark 1.5. Let us recall that the Wigner transform of two complex functions h, g on ℝn, is formally defined as
With a such definition in mind, if 2 ≤ p 1 < ∞, 1 ≤ p2 < ∞, under the hypothesis of Theorem 1.4, a w (x, Dx) : L P1 (ℝn) → L P2 (ℝn), is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition (defined trough of the Wigner transform) of the type
where
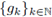 and
and
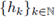 are sequences of functions satisfying
are sequences of functions satisfying
The proof of our main result (Theorem 1.1) will be presented in Section 2 as well as the proof of Theorem 1.4. The nuclearity of Fourier integral operators on the lattice ℤn and on compact Lie groups will be discussed in Section 3 as well as some trace formulae for FIOs on the -dimensional torus 𝕋n = ℝn/ℤn and the unitary special group SU(2). Finally, in Section 4 we consider the nuclearity of FIOs on arbitrary compact homogeneous manifolds, and we discuss the case of the complex projective space ℂℙ2. In this setting, we will prove analogues for the theorems 1.1 and 1.3 in every context mentioned above.
2. Symbol criteria for nuclear Fourier integral operators
2.1. Characterization of nuclear FIOs
In this section we prove our main result for Fourier integral operators F defined as in (1). Our criteria will be formulated in terms of the symbols a. First, let us observe that every FIO F has a integral representation with kernel K(x,y). In fact, straightforward computation shows us that
where
for every
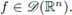 . In order to analyze the r-nuclearity of the Fourier integral operator F we will study its kernel K, by using as a fundamental tool the following theorem (see J. Delgado [13], [15]).
. In order to analyze the r-nuclearity of the Fourier integral operator F we will study its kernel K, by using as a fundamental tool the following theorem (see J. Delgado [13], [15]).
Theorem 2.1. Let us consider 1 ≤ p
1
, p
2
< ∞, 0 < r ≤ 1 and let
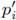 be such that
be such that
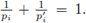 Let (X
1
, μ1) and (X
2
, μ2) be σ-finite measure spaces. An operator T : L
p1 (X
1
, μ1) → L
P2 (X
2
, μ2) is r-nuclear if, and only if, there exist sequences (h
k)k
in L
P2 (μ2), and (g
k) in
Let (X
1
, μ1) and (X
2
, μ2) be σ-finite measure spaces. An operator T : L
p1 (X
1
, μ1) → L
P2 (X
2
, μ2) is r-nuclear if, and only if, there exist sequences (h
k)k
in L
P2 (μ2), and (g
k) in
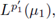 such that
such that
for every f ∈ LP1 (μ1). In this case, if p1 = p2, and μ1 = μ2 , (see Section 3 of [13]) the nuclear trace of T is given by
Remark 2.2. Given f ∈ L1 (ℝn), define its Fourier transform by
If we consider a function f, such that f ∈ L1 (ℝn) with
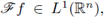 the Fourier inversion formula gives
the Fourier inversion formula gives
Moreover, the Hausdorff-Young inequality
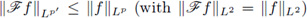 shows that the Fourier transform is a well defined operator on Lp, 1 < p ≤ 2.
shows that the Fourier transform is a well defined operator on Lp, 1 < p ≤ 2.
Proof of Theorem 1.1. Let us assume that F is a Fourier integral operator as in (1) with associated symbol a. Let us assume that F : L p1 (ℝn) → L P2 (ℝn) is r-nuclear.
Then there exist sequences h
k in LP2 and g
kin 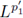 satisfying
satisfying
with
For all z ∈ ℝn, let us consider the set B(z; r), i.e., the euclidean ball centered at z with radius r > 0. Let us denote by |B(z; r)| the Lebesgue measure of B(z; r). Let us choose ξ0 ∈ ℝn and r > 0. If we define
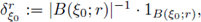 where
where
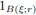 is the characteristic function of the ball B(ξ0; r), the condition 2 ≤ p1 < ∞, together with the Hausdorff-Young inequality gives
is the characteristic function of the ball B(ξ0; r), the condition 2 ≤ p1 < ∞, together with the Hausdorff-Young inequality gives
So, for every r > 0 and ξ0 ∈ ℝn, the function
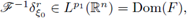 and we get,
and we get,
Taking into account that
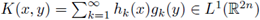 (see, e.g., Lemma 3.1 of [20]), that
(see, e.g., Lemma 3.1 of [20]), that
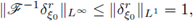 and that (in view of the Lebesgue Differentiation Theorem)
and that (in view of the Lebesgue Differentiation Theorem)
an application of the Dominated Convergence Theorem gives
In fact, for a.e.w. x ∈ ℝn,
Since K ∈ L1 (ℝ2n), and the function k(x, y) := |K(x, y)| is non-negative on the product space ℝ2n, by the Fubinni theorem applied to positive functions, the L1(ℝ2n)-norm of K can be computed from iterated integrals as
By Tonelly theorem, for a.e.w. x ∈ ℝn, the function
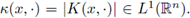 Now, by the dominated convergence theorem, we have
Now, by the dominated convergence theorem, we have
Now, from Lemma 3.4-(d) in [20],
On the other hand, if we compute
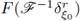 from the definition (1), we have
from the definition (1), we have
From the hypothesis that
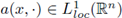 for a.e.w x ∈ ℝ2, the Lebesgue Differentiation theorem gives
for a.e.w x ∈ ℝ2, the Lebesgue Differentiation theorem gives
Consequently, we deduce the identity
which in turn is equivalent to
So, we have proved the first part of the theorem. Now, if we assume that the symbol a of the FIO F satisfies the decomposition formula (32) for fixed sequences h
k in LP2 and gk in
 satisfying (52), then from (1) we can write (in the sense of distributions)
satisfying (52), then from (1) we can write (in the sense of distributions)
where in the last line we have used the Fourier inversion formula. So, by Delgado Theorem (Theorem 2.1) we finish the proof.
Proof of Theorem 1.2. Let us consider the Fourier integral operator F,
associated with the symbol a. The main strategy in the proof will be to analyze the natural factorization of F in terms of the Fourier transform,
Clearly, if we define the operator with kernel (associated to σ = (ϕ, a)),
then
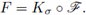 Taking into account the Hausdorff-Young inequality
Taking into account the Hausdorff-Young inequality
the Fourier transform extends to a bounded operator from L
P1 (ℝn) into
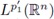 . So, if we prove that the condition (10) assures the r-nuclearity of K
σ from
. So, if we prove that the condition (10) assures the r-nuclearity of K
σ from
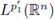 into L
P2 (ℝn), we can deduce the r-nuclearity of F from LP1 (ℝn) into LP2 (ℝn). Here, we will be using the fact that the class of r-nuclear operators is a bilateral ideal on the set of bounded operators between Banach spaces.
into L
P2 (ℝn), we can deduce the r-nuclearity of F from LP1 (ℝn) into LP2 (ℝn). Here, we will be using the fact that the class of r-nuclear operators is a bilateral ideal on the set of bounded operators between Banach spaces.
Now,
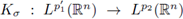 is r-nuclear if, and only if, there exist sequences {h
k
}, {g
k
} satisfying
is r-nuclear if, and only if, there exist sequences {h
k
}, {g
k
} satisfying
Where
for every
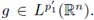 Here, we have used the fact that for
Here, we have used the fact that for
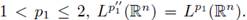 We end the proof by observing that (37) is in turns equivalent to (9).
We end the proof by observing that (37) is in turns equivalent to (9).
Proof of Theorem 1.3. Let a(·, ·) be a symbol such that
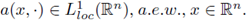 Let 2 ≤ p
1
< ∞, 1 ≤ p
2
< ∞, and let F be the Fourier integral operator associated to a(·, ·). If F : LP1 (ℝn) → LP2(ℝn) is nuclear, then Theorem 1.1 guarantees the decomposition
Let 2 ≤ p
1
< ∞, 1 ≤ p
2
< ∞, and let F be the Fourier integral operator associated to a(·, ·). If F : LP1 (ℝn) → LP2(ℝn) is nuclear, then Theorem 1.1 guarantees the decomposition
where
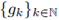 and
and
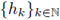 are sequences of functions satisfying
are sequences of functions satisfying
Now, if we use the Hausdorff-Young inequality, we deduce that
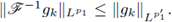 Consequently,
Consequently,
In an analogous way we can prove that
Thus, we finish the proof.
2.2. The nuclear trace for FIOs on ℝn
If we choose a r-nuclear operator T : E
→
E, 0 < r ≤ 1, with the Banach space E satisfying the Grothendieck approximation property (see Grothendieck [31]), then there exist (a nuclear decomposition) sequences
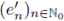 in E’ (the dual space of E) and
in E’ (the dual space of E) and
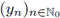 in E satisfying
in E satisfying
and
In this case the nuclear trace of T is (a well-defined functional) given by
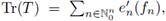 because Lp-spaces have the Grothendieck approximation property and, as consequence, we can compute the nuclear trace of every r-nuclear pseudo-multipliers. We will compute it from Delgado Theorem (Theorem 2.1). For doing so, let us consider a r-nuclear Fourier integral operator F : Lp(ℝn) → Lp(ℝn), 2 ≤ p < ∞. If a is the
because Lp-spaces have the Grothendieck approximation property and, as consequence, we can compute the nuclear trace of every r-nuclear pseudo-multipliers. We will compute it from Delgado Theorem (Theorem 2.1). For doing so, let us consider a r-nuclear Fourier integral operator F : Lp(ℝn) → Lp(ℝn), 2 ≤ p < ∞. If a is the
symbol associated to F, in view of (9), we have (in the sense of distributions)
So, we obtain the trace formula
Now, in order to determinate a relation with the eigenvalues of F, we recall that the nuclear trace of an r-nuclear operator on a Banach space coincides with the spectral trace, provided that
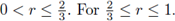 We recall the following result (see [42]).
We recall the following result (see [42]).
Theorem 2.3. Let T : L
P(μ) -> L
P(μ) be a r-nuclear operator as in (40). if
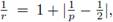 then
then
where λ n(T), n ∈ ℕ is the sequence of eigenvalues of T with multiplicities taken into account.
As an immediate consequence of the preceding theorem, if the FIO F : Lp(ℝn) → Lp(ℝn) is r-nuclear, the relation
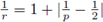 implies
implies
where λ n(T), n ∈ ℕ is the sequence of eigenvalues of F with multiplicities taken into account.
2.3. Characterization of nuclear pseudo-differential operators defined by the Weyl quantization
As it was mentioned in the introduction, the Weyl-quantization of a distribution
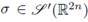 is the pseudo-differential operator defined by
is the pseudo-differential operator defined by
There exist relations between pseudo-differential operators associated to the classical quantization
or in a more general setting, τ-quantizations defined for every 0 < τ ≤ 1, by the integral expression
(with
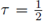 corresponding to the Hörmander quantization), as it can be viewed in the following proposition (see Delgado [12]).
corresponding to the Hörmander quantization), as it can be viewed in the following proposition (see Delgado [12]).
Proposition 2.4. Let
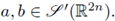 Then,
Then,
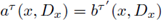 if, and only if,
if, and only if,
provided that 0 < τ,τ’ ≤ 1.
Theorem 2.5. Let 0 < r ≤ 1. Let a(·, ·) be a differentiable symbol. Let 2 ≤ p 1 < ∞,
1 ≤ p2 < ∞, and let a w(x, D x) be the Weyl quantization of the symbol a(·, ·). Then, a w (x, D x): L p1 (ℝn) → L P2 (ℝn) is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition of the form
where
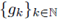 and
and
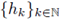 are sequences of functions satisfying
are sequences of functions satisfying
Proof. Let us assume that aτ(x, D x) is r-nuclear from L p1(ℝn) into L P2 (ℝn). By Proposition 2.4, aτ(x, D x) = b(x, D x), where
By Theorem 1.1 applied to
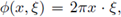 and taking into account that b(x, D
x) is r-nuclear, there exist sequences h
k in L
P2 and g
k in
and taking into account that b(x, D
x) is r-nuclear, there exist sequences h
k in L
P2 and g
k in
 satisfying
satisfying
with
So, we have
Since
we have (in the sense of distributions)
So, we have proved the first part of the characterization. On the other hand, if we assume (49), then
where b(x, ξ) is defined as in (51). So, from Theorem 1.1 we deduce that b(x, D x) is r-nuclear, and from the equality aτ(x, Dx) = b(x, Dx) we deduce the r-nuclearity of aτ(x, Dx). The proof is complete.
Remark 2.6. Let us observe that from Theorem 2.5 with τ = 1/2, we deduce the Theorem 1.4 mentioned in the introduction.
3. Characterizations of Fourier integral operators on ℤn and arbitrary compact Lie groups
3.1. FIOs on ℤn
In this subsection we characterize those Fourier integral operators on ℤn (the set of points in ℝn with integral coordinates) admitting nuclear extensions on Lebesgue spaces. Now we define pseudo-differential operators and discrete Fourier integral operators on ℤn. The discrete Fourier transform of
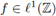 is defined by
is defined by
The Fourier inversion formula gives
In this setting pseudo-differential operators on ℤn are defined by the integral form
These operators were introduced by Molahajloo in [38]. However, the fundamental work of Botchway L., Kibiti G., Ruzhansky M. [5] provides a symbolic calculus and other properties for these operators on
 In particular, Fourier integral operators on ℤn were defined in such reference as integral operators of the form
In particular, Fourier integral operators on ℤn were defined in such reference as integral operators of the form
Our main tool in the characterization of nuclear FIOs on ℤn is the following result, due to Jamalpour Birgani [36].
Theorem 3.1. Let 0 < r ≤ 1, 1 ≤ p
1 < ∞, 1 ≤ p2 < ∞, and let tm
be the pseudo-differential operator associated to the symbol m(·, ·). Then,
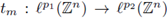 is r-nuclear if, and only if, the symbol m(·, ·) admits a decomposition of the form
is r-nuclear if, and only if, the symbol m(·, ·) admits a decomposition of the form
where
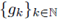 and
and
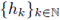 are sequences of functions satisfying
are sequences of functions satisfying
As a consequence of the previous result, we give a simple proof for our characterization.
Theorem 3.2. Let 0 < r ≤ 1, 1 ≤ p
1 < ∞, 1 ≤ p2 < ∞, and let
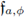 be the Fourier integral operator associated to the phase function 4> and to the symbol a(·, ·). Then,
be the Fourier integral operator associated to the phase function 4> and to the symbol a(·, ·). Then,
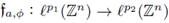 is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition of the form
is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition of the form
where
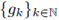 and
and
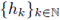 are sequences of functions satisfying
are sequences of functions satisfying
Proof. Let us write the operator
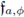 as
as
where
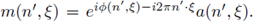 So, the discrete Fourier integral operator
So, the discrete Fourier integral operator
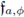 coincides with the discrete pseudo-differential operator tm with symbol m. By using Theorem 3.5, the operator
coincides with the discrete pseudo-differential operator tm with symbol m. By using Theorem 3.5, the operator
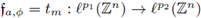 is r-nuclear if, and only if, the symbol m(·, ·) admits a decomposition of the form
is r-nuclear if, and only if, the symbol m(·, ·) admits a decomposition of the form
where
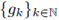 and
and
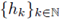 are sequences of functions satisfying
are sequences of functions satisfying
Let us note that from the definition of m we have
which, in turn, is equivalent to
Thus, the proof is complete.
Remark 3.3. The nuclear trace of a nuclear discrete pseudo-differential operator on
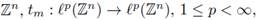 can be computed according to the formula
can be computed according to the formula
From the proof of the previous criterion, we have that
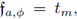 where
where
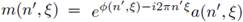 and, consequently, if
and, consequently, if
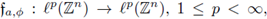 is r-nuclear, its nuclear trace is given by
is r-nuclear, its nuclear trace is given by
Now, we present an application of the previous result.
Theorem 3.4. Let 2 ≤ p1 < ∞, and 1 ≤ p2 < ∞. If
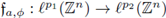 is nuclear, then
is nuclear, then
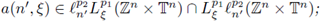 this means that
this means that
and
The proof is only an adaptation of the proof that we have done for Theorem 1.3. We only need to use a discrete Hausdorff-Young inequality. In this case, we use
3.2. FIOs on compact Lie groups
In this subsection we characterize nuclear Fourier integral operators on compact Lie groups. Although the results presented are valid for arbitrary Hausdorff and compact groups, we restrict our attention to Lie groups taking into account their differentiable structure, which in our case could give potential applications of our results to the understanding on the spectrum of certain operators associated to differential problems.
Let us consider a compact Lie group G with Lie algebra
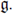 We will equip G with the Haar measure μG. The following identities follow from the Fourier transform on G:
We will equip G with the Haar measure μG. The following identities follow from the Fourier transform on G:
and the Peter-Weyl Theorem on G implies the Plancherel identity on L 2(G),
Notice that, since
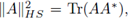 the term within the sum is the Hilbert-Schmidt norm of the matrix
the term within the sum is the Hilbert-Schmidt norm of the matrix
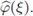 Any linear operator A on G mapping C
∞(G) into D'(G) gives rise to a matrix-valued global (or full) symbol
Any linear operator A on G mapping C
∞(G) into D'(G) gives rise to a matrix-valued global (or full) symbol
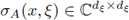 given by
given by
which can be understood from the distributional viewpoint. Then it can be shown that the operator A can be expressed in terms of such a symbol as [48],
So, if
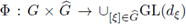 is a measurable function (the phase function), and
is a measurable function (the phase function), and
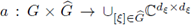 is a distribution on
is a distribution on
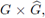 the Fourier integral operator F = FΦ,a associated to the symbol a(·, ·) and to the phase function $ is defined by the Fourier series operator
the Fourier integral operator F = FΦ,a associated to the symbol a(·, ·) and to the phase function $ is defined by the Fourier series operator
In order to present our main result for Fourier integral operators, we recall the following criterion (see Ghaemi, Jamalpour Birgani, Wong [30]).
Theorem 3.5. Let 0 < r ≤ 1, 1 < p1 < ∞, 1 ≤ p2 < ∞, and let A be the pseudo-differential operator associated to the symbol σ A(·, ·). Then, A: L P1 (G) → L P2 (G) is r-nuclear if, and only if, the symbol σ A(·, ·) admits a decomposition of the form
where
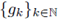 and
and
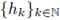 are sequences of functions satisfying
are sequences of functions satisfying
As a consequence of the previous criterion, we give a simple proof for our characterization.
Theorem 3.6. Let Let 0 < r ≤ 1, 1 < p1 < ∞, 1 ≤ p2 < ∞, and let F be the Fourier integral operator associated to the phase function Φ and to the symbol a (·, ·). Then, F : LP1 (G) → LP2 (G) is r-nuclear if, and only if, the symbol a(·, ·) admits a decomposition of the form
where
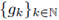 and
and
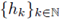 are sequences of functions satisfying
are sequences of functions satisfying
Remark 3.7. For the proof we use the characterization of r-nuclear pseudo-differential operators mentioned above. However, this result will be generalized in the next section to arbitrary compact homogeneous manifolds.
Proof. Let us observe that the Fourier integral operator F, can be written as
where
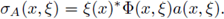 So, the Fourier integral operator F coincides with the pseudo-differential operator A with symbol σA. In view of Theorem 3.5, the operator F = A : LP1 (G) → LP2 (G) is r-nuclear if, and only if, the symbol σA(·, ·) admits a decomposition of the form
So, the Fourier integral operator F coincides with the pseudo-differential operator A with symbol σA. In view of Theorem 3.5, the operator F = A : LP1 (G) → LP2 (G) is r-nuclear if, and only if, the symbol σA(·, ·) admits a decomposition of the form
where
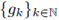 and
and
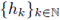 are sequences of functions satisfying
are sequences of functions satisfying
Let us note that from the definition of σA we have
which is equivalent to
Thus, we finish the proof.
Remark 3.8. The nuclear trace of a r-nuclear pseudo-differential operator on G, A : L P(G) → Lp(G), 1 ≤ p < ∞, can be computed according to the formula
From the proof of the previous theorem, we have that F = A, where
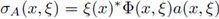 and, consequently, if F : Lp(G) → L
p(G), 1 ≤ p < ∞,, is r-nuclear, its nuclear trace is given by
and, consequently, if F : Lp(G) → L
p(G), 1 ≤ p < ∞,, is r-nuclear, its nuclear trace is given by
Now, we illustrate the results above with some examples.
Example 3.9. (The torus). Let us consider the n-dimensional torus G = 𝕋n: = ℝn/ℤn
and its unitary dual
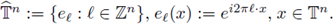 By following Ruzhansky and Turunen
[48]
, a Fourier integral operator F associated to the phase function
By following Ruzhansky and Turunen
[48]
, a Fourier integral operator F associated to the phase function
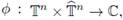 and to the symbol
and to the symbol
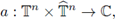 is defined according to the rule
is defined according to the rule
where
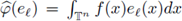 is the Fourier transform of f at
is the Fourier transform of f at
 If we identify
If we identify
 with ℤn, and we define
with ℤn, and we define
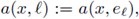 and
and
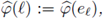 we give the more familiar expression for F,
we give the more familiar expression for F,
Now, by using Theorem 3.6, F is r-nuclear, 0 < r ≤ 1 if, and only if, the symbol a(·, ·) admits a decomposition ofthe form
where
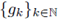 and
and
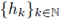 are sequences of functions satisfying
are sequences of functions satisfying
The last condition have been proved for pseudo-differential operators in [29] . In this case, the nuclear trace of F can be written as
Example 3.10. (The group SU(2)). Let us consider the group
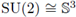 consinting of those orthogonal matrices A in ℂ2x2, with det(A) = 1. We recall that the unitary dual of SU(2) (see
[48]) can be identified as
consinting of those orthogonal matrices A in ℂ2x2, with det(A) = 1. We recall that the unitary dual of SU(2) (see
[48]) can be identified as
There are explicit formulae for t
l
as functions of Euler angles in terms of the so-called Legendre-Jacobi polynomials, see
[48]
. A Fourier integral operator F associated to the phase function
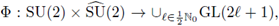 and to the symbol
and to the symbol
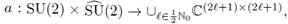 is defined as
is defined as
where
is the Fourier transform of f at tl. As in the case of the n-dimensional torus, if we identify
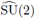 with
with
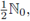 and we define
and we define
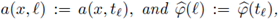 we can write
we can write
Now, by using Theorem 3.6, F is r-nuclear, 0 < r ≤ 1 if, and only if, the symbol a (·, ·) admits a decomposition of the form
where
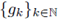 and
and
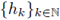 are sequences of functions satisfying
are sequences of functions satisfying
The last condition have been proved for pseudo-differential operators in [30] on arbitrary Hausdorff and compact groups. In this case, in an analogous expression to the one presented above for ℝn, ℤn, and 𝕋n, the nuclear trace of F can be written as
By using the diffeomorphism
 defined by
defined by
we have
where
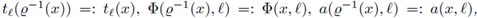 and dσ(x) denotes the surface measure on 𝕊3
. If we consider the parametrization of S3
defined by
and dσ(x) denotes the surface measure on 𝕊3
. If we consider the parametrization of S3
defined by
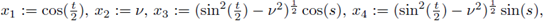 where
where
4. Nuclear Fourier integral operators on compact homogeneous manifolds
The main goal in this section is to provide a characterization for the nuclearity of Fourier integral operators on compact homogeneous manifolds
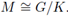 Taking into account that the Peter-Weyl decompositions of L
2(M) and L2(𝔾) (where 𝔾 is a Hausdorff and compact group) have an analogue structure, we classify the nuclearity of FIOs on compact homogeneous manifolds by adapting to our case the proof of Theorem 2.2 in [30], where those nuclear pseudo-differential operators in Lp(𝔾)-spaces were classified.
Taking into account that the Peter-Weyl decompositions of L
2(M) and L2(𝔾) (where 𝔾 is a Hausdorff and compact group) have an analogue structure, we classify the nuclearity of FIOs on compact homogeneous manifolds by adapting to our case the proof of Theorem 2.2 in [30], where those nuclear pseudo-differential operators in Lp(𝔾)-spaces were classified.
4.1. Global FIOs on compact homogeneous manifolds
In order to present our definition for Fourier integral operators on compact homogeneous spaces, we recall some definitions on the subject. Compact homogeneous manifolds can be obtained if we consider the quotient space of a compact Lie groups G with one of its closed subgroups K (there exists an unique differential structure for the quotient M := G/K). Examples of compact homogeneous spaces are spheres
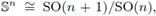 real
real
projective spaces ℝℙn ≅ SO(n + 1)/O(n), complex projective spaces ℂℙn ≅ SU(n + 1)/SU(1) x SU(n), and, more generally, Grassmannians Gr(r, n) ≅ O(n)/O(n - r) x O(r).
Let us denote by
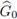 the subset of
the subset of
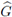 of representations in G that are of class I with respect to the subgroup K. This means that
of representations in G that are of class I with respect to the subgroup K. This means that
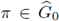 if there exists at least one non trivial invariant vector a with respect to K, i.e., π(h)a = a for every h ∈ K. Let us denote by B
π to the vector space of these invariant vectors, and k
π
= dim B
π
. Now we follow the notion of Multipliers as in [1]. Let us consider the class of symbols Σ(M), for M = G/K, consisting of those matrix-valued functions
if there exists at least one non trivial invariant vector a with respect to K, i.e., π(h)a = a for every h ∈ K. Let us denote by B
π to the vector space of these invariant vectors, and k
π
= dim B
π
. Now we follow the notion of Multipliers as in [1]. Let us consider the class of symbols Σ(M), for M = G/K, consisting of those matrix-valued functions
Following [1], a Fourier multiplier A on M is a bounded operator on L 2(M) such that for some σ A ∈ Σ(M) it satisfies
where
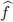 denotes the Fourier transform of the lifting
denotes the Fourier transform of the lifting
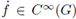 of f to G, given by
of f to G, given by
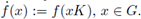
Remark 4.1. For every symbol of a Fourier multiplier A on M, only the upper-left block in σ A (π) of the size k π x k π cannot be the trivial matrix zero.
Now, if we consider a phase function
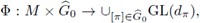 and a distribution
and a distribution
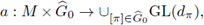 the Fourier integral operator associated to Φ and to a (·, ·) is given by
the Fourier integral operator associated to Φ and to a (·, ·) is given by
We additionally require the condition σ(x,π)ij = 0 for i,j > k π for the distributional symbols considered above. Now, if we want to characterize those r-nuclear FIOs we only need to follow the proof of Theorem 2.2 in [30], where the nuclearity of pseudo-differential operators was characterized on compact and Hausdorff groups. Since the set
provides an orthonormal basis of L 2(M), we have the relation
If we assume that F : L
P1 (M) → L
P2 (M) is r-nuclear, then we have a nuclear decomposition for its kernel, i.e., there exist sequences h
k in LP2 and g
k in
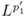 satisfying
satisfying
with
So, we have with 1 ≤ n,m ≤ k π ,
Consequently, if B t denotes the transpose of a matrix B, we obtain
and by considering that Φ(x,π) ∈ GL(dπ) for every x ∈ M, we deduce the equivalent condition,
On the other hand, if we assume that the symbol a(·, ·) satisfies the condition (102) with
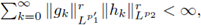 from the definition of Fourier integral operator we can write, for φ ∈ L
P1(M),
from the definition of Fourier integral operator we can write, for φ ∈ L
P1(M),
Again, by Delgado's Theorem we obtain the r-nuclearity of F. So, our adaptation of the proof of Theorem 2.2 in [30] to our case of FIOs on compact manifolds leads to the following result.
Theorem 4.2. Let us assume M = G/K be a homogeneous manifold, 0 < r ≤ 1, 1 ≤ p1, p2
< ∞, and let F be a Fourier integral operator as in (97). Then, F : L
P1 (M) → L
P2 (M) is r-nuclear if, and only if, there exist sequences h
k
in L
P2
and g
k
in
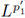 satisfying
satisfying
with
Now, we will prove that the previous (abstract) characterization can be applied in order to measure the decaying of symbols in the momentum variables. So, we will use the following formulation of Lebesgue spaces on
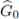 :
:
for 1 ≤ p < ∞.
Theorem 4.3. Let us assume M ≅ G/K be a homogeneous manifold, 2 ≤ p
1
< ∞, 1 ≤ p
2
< ∞, and let F be a Fourier integral operator as in (97) .If F : L
P1 (M) → L
P2 (M) is nuclear, then
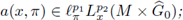 this means that
this means that
provided that
Proof. Let 2 ≤ p 1 < ∞, 1 ≤ p 2 < ∞, and let F be the Fourier integral operator associated to a(·, ·). If F : L P1 (M) → L P2 (M) is nuclear, then Theorem 4.2 guarantees the decomposition
with
Consequently,
Now, if we use the Hausdorff-Young inequality, we deduce,
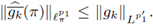 Consequently,
Consequently,
Thus, we finish the proof.
Remark 4.4. If K = {e G } and M = G is a compact Lie group, the condition
arises naturally in the context of pseudo-differential operators. Indeed, if we take Φ(x,ξ = ξ (x), then Φ(x, ξ)-1 = ξ (x)*, and
Remark 4.5. As a consequence of Delgado's theorem, if F: L p(M) - L p(M), M ≅ G/K, 1 ≤ p < ∞, is r-nuclear, its nuclear trace is given by
Example 4.6 (The complex projective plane ℂℙ2). A point
 (the n-dimensional complex projective space) is a complex line through the origin in ℂn+1. For every n, ℂℙn ≅ SU(n +1)/SU(1) x SU(n). We will use the representation theory of SU(3) in order to describe the nuclear trace of Fourier integral operators on ℂℙ2 ≅ SU(3)/SU(1) x SU(2). The Lie group SU(3) (see
[27]) has dimension 8, and 3 positive square roots a, 3 and p with the property
(the n-dimensional complex projective space) is a complex line through the origin in ℂn+1. For every n, ℂℙn ≅ SU(n +1)/SU(1) x SU(n). We will use the representation theory of SU(3) in order to describe the nuclear trace of Fourier integral operators on ℂℙ2 ≅ SU(3)/SU(1) x SU(2). The Lie group SU(3) (see
[27]) has dimension 8, and 3 positive square roots a, 3 and p with the property
We define the weights
With the notations above the unitary dual of SU(3) can be identified with
SU(3) = {A := \(a, b) = aa + br: a,b ∈ N0, }. (116)
In fact, every representation π = πλ(a,b)
has highest weight λ = λ(a, b) for some (a, b) ∈
 In this case
In this case
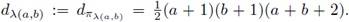 For G = SU(3) and K = SU(1) x SU(2), let us define
For G = SU(3) and K = SU(1) x SU(2), let us define
Now, let us consider a phase function
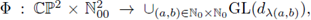 a distribution
a distribution
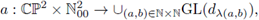 and the Fourier integral operator F associated to Φ and to a (·, ·) :
and the Fourier integral operator F associated to Φ and to a (·, ·) :
where φ ∈ C∞ (ℂℙ2). We additionally require the condition
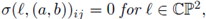 and
and
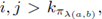 for those distributional symbols considered above. As a consequence of Remark 4.5, if F: Lp(ℂℙ2) → Lp(ℂℙ2), 1 ≤ p < ∞, is r-nuclear, its nuclear trace is given by
for those distributional symbols considered above. As a consequence of Remark 4.5, if F: Lp(ℂℙ2) → Lp(ℂℙ2), 1 ≤ p < ∞, is r-nuclear, its nuclear trace is given by
If
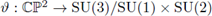 is a diffeomorphism and K = SU(1) x SU(2), then
is a diffeomorphism and K = SU(1) x SU(2), then
where we have denoted
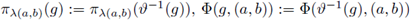 and
and
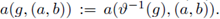 If we consider the parametrization of SU(3) (see, e.g., Bronzan
[4]),
If we consider the parametrization of SU(3) (see, e.g., Bronzan
[4]),
then, the group measure is the determinant given by
and we have the trace formula