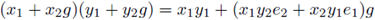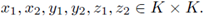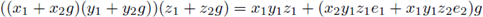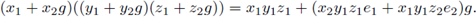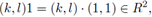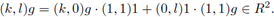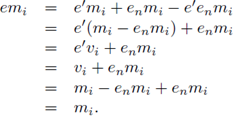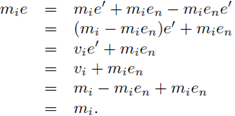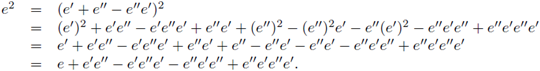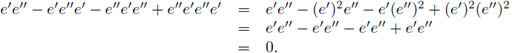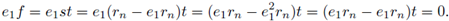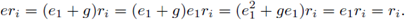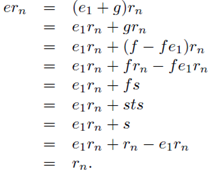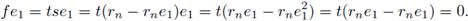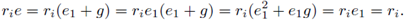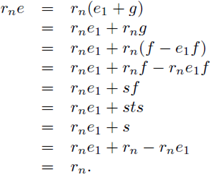1. Introduction
In many presentations of ring theory, authors make the assumption that all rings are unital, that is that they possess a multiplicative identity element. There are, however, lots of natural constructions in ring theory which share all properties of unital rings except the property of having a multiplicative identity. Such constructions include ideals, infinite direct sums of rings, and linear transformations of finite rank of an infinite dimensional vector space. For many examples of rings lacking a multiplicative identity there still exist weaker versions of identity elements. The purpose of the present article is to gather some classical results and examples of rings having different degrees of weak forms of identity elements, ordered in hierarchy. To be more precise, we wish to show the following strict inclusions of families of rings:
In our presentation, we will begin with the class of rings and narrow down our results and examples until we reach the class of unital rings.
2. Idempotent and s-unital rings
Definition 2.1. Throughout this article, R denotes an associative ring. We do not assume that R has a multiplicative identity. Let ℤ denote the set of integers and let ℕ denote the set of positive integers.
Definition 2.2. The ring R is called idempotent if R2 = R. Here R2 denotes the set of all finite sums of elements of the form rs for r, s ∈ R.
Example 2.3. It is easy to construct rings which are not idempotent. In fact, let A be any non-zero abelian group. Define a multiplication on A by saying that ab = 0 for all a, b ∈ A. Then A 2 = {0} ≠ A.
Another generic class of examples is constructed in the following way. If R is a ring and I is a two-sided ideal of R, with I 2 ⊊ I, then I is a ring which is not idempotent. This holds for many rings R, for instance when R = ℤ and I is any non-trivial ideal of R.
The next definition was introduced by Tominaga in 10 and 11.
Definition 2.4. Let M be a left (right) R-module. We say that M is s-unital if for every m ∈ M the relation m ∈ Rm (m ∈ mR) holds. If M is an R-bimodule, then we say that M is s-unital if it is s-unital both as a left R-module and as a right R-module. The ring R is said to be left (right) s-unital if it is left (right) s-unital as a left (right) module over itself. The ring R is said to be s-unital if it is s-unital as a bimodule over itself.
Example 2.5. The following example shows that there exist idempotent rings that are neither left nor right s-unital. Let G = {e, g} denote the associative semigroup defined by the relations e · e = e and e · g = g · e = g · g = g. Let K denote a field and put v = (1,0) and v = (0,1) in K x K. Let R denote the twisted semigroup ring (K x K)[G] where the multiplication is defined by
for x i , x 2 , y 1 , y 2 ∈ K x K. Then R is associative. Indeed, take
A straightforward calculation shows that
and
Also R is neither left nor right s-unital. In fact, take x 1 , y 2 ∈ K x K. If g(x 1 + x 2 g) = g, then e 1 x 1 g = g, so that e 1 x 1 = (1, 1) in K x K which is a contradiction. In the same way (x 1 + x 2 g)g = g leads to x 1 e 2 = (1,1) in K x K which is a contradiction. However, R is idempotent since for all (k, l) G K x K, the following relations hold:
and
Example 2.6. The following example (inspired by [7, Exercise 1.10]) shows that there are lots of examples of rings which are left (right) s-unital but not right (left) s-unital. Let A be a unital ring with a non-zero multiplicative identity 1.
(a) Let B l denote the set A x A equipped with componentwise addition and multiplication defined by the relations
(a, b)(c, d) = (ac, ad)
for a, b, c, d ∈ A. Now we show that Bi is associative. Take a, b, c, d, e, f ∈ A. Then,
((a, b)(c, d))(e, f) = (ac, ad)(e, f) = (ace, acf),
and
(a, b)((c, d)(e, f)) = (a, b)(ce, cf) = (ace, acf).
It is clear that any element of the form (1, a), for a ∈ A, is a left identity for B
l
. However, B
l
is not right unital. Indeed, since (0,1) ∉ {(0, 0)} = (0,1)B
l
it follows that B
l
is not even right s-unital. For each n ∈ ℕ let C
n
denote a copy of B
l
, and put
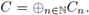 Then C is left s-unital but not left unital. Since none of the C
n
are right s-unital it follows that C is not right s-unital.
Then C is left s-unital but not left unital. Since none of the C
n
are right s-unital it follows that C is not right s-unital.
(b) Let B r denote the set A x A equipped with component wise addition and multiplication defined by the relation
(a, b)(c, d) = (ac, bc)
for a, b, c, ∈ A. Now we show that Br is associative. Take a, b, c, d, e, f ∈ A. Then,
((a, b)(c, d))(e ,f) = (ac, bc)(e, f) = (ace, bce),
and
(a, b)((c, d)(e, f)) = (a, b)(ce, de) = (ace, bce).
It is clear that any element of the form (1, a), for a ∈ A, is a right identity for Bl. However, B
r
is not left unital. Indeed, since (0,1) ∉ {(0, 0)} = B
r (0,1) it follows that Br is not even left s-unital. For each n ∈ ℕ let D
n
denote a copy of B
r
and
 Then D is right s-unital, but not right unital. Since none of the D
n
are left s-unital, it follows that D is not left s-unital.
Then D is right s-unital, but not right unital. Since none of the D
n
are left s-unital, it follows that D is not left s-unital.
Definition 2.7. If e', e'' ∈ R, then put e' V e" = e' + e" - e'e".
Proposition 2.8. Let M be a left (right) R-module. Then M is left (right) s-unital if, and only if, for all n ∈ ℕ and all m1,...,mn ∈ M there is e ∈ R such that for all i ∈ {1,..., n} the relation em¡ = mi (m i e = m i) holds.
Proof. We follow the proof of [11, Theorem 1]. The "if" statements are trivial. Now we show the "only if" statements.
First, suppose that M is a left R-module which is s-unital. Take n ∈ ℕ and m1,..., mn ∈ M. Take en ∈ R such that enmn = mn, and for every i ∈ {1,...,n - 1} put vi = mi - enmi. By induction there is an element e' ∈ R such that for every i ∈ {1,..., n - 1} the equality e 'vi = vi holds. Put e = e' V en. Then
emn = e'mn + enmn - e 'enmn = e 'mn + mn - e'mn = mn,
and for every i ∈ {1,..., n - 1} we get that
Now suppose that M is a right R-module which is s-unital. Take n ∈ ℕ and m1,..., mn ∈ M. Take en ∈ R such that mnen = mn, and for every i ∈ {1,...,n - 1} put vi = m¡ - m¡en. By induction there is an element e' ∈ R such that for every i ∈ {1,..., n - 1} the equality v¡e ' = v¡ holds. Put e = en V e '. Then
mne = mne′ + mnen − mnene′ = mne′ + mn − mne′ = mn,
and for every i ∈ {1,..., n - 1} we get that
Proposition 2.9. Let M be an R-bimodule and suppose that e', e '' ∈ R. Let X be a subset of M such that for all m ∈ X the relations e'm = me '' = m hold. Then; for all m ∈ X the following relations hold:
(e’’ V e’ )m = m(e’’ V e’ ) = m.
Proof. This is essentially the proof of [9, Lemma 1]. Take m G X. Then
(e '' V e ')m = (e' + e'' - e ''e')m = e'm + e''m - e ''e'm = m + e''m - e''m = m,
and
m(e '' V e ') = m(e ' + e'' - e ''e') = me' + me'' - me''e' = me' + m - me ' = m.
Proposition 2.10. Let M be an R-bimodule. Then M is s-unital if, and only if, for all n ∈ ℕ and all m1,..., mn ∈ M there is e ∈ R such that for all i ∈ {1,..., n} the relation emi = mie = mi holds.
Proof. The "if" statement is trivial. Now we show the "only if" statement. Take n ∈ ℕ and mi,..., mn ∈ M. From Proposition 2.8 it follows that there are e', e '' ∈ R such that for all i ∈ {1,..., n} the relations e mi = mie = mi hold. The claim now follows from Proposition 2.9 if we put e = e '' V e' and X = {m1,..., mn}.
Proposition 2.11. The ring R is left (right) s-unital if, and only if, for all n ∈ ℕ and all r1,..., rn ∈ R there is e ∈ R such that for all i ∈ {1,..., n} the relation eri = ri (rie = ri) holds.
Proof. This follows from Proposition 2.8.
Proposition 2.12. The ring R is s-unital if, and only if, for all n ∈ ℕ and all r1,..., rn ∈ R there is e ∈ R such that for all i ∈ {1,..., n} the relations eri = rie = ri hold.
Proof. This follows from Proposition 2.10.
Definition 2.13. An element e ∈ R is called idempotent if e2 = e.
Definition 2.14. We say that R is left (right) locally unital if for all n ∈ N and all
r1,...,rn ∈ R there is an idempotent e ∈ R such that for all i ∈ {1,...,n} the equality eri = rj (rie = ri) holds. We say that R is locally unital if it is both left locally unital and right locally unital.
Example 2.15. Let R denote the ring of real valued continuous functions on the real line with compact support. Then R is s-unital, but neither left nor right locally unital.
3. Locally unital rings
The next definition was introduced by Ánh and Márki in 4.
Definition 3.1. The ring R is said to be locally unital if for all n ∈ ℕ and all r1,...,rn ∈ R there is an idempotent e ∈ R such that for all i ∈ {1,...,n} the equalities eri = rie = ri hold.
Proposition 3.2. Suppose that e , e ∈ R are idempotents, and put e = e V e . Then e 2 = e + e 'e '' - e 'e ''e ' - e ' 'e 'e '' + e ' 'e 'e ''e '. If either of the following equalities hold,
(i) e′e′′ = e′,
(ii) e′e′′ = e′′,
(iii) e′′e′ = e′′,
(iv) e′′e′ = e′,
(v) e′e′′ = e′′e′,
then e is idempotent.
Proof. A straightforward calculation shows that
Now we show the last part. If (i) holds, then
e′e′′ − e′e′′e′ − e′′e′e′′ + e′′e′e′′e′ = e′ − (e′)2 − e′′e′ + e′′(e′)2 = e′ − e′ − e′′e′ + e′′e′ = 0.
If (ii) holds, then
e′e′′ − e′e′′e′ − e′′e′e′′ + e′′e′e′′e′ = e′′ − (e′′)2 − (e′′)2 + (e′′)3 = e′′ − e′′ − e′′ + e′′ = 0.
If (iii) holds, then
e′e′′ − e′e′′e′ − e′′e′e′′ + e′′e′e′′e′ = e′e′′ − e′e′′ − (e′′)2 + (e′′)2 = −e′′ + e′′ = 0.
If (iv) holds, then
e′e′′ − e′e′′e′ − e′′e′e′′ + e′′e′e′′e′ = e′e′′ − (e′)2 − e′e′′ + (e′)2 = −e′ + e′ = 0.
If (v) holds, then
Proposition 3.3. A ring is locally unital in the sense of Definition 2.14 if, and only if, it is locally unital in the sense Definition 3.1.
Proof. The "only if" statement is immediate. Now we show the "if" statement. We use the argument from the proof of [6, Proposition 1.10] (see also [4, Example 1]). Suppose that R is a ring which is locally unital in the sense of Definition 2.14. Take n ∈ ℕ and r1,...,rn ∈ R. Since R is right locally unital, there is an idempotent e’ ∈ R such that for all i ∈ {1,..., n} the equality rie’ = ri holds. Since R is left locally unital, there is an idempotent e’’ ∈ R such that e’’e’ = e’, and for all i ∈ {1,...,n} the equality e’’ri = ri holds. Put e = e’ V e’’. From Proposition 3.2 it follows that e is idempotent. From Proposition 2.9, with X = {ri,...,rn}, it follows that for all i ∈ {1,...,n} the equalities eri = rie = ri hold. So, R is locally unital in the sense of Definition 3.1.
4. Regular rings
Definition 4.1. The ring R is called regular if for every r ∈ R there is s ∈ R such that r = rsr.
The next proposition is [4, Example 1].
Proposition 4.2. Every regular ring is locally unital.
Proof. We proceed in almost the same way as in the proof of Proposition 2.8. Let R be a regular ring. Take n ∈ ℕ and r1,...,rn ∈ R. First we show that R is left locally unital. By induction there is an idempotent e1 ∈ R such that for all i ∈ {1,..., n - 1} the equality e1ri = ri holds. Put s = rn - e1rn. Since R is regular, there is t ∈ R such that s = sts. Put f = st. Then f is idempotent and
Put g = f - fe 1. Then e 1 g = ge 1 = U and
g 2 = f 2 - f 2 e 1 - fe 1 f + fe 1 fe 1 = f - fe 1 = g.
Let e = e1 + g. Then e is an idempotent. Take i ∈ {1,..., n - 1}. Then,
Finally,
Now we show that R is right locally unital. By induction there is an idempotent e1 ∈ R such that for all i ∈ {1,..., n - 1} the equality rie1 = ri holds. Put s = rn - rne1. Since R is regular, there is t ∈ R such that s = sts. Put f = ts. Then f is idempotent, and
Put g = f - e 1 f. Then e 1 g = ge 1 = 0 and
g 2 = f 2 - e 1 f 2 - fe 1 f + e 1 fe 1 f = f - e 1 f = g.
Let e = e 1 + g. Then e is an idempotent. Take i ∈ {1,..., n - 1}. Then,
Finally,
5. Rings with sets of local units
The next definition was introduced by Abrams in 2.
Definition 5.1. Suppose that E is a set of commuting idempotents in R which is closed under the operation V from Definition 2.7. Then E is called a set of local units for R if for all r ∈ R there is e ∈ E such that er = re = r.
Remark 5.2. In [2, Definition 1.1] the condition that E is closed under V was not included. However, since this was intended (personal communication with G. Abrams) we chose to include it here.
Proposition 5.3. If R has a set of local units E, then for all n ∈ N and all r1,...,rn ∈ R there is e ∈ E such that for all i ∈ {1,..., n} the equalities er i = r i e = r i holds.
Proof. Take n ∈ ℕ and r 1 ,...r n ∈ R. By induction there is e1, e2 ∈ E such e2rn = rne2 = rn, and for all i ∈ {1,..., n - 1} the relations e 1 r i = r i e 1 = ri hold. Put e = e1 V e2. Then, since e1e2 = e2e1, we get that
er n = e 1 r n + e 2 r n - e 1 e 2 r n = e 1 r n + r n - e 1 r n = r n
and
r n e = r n e 1 + r n e 2 - r n e 2 e 1 = r n e 1 + r n - r n e 1 = r n,
and for all i ∈ {1,..., n - 1} we get that
er i = e 1 r i + e 2 r i - e 2 e 1 r i = r i + e 2 r i - e 2 r i = r i
and
r i e = r i e 1 + r i e 2 - r i e 1 e 2 = r i + r i e 2 - r i e 2 = r i.
Proposition 5.4. If a ring has a set of local units, then it is locally unital.
Proof. This follows from Proposition 5.3.
Example 5.5. According to [4, Example 1] there are regular rings that do not possess sets of local units in the sense of Definition 5.1.
Definition 5.6. If e, f ∈ R are idempotent, then e and f are said to be orthogonal if ef = fe = 0.
6. Rings with enough idempotents
The following definition was introduced by Fuller in 5.
Definition 6.1. The ring R is said to have enough idempotents in case there exists a set
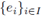 of orthogonal idempotents in R (called a complete set of idempotents for R) such that
of orthogonal idempotents in R (called a complete set of idempotents for R) such that
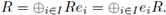
Example 6.2. There exist rings which have sets of local units in the sense of Definition 5.1, but which does not have enough idempotents in the sense of Definition 6.1. To exemplify this we recall the construction from [1, Example 1.6]. Let F denote the field with two elements, and let R be the ring of all functions f : ℕ → F. For each n ∈ ℕ define fn ∈ R by fn(n) = 1, and fn(m) =0, if m ≠ n. For all finite subsets S of ℕ, define fS ∈ R via
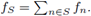 Then I = {fS | S is a finite subset of ℕ} is an ideal of R. Since R is unital, Zorn's lemma implies the existence of a maximal proper ideal M of R with I ⊆ M. Since all elements in R, and hence also in M, are idempotent, it follows that M is a ring with E = M as a set of local units. Seeking a contradiction, suppose that M has a complete set of idempotents {ej}j∈J
. Since I, and hence M, contains all fn, for n ∈ ℕ, it follows that
Then I = {fS | S is a finite subset of ℕ} is an ideal of R. Since R is unital, Zorn's lemma implies the existence of a maximal proper ideal M of R with I ⊆ M. Since all elements in R, and hence also in M, are idempotent, it follows that M is a ring with E = M as a set of local units. Seeking a contradiction, suppose that M has a complete set of idempotents {ej}j∈J
. Since I, and hence M, contains all fn, for n ∈ ℕ, it follows that
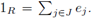 Since M is a proper ideal, we get that 1R ∉ M, and thus it follows that J is an infinite set. Choose any partition J = K ∪ L, with K ∩ L = ∅, and K and L infinite. Define
Since M is a proper ideal, we get that 1R ∉ M, and thus it follows that J is an infinite set. Choose any partition J = K ∪ L, with K ∩ L = ∅, and K and L infinite. Define
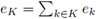 and
and
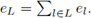 Since the ej
are pairwise orthogonal, we get that eKeL = 0. But M is a maximal ideal of R. Therefore M is a prime ideal of R, and thus eK ∈ M or eL ∈ M. Suppose that eK ∈ M. Since {ej}j∈J
is a complete set of idempotents, there must exist a finite set J' of J with
Since the ej
are pairwise orthogonal, we get that eKeL = 0. But M is a maximal ideal of R. Therefore M is a prime ideal of R, and thus eK ∈ M or eL ∈ M. Suppose that eK ∈ M. Since {ej}j∈J
is a complete set of idempotents, there must exist a finite set J' of J with
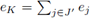 which is a contradiction. Analogously, the case when eL ∈ M leads to a contradiction. Therefore, M is not a ring with enough idempotents.
which is a contradiction. Analogously, the case when eL ∈ M leads to a contradiction. Therefore, M is not a ring with enough idempotents.
Definition 6.3. If M is a left (right) R-module, then M is called left (right) unital if there is e ∈ R such that for all m ∈ M the relation em = m (me = m) holds. In that case e is said to be a left (right) identity for M. If M is an R-bimodule, then M is called unital if it is unital both as a left R-module and a right R-module. The ring R is said to be left (right) unital if it is left (right) unital as a left (right) module over itself. The ring R is called unital if it is unital as a bimodule over itself.
Example 6.4. The ring Bl (or Br) from Example 2.6 is a ring which is left (or right) unital, but not right (or left) unital.
Example 6.5. There are many classes of rings that are neither left nor right unital but still have enough idempotents. Here are some examples:
infinite direct sums of unital rings;
category rings where the category has infinitely many objects (see e.g. [8, Proposition 4]);
Leavitt path algebras with infinitely many vertices (see e.g. [3, Lemma 1.2.12(iv)]).
Proposition 6.6. Let M be an R-bimodule. Then M is unital if, and only if, there is e ∈ R such that for all m ∈ M the relations em = me = m hold.
Proof. The "if" statement is trivial. The "only if" statement follows from Proposition 2.9 if we put X = M.
Proposition 6.7. The ring R is unital if, and only if, there is e G R such that for all r R the relations er = re = r hold.
Proof. This follows from Proposition 6.6 if we put M = R. 0
Remark 6.8. Proposition 6.7 can of course be proved directly in the following way. Let e’ (or e’’) be a left (or right) identity for R as a left (or right) module over itself. Then e' = e’e’’ = e’’.
We end the article with the following remark, which connects unitality and s-unitality.
Proposition 6.9. If R is left (right) s-unital and right (left) unital, then R is unital.
Proof. First suppose that R is left s-unital and right unital. Let f be a right identity of R and take r ∈ R. From Proposition 2.8 it follows that there is e ∈ R with er = r and ef = f. But since f is a right identity of R it follows that ef = e. Thus e = f and hence fr = er = r so that f is a left identity of R. Now suppose that R is right s-unital and left unital. Let f be a left identity of R and take r ∈ R. From Proposition 2.8 it follows that there is e ∈ R with re = r and fe = f. But since f is a left identity of R it follows that fe = e. Thus e = f and hence rf = re = r so that f is a right identity of R.