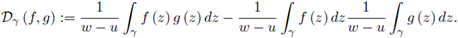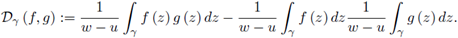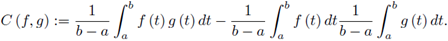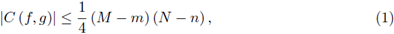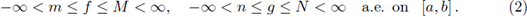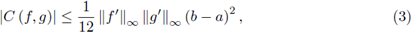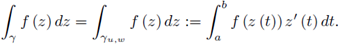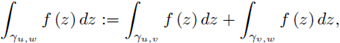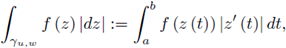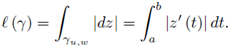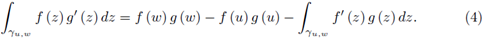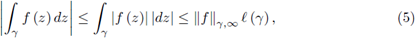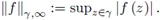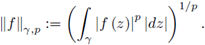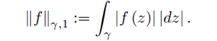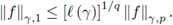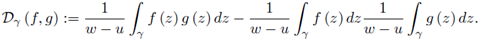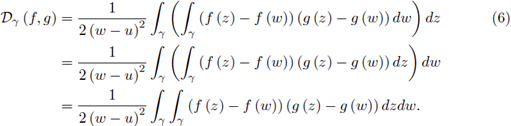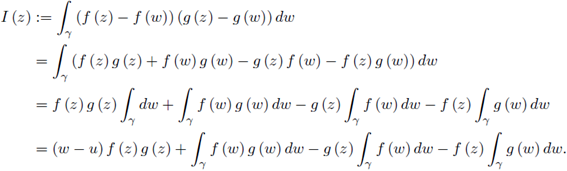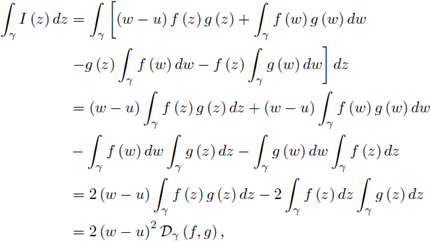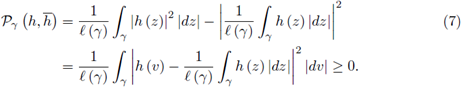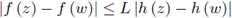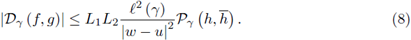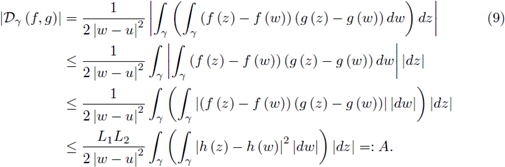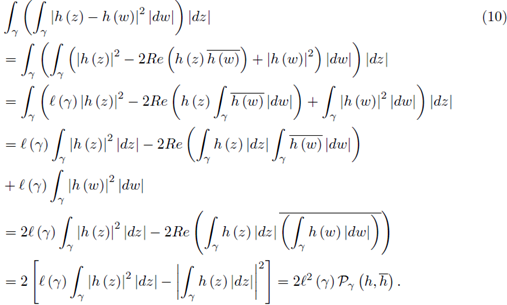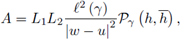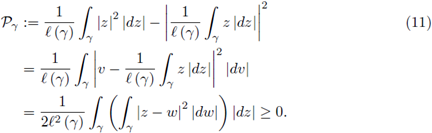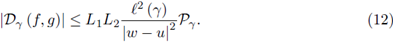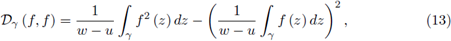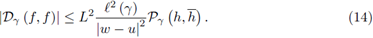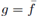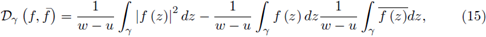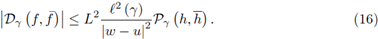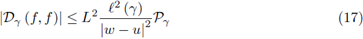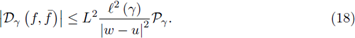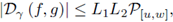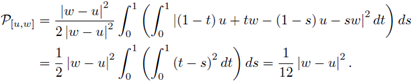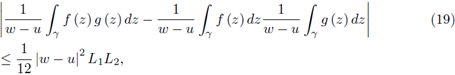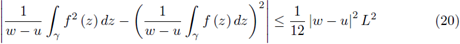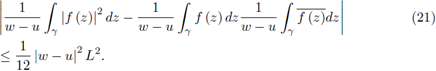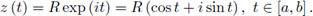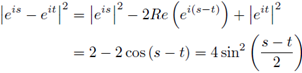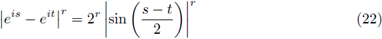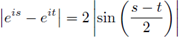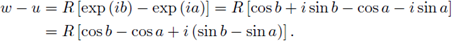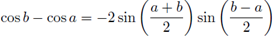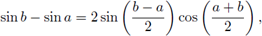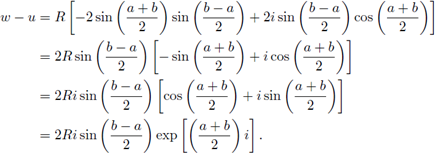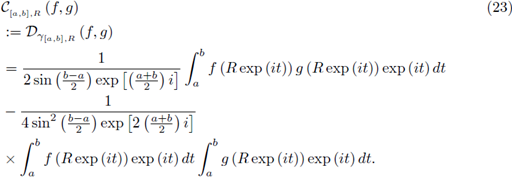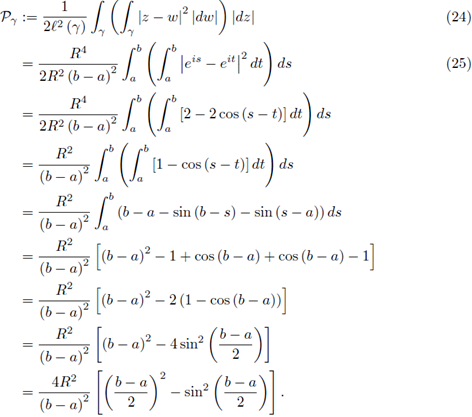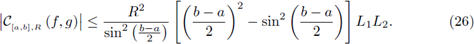1. Introduction

For two Lebesgue integrable functions f, g : [a, b] → ℂ, in order to compare the integral mean of the product with the product of the integral means, we consider the Chebyshev functional defined by

In 1934, G. Grüss [17] showed that

provided m, M, n, N are real numbers with the property that

The constant in (1) is sharp.

Another, however less known result, even though it was obtained by Chebyshev in 1882, [8], states that

provided that f’, g’ exist and are continuous on 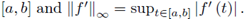The constant 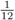cannot be improved in the general case.

The Chebyshev inequality (3) also holds if f, g: [a, b] → ℝ are assumed to be absolutely continuous and f’, g’ ∈ L _∞ [a,b], while

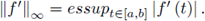
For other inequality of Grüss' type see ^[1]-^[16] and ^[18]-^[28].

In order to extend Grüss' inequality to complex integral we need the following preparations.

Suppose γ is a smooth path parametrized by z (t) , t ∈ [a, b] and f is a complex valued function which is continuous on γ. Put z (a) = u and z (b) = w with u, w ∈ ℂ. We define the integral of f on γ_u,w = γ as

We observe that the actual choice of parametrization of γ does not matter.

This definition immediately extends to paths that are piecewise smooth. Suppose γ is parametrized by z (t), t ∈ [a, b], which is differentiable on the intervals [a, c] and [c, b]; then, assuming that f is continuous on γ, we define

where v: = z (c). This can be extended for a finite number of intervals.

We also define the integral with respect to arc-length:

and the length of the curve γ is then

Let f and g be holomorphic in G, an open domain, and suppose γ ⊂ G is a piecewise smooth path from z (a) = u to z (b) = w. Then we have the integration by parts formula

We recall also the triangle inequality for the complex integral, namely,

where

We also define the p-norm with p≥1 by

For p = 1 we have

If p, q > 1 with 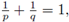then, by Hölder’s inequality, we have

Suppose γ ⊂ ℝ is a piecewise smooth path parametrized by z (t), t ∈ [a, b] from z (a) = u to z (b) = w with w ≠ u. If f and g are continuous on γ, we consider the complex Chebyshev functional defined by

In this paper we establish some bounds for the magnitude of the functional D_γ (f, g) under various assumptions for the functions f and g, and provide a complex version for the Chebyshev inequality (3).

2. Chebyshev type results

We start with the following identity of interest:

Lemma 2.1. Suppose γ ⊂ ℝ is a piecewise smooth path parametrized by z (t), t ∈ [a, b] from z (a) = u to z (b) = w with w ≠ u. If f and g are continuous on γ, then

Proof. For any z ∈ γ the integral 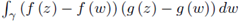exists and

The function I (z) is also continuous on γ, then the integral 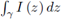exists and

which proves the first equality in (6).

The rest follows in a similar manner and we omit the details. 0

Suppose γ ⊂ ℂ is a piecewise smooth path from z (a) = u to z (b) = w and h: γ → ℂ a continuous function on γ. Define the quantity:

We say that the function f: G ⊂ ℂ → ℂ is L-h-Lipschitzian on the subset G if

for any z, w ∈ G. If h (z) = z, we recapture the usual concept of L-Lipschitzian functions on G.

Theorem 2.2. Suppose γ ⊂ ℂ is a piecewise smooth path parametrized by z (t), t ∈ [a, b] from z (a) = u to z (b) = w with w ≠ u, h : γ → ℂ is continuous, f and g are L₁, L₂ -h-Lipschitzian functions on γ; then

Proof. Taking the modulus in the first equality in (6), we get

Now, observe that

Therefore, by (10) we get

and by (9) we get the desired result (8).

Further, for γ ⊂ ℂ a piecewise smooth path parametrized by z (t), and by taking h (z) = z in (7), we can consider the quantity

Corollary 2.3. Suppose γ ⊂ ℂ is a piecewise smooth path parametrized by z (t), t ∈ [a, b] from z (a) = u to z (b) = w with w ≠ u and f and g are L₁, L₂ -Lipschitzian functions on γ; then

Remark 2.4. Assume that f is L-h-Lipschitzian on γ. For g = f we have

and by (8) we get

For we have

and by (8) we get

If f is L-Lipschitzian on γ, then

And

If the path γ is a segment [u, w] connecting two distinct points u and w in ℂ, then we write 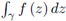as

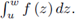
Now, if f and g are L₁, L₂-Lipschitzian functions on [u, w] := {(1 - t) u + tw, t ∈ [0,1]} , then by (12) we have

where

Therefore,

if f and g are L ₁ , L ₂-Lipschitzian functions on [u, w].

If f is L-Lipschitzian on [u, w] , then

and

3. Examples for circular paths

Let [a, b] ⊆ [0, 2π] and the circular path γ[ _a,b ],R centered in 0 and with radius R > 0:

If [a, b] = [0, π], then we get a half circle, while for [a, b] = [0, 2π] we get the full circle.

Since

for any t, s ∈ ℝ, then

for any t, s ∈ ℝ and r > 0. In particular,

for any t, s ∈ ℝ.

If u = R exp (¿a) and w = R exp(ib), then

Since

and

hence

If γ = γ _[a,b],_R then the circular complex Chebyshev functional is defined by

If γ = γ _[a,b],R then

We have the following result:

Proposition 3.1. Let γ_[a,b],_R be a circular path centered in 0, with radius R > 0 and [a, b] ⊂ [0, 2π]. If f and g are L ₁, L ₂ -Lipschitzian functions on γ_[a,b],R, then