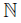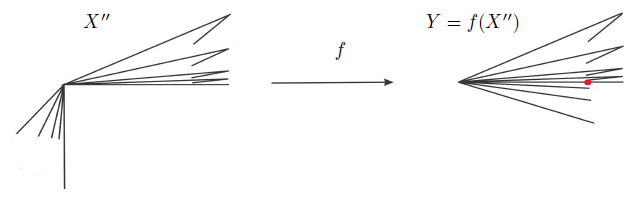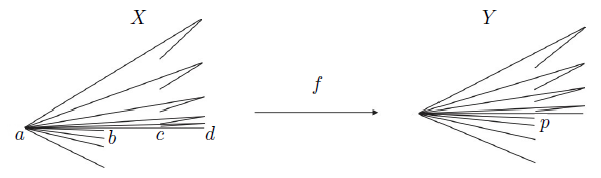1. Preliminaries and auxiliary results
All spaces considered are metric and all mappings are assumed surjective and continuous. A continuum means a nonempty compact connected metric space. A subcontinuum is a continuum which is a subset of a space. A continuum is said to be hereditarily unicoherent if the intersection of any two of its continua is connected. An arc is understood as a homeomorphic image of a closed unit interval of the real line. For each x, y into a space, we denote by xy any arc into a space joining x to y and we denote by 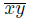 the straight line segment into a space joining x to y. If any two points of a space can be joined by an arc lying in it, then it is said to be arcwise connected.
the straight line segment into a space joining x to y. If any two points of a space can be joined by an arc lying in it, then it is said to be arcwise connected.
A dendroid is defined as an arcwise connected and hereditarily unicoherent continuum. A point p of a dendroid X is called a ramification point of X, if there exist three arcs emanating from p in X, with the intersection of each two of them being just the singleton {p}. A fan means a dendroid having exactly one ramification point, this point is called its vertex.
The symbol 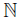 stands for the set of all positive integers. Let X be a topological space, and {An}n∈N be a sequence of subsets of X.
stands for the set of all positive integers. Let X be a topological space, and {An}n∈N be a sequence of subsets of X.
— Li An={x ∈ X: for each open subset U of X such that x ∈ U, U ∩ An ̸= ∅ for all but finitely many n}, is the limit inferior of the sequence {An}n∈N.
— Ls An={x ∈ X: for each open subset U of X such that x ∈ U, U ∩ An ̸= ∅ for infinitely many}, is the limit superior of the sequence {An}n∈N.
— Lim An = Li An = Ls An, is the limit of the sequence {An}n∈N. In this way, it is said that the sequence {An}n∈N converges to the limit L =Lim An.
The following concepts are related to contractility which will be used throughout this paper.
A continuum X is said to be of type N provided there exist in X: two points p, q, an arc A = pq; two sequences of arcs {An}n∈N = {pnp′n}n∈N and {Bn}n∈N = {qnq′n}n∈N; and points p′′n ∈ Bn\ {qn, q′n} and q′′n ∈ An \ {pn, p′n} such that the following conditions are satisfied:
(1) A = Lim An = Lim Bn;
(2) p = lim pn = lim p′n = lim p′′n ;
(3) q = lim qn = lim q′n= lim q′′n ;
(4) each arc in X joining pn and p′ncontains q′′n ;
(5) each arc in X joining qn and q′ncontains p′′n .
A dendroid X contains a zig-zag provided there exist in X: an arc A with end points p and q, and a sequence of arcs {An}n∈N with end points pn, qn, and points p1n, q1n ∈ An\{pn, qn} such that:
Note that each dendroid containing a zig-zag is of type N. The converse is not always true, even on fans (see [5, Example 2.7]).
Let X be a continuum, and let A and B be nonempty compact subsets of X. A subcontinuum C of X is said to be irreducible between A and B provided that C ∩ A ‡ ∅, C ∩ B ‡ ∅, and no proper subcontinuum of C intersects both A and B.
A point p of a dendroid X is called a Q-point if there is a sequence {pn}n∈N in X converging to p such that Ls ppn ‡ {p} and, if pnqn denotes the arc which is irreducible between pn and Ls ppn, then the sequence {qn}n∈N converges to p.
Let X be a dendroid and r a point in X, suppose that there exist two sequences { r } n∈N , { r
} n∈N , { r } n∈N in X, both converging to r. The former sequence dominates the latter provided that whenever there is a point s ∈ X and a sequence { s
} n∈N in X, both converging to r. The former sequence dominates the latter provided that whenever there is a point s ∈ X and a sequence { s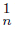 } n∈N in X converging to the point s with the property that the sequence of arcs r
} n∈N in X converging to the point s with the property that the sequence of arcs r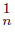 s
s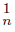 converges to the arc rs, then it follows that there exists another sequence { s
converges to the arc rs, then it follows that there exists another sequence { s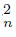 } n∈N in X converging to s such that the sequence of arcs r
} n∈N in X converging to s such that the sequence of arcs r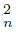 s
s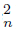 converges to the arc rs. A dendroid is said to be pairwise smooth provided that whenever a pair of sequences converge to a common limit point, then one of the pairs dominates the other.
converges to the arc rs. A dendroid is said to be pairwise smooth provided that whenever a pair of sequences converge to a common limit point, then one of the pairs dominates the other.
Let X be a topological space, X is called contractible if there is a mapping H: X×[0, 1] → X such that H(x, 0) = x for all x and H(x, 1) = p for all x and some p ∈ X. The following internal characterization of contractibility of fans is due to L. G. Oversteegen (see [12, Theorem 3.4, p. 393]).
Theorem 1.1. For a fan X, the following conditions are equivalent:
X is contractible;
X contains no Q−points, is not of type N and is pairwise smooth;
X contains no Q−points, contains no zig-zag and is pairwise smooth.
The following concepts are related to contractibility of continua too. A nonempty closed subset (subcontinuum) K of a continuum X is called an:
R1−set (continuum), if there exist an open set U of X containing K and if {C
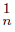 }n∈N and {C
}n∈N and {C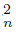 }n∈N are two sequences of components of U such that K = Ls C
}n∈N are two sequences of components of U such that K = Ls C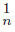 ∩ Ls C
∩ Ls C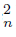 .
.R2 -set (continuum), if there exist an open set U of X containing K and two sequences {C
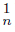 }n∈N and {C
}n∈N and {C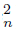 }n∈N of components of U such that K = Lim C
}n∈N of components of U such that K = Lim C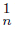 ∩ Lim C
∩ Lim C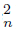 .
.R3 -set (continuum), if there exist an open set U of X containing K and a sequence {Cn}n∈N of components of U such that K = Li Cn.
The following proposition was first shown for dendroids (see [8, Proposition 5, p.77; and, Corollary 11, p.78]) but it holds for continua.
Proposition 1.2. If a continuum X contains an R i−continuum for some i ∈ {1, 2}, then it contains an R3−continuum.
In fact, if X contains an R1−continuum, then taking a subsequence if necessary, it contains an R2−continuum, and each R2−continuum is both an R1−continuum and an R3−continuum (see [7, 3.3, p.34]). For R i−sets (see [13, Theorem 2.3, Theorem 2.4 and Corollary 2.5, p.310]).
The following result is well known (see [13, Corollary 3.3, p. 317], [8, Theorem 9, p. 78]).
Theorem 1.3. If a continuum X contains an R i−set (continuum) for i ∈ {1, 2, 3}, then X is not contractible.
In this paper, we will use the following kinds of mappings.
A mapping f: X → Y between continua is said to be:
— Monotone, if f −1 ({p}) is connected for each point p of Y .
— Almost monotone, if f −1 (B) is connected for each subcontinuum B of Y with nonempty interior.
— Quasi monotone, if for each subcontinuum B of Y with nonempty interior, f −1 (B) has a finite number of components and if D is a component of f −1(B), then f (D) = B.
— Confluent, provided that for each subcontinuum B of Y and each component C of f −1 (B), f (C) = B.
— Weakly confluent, provided that for each subcontinuum B of Y there exists a component C of f −1 (B), such that f (C) = B.
— Freely decomposable, if whenever A and B are proper subcontinua of Y such that Y = A∪B, then there exist two proper subcontinua A′ and B′ of X such that X = A′ ∪B′ , where A′ ⊆ f −1 (A) and B′ ⊆ f −1 (B).
— Strongly freely decomposable, if whenever A and B are proper subcontinua of Y such that Y = A ∪ B, then f −1 (A) and f −1 (B) are connected.
— Light, provided that f −1 ({z}) is totally disconnected for each z ∈ Y .
— Open, provided that for any open subset U of X, f (U) is an open subset of Y .
We will use the following characterization for monotone mappings (see for instance [9, Lemma 2.1.12, p. 74]).
Theorem 1.4. Let f : X → Y be a mapping between continua. Then, f is monotone if and only if f −1 (C) is connected for each connected subset C of Y .
In the following diagram, we show the relationship among the above mappings.
Let 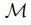 be a class of mappings between continua. A mapping f : X → Y is said to be hereditarily
be a class of mappings between continua. A mapping f : X → Y is said to be hereditarily 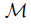 if the restriction to every subcontinuum of X belongs to
if the restriction to every subcontinuum of X belongs to 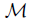 . Also, we will use the following language. If a mapping f belongs to two different classes of mapping M and M′ , we say that f is a MM′ mapping. For instance, if the mapping f is light and confluent, we say that f is a light confluent mapping.
. Also, we will use the following language. If a mapping f belongs to two different classes of mapping M and M′ , we say that f is a MM′ mapping. For instance, if the mapping f is light and confluent, we say that f is a light confluent mapping.
The main goal of this paper is to show some partial answers to the following general problems:
([5, Problem 8.1, p.589]) What are all mappings that preserve contractibility (noncontractibility) of dendroids?
Let X be a dendroid (fan). What kinds of mappings f defined on X have the property that whether X contains an R i -set (continuum) where i ∈ {1, 2, 3}, then f(X) also contains an R i -set (continuum)?
Particular cases of these problems are given in the following questions:
Question 1.5 ([6, Question 13.10, p.72]). What kinds of confluent mappings preserve contractibility of fans?
Question 1.6 ([6, Question 13.22, p.75]). What kinds of confluent mappings preserve noncontractibility of fans?
Question 1.7 ([6, Question 13.24, p.76]). Let a fan (a dendroid) X be given. What confluent mappings f defined on X have the property that if X contains an R i−continuum, where i ∈ {1, 2, 3}, then f(X) also contains an R i−continuum?
Question 1.8 ([6, Question 13.26, p.76]). Let a fan (dendroid) X be given. What confluent mappings f defined on X have the property that if f(X) contains an R i−continuum, where i ∈ {1, 2, 3}, then X also contains an R i−continuum?
This paper is divided into four sections. After preliminaries and auxiliaries results, in Section 2, we discuss the questions formulated for Ri−continua. In Section 3, we discuss the behaviour of Q−points, zig-zag, and pairwise smooth under the above mappings. Finally, in Section 4, we work with the function T and some classes of mappings.
2. Ri −continua and mappings
Given a topological property 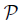 and a class
and a class 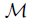 of mappings, we say that
of mappings, we say that 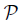 is invariant under mappings in
is invariant under mappings in 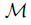 provided that for each mapping f: X → Y with f ∈
provided that for each mapping f: X → Y with f ∈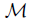 if X has
if X has 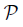 then Y has
then Y has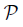 . Given a topological property
. Given a topological property 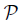 and a class
and a class 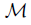 of mappings, we say that
of mappings, we say that 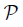 is coinvariant under mappings in
is coinvariant under mappings in 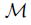 provided that for each mapping f : X → Y with f ∈
provided that for each mapping f : X → Y with f ∈  if Y has
if Y has , then X has
, then X has . Concerning Problem 1, we start our study mentioning a known result for monotone mappings and Ri−continua.
. Concerning Problem 1, we start our study mentioning a known result for monotone mappings and Ri−continua.
Example 2.1. Containing an R i−continuum for i ∈ {1, 2, 3} is not invariant under monotone mappings of fans, even all but one point inverses are degenerate (see [6, Example 13.17, p.74] and [6, Corollary 13.23, p.75]). As a corollary, noncontractibility is not invariant under monotone mappings between fans.
We have the following results.
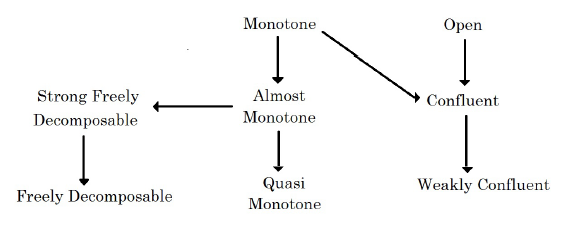
Example 2.2. Containing an R i−continuum for i ∈ {1, 2, 3} is not invariant under light confluent and strongly freely decomposable mappings between fans.
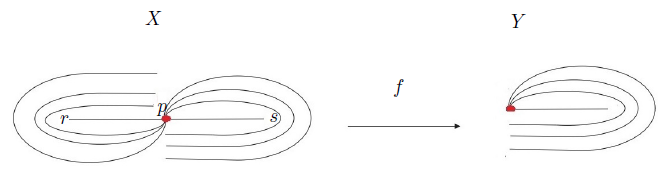
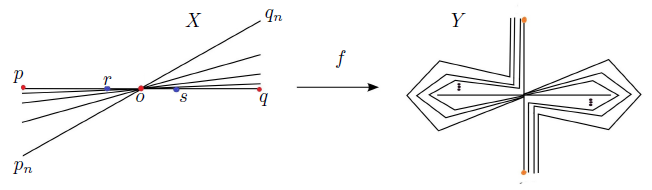
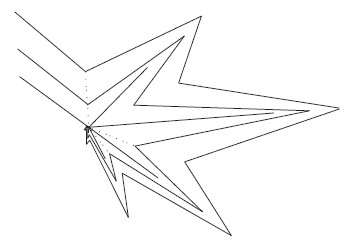
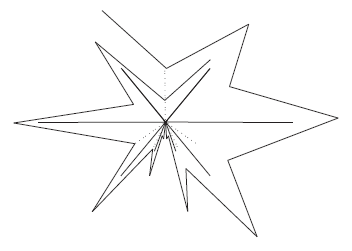
Proof. Let X = Z1 ∪ Z2 and Y be fans, where Z1 ∩ Z2= {p} and Z1, Z2 and Y are homeomorphic spaces to the continuum X described in [6, Example 11.16, p.53] (see Figure 2). Consider a decomposition of X whose nondegenerate elements are obtained identifying in a point any pair of the symmetric points with respect to the point p of the arc rs. The mapping f: X → Y is the quotient mapping under this decomposition. The mapping is light confluent and strongly freely decomposable, even f is almost monotone mapping.
Note that {p} is an R i−continuum in X and Y contains no Ri−continuum, i ∈ {1, 2, 3}. Unfortunately, by Theorem 1.1, the fan Y is not contractible. It is still open to find two fans X and Y , and a confluent (light confluent, strongly freely decomposable, almost monotone) mapping between them such that X contains an R i−continuum and Y is contractible.
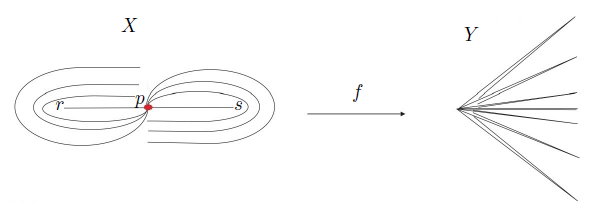
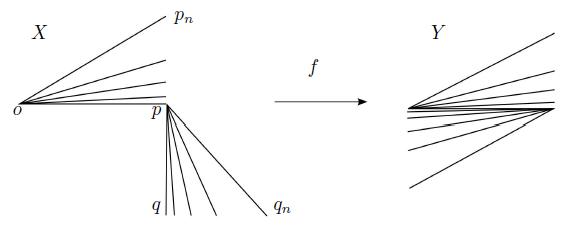
Example 2.3. Containing an R i−continuum for i ∈ {1, 2, 3} is not invariant under light open and quasi monotone mappings between dendroids.
Proof. Let p = (−1, 0), o = (0, 0), q = (1, 0). Put an = (0, 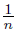 ) and bn = (0, −
) and bn = (0, − 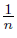 ) for each n ∈
) for each n ∈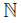 . Let X =
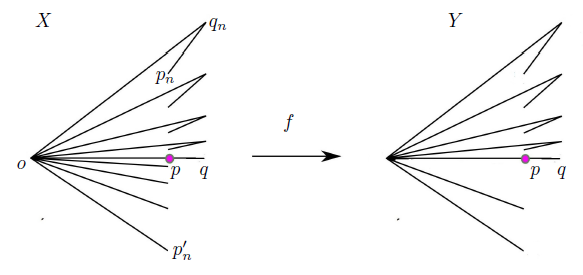
. Let X =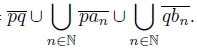 Consider the decomposition whose elements are obtained by identifying every point x ∈ X with −x. The function f : X → f(X) = Y is the quotient mapping under this decomposition. Note that f is light open and quasi monotone mapping. On the other hand, the set {o} is an R i−continuum in X and Y does not contain any R i−continuum, i ∈ {1, 2, 3}. Even Y is contractible.
Consider the decomposition whose elements are obtained by identifying every point x ∈ X with −x. The function f : X → f(X) = Y is the quotient mapping under this decomposition. Note that f is light open and quasi monotone mapping. On the other hand, the set {o} is an R i−continuum in X and Y does not contain any R i−continuum, i ∈ {1, 2, 3}. Even Y is contractible.
Corollary 2.4. Noncontractibility is not invariant under light open and quasi monotone mappings between dendroids.
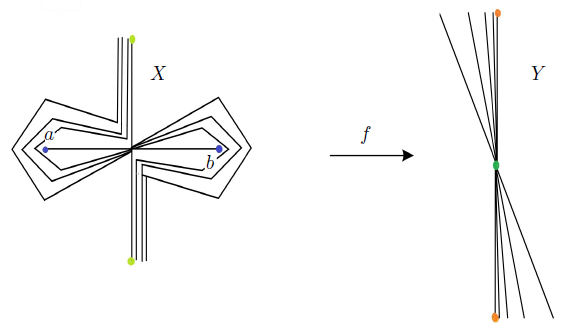
Example 2.5. Containing an R i−continuum, i ∈ {1, 2, 3}, is not invariant under light open and quasi monotone mappings between fans.
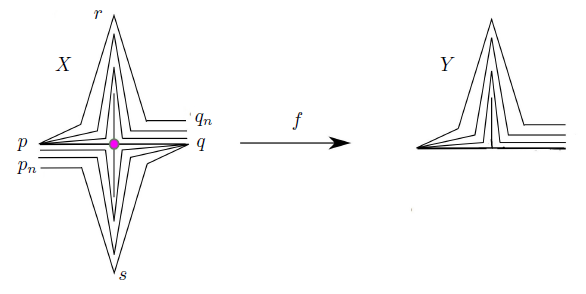
Proof. Let X be the fan defined in Example 2.2 and let Y be a fan homeomorphic to the fan described in [6, Example 11.16, p.53]. Let p = (0, 0). We consider the decomposition on X by identifying every point x ∈ X with −x (see Figure 4). The quotient mapping f : X → Y is the result of this identification. It is not difficult to prove that the mapping f is light open and quasi monotone. The set {p} ⊆ X is an R i−continuum. However, Y does not contain an R i−continuum for each i ∈ {1, 2, 3}. Unfortunately, by Theorem 1.1, the fan Y is not contractible. It is still open to find two fans X and Y and an open (quasi monotone) mapping between them such that X contains an R i−continuum and Y is contractible.
Example 2.6. Containing an R i−continuum for i ∈ {1, 2, 3} is not invariant under freely decomposable and weakly confluent mappings between dendroids.
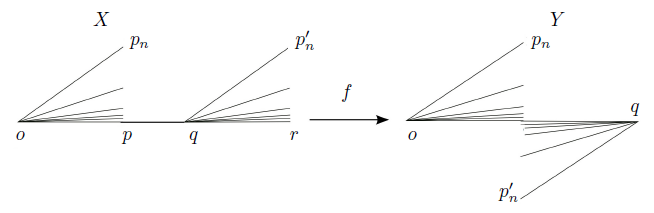
Proof. Put o = (0, 0), p = (−1, 0), q = (1, 0), r = (0, 1), s = (0, −1) and let pn = (−1, − 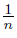 ), qn = (1,
), qn = (1, 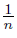 ), un = (−
), un = (− 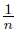 ,
, 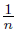 ), vn = (
), vn = ( 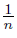 ,
, 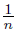 ), wn = (
), wn = ( 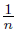 , −
, − 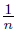 ), zn = (−
), zn = (− 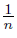 , −
, − 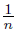 ), sn = (0, −1 −
), sn = (0, −1 − 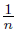 ) and rn = (0, 1 +
) and rn = (0, 1 + 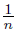 ) for each n ∈ N. Define X =
) for each n ∈ N. Define X =
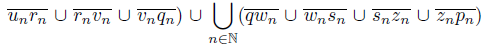 and let f : X → Y be the mapping defined by f(x) = x if x ∈
and let f : X → Y be the mapping defined by f(x) = x if x ∈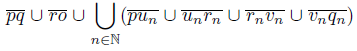 and if
and if 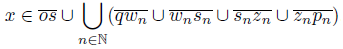 , f(x) is the projection over the arc
, f(x) is the projection over the arc . So, Y = f(X) =
. So, Y = f(X) =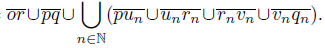 The set {o} is an R i−continuum and Y does not contain an R i−continuum, i ∈ {1, 2, 3}. Moreover, Y is contractible.
The set {o} is an R i−continuum and Y does not contain an R i−continuum, i ∈ {1, 2, 3}. Moreover, Y is contractible.
Corollary 2.7. Non contractibility is not invariant under freely decomposable and weakly confluent mappings between dendroids.
Example 2.8. Containing an R i−continuum for i ∈ {1, 2, 3} is not invariant under strongly freely decomposable and weakly confluent mappings between fans.
Proof. To describe the continua X and Y, we consider the following points: o = (0, 0), p = (1, 0) and q = (2, 0). Put pn = (1, 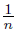 ), p′n = (1, −
), p′n = (1, −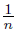 ) and qn = (2,
) and qn = (2, 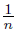 ) for each n ∈
) for each n ∈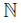 . Let X =
. Let X =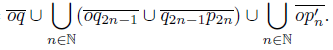 To describe the mapping f: X → Y , let 0 < ε <
To describe the mapping f: X → Y , let 0 < ε <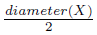 and let B={p ′ n : d(p ′ n , p) < ε}. Then, f(x) = x if x
and let B={p ′ n : d(p ′ n , p) < ε}. Then, f(x) = x if x 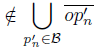 and f(x) is the projection over the arc
and f(x) is the projection over the arc 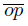 if x
if x 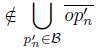 .
.
Notice that f is a strongly freely decomposable mapping, the set {p} is an R i−continuum of X while Y does not contain an R i−continuum for each i ∈ {1, 2, 3}. Even f is almost monotone and Y is contractible. Therefore, noncontractibilty is not invariant under strongly freely decomposable, almost monotone and weakly confluent mappings between fans.
On the other hand, in [6] the authors asked the following:
Question 2.9 ([6, Question 13.26, p.76]). Is the property of containing an R i−continuum, i ∈ {1, 2, 3}, coinvariant under confluent mappings between fans (dendroids)?
We can ask a more general question as follows:
Question 2.10. What kinds of mappings satisfy that the property of containing an R i−continuum is coinvariant between fans (dendroids)?
For this question, we consider the following classes of mappings: monotone, weakly confluent, strongly freely decomposable, freely decomposable, almost monotone, and quasi monotone.
It is known that containing an R i−continuum for i ∈ {1, 2, 3} is not coinvariant under light confluent mappings of fans (see [6, Corollary 13.25, p.76]). The same corollary shows that the contractibility is not invariant under light confluent mappings of fans. The fans pictured in Figure 7 are the same as Figure 9 and Figure 10 in [6, p.71].
Example 2.11. Containing an R i−continuum for i ∈ {1, 2, 3} is not coinvariant under monotone mappings of dendroids.
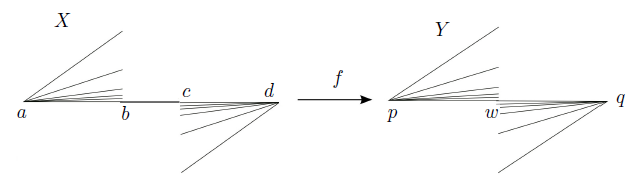
Proof. To define the dendroid X, we consider the following points: a = (0, 0), b = (1, 0), c = (2, 0) and d = (3, 0). Let bn = (1, 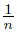 ) and cn = (2, −
) and cn = (2, − 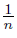 ) for each n ∈
) for each n ∈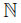 . Put X = ad∪
. Put X = ad∪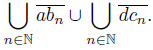 . Consider the decomposition of X whose only nondegenerate element is the arc bc. Then, the mapping f is the quotient mapping under this decomposition, and f(X) = Y is homeomorphic to the dendroid X in Figure 8. Observe that f is a monotone mapping. Notice that {w} is an R i−continuum of Y, for every i ∈ {1, 2, 3}. However, X is contractible.
. Consider the decomposition of X whose only nondegenerate element is the arc bc. Then, the mapping f is the quotient mapping under this decomposition, and f(X) = Y is homeomorphic to the dendroid X in Figure 8. Observe that f is a monotone mapping. Notice that {w} is an R i−continuum of Y, for every i ∈ {1, 2, 3}. However, X is contractible.
Example 2.12. Containing an R i−continuum for i ∈ {1, 2, 3} is not coinvariant under monotone mappings between fans.
Proof. In order to define the fan X, we consider the following points: a = (0, 0), b = (1, 0), c = (2, 0) and d = (3, 0). For each n ∈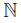 , let bn = (1, −
, let bn = (1, − 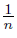 ), cn = (2,
), cn = (2, 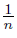 ) and dn = (3,
) and dn = (3, 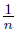 ). Put X =
). Put X =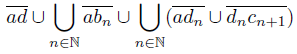 .
.
Consider the decomposition of X such that the only non degenerate is the arc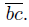 Then, the mapping f is the quotient mapping under this decomposition, and f(X) is homeomorphic to the fan Y in Figure 9. Clearly f is a monotone mapping. Notice that the set {p} is an R i−continuum of f(X) for i ∈ {1, 2, 3}. However, X is contractible.
Then, the mapping f is the quotient mapping under this decomposition, and f(X) is homeomorphic to the fan Y in Figure 9. Clearly f is a monotone mapping. Notice that the set {p} is an R i−continuum of f(X) for i ∈ {1, 2, 3}. However, X is contractible.
Notice that in the previous two examples, for every proper open subset U of Y containing two sequences {C 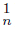 }n∈N and {C
}n∈N and {C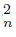 }n∈N of components satisfying that {x} = Ls C
}n∈N of components satisfying that {x} = Ls C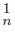 ∩ Ls C
∩ Ls C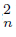 ⊆ U, we have that Ls f −1 (C
⊆ U, we have that Ls f −1 (C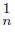 )∩ Ls f −1 (C
)∩ Ls f −1 (C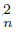 ) = ∅. On the other hand, if we also consider a sequence {Cn}n∈N of components of U fulfilling that Li Cn = {x}, we have that Li f −1 (Cn) is not R3−set (continuum) in X.
) = ∅. On the other hand, if we also consider a sequence {Cn}n∈N of components of U fulfilling that Li Cn = {x}, we have that Li f −1 (Cn) is not R3−set (continuum) in X.
Now, with additional conditions, we have that containing an Ri−set (continuum) for i ∈ {1, 2, 3} is coinvariant under monotone mappings between fans (dendroids).
The following lemma is a consequence of [10, 8.15, p.127].
Lemma 2.13. Let f : X → Y be a mapping between topological spaces. If C is a component of D ⊆ Y and E ⊆ X is a component of f −1 (C), then E is a component of f −1(D).
Lemma 2.14. Let X and Y be topological spaces and let f : X −→ Y be a mapping. If {An}n∈N is a sequence of subsets of Y , then:
Proof. We will just prove the first proposition. The proof of the second one is similar. The third one follows from 1. and 2. We will prove that if x 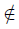 f −1 ( Li An), then x
f −1 ( Li An), then x 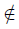 Li f −1 (An). So, there exists an open set of Y containing f(x) such that U ∩ An = ∅ for infinitely many indices n ∈
Li f −1 (An). So, there exists an open set of Y containing f(x) such that U ∩ An = ∅ for infinitely many indices n ∈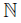 . So, f −1 (U ∩An) = ∅. Note that f −1 (U ∩An) = f −1 (U)∩ f −1 (An). Then, f −1 (U) is an open set of X containing x such that f −1 (U)∩f −1 (An) = ∅ for infinitely many indices n ∈
. So, f −1 (U ∩An) = ∅. Note that f −1 (U ∩An) = f −1 (U)∩ f −1 (An). Then, f −1 (U) is an open set of X containing x such that f −1 (U)∩f −1 (An) = ∅ for infinitely many indices n ∈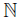 . Hence, x
. Hence, x 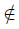 Li f −1 (An).
Li f −1 (An).
Proposition 2.15. Let X and Y be continua and let f : X → Y be a monotone mapping. If Y contains a proper subcontinuum K and an open subset U containing two sequences {C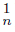 }n∈N and {C
}n∈N and {C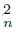 }n∈N of components of U such that K =Ls C
}n∈N of components of U such that K =Ls C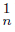 ∩ Ls C
∩ Ls C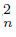 ⊆ U, Li f−1 (C
⊆ U, Li f−1 (C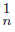 ) ‡ ∅, Li f−1 (C
) ‡ ∅, Li f−1 (C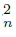 ) ‡ ∅ and H =Ls f−1 (C
) ‡ ∅ and H =Ls f−1 (C 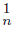 )∩ Ls f −1 (C
)∩ Ls f −1 (C 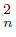 ) ‡ ∅, then X has an R1−set. If X is hereditarily unicoherent, then X contains an R1−continuum. Therefore, X is not contractible.
) ‡ ∅, then X has an R1−set. If X is hereditarily unicoherent, then X contains an R1−continuum. Therefore, X is not contractible.
Proof. Because f is a mapping, f−1 (U) is an open set of X. Since f is monotone and by Lemma 2.13, we have that for every n ∈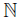 , and i ∈ {1, 2}, the component C
, and i ∈ {1, 2}, the component C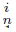 of U, satisfies that f −1 (C
of U, satisfies that f −1 (C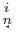 ) is a component of f−1 (U). Thus, we get sequences {f−1 (C
) is a component of f−1 (U). Thus, we get sequences {f−1 (C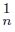 )}n∈N and {f−1 (C
)}n∈N and {f−1 (C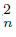 )}n∈N of components of f−1 (U).
)}n∈N of components of f−1 (U).
On the other hand, Ls f−1 (C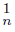 ) and Ls f−1 (C
) and Ls f−1 (C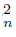 ) are subcontinua of X because of Li f −1 (C
) are subcontinua of X because of Li f −1 (C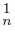 ) ‡ ∅, Li f−1 (C
) ‡ ∅, Li f−1 (C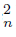 ) ‡ ∅. Notice that H is a closed subset of X and ∅ ‡ H = Ls f−1 (C
) ‡ ∅. Notice that H is a closed subset of X and ∅ ‡ H = Ls f−1 (C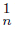 )∩ Ls f−1 (C
)∩ Ls f−1 (C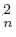 ) ⊆ f−1 (Ls C
) ⊆ f−1 (Ls C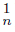 ) ∩ f−1 (Ls C
) ∩ f−1 (Ls C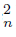 ) = f−1 (Ls C
) = f−1 (Ls C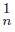 ∩Ls C
∩Ls C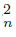 ) = f −1 (K) ⊆ f−1 (U). So, H is R1 -set. If X is hereditarily unicoherent, then H is connected. Therefore, H is an R1 -continuum. So, X is not contractible.
) = f −1 (K) ⊆ f−1 (U). So, H is R1 -set. If X is hereditarily unicoherent, then H is connected. Therefore, H is an R1 -continuum. So, X is not contractible.
Proposition 2.16. Let X and Y be continua and let f : X → Y be a monotone mapping. If Y contains a proper subcontinuum K, an open subset U of Y and a sequence {Cn}n∈N of components of U such that K =Li Cn ⊆ U and H =Li f −1 (Cn) ‡ ∅, then X has an R3−set. If X is hereditarily unicoherent, then H is an R3−continuum. Therefore, X is not contractible.
Proof. Since f is a mapping, f−1 (U) is an open subset of X. Because Cn is a component of U and f is a monotone mapping, by Lemma 2.13, f−1 (Cn) is a component of f−1 (U). Hence, {f−1 (Cn)}n∈N is a sequence of components of f−1 (U).
Notice that H =Li f−1 (Cn) ⊆ f−1 (Li Cn) = f−1 (K) ⊆ f−1 (U). Thus, H is an R3 -set. If X is hereditarily unicoherent and since ∅ ̸= H =Li f−1 (Cn) = Li 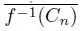 , then H is a subcontinuum of X (see [4, Lemma 1, p.6]). So, H is an R3 -continuum. Therefore, X is not contractible.
, then H is a subcontinuum of X (see [4, Lemma 1, p.6]). So, H is an R3 -continuum. Therefore, X is not contractible.
Proposition 2.17. Let X and Y be continua and let f : X → Y be a monotone mapping. If Y contains a proper subcontinuum K, and an open subset U of Y such that K ⊆ U and two sequences {C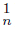 }n∈N and {C
}n∈N and {C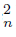 }n∈N of components of U such that K =Lim C
}n∈N of components of U such that K =Lim C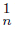 ∩ Lim C
∩ Lim C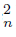 , Li f −1 (C
, Li f −1 (C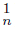 ) ‡ ∅, Li f−1 (C
) ‡ ∅, Li f−1 (C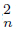 ) ‡ ∅ and H =Lim f−1 (C
) ‡ ∅ and H =Lim f−1 (C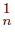 )∩ Lim f−1 (C
)∩ Lim f−1 (C 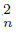 ) ‡ ∅, then X has an R 2−set. If X is hereditarily unicoherent, X has an R2−continuum. Therefore, X
is not contractible.
) ‡ ∅, then X has an R 2−set. If X is hereditarily unicoherent, X has an R2−continuum. Therefore, X
is not contractible.
Proof. Since K is an R2−set of Y , K is an R 1−continuum of Y . By Proposition 2.15, H is an R1−continuum of X. Therefore, X contains an R2−set.
In particular, if X and Y are dendroids fulfilling the conditions of propositions 2.15, 2.16 and 2.17, then X is not contractible.
Example 2.18. Containing an Ri−continuum for i ∈ {1, 2, 3} is not coinvariant under light weakly confluent and freely decomposable mappings between dendroids.
Proof. First, we define the following points: o = (0, 0), p = (1, 0), q = (2, 0) and r = (3, 0). For each n ∈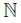 , put pn = (1,
, put pn = (1, 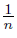 ), p′n = (1, −
), p′n = (1, − 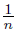 ), rn = (3,
), rn = (3, 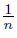 ). Let X =
). Let X =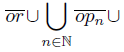
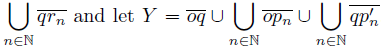 . We now consider the decomposition of X, whose nondegenerate elements are obtained by identifying in a point, the symmetric points with respect to the point q into the arc
. We now consider the decomposition of X, whose nondegenerate elements are obtained by identifying in a point, the symmetric points with respect to the point q into the arc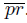 . Then, Y is homeomorphic to the image of the quotient mapping f defined under this identification.
. Then, Y is homeomorphic to the image of the quotient mapping f defined under this identification.
Notice that f is a light weakly confluent and freely decomposable mapping, X contains no Ri−continuum (X is contractible) and {p} ⊆ Y is an R i−continuum, for each i ∈ {1, 2, 3} (Y is not contractible).
Example 2.19. Containing an R i−continuum for i ∈ {1, 2, 3} is not coinvariant under almost monotone mapping between fans.
Proof. We consider the fans X ′′ and f(X ′′) = Y, and the mapping described in [6, Example 13.7, p.70]. Observe that f is almost monotone, also is a strongly freely decomposable mapping, X does not contain an Ri−continuum and the subset {p′} of Y is an Ri−continuum, for each i ∈ {1, 2, 3}.
Then, non contractibility is not coinvariant under almost monotone and strongly freely decomposable mappings between fans.
Example 2.20. Containing an Ri−continuum for i ∈ {1, 2, 3} is not coinvariant under light freely decomposable mappings between fans.
Proof. We define the points o = (0, 0), p = (−1, 0), q = (1, 0), and for each n ∈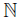 , pn = (−1, −
, pn = (−1, − 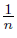 ) and qn = (1,
) and qn = (1, 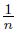 ). Let X =
). Let X =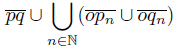 .
.
Let 0 < ε < 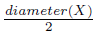 . Consider r ∈
. Consider r ∈ 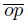 and s ∈
and s ∈ 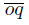 such that d(o, r) = d(s, o) =
such that d(o, r) = d(s, o) = 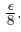 Now we identify each point x with its symmetric point respect to r if x ∈ ro and if x ∈ os, we identify x with its symmetric point respect to s. The mapping f is the quotient mapping under this identification, f(X) is homeomorphic to the fan Y in Figure 11.
Now we identify each point x with its symmetric point respect to r if x ∈ ro and if x ∈ os, we identify x with its symmetric point respect to s. The mapping f is the quotient mapping under this identification, f(X) is homeomorphic to the fan Y in Figure 11.
It is not difficult to see that f is light freely decomposable but not strongly freely decomposable mapping.
Therefore, non contractibility is not coinvariant under light freely decomposable between fans.
3. Zig-zag, Type N, Q − points, pairwise smooth, and mappings.
The characterization given in Theorem 1.1 describes three possible reasons for non contractibility of a fan:
being of type N (in particular containing a zig-zag),
containing a Q−point, and
being not pairwise smooth.
In this sense, J. J. Charatonik, W. J. Charatonik, and S. Miklos asked the following questions in [6]:
Question 3.1 (Question 13.5). Is the property of not containing a) a Q−point, b) a zig-zag, invariant under a) light open, b) open, c) light confluent mappings?
Question 3.2 (Question 13.19). Does there exist an open (or even light open) mapping from a fan containing a) a Q-point, b) a zig-zag, onto a fan that contains neither a Q−point nor a zig-zag?
Question 3.3 (Question 13.11). Is contractibility of fans invariant under light open or under open mappings?
Question 3.4 (Question 13.9). Is the property of being a pairwise smooth fan, invariant under light open or open mappings?
Question 3.5 (Question 13.20). Does there exist an open (or even a light open) mapping from a not pairwise smooth fan onto a fan that is pairwise smooth (contractible)?
We will give some partial answers to these questions. Additionally, we discuss these questions considering the families of strongly freely decomposable, freely decomposable, weakly confluent, almost monotone, and quasi monotone mappings. The following result is known: The property of not containing Q−point or a zig-zag is not invariant under monotone mappings (see [6, Example 13.3, p.68]). As a corollary, contractibility between fans under monotone mapping is not invariant (see [6, Corollary 13.4, p.69]).
The property of containing a Q−point and a zig-zag is not invariant under monotone mappings (see [6, Example 13.15, p.74]). Therefore, noncontractibility between fans under monotone mapping is not invariant (see [6, Corollary 13.16, p.74]).
Neither the existence of Q-point nor the existence of a zig-zag is invariant under open mappings of a fan onto an arc (see [6, Corollary 13.18, p.74]).
Neither the existence of Q−point nor the existence of a zig-zag is invariant under nonlight open mappings between fans (see [6, Corollary 13.18, p.74]).
The property of not being pairwise smooth is not invariant under monotone mappings between fans (see [6, Example 13.17, p.74]).
The property of being pairwise smooth is not invariant under monotone mappings between fans (see [6, Example 13.6, p.70]).
The property of being pairwise smooth is not invariant under light confluent mappings between fans (see [6, Example 13.7, p.70]). As a corollary, contractibility between fans under light confluent mapping is not invariant (see [6, Corollary 13.8, p.72]).
Hereditarily contractibility is invariant under confluent mappings and coinvariant under light confluent mappings (see [6, Theorem 13.13, p.73]).
In this part, we discuss our answers regarding questions 3.1 and 3.2 and Q−points. Let X be a topological space and let L(X) be the set of all points at which X is locally connected. The following proposition is known.
Proposition 3.6. If a mapping f : X → Y is open, then f(L(X)) ⊆ L(f(X)).
It is easy to see from the definition of Q−point that if X is locally connected at a point p, then p is not a Q−point.
The following theorem is known.
Theorem 3.7 ([3, Theorem 2.2, p.87]). Let X be a dendroid. Suppose that X is locally connected at each point of the closure of the set of ramification points of X. Then X does not have Q-points.
Theorem 3.8. Let X and Y be fans such that X is locally connected at its vertex. Let f : X → Y be a light confluent mapping, then Y is locally connected at its vertex.
Proof. Since f : X → Y is a light confluent mapping, by [6, Corollary 4.13, p.18], f −1 (v′ ) = {v} where v is the vertex of X and v′ is the vertex of Y . By Proposition 3.6, Y is locally connected in v′ .
As a consequence, we have to light open mappings and Q−points the following result.
Corollary 3.9. If f : X → Y be a light and open mapping and X and Y are fans such that X is locally connected at its vertex, then Y does not contain Q−points.
Recall that a topological space X is said to be planable provided there is a homeomorphism of X into the Euclidean plane. Besides, we can see that planability of fans is invariant under light open mapping if the domain is locally connected at its vertex. So, we respond partially to [6, Question 10.4, p.45].
In relation to questions 3.1 and 3.2 and zig-zags, we have the following results: the fan X used in Example 3.10 to shows that the property of not containing a zig-zag is not invariant under light confluent and almost monotone mapping between fans and the property of not containing a zig-zag is not invariant under light open and quasi monotone mapping between fans.
Example 3.10. Not containing a zig-zag is not invariant under light confluent and almost monotone mapping between fans.
Proof. Now, consider the following points in cylindrical coordinates in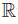 3 . Let p = (0, 0, 0), a0 =
3 . Let p = (0, 0, 0), a0 = 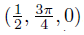 , a′0 =
, a′0 = 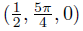 , an =
, an = 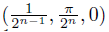 a0,m =
a0,m = 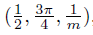 , a′0,m =
, a′0,m = 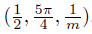 , p0,m =
, p0,m = 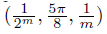 , p′0,m =
, p′0,m = 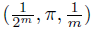 , and for every n, m ∈
, and for every n, m ∈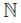 , let an,m =
, let an,m =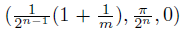 , pn,m =
, pn,m =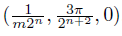 . Consider T =
. Consider T =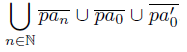 . For each m ∈
. For each m ∈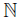 , put pa′m =
, put pa′m = 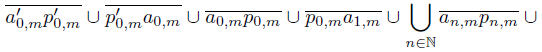
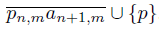 .
.
Notice that the sequence of arcs {pa′m}m∈N converges to the continuum T. So, X = T ∪( 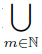 pa′m) is a countable fan with vertex p. The fan X is homeomorphic to the plane fan X ′ in Figure 12. Moreover, X ′ is a rotation about 90o with respect to the fan X.
pa′m) is a countable fan with vertex p. The fan X is homeomorphic to the plane fan X ′ in Figure 12. Moreover, X ′ is a rotation about 90o with respect to the fan X.
Now, we define an equivalence relation in X: let x, y ∈ X, x ∼ y if and only if either x 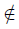 pa0 ∪ pa′0 and y = x or x ∈ pa0, y ∈ pa′0 and ||x|| = ||y||.
pa0 ∪ pa′0 and y = x or x ∈ pa0, y ∈ pa′0 and ||x|| = ||y||.
Consider Z = X/ ∼. Then, Z is homeomorphic to the fan Z ′ in Figure 13. Notice that X contains no zig-zag, Z contains a zig-zag and the quotient mapping is light confluent, and quasi monotone. We observe that X and Z are not contractible, because X has a Q−point and Z has a Q−point and zig-zags.
Example 3.11. Not containing a zig-zag is not invariant under light open and quasi monotone mapping between fans.
Proof. Consider the fan X in Example 3.10 with the same notation. Let f : X \ (pa0 ∪ pa′0 ) → 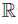 3 be the mapping defined by f((r, θ, z)) = (r, −θ, −z). Put W = X ∪ f(X \ (pa0 ∪ pa′0 )). Then, W is a countable plane fan with vertex p which is homeomorphic to the plane fan W′ in Figure 14. Now, we define an equivalence relation in W: let x, y ∈ W, x ∼ y if and only if either y = f(x) or x ∈ pa0, y ∈ pa′0 and ||x|| = ||y||.
3 be the mapping defined by f((r, θ, z)) = (r, −θ, −z). Put W = X ∪ f(X \ (pa0 ∪ pa′0 )). Then, W is a countable plane fan with vertex p which is homeomorphic to the plane fan W′ in Figure 14. Now, we define an equivalence relation in W: let x, y ∈ W, x ∼ y if and only if either y = f(x) or x ∈ pa0, y ∈ pa′0 and ||x|| = ||y||.
The quotient space Z is homeomorphic to the fan Z ′ in Figure 13. The fan W does not contain a zig-zag, but it has a Q−point. Therefore, it is not contractible and Z contains zig-zags and a Q−point (it is not contractible) and the quotient mapping is light open, and quasi monotone.
Example 3.12. Containing a zig-zag is not coinvariant under freely decomposable, weakly confluent and light mappings between dendroids.
Proof. To describe the dendroid X, we consider the following points in the plane; o = (0, 0), p = (1, 0) and q = (1, −1). For each n ∈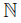 , let pn = (1,
, let pn = (1, 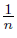 ) and qn = (1 +
) and qn = (1 + 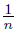 , −1). Put X =
, −1). Put X =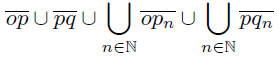 .
.
Now, we identify the point (x, 0) with the point (1, −1+x). Let f: X → f (X) the quotient mapping under this identification. Notice that X is contractible, f(X) is homeomorphic to the dendroid Y in Figure 15, Y contains a zig-zag and the quotient mapping is light freely decomposable and weakly confluent.
Example 3.13. Containing a zig-zag and Q−points is not coinvariant under light freely decomposable mappings between fans.
Proof. We consider the spaces X and Y and the mapping f of Example 2.20. The fan Y contains a zig-zag and its vertex is a Q−point, X is contractible and f is a light freely decomposable mapping.
Example 3.14. Containing a zig-zag and Q−points is not coinvariant under light weakly confluent and freely decomposable mappings between fans.
Proof. We consider a fan Y ′ homeomorphic to the fan Y in Example 2.5 and the armonic fan X′ =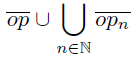 , where o = (0, 0), p = (1, 0), pn = (1,
, where o = (0, 0), p = (1, 0), pn = (1, 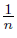 ) for each n ∈
) for each n ∈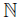 . Now, we define the following decomposition of X. Let m be the middle point of the arc
. Now, we define the following decomposition of X. Let m be the middle point of the arc 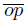 . The non degenerate elements of this decomposition are obtained by identifying in a point each pair of symmetric points respect to the point m in the arc
. The non degenerate elements of this decomposition are obtained by identifying in a point each pair of symmetric points respect to the point m in the arc 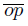 . The mapping f : X′ → f(X′ ) = Y ′ is the quotient mapping under this decomposition. Note that X is contractible, Y contains a Q−point and a zig-zag and f is a light weakly confluent and freely decomposable mapping.
. The mapping f : X′ → f(X′ ) = Y ′ is the quotient mapping under this decomposition. Note that X is contractible, Y contains a Q−point and a zig-zag and f is a light weakly confluent and freely decomposable mapping.
Let X be a continuum. The hyperspace 2 X is defined as the family of nonempty closed subset of X, C(X) is defined as the family of continua of X and F1(X) is the family of singletons of X, all endowed with the Hausdorff metric (see [10, p.53]. Observe that F1(X) ⊂ C(X) ⊂ 2 X.
The following result is well known.
Theorem 3.15 ([11, Theorem 16.39]). If X is a continuum such that 2 X (or C(X)) is contractible and if Y is a continuum which is an open image of X, then 2 Y and C(Y ) are contractible.
Concerning Question 3.3, we have the following.
Corollary 3.16. Let X be a contractible continuum. If f : X → Y is an onto open mapping and F1(Y ) is a retract of 2 Y (C(X)), then Y is contractible.
Proof. Since X is contractible, by [11, Corollary 16.8], 2 X and C(X) are each contractible. By Theorem 3.15, 2 Y and C(Y ) are contractible. Then Y is contractible, because F1 (Y ) is a retract of 2 Y(C(Y )) and retracts preserve contractibility.
To end this section, for pairwise smooth, we have the following two examples.
Example 3.17. There exists a light confluent and almost monotone mapping from a nonpairwise smooth fan onto a pairwise smooth fan.
Proof. Consider the fans X, Y and the mapping f of Example 2.2. The fan X is nonpairwise smooth, Y is pairwise smooth and the mapping f is light confluent and almost monotone. Unfortunately, Y is not contractible, because Y has a zig-zag and a Q−point.
Example 3.18. There exists a light open and quasi monotone mapping from a nonpairwise smooth fan onto a pairwise smooth fan.
Proof. Consider the fans X, Y and the mapping f of Example 2.5. The fan X is not pairwise smooth, the fan Y is pairwise smooth and the mapping f is light open and quasi monotone. Unfortunately, Y is not contractible, because Y has a zig-zag and a Q−point.
The following questions are still open.
Question 3.19. Does there exist a confluent (or even a light confluent) mapping from a non pairwise smooth fan onto a fan which is contractible?
Question 3.20. Does there exist an open (or even a light open) mapping from a non pairwise smooth fan onto a fan which is contractible?
4. Set function T, contractibility and mappings
Another concept related to contractibility is the set function T. We recall the definition.
Let X be a continuum, the power set of X is defined and denoted by P(X) = {A: A ⊂ X}. The Jones’s set function T: P(X) → P(X) is defined by T(A) = {x ∈ X: for each subcontinuum K of X such that x ∈ int(K), K ∩ A ‡ ∅} for each A ∈ P(X).
On the other hand, a continuum X is said to satisfy the condition (∗) provided that there are two closed subsets H and K of X such that
T(H) ∩ T(K) ‡ ∅, H ∩ T(K) = ∅ and T(H) ∩ K = ∅.
The following theorem gives a relationship between the set function T and contractibility.
Theorem 4.1 ([1, Corollary 1, p.48]). If X is a continuum satisfying condition (∗), then X is not contractible.
To prove the following theorem we need the next proposition given in [9, Corollary 3.1.64, p.167].
Proposition 4.2. Let X and Y be continua and let f : X → Y be a monotone open mapping. If C a subset of Y, then f −1 (T(C)) = T(f −1 (C)).
It is possible to extend the previous result for open almost monotone mappings.
Proposition 4.3. Let X and Y be continua and let f : X → Y be an open almost monotone mapping. If C a subset of Y, then f −1 (T(C)) = T(f −1 (C)).
The following theorem proves that condition (∗) is coinvariant under open almost monotone mappings between continua (dendroids).
Theorem 4.4. Let f : X → Y be an open almost monotone mapping between continua. If Y satisfies condition (∗), then X satisfies the condition (∗). Therefore, X is not contractible.
Proof. Let A and B be closed subsets of Y satisfying (∗). If z ∈ T(A) ∩ T(B), then f −1(z) ⊆ f −1 (T(A) ∩ T(B)) = f−1 (T(A)) ∩ f−1 (T(B)) = T(f−1 (A)) ∩ T(f−1 (B)). Therefore, T(f−1 (A)) ∩ T(f −1 (B)) ‡ ∅.
We can see that f −1 (A)∩T(f −1 (B)) = ∅. Otherwise, if f −1 (A)∩T(f −1 (B)) ‡ ∅, would exist w ∈ f −1 (A) ∩ T(f−1 (B)). Then, f (w) ∈ A and w ∈ T(f−1 (B)) = f −1 (T(B)), thus f (w) ∈ T(B). So, A ∩ T(B) ‡ ∅, a contradiction. Analogously, we prove that f−1 (B) ∩ T(f−1 (A)) = ∅.
So, H = f −1 (A) and K = f −1(B) fulfil condition (∗).
Since every monotone mapping is almost monotone, we have the following result.
Corollary 4.5. Let f : X → Y be an open monotone mapping between continua. If Y satisfies the condition (∗), then X satisfies the condition (∗). Thus, X is not contractible.
Corollary 4.6. Let f : X → Y be an open hereditarily freely decomposable mapping between continua. If Y is a hereditarily decomposable continuum fulfilling the condition (∗), then X satisfies the condition (∗). Therefore, X is not contractible.
Proof. Since Y is a hereditarily decomposable continuum and f is a hereditarily freely decomposable mapping, by [2, Theorem 5.4], f is a monotone mapping. By Theorem 4.4, X satisfies the condition (∗). So, X is not contractible.
Example 4.7. There is a map f : X → Y between dendroids such that f is monotone and not open, Y satisfies the condition (∗) and X is contractible.
Proof. We consider X and Y as in Example 2.11. Observe that f is a monotone mapping and it is not open. Notice that the closed subsets {p} and {q} of Y satisfy the condition (∗). However, X is contractible. Therefore, we need that the mapping f must be open in the Corollary 4.5.
We don’t know if there are dendroids X and Y , and an open mapping non-monotone between them such that Y satisfies the condition (∗) and X does not (or X contractible). Moreover, X is contractible.
Example 4.8. Condition (∗) is not coinvariant between dendroids under light weakly confluent and freely decomposable mappings.
Proof. Example 2.18 shows a light weakly confluent and freely decomposable mapping f between dendroids X and Y such that the closed subsets {o} and {q} of the continuum Y satisfy the condition (∗) and X does not satisfy the condition (∗). Moreover, X is contractible.
Example 4.9. Condition (∗) is not coinvariant between fans under light freely decomposable mappings.
Proof. Example 2.20 shows a light freely decomposable mapping f : X → Y between fans such that the subsets { f (r) } and { f (s) } of the continuum Y satisfies the condition (∗) and X does not.
The following examples show that the condition (∗) is not invariant under the following kind of mappings: light open and quasi monotone; light confluent and strongly freely decomposable, and monotone.
Example 4.10. Condition (∗) is not invariant under light confluent and strongly freely decomposable mappings between fans.
Proof. Example 2.2 shows a light confluent and strongly freely decomposable mapping f between fans X and Y such that the closed subsets {r} and {s} of the continuum X satisfy the condition (∗) while Y does not satisfy the condition (∗), but Y is not contractible.
Example 4.11. Condition (∗) is not invariant under light open and quasi monotone mappings between fans.
Proof. Example 2.5 shows a light open and quasi monotone mapping f between fans X and Y such that the closed subsets {r} and {s} of the continuum X satisfy the condition (∗) but Y does not. However, Y is not contractible.
Example 4.12. The condition (∗) is not invariant under monotone mappings between fans.
Proof. Consider the fans X and Y given in Figure 4, and the decomposition of X whose only nondegenerate element is the arc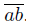 . So, f : X
→ Y is the quotient mapping under this decomposition. Notice that f is a monotone mapping and the closed subsets {a} and {b} satisfy the condition (∗) while Y is contractible.
. So, f : X
→ Y is the quotient mapping under this decomposition. Notice that f is a monotone mapping and the closed subsets {a} and {b} satisfy the condition (∗) while Y is contractible.