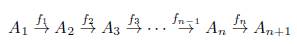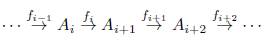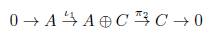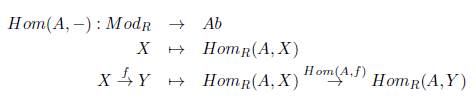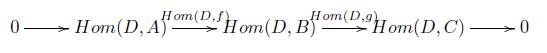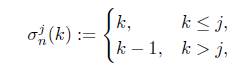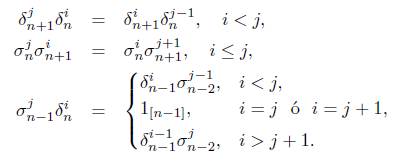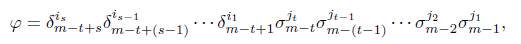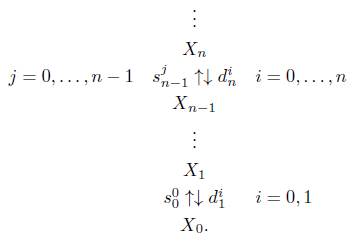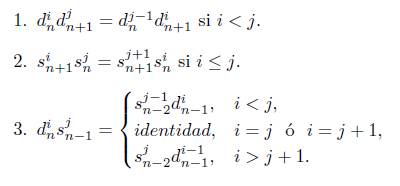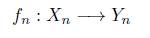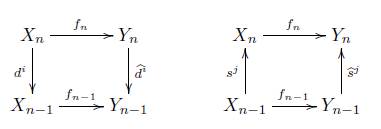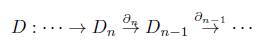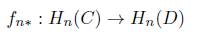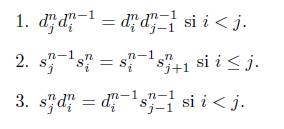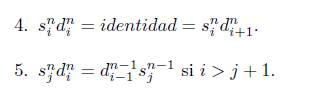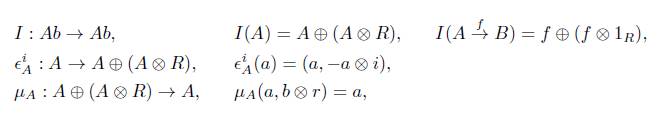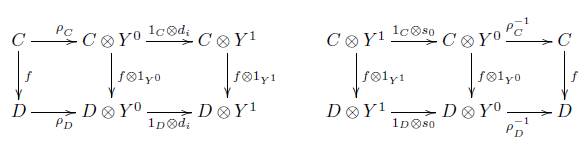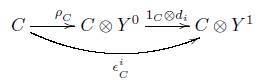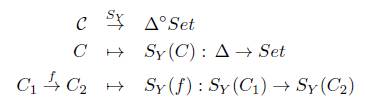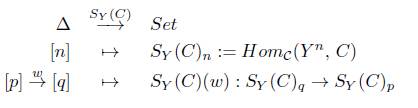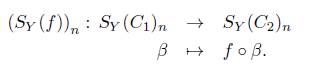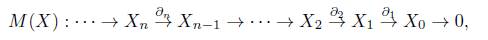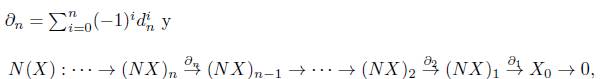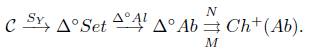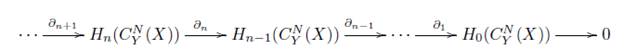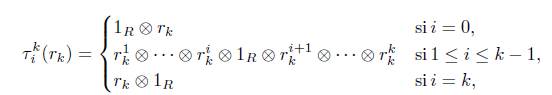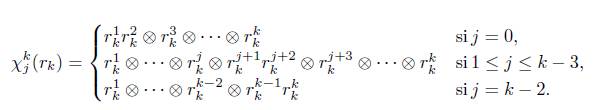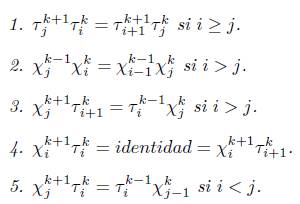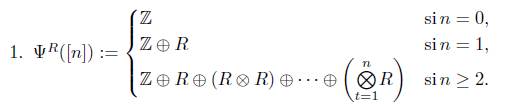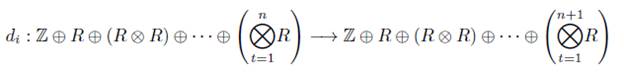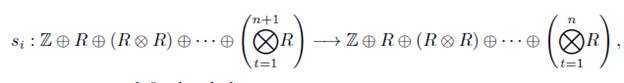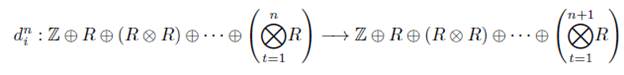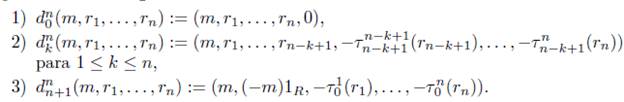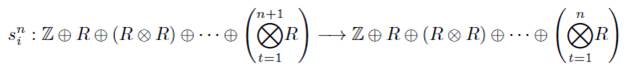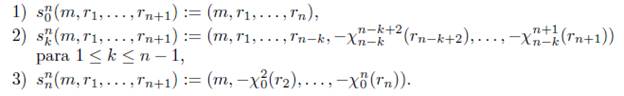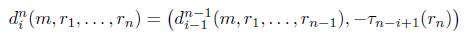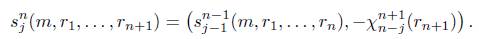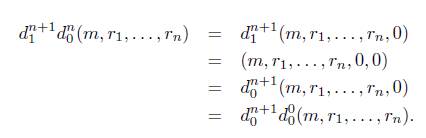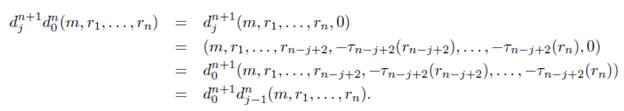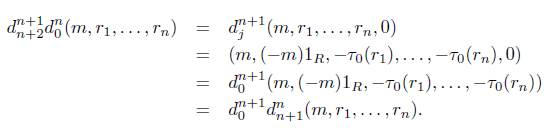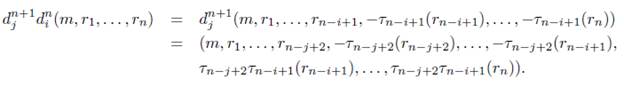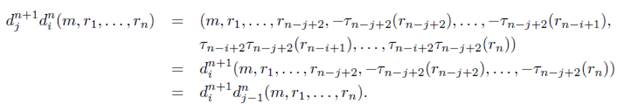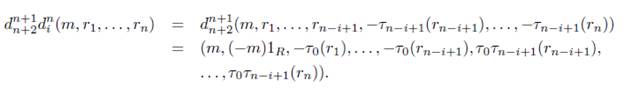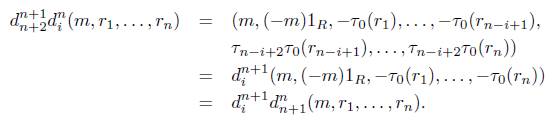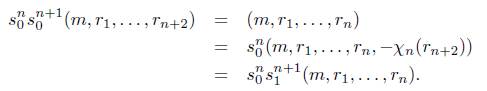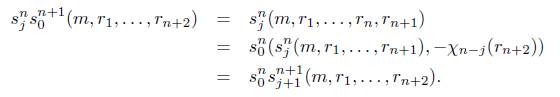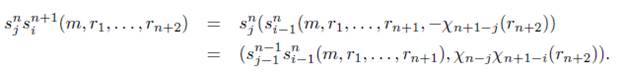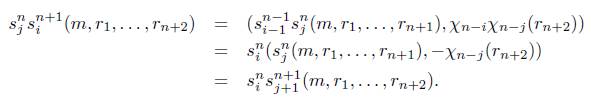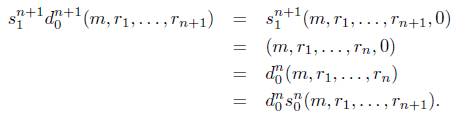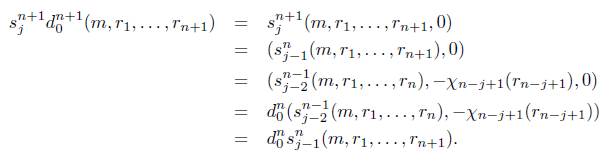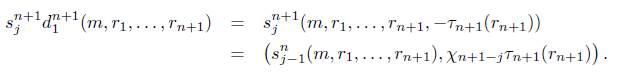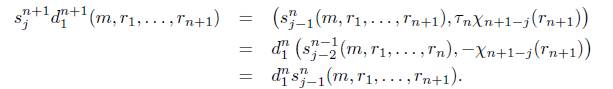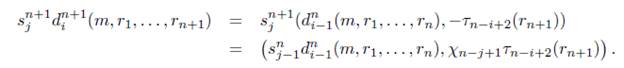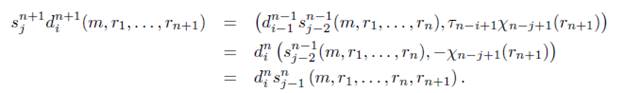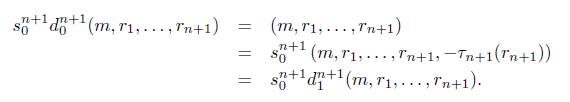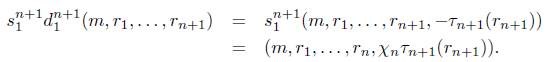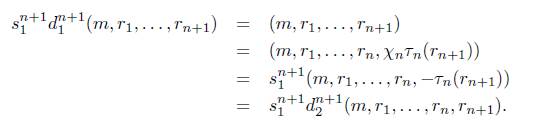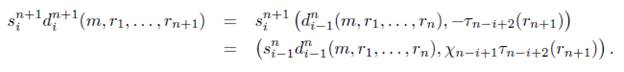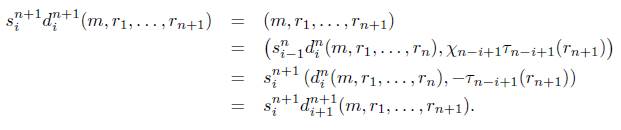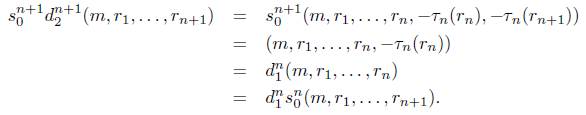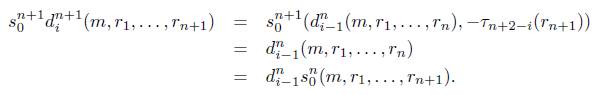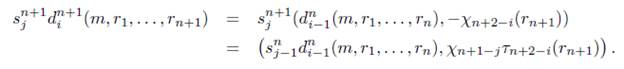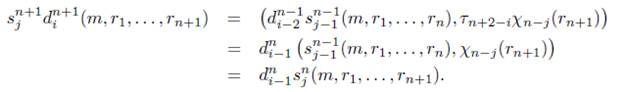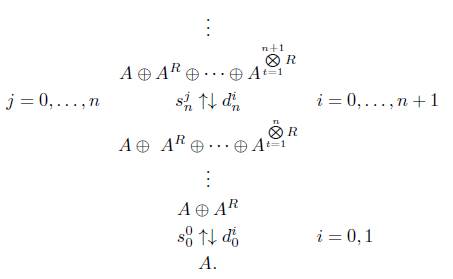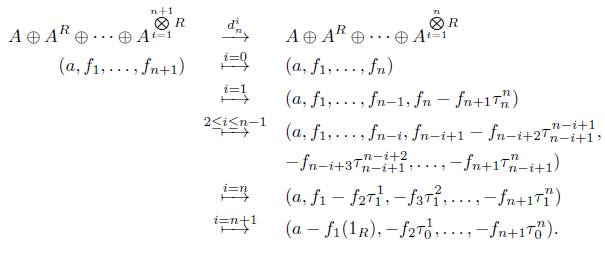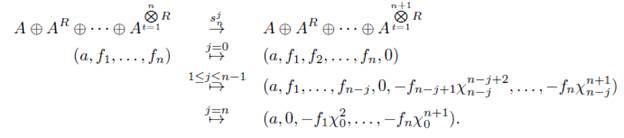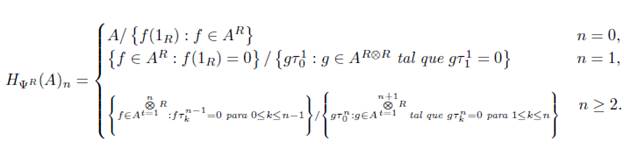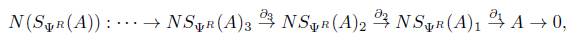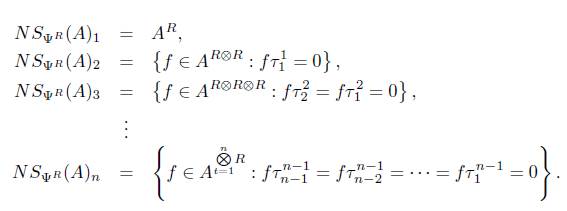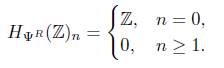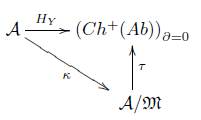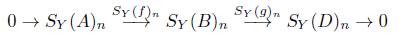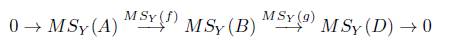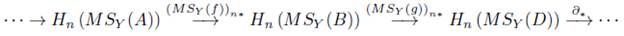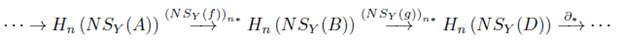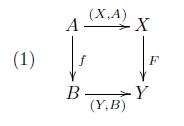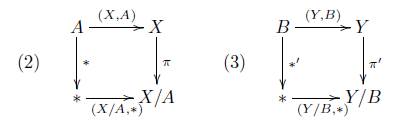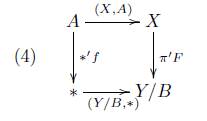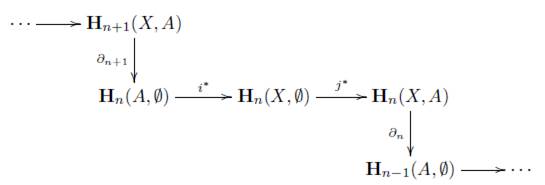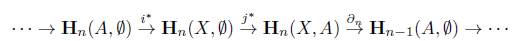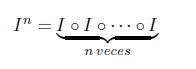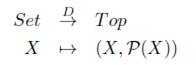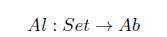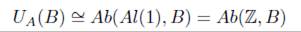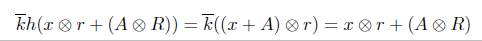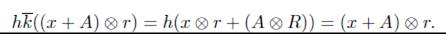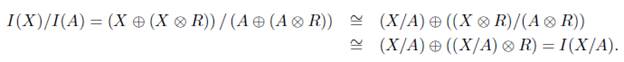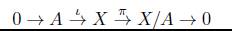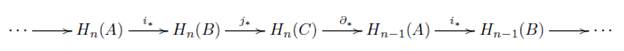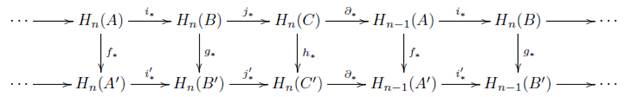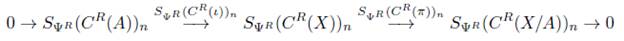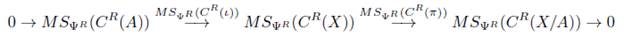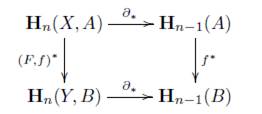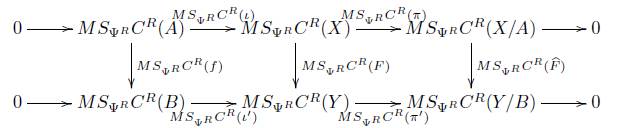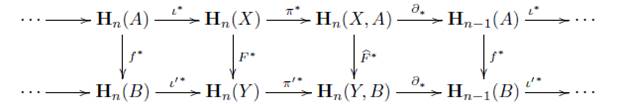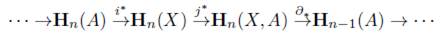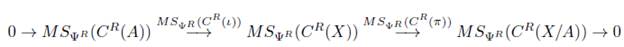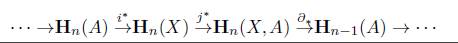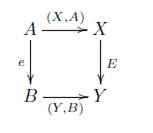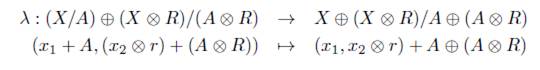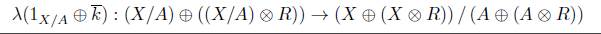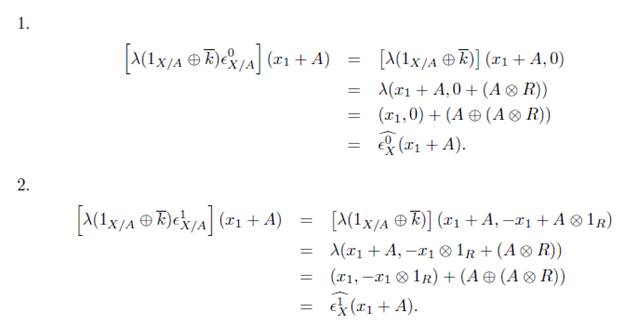1. Introducción
En el trabajo doctoral de R. Ruiz, Change of Models In Algebraic Topology [21], se evidenció que la topología algebraica estaba determinada por un funtor Λ : Δ - Top, que el autor denominó objeto modelo sobre la categoría Top, en el cual Λ ([n]) es el n-simplejo topológico Δn para n = 0,1,..., con el cual se determina la homotopía en Top y por medio del funtor singular del objeto A se obtiene la homología singular la cual cumple el axioma de homotopía de teorías de homologías dado por Eilenberg-Steenrod [9, pág. 111]. Además se mostró que cambiando el modelo A por un funtor covariante F : Δ → Top con la condición de que F([0]) sea un punto, se producen resultados paralelos, algo así como otra topología algebraica. De este trabajo quedó abierta la pregunta de si estos modelos producen, por medio del correspondiente funtor singular, teorías de homología
Posteriormente en el artículo Overview on Models in Homotopical Algebra [20], se extiende y se estudia el concepto de objeto modelo para categorías en general. De nuevo queda abierta la pregunta si con estos objetos modelos se pueden hacer teorías de homología. Sin embargo para definir un concepto análogo al de teoría de homología en categorías no topológicas, es decir en categorías donde sus objetos no son espacios topológicos, era necesario determinar qué es una teoría de homología, para categorias en general, comenzando por el concepto de categoría admisible para homología, tal como se tiene en las teorías de homología en los espacios topológicos [12, pág. 1]. En particular era necesario axiomatizar el concepto de categoría admisible para homología, trabajo desarrollado en el texto Introducción a la Teoría de Homología General [22] en el cual se demuestran las principales consecuencias y está abierto el problema de precisar cuándo un objeto modelo realmente produce una teoría de homología general. Este problema puede enfrentarse de manera general pero las bondades de la categoría misma producen diferencias significativas en la necesidad de la construcción de dicha teoría. Es por esta razón que este trabajo se enfoca en la categoría de los grupos abelianos (Ab), además de la posibilidad de extenderlo a categorías abelianas.
Así pues en este artículo presentamos una teoría de homología general, en el sentido de R. Ruiz [22], en la categoría de los grupos abelianos, definida por medio de lo que llamamos Esqueleto Homoto-Homológico.
2. Preliminares
Definición 2.1. Consideremos Mod R la categoría que tiene por objetos ñ-módulos y por morfismos a los homomorfismos de ñ-módulos, los cuales llamamos ñ-homomorfismos. Una sucesión finita de ñ-homomorfismos
es exacta si Ker(f i + 1) = Im(fi) para i = 1, 2,... ,n - 1. Una sucesión infinita
es exacta si Ker(fi+1) =Im(fi) para todo i Є ℤ.
Una suceción exacta de la forma
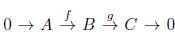 es llamada
sucesión exacta corta.
es llamada
sucesión exacta corta.
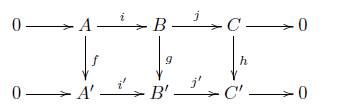
Teorema 2.2 ([11, Tma 1.18. pág. 177]). Consideremos en Mod R la siguiente sucesión exacta corta
entonces las siguientes condiciones son equivalentes.
Existe un R-homomorfismo h : C → B tal que gh = 1 c .
Existe un R-homomorfismo k : B → A tal que kf = 1 a .
La sucesión (1) es isomorfa a la sucesión exacta corta
en particular, B ≅ A ⊕ C.
Una sucesión exacta corta que cumpla las condiciones equivalentes del Teorema 2.2 se dice que se descompone.
Definición 2.3. Se define el funtor Hom(A, -), para A un R-módulo, como sigue:
donde Hom(A,f )(α) = fα, para α Є Hom R (A, X).
Proposición 2.4 ([11, Prop. 4.4, pág. 201]). Sea
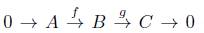 una sucesión exacta de R-módulos que se descompone, entonces la sucesión
una sucesión exacta de R-módulos que se descompone, entonces la sucesión
es exacta y se descompone, para todo R-módulo D.
Definición 2.5. La categoría Δ es aquella en la cual sus objetos son los conjuntos ordenados [n] = {0,1... ,n}, para n ≥ 0. Los morfismos en Δ son las funciones no decrecientes, esto es funciones f : [n] - [m] tales que i < j implica que f (i) ≤ f (j), para 0 ≤ i,j ≤ n.
En la categoría Δ se tienen los monomorfismos δ i n : [n - 1] - [n], para i = 0,... ,n y los epimorfismos σ j n : [n + 1] → [n], para j =0,... ,n dados por
los cuales satisfacen las siguientes propiedades:
Teorema 2.6 ([5, Lema 2.2, pág. 24]). Todo morfismo φ Є Hom Δ ([m], [n]) puede ser escrito como composición de epimorfismos y monomorfismos de forma única como sigue:
donde n = m - t + s y n ≥ i s > ... > i 1 ≥ 0, 0 < j t < ... < j 1 < m.
Definición 2.7.
La categoría de los Conjuntos Simpliciales, denotada como Δ ° Set, es aquella en la que sus objetos son funtores contravariantes X : Δ → Set, donde Set es la categoría de los conjuntos. Los morfismos son transformaciones naturales entre estos funtores.
La categoría de los Grupos Abelianos Simpliciales, denotada como Δ °Ab, es aquella en donde los objetos son funtores contravariantes X : Δ →Ab donde Ab es la categoría de los grupos abelianos. Los morfismos son transformaciones naturales entre estos funtores.
La Definición 2.7 es lo que P. May en [18, pág. 4], denomina como objeto simplicial. Los objetos de la categoría de los Conjuntos Simpliciales (Grupos Abelianos Simpliciales), también pueden ser vistos como una sucesión [Xn}n≥o de conjuntos (grupos abelianos) junto con funciones (homomorfismos) entre ellos como sigue
donde X n = X([n]), d i n = X(δ i n ) y s j n = X(σ n j ), para X un conjunto simplicial (grupo abeliano simplicial), es decir X : Δ → Set (X : Δ → Ab) un funtor contravariante. Estas funciones (homomorfismos) satisfacen las siguientes propiedades, llamadas propiedades combinatorias:
El subíndice n de d i n y s j n se omitirá en la mayoría de los casos, siempre que no haya confusión.
Definición 2.8. Si X y Y son conjuntos simpliciales, se define como función simplicial, digamos f : X → Y, a una familia de funciones
tal que los siguientes diagramas conmutan
para todo n Є ℕ, i = 0,...,n y j =0,...n-1.
Definición 2.9. Denotamos como Δ[n] al conjunto simplicial el cual para q Є ℕ se define Δ [n]q = Hom Δ ([q], [n]), y para f : [p] → [q] un morfismo en la categoría Δ, el morfismo Δ [n](f) : Δ[n]q → Δ[n]p está definido por Δ[n](f)(α) = αf.
Definición 2.10.
1. Un complejo de cadenas D de grupos abelianos, es una familia de grupos abelianos [Dn}nЄ ℤ junto con homomorfismos de grupos como sigue
tales que ∂ n-1 o ∂ n = 0 para todo n Є ℤ. El subíndice n de ∂ n se omitirá en la mayoría de los casos, siempre que no haya confusión.
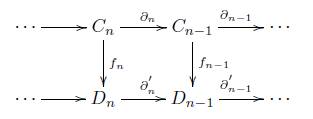
2. Si C y D son complejos de cadenas de grupos abelianos, una transformación de cadenas f : C → D es una familia de homomorfismos {fn: Dn → Cn} n Єℕ tal que el siguiente diagrama conmuta para todo n
3. La categoría Ch(Ab) es aquella en donde los objetos son complejos de cadenas de grupos abelianos y los morfismos son transformaciones de cadenas.
Denotamos como Ch + (Ab) a la categoría la cual sus objetos son complejos de cadenas C positivas, es decir C n = 0 si n < 0 y (Ch+ (Ab)) d=0 a la categoría de cadenas positivas tales que d n : C n → C n-i son homomorfismos nulos para todo n Є ℤ.
Existe en la literatura una definición más general de complejos de cadenas sobre R-módulos, para R un anillo, la cual denotan por Ch(R) o Chain R (ver [10, pág. 40]), más en este trabajo nos enfocamos en el caso de complejos de cadenas sobre ℤ -módulos.
Definición 2.11 (Grupos de Homología). Sea C un complejo de cadenas, entonces los grupos de homología de C están definidos por H n (C) = Ker∂ n /Im∂ n + i para n Є ℤ.
Sea f: C → D una transformación de cadenas, entonces f induce un homomorfismo
como sigue: Sea C n +∂ (Cn+1) Є Hn(C), entonces f n* (cn + ∂ (Cn+1)) = fn(cn)+ ∂ (Dn+1). El subíndice n generalmente se omite de f n* para dar la notación f * : H n (C) → H n (D) siempre que no haya confusión.
3. Objetos modelo para homotopía y homología
Los objetos modelo en una categoría C que se presentan en [20] son importantes en el estudio de homotopía y homología, pues ellos bajo ciertas condiciones, que se presentan en esta sección, pueden generar grupos de homología y una relación de homotopía en la categoría C, por medio de un sistema homotópico en el sentido de [14] y [15].
Definición 3.1. Sea C una categoría. Un objeto modelo sobre la categoría C es un funtor covariante Y: Δ → C, es decir un objeto cosimplicial en la categoría C, para el cual usaremos la notación Y([n]) := Y n , Y(δ i n : [n - 1] → [n]) := d n i y Y(σ n j : [n +1] → [n]) := s n j , similar a conjuntos simpliciales, donde los morfismos δ i n y , para i, j = 0,1,... ,n, son los monomorfismos y epimorfismos, respectivamente, que generan a todos los morfismos de la categoría Δ. Los morfismos d n i y s n j satisfacen las siguientes identidades combinatorias:
El superíndice n de d n i y sn j se omitirá en la mayoría de los casos, siempre que no haya confusión.
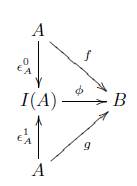
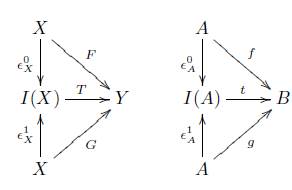
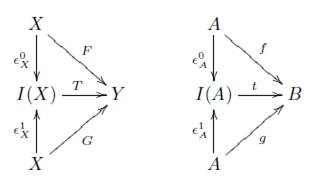
Definición 3.2. Un sistema homotópico en una categoría C, es una cuádrupla η = (I,Є 0 , Є 1 ,μ) donde I: C → C es un funtor covariante, y Є i : 1c - I, μ: I → 1 c son transformaciones naturales tales que μ◦ Є i = 1 para i = 0, 1, donde 1 denota la transformación idéntica 1c → 1c. Sean f,g: A → B dos morfismos en C, entonces decimos que f es η-homótopo a g (f ~η g) si existe un morfismo ∅ : I (A) → B en C tal que el siguiente diagrama conmuta
Ejemplo 3.3. Sea Ab la categoría en donde sus objetos son grupos abelianos y los morfismos son los homomorfismos de grupos abelianos. Dado un anillo unitario R, entonces en Ab existe un sistema homotópico, presentado en [8], dado por
para i = 0,1 y donde ⊗ denota el producto tensorial como ℤ -módulos.
Un objeto modelo sobre una categoría C puede generar un sistema homotópico en C bajo ciertas condiciones que presentamos a continuación.
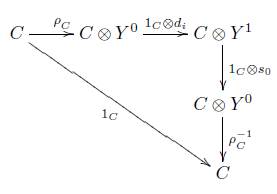
Sea Y: Δ → C un objeto modelo y supongamos que existe un bifuntor (-)⊗ ( -) : C xC → C y existe un isomorfismo p C : C → C⊗ Y 0 natural en C, entonces los siguientes diagramas son conmutativos
Se puede generar entonces un sistema homotópico en la categoría C por medio de un objeto modelo Y : Δ → C como sigue.
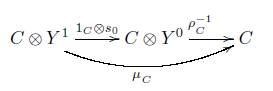
Definición 3.4. Sea Y Δ →C un objeto modelo en la categoría C, ( - ) ⊗ (-): C xC → C un bifuntor y p : (-)→ ( - ) ⊗ Y 0 un isomorfismo natural. Entonces la terna (Y, ⊗,p) induce un sistema homotópico η Y = (I,Є°, Є 1 ,μ) como sigue:
1. I : C → C; donde I(C) = C ⊗ Y 1 y I(f) = f ⊗ 1 y1 .
2. Є i : 1c →I, definido para i = 0,1 por
para C Є ObjC.
3. μ : I → 1c , definido por
para C Є ObjC.
Ejemplo 3.5 (Homotopía en Categorías Monoidales). En una categoría monoidal (M, ⊗, 1) se tiene un bifuntor ⊗: M x M → M, llamado producto tensorial y un objeto identidad 1 el cual cumple que M ⊗ 1 ≅ M naturalmente para todo objeto M en M (ver [4, pág. 21]). Así pues, si se tiene un objeto modelo Y : Δ → M tal que Y 0 = 1, entonces Y genera un sistema homotópico en M.
Los objetos modelos también juegan un papel importante para la construcción de funtores de homología de la forma H : C → (Ch + (Ab)) ∂=0 , los cuales se generan por medio de los grupos de homología en la categoría Ch(Ab) (ver Definición 2.11) y a partir del funtor singular S Y que definimos a continuación.
Definición 3.6 (Funtor Singular). Sea C una categoría y Y : Δ → C un objeto modelo sobre C, entonces el Funtor Singular S Y está dado por
donde
1. Para C un objeto en C, se define el funtor contravariante S y (C) por
y para α Є Sy (C)q se define Sy (C)(ω)(α) = α o Y(ω).
2. Para
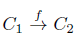 un morfismo en C, la función simplicial S
y
(f) : S
y
(C
1
) 4 S
y
(C
2
) se define por la siguiente familia de funciones
un morfismo en C, la función simplicial S
y
(f) : S
y
(C
1
) 4 S
y
(C
2
) se define por la siguiente familia de funciones
Puesto que para un objeto de Ch(Ab) existen sus grupos de homología y el funtor singular de un objeto modelo Y : Δ → C asigna a un objeto C de C un conjunto simplicial1, para definir grupos de homología de C es necesario un funtor desde la categoría Δ °Set a la categoría Ch(Ab), el cual se construye pasando primero por una categoría que es equivalente a Ch+(Ab), la cual es la categoría de los grupos abelianos simpliciales Δ °Ab.
Para pasar de Δ °Set a Δ ° Ab, considere el funtor Set
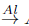 Ab tal que para B un conjunto, Al(B) es el grupo abeliano libre generado por los elementos de B, y para f : A → B una función entre conjuntos, Al(f) : Al(A) 4 Al(B) es el homomorfismo definido por Al(f)( α) = f(α) para todo a perteneciente al conjunto generador A. Así, si X es un conjunto simplicial, es decir un funtor contravariante de Δ a Set, entonces Al o X es un grupo abeliano simplicial, con esto se define un funtor desde la categoría Δ ° Set a Δ ° Ab, denotado por Δ
°
Al, el cual puede ser presentado también de la forma de sucesión, en donde cada nivel del grupo abeliano simplicial es de la forma Al(X
n
) y los morfismos que cumplen las propiedades combinatorias son Al(di) y Al(si).
Ab tal que para B un conjunto, Al(B) es el grupo abeliano libre generado por los elementos de B, y para f : A → B una función entre conjuntos, Al(f) : Al(A) 4 Al(B) es el homomorfismo definido por Al(f)( α) = f(α) para todo a perteneciente al conjunto generador A. Así, si X es un conjunto simplicial, es decir un funtor contravariante de Δ a Set, entonces Al o X es un grupo abeliano simplicial, con esto se define un funtor desde la categoría Δ ° Set a Δ ° Ab, denotado por Δ
°
Al, el cual puede ser presentado también de la forma de sucesión, en donde cada nivel del grupo abeliano simplicial es de la forma Al(X
n
) y los morfismos que cumplen las propiedades combinatorias son Al(di) y Al(si).
Así pues tenemos el funtor
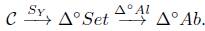 . Ahora para un objeto X en Δ °Ab se tiene la sucesión {Xn}n≥0 donde cada X
n
con n ≥ 0 es un grupo abeliano y también para cada n > 0 se tienen homomorfismos d
i
n
: X
n
→ X
n-1
, para i = 0,1, 2,... ,n, con esto formamos los complejos de cadenas N(X) y M(X), conocidos en la literatura como Complejo de Moore y Complejo Normalizado, respectivamente, dados por
. Ahora para un objeto X en Δ °Ab se tiene la sucesión {Xn}n≥0 donde cada X
n
con n ≥ 0 es un grupo abeliano y también para cada n > 0 se tienen homomorfismos d
i
n
: X
n
→ X
n-1
, para i = 0,1, 2,... ,n, con esto formamos los complejos de cadenas N(X) y M(X), conocidos en la literatura como Complejo de Moore y Complejo Normalizado, respectivamente, dados por
donde
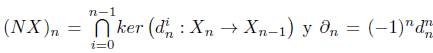 . Por tanto obtenemos dos
. Por tanto obtenemos dos
funtores desde la categoría C a la categoría Ch+(Ab) (un funtor tomando N y otro funtor tomando M) de la siguiente forma
Observación 3.7. El morfismo inclusión i : N(X) → M(X) es una transformación de cadenas la cual es una equivalencia de cadenas (ver [6, Tma 2.4, pág. 150]), entonces los grupos de homología de los complejos M(X) y N(X), para X un grupo abeliano simplicial, son isomorfos (ver [17, Cor 2.2, pág. 40]).
Notación. Denotaremos por C y N a la composición N o Δ ° Al o S y y Cy M a la composición M o Δ° Al o S y , por lo tanto, para un objeto X en la categoría C, se pueden definir grupos de homología de X por medio de los grupos de homología del complejo de cadenas (X), los cuales por la Observación 3.7 son iguales a los grupos de homología del complejo de cadenas Cy 1 (X). Así pues, en algunos casos realizaremos cálculos de grupos de homología por medio del funtor y en otros por medio del funtor Cy M por conveniencia. En particular para objetos modelos Y : Δ → Ab, puesto que S llega a la categoría de los grupos abelianos simpliciales, es decir S : Ab → Δ ° Ab, entonces para estos objetos modelos denotamos por C y N al funtor N o S y y C y N a la composición M o S y .
En particular para objetos modelos Y : Δ → Ab sobre la categoría de los grupos abelianos, al aplicar el funtor singular S a una sucesión exacta que se descompone en Ab, es decir que satisface una de las condiciones del Teorema 2.2, se obtiene por cada nivel n ≥ 0 una sucesión exacta. Este resultado es de interés en este trabajo puesto que por medio de él se define una transformación natural necesaria para teorías de homología general la cual se presenta posteriormente en la sección 8 en la Observación 8.8.
Corolario 3.8. Sea Y : Δ → Ab un objeto modelo y
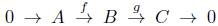 una sucesión exacta en Ab que se descompone, entonces la sucesión
una sucesión exacta en Ab que se descompone, entonces la sucesión
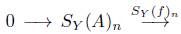
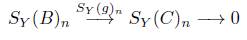 es exacta para todo n ≥ 0.
es exacta para todo n ≥ 0.
Demostración. La sucesión
 es por definición
es por definición
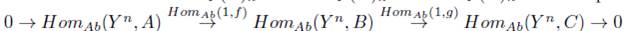 la cual es exacta por la Proposición 2.4, puesto que
la cual es exacta por la Proposición 2.4, puesto que
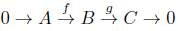 es exacta y se descompone.
es exacta y se descompone.
Definición 3.9. Sea Y : Δ → C un objeto modelo sobre una categoría C, entonces el funtor H y : C → (Ch + (Ab)) ∂=0 , que llamaremos el funtor de homología generado por Y, está definido como sigue:
1. Para un objeto en C, H ( ) es el complejo de cadenas siguiente
donde ∂ n = 0 para todo n.
2. Para f : X → Z un morfismo en la categoría C, H y (f) : Hy (X) → Hy (Z) es la transformación de cadenas tal que H y (f) n = H n (Cp(f)).2
4. Objeto modelo en los grupos abelianos
En esta sección definimos el objeto modelo ΨR en la categoría de los grupos abelianos, la relación de homotopía y grupos de homología que genera, donde la relación de homotopía es igual a la presentada por L. Hernández en su tesis doctoral [13].
Sea R un anillo unitario y consideremos los siguientes homomorfismos de grupos abelianos
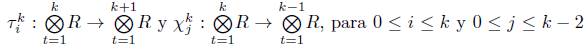 definidos como sigue. Sea
definidos como sigue. Sea
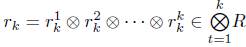 entonces
entonces
Y
Estos homomorismos satisfacen unas identidades las cuales son de importancía para la construcción de el objeto modelo ΨR.
Proposición 4.1 ([7, Prop. 1.39 pág. 57]). Los homomorfismos T i k y x k j satisfacen las siguientes identidades:
A continuación presentamos la aplicación ΨR que posteriormente en el Teorema 4.4 se prueba que es, en efecto, un objeto modelo sobre la categoría Ab.
Definición 4.2. Sea ΨR : Δ → Ab, donde R es un anillo unitario, la aplicación tal que
2. La imagen de los morfismos δ i y σ i presentados en la categoría A son
Y
respectivamente, definidos de la siguiente manera:
a) Para n = 0 definimos d i 0 : ℤ - ℤ ⊕ R, donde d i 0 (m) = (m, (-m i)1 R ) para i = 0,1 y s 0 0 : ℤ ⊕ R → Z, donde s0(m, r) = m.
b) Para n ≥ 1, se define
por casos como sigue:
c) Para n ≥ 1, se define
por casos como sigue:
Observación 4.3. Nótese que para 2 ≤ i ≤ n + 1 y n ≥ 1 se tiene que
y para 1 ≤ j ≤ n se tiene que
s n (m,rk,...,rn+k) = (s n- ^(m,rk,. .. ,rn), -xVji (rn+k)) .
Ahora, con esta observación y la Proposición 4.1, podemos demostrar que la aplicación Ψ R de la Definición 4.2 es un objeto modelo sobre la categoría Ab.
Teorema 4.4. Los morfismos d i n y s n j de 4-2 satisfacen las identidades combinatorias presentadas en 3.1.
Demostración. Actuemos por inducción sobre n.
I. Sea n = 1, entonces
II. Supongamos que se cumple para algún n Є ℕ, verifiquemos para n + 1.
1. Sea j = 1 y i = 0, entonces
Sea i = 0 y 1 < j ≤ n + 1, entonces
Sea i = 0 y j = n + 2, entonces
Sea 0 < i < j ≤ n + 1, entonces
Puesto que i < j, entonces n - i + 1 ≥ n - j + 2, por tanto por el ítem 1 de la Proposición 4.1 se tiene que Tn-j+2Tn-i+i = Tn-i+2Tn-j+2. Luego
Sea 0 < i < j = n + 2, entonces
Puesto n - i + 1 ≥ 0, entonces por el ítem 1 de la Proposición 4.1 se tiene que T 0 T n -i+i = T n -i+ 2 T0, entonces
2. Sea i = 0 = j, entonces
Sea i = 0 < j, entonces
Sea 0 < i < j, entonces
Por hipótesis de inducción
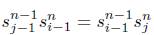 y por el ítem 2 de la Proposición 4.1 se tiene que X
n-
jX
n
+i
-i
= X
n-i
X
n-
j, puesto que j > i implica que n+1 - i > n - j, entonces
y por el ítem 2 de la Proposición 4.1 se tiene que X
n-
jX
n
+i
-i
= X
n-i
X
n-
j, puesto que j > i implica que n+1 - i > n - j, entonces
3. Sea i = 0 y j = 1, entonces
Sea 0 = i < j, entonces
Sea 1 = i < j, entonces
Ahora, puesto que j > 1, tenemos que n > n +1 - j, por lo tanto, por el ítem 3 de la Proposición 4.1, se obtiene que X n + 1 -jT n + 1 = T n Xn+ 1 -j. Luego,
Sea 2 ≤ i < j < n + 2, entonces
Por hipótesis de inducción
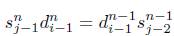 y por el ítem 3 de la Proposición 4.1 se tiene que Xn
_
j+
1
T
n-i+2 = T
n
_
i
+
1
X
n
_
j+
1
. Ya que i < j, tenemos que n - i + 1 > n - j + 1 y luego
y por el ítem 3 de la Proposición 4.1 se tiene que Xn
_
j+
1
T
n-i+2 = T
n
_
i
+
1
X
n
_
j+
1
. Ya que i < j, tenemos que n - i + 1 > n - j + 1 y luego
4. Sea i = 0, entonces
Sea i = 1, entonces
Por el ítem 4 de la Proposición 4.1 se tiene que Xn T n+ 1 = identidad = Xn T n. Luego
Sea 2 ≤ i ≤ n + 1 , entonces
Por hipótesis de inducción s n i - 1 d n i-1 = identidad = s n i - 1 d n i y por el ítem 4 de la Proposición 4.1 se tiene que X n _ i+1 T n _ i+2 = identidad = X n _ i+1 T n _ i+1. Luego
5. Sea i = 2 y j = 0, entonces
Sea i > 2 y j = 0, entonces
Sea i > j + 1 y j > 1, entonces
Por hipótesis de inducción
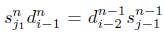 y por el ítem 5 de la Proposición 4.1 se tiene que X
n
+
1
_
j
T
n
+
2
_
j =
T
n
+
2
_
iX
n
_
j. Ya que i > j + 1, tenemos que n + 2 - i < n + 1 - j y luego
y por el ítem 5 de la Proposición 4.1 se tiene que X
n
+
1
_
j
T
n
+
2
_
j =
T
n
+
2
_
iX
n
_
j. Ya que i > j + 1, tenemos que n + 2 - i < n + 1 - j y luego
Así pues la propiedad se cumple para n + 1. Entonces las identidades se cumplen para todo n Є ℕ.
Teorema 4.5. Consideremos el bifuntor (-)⊗ (-) : Ab x Ab → Ab dado por A ⊗ B := A⊗ ℤ B, donde (&% denota el producto tensorial como ℤ -módulos. La relación de homotopía que genera el objeto modelo Ψ r , junto con el bifuntor (-)⊗ (-), por el proceso descrito en 3.4, es la relación de homotopía en Ab descrita en [13].
Demostración. Puesto que (Ψ r ) 0 = ℤ, entonces X⊗(Ψ r ) 0 ≅ X naturalmente para todo grupo abeliano X, por lo tanto Ψ r genera un sistema homotópico ηФ R = (I,Є 0 ,Є 1 ,μ), donde I(X) = X ⊗ (ℤ ⊕ R) ≅ X ⊕ (X ⊗R) ,Є 0 X (x) = (x, 0),Є 1 x (x) = (x, -x ⊗1r) y μ X (x,y ⊗r) = x, el cual es el sistema homotópico descrito en el Ejemplo 3.3, donde la relación de homotopía que genera es la homotopía en la categoría de los grupos abelianos, no trivial, descrita por L. Hernández en su tesis doctoral [13]. 0
A continuación explicitamos la construcción dada en la Definición 3.6 asociada al objeto modelo Y = Ψ
r
definido en 4.2, para ello utilizaremos la notación de tipo exponencial, HomAb(A,B) = B
A
: Sea A un grupo abeliano y R un anillo unitario, entonces
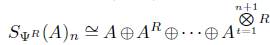
, por tanto obtenemos que SΨ R (A) es el siguiente grupo abeliano simplicial
donde los morfismos d i n para i = 0,...,n +1 y s j n para j = 0,..., n son como sigue:
1. Para
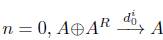 , donde
, donde
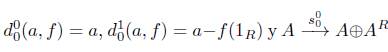 , donde s0
0(α) = (α, 0).
, donde s0
0(α) = (α, 0).
2. Para n ≥ 1
Y
Por la Definición 3.9 tenemos que el objeto ΨR modelo definido en 4.2, genera al funtor de homología HΨr donde HΨr (A) n : = H n (C Ψ N R (A)) = Ker(∂ n )/Im(∂ n+1 ), donde ∂ n : = ( -1) n d n n para d n n definido por el grupo abeliano simplicial SΨr (A) el el ítem 1 al inicio de esta sección. Veamos pues los grupos de homología que genera el objeto modelo para un grupo abeliano A, grupos de homología introducidos en este trabajo, los cuales presentamos en el siguiente teorema.
Teorema 4.6. Sea A un grupo abeliano y R un anillo unitario, entonces
Demostración. Sea A un grupo abeliano y R un anillo unitario, entonces aplicando el funtor N : Δ°Ab → Ch+(Ab) al grupo abeliano simplicial SФ,r(A), se obtiene el siguiente complejo de cadenas
Donde
y
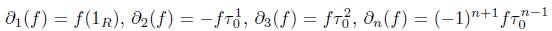 para todo n ≥ 3, con lo cual se tiene el resultado.
para todo n ≥ 3, con lo cual se tiene el resultado.
Ejemplo 4.7.
1. Sea R un cuerpo, entonces
2. Consideremos R = ℚ y A = ℚ / ℤ. Afirmación: todo objeto en ℚ ⊗ ℚ es de la forma r ⊗ 1 para r Є ℚ. En efecto, consideremos p
(g> J un elemento del conjunto generador de ℚ ⊗ ℚ, entonces
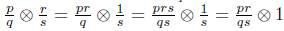 . Análogamente también se prueba que en ℚ ⊗ ℚ se tiene que r ⊗ 1 = 1 ⊗ r, para todo r Є ℚ. Así pues, si un homomorfismo g : ℚ ⊗ ℚ → ℚ / ℤ satisface que gt
1
1
= 0, entonces gt
1
0
= 0, por lo tanto HΨr (ℚ / ℤ)
1
= {f Є ( ℚ / ℤ) ℚ
: f (1) = 0} con lo cual obtenemos HΨr (ℚ / ℤ)
1
= 0, puesto que la proyección canónica π : ℚ → ℚ / ℤ dada por π(r) = r + ℤ, para r Є ℚ, está en el conjunto {f Є (ℚ / ℤ)
ℚ
: f (1) = 0} y no es el homomorfismo nulo.
. Análogamente también se prueba que en ℚ ⊗ ℚ se tiene que r ⊗ 1 = 1 ⊗ r, para todo r Є ℚ. Así pues, si un homomorfismo g : ℚ ⊗ ℚ → ℚ / ℤ satisface que gt
1
1
= 0, entonces gt
1
0
= 0, por lo tanto HΨr (ℚ / ℤ)
1
= {f Є ( ℚ / ℤ) ℚ
: f (1) = 0} con lo cual obtenemos HΨr (ℚ / ℤ)
1
= 0, puesto que la proyección canónica π : ℚ → ℚ / ℤ dada por π(r) = r + ℤ, para r Є ℚ, está en el conjunto {f Є (ℚ / ℤ)
ℚ
: f (1) = 0} y no es el homomorfismo nulo.
Observación 4.8. En [13] se define lo siguiente: Sea i : ℤ → R el homomorfismo de grupos abelianos dado por i(1 ℤ)= 1r y sea S = Coker(i), por tanto S = R/i(ℤ), donde i(ℤ) es el grupo abeliano generado por 1R, es decir i(ℤ) = {n1 R \n Є ℤ }. Se define
y con esto el n-ésimo grupo de homotopía π n (A) = [⊗ n S, A] R para un grupo abeliano A, donde [A, B] R = HomAb(A, B)/ η para η el sistema homotópico presentado en el ítem 3 del Ejemplo 3.3. Así pues tenemos que π 0 (A) = [ℤ, A] R . Posteriormente en este trabajo, en el Teorema 6.8, se demuestra que HΨr (A) 0 ≅ π 0 (A).
5. Esqueletos homoto-homológicos
Definición 5.1. Un Esqueleto Homoto-Homológico en una categoría A consiste de lo siguiente:
1. Un objeto modelo Y : Δ → A.
2. Una relación de homotopía ~ que sea compatible con la composición; es decir, si f, g : A → A' y f', g' : A → A" son tales que f ∼ g y f' ∼ g', entonces f’f ∼g'g.
3. Un funtor H: A → (Ch+ (Ab)) ∂=0 tal que si dos morfismos f, g son tales que f ∼ g, entonces H(f) =H(g).
Por ejemplo, la relación ∼ puede ser definida por medio del sistema homotópico n Y presentado en 3.4, si existe, o definida por medio del funtor H y : A → (Ch + (Ab)) ∂=0 definido en 3.9. 3. Como funtor H podemos considerar H= H y : A → (Ch + (Ab)) ∂=0 definido en 3.9, en el caso que este funtor sea invariante bajo la relación ∼, es decir que cumpla la condición exigida en 3 de la Definición 5.1. Usaremos la abreviación (A,Y, ∼ , H) para referirnos a esqueletos homoto-homológicos sobre la categoría A.
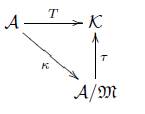
En [2] se deine una relación de homotopía en una categoría A por medio de la categoría de cocientes (A/ ℳ, k) (o llamada también en [5] como categoría de fracciones de A por M), donde A/ ℳ es una categoría con los mismos objetos de A y k : A → A/ ℳ es un funtor covariante que preserva los objetos de A y satisface las siguientes dos condiciones:
1. Si α Є ℳ, entonces K(α) es invertible en A/ ℳ, es decir K(α) es un isomorfismo en A/ ℳ.
2. Si T : A →K es un funtor, donde K es una categoría cualquiera, tal que T(α) es invertible para todo α Є M, entonces existe un único funtor t : A/ ℳ → K tal que T = t o k, es decir que el siguiente diagrama conmuta
Dada una categoría A cualquiera y ℳ una clase arbitraria de morfismos en una categoría A, entonces en [2, Tma 1.1, pág. 240] demuestran que la categoría cociente (A/ ℳ,k) existe. Con esto, definen M-homotopía en A como sigue: Dos morfismos f,g : A → B en A son llamados M-homótopos (f ℳ g) si y sólo si n(f) = n(g).
Observación 5.2. Si F : A → C es un funtor covariante cualquiera, se define la familia de morfismos ℳ (F) := {f Є A | F(f) es invertible en C}, por tanto existe la categoría cociente (A/ ℳ (F), k) la cual genera la relación ℳ(F) en A. Ahora, dado un objeto modelo Y : Δ → A, entonces por la Definición 3.9 existe el funtor de homología
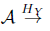 (Ch
+
(Ab))
∂=0
el cual genera entonces la relación
(Ch
+
(Ab))
∂=0
el cual genera entonces la relación
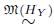 en la categoría A.
en la categoría A.
Veamos que el funtor H
Y
es invariante bajo la relación
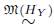 en A.
en A.
Teorema 5.3. Dado un objeto modelo Y sobre la categoría A y f,g : A → B morfismos en A tales que f es ℳ (Hy)-homótopo a g, entonces Hy(f) = Hy(g).
Demostración. Por definición ℳ (H Y ) = {f G A | Hy(f) es invertible en (Ch+ (Ab)) d=0 ], entonces existe un único funtor t : A/ ℳ - (Ch + (Ab)) ∂=0 tal que el siguiente diagrama conmuta
Luego, por otro lado, puesto que f es ℳ (Hy)-homótopo a g, entonces K(f) = K(g) y por tanto TK(f) = TK(g), es decir, H y (f) = H y (g).
Así pues, dado un objeto modelo Y sobre A, entonces
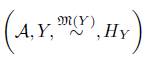 es un Esqueleto Homoto-Homológico.
es un Esqueleto Homoto-Homológico.
5.1. Esqueletos homoto-homológicos en categorías simpliciales
En [6, pág. 81] se define categoría simplicial, a una categoría C para la cual existe un bifuntor Hom c : C x C → Δ° Set con las siguientes propiedades para A y B objetos en C:
1. Hom C (A,B) 0 = Hom C (A, B).
2. Cada funtor Hom c (A, •) : C → Δ° Set tiene un adjunto a izquierda A⊗ C • : Δ°Set → C el cual es asociativo en el sentido que existe un isomorfismo A⊗ C (K x L) ≅ (A ⊗ C K) ⊗ C L natural en A ЄC y K, L Є Δ°Set.
3. Cada funtor Hom c (•, B) : C op → A°Set tiene un adjunto a izquierda homc(•, B) : Δ°Set → C op .
Ahora, si una categoría simplicial C tiene objeto final *, entonces en C se puede obtener un Esqueleto Homoto-Homológico, como lo muestra el siguiente corolario.
Corolario 5.4. Sea C una categoría simplicial con objeto final * y Y : Δ → C el objeto modelo definido por Y
n
= *⊗
C
Δ[n]4, Y(δ
i
n
) = 1* ⊗
C
d
n
i
e Y(σ
j
n
) = 1* ⊗
C
s
n
j
, para d
n
i
y s
n
j
definidas por (d
n
i
)
p
(α) = δ
n
i
α y (s
j
n
)
p
(β) = σ
n
j
β, donde α Є HomΔ([p], [n - 1]) y β Є HomΔ([p], [n +1]), entonces
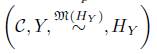 es un Esqueleto Homoto-Homológico.
es un Esqueleto Homoto-Homológico.
Demostración. Dado que Y es un objeto modelo en C, entonces por el Teorema 5.3 se obtiene el resultado. 0
Por lo visto en la Observación 5.2 se tiene que un objeto modelo Y : Δ→ A genera una relación de homotopía por medio de la categoría cociente A/M y con lo visto en la Definición 3.4, Y genera bajo ciertas condiciones un sistema homotópico en A, el cual a su vez define una relación de homotopía. Queda aquí pues abierta la pregunta de que tipo de relación hay entre estas dos relaciones de homotopía.
6. Esqueleto homoto-homológico en Ab
En la categoría de los grupos abelianos, existe la relación de homotopía presentada por L. Hernández en su tesis doctoral (ver [13]), la cual utilizó para definir los grupos de homotopía para un grupo abeliano, entre otras cosas. Por tanto, dada la importancia de esta relación de homotopía, en este trabajo se presentará un Esqueleto Homoto-Homológico en Ab para el cual la relación ~ de la propiedad 2 de la Definición 5.1, sea la descrita en [13], la cual es generada por medio del objeto modelo Ψ R , definido en 4.2. Ahora, este modelo genera el funtor de homología HΨr (ver Definición 3.9), al cual se le hizo una modificación a los objetos de la categoría de partida, es decir a los grupos abelianos.
Para R un anillo unitario, en [8, pág. 163] se define una relación de homotopía en la categoría de los grupos abelianos dada como sigue: Sean f,g : A → B homomorfismos de grupos abelianos, entonces se dice que f es nulo-homótopo
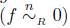 si existe una función bilineal F : A x R → B tal que F(α, 1
R
) = f (α), para todo α Є A. Luego f es homótopo a g (f ≅R
g) si y sólo si
si existe una función bilineal F : A x R → B tal que F(α, 1
R
) = f (α), para todo α Є A. Luego f es homótopo a g (f ≅R
g) si y sólo si
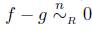 .
.
Ahora, sea A un grupo abeliano, entonces A ≅Hom Ab (ℤ, A), así pues se puede definir una relación en A por medio de la relación ≅ R en HomA b (ℤ, A) como sigue.
Definición 6.1. Sea A un grupo abeliano y α
i
,α
2
Є A, entonces
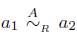 si y solo si ψ
a1
≃
R
ψ
a2
, donde ψ
ai
: ℤ → A es el homomorfismo de grupos abelianos dado por ψ
ai
(n) = nα
i
, para i = 1, 2. Así pues
si y solo si ψ
a1
≃
R
ψ
a2
, donde ψ
ai
: ℤ → A es el homomorfismo de grupos abelianos dado por ψ
ai
(n) = nα
i
, para i = 1, 2. Así pues
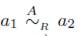 si y sólo si existe una función bilineal F : ℤ x R → A tal que F(n, 1
R
) = n(α
1
- α
2
), para todo n Є ℤ.
si y sólo si existe una función bilineal F : ℤ x R → A tal que F(n, 1
R
) = n(α
1
- α
2
), para todo n Є ℤ.
Puesto que la relación ≃
R
es de equivalencia, entonces
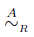 también lo es. Usaremos la notación ∿
R
en cambio de
también lo es. Usaremos la notación ∿
R
en cambio de
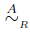 , cuando se entienda el grupo abeliano A.
, cuando se entienda el grupo abeliano A.
Tomando la operación del grupo A, el conjunto {f(1 R ) : f Є HomAb(R,A)} es un subgrupo de A. Este subgrupo es de interés aquí, pues él es el que determina la relación ∿ R , lo cual mostramos en la siguiente proposición:
Proposición 6.2. Sea A un grupo abeliano y α 1 , α 2 Є A, entonces α 1 ∿ R α 2 si y sólo si α 1 - α 2 Є{f (1r) : f Є HomAb(R A)}. Así pues A/ ∿r ≅ A/{f (1r) : f Є HomAb(R A)}.
Demostración. (⇒) Supongamos α 1 ∿ R α 2 , entonces existe una función bilineal F : ℤ x R → A tal que F(n, 1 R ) = n(α 1 - α 2 ), para todo n Є ℤ, la cual induce un homomorfismo f : R → A dado por f(r) = F(1 ℤ ,r). Puesto que F es bilineal, entonces f es homomorfismo de grupos. Así pues f (1 R ) = F(1 ℤ, 1 R ) = α 1 - α 2 . Por lo tanto α 1 - α 2 Є {f (1r) : f Є HomAb(R, A)}.
(⇐) Supongamos ahora α 1 - α 2 Є A tales que α 1 - α 2 Є {f(1 R ) : f Є HomA b (R,A)}, entonces existe un homomorfismo de grupos abelianos f : R → A tal que f (1 R ) = α 1 - α 2 . Considere la aplicación F : ℤ x R → A dada por F(n, r) := nf (r). Así pues F es bilineal y F(n, 1r) = nf (1 R ) = n(α 1 - α 2 ), por lo tanto α 1 ∿ R . 0
De la Proposición 6.2 podemos ver que para el caso que HomA b (R, A) = 0 entonces el grupo abeliano A/ ∿ R es el mismo grupo abeliano A.
La relación de homotopía ≃ R en HomA b (A, B), presentada en [13], induce el grupo HomA b (A, B)/ ≃ R , el cual en [13, pág. 37] lo denotan por [A, B] R . Por otro lado, puesto que HomAb(A, B) es un grupo abeliano entonces tenemos el grupo abeliano HomA b (A, B)/ ∿ R . El siguiente teorema nos muestra que estos grupos abelianos son isomorfos.
Teorema 6.3. Sean A y B grupos abelianos y f,g Є HomAb(A, B), entonces f ≃ R g si y sólo si f ≅r g. Así pues [A,B]r = HomAb(A,B)/ . ∿R.
Demostración. (⇒) Supongamos que f ≃
R
g, entonces
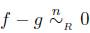 , es decir que existe una función bilineal F : A x R → B tal que F(α, 1R) = (f - g)(a). Considere ahora la función G : ℤ x R → HomA
b
(A, B) donde G(n,r) = F o in
r, donde i
n
r
: A → A x R es la función definida por i
n
r
(α) := (n a, r). La función G es bilineal. Ahora G(n, 1R)(α) = F(n α, 1R) = (f - g)(n a) = n(f - g)(a), para todo α Є A, entonces G(n, 1R) = n(f - g), es decir f ∿
R
g.
, es decir que existe una función bilineal F : A x R → B tal que F(α, 1R) = (f - g)(a). Considere ahora la función G : ℤ x R → HomA
b
(A, B) donde G(n,r) = F o in
r, donde i
n
r
: A → A x R es la función definida por i
n
r
(α) := (n a, r). La función G es bilineal. Ahora G(n, 1R)(α) = F(n α, 1R) = (f - g)(n a) = n(f - g)(a), para todo α Є A, entonces G(n, 1R) = n(f - g), es decir f ∿
R
g.
(⇐ ) Supongamos que f ∿ R g, entonces existe una función bilineal G : ℤ x R → HomAb(A, B) tal que G(n, 1R) = n(f - g). Considere ahora la función F : A x R → B definida por F(α, r) = G(1 Z , r)( α). La función F es bilineal. En efecto, F (α 1 + α 2 ,r) = G(1 ℤ ,r)( α 1 + α 2 ) = G(1 ℤ ,r)( α 1 ) + G(1 ℤ ,r)( α 2 ) = F (α 1 ,r) + F (α 2 ,r) y F(α,r 1 + r2) = G(1 ℤ, r 1 + r2 )( α) = [G(lz,n) + G(1 ℤ,r2)]( α) = G(1 ℤ,n)( α) + G(lz,r2)( α) = F (α,r 1 ) + F (α,r 2 ).
Así pues se obtiene que el homomorfismo identidad l : HomA b (A, B) → HomA b (A, B) pasa al cociente 1 : [A, B] R → HomAb(A, B)/ ∿ R , es decir [A, B] R = HomA b (A, B)/ ∿ R .
Teorema 6.4. Sea f : A → B un homomorfismo de grupos abelianos. Si α 1 ∿ R α 2 , entonces f (α 1 ) ∿ R f (α 2 ).
Demostración. Si α 1 ∿ R α 2 , entonces ψα 1 ≃ R ψ α 2, luego puesto que la relación ≃ R es representada por un sistema homotópico, entonces fψ α 1 ≃ R fψ α 2 es reflexiva (ver [19, Lema 2.3, pág. 4]). Ahora ψ f(ai) (n)= nf (α 1 ) = f (n α 1 ) = f (ψ ai ,(n)) = fψ ai ,(n), asípues, si ai ∿r α 2 entonces ψ f (α 1 ) ≃r ψf(α 2 ), por lo tanto f (α 1 ) ∿r f (α 1 ).
Con lo anterior tenemos que todo homomorfismo de grupos abelianos f : A → B pasa al cociente por ∿ R , por tanto se tiene el homomorfismo de grupos abelianos [f] R : A/ ∿ R → B/ ∿ R donde [f]R ([α]A) = [f (α)] B . Entonces definimos el siguiente funtor.
Definición 6.5. Se define el endofuntor C R : Ab →Ab por C R (A) = A/ ∿ R , para A un grupo abeliano y C R (f) = [f] R , para f un homomorfismo de grupos abelianos.
Teorema 6.6. Sean f,g : A → B homomorfismos de grupos abelianos. Si f ∿ R g, entonces C R (f) = C R (g).
Demostración. Supongamos f ≃
R
g, entonces existe una función bilineal F : A x R → B tal que F(α, 1
R
) = (f - g)(α), para todo a Є A. Consideremos la función
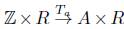 , para cada α Є A, donde T
α
(n,r) = (n α,r). La función FT
a
es bilineal, más aún, se tiene que FTa(n, Ir) = F (n α, Ir) = (f - g)(na) = nf (α) - ng(α) = n(f (α) - g(α)), por tanto f(a) ∿ g(α) para cada a Є A, es decir C
R
(f)(a) = C
R
(g)( α) en B/ ∿, entonces C
R
(f )= C
R
(g). 0
, para cada α Є A, donde T
α
(n,r) = (n α,r). La función FT
a
es bilineal, más aún, se tiene que FTa(n, Ir) = F (n α, Ir) = (f - g)(na) = nf (α) - ng(α) = n(f (α) - g(α)), por tanto f(a) ∿ g(α) para cada a Є A, es decir C
R
(f)(a) = C
R
(g)( α) en B/ ∿, entonces C
R
(f )= C
R
(g). 0
Observación 6.7. Para el objeto modelo ΨR sobre la categoría Ab, se obtuvo por el Teorema 4.6 que HΨr (A) 0 = A/{f (Ir) : f Є HomA b (R, A)}, es decir que HΨr (A) 0 ≅ C R (A), para todo grupo abeliano A y en [13] se define el grupo cero de homotopía por π 0 (A) = [ℤ,A]r, para A un grupo abeliano. Veamos que π 0 (A) = HΨr(A) 0 .
Teorema 6.8. Sea A un grupo abeliano, entonces no(A) ≅ HΨr(A) 0 .
Demostración. En [13] definen π 0 (A) = [ℤ,A] R , luego por el Teorema 6.3 tenemos que [ℤ, A] R ≅ HomA b (ℤ, A)/ ∿. Por otro lado, existe un isomorfismo φ : A → HomA b (ℤ, A), luego puesto que C R es un funtor entonces C R (φ) : A/ ∿ → HomA b (ℤ, A)/ ∿ es un isomorfismo, es decir A/ ∿ ≅ HomA b (ℤ, A)/ ∿. Por último, por la Observación 6.7 tenemos que C R (A) = HΨr(A) 0 . Así pues con lo anterior obtenemos n 0 (A) = [ℤ,A] R = HomAb(Z,A)/ ∿ ≅ A/ ∿≅ HyR (A) 0 .
El funtor C R preserva sucesiones exactas que se descomponen en Ab, propiedad que mostramos en la siguiente proposición.
Proposición 6.9. Consideremos una sucesión exacta corta en
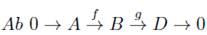 que se descompone, entonces la sucesión corta en
que se descompone, entonces la sucesión corta en
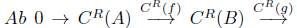 C
R
(D) → 0 es exacta y se descompone.
C
R
(D) → 0 es exacta y se descompone.
Demostración. Para la exactitud hay tres cosas por demostrar:
1. (C R (f) es monomorfismo) Puesto que la sucesión se descompone, entonces f es una sección y por tanto C R (f) es una sección, además toda sección es un monomorfismo. Así pues C R (f) es un monomorfismo.
2. (C R (g) es epimorfismo) Afirmación; si g es epimorfismo, entonces C R (g) es también un epimorfismo. En efecto, sea [d] Є D/ ~, donde d Є D, puesto que g es sobreyectiva, entonces existe un b Є B tal que g( b) = d, por tanto [g(b)] = [d], luego CR(g)(b) = [g(b)], asípues C R (g)(b) = [d].
3. (Ker (C
R
(g)
)
= Im((C
R
(f)
)
) Puesto que la sucesión
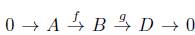 se descompone, entonces por el corolario 3.8 la sucesión
se descompone, entonces por el corolario 3.8 la sucesión
es exacta para todo n ≥ 0 . Ahora al aplicar el funtor M : Δ°Ab → Ch + (Ab) obtenemos la sucesión
en Ch+(Ab), la cual es exacta por niveles para cada n ≥ 0. Así pues obtenemos que la sucesión
es exacta para todo n ≥ 0 (ver [1, Theorem 1.3, pág. 6], la cual por la Observación 3.7 es igual a la sucesión
Así pues Ker ((NS Y (g)) n* ) = Im ((NS Y (f )) n* ). Ahora si tomamos Y = Ψ R y n = 0, entonces por la Observación 6.7 obtenemos que KerC R (g) = ImC R (f).
Puesto que C
R
(f) es una sección, entonces la sucesión exacta
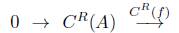
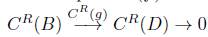 se descompone.
se descompone.
Así pues con el funtor C
R
y H
y
para un objeto modelo Y : Δ → Ab (ver Definición 3.9) se tiene el funtor
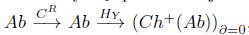 , este funtor satisface que si f ≃
R
g en Ab, lo cual es equivalente a que
, este funtor satisface que si f ≃
R
g en Ab, lo cual es equivalente a que
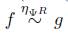 (Teorema 4.5), entonces H
y
C
R
(f) = H
y
C
R
(g) (Teorema 6.6), para R un anillo unitario. Así pues tomando a Y como el objeto modelo Ψ
R
, entonces tenemos el siguiente teorema.
(Teorema 4.5), entonces H
y
C
R
(f) = H
y
C
R
(g) (Teorema 6.6), para R un anillo unitario. Así pues tomando a Y como el objeto modelo Ψ
R
, entonces tenemos el siguiente teorema.
Teorema 6.10. Sea Ψ
R
el objeto modelo definido en 4.2, entonces
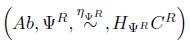 es un Esqueleto Homoto-Homológico en Ab.
es un Esqueleto Homoto-Homológico en Ab.
7. Teoría de homología general
En [22] se define lo que es una Teoría de Homología General, empezando con lo que es una Categoría Admisible para Homología en una categoría C, con objeto inicial 0 y con un sistema homotópico n. Con ello muestra los resultados que se obtienen para teoría de homología general. Para dar claridad al artículo, presentamos en esta sección las definiciones fundamentales para teoría de homología general presentadas en [22], para con esto mostrar posteriormente una teoría de homología general en la categoría de los grupos abelianos, utilizando el esqueleto homoto-homológico
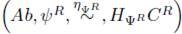 del Teorema 6.10. Si para el lector es de interés el conocer más propiedades de las teorías de homología general, se pueden consultar en [22].
del Teorema 6.10. Si para el lector es de interés el conocer más propiedades de las teorías de homología general, se pueden consultar en [22].
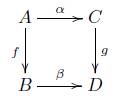
Definición 7.1. Consideremos C una categoría. Se define la categoría Mor (C) por:
1. Los objetos de Mor (C) son los morfismos de C,
2. Un morfismo entre f y g es una pareja (β, α), donde α : A → C y β : B → D son morfismos en C tales que el siguiente diagrama conmuta
3. Sean (β 1 , α 1 ) : f → g y β 2 , α 2 ) : g → h, morfismos en Mor (C), la composición está dada por (β 2 , α 2) (β 1 , α 1): = (β 2 β 1, α 2 α 1 ).
Consideremos de ahora en adelante a (C, η) como una categoría C con objeto inicial 0 único y η = (I, Є0 , Є 1 , μ) un sistema homotópico en C tal que I(0) = 0.
Definición 7.2 (Categoría de Parejas). Llamaremos por categoría de parejas V a una subcategoría cualquiera de Mor (C) que cumpla lo siguiente:
1. Para cada par de objetos A y B de C, existe a lo más un único morfismo α : A → B, es decir no existe otro morfismo de C como objeto en V con el mismo dominio y codominio de a.
2. V es cerrada para composiciones, es decir si α Є Home (A, B) y β Є Home (B, C) son objetos en V, entonces βα es un objeto en V.
3. Para cada objeto X en C, se tiene que el morfismo identidad 1 X : X → X y el morfismo 0 → X (el cual es único por 0 ser objeto inicial) son objetos en V.
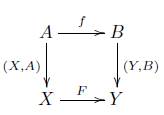
Notación. Sea α : A → X un objeto de V. Puesto que solo existe un morfismo en V con dominio A y codominio X, entonces denotamos este objeto como (X,A). Así pues con esta notación tenemos que para dos objetos (X, A) y (Y, B) en la categoría V, un morfismo (F, f) : (X,A) → (Y, B) en V es una pareja F : X → Y, f : A → B de morfismos de C tales que el siguiente diagrama conmuta
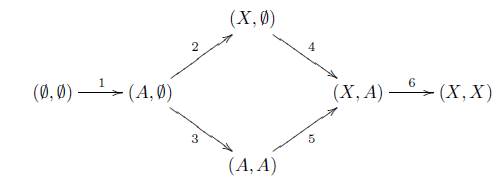
Definición 7.3 (Diagrama de (X, A)). Sea (X, A) un objeto en V, entonces se define el diagrama de (X,A), denotado por D(X,A), a
en donde los morfismos del 1 al 6 son los evidentes. Por ejemplo, (X, A) es un morfismo α : A → X en C, entonces el morfismo 5 es (α, 1a).
Con las definiciones anteriores se abre paso a la definición de Categoría Admisible.
Definición 7.4 (Categoría Admisible para Homología). Sea V una categoría de parejas sobre una categoría (C,n). Se dice que V es una categoría esencialmente admisible para homología si satisface las siguientes condiciones:
(AC1) Si (X,A) es un objeto en V, entonces V contiene a D(X,A).
(AC1) Si (X,A), (Y,B) GV y (F, f) : (X,A) → (Y, B) es un morfismo en V, entonces todos los morfismos inducidos por (F, f), desde los miembros de D(X,A) a los correspondientes miembros de D(Y, B) están en V.
(AC1) Si (X,A) Є V, entonces I(X, A) = (I(X),I(A)) está en V, donde I es el funtor del sistema homotópico n que acompaña a C.
Si V es una categoría esencialmente admisible para homología y además admite al menos un objeto (*, 0), donde * es un objeto final y 0 el objeto inicial en la categoría C, entonces se dice que V es una categoría admisible para homología.
Para V una categoría admisible para homología, a los objetos de V se les llama admisibles y a los morfismos de V morfismos admisibles.
Ejemplo 7.5 (La categoría de pares topológicos). Consideremos la categoría de los espacios topológicos con la homotopía usual. Sea Top par la categoría en la cual los admisibles son las parejas topológicas (X,A), es decir las inclusiones A → X, para A un subespacio de X. Los morfismos entre dos admisibles (X,A) y (Y, B) son todas las funciones continuas f : X →Y que satisfacen f (A) ⊆ B. Así pues Top par satisface las condiciones (AC1)-(AC3) y admite el morfismo 0 → *, donde * es un espacio singleton, por tanto Top par es un categoría admisible para homología.
Con la relación de homotopía generada por el sistema homotópico n en la categoría C, se puede definir también una relación de homotopía en una categoría admisible V sobre la categoría (C,η), la cual presenta [22] de la siguiente manera.
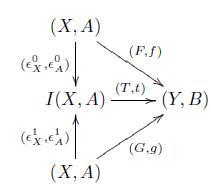
Definición 7.6 (Homotopía en Categorías Admisibles). Sean V una categoría admisible para homología sobre una categoría (C, η) y (F, f), (G,g) : (X,A) → (Y, B) morfismos admisibles en V, entonces decimos que (F,f) es n homótopo a
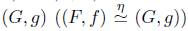 si existe un morfismo admisible (T, t) : I(X, A) → (Y, B) tal que el siguiente diagrama conmuta
si existe un morfismo admisible (T, t) : I(X, A) → (Y, B) tal que el siguiente diagrama conmuta
es decir, que los siguientes diagramas son conmutativos
En [22] se define el objeto cociente en una categoría como sigue.
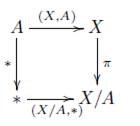
Definición 7.7. Sea V una categoría de parejas sobre una categoría C con objeto final * y (X, A) un objeto en V, entonces definimos el cociente X/A por medio del siguiente diagrama cocartesiano
siempre y cuando exista.
Observación 7.8. En la categorías de parejas Top par del Ejemplo 7.5, el cociente definido en 7.7 coincide con el cociente de espacios topológicos.
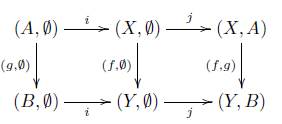
Para el caso de un morfismo (F, f) : (X, A) → (Y, B) en una categoría de parejas se cumple una propiedad de isomorismo entre cocientes, propiedad demostrada en este trabajo y presentada en la siguiente proposición.
Teorema 7.9. Sea V una categoría de parejas sobre una categoría C con objeto final * y supongamos el siguiente diagrama es cocartesiano
entonces X/A ≅ Y/B, siempre y cuando existan estos cocientes.
Demostración. Por la Definición 7.7 tenemos que los siguientes diagramas son cocartesianos
luego componiendo el diagrama (1) con el diagrama (3) obtenemos el siguiente diagrama
el cual es cocartesiano. Por tanto tenemos que (2) y (4) son cocartesianos, entonces X/A ≅ Y/B. 0
Definición 7.10 (Escisión Categórica). Un morfismo (E,e) : (X,A) → (Y,B) en V es una escisión categórica si el siguiente diagrama es cocartesiano
Definición 7.11. En D(X,A), definido en 7.3, la composición
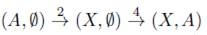 será llamada la descomposición esencial de (X,A) con notación genérica
será llamada la descomposición esencial de (X,A) con notación genérica
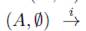
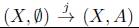 y que denotaremos por E(X,A). Para un morfismo (f,g) : (X,A) → ( Y, B) su diagrama esencial es el siguiente
y que denotaremos por E(X,A). Para un morfismo (f,g) : (X,A) → ( Y, B) su diagrama esencial es el siguiente
el cual denotaremos por E(f,g).
Ahora, consideremos una categoría admisible para homología V sobre (C ,η) y H : V → Ch(Ab) un funtor covariante, entonces H induce los funtores H n : V → Ab y PR n : V - Ab, donde H n (X,A) = H(X,A) n , PR n (X,A) = H(A, 0) n , para (X,A) un objeto en V y Hn(F,f) = (F,f )n, PRn(F,f) = (f, 1 0 )n, para (F,f) un morfismo en V, para cada n Є ℤ, donde H(X, A) n es n-ésimo grupo abeliano del complejo de cadenas H(X, A) y (F, f )n = H(F, f) n . Al funtor PR n lo llamaremos proyección n-ésima de H.
Para las teorías de homología generales, como en las teorías de homología en espacios topológicos, se pide la existencia de una transformación natural ∂ n : H n → PR n_1 para cada n Є ℤ, para la cual tenemos entonces la siguiente sucesión
Así pues con el anterior breve resumen se abre paso a la definición de teoría de homología general, presentada en [22].
Definición 7.12 (Teoría de Homología General). Sea V una categoría admisible para homología sobre una categoría (C, η) y H: V → Ch(Ab) un funtor covariante. Decimos que H es una teoría de homología general si satisface los siguientes axiomas:
1. Axioma de Exactitud. Si (X,A) es un objeto en V, entonces
es una sucesión exacta.
2. Axioma de Homotopía. Sean (F, f), (G,g) : (X,A) → (Y, B) morfismos en P tales que
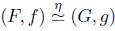 , entonces H(F,f) =H(G,g).
, entonces H(F,f) =H(G,g).
3. Axioma de Dimensión. Si n = 0, entonces H n (*, 0) = 0, para todo admisible (*, 0), donde * es un objeto final en C.
4. Axioma de Escisión. Si (E,e) : (X,A) → (Y,B) es una escisión categórica, entonces H(E,e) es un isomorfismo. Más aún H(X/A) ≅ H(Y/B), si X/A y Y/B existen.
Nota. Toda categoría C con objeto inicial y final se puede cambiar para todo propósito en C igual que
 pero con un solo objeto inicial 9 y un solo objeto final * y trabajar con
pero con un solo objeto inicial 9 y un solo objeto final * y trabajar con
 .
.
8. Teoría de homología general en Ab
Presentaremos una categoría de parejas en la categoría de los grupos abelianos (Ab) desarrollada en este trabajo, la cual utilizaremos posteriormente para mostrar una teoría de homología general en la categoría Ab.
Definición 8.1. Definimos la categoría Ab inj como sigue:
1. Consideramos como objetos admisibles los siguientes morfismos
a) Para todo grupo abeliano A, consideramos el morfismo 0 → A y el morfismo identidad 1a : A → A.
b) Las inclusiones A → X, donde A es un ℤ -módulo inyectivo.
c) Para las inclusiones i : A → X del ítem anterior, consideramos también como admisibles a I n (i : A → X), para n Є ℤ +, donde
para I el funtor cilindro del sistema homotópico en Ab mostrado en el ítem 4 del Ejemplo 3.3, el cual I(f : X → Y) = f ⊕ (f ⊗1r), para f un homomorfismo de grupos abelianos.
2. Como morfismos entre objetos admisibles (X, A) y (Y, B), consideramos los morfismos en la categoría Mor(Ab) entre estos objetos, es decir una pareja de homomor-fismos de grupos abelianos (F, f) : (X, A) → (Y, B) tal que f (A) ⊂ B y f = F|a.
Consideremos el funtor H: Ab inj → (Ch + (Ab)) ∂=0 definido por medio del funtor de homología HΨr, presentado explícitamente en el Teorema 4.6, como H(X,A) = HΨr (C R (X/A)), donde C R es el funtor definido en 6.5. Para (F, f) : (X, A) → (Y, B) un morfismo en Ab inj definimos H(F, f) := HΨr (C r (F)), el cual denotamos por (F, f )*, donde el homomorfismo F : X/A - Y/B es dado por F(x + A) = F(x) + B.
Nótese que H(X, 0) = HΨr (C(X)), por tanto a las parejas de la forma (X, 0) las denotaremos solo por X, para X un grupo abeliano. Así pues un morfismo f : X → (Y,B) es un morfismo de la forma (f, 0) : (X, 0) → (Y,B), donde f es un homomorfismo de X a Y. Por lo visto en la sección 7 tenemos los funtores H n y PR n .
8.1. Dimensión
Teorema 8.2. H n (0) = 0 para todo n ≥ 0.
Demostración. Por definición H n (0) = HΨr(C R (0)) n , luego C R (0) = 0 y por el Teorema 4.6 tenemos que HΨr (0) n = 0 para todo n ≥ 0, entonces H n (0) = 0 para todo n ≥ 0.
Toda teoría de homología general H debe satisfacer que H n (X,X) = 0 para todo n (ver [22, pág. 47]), luego en Ab se tiene que H n (*) = H n (*, 0) = 0 puesto que * = 0 = 0, donde * es el objeto final y 0 es el objeto inicial, lo cual quiere decir que toda teoría de homología H en Ab sería una homología reducida. En busca de una teoría de homología general no reducida en Ab nos vemos en la necesidad de cambiar el axioma de dimensión en el sentido de que * no sea el objeto final pero sin alterar lo establecido en teorías de homología en la categoría Top. Nótese lo siguiente; el funtor olvido U T : Top → Set es representable (ver [16, Proposición 4.1.11, pág. 87]) puesto que tiene como adjunto a izquierda al funtor
donde V( X) denota partes de X, es decir la topología discreta, así pues tenemos que U T (X) ≅ Top(D(l), X), para X un espacio topológico y donde 1 es un conjunto uni-puntual y en Top el objeto D(1) coincide con el objeto inicial, lo cual no sucede en la categoría Ab. El funtor olvido Ua : Ab → Set tiene como adjunto a izquierda el funtor abeliano libre
así pues tenemos
por tanto en Ab, tomamos * = ℤ, luego por el ítem 1 del Ejemplo 4.7 tenemos que la homología no es reducida, en el caso que R sea un cuerpo. Por otra parte, pensando en el cálculo de los grupos de homotopía, tomando * = Z, se presenta una diicultad en la construcción de las esferas por suspensión, puesto que se requiere de un morfismo único S
n-1
→ * para generar S
n
, partiendo de S
0
= * + * = ℤ ⊕ ℤ, donde + denota la suma categórica, así pues estudiamos actualmente la categoría Ab ℤ, en donde
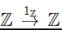 es el objeto inal, el cual es diferente al objeto inicial el cual es el morismo 0 - ℤ.
es el objeto inal, el cual es diferente al objeto inicial el cual es el morismo 0 - ℤ.
8.2. Exactitud y escisión
Lema 8.3. Sea X un grupo abeliano y A un subgrupo de X, entonces
1. I(X/A) ≅ I(X)/I(A).
2. Si A es un ℤ -módulo inyectivo, entonces I(i : A → X) = i : I(A) → I(X), donde i es el monomorfismo inclusión.
Demostración.
1. Consideremos la aplicación h : (X ⊗R)/(A ⊗ R) → (X/A) ⊗ R, donde h(x ⊗ r +(A ⊗ R)) = (x+A) ⊗r. Veamos que h está bien definida. Supongamos x\⊗r\ + (A⊗ R) = x 2 ⊗r 2 + (A ⊗R), entonces tenemos los siguientes casos:
a) Si r 1 = r 2 , entonces x 1 - x 2 Є A, por tanto (x 1 + A) ⊗ r 1 = (x 2 + A) ⊗r 2 .
b) Si r 1 = r 2 , entonces x 1 ,x 2 Є A, por tanto (x 1 + A) ⊗ r 1 = 0 = (x 2 + A) ⊗ r2.
Por otro lado, consideremos la aplicación k : (X/A) x R - (X ⊗ R)/(A ⊗ R), donde k(x + A, r) = x ⊗ r + (A ⊗ R). Veamos que k está bien definida. Supongamos (x 1 + A,r i ) = (x 2 + A,r 2 ), entonces tenemos que x 1 + A = x 2 + A y r 1 = r 2 , por tanto (x 1 - x 2 ) ⊗ r 1 + (A ⊗ R) = 0 + (A ⊗ R), es decir x 1 ⊗ r 1 + (A ⊗ R) = x 2 ⊗ r 2 + (A ⊗ R).La función k es una función bilineal. En efecto, k((x 1 + A) + (x 2 + A), r) = k((x 1 + x 2 ) + A,r) = (x 1 + x 2 ) ⊗ r + (A ⊗R) = (x i ⊗r + x 2 ⊗r) + (A ⊗ R) = (x 1 ⊗ r +(A ⊗ R)) + (x2 ⊗ r + (A ⊗ R)) = k((xi + A),r) + k((x2 + A),r) y k(x + A,r 1 + r 2 ) = x ⊗ (r 1 + r 2 ) + (A ⊗ R) = (x ⊗ r1+ x ® r2) + (A ⊗ R) = (x ⊗ri + (A ⊗ R)) + (x ® r2 + (A ⊗R)) = k(x + A, ri) + k(x + A,r 2 ).
Así pues, existe un homomorfismo de grupos abelianos k : (X/A) ⊗ R → (X ⊗ R)/(A ⊗ R), tal que k((x + A) ⊗ r) = k(x + A, r). Ahora
y
Por lo tanto k es un isomorfismo, es decir (X/A) ⊗ R ≅ (X ⊗ R)/(A ⊗ R). Entonces tenemos lo siguiente
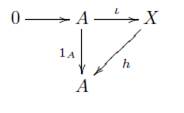
2. Puesto que la inclusión i : A → X es monomorfismo, entonces la sucesión 0 → A X es exacta, ahora puesto que A es inyectivo, entonces existe un homomorfismo de grupos abelianos h : X → A tal que el siguiente diagrama conmuta
Así pues i : A → X es una sección, por lo tanto i ⊕ (i ⊗ 1 r ) es una sección, luego toda sección es monomorfismo, entonces i ⊕ (i ⊗ 1 r ) es un monomorfismo, más aún I (i)(a, b ⊗ 1r ) = [i ⊕ (i ⊗ 1r )] (a, b ⊗ r) = (a,b ⊗ r), para (a,b ⊗ r) Є A ⊕ (A ® R), por tanto I(i) : A ⊕ (A ⊗ R) → X ⊕ (X ⊗ R) es el monomorfismo inclusión. 0
Teorema 8.4. Sea (X,A) un objeto en Ab inj , entonces la sucesión exacta
se descompone, donde i es el monomorfismo inclusión y π la proyección canónica.
Demostración. Sea (X,A) un objeto en Ab inj, entonces tenemos los siguientes casos:
1. Si A = 0, entonces tenemos la sucesión
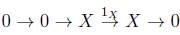 , la cual es exacta y se descompone.
, la cual es exacta y se descompone.
2. Si A = X, es decir (X,A) = (A, A) = 1a, entonces tenemos la siguiente sucesión
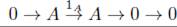 , la cual es exacta y se descompone.
, la cual es exacta y se descompone.
3. Si A = 0 es un ℤ -módulo inyectivo, entonces la sucesión exacta
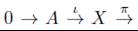
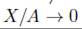 se descompone (ver [11, Prop. 3.13, pág. 197]).
se descompone (ver [11, Prop. 3.13, pág. 197]).
4. Si (X,A) = I
n
(X',A'), para algún n ≥ 0, donde A' es un ℤ -módulo inyectivo y X un grupo abeliano que contiene a A , entonces tenemos por el ítem 3 que la sucesión exacta
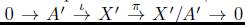 se descompone, entonces existe un homomorfismo z : X' → A' tal que zi = 1a' . Luego por el ítem 2 del lema 8.3, puesto que A es un Z-módulo inyectivo, tenemos que I(i : A' → X') = i : I(A') - I(X'), entonces I
n
(i : A' → X') = i : I
n
(A') - I
n
(X'), por tanto I
n
(z)i = I
n
(z)I
n
(i) = 1¡n(x). Así pues tenemos que la sucesión exacta
se descompone, entonces existe un homomorfismo z : X' → A' tal que zi = 1a' . Luego por el ítem 2 del lema 8.3, puesto que A es un Z-módulo inyectivo, tenemos que I(i : A' → X') = i : I(A') - I(X'), entonces I
n
(i : A' → X') = i : I
n
(A') - I
n
(X'), por tanto I
n
(z)i = I
n
(z)I
n
(i) = 1¡n(x). Así pues tenemos que la sucesión exacta
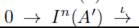
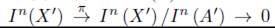 se descompone, es decir que la sucesión exacta
se descompone, es decir que la sucesión exacta
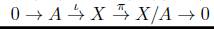 se descompone.
se descompone.
Observación 8.5. Sea
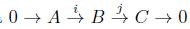 una sucesión exacta en Ch(Ab). Entonces un conjunto de homomorfismos ∂
n
* : H
n
(C) → H
n-1
(A) es definido en [1, pág. 5] como sigue: Los elementos de H
n
(C) tienen la forma c
n
+ ∂C
n
+
1
, donde ∂c
n
= 0. Puesto que j
n
es un epimorfismo, existe un b Є B
n
tal que j
n
(b
n
) = c
n
. Así pues j
n-1
(∂b
n
) = ∂ (j
n
b
n
) = ∂c
n
= 0 y por la exactitud en la n-ésima posición existe un an-1
Є A
n-1
, para el cual i
n
-
1
(a
n
-i) = ∂b
n
. Por tanto definimos ∂
n
* (c
n
+ ∂C
n
+
1
) = a
n-1
+ ∂A
n
. El símbolo ∂* será escrito en lugar de ∂
n
*
una sucesión exacta en Ch(Ab). Entonces un conjunto de homomorfismos ∂
n
* : H
n
(C) → H
n-1
(A) es definido en [1, pág. 5] como sigue: Los elementos de H
n
(C) tienen la forma c
n
+ ∂C
n
+
1
, donde ∂c
n
= 0. Puesto que j
n
es un epimorfismo, existe un b Є B
n
tal que j
n
(b
n
) = c
n
. Así pues j
n-1
(∂b
n
) = ∂ (j
n
b
n
) = ∂c
n
= 0 y por la exactitud en la n-ésima posición existe un an-1
Є A
n-1
, para el cual i
n
-
1
(a
n
-i) = ∂b
n
. Por tanto definimos ∂
n
* (c
n
+ ∂C
n
+
1
) = a
n-1
+ ∂A
n
. El símbolo ∂* será escrito en lugar de ∂
n
*
Teniendo en cuenta este conjunto de homomorfismos ∂ n * : H n (C) → H n-1 (A), en [1] demuestran los dos siguientes teoremas (8.6 y 8.7), los cuales son de importancia en este trabajo, puesto que definen la transformación natural a utilizar para la teoría de homología general que estamos construyendo en la categoría Ab.
Teorema 8.6. Si
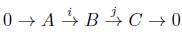 es una sucesión exacta en Ch(Ab), entonces la sucesión
es una sucesión exacta en Ch(Ab), entonces la sucesión
es exacta en Ab.
Teorema 8.7. En el diagrama de complejos de cadenas
sean las sucesiones exactas y cada diagrama conmutativo, entonces el siguiente diagrama
en Ab
es conmutativo.
Observación 8.8. Sea (X,A) un objeto en Ab
inj
. Entonces, por el Teorema 8.4, la sucesión exacta
 se descompone. Luego, por la Proposición 6.9, la sucesión
se descompone. Luego, por la Proposición 6.9, la sucesión
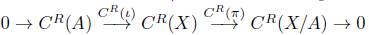 es exacta y se descompone en Ab y, por el Corolario 3.8, la sucesión
es exacta y se descompone en Ab y, por el Corolario 3.8, la sucesión
es exacta para todo n ≥ 0. Así pues, al aplicar el funtor M obtenemos la sucesión exacta en Ch+ (Ab)
entonces por la Observación 8.5 se tiene un conjunto de homomorfismos ∂* :H n (X,A) →U n-1 (A, 0).
Veamos que efectivamente ∂* : H n (X,A) →H n-1 (A) es transformación natural.
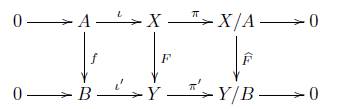
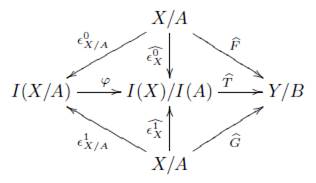
Proposición 8.9. Sea (F, f) : (X,A) → (Y,B) un morfismo en Ab inj , entonces el siguiente diagrama es conmutativo
Demostración. Puesto que (F, f) es un morfismo en Ab inj , entonces tenemos en Ab el siguiente diagrama conmutativo
en el cual las flechas horizontales forman sucesiones exactas. Aplicando el funtor MSΨrC R obtenemos en Ch+(Ab) el siguiente diagrama conmutativo
donde las flechas horizontales forman sucesiones exactas (Obs. 8.8), y por el Teorema 8.7 el siguiente diagrama es conmutativo
A continuación mostramos que el funtor H : Ab inj → Ch+(Ab) satisface el axioma de exactitud y posteriormente el axioma de escisión.
Teorema 8.10. Considere (X,A) un objeto en Ab inj y E(X,A), definido en 7.11, entonces
es una sucesión exacta.
Demostración. Para (X, A) tenemos que E(X, A) es la sucesión
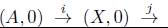 (X, A), donde i es el homomorfismo inclusión de A a X y j es el homomorfismo identidad del objeto X. Así pues i* = HΨr (C
R
(i))
n
y j* = HΨr (C
R
(n))
n
, para los morfismos i y π del Teorema 8.4. Luego por la Observación 8.8 tenemos que la sucesión
(X, A), donde i es el homomorfismo inclusión de A a X y j es el homomorfismo identidad del objeto X. Así pues i* = HΨr (C
R
(i))
n
y j* = HΨr (C
R
(n))
n
, para los morfismos i y π del Teorema 8.4. Luego por la Observación 8.8 tenemos que la sucesión
es exacta en Ch+ (Ab), por tanto, aplicando el Teorema 8.6, obtenemos que la sucesión
es exacta en Ab. 0
Teorema 8.11. Si (E, e) : (X, A) → (Y, B) es una escisión categórica en Ab in j, entonces H(E,e) es un isomorfismo.
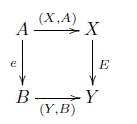
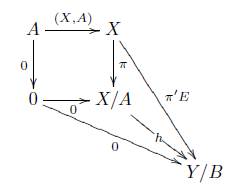
Demostración. Por definición tenemos que
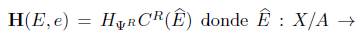 - Y/B es dado por E(x + A) = E(x) + B, por otro lado por la Definición 7.10 tenemos el siguiente diagrama cocartesiano
- Y/B es dado por E(x + A) = E(x) + B, por otro lado por la Definición 7.10 tenemos el siguiente diagrama cocartesiano
Ahora, por la Proposición 7.9 tenemos que X/A ≅ Y/B, donde el isomorfismo h : X/A → Y/B es definido por medio del siguiente diagrama conmutativo
es decir h(x + A) = hπ(x) = π'E(x) = E(x) + B, entonces h =
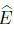 . Por lo tanto
. Por lo tanto
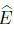 es un isomorfismo, entonces HΨrC
r
(
es un isomorfismo, entonces HΨrC
r
(
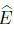 ) es un isomorfismo, es decir H(E, e) es un isomorfismo.
) es un isomorfismo, es decir H(E, e) es un isomorfismo.
8.3. Invarianza homotópica del funtor H
El objeto modelo Ψ r genera un sistema homotópico η = (I,Є 0 ,Є 1 ,μ) por medio de la Definición 3.4, utilizando como bifuntor ⊗: CxC → C el producto tensorial de Z-módulos, entonces I(X) = X ⊕ (X ⊗ R), Є 0 X (x) = (x, 0), Є 1 X (x) = (x, -x⊕ 1 R ) y μ X (x, y ⊗ r) = x) y este sistema homotópico define la relación de homotopía en Ab descrita en [13] (Teorema 4.5). Así pues (Ab, η) define una relación de homotopía en Ab inj por medio de la Definición 7.6, la cual cumple el siguiente teorema.
Teorema 8.12. Sean (F, f), (G,g) : (X,A) → (Y,B) morfismos en la categoría Ab
in
j, tales que
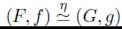 , entonces H(F, f) =H(G,g).
, entonces H(F, f) =H(G,g).
Demostración. Por hipótesis tenemos que
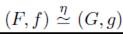 , entonces existe un morfismo admisible (T,t) : I(X,A) → (Y,B) en Ab
in
j tal que los siguientes diagramas conmutan
, entonces existe un morfismo admisible (T,t) : I(X,A) → (Y,B) en Ab
in
j tal que los siguientes diagramas conmutan
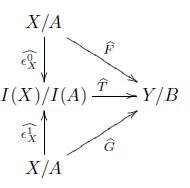
entonces el siguiente diagrama conmuta
Ahora, de la teoría de grupos tenemos que el homomorfismo λ : X 1 /A 1 ⊕ X 2 /A 2 - (X 1⊕X 2 )/(A 1⊕A 2 ) dado por A(x 1 +A 1 ,x 2 +A 2 ) = (x 1 ,x 2 ) + (A 1⊕A 2 ) es un isomorfismo, donde Ai es un subgrupo del grupo abeliano X i para i = 1, 2. Por tanto
es un isomorfismo. En la prueba del ítem 1 del lema 8.3 se mostró que el homomorfismo
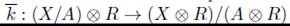 es un isomorfismo, por lo tanto
es un isomorfismo, por lo tanto
es un isomorfismo. Ahora nótese lo siguiente
Por lo tanto el siguiente diagrama es conmutativo
donde
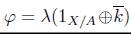 . Entonces
. Entonces
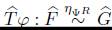 , luego puesto que
, luego puesto que
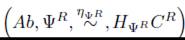 es un Esqueleto Homoto-Homológico (Teorema 6.10) entonces
es un Esqueleto Homoto-Homológico (Teorema 6.10) entonces
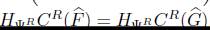 , por lo tanto H
n
(F, f) =H
n
(G,g), para todo n ≥ 0, es decir H(F, f) =H(G,g).
, por lo tanto H
n
(F, f) =H
n
(G,g), para todo n ≥ 0, es decir H(F, f) =H(G,g).