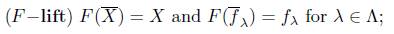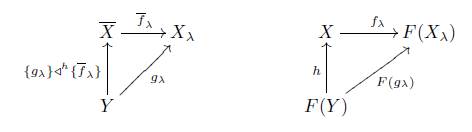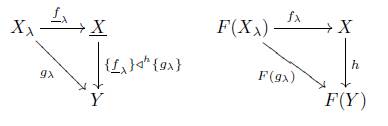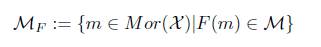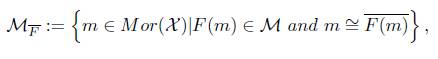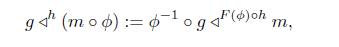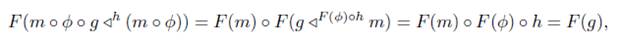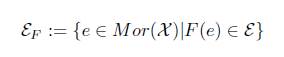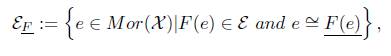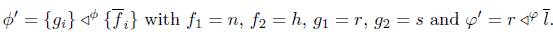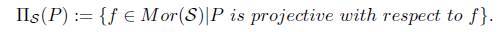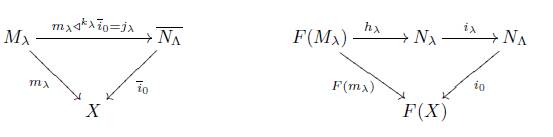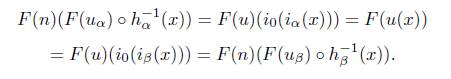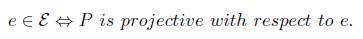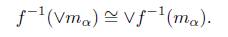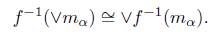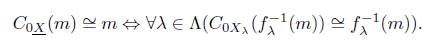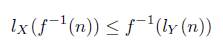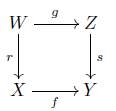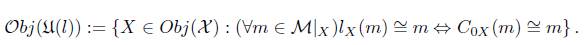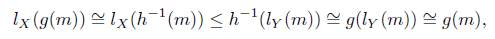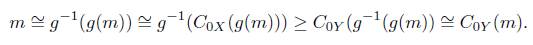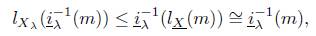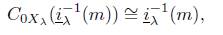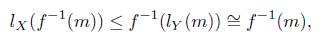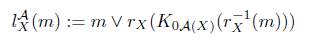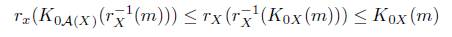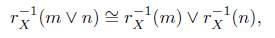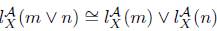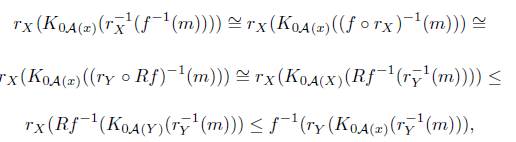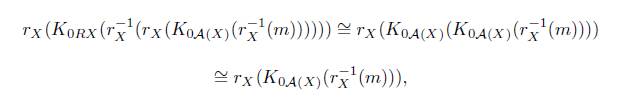2. Preliminaries and notation

Let {(X _i ,T _i )\i Є I} be a family of topological spaces. For each family of functions {f _i : Y → X _i \i Є I} there is the coarser topology ρ on Y that makes continuous each f _i : (Y, ρ) → (X _i ,T _i ). This fundamental construction in the Top category can be generated in many categories similar to Top. The following definitions and results are on 12 of [¹⁴].

For a generic category S a functor F: X → S is said to be a topological functor if for any F−source (X, (f _λ : X → F(X _λ )) _λ∈Λ ), there exists a unique X−source (X, (f _λ : X → X _λ ) _λ∈Λ ), which will be called F− initial lift of (f _λ ) _λ∈Λ , satisfying the following conditions:

1.

2. (F- initiality) For an X-source (Y, (g _λ : Y → X _λ ) _λ∈Λ ) and an S-morphism h : F(Y) → X such that f _λ o h = F(g _λ ) for any A Є Λ, there exists a unique X- morphism 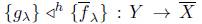such that 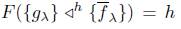and

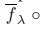
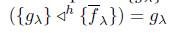
An X -morphism f : X → Y is said to be an F -initial morphism in X if the X- source (X, (f )) is an F-initial lift of (F(X), (F(f ))).

Dual: S-sink, F-sink, cotopological functor, F-final morphism and F-final lift described by the commutative diagram

Proposition 2.1 (See 12.4 of [¹⁴]). If a functor F : X → S is topological, then it is faithful.

Theorem 2.2 (See 12.7 of [¹⁴]). A functor F : X → S is topological if and only if it is co-topological.

The next result gives a property of lifting of limits and colimits.

Corollary 2.3 (See 12.9 of [¹⁴]). Suppose that F : X → S is a topological functor. If S is complete, then X is complete and, if S is cocomplete, then X is cocomplete.

Definition 2.4 (See 13.1 of [¹⁴]). Let F : X → S be a functor. A pair (X,F) with X a locally small category is said to be a topological category if the following conditions hold:

1. S = S et and F is a topological functor.

2. For any A Є Obj(Set), the class F ^-1 (A) := {X Є Obj(X)\F(X) = A} is a set.

3. For a set {p} consists of precisely one point p, F ^-1 ({p}) consist of precisely one X- object.

The proof of the dual theorem of next theorem is in 8 of [¹⁴].

Theorem 2.5 (Characterization of ℳ - coreflective subcategories). Suppose that X is an M - wellpowered (ℰ, ℳ) -category with ℳ ⊆ Mono(X) and that X has coproducts. Then, for a full and isomorphism-closed subcategory U of X, the following conditions are equivalent:

1. U is M - coreflective in X.

2. U is closed under coproducts and satisfies that if f : X → Y belongs to ℰ and X Є Obj (U), then Y Є Obj (U).

3. Lifted structures to topological categories

A topological category (X, F ) is based on the category S et through the functor F, in order to give a structure on X, we use the lifting property of F (initial or final) to lift every structure of (ℳ, ℰ )- category on S et to a structure of (ℳ ', ℰ ') -category on X, this structure inherits closure properties respect to composition, limits, and existence of unions.

Notation. Let F : X → S be a topological functor and ℳ ⊆ Mono(S),

And

where 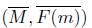is an F-initial lift of (F (M ),F (m)), and for every pair of X- morphisms f and g, f ≅ g denotes that there is an X- isomorphism φ with f = g o p. For every X-object X, an element of ℳ _F (or ℳ _F ) with codomain X is called ℳ _F - subobject (or ℳ _F -subobject of X).

Proposition 3.1. If F : X → S is a topological functor with X locally small and ℳ ⊆ Mono(S), then:

1. ℳ _F ⊆ Mono(X) and ℳ _F ⊆ Mono(X).

2. If ℳ contains all identity morphisms of S, ℳ f and ℳ _F contain all identity morphisms of X.

3. If M is closed under composition with isomorphisms, then ℳ f and ℳ ^F are closed under composition with isomorphisms.

Proof. 1. It follows from proposition 21.13 part (1) of [¹].

2. Let I _X be an identity morphism of X, F(I _X ) = I _F(X) ∈ ℳ, next we show that IX is an F−initial morphism, suppose that g: Y → X is an X-morphism and h: F(Y ) → F(X) is an S−morphism such that IF(X) ◦ h = F(g), then h = F(g), letting g ◁h IX: = g, we have F(g◁ ^h IX) = F(g), the unicity of g◁ ^h IX is a consequence of Proposition 2.1. Finally, since all F−initial lifts of the same morphism are isomorphic, we have that IX ≅IF(X).

3. Let m: M → X be an ℳ F−subobject of X, i.e., m ∈ ℳ F and Cod(m) = X, and ϕ: Z → M an X−isomorphism, we have F(m ◦ ϕ) = F(m) ◦ F(ϕ) ∈ M, next we show that if m ∈ M F , then m ◦ ϕ is an F−initial morphism, suppose that g: Y → X is an S−morphism and h: F(Y ) → F(Z) such that F(ϕ ◦ m) ◦ h = F(g), by the property of F−initiality of m, there is a morphism g ◁ ^F (ϕ)◦h m, letting

we have that F (g ◁ ^h (m o Ф)) = h, and

hence m o Ф o g◁ ^h (m o Ф) = g by Proposition 2.1, the unicity of g◁ ^h (m o $) is a consequence of Proposition 2.1. Finally since all F-initial lifts of the same morphism are isomorphic, we obtain that m o Ф ≅ F (m o Ф).

Notation. Let F : X → S be a topological functor and ℰ ⊆ Epi(S),

And

with (E,F(e)) an F-final lift of (F(E),F(e)).

Proposition 3.2. If F : X → S is a topological functor and ℰ ⊆ Epi(S), then:

1. ℰ _F ⊆ Epi(X) and ℰ _F ⊆ Epi(X).

2. If ℰ contains all identity morphisms of S, ℰ p and ℰ p contains all identity morphisms ofX.

3. If ℰ is closed under composition with isomorphisms, then ℰ p and ℰ p are closed under composition with isomorphisms.

For a topological category (X, F) it is well known that X is well-powered and cowell-powered (see 13.1 of [¹⁴] and 21.16 of [¹]), that is X is Mono(Set) _F -well-powered. A similar result, with a similar proof, but with a minor variant is the following:

Proposition 3.3. Let F : X → S be a topological functor with X a locally small category and ℳ a class of monomorphisms in S closed under composition with isomorphism. If S is ℳ -wellpowered, then X is Mf - wellpowered and ℳ f -wellpowered.

Another property of topological functors is that it can reflect and preserve separators (see 21.16 of [¹]), we indicate in particular the following separator object P in a topological category (X, F) since it can be detected as an object of a certain specific subcategory of X (Proposition 5.6).

Proposition 3.4. Let (X ,F) be a topological category, for any set {p} consisting of precisely one point p, the object P Є F ^-1 ({p}) is a separator on X.

A version of the following Proposition for factorizations of initial sources or a version for initial morphisms and (ℰ, ℳ)- topological functor can be seen at 4.2 of [¹⁰] and 21.14 of [¹] respectively.

Proposition 3.5. Let F : X → S be a topological functor. If S has (ℰ, ℳ)- factorization, then X has (ℰ f, Mf) and (ℰ f, ℳ f)-factorization.

Proposition 3.6. Let F : X → S be a topological functor. If S has ℳ -pullbacks, then X has ℳ f-pullbacks and Mf-pullbacks.

Proof. Let f : X → Y, m : M - Y and k : K → Y be A⁷-morphisms with m G M _F and k Є M _F • Let n,h, and l,g be the M-pullbacks of F(m),F(f) and F(k),F(f), respectively. Notice that n, h, and l,g' are the M _F -pullback and the Mf-pullback, respectively, where g' = (f o 1) ◁g k. The universal property follows from the next commutative diagrams

where

Corollary 3.7. Let F : X → S be a topological functor. If S is a finitely ℳ -complete category, then X is finitely Mf - complete and finitely ℳ f -complete.

The (ℰ, M)- situations generated by Herrlich in [¹⁰] has a similar construction of (ℰ, ℳ)- structures for the concepts of (ℰ, ℳ)- topological category and (ℰ, ℳ)- topological functor.

4. Lifting of projective objects

Definition 4.1. Let f : X → Y be an S-morphism, an S-object P is said to be projective with respect to / if for every S-morphism y : P → Y there is an S-morphism x : P → X with / o x = y. For every S-object P, one defines

Let (f _λ : X _λ → Y) _λЄ∧ be a sink in X, P is projective with respect to (f _λ ) _λЄ∧ if for every X- morphism y : P → Y there is a X ₀ Є ∧ and a morphism x : P - X _λ0 , with f _λ0 ^o x = y.

Remark 4.2. Let {p} be a set consisting of precisely one point, Πs _et ({p}) = Epi(Set) and (ΠSet({p}))⊥ = Mono(Set)..

Proposition 4.3. If (X,F) is a topological category and P Є F ^-1 ({p}), then the following holds:

1. Πx(P) is stable under pullbacks and Πx(P) ⊂ Epi(X).

2. (Πx(P)) ⊥ = Mono(Set) _F .

3. X is a (Πx(P), (Πx(P)) ⊥) - category.

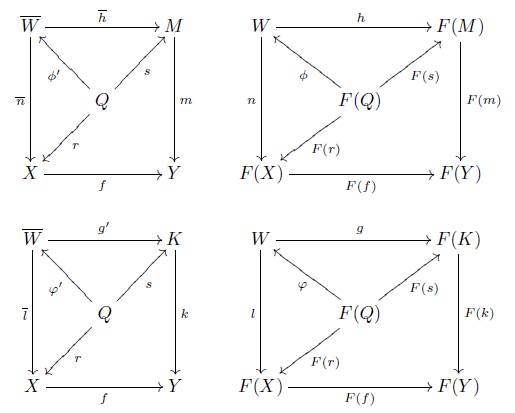
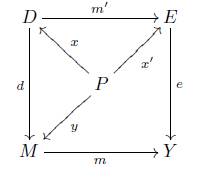
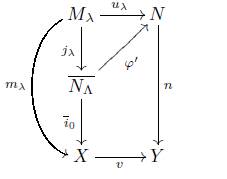
Proof. 1. Consider a pullback

with e Є Πx (P), since P is projective with respect to e for every morphism y : P → M, there is a morphism x' : P →E with e o x' = m o y, by the pullback property there is a morphism x : P → D with d o x = y and m' o x = x'

hence d Є Π _X (P).

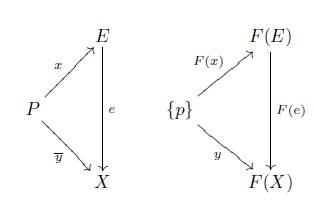
Let e Є Πx(P), one has F(e) Є Π _Set ({p}), since for every y : {p} - F(X), there is an X-morphism X such that the following diagram commutes

For any two X−morphisms u, v: X → Z with u ◦ e = v ◦ e, one has F(u) ◦ F(e) = F(v) ◦ F(e) hence F(u) = F(v) and u = v.

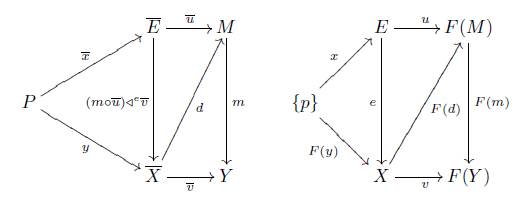
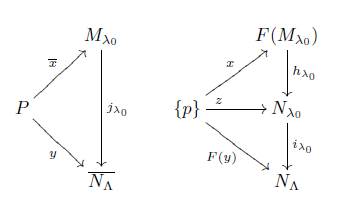
2. Let m ∈ (ΠX (P))⊥, suppose that v ◦ e = F(m) ◦ u with e ∈ ΠSet({p}), consider u: E → M and v: X → Y the F−initial lifts of u and v respectively. By F−initiality of v, there is a X−morphism t = (m◦u) ◁ ^e v. Next we shown that t ∈ ΠX (P), if y: P → X is an X−morphism, there is a Set−morphism x: p → E with F(y) = e ◦ x, and the F−initial lift x: P → E of x is an X−morphism with F(t ◦ x) = F(y), hence t ◦ x = y. Since m ◦ u = v ◦ t, there exists an X−morphism with v = m ◦ d and u = d ◦ t. The Set−morphism F(d) satisfies v = F(m) ◦ F(d) and u = F(d) ◦ e, and considering that e is an epimorphism, F(d) is the unique Set−morphism with that property.

Hence F(m) ∈ (Π _Set ({p}))⊥, and F(m) is a Set−monomorphism. To show the F−initiality of m suppose that F(m) ◦ h = F(g) with g: Y → X a X−morphism and h: F(Y ) → F(M) a Set−morphism, one has the following commutative diagram:

for (F(Y ), (h, Id)) a F−initial lift of (F(Y ), (h, Id)) and letting g ◁ ^h m: = d one has the commutative diagram

hence m is F initial.

Let m Є Mono(Set)F and e Є Πx (P) with m o u = v o e we have the commutative diagrams:

with d′ = v ◁ ^d m, hence m ∈ (ΠX (P))⊥.

3. Let f: X → Y be an X−morphism. Consider the factorization of F(f) in Set given by the inclusion i of A = F(f)(F(X)) to F(Y ) and e the restriction of F(f) to A, then F(f) = i ◦ e. Consider the F−initial lift i: A → Y of i, and t = f ◁ ^e i, we have that f = i ◦ t and, by (2), i ∈ (ΠX (P))⊥, also as in the proof of (2) we have that t ∈ ΠX (P). Now we showed that the factorization f = i ◦ t has the diagonalization property. For every n ∈ (ΠX (P))⊥ and X−morphisms u: X → N and v: Y → Z with v ◦ f = n ◦ u we have the following commutative diagrams

with d′ = (v ◦ i) ◁ ^d n, the existence, and uniqueness of d′ follow from the fact that n ∈ Mono(Set)F , this last by (2). Therefore, f = i◦t is a (ΠX (P), (ΠX (P))⊥)−factorization of f.

Lemma 4.4. Let (X, F) be a topological category, P ∈ F−1({p}) and (m _λ : Mλ → X) _λ∈Λ a family of elements of (ΠX (P))⊥, then

1. For N _Λ = ∪F(m _λ )(F(M _λ )) and i ₀: N _Λ → F(X) the inclusion, ∨mλ≅ i ₀ holds.

2. P is projective with respect to the sink, belonging to (ΠX (P))⊥−union, (j _λ : M _λ →∨M _λ ) _λ∈Λ .

Proof. Let (m _λ : M _λ → X) _λ∈Λ be a class of elements of (ΠX (P))⊥. For each λ ∈ Λ we define:

(a) h _λ as the restriction of F(m _λ ) to its image and N _λ as F(m _λ )(F(M _λ )), note that by definition and (2) of Proposition 4.3 we have that h _λ is a bijection.

(b) i _λ as the inclusion from Nλ to ∪F(m _λ )(F(M _λ )).

(c) k _λ : F(M _λ ) → ∪F(m _λ )(F(M _λ )) as kλ: = i _λ ◦ _hλ.

Since i ₀ is an initial morphism, for every λ ∈ Λ there is a j _λ : = m _λ ◁ ^k λ i ₀ with m _λ = i ₀ ◦j _λ , i.e., m _λ ≤ i ₀.

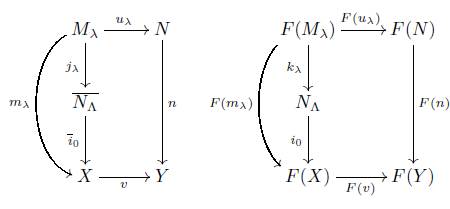
Next, we show that for every n ∈ (ΠX (P))⊥, if {u _λ : M _λ → N} _λ∈Λ is a family of X−morphisms and v: X → Y is an X−morphism such that for every λ ∈ Λ, n ◦ u _λ =v ◦m _λ , then there is a uniquely determined morphism d: N → N with n ◦ d = v ◦ i ₀ and d ◦ j _λ = u _λ for all λ ∈ Λ, definition of M−union (see 1.9 of [⁵]). Suppose that, for each λ ∈ Λ there is a commutative diagram on X

with n ∈ (ΠX (P))⊥. Considering the commutative diagram

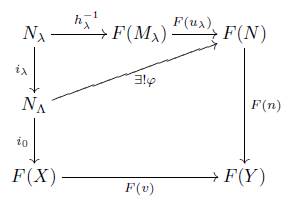
where φ is defined as follows, for every x ∈ NΛ, there is a λ _x ∈ Λ such that x ∈ N _λx ,and φ(x) := F( _uλx ) ◦ h ⁻¹ _λx (x), note that if x ∈ N _α ∩ N _β , then

By (2) of Proposition 4.3, F(n) is a monomorphism, then F( _uα ) ◦ h ⁻¹ _α (x) = F(u _β ) ◦h _−1β (x)), hence φ is well defined. We can define φ′ = (v ◦ i ₀) ◁ _φ n, it makes the next diagram commute

hence ∨m _λ ≅ i ₀ and for each λ ∈ Λ, j _λ = m _λ ◁ ^kλ i ₀.

Finally, for any X−morphism y: 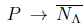, there is a λ ₀ ∈ Λ with F(y)(p) ∈ N _λ0 ,let z: {p} → N _λ0 the constant function with value F(y)(p), we have the commutative diagrams

where x : {p} → F(M _λ0 ) is the constant function with value h ^-1 _λ0 (F(y)(p)) and x̅ is an F-initial lift of x. Thus, P is projective with respect to (j _λ ) _{λЄ Λ} . 0

Next result gives a property of good behavior of inverse images with respect to unions (see 1.L of [⁵]).

Proposition 4.5. Let X be an ℳ -complete category with an object P such that for every X - morphism e:

For every X - morphism f : X → Y and non-empty family (m _λ ) _λЄΛ in M\y, if P is projective with respect to (j _λ : M _λ → M) _{λЄ Λ} , the sink belonging to a union m = Vm _λ , then f ^-1 (Vm _λ ) ≅ Vf ^-1 (m _λ ).

Corollary 4.6. Every topological category (X, F) with P ∈ F ⁻¹ (p) is a category with (ΠX (P), (ΠX (P))_⊥)−factorization, and for every X−morphism f: X → Y and nonempty families (m _α : M _α → Y ) _α∈Λ in (ΠX (P))_⊥ , one has

Corollary 4.7. Let (X, F) be a topological category and P ∈ F ⁻¹ ({p}), then the following holds:

1. X is a (ΠX (P),Mono(Set)F )−category.

2. (ΠX (P))⊥ ⊂ Mono(X).

3. For every X−morphism f: X → Y and every non-empty class (m _λ ) _λ∈Λ in (ΠX (P))⊥|Y one has

Proof. By Proposition 3.1 and Proposition 4.3 we have (1) and (2), by Lemma 4.4 and Proposition 4.5 we have (3).

Theorem 4.8. Let (X, F) be a topological category and P ∈ F−1({p}). IfM= (ΠX (P))⊥ and ℰ = ΠX (P), then the following holds:

1. X satisfies the hypothesis of the characterization of M−coreflective subcategories (see Theorem 2.5).

2. Any object P with F(P) = {p} is a separator in X; furthermore, any M−coreflective subcategory, with P as an object, is bicoreflective.

3. For every morphism f, the operator f ⁻¹ (_) preserves M−unions.

Proof. 1. By (2) of Proposition 4.3, we have that M = Mono(Set)F , and by (1) of Proposition 3.1, we have that ℳ ⊂ Mono(X). By (3) of Proposition 4.3, X is an (ℰ, ℳ)−category. Note that in Set for every set X a representative set of Mono(Set)−subobjects of X is the set of inclusion functions with codomain X, thus Set is Mono(S)−wellpowered, and by Proposition 3.3 we have that X is M−wellpowered.

2. It follows from Proposition 3.4 and Proposition 6.11 of [¹⁴].

3. It follows from (3) of Corollary 4.7.

5. Lower limit-operators and bicoreflective subcategories

The bicoreflective subcategories of Top have been related to limit-operators of Kura-towski closure operator (see Method 3 of [⁹]), as we will see below, the (ℰ, ℳ f) and (ℰ _F , ℳ )- category structures inherited by the Set category to any topological category, is ideal for extending the relationship presented in Top to a topological category (X, F).

Let (X,F) be a topological category, we denote by C ₀ an additive, grounded (see [⁵]) and defined by final sinks closure operator in X respect to ℳ _F , which is defined below.

Definition 5.1. A closure operator C ₀ in X with respect to MF is said to be a closure operator defined by final sinks if for all F−final sink (f _λ : X _λ → X) _λ∈λ , and any ℳ F subobject m of X, is C ₀ −closed iff for all λ ∈ Λ, f ⁻¹ _λ (m) is C ₀ −closed, i.e.,

Definition 5.2. Let C ₀ be a closure operator in X with respect to N ⊂ Mono(X), a lower limit-operator with respect to C ₀, is given by a family l = {lX} _X∈X of maps l _X : N| _X → N| _X such that for every X ∈ Obj(X):

1. (Extension) m ≤ l _X (m) ≤ C _0X (m) for all m ∈ N| _X ;

2. (Additivity) l _X (m ∨ n) ≅ lX(m) ∨ l _X (n) for m, n ∈ N| _X ;

3. (Continuity) f: X → Y , f(l _X (m)) ≤ lY (f(m)) for all f: X → Y and m ∈ N.

Remark 5.3. The additivity property implies the monotonicity of l (and then the well defined by isomorphism, m ≅ n implies l _X (m) ≅ l _X (n)), hence the continuity condition can equivalently be expressed as

for all f: X → Y and n ∈ ℳ | _Y .

Remark 5.4. Let X have (ℰ, ℳ)−factorizations and ℳ −pullbacks:

1. If h: X → Y is a X−isomorphism with g = h ⁻¹ : Y → X, for every ℳ −subobject m of Y , g(m) ≅h−1(m);

2. for every commutative diagram in X

and every ℳ - subobject m of Z, r(g ^-1 (m)) ≤ f ^-1 (s(m)).

For every lower limit-operator l with respect to C₀, note that for every ℳ ≅ subobject with C _0X (m) = m we have that m ≤ l _x (m) ≤ C _0X (m) ≤ m, so we have that l _x (m) ≅ m. We denote by U(l) the full subcategory of x with class of objects:

Proposition 5.5. For every lower limit-operator l with respect to C ₀ the subcategory U(l) is replete.

Proof. Let X ∈ U(l) and h: X → Y be a X−isomorphism, suppose that m ∈ ℳ | _Y with l _Y (m) ≅ m, for g: = h−1 : Y → X, we have that for every n ∈ M| _Y

hence l _x (g(m)) ≅ g(m). Since X Є U(l) we have that C _0x (g(m)) ≅ g(m), then

Thus, m ≅ C _0Y (m) and Y G U(l)

Proposition 5.6. Let l be a lower limit-operator with respect to C ₀ and P be an object such that F(P) - {p}. The subcategory U(l) has P as an object.

Proof. Let m: M → P be an ℳ−subobject of P. Suppose that m = o _X , then C _0X (o _X ) ≅ o _X since C ₀ is grounded. On the other hand, if F(m) is the constantfunction {q} → {p}, then F(C _0X (m)) is a constant function {r} → {p}. The F−initiallift of the constant function {r} → {q} shows that C _0X (m) ≤ m.

Proposition 5.7. For every lower limit-operator l with respect to C ₀ one has:

1. U(l) is closed under coproducts.

2. If f : X → Y is in E _F and X Є Objthen Y Є Obj (U(l)).

Proof.

1 Let {X _λ } _λ∈Λ be a class of X-objects indexed by a set Λ. The final lift (X, (i _λ ) _λ∈Λ ) of the F−sink (⨿F(X _λ ), (i _λ : F(X _λ ) →⨿F(X) _λ ) _λ∈Λ ) is the coproduct of {Xλ} _λ∈Λ in X.

Let m ∈ ℳ|X with lX(m) ≅m, for every λ ∈ Λ one has that

hence 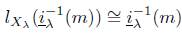, since every X _λ is an U(l)-object one has that

finally C _0X (m) ≅ m.

2 Let f: X → Y in ℰF and X ∈ Obj(U(l)), and m ∈ MF |Y with lY (m) ≅ m, one has

hence lX(f ⁻¹ (m)) ≅ f−1(m), since X ∈ Obj(U(l)), one has C _0X (f−1(m)) ≅ f ⁻¹ (m),and C _0Y (m) ≅ m since C0 is defined by final sink.

Theorem 5.8. For every lower limit-operator l with respect to C ₀ , the full subcategory U(l) is a bicoreflective subcategory of X.

Proof. The Theorem of characterization of ℳ-coreflective subcategories applied to the (ℰf, ℳ _F ) structure on X, Theorem 4.8 part (1) and Proposition 5.7, shows that U(l) is ℳ- coreflective in X. By Proposition 5.6 and (2) of Theorem 4.8 one has that U(l) is bicoreflective in X

For ℳ - Mono(Set) and a topological category (X,F) we consider the (ℰ _F , ℳF)-structure for X induced by F. We consider K _o an additive closure operator on X with respect to MF.

Theorem 5.9. Let A be a bicoreflective subcategory of X, and for every X-object X let rX: A(X) → X be an A-coreflector of X . The operator 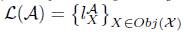defined(up to isomorphism) by:

for every m Є ℳp|x, is a lower-limit operator with respect to K ₀ . Furthermore, if C ₀ is idempotent, and A is ℳp-coreflective, then (A) is idempotent.

Proof. Let X be a X- object, and m Є ℳp| _x , by (2) of Lemma 4.4 and (2) of Proposition 4.3 we have that l^A _x (m) is in ℳ _F , by definition m ≤ l^A _x (m). Since

one has that l ^A _x (m) ≤ K _0x (m).

For m,n Є ℳ _f | _x , by Corollary 4.6 one has that

Hence .

Let f: X → Y an X−morphism and m ∈ MF|Y , and Rf the X-morphism withf ◦ rX = rY ◦ Rf, one has that:

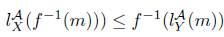then . If K ₀ is idempotent, and every r _X is in ℳF , then