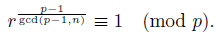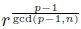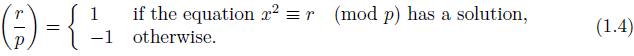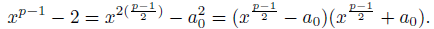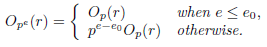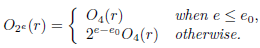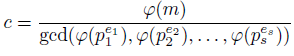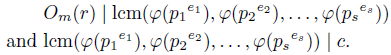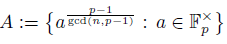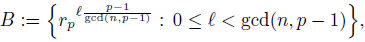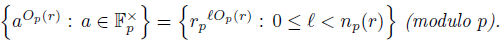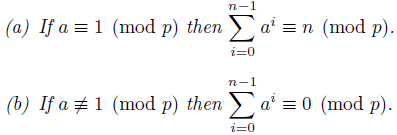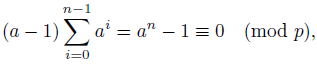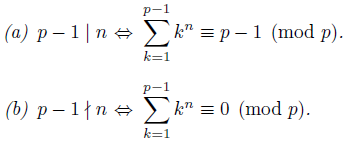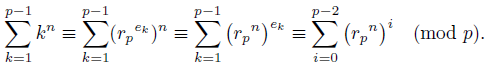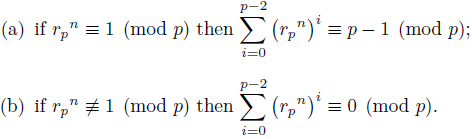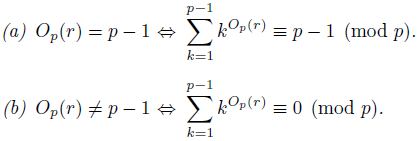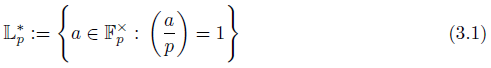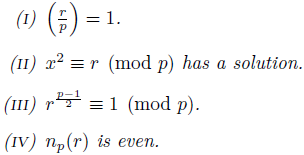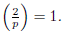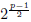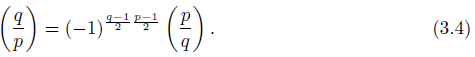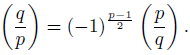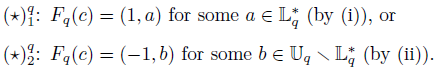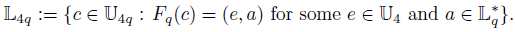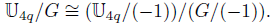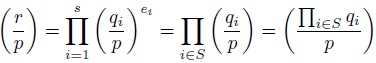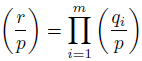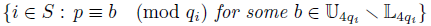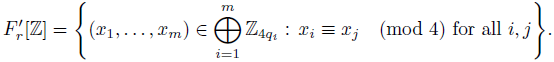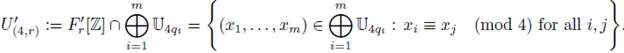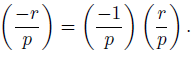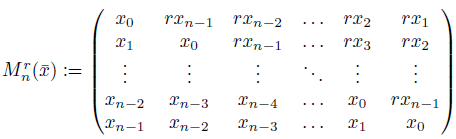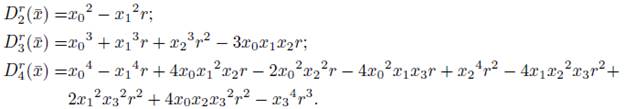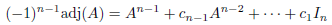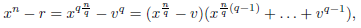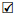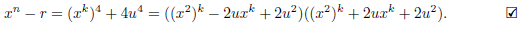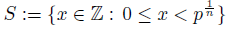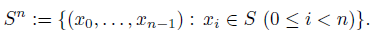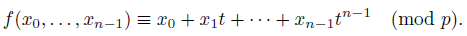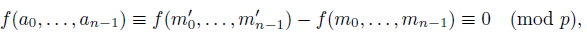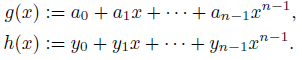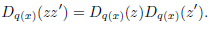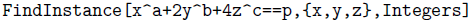1. Introduction
In this work, we prove several properties and present problems related with quadratic residues and its generalization to n-th power residues modulo prime, all in the framework of elementary number theory.
Before entering into the subject, we first fix some basic notations.
Notation 1.1. In the following, m > 1 is an integer and q is a prime.
(1) 𝔽q denotes the field of integers modulo q, which is the prime field of order q, and 𝔽x q denotes its associated multiplicative group.
(2) More generally, Um denotes the multiplicative group of integers modulo m that are relatively prime with m. Note that 𝕌q = 𝔽x q.
(3) Let G be a group with identity element 1 G . For any r ∈ G, the order of r in G, which we denote by O G (r), is the smallest positive integer n satisfying r n = 1G in case it exists, otherwise OG(r) is infinite. When G = 𝕌m, for r ∈ 𝕌 m we abbreviate O m (r): = O 𝕌 m (r), which is the smallest positive integer n such that r n ≡ 1 (mod m) (which always exists because 𝕌m is finite). We can of course extend this notion for any r ∈ ℤ that is relatively prime with m, so O m (r) = O m (r 0 ) where r 0 is the residue obtained after dividing r by m.
(4) The number of elements of a set A is denoted by #A. When G is a group, #G is also called the order of G. When G is a finite group and r ∈ G, OG(r) divides #G. Therefore, since # 𝕌m = φ (m) where φ denotes Euler's phi function, O m (r) | φ (m) for any integer r relatively prime with m. In particular, if q does not divide r then O q (r) | φ (q) = q - 1.
(5) Let r ∈ ℤ be relatively prime with m. Since O
m
(r) | ((m), there is a unique (positive) integer n
m
(r) satisfying O
m
(r)n
m
(r) = ((m). Therefore, due to the definition of O
m
(r), n
m
(r) is the largest n | ((m) such that r
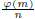 ≡ 1 (mod m).
≡ 1 (mod m).
The notion of n m (r) is not standard, but it will be very useful in the context of power residues modulo prime, as well as in characterizations of Om(r).
Euler's criterion for quadratic residues modulo prime can be easily generalized to power residues as follows (see e.g. [5, Thm. 3.11], [8, Thm. 1.29] and [3, Prop. 4.2.1]).
Theorem 1.2 (Generalized Euler's criterion). Let r Є ℤ , p a prime not dividing r and let n be a positive integer. Then the equation x n = r (mod p) has a solution iff
Even more, if the equation x n = r (mod p) has a solution then it has gcd(p - 1,n)-many incongruent solutions modulo p in total.
As a consequence,
Corollary 1.3. Let r Є ℤ and p a prime not dividing r. Then n p (r) is the largest n | p - 1 such that r has an n-th root modulo p. Moreover, the fol lowing statements are equivalent for any positive integer n:
(I) x n = r (mod p) has a solution.
(III) gcd(p - 1,n) | n p (r).
Proof. The equivalence (i) ⇔ (ii) is Theorem 1.2; the equivalence (ii) ⇔ (iii) can be seen from the definition of n
p
(r) (see Notation 1.1(5)).
In this view, n p (r) plays a very important role in relation with power residues modulo p.
The main results of this paper are divided in two parts, the first about quadratic reciprocity, and the second about power reciprocity modulo prime.
Main results 1: On quadratic residues
Fix r Є ℤ. When p is an odd prime not dividing r (i.e. gcd(p, r) = 1), whether r is a quadratic residue modulo p is determined by the Legendre symbol, which is defined by
In the case r = 2, the problem of whether 2 is a quadratic residue modulo an odd prime is already solved.
Theorem 1.5
(See e.g. [1, Thm. 9.6]). If p is an odd prime then
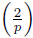 = 1 if p ≡
±1 (mod 8).
= 1 if p ≡
±1 (mod 8).
We ask about similar characterizations for any integer r.
Problem 1.6.
Let r
Є ℤ Is there a positive integer m(r) and a set L(r) ⊆ 𝕌m (r) such that, for any prime p not dividing r
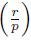 =1 iff the residue of p modulo m(r) is in L(r) ?
=1 iff the residue of p modulo m(r) is in L(r) ?
If so, can L(r) be characterized in some way?
The answer to the first question should not be difficult due to the quadratic reciprocity law, but the characterization of L( r) is more interesting for settling the general problem. In fact, due to the property
the interesting case of Problem 1.6 is when r is a prime. In this case, we proved the following main result:
Theorem A (Theorem 3.5). Let q be a prime. Then
(a) There is only one subgroup of 𝕌4q with order
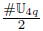 containing -1. This subgroup is denoted by 𝕃4q.
containing -1. This subgroup is denoted by 𝕃4q.
(b) For any prime p ≠ q,
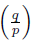 =1 if the residue of p modulo 4q is in 𝕃
4q
.
=1 if the residue of p modulo 4q is in 𝕃
4q
.
This theorem becomes a tool to calculate 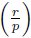 for any r Є ℤ relatively prime with p. This is presented in Theorem 3.6 (and at the end of Section 3).
for any r Є ℤ relatively prime with p. This is presented in Theorem 3.6 (and at the end of Section 3).
In the case of composite r, due to Equation (1.7) an extension of Theorem A is reasonable when r is square free. In this case we can find a subgroup 𝕃 4q of 𝕌4r containing -1 as in (b), but in general this group is not unique as in (a). Details are presented in Theorem 3.7 and in the discussion that follows it.
Main results 2: On power residues
We aim to generalize the following result to power residues.
Theorem 1.8 (See e.g. [2, Thm. 256] and [9]). Let p be an odd prime. Then the following statements are equivalent.
(I) The equation x2 ≡ 2 (mod p) has a solution.
(II) The equation x2 - 2y2 = p has an integer solution.
This is related to the characterization of irreducible elements of the ring ℤ [√2]. an odd prime p in ℤ is still a prime in ℤ [√2] iff the equation x2 - 2y2 = p does not have integer solutions (see [2, Thm. 256]). Recall that x2 - 2y2 is the norm of x + y√2 in the field extension ℚ (√2) of ℚ.
For any n ≥ 2, denote by D
2
n
(x
0
,..., x
n-1
) the norm of x
0
+ xi n
√2 + ... x
n-1
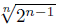 in the field extension ℚ (n
√2) of ℚ. This norm is defined (even in a more general context) in Section 4, but we just state here that
D
2
п
(x
0
,..., x
n-1
) is an integer when x
0
,..., x
n-1
Є ℤ. So we ask whether Theorem 1.8 can be generalized in the following sense.
in the field extension ℚ (n
√2) of ℚ. This norm is defined (even in a more general context) in Section 4, but we just state here that
D
2
п
(x
0
,..., x
n-1
) is an integer when x
0
,..., x
n-1
Є ℤ. So we ask whether Theorem 1.8 can be generalized in the following sense.
Problem 1.9. Let n > 2 and p a prime such that p ≡ 1 (mod n). Are the following statements equivalent?
(1) The equation x n ≡ 2 (mod p) has a solution.
(2) The equation D 2 n (x0,. .., x n-1 ) = p has an integer solution.
The solution of this problem seems to rely on tools in algebraic number theory that would go beyond elementary number theory. In these terms, we managed to solve weaker versions of the problem, where in some of them (2) is replaced by D 2 n (x n ,..., x n-1 ) ≡ 0 (mod p). The trivial solution of this equation is x 0 = ... = x 0-1 = 0, so we aim for non-trivial solutions. On the other hand, our results deal with any integer r in place of 2, so we used a general version D r n (x 0 ,..., x n-1 ) of the norm (which is defined in detail in Section 4).
Theorem B (Theorem 5.1). Let p be a prime, r Є ℤ, n Є ℤ + and r n Є 𝔽 p such that r ≡ r n (mod p) .
(a) The polynomial x n - r 0 is irreducible in 𝔽 p [x] if the equation D r n (x 0 , ..., x n-1 ) = 0 (mod p) does not have a non-trivial solution in the integers.
(b) If n ≥
2 and the equation x
n
≡ r (mod p) has a solution, then D
r
n
(x
0
, .. ., x
n-
i) = 0 (mod p) has a non-trivial solution in ℤn
satisfying -p
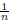 < x
i
< p
< x
i
< p
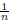 for all 0
≤
i < n.
for all 0
≤
i < n.
The proof of Theorem B(b) is inspired in the proof of Theorem 1.8 presented in the post [9]. As a consequence, we obtain the following equivalence when n is a prime.
Corollary (Corollary 5.2). Let p and q be primes, r Є ℤ. Then the following statements are equivalent:
(I) x q = r (mod p) has a solution.
(II) D r q (x 0 ,.. ., x n-1 ) ≡ 0 (mod p) has a non-trivial solution.
We can also conclude some weakening of the implication (2) ⇒ (1) of Problem 1.9, which yields the real implication when n is a prime.
Theorem C ( Theorem 5.3) . Assume that p is a prime, n ≥2, r Є 𝔽 p and r n Є 𝔽 p such that r ≡ r 0 (mod p). If the polynomial x n - r 0 is irreducible in 𝔽 p [x] then D r n (x̄) = p does not have a solution in the integers.
In particular, (2) ⇒ (1) of Problem 1.9 is true when n is a prime.
We also present a simple proof of Theorem 1.8 using Theorem B (see Theorem 5.4), where 2 can also be replaced by r Є {-2, -1}. This shortens the proof in [9] a little bit.
We remark that "xn - r is irreducible in 𝔽 p [x]" is stronger than "xn = r (mod p) does not have a solution". For instance, if p Є {7,17, 23, 31,41,47, 71}, the equation x 2 ≡ 2 (mod p) has a solution, but x p-1 ≡ 2 (mod p) does not have one. On the other hand, if a n is a solution of x 2 - 2 = 0 in 𝔽 p then, in 𝔽 p [x] :
This means that x p-1 - 2 is reducible in 𝔽 p [x]. More details about irreducibility of x n - r are presented in Section 4.
We do not have any counter-example for Problem 1.9 even when x n - 2 is reducible in 𝔽 p [x].
Indirect motivation
The motivation of this work is related with the study of Mersenne primes, although we do not present explicit results about them. A Mersenne number is an integer of the form 2 n - 1 with n Є ℤ + (positive integer), and a Mersenne prime is a primer number of this form. It is well known that, whenever 2n - 1 is a prime, n must be a prime. Another curious fact is that, whenever 2n - 1 is a Mersenne prime, there is only one (odd) prime p such that Op(2) | n, that is, such that 2n ≡ 1 (mod p). Even more, since n must be prime, n = O p (2). The converse situation is interesting: if n is a prime and there is only one prime p such that O p (2) | n, then 2n - 1 = p e for some e Є ℤ +. Hence, when e = 1, 2n ≡ 1 is a Mersenne prime; but if e > 1 then p is a Wieferich prime, i.e., a prime number p satisfying 2p-1 ≡ 1 (mod p2). Recall that so far only two Wieferich primes are known, namely 1093 and 3511, and Silverman proved under the abc-conjecture that there are infinitely many non-Wieferich primes [7].
The previous observation indicates that understanding O p (2) would lead to a better understanding of Mersenne primes and would trigger possible characterizations. On the other hand, since O p (2) is associated with n p (2), according to Corollary 1.3 we can discover a lot about n p (r) in general by studying power residues modulo p.
Concerning O p (r) for some fixed integer r > 1, the pattern of the sequence of O p (r) for prime p relatively prime with r seems to be very erratic [6], but O n (r) in general can be determined in terms of O p (r) for prime p | n, see Theorems 2.1-2.3. In particular, O pe (r) is deeply related with Wieferich primes (in base r). A more detail discussion is presented in Section 2.
Structure of the paper
Section 2. We discuss some simple aspects related with O m (r) and np(r). In particular, we show expressions of O m (r) for composite m, and a method to obtain n-th roots of 1 modulo a prime p, in particular n p (r) -th roots of 1 . The contents of this section are known and unrelated with the main results, but we present them in accordance with the "indirect motivation" above.
Section 3. This is dedicated to the proof of Theorem A and to further discussions about groups associated with quadratic reciprocity.
Section 4. We present some preliminaries in algebra that are going to be required in the proof of the main results about power residues modulo prime.
Section 5. We prove our main results about power residues modulo prime, in particular Theorems B and C.
Section 6. We discuss research related to this work.
2. Multiplicative order
We first show how the multiplicative order modulo composite numbers can be calculated.
Theorem 2.1 (See e.g. [5, §3.2, Thm. 3.6]). Let p be an odd prime and r Є ℤ, r ≠ ±1 relatively prime with p. Assume that en is the maximum integer such that O pe0 (r) = Op(r). Then, for any e ≥ 1,
The previous result has a deep connection with Wieferich primes. In fact, an odd prime p is a Wieferich prime in base r if p ł r and Op2 (r) = Op(r).1 Very few of these numbers are known for each r > 1 .
The following is a version of Theorem 2.1 for p = 2. The proof is almost the same, so we omit it.
Theorem 2.2. Assume r Є ℤ is odd, r ≠ ±1 . If e 0 ≥ 2 is the maximum integer such that O2e0 (r) = O4 (r) then, for any e ≥ 2,
Now we look at the case when m > 1 is composite but not a prime power, so we assume that it has prime factorization m= 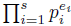 (s ≥ 2).
(s ≥ 2).
Theorem 2.3. When gcd(r, m)=1, Om(r) =
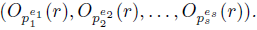 .
.
Proof. Let us suppose b := lcm
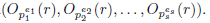 We need to prove the following.
We need to prove the following.
1. rb ≡ 1 (mod m). For any i ≤ s we know that r 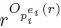 ≡ 1 (mod peii) and O peii (r) | b, so rb ≡ 1 (mod peii), i.e. peii | rb - 1. Since peii and pejj are relatively prime when i ≠ j, we conclude that m | rb - 1.
≡ 1 (mod peii) and O peii (r) | b, so rb ≡ 1 (mod peii), i.e. peii | rb - 1. Since peii and pejj are relatively prime when i ≠ j, we conclude that m | rb - 1.
2. b is the minimal number satisfying the equation rx = 1 (mod p) Assume rx ≡ 1 (mod m). This implies rx ≡ 1 (mod peii) for any i ≤ s, so O peii (r) | x. Therefore b | x, so by (1) b is the minimum we claim.
Notice that, by the Chinese remainder theorem, the map ℤ m (⊕si=1 ℤ peii that sends α to the tuple (αi,... , αs) of residues modulo peii is a ring isomorphism, and when restricted to 𝕌m it gives a group isomorphism onto
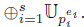 . So the previous result can be seen as a particular case of the following fact: if G =
. So the previous result can be seen as a particular case of the following fact: if G =
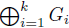 is a direct sum of groups of finite order and
is a direct sum of groups of finite order and 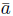 = (α1,... αk) Є G, then O
G
(
= (α1,... αk) Є G, then O
G
(
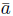 ) = lcm(OG1 (α1),..., O
G
k
(α
k
)). (A similar proof works.)
) = lcm(OG1 (α1),..., O
G
k
(α
k
)). (A similar proof works.)
As a consequence, we obtain the following modular equation using Euler's phi function.
Corollary 2.4. If gcd(r, m) = 1 and
Then r c ≡1 (mod m)
Proof. Since lcm(α 1 , α 2 ,..., α m ) gcd(α 1 , α 2 ,..., α m ) | α 1 α 2 ... α m , by Theorem 2.3 we can prove that
The theorem follows immediately.
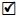
The previous result can be generalized as well in the context of direct sums of groups: if
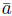 Є G and c =
Є G and c =
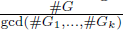 then
then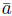 c
= 1G, i.e. O G
(
c
= 1G, i.e. O G
(
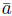 ) | c.
) | c.
From here until the end of this section, we assume that p is a prime and gcd(r,p) = 1. We look at the effect of the power of O p (r) in 𝔽 x p, namely, properties of k Op(r) for к Є𝔽 p . In fact, these properties come from more general results. First, we show that {k Op(r) : k Є 𝔽 x p } gives the full set of n p (r)-th roots of 1 modulo p, which can be generalized as follows.
Theorem 2.5. Let n ≥ 1 be an integer. Then all the n-th roots of unity can be obtained from the set
Moreover, if r p is a primitive root of p then the set above coincides modulo p with
and their members are pairwise incongruent modulo p.
Proof. We define m(n) :=
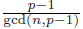 and b := r
p
m(n)
. For any α Є𝔽
x
p, if α ≡ r
p
k
(mod p)
and b := r
p
m(n)
. For any α Є𝔽
x
p, if α ≡ r
p
k
(mod p)
then α m(n) = r p km(n) (mod p). If we put к = d . gcd(n,p - 1) + ℓ for some d Є ℤ and 0 ≤ ℓ < gcd(n,p - 1), then km(n) = d(p - 1) + ℓ m(n). So we get a m(n) = (r p m(n) ) ℓ ≡ b ℓ (mod p). This shows A ⊆ B (modulo p). The converse inclusion is trivial.
By Theorem 1.2, the equation x
n
= 1 (mod p) has exactly gcd(n,p - 1)-many solutions in 𝔽p. On the other hand, since O
p
(b) = gcd(n,p - 1), it is clear that (bℓ)
n
≡ 1 (mod p) for all 0 < ℓ < gcd(n,p - 1), and that the b
ℓ
are pairwise incongruent modulo p. This shows that B is the complete set of n-th roots of unity.
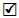
Corollary 2.6. The set of solutions for the equation x np(r) = 1 (mod p) (i.e. the set of n p (r) -th roots of unity modulo p) is
Recall the following properties of roots of unity modulo p.
Lemma 2.7. Let n ≥ 1 and assume that a is an n-th root of 1 modulo p. Then:
Proof. Property (a) is trivial; since
it is clear that α
 1 (mod p) implies (b).
1 (mod p) implies (b).
As a consequence, we can show the behaviour of the sum of k Op(r) for 1 ≤ k ≤ p - 1, or even more generally:
Theorem 2.8 (See e.g. [8, Pg. 67]). Let n Є ℤ + . Then:
Proof. Fix a primitive root r p of p, and for each 1 ≤ k < p choose e k < p - 1 such that r p ek ≡ k (mod p). We have the following:
Note that any member of 𝔽x p is a (p - 1)-th root of 1, so we can apply Lemma 2.7 to conclude:
It is easy to verify that r
p
n
≡ 1 (mod p) is equivalent to p-1 | n, so the result follows.
Corollary 2.9. Let r Є ℤ such that gcd(r, p) = 1. Then:
3. Groups associated with quadratic residues
This section is dedicated to the proof of Theorem A.
Recall the Legendre symbol
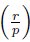 as presented in Equation (1.4). It is known that the map
as presented in Equation (1.4). It is known that the map
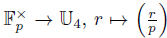 is a group homomorphism, where 𝕌4 = {1, -1} as a multiplicative group,2 so
is a group homomorphism, where 𝕌4 = {1, -1} as a multiplicative group,2 so
is a subgroup of 𝔽x
p of order
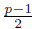 (half of the order of 𝔽x
p ).
(half of the order of 𝔽x
p ).
We look at the following converse situation: given an integer r, characterize the odd primes p relatively prime with r such that = 1. This is associated with n p (r) in the following sense.
Lemma 3.2. Let p be an odd prime, r Є ℤ such that gcd(r,p) = 1. Then the following statements are equivalent:
Proof. The equivalence (i) ⇔ (ii) follows from the definition of Lagrange's symbol. The others are a direct consequence of Corollary 1.3 (applied to n = 2).
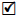
First, we look at the case when r = q is a prime. If q = 2 we have the following situation.
Theorem 3.3. If p is an odd prime then the following statements are equivalent.
(II) p ≡ ± (mod 8)
(IV) n p (2) is even.
Proof. (i) ⇔ (ii) is known, see Theorem 1.5. The rest follows by Lemma 3.2.
We aim to generalize Theorem 3.3 for any r in the place of 2, concretely, to find a condition like in (ii) that characterizes
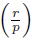 for any odd prime p relatively prime with r.
for any odd prime p relatively prime with r.
An observation about the case r = 2: Denote 𝕃8: = {1, -1} as a subgroup of 𝕌8. Note that this is the only subgroup of 𝕌8 of order 2 (half of the order of 𝕌8) that contains - 1 . Theorem 3.3 says that (j) ≡ 1 iff p = c (mod 8) for some c Є 𝕃 8 , which validates
Theorem A for r = 2.
Assume that r = q is an odd prime. If p ≠ q is an odd prime then, by the quadratic reciprocity law:
We start assuming q = - 1 (mod 4),3 in which case
Therefore,
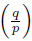 ≡1 iff one of the following cases hold:
≡1 iff one of the following cases hold:
(I) p ≡ 1 (mod 4) and p = a (mod q) for some a Є 𝕃 * q (see Equation (3.1)), or
(II) p ≡ - 1 (mod 4) and p = b (mod q) for some b Є 𝕌 q \ 𝕃 * q.
For any odd prime q 0 : by the Chinese remainder theorem, the map F qo : ℤ 4qo( ℤ 4⊕ 𝔽qo that sends any x to the pair (x 0 ,x 1 ) of remainders modulo 4 and q 0 respectively, is a ring isomorphism. When this map is restricted to 𝕌 4qo it becomes a group isomorphism onto 𝕌 4 ⊕ 𝔽x qo .
Coming back to our argument, using the previous terminology we conclude that
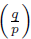 = 1 iff p
≡
c (mod 4q) for some c Є 𝕌
4qo
such that c satisfies one of the following conditions:
= 1 iff p
≡
c (mod 4q) for some c Є 𝕌
4qo
such that c satisfies one of the following conditions:
Let 𝔽4q be the set of c Є 𝕌
4q
satisfying either
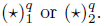 or Since
or Since
L’( 4 q ): = {(e, a) Є 𝕌 4 ⊕ 𝕌 q : either e =1 and a Є 𝕃* q, or e ≠1 and α ∉ 𝕃 * q } is a subgroup of 𝕌 4 ⊕ 𝕌 q and 𝕃4q is the inverse image under F q of this subgroup, we conclude that 𝕃4q is a subgroup of 𝕌 4q .
Moreover, 𝕃4q has order q - 1, which is half of the order of 𝕌
4q
, and -1 Є 𝕃4q: Since 𝕃*
q
has order
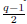 it is clear that the order of L’(
4 q
) is double, that is, q - 1, and this is the order of 𝕃 4q; note that F
q
( -1) = ( - 1, -1) and -1 ∉ 𝕃*
q
because q ≡ - 1 (mod 4), so it satisfies (★)q
2 and we get -1 Є 𝕃4q.
it is clear that the order of L’(
4 q
) is double, that is, q - 1, and this is the order of 𝕃 4q; note that F
q
( -1) = ( - 1, -1) and -1 ∉ 𝕃*
q
because q ≡ - 1 (mod 4), so it satisfies (★)q
2 and we get -1 Є 𝕃4q.
We turn to the case when q = 1 (mod 4). By Equation (3.4) we obtain that
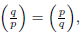 so
so
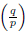 =1 iff p = α (mod q) for some α Є 𝕃*
q
. Using the ring isomorphism F
q
introduced before, define
=1 iff p = α (mod q) for some α Є 𝕃*
q
. Using the ring isomorphism F
q
introduced before, define
Since this is the inverse image under F q of 𝕌 4 ⊕ 𝕌 q * and this is a subgroup of 𝕌 4 ⊕ 𝕌 q of size q - 1, we conclude that 𝕃 4q is a subgroup of 𝕌 4q of order q - 1 (half of the order of 𝕌 4q ). Even more, -1 Є 𝕃4q because F q (- 1) = (-1, -1) and, since q ≡ 1 (mod 4), - 1 Є 𝕃* q .
The previous argument is then summarized in the following result, which generalizes Theorem 3.3 and concludes the proof of Theorem A.
Theorem 3.5.
Let q ≠ p be prime numbers with p odd.
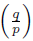 = 1 iff p ≡ c (mod 4q) for some c Є 𝕃4q.
= 1 iff p ≡ c (mod 4q) for some c Є 𝕃4q.
Moreover, 𝕃4q is the unique subgroup of 𝕌4q with order q - 1 (half of the order of 𝕌4q) that contains - 1.
Proof. According to the previous discussion, it remains to show that, whenever q is an odd prime, 𝕃4q is the unique subgroup of 𝕌4q as in the statement. So let Є be a subgroup of 𝕌4q of order q - 1 with -1 Є G. This indicates that (- 1) := {1, -1} is a subgroup of G, so when taking quotients
Note that 𝕌4q /(-1) ≅ 𝕌2q and G/( - 1) is a subgroup of 𝕌4q/(-1) of order
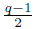 . So it is enough to show that
. So it is enough to show that
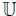 2q contains only one subgroup of order
2q contains only one subgroup of order
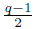 .
.
By the Chinese remainder theorem, 𝕌2q is isomorphic to 𝕌2 ⊕ 𝔽xq, which is isomorphic to 𝔽xq itself. Since 𝔽xq is a cyclic group, it only contains one subgroup of order
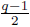 , which concludes the proof.
, which concludes the proof.
Now we turn to the more general case r Є ℤ+. If r is a square then trivially
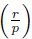 = 1 for any odd prime p relatively prime with r; if
= 1 for any odd prime p relatively prime with r; if
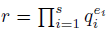 is the prime factorization of r and r is not a square, and p is an odd prime relatively prime with r, then by (1.7):
is the prime factorization of r and r is not a square, and p is an odd prime relatively prime with r, then by (1.7):
where S := {i : ei is odd}.
Therefore, the general case reduces to when r is square free, that is, it has its prime factorization of the form qi ... qm (when all prime powers are 1). Since
we obtain that
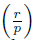 =1 iff the number of elements of the set {i :
=1 iff the number of elements of the set {i :
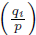 =
-
1} is even. We can express this in terms of the groups 𝕃4q thanks to Theorem 3.5.
=
-
1} is even. We can express this in terms of the groups 𝕃4q thanks to Theorem 3.5.
Theorem 3.6. Let r Є ℤ+.
(a) If r is a square then
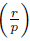 = 1 for any odd prime p with gcd(p, r) = 1.
= 1 for any odd prime p with gcd(p, r) = 1.
(b) Assume that r is not a square and r= 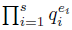 is its prime factorization. If S :=
is its prime factorization. If S :=
{i : ei is odd} then, for any odd prime p with gcd(p, r) = 1,
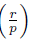 = 1 iff the number of elements of the set
= 1 iff the number of elements of the set
is even.
We develop the case r = qi ... qm (prime factorization) a bit more. Consider the ring homomorphism F’r :
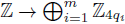 that sends x to the tuple (xi,..., xm) where x ≡ xi (mod 4qi) for any i. Although the kernel of this map is (4r) ℤ, the image is not everything: as a consequence of the Chinese remainder theorem (for non-coprime moduli),4
that sends x to the tuple (xi,..., xm) where x ≡ xi (mod 4qi) for any i. Although the kernel of this map is (4r) ℤ, the image is not everything: as a consequence of the Chinese remainder theorem (for non-coprime moduli),4
Therefore, the map Fr : ℤ 4r ( F‘r [ℤ] defined by Fr (α) = F‘r (α), is a ring isomorphism. If we restrict this map to 𝕌4r, we get a group isomorphism onto
According to (b), define
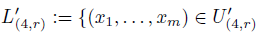 : the number of elements of the set
: the number of elements of the set
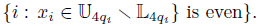
And let 𝕃4r = {x Є 𝕌4r : Fr (x) Є L’(4r)}. Therefore, for any odd prime p with gcd(p, r) = 1,
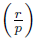 =1 iff p = c (mod 4r) for some c Є 𝕃4r.
=1 iff p = c (mod 4r) for some c Є 𝕃4r.
It is easy to check that L’(4 r) is a subgroup of U'(4,r) of half order, so 𝕃4r is a subgroup of 𝕌4r of half order. Moreover, -1 Є 𝕃4r because {i : -1 Є 𝕌4qi \ 𝕃4qi} is empty by Theorem 3.5 (so it has zero elements). To summarize:
Theorem 3.7. Let r Є ℤ+ with prime factorization r = q1 ... qm. Then there is a subgroup 𝕃4r of 𝕌4r of half order, containing -1, such that for any odd prime p with gcd(p, r) = 1,
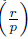 = 1 iff p = c (mod 4r) for some c Є 𝕃4r.
= 1 iff p = c (mod 4r) for some c Є 𝕃4r.
However, it may be that 𝕃4r is not the only subgroup of 𝕌4r of half order containing - 1. For example, consider r = 15: 𝕃60 = {±1, ±7, ±11, ±17}, but {±1, ±11, ±19, ±29} is another subgroup of 𝕌60 of half order containing -1.
To finish this section, we consider negative integers. If r Є ℤ+ and p is an odd prime with gcd(r,p) = 1 then
Since
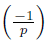 =1 iff p ≡ 1 (mod 4),
=1 iff p ≡ 1 (mod 4),
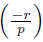 can be easily calculated by Theorem 3.6.
can be easily calculated by Theorem 3.6.
4. Preliminaries about modules and fields
Throughout this section, we fix an arbitrary integral domain R, r Є R and a natural number n. We first discuss the ring quotient Rrn := R[x]/(xn - r). It is very common to look at this ring quotient when R is a field and xn - r is irreducible in R[x], in which case Rrn is a field. But in this work we also want to look at the situation when xn - r is reducible in R[x] , in which case Rrn is not an integral domain. In any case:
Lemma 4.1. The ring Rrn is a free R-module with basis {1,u,... ,un-1} where u := x (mod ( xn-r)) , even more Rrn is an R-algebra.
Proof. Recall that R[x] satisfies the division algorithm with monic polynomials: for any f (x), g(x) Є R[x], if g(x) is of the form xm + am-1 xm-1 + ... + a0 (m = 0 is allowed, in which case g(x) = 1) then there are unique q(x),t(x) Є R[x] such that f (x) = q(x)g(x) + t(x) and t(x) has degree smaller than g(x).
Now, if 0 ≠ f( x) Є R[x] has degree smaller than n then, by applying the previous division algorithm to g(x) = xn - r, we obtain that f (x) = q(x)g(x) + t(x) for unique q(x) and t(x), the latter with degree smaller than n. Hence q(x) = 0: if q(x) ≠ 0 has degree m ≥ 0, then q(x)g(x), and thus f (x), have degree n + m, which contradicts that f (x) has degree smaller than n. Therefore t(x) = f (x) ≠ 0, meaning that f (x) is not a multiple of xn - r (otherwise, t(x) = 0 by the division algorithm with monic polynomials).
Let R’ be the R-submodule of R[x] generated by { 1 , x, . . . , xn-1 } , which is a free R-module. The previous paragraph shows that the surjective R-module homomorphism R' → Rrn that sends each xi to ui has kernel equal to the zero ring, so it is an Rrn -module isomorphism. This shows that Rrn is a free R-module with basis {1,u,...,un-1}.
It is clear that Rrn is an R-algebra.
If xn - r is reducible in R[x] then Rrn is not an integral domain, but it is an integral domain when R is a unique factorization domain and xn - r is irreducible in R[x]. In general, Rrn can be expressed as a ring of matrices 𝕄rn(R) such that the determinant works as the norm of the elements of the ring.
Definition 4.2. (1) For x̄ = (x0,... ,xn-1) Є Rn define
and denote its determinant by Drn (x̄).
(2) If z Є Rrn we denote Mrn(z) := Mrn (x̄) and Drn(z) := Drn(x̄) where x = (xo,..., xn-1) Є Rn is the unique tuple such that z =
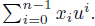
(3) Define 𝕄rn (R) := {Mrn (x̄) : x̄ Є Rn}. When R is understood from the context we just write 𝕄rn.
These matrices actually describe the shift endomorphisms in Rrn:
Lemma 4.3. If z Є Rrn then the matrix Mrn (z) characterizes the endomorphism Rrn → Rrn given by w ↦ zw. Concretely, Mrn (z) is the unique matrix with the following property: if w =
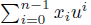 for some x̄ Є Rn, then zw =
for some x̄ Є Rn, then zw =
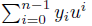 where
where
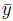 = Mrn (z) x̄.
= Mrn (z) x̄.
As a consequence 𝕄rn is a subring of the ring of n x n matrices with entries in R, even more, 𝕄rn is commutative and so it is an R-algebra. In fact, it characterizes Rrn.
Lemma 4.4. The function Mrn : Rrn → 𝕄rn is an R-algebra isomorphism, and the map Drn : Rrn → R satisfies Drn (zz') = Drn (z) Drn (z') for any z, z' Є Rrn
The function Drn has the role of a norm for Rrn. In fact, when F is a field and xn - r is irreducible in F[x], Frn is a field and Drn is its norm as an F-extension.
We list the exact form of some few Drn(x̄) with x Є Rn:
We can also talk about conjugates in Rrn. In field extensions like ℚ(i) and ℚ (√2), the conjugate z of some element z satisfies that
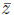 is the norm of z. In the general case we can look at the matrix characterization: for any matrix A of dimensions n x n (with entries in R), A .adj(A) = |A|In where In is the identity matrix of dimensions n x n, adj(A) is the adjugate of A and |A| is the determinant of A. Since the determinant acts as a norm, then adj(A) works as the (analog of the) conjugate of A. Recall that the matrix A is invertible if there is some unique matrix A-i of dimensions n x n, with entries in R, such that AA-1 = A-1A = In. Recall that A is invertible iff |A| is a unit in R, in which case A-1 = |A| - 1adj(A). In 𝕄rn(R) we obtain:
is the norm of z. In the general case we can look at the matrix characterization: for any matrix A of dimensions n x n (with entries in R), A .adj(A) = |A|In where In is the identity matrix of dimensions n x n, adj(A) is the adjugate of A and |A| is the determinant of A. Since the determinant acts as a norm, then adj(A) works as the (analog of the) conjugate of A. Recall that the matrix A is invertible if there is some unique matrix A-i of dimensions n x n, with entries in R, such that AA-1 = A-1A = In. Recall that A is invertible iff |A| is a unit in R, in which case A-1 = |A| - 1adj(A). In 𝕄rn(R) we obtain:
Lemma 4.5. If A Є 𝕄rn(R) then adj(A) Є 𝕄rn(R). In particular, if A Є 𝕄Tn(R) is invertible (as a matrix) then A-1 Є 𝕄rn (R).
Proof. An analog of the Caley-Hamilton Theorem indicates that
where cn-1,... ,co Є R and λn + cn-1λn-1 + ... + c0 is the characteristic polynomial of A. If A Є 𝕄rn. then ( - 1)n-1 adj(A) Є 𝕄rn by the expression above, so adj(A) Є 𝕄rn.
In particular, when A is invertible, A-1 = |A|-1 adj(A) Є 𝕄rn.
We also present an elementary proof in the case when A Є 𝕄rn ( R) is invertible as a matrix with entries in F, where F is the field of fractions of R. Choose z Є R such that A = Mrn (z). Since A is invertible, by Lemma 4.3 the map w ↦ zw is an automorphism on Frn, so there is some z' Є F such that zz' = 1, hence w ↦ z'w is the inverse of the previous map. Therefore A-1 = 𝕄rn (z') Є 𝕄rn (F ), which implies that adj(A) = |A|A-1 Є 𝕄rn (F ). But adj(A) is a matrix with entries in R, so adj(A) Є 𝕄rn (R).
Now that we know a bit more about the structure of Rrn, we now look at sufficient and necessary conditions for the polynomial xn - r to be irreducible.
Lemma 4.6. If xn - r is irreducible in R[x] then: whenever q | n is prime, xq - r = 0 does not have a solution in R.
Proof. Assume that q | n is prime and xq - r = 0 has a solution v in R, that is, vq = r in R. Then, in R[x],
We will prove the converse in some cases of interest by using the following result. From now on, fix a field F and r Є F.
Theorem 4.7 (See [4, Ch. VI §9]). The polynomial xn - r is irreducible in F[x] iff the following two conditions hold.
(i) If q | n is prime then the equation xq - r = 0 does not have a solution in F.
(ii) If 4 | n then the equation 4x4 + r = 0 does not have a solution in F.
Proof. The cited reference states and proves that (i) and (ii) implies that xn - r is irreducible in F[x] . The converse implication is true for any ring R and it is easy to prove. Assume that r Є R. Lemma 4.6 shows that xn - r irreducible in R[x] implies (i). To show that (ii) is also implied we prove that, whenever 4 | n and 4u4 + r = 0 for some u Є R, xn - r is reducible in R[x]. Since n = 4k for some к ≥ 1, we get
Corollary 4.8. Let q be a prime and let F be a field. Then xq - r = 0 does not have a solution in F iff xq - r is irreducible in F[x].
Condition (ii) can be suppressed when we look at fields of prime characteristic.
Theorem 4.9. Let p be a prime and assume that 4 ł n or 4 | p - 1 or p = 2. If F has characteristic p then xn - r is irreducible in F[x] iff, for any prime q | n, xq - r = 0 does not have a solution in F.
Proof. We showed one direction in Lemma 4.6. To see the converse, assume that, for any prime q | n, xq - r = 0 does not have a solution in F, which means that (i) of Theorem 4.7 is valid. By using the same theorem, it is enough to show that (ii) holds, that is, the equation 4x4 + r = 0 does not have a solution in F when 4 | n.
Assume that 4 | n, so either 4 | p - 1 or p = 2 by hypothesis. In the case 4 | p - 1 assume towards a contradiction that 4x4 + r = 0 has a solution xo Є F. So -r = 4x40 = (2x20)2. Let yo := 2 x20, so y20 = -r.
On the other hand, by properties of the Legendre symbol,
which means that -1 ≡ z20 (mod p) for some z0 Є 𝔽p. Hence, r = (-r)( - 1) = (y0z0)2, that is, the equation x2 - r = 0 has a solution in F, but this is not true by hypothesis: since 2 is prime and 2 | n, x2 - r = 0 does not have a solution in F.
In the case p = 2 we have 4x4 + r = r. If 4x4 + r = 0 has a solution in F then r = 0, but 4 | n so the hypothesis says that the equation x2 = 0 does not have a solution in F, which is absurd.
Corollary 4.10. Let p be a prime and assume that n | p - 1. If F has characteristic p then xn - r is irreducible in F[x] iff, for any prime q | n, xq - r = 0 does not have a solution in F.
Proof. Immediate by Theorem 4.9 because 4 | n implies 4 | p - 1 when p is odd.
In some cases, we can also characterize irreducibility of xn - r in ℚ[x].
Theorem 4.11. Let n be a natural number. If r Є ℚ and r > 0 then xn - r is irreducible in ℚ[x] iff xq - r = 0 does not have a solution in ℚ for any prime q | n.
Proof. This is a direct consequence of Theorem 4.7 since condition (ii) there is always satisfied.
The previous result actually applies to any ordered field.
To finish this section, we show that irreducible in 𝔽p[x] is stronger than irreducible in ℚ[x] when r Є ℤ.
Corollary 4.12. Let p be a prime, r Є ℤ and n Є ℤ+. If r ≡ r0 (mod p) and xn - r0 is irreducible in 𝔽p[x] then xn - r is irreducible in ℚ[x].
Proof. Assume that xn - r0 is irreducible in 𝔽p[x]. We first prove that xq - r = 0 does not have a solution in Q for any prime q | n. Using Lemma 4.6 with R = 𝔽p, we know that xq - ro = 0 does not have a solution in 𝔽p for any prime q | n, which implies that the equation xq - r = 0 does not have a solution in ℤ, so neither in ℚ: if a,b Є ℤ are relative prime, b > 0, and
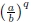 - r = 0, then αq = rbq, which implies that b = 1 (if b > 1 then r = 0, so a = 0 and, since gcd(a, b) = 1, b = 1, contradiction), thus xq - r has a solution in ℤ.
- r = 0, then αq = rbq, which implies that b = 1 (if b > 1 then r = 0, so a = 0 and, since gcd(a, b) = 1, b = 1, contradiction), thus xq - r has a solution in ℤ.
In the case r > 0 the result follows by Theorem 4.11; in the case n ł 4, the result follows by Theorem 4.7; and when r = 0, we must have n = 1 (because we assumed xn - r0 irreducible in 𝔽p[x]) and then xn - r = x is irreducible in ℚ.
So it remains to consider the case when r < 0 and n | 4. Here it remains to show that (ii) of Theorem 4.7 holds for 𝔽 = ℚ. Towards a contradiction, assume that 4 α 4 + r = 0 for some α Є ℚ. Since r Є ℤ and α4 =
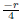 , we must have that α Є ℤ. Therefore, modulo p we get that 4x4 + ro = 0 has a solution in 𝔽p, but this contradicts (ii) of Theorem 4.7 for xn - ro in 𝔽p [x].
, we must have that α Є ℤ. Therefore, modulo p we get that 4x4 + ro = 0 has a solution in 𝔽p, but this contradicts (ii) of Theorem 4.7 for xn - ro in 𝔽p [x].
5. Power residues
In this section we show the main results concerning power residues. We start with Theorem B.
Theorem 5.1. Let p be a prime, n Є ℤ +, r Є ℤ and let ro Є 𝔽p such that r ≡ r0 (mod p).
(a) The polynomial xn - r0 is irreducible in 𝔽p[x] iff the equation DTn(x0,..., xn-1) ≡ 0 (mod p) does not have a non-trivial solution in the integers.
(b) If xn -r is reducible in ℚ[x] then Drn(x) = 0 has a non-trivial solution in the integers.
(c) If n ≥2 and the equation xn ≡ r (mod p) has a solution, then DTn(x0, ... ,xn-1) ≡ 0 (mod p) has a non-trivial solution in the integers. Even more, this solution satisfies -
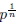 <
<
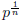 for all 0 ≤ i < n.
for all 0 ≤ i < n.
Proof. Set F := 𝔽p. We first show (a). Assume that xn - ro is irreducible in F[x]. Then Fnro = F(u) is a field extension of F with u :=
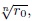 , which is isomorphic to 𝕄r0n (F) by Lemma 4.4. Let x̄ = (xo, ..., xn-1) ≠ (0, ..., 0) with xi Є 𝔽p (0 ≤i < n), and set A := Mnr0 (x). By Lemma 4.5 A-1 Є 𝕄rn0, so Drn° (x) ≠ 0 in 𝔽p, that is, Drn(x̄) = 0 (mod p) .
, which is isomorphic to 𝕄r0n (F) by Lemma 4.4. Let x̄ = (xo, ..., xn-1) ≠ (0, ..., 0) with xi Є 𝔽p (0 ≤i < n), and set A := Mnr0 (x). By Lemma 4.5 A-1 Є 𝕄rn0, so Drn° (x) ≠ 0 in 𝔽p, that is, Drn(x̄) = 0 (mod p) .
For the converse, assume that xn - r0 is reducible in F[x]. Then Fnro is not an integral domain, so there are non-zero z,w Є Fnro such that zw = 0. Then, by Lemma 4.4, Dnr ( z) Dnr ( w) ≡ 0 (mod p) , so either Dnr ( z) = 0 (mod p) or DnT ( w) ≡ 0 (mod p) .
To see (b): if xn - r is reducible in ℚ[x] then there are non-zero z, w Є ℚ rn such that zw = 0. Even more, we can find non-zero vectors
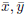 Є ℤn such that z'w' = 0 where z' =
Є ℤn such that z'w' = 0 where z' =
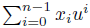 and w' =
and w' =
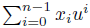 (here u determines the basis of ℚrn as a ℚ-vector space). Therefore Drn(x̄)Drn(
(here u determines the basis of ℚrn as a ℚ-vector space). Therefore Drn(x̄)Drn(
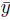 ) = 0, so Drn(x̄) = 0 or Drn(
) = 0, so Drn(x̄) = 0 or Drn(
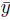 ) = 0.
) = 0.
Now we show (c). Assume that xn ≡ r (mod p) has a solution t, that is, tn ≡ r (mod p).
Consider the set
and let
Note that Sn has more than p elements (because n ≥ 2). Now define the function f : Sn - 𝔽p by
Since 𝔽p has p many elements, Sn has more elements than 𝔽p, so by the pigeonhole principle there are two (m0, ..., mn-1) ≠ (m'0, ..., m' n-1) in Sn such that f (mo,..., mn-1) = f (m'0, ..., m' n-1). For 0 ≤ i < n let ai := m'i - mi, so
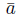 := (ao, ..., an-i) ≠ (0, ..., 0) and -
:= (ao, ..., an-i) ≠ (0, ..., 0) and -
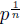 < ai <
< ai <
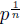 , We show that
, We show that
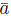 is as desired.
is as desired.
We proceed in a similar way as in the proof of (a) first assuming that xn - r is irreducible in ℚ[x]. Then K := ℚ rn = ℚ (v) is a field extension of ℚ with v =
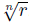 , and it is isomorphic to 𝕄rn(ℚ) by Lemma 4.4. Set A := Mrn(
, and it is isomorphic to 𝕄rn(ℚ) by Lemma 4.4. Set A := Mrn(
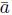 ). Since this matrix is not zero, it is invertible, so A-1 Є 𝕄rn(ℚ), and even more B := adj(A) Є 𝕄rn(ℤ) by Lemma 4.5. So choose y Є ℤ n such that B = Mrn (
). Since this matrix is not zero, it is invertible, so A-1 Є 𝕄rn(ℚ), and even more B := adj(A) Є 𝕄rn(ℤ) by Lemma 4.5. So choose y Є ℤ n such that B = Mrn (
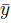 ).
).
Since K is ℚ[x]/(q(x)) with q(x) := xn - r, we have that A = Mrn (g(x) (mod (q(x)))) and B = Mrn(h(x) (mod (q(x)))) where
Since AB = |A|In, we get that xn - r divides g(x)h(x) - |A| in ℚ[x], and actually in ℤ[x] because both polynomials have coefficients in ℤ and xn - r is monic. Then g(x)h(x) = j(x)q(x) + |A| for some j(x) Є ℤ[x].
To finish the proof, note that g(t)h(t) - |A| = (tn - r)j(t) ≡ 0 (mod p), so g(t)h(t) = |A| (mod p). On the other hand, we know that g(t) ≡ f (α0, ..., αn-1) = 0 (mod p) so |A| = 0 (mod p) , that is, Dn(α0 , … , αn-1) ≡ 0 (mod p) .
For the general proof of (c) we work in Fn , which is isomorphic to Mn( F) . Again set A := Mrn (
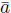 ) which is in Mrn (F ), so B := adj(A) Є 𝕄rn (F ) by Lemma 4.5. Like above, since AB = |A| In we have two polynomials g(x) , h( x) Є F[x] , which g( x) as above, such that xn - r divides g(x)h(x) - |A|, so g(x)h(x) = j (x)q(x) + |A| for some j(x) Є F[x]. Exactly as in the last part of the previous argument, we conclude that Drn(
) which is in Mrn (F ), so B := adj(A) Є 𝕄rn (F ) by Lemma 4.5. Like above, since AB = |A| In we have two polynomials g(x) , h( x) Є F[x] , which g( x) as above, such that xn - r divides g(x)h(x) - |A|, so g(x)h(x) = j (x)q(x) + |A| for some j(x) Є F[x]. Exactly as in the last part of the previous argument, we conclude that Drn(
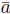 ) ≡ 0 (mod p).
) ≡ 0 (mod p).
Thanks to the results in Section 4, the previous result takes a simple form when n is a prime.
Corollary 5.2. Let p and q be primes. Then the equation xq ≡r (mod p) has a solution iff the equation Dqr(x0, ..., xn-1) = 0 (mod p) has a non-trivial solution.
Proof. The direction from left to right follows from Theorem 5.1(c). For the converse, if the equation xq ≡ r (mod p) does not have a solution then the polynomial xq - ro is irreducible in 𝔽p[x] by Corollary 4.8 where r0 Є 𝔽p is the residue of r modulo p, so Dqr( x0 , … , xn-1) ≡ 0 (mod p) does not have a non-trivial solution by Theorem 5.1(a).
The next result is Theorem C, which is a weakening of (2) ⇒ (1) of Problem 1.9. This actually checks this implication when n is a prime (for any r Є ℤ).
Theorem 5.3. Assume that p is a prime, r Є ℤ, r = ro (mod p) with ro Є 𝔽p and n ≥ 2.
If the polynomial xn - r0 is irreducible in 𝔽p[x] then Drn (x0, ..., xn-1) = p does not have a solution in the integers.
In particular, if q is a prime and xq ≡ r (mod p) does not have a solution then Drq(x0, ..., xn-1) = p does not have a solution in the integers.
Proof. By Theorem 5.1, if xn - r0 is irreducible in 𝔽p[x] then Drn (x0…,xn-1) ≡ 0 (mod p) does not have a non-trivial solution. Thus, if Dnr ( x0, … , xn-1 ) = p has a solution α0, ..., αn-1 Є ℤ, then every must be a multiple of p. But this implies that Dnr (α 0, ..., αn-1) is a multiple of pn, so it cannot be equal to p because n ≥ 2.
We can use Theorem 5.1 to solve Problem 1.9 for n = 2, i.e., Theorem 1.8. In fact, this is valid for -1 and -2 in the place of 2, which yield well known results.
Theorem 5.4. Let r Є {-2, -1, 2}. If p is a prime then the equation x2 ≡ r (mod p) has a solution iff the equation Dr2(x0,x1) = p has a solution in the integers.
Proof. One implication follows by Theorem 5.3 because 2 is prime. So we show that, whenever x2 ≡ r (mod p) has a solution, the equation D2r ( x0 , x1) = p has a solution in the integers, for r Є {- 2, - 1 , 2} .
By Corollary 5.2, the equation D2r (x0,x1) = 0 (mod p) has a non-trivial solution (a,b). Hence p divides D2q (α, b) ≡ α2 - b2r. According to Theorem 5.1(c), we can find a and b between -p
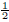 and p
and p
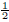 .
.
Case r = 2. We claim that - 2p < α 2 - 2b 2 < p. Two cases: if α 2 ≥ 2b 2 then 0 ≤ α 2 - 2b 2 ≤ α 2 < p; if α 2 < 2b 2 then - 2p < - 2b 2 ≤ α 2 - 2b 2 < 0, so the claim follows.
Now, since - 2p < D 2 2 (α, b) = α 2 - 2b 2 < p and p | D 2 2 ( a, b) , we must have that D 2 2 ( a, b) = - p (it can not be zero because p must not divide both a and b).
Note that D 2 2 (1 , 1) = 12 -2 . 12=-1, SO
Hence x 0 : = α + 2b and x i = α + b form an integer solution of D 2 2 (x 0 , x 1 ) = p. Case r = -1. It is clear that 0 < α 2 + b2 < 2p, so α 2 + b 2 = p.
Case r = -2. Note that 0 < α
2
+ 2b
2
< 3p, so either α
2
+ 2b
2
= p or α
2
+ 2b
2
= 2p. In the first case we are done; in the second case a must be even, so a = 2 α
0
for some a
o
Є ℤ, and 2p = α
2
+ 2b
2
= + 2b
2
, hence D
-2
(b, α
0
) = p.
6. Discussions
Problem 1.9 cannot be generalized by simply replacing 2 by any r Є ℤ. For n = 2, it is known it is fine for r Є {-2, -1, 2} as shown in Theorem 5.4, but other values of r are problematic. For example, 3y 2 + p is never a square when p ≡ 3 (mod 4) (because it is 3 or 2 modulo 4), so D 3 2 (x, y) = p does not have a solution for those p. However, there are primes p = 3 (mod 4) such that x 2 ≡ 3 (mod p) has a solution, for example, p =11. In this case, it could be conjectured that the equation D 3 2 (x, y) = p has a solution iff x 2 ≡ 3 (mod p) has a solution and p = 1 (mod 4). This motivates:
Problem 6.1. For n ≥ 2 (particularly n = 2) and r Є ℤ (or just free of n-powers), what are suitable necessary and sufficient conditions for a prime p to get that D r n (x̄) = p has a solution in the integers?
As discussed in the introduction, the solution of Problem 1.9 should be related to the characterization of primes (or irreducible) elements in ℤ
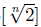 , which looks very complex for general values of n. In the post [10] it is hinted that Problem 1.9 is true for n = 3 by looking at ℤ
, which looks very complex for general values of n. In the post [10] it is hinted that Problem 1.9 is true for n = 3 by looking at ℤ
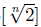 with tools that we did not deal with in this paper.
with tools that we did not deal with in this paper.
Some results of Section 5 can be generalized when x n - r is replaced by any monic polynomial in ℤ[x]. If R is an integral domain and q(x) Є R [x] is a monic polynomial of degree n > 0, the theory in the first part of Section 4 can be generalized in the context of R q (x) : = R[x]/(q(x)):
(I) R q ( x ) is a free R-module (and an R-algebra) with basis {1,u, ... ,u n-1 } where u := x (mod (q(x)))
(II) For any z Є R q ( x ) there is a unique matrix M q ( x )(z) that characterizes the endo-morphism R q ( x ) - R q ( x ), w - zw as in Lemma 4.3.
(III) Set 𝕄 q(x) := 𝕄 q(x) (R) = {M q(x) (z) : Z Є R q(x) }. The function M q(x) : R q(x) → 𝕄 q(x) is an R-algebra isomorphism.
(IV) For any z Є R q(x) set D q(x) (z) := | M q(x) (z)|. Then, for any z,z' Є R q(x) ,
When x̄ = (xo, ..., x
n1
) Є
R,
denote D
q(x)
(x̄) := D
q(x)
(z) where z =
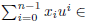 R
q(x)
.
R
q(x)
.
(V) If A Є 𝕄 q(x)(R) then adj(A) Є 𝕄 q(x) (R).
Using this theory, we obtain the following results (with similar proofs as in Section 5).
Theorem 6.2. Let p be a prime, q(x) Є ℤ[x] α monic polynomial of degree n> 0, and let qo(x) Є 𝔽 p [x] be the polynomial resulting from q(x) by changing its coefficients by their residues modulo p. Then:
(1) qo(x) is irreducible in 𝔽 p [x] iff the equation D q ( x )(x 0 , ..., x n-1 ) ≡ 0 (mod p) does not have a non-trivial solution in the integers.
(2) If q(x) is reducible in ℚ [x] then the equation D q ( x )(x̄) = 0 has a non-trivial solution in the integers.
(3) If n ≥ 2 and the equation q
0
(x) ≡ 0 (mod p) has a solution then the equation D
q
(
x
) (x
0
, ... ,x
n-1
) ≡ 0 (mod p) has a non-trivial solution in the integers with -
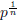 < xi <
< xi <
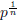 for any i.
for any i.
(4) If n ≥ 2 and qo(x) is irreducible in 𝔽 p [x] then the equation D q ( x )(x̄) = p does not have a solution in the integers.
As a digression, the equation D 2 3 (x o ,x 1 ,x 2 ) = p motivates the following.
Problem 6.3. Assume that a,b,c Є {1, 2, 3} and that p is a prime. Does the equation x a + 2y b + 4z c = p have a solution in the integers?
Table 1 Instances among the first 1000 primes where a solution of x a + 2y b + 4z c = p was not found in Wolfram Mathematica with the command Findlnstance, in the case when at least two of a,b,c are equal to 3.
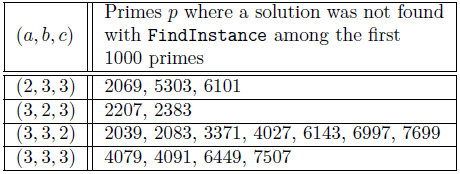
Table 2 First four prime p instances where a solution of x a + 2yb + 4zc = p was not found in Wolfram Mathematica with the command Findlnstance, in the case when only one of a,b,c is equal to 3.

For any p Є ℤ (not necessarily prime): it is easy to find a solution when either a, b or c is equal to 1; and the case a = b = c = 2 has a positive answer, as mentioned in [1, §13.3, Prob. 8(a)].
So this leaves the case 2 ≤ min{a, b, c} ≤ max{a, b, c} = 3. By running computations in Wolfram Mathematica with the command Findlnstance (see below), a solution was not found for some primes in all the subcases (but this is not a proof that the solution does not exist).
See details in Tables 1 and 2: in Table 1 we look at the case when at least two of a, b, c are equal to 3, where solutions were not found for some primes below 10000; in Table 2 we look at the case when only one of a, b, c is equal to 3, where solutions were not found for some primes beyond 20000.