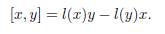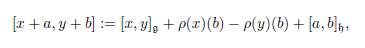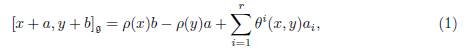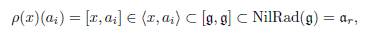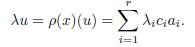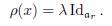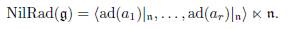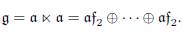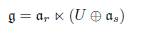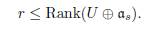1. Introduction

First, let us emphasize that throughout this work, we understand that negative means less than or equal to zero. In geometry, a really important problem is to determine which connected Lie groups admit a left invariant Riemannian metric with negative sectional curvature. The work of professors J. A. Wolf and E. Heintze shows that this problem is closely related to the classification of connected, homogenous Riemannian manifolds with negative curvature (see [¹³], [⁷]). So, motivated by this, the aim this work is to completely describe two families of Lie groups with negative sectional curvature through their Lie algebras.

In 1976 professor J. Milnor published the paper Curvature of Left Invariant Metrics on Lie Groups (see [⁹]). In this survey, as its title suggests, he described the properties of the curvature of a large class of Riemannian manifolds, namely, Riemannian Lie groups, i.e., Lie groups endowed with a left-invariant Riemannian metric. In this work, professor Milnor proved many results that are classic and well-known nowadays, and he also conjectured many new ones. Through the years some of these conjectures have been proved, for example, Uesu (see [¹²], 1981) proved that in a Riemannian Lie group the central elements u ∈ g are the only ones that satisfy K(u, v) ≥ 0 for all v ∈ g (see Corollary 1.3. in [⁹]); on the other hand, Cairns (see [⁴], 2017) recently stated that “motivated by classic results (that is, motivated by [⁹]), we determine the subsets of a given nilpotent Lie algebra g whose sign of Ricci curvature remains unchanged for an arbitrary choice of a positive definite inner product on g”.

In particular, the work of professor Milnor [⁹] presented examples of Riemannian Lie groups with constant negative sectional curvature. More precisely, in the special example 1.7, two equivalent conditions are given to ensure constant negative sectional curvature on a connected Lie group, and these conditions are formulated in terms of the corresponding Lie algebra:

(P1) For all x, y ∈ g, the Lie product [x, y] is always equal to a linear combination of x and y,

(P2) There exists a linear map l ∈ g^∗ such that, for all x, y ∈ g

We need to point out that the (P1) and (P2) conditions have been studied in several works. For example, in the work of Barnet (see [²]), a Lie algebra satisfying the (P1) condition is called a Lie algebra of special type, and thus, a Lie group is called of spe-cial type if its Lie algebra g is of special type. In this work, it is stated that every left-invariant Riemannian metric on a Lie group of special type is of constant negative sectional curvature (see the first paragraph in the introduction of [²]). A second example can be found in the work of Reyes (see [¹¹]), where the Lie groups associated to a Lie algebra satisfying the (P2) condition are explicitly calculated. As the last examples, we shall mention that in [⁶] and [⁸], a Lie algebra satisfying the (P1) condition is called a modular Lie algebra because its associated lattice of subalgebras is a modular lattice.

On the other hand, we are also interested in studying a second family of Lie groups with negative sectional curvature. This family consists of Lie groups whose Lie algebras are reduced Lie algebras of Iwasasa type. Following [¹⁴], all symmetric spaces of non-compact type with a metric induced by the Killing form have contact Ricci curvature. By the Iwasawa decomposition Theorem, these spaces can be identified with solvable Lie groups whose Lie algebras are of Iwasawa type. Moreover, the results of R. Azencott and E. Wilson imply that Lie groups of Iwasawa type always admit left invariant metrics of non-positive sectional curvature (see [¹]).

In order to completely describe both families of Lie groups, we shall use the very well-known theory of Lie algebras. We shall use the well-known classification of nilpotent Lie algebras given by Gong in [⁵], as well as the Lie algebra of derivations of these Lie algebras.

This paper is organized as follows: Section 2 is devoted to understand the Lie algebras that satisfy the (P1) condition, and to prove our main result given by Theorem 2.9. Section 3 is devoted to completely describe the Lie algebras associated to Lie groups of Iwasawa type. To do this, we consider two cases depending on whether the nilradical of a Lie algebra is abelian or not. In the non-abelian case we use the existence of a maximal abelian ideal contained in the nilradical to describe all reduced Lie algebras of Iwasawa type. Finally, Section 4 is devoted to listing all low-dimensional Lie algebras of Iwasawa type having an indecomposable nilradical.

2. Lie algebras satisfying the (P1) condition

Let g be a finite dimensional complex Lie algebra. We say that g satisfies the (P1) condition if g satisfies the condition given by Milnor in [⁹], namely, given x, y ∈ g, the Lie product [x, y] is always equal to a linear combination of x and y. This condition is equivalent to the fact that the linear subspace x, y is a Lie subalgebra of g.

From the (P1) condition, the following Lemma is easy to prove:

Lemma 2.1. Let g be a Lie algebra. Then, the following statements are equivalent

On the other hand, recall that the space of derivations of a Lie algebra g is given by Der(g) := {D ∈ End(g) | D([x, y]) = [Dx, y] + [x, Dy] for all x, y ∈ g}, and a straightfor-ward calculation shows that Der(g) is a Lie algebra. Now, let g and h be Lie algebras, we say that g acts on h by means of derivations if there is a homomorphism of Lie algebras ρ: g → Der(h). Then the vector space g ⊕ h is a Lie algebra defining the Lie bracket as follows:

for all x, y ∈ g, a, b ∈ h. This Lie algebra is called the semidirect sum of g and h, and it is denoted by

As a consequence of Lemma 2.1, we can state the following result:

Lemma 2.2. Let g be a Lie algebra satisfying the (P1) condition.

Now, we can provide a characterization of a nilpotent Lie algebra in terms of its 2-dimensional Lie subalgebras:

Lemma 2.3. Let g be a Lie algebra. Then the following conditions are equivalent:

Proof. Let h ⊂ g be a 2-dimensional Lie subalgebra. Clearly, such h is nilpotent and thus, it is abelian. On the other hand, suppose that any 2-dimensional Lie subalgebra of g is abelian. For any x ∈ g − {0} consider the linear transformation ad(x), and let λ be one of its eigenvalues and y be the corresponding eigenvector. Since x, y is a 2-dimensional Lie subalgebra of g, it follows that λ = 0, that is, ad(x) is a nilpotent linear transformation for all x ∈ g. Then g is a nilpotent Lie algebra.

Lemma 2.4. Let g be a Lie algebra satisfying the (P1) condition. Then g is a solvable Lie algebra.

Proof. Let us suppose that g = g_L ⋉ Rad(g) where g_L is a Levi subalgebra of g and Rad(g) is the radical of g. Let x_E ∈ g_L be a nilpotent element, then the Morozov-Jacobson Lemma implies that there exist elements x_F , x_H ∈ g_L such that [x_E, x_F ] = x_H .

In other words, if g_L #= {0}, then g does not satisfy the (P1) condition.

As usual, let us denote by NilRad(g) the maximal nilpotent ideal of a Lie algebra g. Clearly, NilRad(g) ⊂ g.

Lemma 2.5. Let g be a solvable Lie algebra satisfying the (P1) condition. Then NilRad(g) is abelian.

Proof. From Lemma 2.2 follows that NilRad(g) satisfies the (P1) condition. Let {u₁, . . . , u_r} be a basis of NilRad(g). Then, for each i #= j, Lemma 2.1 implies that ⟨u_i, u_j⟩ is a 2-dimensional Lie subalgebra of NilRad(g), then ⟨u_i, u_j⟩ is abelian, and hence, [u_i, u_j ] = 0 for all i, j = 1, . . . , r.

If g is a solvable Lie algebra satisfying the (P1) condition, let us denote by a_r = NilRad(g) its abelian nilradical. As a vector space, g can be decomposed as a direct sum of vector spaces, g = h ⊕ a_r, where h is a complementary subspace of a_r. In this case, observe that the Lie algebra structure of g is completely determined by the following data:

Thus, if {a₁, . . . , a_r} is a basis for a_r, the Lie bracket of g can be written in terms of the data (ρ, θⁱ) as follows:

where x, y ∈ h and a, b ∈ a_r.

Lemma 2.6. Let g be a solvable Lie algebra satisfying the (P1) condition. Let (ρ, θⁱ) be the data characterizing the Lie bracket of g, as in Equation (1). Then:

Proof. We have that, as vector space, g = h ⊕ a_r, where a_r is the nilradical of g and h is a complementary subspace of a_r. Let {a₁, . . . , a_r} be a basis for a_r. From Equation (1) follows that for any x, y ∈ h, [x, y]_g = Σ^r _i=1 θⁱ(x, y)α_i ∈ x, y if and only if θⁱ(x, y) = 0 for all i = 1, . . . , r. Hence, h is an abelian Lie algebra.

Now, let x ∈ h and consider the linear transformation ρ(x). If we evaluate ρ(x) in any basis element a_i, we have that

therefore, there exists λ_i ∈ 𝔽 such that ρ(x)(α_i) = λ_iα_i.

On the other hand, let u ∈ ar be a linear combination of the basis elements {α₁, . . . , α_r}, that is, u = Σ^r _i=1 c_iα_i where c_i ∈ 𝔽 (i = 1, . . . , r). The previous argument shows that

Thus, λc_i = λ_ic_i for all i = 1, . . . , r and all c_i ∈ 𝔽. Therefore, we get that λ = λ_i for all i = 1, . . . , r and we conclude that

Lemma 2.6 implies that a solvable Lie algebra satisfying the (P1) condition can be written as the semidirect product of two abelian Lie algebras, namely, if a_k denotes the abelian Lie algebra h in (1) of Lemma 2.6, then g = a_k ⋉_ρ a_r. Thus, the next result follows easily:

Corollary 2.7. Let g = a_k ⋉_ρ a_r be a solvable Lie algebra satisfying the (P1) condition.

Then, NilRad(g) = a_r if and only if k = 1.

As a consequence, we get the main theorem of this section:

Theorem 2.8. Let g be a Lie algebra satisfying the (P1) condition. Then g is isomorphic to one of the following Lie algebras:

3. Lie algebras of Iwasawa type

We start with the following:

Definition 3.1. A simply connected solvable Lie group G is said to be of Iwasawa type if its Lie algebra g satisfies the following conditions:

If G is a Lie group of Iwasawa type, it is said that its Lie algebra g is of Iwasawa type.

It follows that a Lie algebra g of Iwasawa type satisfies conditions (1)-(3) of Definition 3.1 above. The aim of this section is to completely describe this kind of Lie algebras.

Lemma 3.2. Let g = α + n be a Lie algebra of Iwasawa type. Then g can be decomposed as a direct sum of Lie algebras, g = α_r ⊕ h, where h = α_s + n is a Lie algebra of Iwasawa type such that NilRad(h) = n and α_r is an abelian Lie algebra such that α = α_r ⊕ a_s.

Proof. Since g = a + n is a Lie algebra of Iwasawa type, it is clear that n = [g, g] ⊂ NilRad(g). Moreover, if n ̸= NilRad(g), then there exist α₁, . . . , a_r ∈ a such that

This implies that ad(α_i) = 0, i = 1, . . . , r, which proves the Lemma.

Observe that Lemma 3.2 reduces the problem of studying Lie algebras g of Iwasawa type to the problem of studying Lie algebras of Iwasawa type satisfying that NilRad(g) = n.

Definition 3.3. A Lie algebra of Iwasawa type g = a + n is called reduced if it satisfies NilRad(g) = n.

From now on, without loss of generality, we can suppose that g is a reduced Lie algebra of Iwasawa type.

Lemma 3.4. Let g be a solvable Lie algebra of Iwasawa type. Then Z(g) = {0}.

Proof. Note that Z(g) ⊆ n, and let x be a non-zero element in Z(g), then for all a ∈ a, we have that ad(a)(x) = 0.

To describe the reduced Lie algebras of Iwasawa type, Lemma 3.4 implies that it is enough to study two cases: (a) reduced Lie algebras of Iwasawa type having an abelian nilradical, and (b) reduced Lie algebras of Iwasawa type having a non-abelian nilradical. Our next task is to study both cases.

3.1. Reduced Lie algebras of Iwasawa type having an abelian nilradical

Let us recall that the 2-dimensional Lie algebra e₁, e₂ defined by [e₁, e₂] = e₂ is called the affine Lie algebra and it is denoted by af₂.

Proposition 3.5. Let g = α + n be a complex reduced Lie algebra of Iwasawa type having an abelian nilradical. If dim α = dim n, then

Proof. Clearly, from the assumption follows that n = α. Now, we can apply Theorem 3 from [¹⁰] to get the desired conclusion.

Observe that in any other case, if g = a + n is a reduced Lie algebra of Iwasawa type having an abelian nilradical, then dim a < dim n. Therefore, ad(a) ⊂ gl(n), and there exists an invertible element with positive real part for each eigenvalue, and thus ad(α) is a semisimple linear map for any α ∈ α.

Lemma 3.6. Let a and n be Lie algebras and let ρ_i: α → gl(n) be a linear representation, i = 1, 2. Then ρ₁ ≃ ρ₂ if and only if, there exists an isomorphism T ∈ Aut(n) such that ρ₁(x) = T ⁻¹ ◦ ρ₂(x) ◦ T for all x ∈ α.

Let g = α + n be a Lie algebra of Iwasawa type having an abelian nilradical, then α = α_r and n = a_k with r ≤ k. Let us suppose that r < k. Then we can state the following result:

Proposition 3.7. Let g_i = α_r ⋉_ρi α_k be a Lie algebra of Iwasawa type, i = 1, 2. Then g₁ ≃ g₂ if and only if ρ₁(α_i) = ρ₂(α_i), i = 1, . . . , r, and α_r = {α₁, . . . , α_r} .

3.2. Reduced Lie algebras of Iwasawa type having a non-abelian nilradical

Let g be a finite-dimensional Lie algebra. Let us denote by α(g) the maximal dimension of an abelian subalgebra of g, and by β(g) the maximal dimension of an abelian ideal of g. Both quantities α(g) and β(g) are useful invariants associated to g. In this direction, let us recall a result proved by Burde and Ceballos (see [³]):

Theorem 3.8. Let g be a solvable Lie algebra over an algebraically closed field F of characterstic zero. Then β(g) = α(g).

On the other hand, suppose that g = a + n is a complex reduced Lie algebra of Iwasawa type. Let t be a commutative subalgebra of Der(n) consisting of semisimple endomor-phisms. Such t is called a torus on n. Then we define Rank(n) as the dimension of a maximal torus over n.

Now, from Theorem 3.8 we can obtain the following Corollary:

Corollary 3.9. Let g = a + n be a complex reduced Lie algebra of Iwasawa type. Then there exists an abelian ideal b ⊆ n such that dim a ≤ dim b. Moreover, dim a ≤ Rank(n).

Although there is not a complete classification of nilpotent Lie algebras, from Theorem 3.8 we can conclude that if g is a complex reduced Lie algebra of Iwasawa type, then g is a semidirect sum of Lie algebras, namely,

where n = U ⊕ α_s and a_s is a maximal abelian ideal of n and U is a complementary subspace of α_s, i.e., r ≤ s and moreover

Remark 3.10. Let n = U ⊕ a_s be an idecomposable nilpotent Lie algebra. To construct a Lie algebra g of Iwasawa type from such n, the fact that r ≤ Rank(U ⊕ α_s) indicates that we can only add a tours α_r to n if and only if r ≤ Rank(n).

In the next section, we will use Remark 3.10 to provide a complete list of low-dimensional complex Lie algebras of Iwasawa type.

4. Low-dimensional reduced Lie algebras of Iwasawa type

The goal of this section is to construct all low-dimensional complex Lie algebras of Iwa-sawa type. For doing this, we will use the well-known classification of low-dimensional indecomposable nilpotent Lie algebras, and we proceed in the following way: first, for each indecomposable nilpotent Lie algebra n we compute its maximal abelian ideal α _s, and as a consequence we obtain the invariant α(n). Then, for such indecomposable n, we compute its Lie algebra of derivations, Der(n), and the subspace of semisimple deriva-tions in n, Der_S(g), i.e., we obtain Rank(n). Finally, we apply Remark 3.10 to construct the reduced complex Lie algebras of Iwasawa type.

4.1. Low-dimensional indecomposable nilpotent Lie algebras

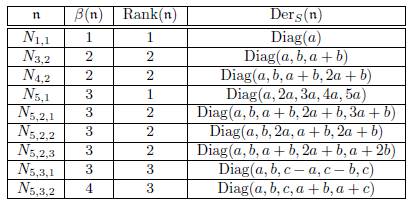
Following the notation used by Gong (see [⁵]), we provide the complete list of indecom-posable non-isomorphic nilpotent Lie algebras n having dimension less than or equal to 5. In this list, N_i,j,k denotes the k-th algebra of dimension i and rank j. When there is only one algebra with the specified dimension and rank, we simply denote it by N_i,j.

• Dimension 3, N_3,2: = h₃, [e₂, e₃] = e₁.

• Dimension 3, N_3,2: = h₃, [e₂, e₃] = e₁.

• Dimension 4, N_4,2, [e₁, e₂] = e₃, [e₁, e₃] = e₄.

• Dimension 5

1. N_5,1, [e₁, e₂] = e₃, [e₁, e₃] = e₄, [e₁, e₄] = e₅, [e₂, e₃] = e₅.

2. N_5,2,1, [e₁, e₂] = e₃, [e₁, e₃] = e₄, [e₁, e₄] = e₅.

3. N_5,2,2, [e₁, e₂] = e₄, [e₁, e₄] = [e₂, e₃] = e₅.

4. N_5,2,3, [e₁, e₂] = e₃, [e₁, e₃] = e₄, [e₂, e₃] = e₅.

5. N_5,3,1 = h₅, [e₁, e₂] = [e₃, e₄] = e₅.

6. N_5,3,2, [e₁, e₂] = e₄, [e₁, e₃] = e₅.

In the following table we describe an indecomposable nilpotent Lie algebra g, β(g), Rank(g) and, in the last column we describe a basis for the subspace of semisimple derivations in g, Der_S(g).

Now, for each indecomposable nilpotent Lie algebra n having dimension less or equal than five, straightforward calculations allow us to obtain β(n) the maximal dimension of an abelian ideal of n, Rank(g) the dimension of a maximal torus over n, and a basis for Der_S(n) the subspace of semisimple derivations in n. This information is summarized in Table 1 below.

Table 1 Indecomposable nilpotent Lie algebras having dimension less or equal than 5. 

These examples of low-dimensional indecomposable nilpotent Lie algebras suggest the following definition:

Definition 4.1. Let g = α + n be a complex reduced Lie algebra of Iwasawa type. We say that a is maximal if dim α = Rank n.

Lemma 4.2. Let g = a + n be a complex non-maximal reduced Lie algebra of Iwasawa type. Then there exists a complex maximal reduced Lie algebra of Iwasawa type h = b + n such that g ⊂ h.

Observe that Lemma 4.2 implies that we only need to construct maximal reduced Lie algebras of Iwasawa type. Thus we can state the following result:

Theorem 4.3. Let g = a + n be a complex Lie algebra of Iwasawa type such that n is an indecomposable nilpotent Lie algebra and a is a maximal abelian Lie algebra. Then g is isomorphic to:

1. dim g = 2, g ≃ af₂ = a₁ ⋉ a₁.

2. dim g = 5, g ≃ a₂ ⋉ N_3,2.

3. dim g = 6, g ≃ a₂ ⋉ N_4,2, a₁ ⋉ N_5,1.

4. dim g = 7, g ≃ a₂ ⋉ N_5,2,1, a₂ ⋉ N_5,2,2, a₂ ⋉ N_5,2,3.

5. dim g = 8, g ≃ a₃ ⋉ N_5,3,1, a₃ ⋉ N_5,3,2.