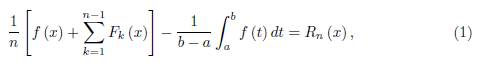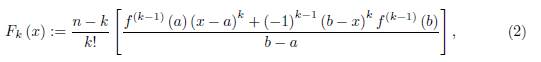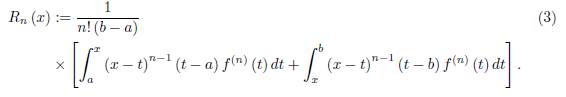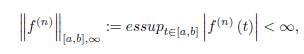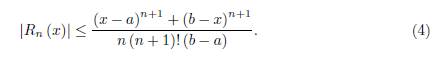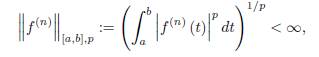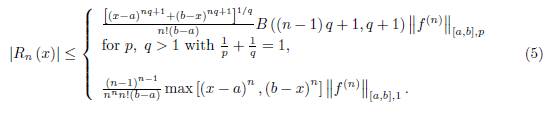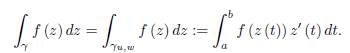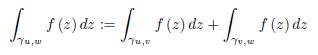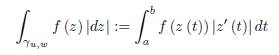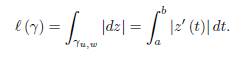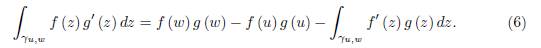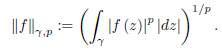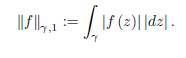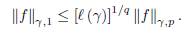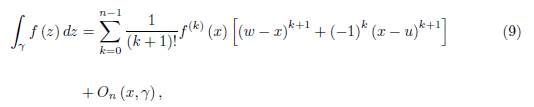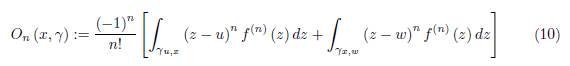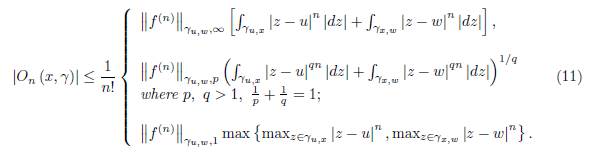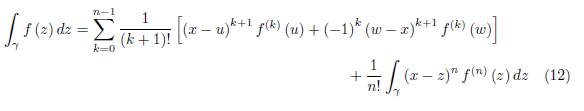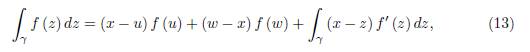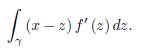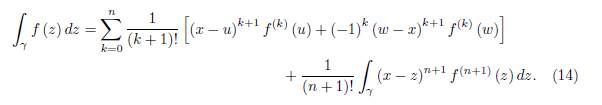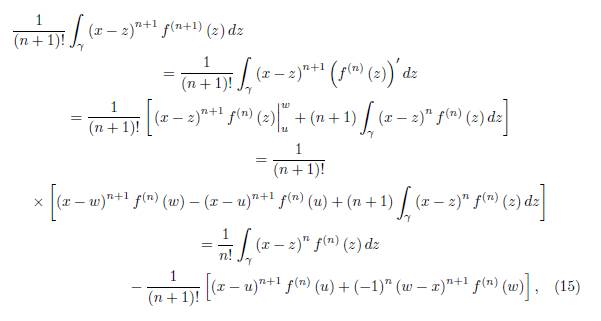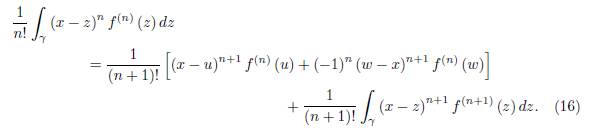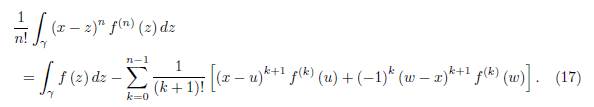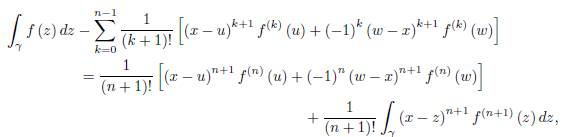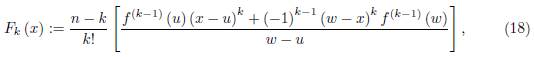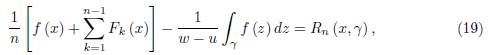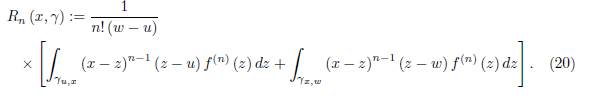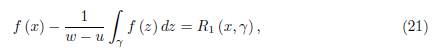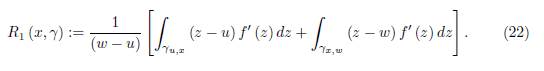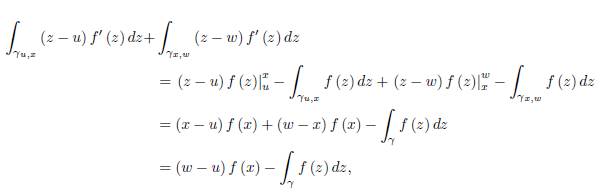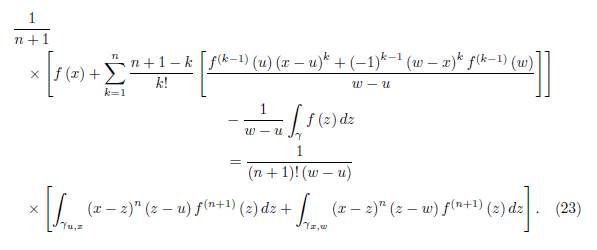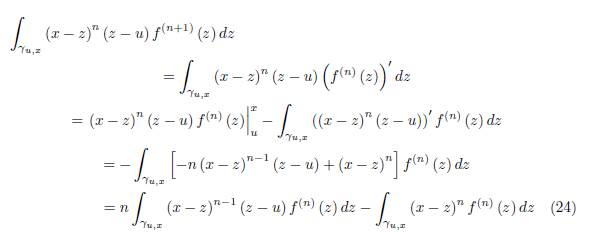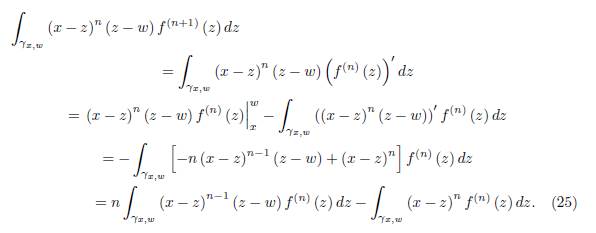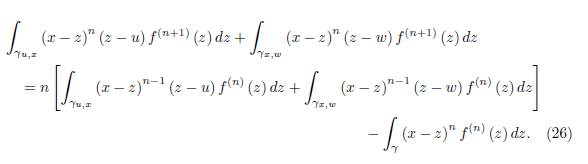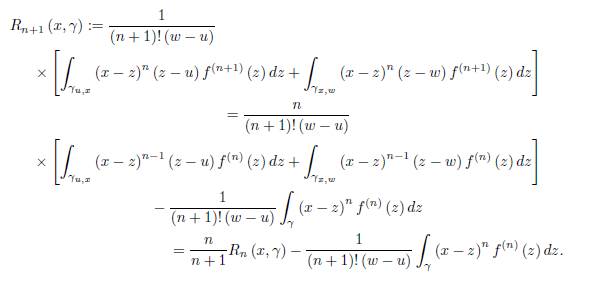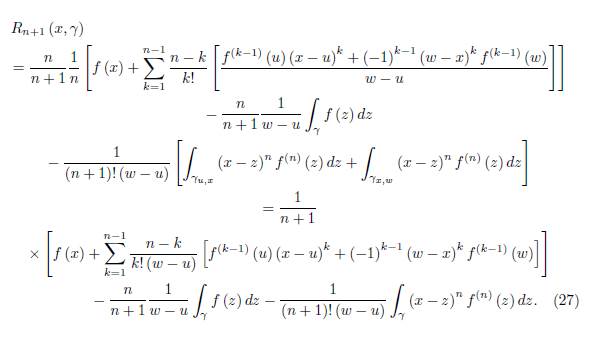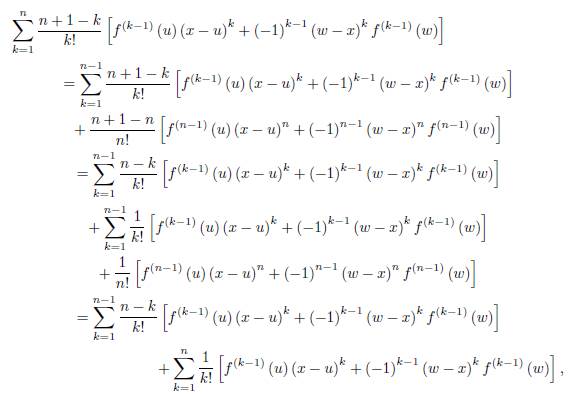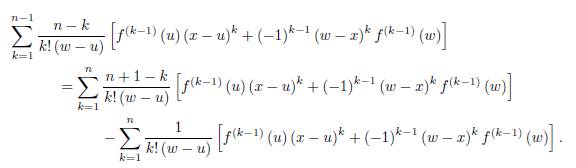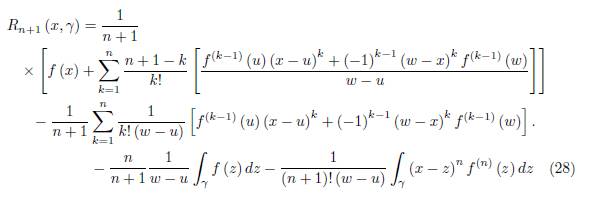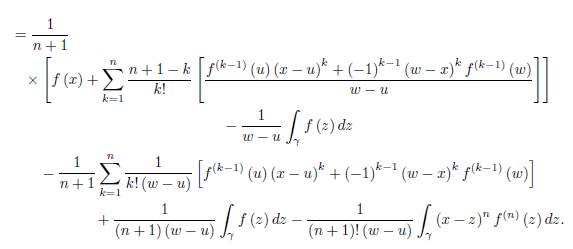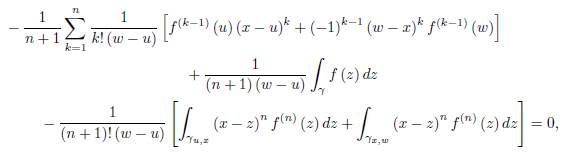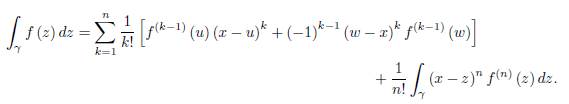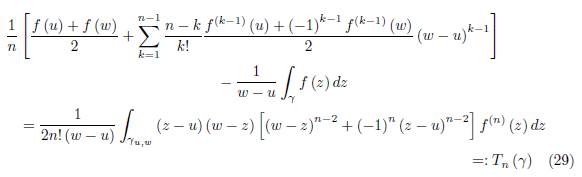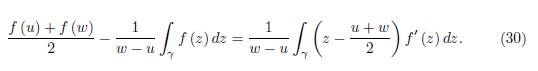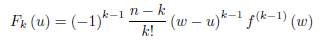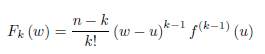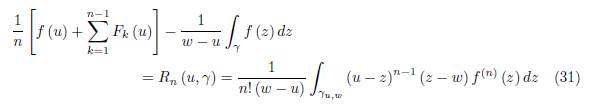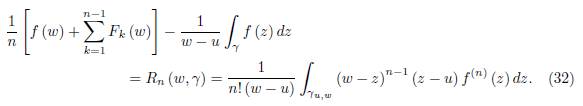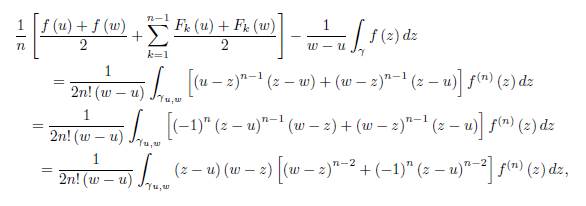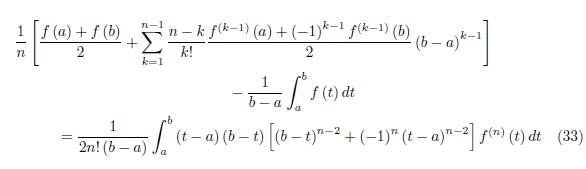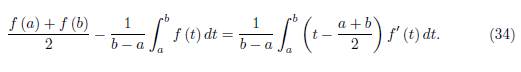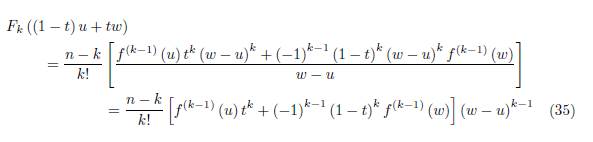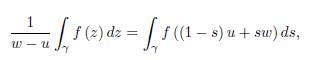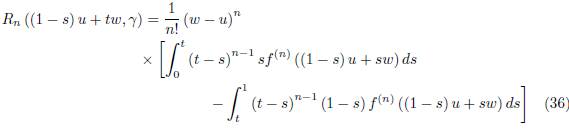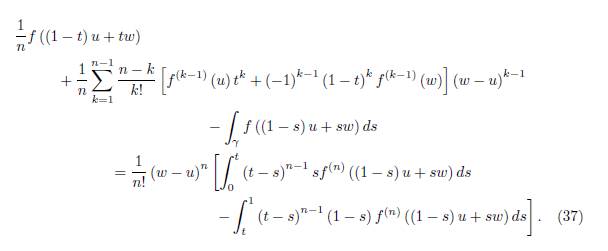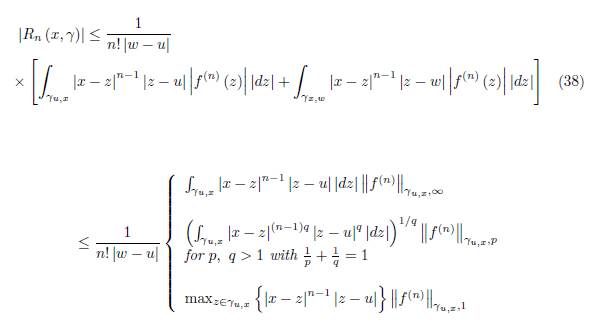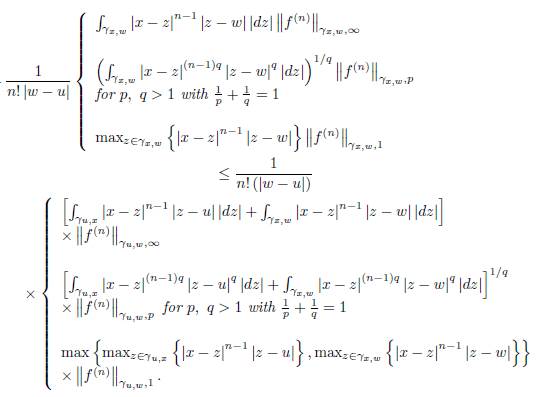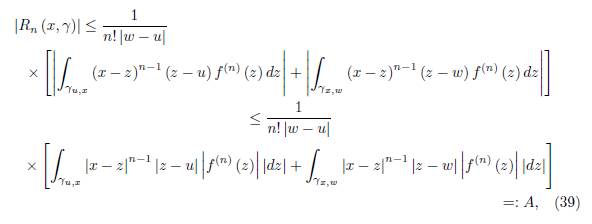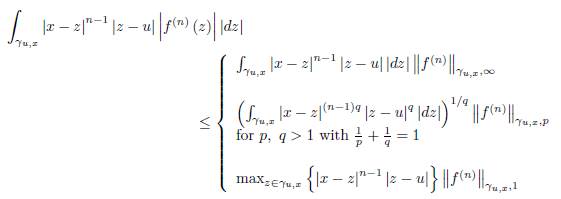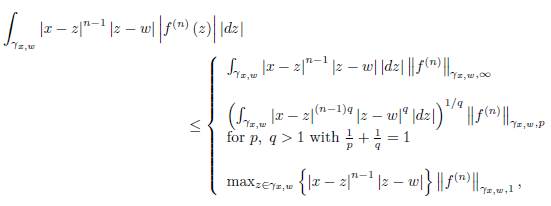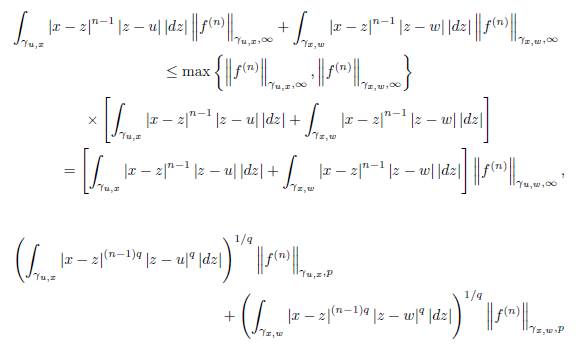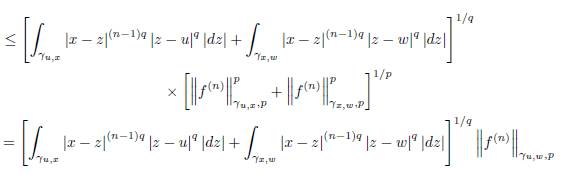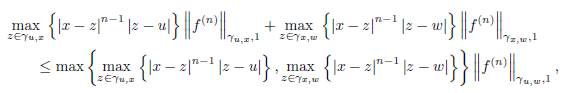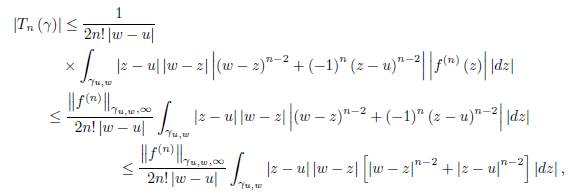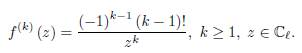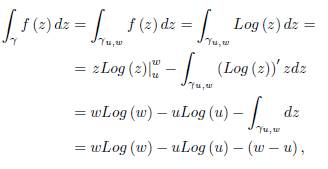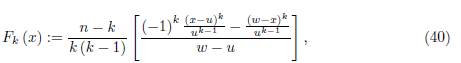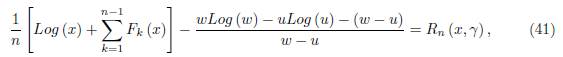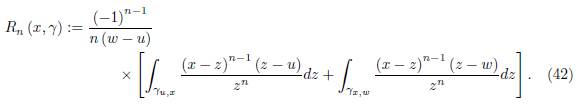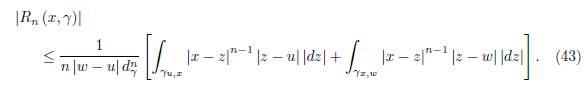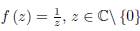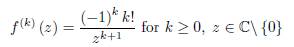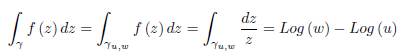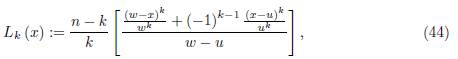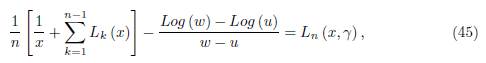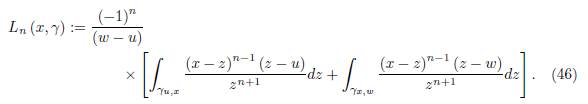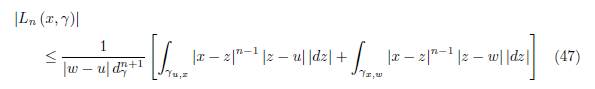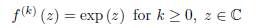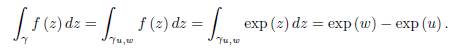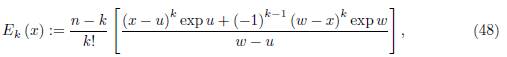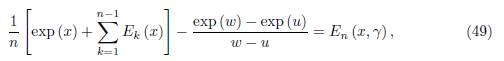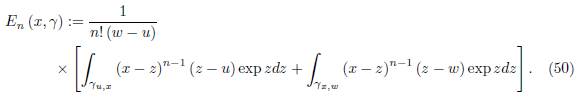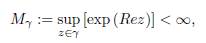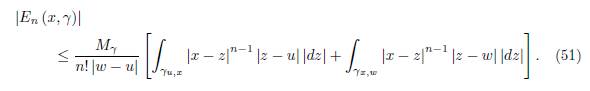1. Introduction

In 1992, [⁶] A. M. Fink obtained the following identity for a function f: [α, b] → ℝ whose (n − 1)-derivative f ⁽ⁿ⁻¹⁾ with n ≥ 1 is absolutely continuous on [α, b]

for x ∈ [a, b] , where

for k = 1, ..., n − 1 where n ≥ 2, and

If n = 1 the sum Σ ⁿ⁻¹ _k=1 F _k (x) is taken to be zero.

In the case f ⁽ⁿ⁾ ∈ L∞ [a, b] , namely

then the following bound for the remainder obtained by Milovanović and Pečarić in 1976, [⁸] holds

In the case of f ⁽ⁿ⁾ ∈ L _p [a, b] , p ≥ 1, namely

then the following bounds for the remainder obtained by Fink in 1992, [⁶] hold

For other results connected with Fink’s identity, see [¹], [²], [³] and [⁷].

In order to extend these results for the complex integral, we need the following preparations.

Suppose γ is a smooth path parametrized by z (t) , t ∈ [a, b] and f is a complex function which is continuous on γ. Put z (a) = u and z (b) = w with u, w ∈ ℂ. We define the integral of f on γ _u,w = γ as

We observe that the actual choice of parametrization of γ does not matter.

This definition immediately extends to paths that are piecewise smooth. Suppose γ is parametrized by z (t), t ∈ [a, b], which is differentiable on the intervals [a, c] and [c, b], then assuming that f is continuous on γ we define

where v: = z (c) . This can be extended for a finite number of intervals.

We also define the integral with respect to arc-length

and the length of the curve γ is then

Let f and g be holomorphic in G, an open domain and suppose γ ⊂ G is a piecewise smooth path from z (a) = u to z (b) = w. Then we have the integration by parts formula

Where

We also define the p-norm with p ≥ 1 by

For p = 1 we have

If p, q > 1 with 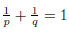, then by Hölder’s inequality we have

For p = ∞ the norm is defined by (8).

In the recent paper [⁴] we obtained the following identity:

Theorem 1.1. Let f: D ⊆ ℂ → ℂ be an analytic function on the domain D and x ∈ D. Suppose γ ⊂ D is a smooth path parametrized by z (t) , t ∈ [a, b] with z (a) = u, z (t) = x and z (b) = w where u, w ∈ D. Then we have the equality

where the remainder On (x, γ) is given by

and n is a natural number, n ≥ 1.

The remainder On (x, γ) satisfies the following bounds

In this paper, we established an identity of Fink type for approximating the integral of analytic complex functions on paths from general domains. Error bounds for these expansions in terms of p-norms were also provided. Examples for the complex logarithm and the complex exponential were given as well.

2. Representation Results

We started with the following preliminary result that was of interest in itself [⁴]. For the sake of completeness, we gave here a short proof as well.

Lemma 2.1. Let f: D ⊆ ℂ → ℂ be an analytic function on the domain D and x ∈ D. Suppose γ ⊂ D is a smooth path parametrized by z (z) , t ∈ [a, b] with z (a) = u, z (t) = x and z (b) = w where u, w ∈ D. Then we have the equality

for n ≥ 1.

Proof. The proof is by mathematical induction over n ≥ 1. For n = 1, we have to prove that

which is straightforward as may be seen by the integration by parts formula applied for the integral

Assume that (12) holds for “n” and let us prove it for “n + 1”. That is, we wish to show that:

Using the integration by parts rule, we have

which gives that

From the induction hypothesis we have

By making use of (16) and (17) we get

which is equivalent to (14).

We have the following generalization of Fink identity for the complex integral.

Theorem 2.2. Let f: D ⊆ ℂ → ℂ be an analytic function on the domain D and x ∈ D. Suppose γ ⊂ D is a smooth path parametrized by z (t) , t ∈ [a, b] with z (a) = u, z (t) = x and z (b) = w where u, w ∈ D, u ≠ w. Define

for k = 1, ..., n − 1 where n ≥ 2.

Then we have the equality

where the remainder Rn (x, γ) is given by

For, n = 1 the identity (19) reduces to

Where

Proof. We prove the identity by induction over n. For n = 1, we have to prove the equality (21) with the remainder R ₁ (x, γ) given by (22).

Integrating by parts, we have:

which proves the statement.

Assume that the representation (19) holds for “n” and let us prove it for “n + 1”. That is, we have to prove the equality

Using the integration by parts, we have

And

If we add these two equalities, we get

By dividing with (n + 1)! (w − u) in (26) we get

Using the representation (20) for R _n (x, γ) , which is assumed to be true by the induction hypothesis, we get

Observe that

which implies that

Therefore, by (27) we get

We must prove now that

Namely

This however follows by Lemma 2.1.

We have the following trapezoid type representation:

Corollary 2.3. With the assumptions of Theorem 2.2 we have

for n ≥ 2.

For n = 1, we have

Proof. We have

and

for k = 1, ..., n − 1 where n ≥ 2.

From (19) we have

And

If we add the equalities (31) and (32) and divide by 2, then we get

which proves (29).

Remark 2.4. If the function f is of real variable and defined on the interval [a, b] then from (29) we obtain the following trapezoid identity obtained by Dragomir & Sofo in [⁵]

for n ≥ 2.

If n = 1, then we have

It is natural to consider the case of linear path γ, namely the path parametrized by z (s) := (1 − s) u + sw, s ∈ [0, 1] that join the distinct complex numbers u, w ∈ D. If x = (1 − t) u + tw for some t ∈ [0, 1] , then

for k = 1, ..., n − 1 where n ≥ 2,

and the equality (19) becomes

3. Error Bounds

We have the following error bounds:

Theorem 3.1. Let f: D ⊆ ℂ → ℂ be an analytic function on the domain D and x ∈ D. Suppose γ ⊂ D is a smooth path parametrized by z (t) , t ∈ [a, b] with z (a) = u, z (t) = x and z (b) = w where u, w ∈ D, u ≠ w. Then we have the representation (19) and the remainder R _n (x, γ) satisfies the bounds

Proof. By the equality (20) we have

which proves the first inequality in (38).

Using Holder’s integral inequality we have

and

which proves the last part of 38).

We also have

and

which proves the last part of 38).

We have the following error bounds:

Theorem 3.2. Let f: D ⊆ ℂ → ℂ be an analytic function on the domain D and x ∈ D. Suppose γ ⊂ D is a smooth path parametrized by z (t) , t ∈ [a, b] with z (a) = u, z (t) = x and z (b) = w where u, w ∈ D, u ≠ w. Then we have the representation (29) and the remainder T _n (γ) satisfies the bounds

provided that .

The proof follows by the identity (29) by taking the modulus and using the integral properties.

4. Examples for Logarithm and Exponential

Consider the function f(z) = Log (z) where Log (z) = ln |z| + iArg (z) and Arg (z) are such that −π < Arg (z) ≤ π. Log is called the "principal branch" of the complex logarithmic function. The function f is analytic on all of ℂ _ℓ : = ℂ \ {x + iy: x ≤ 0, y = 0} and

Suppose γ ⊂ ℂ _ℓ is a smooth path parametrized by z (t) , t ∈ [a, b] with z (a) = u and z (b) = w where u, w ∈ ℂ _ℓ , u ≠ w. Then

where u, w ∈ ℂ _ℓ .

Define

for k = 2, ..., n − 1, where n ≥ 3.

Then we have the equality

where the remainder Rn (x, γ) is given by

If d _γ : = infz∈γ |z| is positive and finite, then from (42) we get the inequality

Consider the function . Then

and suppose γ ⊂ ℂ _ℓ is a smooth path parametrized by z (t) , t ∈ [a, b] with z (a) = u and z (b) = w where u, w ∈ ℂ _ℓ , u # w. Then

for u, w ∈ ℂ _ℓ .

Define as

for x ∈ γ, k = 1, ..., n − 1, where n ≥ 2.

Then we have the equality

where the remainder L _n (x, γ) is given by

If d _γ defined above is positive and finite, then from (42) we get the inequality

Consider the function f (z) = exp (z) , z ∈ ℂ. Then

and suppose γ ⊂ ℂ is a smooth path parametrized by z (t) , t ∈ [a, b] with z (a) = u and z (b) = w, where u, w ∈ ℂ, u ≠ w. Then

Define for x ∈ γ

for k = 1, ..., n − 1, where n ≥ 2.

Then we have the equality

where the remainder E _n (x, γ) is given by

Since |exp z| = exp (Rez) and if assumed that for γ ⊂ ℂ we have

then by (50) we get the inequality