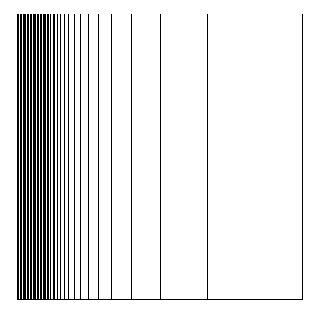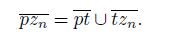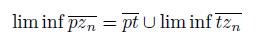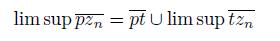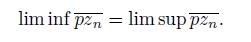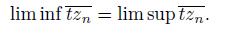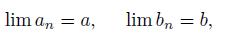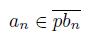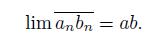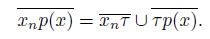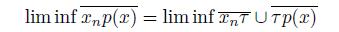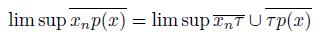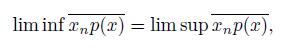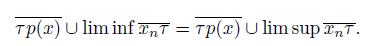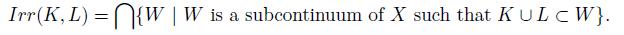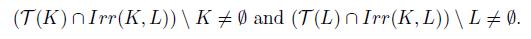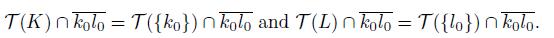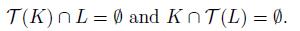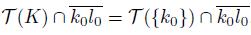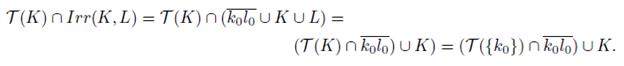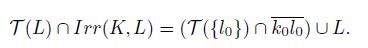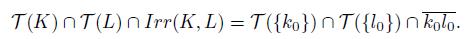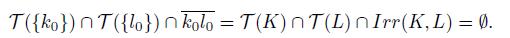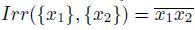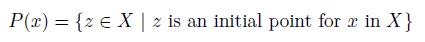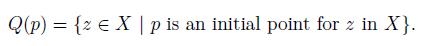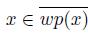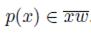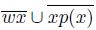1. Introduction

This is a survey paper on dendroids, smooth dendroids and mainly on pointwise smooth dendroids based on the work of Janusz J. Charatonik and Carl Eberhart [²], [⁴] and [¹²] (dendroids and smooth dendroids) and of Stanisław T. Czuba [⁷], [⁹], [¹⁰], and [¹¹] (pointwise smooth dendroids). We present several characterizations of pointwise smooth dendroids. In particular, a new one using the strict point T -asymmetry property (defined by David P. Bellamy [¹⁹, p. 392]) and the nonexistence of R ³-continua in the dendroid. We give the appropriate references for the results whose proofs we do not include.

The paper is divided in six sections. After this Introduction, in section 2, we have the preliminaries, here we include the definitions and some needed results for the rest of the paper. In section 3, we introduce dendroids and present some of their properties, for example that each subcontinuum of a dendroid is a dendroid (Theorem 3.1); that dendroids are hereditarily decomposable continua (Theorem 3.2); that being a dendroid is preserved by monotone maps (Theorem 3.4); we prove a characterization of monotone maps between dendroids (Theorem 3.5), and characterize dendrites as aposyndetic den-droids (Corollary 3.9). In section 4, we talk about smooth dendroids and prove that each subcontinuum of a smooth dendroid is a smooth dendroid (Theorem 4.2); that smoothness allows us to construct certain types of subcontinua (Theorem 4.6); and that smooth dendroids are contractible (Theorem 4.7). In section 5, we introduce the main topic of the paper, pointwise smooth dendroids, we show that a subcontinuum of a pointwise smooth dendroid is a pointwise smooth dendroid (Theorem 5.1); that a fan is pointwise smooth if and only if it is smooth (Theorem 5.3); we present a characterization of pointwise smooth dendroids using Professor F. Burton Jones’ set function T and irreducible sub-continua (Theorem 5.11); we give another characterization of pointwise smooth dendroids using the images of singletons using Professor Jones’ set function K (Theorem 5.19); we present some interrelationships of the set functions T and K on pointwise smooth den-droids (Theorem 5.22); we show a characterization of pointwise smooth dendroids using semi-aposyndesis and the nonexistence of R ³-continua in the dendroid (Theorem 5.24). In section 6, we introduce strict point T -asymmetry for continua, defined by David P. Bellamy [19, p. 392]. We present new results about strict point T -asymmetry. We show that strict point T -asymmetry is equivalent to semi-aposyndesis (Theorem 6.2); we prove that each pointwise smooth dendroid is strictly point T -asymmetric (Corol-lary 6.3); we demonstrate that, for fans, smoothness, pointwise smoothness and strict point T -asymmetry are equivalent properties (Corollary 6.6) and we give a new charac-terization of pointwise smooth dendroids using the strict point T -asymmetry property and the nonexistence of R ³-continua in the dendroid (Theorem 6.7).

2. Preliminaries

Let Z be a metric space. If A is a subset of Z, then Int(A), Bd(A) and Cl(A) denote the interior, the boundary and the closure of A in Z, respectively. A map is a continuous function. The symbol N   denotes the set of positive integers.

A continuum is a nonempty compact, connected, metric space. A subcontinuum is a continuum contained in a metric space. A continuum X is connected im kleinen at a point p of X provided that for each open subset U of X containing p, there exists a subcontinuum W of X such that p ∈ Int(W ) ⊂ W ⊂ U. A continuum X is locally connected at a point p if for every open subset U of X containing p, there exists a connected open subset V of X such that p ∈ V ⊂ U. A continuum X is locally connected provided that it is locally connected at each of its points. We do not define connectedness im kleinen globally because a continuum is connected im kleinen at each of its points if and only if it is locally connected [²², Theorem 1.4.18]. An arc is a continuum Z that is homeomorphic to [0, 1]. If h: [0, 1] → Z is a homeomorphism, then h(0) and h(1) are the endpoints of Z.

Let X be a continuum and let p be a point of X. Then p is an endpoint of X provided that it is an endpoint of every arc in X that contains it. A simple triod is a continuum Z such that Z is the union of three arcs α ₁, α ₂ and α ₃ such that α ₁ ∩α ₂ = α ₁ ∩α ₃ = α ₂ ∩α ₃ = {v}, where v is called the vertex of the simple triod.

A continuum X is unicoherent if each time A and B are subcontinua of X such that X= A ∪ B, we have that A ∩ B is connected. A continuum X is hereditarily unicoherent provided that each of its subcontinua is unicoherent. Note that this is equivalent to say that a continuum is hereditarily unicoherent if the intersection of each pair of its subcontinua is connected.

Let X and Y be continua and let f: X → Y be a surjective map. We say that f is monotone provided that for each connected subset C of Y , we have that f ⁻¹ (C) is a connected subset of X.

Theorem 2.1. Let X and Y be continua and let f: X → Y be a map. If X is hereditarily unicoherent and f is monotone, then Y is hereditarily unicoherent.

Proof. Suppose Y has a subcontinuum Z that is not unicoherent. Then there exist two subcontinua K and L of Z such that Z = K ∪ L and K ∩ L is not connected. Since f is monotone, f ⁻¹ (Z), f ⁻¹ (K) and f ⁻¹ (L) are subcontinua of X, and f ⁻¹ (Z) = f ⁻¹ (K) ∪ f ⁻¹ (L). Since f ⁻¹ (K)∩ f ⁻¹ (L) = f ⁻¹ (K ∩L), we obtain that f ⁻¹ (K)∩f ⁻¹ (L) is not connected. Hence, X is not hereditarily unicoherent.

A continuum is decomposable if it can be written as the union of two of its proper subcontinua; it is indecomposable if it is not decomposable. A continuum is hereditarily decomposable provided that every nondegenerate subcontinuum of it is decomposable. A continuum is hereditarily indecomposable if each of its subcontinua is indecomposable.

Let X be a continuum and let G be a family of subcontinua of X. Then G is a clump if ∪G is a subcontinuum of X and there exists a subcontinuum C of X, called the centre of the clump, such that C is a proper subcontinuum of every element of G, and for each pair G and G ^′ of elements of G, we have that G ∩ G ^′ = C.

A continuum X is contractible provided that there exist a point p and a map F: X × [0, 1] → X such that, for each element x of X, F ((x, 0)) = x and F ((x, 1)) = p.

Given a continuum X, we define its n-fold hyperspace as:

C _n (X) = {A ⊂ X | A is a nonempty closed subset of X with at most n components}.

We topologize C _n (X) with the topology given by the Hausdorff metric [²¹, Theorem 1.8.3]. With this topology, C _n (X) is an arcwise connected continuum [²¹, Theorem 1.8.12]. A Whitney map for C _n (X) is map µ: C _n (X) → [0, 1] such that µ({x}) = 0, for all points x ∈ X, µ(X) = 1, and if A and B are two elements of C _n (X) and A ⊊ B, then µ(A) < µ(B) [²⁴, (0.50)].

A continuum X is semi-aposyndetic provided that for each pair of points p and q of X, there exists a subcontinuum W of X such that {p, q}∩Int(W ) # ∅ and {p, q}∩(X \W ) # ∅. A continuum X is aposyndetic if for each pair of points p and q of X, there exists a subcontinuum W of X such that p ∈ Int(W ) ⊂ W ⊂ X \ {q}.

Given a continuum X and a point p of X, the composant of p in X, κ _p , consists of the union of all proper subcontinua of X that contain p.

Let X be a continuum and let 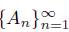be a sequence of nonempty closed subsets of X. The limit inferior of the sequence, denoted by lim sup A _n , is the set:

{x ∈ X | for each open subset U of X such that x ∈ U, there exists N ∈ ℕ such that U ∩ A _n # ∅ for all n ≥ N}.

The limit superior of the sequence, denoted by lim sup A _n , is the set:

{x ∈ X | for every open subset U of X such that x ∈ U, we have that U ∩ A _n # ∅ for infinitely many indexes n ∈ IN}.

If there exists a subset A of X such that lim inf A _n = lim sup A _n = A, we say that the sequence 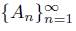converges to A.

Theorem 2.2. [², Lemma 1] Let X be a hereditarily unicoherent continuum. If {W _n} 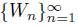is a sequence of subcontinua of X, then lim inf W _n is a subcontinuum of X.

The following result is useful for studying smooth dendroids.

Theorem 2.3. Let X be a continuum and let p and q be two elements of X and let α be an arc contained in X whose endpoints are p to q. If U is an open subset of X such that p ∈ U and q ∈ X \ U, then there exists an open subset V of X such that Bd(V ) ∩ α consists of just one point.

Proof. Let U be an open subset of X such that p ∈ U and q ∈ X \ U. Since X is a regular space, there exists an open subset W of X such that p ∈ W ⊂ Cl(W ) ⊂ U. Since α is a connected set, p ∈ W and q ∈ X \ W , we have that α ∩ Bd(W ) # ∅ [¹⁸, Theorem 1, p. 127]. Let t be the first element of α in Bd(W ), from p to q. Since X is a completely normal space, there exist two disjoint open subsets Y and Z of X such that pt \ {t} ⊂ Y and tq \ {t} ⊂ Z, where pt and tq are the subarcs of α, from p to t and from t to q, respectively. Let V = Y ∩U. Hence, t ∈ Bd(V ). Suppose that there exists a point s in (Bd(V ) \ {t}) ∩ α. Then, we obtain that s ∈ tq \ {t}, because pt \ {t} ⊂ V ⊂ Y .

This implies that Y ∩ Z # ∅, a contradiction. Therefore, α ∩ Bd(V ) = {t}. Also p ∈ V ⊂ Cl(V ) ⊂ Cl(W ) ⊂ U.

Let X be a continuum. Define Professor F. Burton Jones set functions T and K as follows: if A is a subset of X, then

T (A) = X \ {x ∈ X | there exists a subcontinuum

W of X such that x ∈ Int(W ) ⊂ W ⊂ X \ A}.

Observe that for any subset A of X, T (A) is a closed subset of X and A ⊂ T (A). A continuum X is T -additive provided that for each pair A and B of closed subsets of X, we have that T (A ∪ B) = T (A) ∪ T (B).

Next, if A is a subset of X, then

K(A) =∩{W | W is a subcontinuum of X and A ⊂ Int(W)}.

Note that for any subset A of X, K(A) is a closed subset of X and A ⊂ K(A).

The next theorem follows from the definition of the set function K:

Theorem 2.4. If X is a hereditarily unicoherent continuum and A is a nonempty closed subset of X, then K(A) is a subcontinuum of X.

Theorem 2.5. [22, Theorem 7.7.2] Let X be a continuum and let W be a subcontinuum of X. Then K(W ) = {x ∈ X | T ({x}) ∩ W } # ∅.

Let X be a continuum and let K be a proper subcontinuum of X. Then K is an R ¹ -continuum if there exist an open subset U of X, containing K, and two sequences 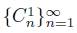and 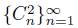of components of U such that lim sup C _n ¹ ∩ lim sup C _n ² = K.

Remark 2.6. In [²²] an R ¹-continuum is called an R-continuum.

Let X be a continuum and let K be a proper subcontinuum of X. Then K is an R ³ -continuum if there exist an open subset U of X, containing K, and a sequence 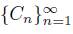of components of U such that lim inf C _n = K.

From [⁸, Corollary 11], we have the following:

Lemma 2.7. Let X be a dendroid. Then each R ¹ -continuum contains an R ³ -continuum. Also, if an R ¹ -continuum is a single point, then it is also both an R ² and an R ³ -continuum.

3. Dendroids

The class of dendroids was introduced by Bronisław Knaster in his seminar at the Insti-tute of Mathematics of the University of Wrocław. We present properties of them.

A dendroid is an arcwise connected continuum that is hereditarily unicoherent; i.e., a dendroid is an arcwise connected continuum in which the intersection of every pair of its subcontinua is connected.

As an example of a dendroid, we have the comb space:

Theorem 3.1. If X is a dendroid and Z is a subcontinuum of X, then Z is a dendroid.

Proof. Let X be a dendroid and let Z be a subcontinuum of X. We only need to show that Z is arcwise connected. Let z ₀ and z ₁ be two points of Z. Since X is arcwise connected, there exists an arc α in X whose endpoints are z ₀ and z ₁. Consider α ∩ Z. Since X is hereditarily unicoherent, α ∩ Z is connected. Hence, since {z ₀ , z ₁ } ⊂ (α ∩ Z), we obtain that α ∩ Z = α. Therefore, α ⊂ Z and Z is a dendroid.

Theorem 3.2. If X is a dendroid, then X is hereditarily decomposable.

Proof. Let X be a dendroid. By Theorem 3.1, we only need to show that X is decomposable. Suppose that X is an indecomposable continuum. Let x ₁ and x ₂ be two points of X that belong to two distinct composants of X (indecomposable continua have uncount-ably many composants [¹⁶, Theorem 3-46] and they are pairwise disjoint [¹⁶, Theorem 3-47]). Since X is arcwise connected, there exists an arc α in X having x ₁ and x ₂ as its endpoints. Since x ₁ and x ₂ are in distinct composants of X and X is indecompos-able, the only subcontinuum of X containing {x ₁ , x ₂ } is X. Hence, α = X. This is a contradiction, since an arc is a decomposable continuum. Therefore, X is hereditarily decomposable.

Notation. Let X be a dendroid. Since X is hereditarily unicoherent and arcwise con-nected, given to elements x ₀ and x ₁ of X, there exists a unique arc whose endpoints are x ₀ and x ₁, this arc is denoted by .

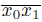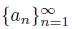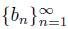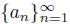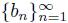Theorem 3.3. [², Corollary 1] Let X be a dendroid, let and be two convergent sequences of elements of X. If and converge to a and b, respectively, then lim inf 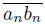is a subcontinuum of X, and ab ⊂ lim inf .

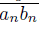Theorem 3.4. Let X and Y be continua and let f: X → Y be a surjective map. If X is a dendroid and f is monotone, then Y is a dendroid.

Proof. Suppose X is a dendroid and f: X → Y is a surjective monotone map. By Theorem 2.1, Y is hereditarily unicoherent. We need to show that Y is arcwise connected. Let y ₀ and y ₁ be two elements of Y . Since f is surjective, there exist two points x ₀ and x ₁ in X such that f(x ₀) = y ₀ and f(x ₁) = y ₁. Consider the arc x ₀ x ₁ in X. By [²⁵, Theorem 8.14], we have that f(x ₀ x ₁) is a locally connected subcontinuum of Y containing f(x ₀) and f(x ₁). Since locally connected continua are arcwise connected [²⁵, Theorem 8.23], the arc y ₀ y ₁ exists and is contained in Y . Therefore, Y is arcwise connected and it is a dendroid.

The following result gives a characterization of monotone maps between dendroids.

Theorem 3.5. Let X and Y be dendroids and let f: X → Y be a surjective map. Then f is monotone if and only if 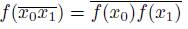for each pair of points x ₀ and x ₁ of X.

Proof. Suppose f is monotone and let x ₀ and x ₁ be two elements of X. Note that 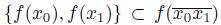. Hence, 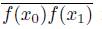is an arc contained in the subdendroid 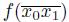(Theorem 3.1). Since f is monotone, 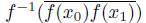is a subdendroid of X that contains {x ₀ , x ₁ }. Thus, 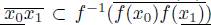. This implies that 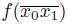⊂ 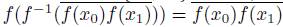. Thus, .

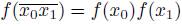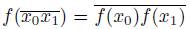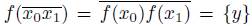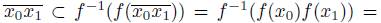
Now, assume that for each pair of points x ₀ and x ₁ of X. Let y be an element of Y and let x ₀ and x ₁ be two elements of f ⁻¹ (y). By our assumption, . Note that 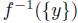. Hence, f ⁻¹ (y) is a connected subset of X. Thus, by [22, Theorem 1.4.46], f is a monotone map.

Important properties of dendroids are the following:

Theorem 3.6. [¹, p. 18] Let X be a dendroid. If ξ: [0, ∞) → X is a one-to-one map, then the closure of ξ([0, ∞)) is an arc (ξ([0, ∞)) is called a Borsuk ray).

Theorem 3.7. [¹, Theorem 2] If X is a dendroid and f: X → X is a map, then there exists a point x in X such that f(x) = x.

A dendrite is a locally connected dendroid. Dendrites constitute an important class of continua, the main properties of these spaces are given in [³].

Theorem 3.8. A dendroid is a dendrite if and only if T ({x}) = {x}, for all x in X.

Proof. If X is a dendrite, by [²², Theorem 2.1.37], T ({x}) = {x}, for all x in X.

Suppose X is a dendroid that satisfies that T ( {x}) = {x}, for all x in X. Let p be an element of X and let A be a nonempty closed subset of X such that p ∈ T (A). Since X is hereditarily unicoherent, X is T -additive [²², Theorem 2.2.12]. Hence, by [²², Corollary 2.2.13], we have that T (A) = ∪{T ({a})| a ∈ A}. Thus, there exists a point a in A such that p ∈ T ( {a}). Since T ({a}) = {a}, we obtain that p = a, and p ∈ A. Hence, by [²², Corollary 2.1.31], X is connected im kleinen at p. Since p is an arbitrary point of X, we have that X is connected im kleinen at each of its points. Therefore, X is locally connected [²², Theorem 1.4.18], and X is a dendrite.

The next result says that for the class of dendroids aposyndesis is equivalent to local connectedness.

Corollary 3.9. A dendroid is a dendrite if and only if X is aposyndetic.

Proof. Let X be a dendroid. If X is a dendrite, by Theorem 3.8, we have that T ({x}) = {x}, for all x in X. Hence, by [²², Theorem 2.1.34], X is aposyndetic. If X is an aposyndetic dendroid, we obtain that, by [²², Theorem 2.1.34], that T ({x}) = {x}, for all x in X. Thus, by Theorem 3.8, X is a dendrite.

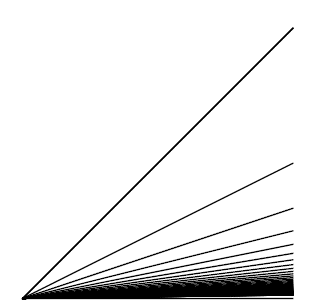
A fan is a dendroid with exactly one ramification point; i.e., a point that is the only endpoint in common of at least three otherwise disjoint arcs. This point is called the top of the fan. The cone over the harmonic sequence 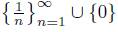is an example of a fan, the so-called harmonic fan:

4. Smooth Dendroids

The class of smooth dendroids was introduced by Janusz J. Charatonik and Carl Eberhart [⁴] and [¹²].

A dendroid X is smooth at a point p of X provided that for each sequence {x _n } _n=1 of points of X converging to a point x in X, the sequence of arcs 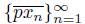converges to the arc px. The point p is called a point of smoothness of X. A dendroid X is smooth if it is smooth at so me of its points. A fan is smooth provided that it is smooth at its top.

As an example of a smooth dendroid we have the comb space and the harmonic fan (Figures 1 and 2, respectively). Also, the cone over the Cantor set, called the Cantor fan, is a smooth dendroid:

As a consequence of [2, Theorem 9, p. 27] and [¹², Corollary 4], we have:

Theorem 4.1. A fan is smooth if and only if it can be embedded in the Cantor fan.

Theorem 4.2. If X is a smooth dendroid and Z is a subcontinuum of X, then Z is a smooth dendroid.

Proof. Let X be a smooth dendroid, let Z be a subcontinuum of X, and let p be the point of smoothness of X. By Theorem 3.1, Z is a dendroid. If p belongs to Z, we are done. Assume that p ∈ X \ Z. Let z ^′ be an element of Z and consider the arc 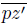. Let t be the first element of the arc 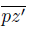in Z. We show that Z is smooth at t. Let 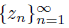be a sequence of elements of Z converging to a point z in Z. Note that, for each n ∈ IN,

Hence,

[¹⁷, p. 336], and

[¹⁷, p. 337]. Since X is smooth at p,

Thus,

Since 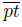∩ lim inf 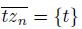and 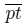∩ lim sup 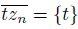, we obtain that:

Therefore, Z is smooth at t.

Remark 4.3. An important characterization of smooth dendroids in terms of prohibited subdendroids is given in [¹⁵].

Theorem 4.4. [⁴, Corollary 10] Let X and Y be dendroids and let f: X → Y be a surjective map. If X is smooth and f is monotone, then Y is smooth.

Note that if X is a dendroid that is not smooth at the point p, then there exists a sequence 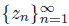of elements of X converging to a point z of X such that the sequence of arcs 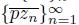either does not converge or lim 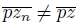. The next theorem shows that we may always assume the second possibility.

Theorem 4.5. Let X be a dendroid and let p be a point of X. If X is not smooth at p, then there exists a sequence 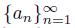of points of X converging to an element a of X such that the sequence of arcs 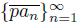converges to a subdendroid L of X and .

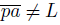Proof. Suppose that X is not smooth at p. Let 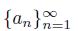be a sequence of points of X that converges to an element a of X and the sequence 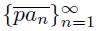does not converge. Since 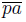⊂ lim inf pa _n , we have that there exists a subsequence 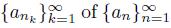such that lim 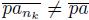. To see this, note that, since 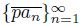does not converge, we have that lim inf 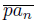# lim sup 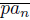. Let x ∈ lim sup 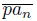\ lim inf 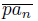and let V be an open subset of X containing x. Since x ∈ lim sup 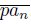we obtain that V intersects infinitely many arcs 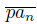. Hence, since C ₁(X) is compact [²¹, Theorem 1.8.5], we have that the sequence of arcs 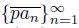has a convergent subsequence 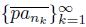. Thus, 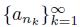is a subsequence of 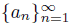such that the sequence of arcs 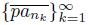converges. Since x ∈ lim 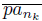, pa ⊂ lim inf 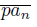⊂ lim 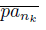and x ∈ X \ lim inf 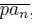, we obtain that lim .

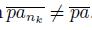Theorem 4.6. Let X be a dendroid that is smooth at the point p. If K is a closed subset of X, then 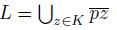is a subcontinuum of X.

Proof. Note that L is a connected subset of X since L is the union of arcs all containing the point p. Let x ∈ Cl(L). Then there exists a sequence 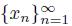of elements of L that converges to x. For each n ∈ IN, there exists an element z _n in K such that x _n ∈ 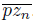. Since K is compact, without loss of generality, we assume that there exists a point z in K such that the sequence 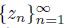converges to z. Since X is smooth at p, we have that the sequence of arcs 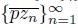converges to the arc 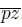Observe that we have that x ∈ 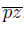. Hence, x ∈ L and L is a subcontinuum of X.

The following result is originally proved in [²³, Theorem 1.16]. The proof given here is a modification of [²⁰, p. 41].

Theorem 4.7. If X is a smooth dendroid, then X is contractible.

Proof. Suppose X is a dendroid that is smooth at the point p. Let µ: C ₁(X) → [0, 1] be a Whitney map. For each element x of X and every number t ∈ [0, 1], let x _t be the unique point in the arc 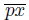such that 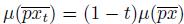. Let F: X × [0, 1] → X be given by F ((x, t)) = x _t . Note that, for every x ∈ X, F ((x, 0)) = x and F ((x, 1)) = p.

We need to show that F is continuous. Let 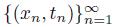be a sequence of points of X × [0, 1] converging to a point (x, t) in X × [0, 1]. For each n ∈ IN, we have that F ((x _n , t _n )) = x _ntn . Since X is a continuum, we may assume that there exists an element w of X such that the sequence 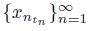converges to w. We prove that F ((x, t)) = w.

From the definition of F, we obtain that, for every n ∈ IN, µ(px _ntn ) = (1 − t _n )µ(px _n ). Since X is smooth at p, 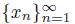converges to x and 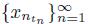converges to w, we have that lim 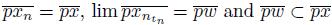. Using the continuity of µ and the fact that lim t _n = t, these equalities imply that 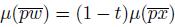. Hence, F ((x, t)) = w. Therefore, F is continuous.

We end this section with a couple of characterizations of smooth dendroids.

Theorem 4.8. [⁴, Theorem 12] A dendroid X is smooth if and only if there exists a point p in X such that for each pair of convergent sequences and 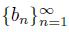, the conditions:

and

imply that:

Theorem 4.9. [⁴, Theorem 6] A dendroid X is smooth if and only if for each pair of points x ₁ and x ₂ of X, we have that x ₁ x ₂ ∩ T ({x ₁ }) = {x ₁ } or x ₁ x ₂ ∩ T ({x ₂ }) = {x ₂ }.

5. Pointwise Smooth Dendroids

The class of pointwise smooth dendroids was introduced by Stanisław T. Czuba [⁷] as a generalization of the class of smooth dendroids. He continued the study of this class of dendroids in [⁹], [¹⁰], and [¹¹].

A dendroid X is said to be pointwise smooth if, for each point x of X, there exists a element p(x) of X such that for every sequence 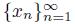of points of X that converges to x, the sequence of arcs 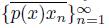converges to the arc 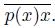. The point p(x) is called an initial point for x in X. Note that in the case of a smooth dendroid the point of smoothness is the initial point of every element of the dendroid.

Theorem 5.1. If X is a pointwise smooth dendroid and Z is a subcontinuum of X, then Z is a pointwise smooth dendroid.

Proof. Let X be a pointwise smooth dendroid and let Z be a subcontinuum of X. By Theorem 3.1, Z is a dendroid. Let z be a point of Z. Since X is pointwise smooth, there exists a point p(z) in X that is an initial point for z in X. We assume that p(z) ∈ X \ Z. Let p ^′ (z) be the first point of the arc 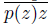that is in Z. We show that p ^′ (z) is an initial point for z in Z. To this end, let 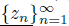be a sequence of elements of Z converging to z. Note that 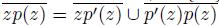and, for each n 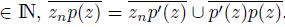. A similar argument to the one given in Theorem 4.2 shows that the sequence of arcs 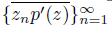converges to the arc zp ^′ (z) Therefore, Z is pointwise smooth.

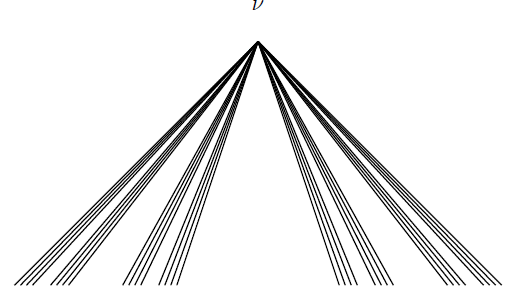
Remark 5.2. Note that the following dendroid:

is pointwise smooth but not smooth.

The next theorem shows that for the class of fans, pointwise smoothness and smoothness are equivalent [⁷, Theorem 1].

Theorem 5.3. A fan X is pointwise smooth if and only if X is smooth.

Proof. Suppose X is a pointwise smooth fan, let τ be the top of X, and let x be a point of X. We prove that τ is the initial point for x. Let 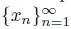be a sequence of elements of X converging to x. If there exists N ∈ IN such that for n ≥ N, we have that both x _n and x belong to the same component of X \ {τ} (this is a semi-open arc), we obtain that lim 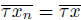. Without loss of generality, we assume that for each n ∈ IN, we have that 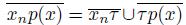(if there exists an infinite set IK of IN and there exists a component Z of X \ {τ} such that if n ∈ IK, then x _n ∈ Z, we obtain that lim 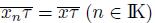and we only need to take care of the indexes that belong to IN \ IK, this set is infinite and if n ₁ and n ₂ are two distinct elements of IN \ IK, then x _n1 and x _n2 belong to two distinct components of X \ {τ}). Thus, for each n ∈ IN, we have that

Hence,

[¹⁷, p. 336] and that

[¹⁷, p. 337]. Since X is pointwise smooth fan and p(x) is the initial point for x in X, we obtain that

from this, we have

Observe that 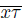⊂ lim inf 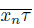⊂ lim sup 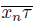. We prove that lim sup 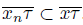. Suppose that (lim sup 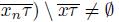and that (lim sup 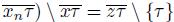[²², Theorem 1.1.30]. Let w ∈ 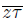\ {z, τ}. Let 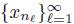be a subsequence of 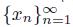such that 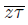⊂ lim .

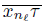For every ℓ ∈ IN, let wℓ be the first point of the arc 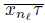, from x _nℓ to τ , such that d(w,wℓ) ≤ 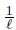. The sequence 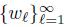converges to w. Note that 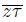⊂ lim inf .

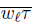Hence, there does not exist an initial point p(w) for w in X, a contradiction. Thus, lim sup 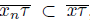and lim 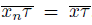. Therefore, X is a smooth fan. The reverse implication is clear.

The following two theorems give characterizations of pointwise smooth dendroids.

Theorem 5.4. [²², Theorem 7.3.15] Let X be a dendroid. Then X is pointwise smooth if and only if for each pair of different points x ₁ and x ₂ of X, we have that either x ₁ x ₂ ∩ T ({x ₁ }) = {x ₁ } or x ₁ x ₂ ∩ T ({x ₂ }) = {x ₂ } or T ({x ₁ }) ∩ T ({x ₂ }) = ∅.

Theorem 5.5. [²², Corollary 7.3.16] A dendroid X is pointwise smooth if and only if for each point x of X, there exists a point p(x) in X such that for each sequence 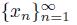of points of X converging to x, the sequence of arcs 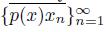converges to the arc 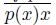and x ∈ T ({p(x)}).

Lemma 5.6. [²², Lemma 7.3.10] If X is a dendroid and A and B are closed subsets of X such that A ∩ T (B) = ∅, T (A) ∩ B = ∅ and T (A) ∩ T (B) # ∅, then there exist two points p ∈ A and q ∈ B such that p ∈ X \ T ({q}), q ∈ X \ T ({p}) and T ({p}) ∩ T ({q}) # ∅.

Remark 5.7. Lemma 5.6 is important since it gives a simple way to obtain the noncon-tractibility of a dendroid [²², Theorem 7.2.2].

The next theorem gives a sufficient condition for a continuum to contain an R ¹-continuum (R ³-continuum (Lemma 2.7)).

Theorem 5.8. [²², Theorem 7.3.11] If X is a dendroid and A and B are subcontinua of X such that A ∩ T (B) = ∅, T (A) ∩ B = ∅, and T (A) ∩ T (B) ≠ ∅, then T (A) ∩ T (B) is an R ¹ -continuum. Therefore, it contains an R ³ -continuum.

Corollary 5.9. [²², Corollary 7.3.12] If X is a dendroid and A and B are closed subsets of X such that A ∩ T (B) = ∅, T (A) ∩ B = ∅ and T (A) ∩ T (B) # ∅, then X contains an R ¹ -continuum. Therefore, it contains an R ³ -continuum.

If X is a dendroid and K and L are two disjoint and nonempty closed subsets of X, then

The set Irr(K, L) is called the irreducible subcontinuum of X about K ∪ L.

Remark 5.10. If X is a dendroid and K and L are two disjoint subcontinua of X, then by the arcwise connectedness and the hereditary unicoherence of X, we have that there exist two points k ₀ in K and l ₀ in L such that the arc 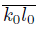satisfies that 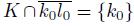, 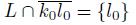and .

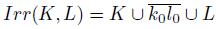The following result is [⁹, Corollary (3.3)].

Theorem 5.11. A dendroid is pointwise smooth if and only if for any two disjoint sub-continua K and L of X, we have that T (K) ∩ Irr(K, L) = K or T (L) ∩ Irr(K, L) = L or T (K) ∩ T (L) = ∅.

Proof. Assume that X is a pointwise smooth dendroid and that K and L are two disjoint subcontuna of X such that

Observe that (Remark 5.10),

We show these two equalities are true. Note that T ({k ₀ }) ∩ 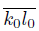⊂ T (K) ∩ 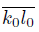[²², Proposition 2.1.7]. Let z be an element of T (K) ∩ 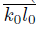. Hence, if W is a subcontinuum of X such that z ∈ Int(W ), then W ∩ K # ∅. Since X is hereditarily unicoherent, we obtain that k ₀ ∈ W. Thus, z ∈ T ({k ₀ }), and z ∈ T ({k ₀ }) ∩ 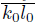. Therefore, T (K) ∩ 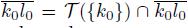. Similarly, we have that T (L) ∩ 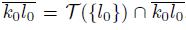. Next, we claim that

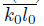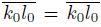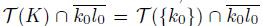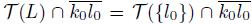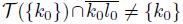Assume that T (K) ∩ L # ∅. Since T (K) is a subcontinuum of X [²², Theorem 2.1.27] and X is a dendroid, we have that ⊂ T (K). Hence, T (K) ∩ . Since and , we obtain that l ₀ ∈ T ({k ₀ })∩T ({l ₀ }). Also, since (T (K)∩Irr(K, L))\K # ∅ and (T (L)∩Irr(K, L))\L # ∅, we have that and 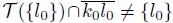. Similarly, if K ∩T (L) # ∅, then 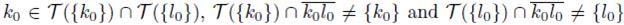. Thus, in any case, we obtain a contradiction to Theorem 5.4. Therefore, T (K) ∩ L = ∅ and K∩T(L)=∅.

Since , we have that:

Similarly, we obtain:

Hence,

Recall that (T (K) ∩ Irr(K, L)) \ K # ∅ implies that 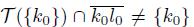and that (T (L) ∩ Irr(K, L)) \ L # ∅ implies that 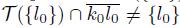. Thus, by Theorem 5.4, we have that

Since X is hereditarily unicoherent, we obtain that T (K) ∩ T (L) = ∅.

The reverse implication is obtained by Theorem 5.4, taking K = {x ₁ } and L = {x ₂ }.

Note that, in this case, .

Let X be a dendroid and let p and x two be points of X. Define the sets:

and

Some consequences of the definition of these sets are:

Theorem 5.12. Let X be a dendroid. Then the following hold:

(1) X is pointwise smooth if and only if ∪{Q(p) | p ∈ X} = X.

(2) X is smooth if and only if ∩ {P(x) | x ∈ X} ̸= ∅.

(3) X is smooth if and only if there exists an element p of X such that Q(p) = X.

Theorem 5.13. Let X be a dendroid and let x ₀ be a point of X. Then the following are equivalent:

(1) P (x ₀) = X;

(2) x ₀ ∈ Q(x ₀);

(3) x ₀ ∈ P (x ₀);

(4)x ₀ ∈ X \ T ({x}), for all x ∈ X \ {x ₀ };

(5) X is connected im kleinen at x ₀ .

Proof. Assume that P (x ₀) = X. This means that each element x of X is an initial point for x ₀ in X. In particular, x ₀ is an initial point for itself in X. Thus, x ₀ ∈ Q(x ₀). Next, if x ₀ ∈ Q(x ₀), then x ₀ is an initial point for itself in X. Hence, x ₀ ∈ P (x ₀). Now, assume that x ₀ ∈ P (x ₀). 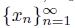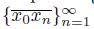This implies that for each sequence of elements of X converging to x ₀, we have that the sequence of arcs converges to {x ₀ }. Thus, lim diam 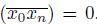. 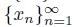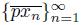From this, we obtain that if p is a point of X and is a sequence of elements of X converging to x ₀, we have that the se quence of arcs converges to the arc 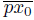. Therefore, P (x ₀) = X. Hence, (1), (2) and (3) are equivalent.

Suppose that x ₀ ∈ X \T ({x}), for every point x in X \{x ₀ }. We show that X is connected im kleinen at x ₀. To this end, let A be a closed subset of X such that x ₀ ∈ T (A). Since X is hereditarily unicoherent, by [²², Theorem 2.2.12], X is T -additive. Thus, by [22, Corollary 2.2.13], we have that T (A) = ∪{T ({a})| a ∈ A}. Hence, there exists a point a in A such that x ₀ ∈ T ({a }). By our assumption, we obtain that x ₀ = a and x ₀ ∈ A. By [²², Corollary 2.1.31], we conclude that X is connected im kleinen at x ₀. Now, assume that X is connected im kleinen at x ₀, let x be an element of X \ {x ₀ } and let U be an open subset of X \ {x} that contains x ₀. Since X is connected im kleinen at x ₀, there exists a subcontinuum W of X such that x ₀ ∈ Int(W ) ⊂ W ⊂ U ⊂ X \{x}. This implies that x ₀ ∈ X \ T ({x}). Thus, (4) and (5) are equivalent.

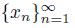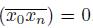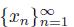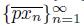Suppose that X is connected im kleinen at x ₀. Then x ₀ is in the interior of subcon-tinua of X of arbitrary small diameters. By Lemma 3.1 each of these subcontinua is a dendroid. This implies that if is a sequence of points of X converging to x ₀, then lim diam . Hence, if p is an element of X and is a sequence of points of X converging to x ₀, then the sequence of arcs converges to the arc 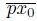. Therefore, P (x ₀) = X. Now, assume that X is not connected im kleinen at x ₀. Thus, there exists an open subset U of X containing x ₀ such that no subcontinuum of X contained in U has x ₀ in its interior. Since X is a regular space, there exists an open subset V of X such that x ₀ ∈ V ⊂ Cl _X (V ) ⊂ U. Let W be the component of Cl(V ) that contains x ₀. By [²², Theorem 1.4.36], we have that W is a nondegenerate subcontinuum of X. By our assumption, x ₀ ∈ W \ Int(W ). 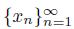Hence, there exists a sequence of points of X \W that converges to x ₀. Consider the sequence of arcs 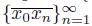. Observe that, for each n ∈ IN, we obtain that 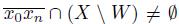. We have two possibilities, either the sequence 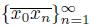converges and in this case, 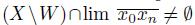or such sequence does not converge. In either case, we obtain that x ₀ ∈ X \ P (x ₀). Therefore, P (x ₀) ̸= X. Hence, (5) and (1) are equivalent.

By Theorem 4.7, we know that a smooth dendroid is contractible. It was asked if the same was true for pointwise smooth dendroids. Note the following result.

Theorem 5.14. Let X be a dendroid. Then X is pointwise smooth if and only if C _n (X) is contractible, for each n ∈ IN.

Proof. By [⁵, Corollary, p. 411], we have that X is a pointwise smooth dendroid if and only if C ₁(X) is contractible. Hence, by [21, Theorem 6.1.17], we obtain the result for n ≥ 2.

A dendroid X has property (CS) if there exists a clump G of smooth subdendroids of X whose centre is C such that:

(1)∪G=X;

(2)there exists an element p ∈ C such that p is the point of smoothness of each of the elements of G;

(3) the set Cl(∪G \ C) ∩ C is totally disconnected.

Theorem 5.15. [¹¹, Theorem 3] If X is a pointwise smooth dendroid having property (CS), then X is a smooth dendroid.

Regarding the contractibility of a pointwise smooth dendroid, we have:

Theorem 5.16. [¹¹, Corollary 4] Let X be a dendroid having property (CS). Then the following are equivalent:

(1)X is hereditarily contractible;

(2)X is pointwise smooth;

(3)X is smooth.

Let X be a continuum. If L is a subcontinuum of X that is contained in a subset A of X, then C(A, K) denotes the component of A containing L.

Theorem 5.17. Let X be a dendroid. Then the following are equivalent:

(1) X is pointwise smooth;

(2) for each point x of X, there exists a point z of X such that for every subcontinuum K of X which contains an arc 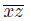and for each open subset U of X that contains K, we have that x ∈ Int(C(U, K));

(3) for each element x of X, there exists a point z of X such that for every open subset U of X containing 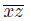, we have x ∈ Int(C(U, K)).

Proof. To show that (1) implies (2), let x be a point of the pointwise smooth dendroid X and let K be a subcontinuum of X containing the arc 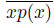. Let U be an open subset of X containing K. If x ∈ X \ Int(C(U, K)), then there exists a sequence 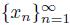of points of X \ C(U, K) converging to x. Observe that 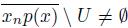. Thus, since X is pointwise smooth, lim 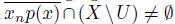. Since K ⊂ U, we have that K ∩(X \U) = ∅. By Theorem 3.1, lim 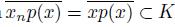, a contradiction. Hence, x ∈ Int(C(U, K)).

It is clear that (2) implies (3). Suppose (3), we prove (1). Let z be a point of X and let 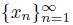be a sequence of elements of X converging to an element x of X. If lim sup 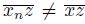, then let w ∈ lim sup 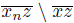. Let U be an open subset of X such that w ∈ Cl(U) and 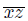⊂ U. Note that for each n ∈ IN, x _n ∈ X \ C(U, {x}). Thus, x ∈ X \ Int(C(U, {x})), a contradiction. Since lim inf 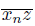is a continuum (Theorem 2.2) containing x and z, we have that lim inf 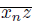= lim sup 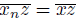. Hence, we may take z to be p(x), the initial point of x in X.

Theorem 5.18. [¹⁰, Proposition 4] A dendroid X is pointwise smooth if and only if for each point x of X and every sequence 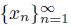of elements of X converging to x, there exists a point q of X such that lim sup 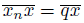and for each initial point p(x) for x in X, we have that .

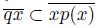Theorem 5.19. A dendroid X is pointwise smooth if and only if for each point x of X, K({x}) is an arc xz, where z may be taken as an initial point for x in X (z = p(x), in the sense of Theorem 5.5).

Proof. Let X be a pointwise smooth dendroid, let x be an element of X and let p(x) be an initial point for x in X (Theorem 5.5). Since x ∈ T ({p(x)}), by [²², Lemma 7.7.3], p(x) ∈ K({x}). Thus, {x, p(x)} ⊂ K({x}) and, by Theorem 2.4, we have that 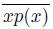⊂ K({x}). If K({x}) \ xp(x) # ∅, let w ∈ K({x}) \ xp(x). We consider three cases.

Case (1). .

In this case, {w} # 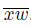. Since w ∈ K({x}), by [²², Lemma 7.7.3], x ∈ T ({w}). Hence, 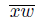⊂ wp(x) ⊂ T ({w}) [²², Theorem 2.1.27]. Also, {p(x)} # 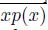. Since x ∈ T ({p(x) }), we obtain that 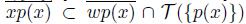. Form all of this, we have that {w} # 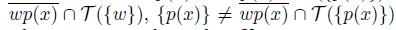and x ∈ T ({w}) ∩ T ({p(x)}). Thus, by Theorem 5.4, we have that X is not a pointwise smooth dendroid.

Case(2). .

It follows from Theorem 5.18 that p(x) is not an initial point for x in X.

Case (3). is a simple triod.

In this case, there exists an element t of X such that 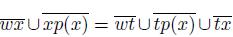, where t is the vertex of the simple triod. Hence, 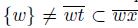. Since w ∈ K({x}), by [²², Lemma 7.7.3], x ∈ T ({w}). Thus, 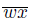⊂ T ({w}) [²², Theorem 2.1.27]. Also, {x} # 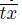⊂ 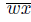. Since w ∈ K({x}), we obtain that 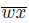⊂ T ({x}) [²² , Theorem 2.1.27]. From all this, we have that{w} 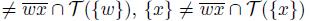and t ∈ T ({w}) ∩ T ({x}). Thus, by Theorem 5.4, we have that X is not a pointwise smooth dendroid.

From these cases, we obtain that .

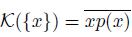Now, suppose X is not a pointwise smooth dendroid. Then, by Theorem 5.4, there exist two elements a and b of X such that 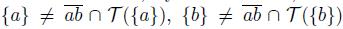, and T ({a}) ∩ T ({b}) # ∅. Since X is hereditarily unicoherent, there exists a point 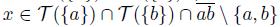. By [²², Lemma 7.7.3], we have that {a, b} ⊂ K({x}). This implies that K({x}) is not an arc with x as one of its endpoints.

As a consequence of Theorems 5.5 and 5.19, we have:

Corollary 5.20. If X is a pointwise smooth dendroid, then for each element x of X, there exists a unique point p(x) (namely, the endpoint of the arc K({x}) different from x) such that for each sequence 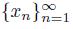of points of X converging to x, lim 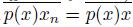, and x ∈ T ({p(x)}).

Corollary 5.21. If X is a pointwise smooth dendroid, then no point from the open arc K({x}) \ {x, p(x)} is an initial point for x in X, where

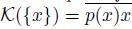
Theorem 5.22. If X is a pointwise smooth dendroid, then for each pair of points x ₁ and x ₂ of X, the following are satisfied:

(1) K({x ₁ }) = K({x ₂ }) if and only if x ₁ = x ₂ ;

(2) T ({x ₁ }) = T ({x ₂ }) if and only if x ₁ = x ₂ ;

(3) T ({x ₁ }) ∩ K({x ₁ }) = {x ₁ };

(4) K(T ({x ₁ })) = T ({x ₁ }) ∪ K({x ₁ }).

Proof. We show (1). If K({x ₁ }) = K({x ₂ }), by Theorem 5.19, 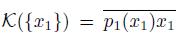and 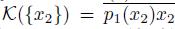. Hence, either, x ₁ = x ₂ or p(x ₁) = x ₂ or p(x ₂) = x ₁. If p(x ₁) = x ₂, then 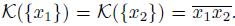. This implies, by [²², Lemma 7.7.3], that 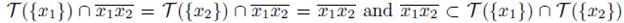. Hence, by Theorem 5.4, X is not a pointwise smooth dendroid, a contradiction. Similarly, we obtain a contradiction if p(x ₂) = x ₁. Therefore, x ₁ = x ₂. The reverse implication is clear.

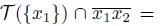
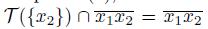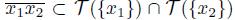To prove (2), note that if T ({x ₁ }) = T ({x ₂ }) and x ₁ # x ₂, then and . Thus, by Theorem 5.4, X is not a pointwise smooth dendroid, a contradiction. Therefore, x ₁ = x ₂. The reverse implication is clear.

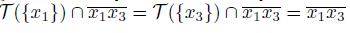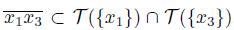To see (3), let x ₃ ∈ T ({x ₁ }) ∩ K({x ₁ }) \ {x ₁ }. Then, by [²², Lemma 7.7.3], we have that x ₁ ∈ T ({x ₃ }) and x ₃ ∈ T ({x ₁ }). Hence, and . Thus, by Theorem 5.4, X is not a pointwise smooth dendroid, a contradiction. Therefore, T ({x ₁ }) ∩ K({x ₁ }) = {x ₁ }.

To show (4), observe that since x ₁ ∈ T ({x ₁ }), we have that K({x ₁ }) ⊂ K(T ({x ₁ })) and, by definition, T ({x ₁ }) ⊂ K(T ({x ₁ })). Hence, T ({x ₁ }) ∪ K({x ₁ }) ⊂ K(T ({x ₁ })). Let x ₃ ∈ K(T ({x ₁ })). By Theorem 2.5, we obtain that T ({x ₃ }) ∩ T ({x ₁ }) # ∅. By Theorem 5.4, we have that either 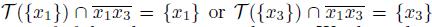. Suppose 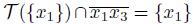, the proof of the other case is analogous. We claim that, in this case, 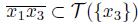. If this is not true, then 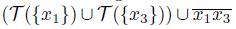would contain a nonunicohenrent subcontinuum of X (Let x ₄ be the first point of the arc 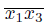in T ({x ₃ }), and let x ₅ ∈ T ({x ₃ }) ∩ T ({x ₁ }). Then 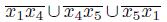is a simple closed curve contained in X.), a contradiction. Hence, x ₁ ∈ T ({x ₃ }) and, by [²², Lemma 7.7.3], Therefore, K(T ({x ₁ })) = T ({x ₁ }) ∪ K({x ₁ }).

Theorem 5.23. [⁹, Theorem 3.7] If X is a pointwise smooth dendroid, then X does not contain an R ³ -continuum.

The following result is [¹⁰, Theorem 16].

Theorem 5.24. If X is a dendroid, then the following are equivalent:

(1)X is pointwise smooth dendroid.

(2)X is semi-aposyndetic and X does not contain an R ³ -continuum.

(3)X is semi-aposyndetic and X does not contain two points x ₁ and x ₂ such that x ₁ ∈ X \ T ({x ₂ }), x ₂ ∈ X \ T ({x ₁ }) and T ({x ₁ }) ∩ T ({x ₂ }) # ∅.

Proof. We prove that (1) implies (2). Suppose X is a pointwise smooth dendroid. Let x ₁ and x ₂ be two points of X. By Theorem 5.4, either x ₁ ∈ X \T ({x ₂ }) or x ₂ ∈ X \T ({x ₁ }). Hence, by [²², Theorem 2.1.32], X is semi-aposyndetic. By Theorem 5.23, X does not contain an R ³-continuum. The fact that (2) implies (3) follows from Corollary 5.9 and [²², Lemma 7.3.10]. To show (3) implies (1), let x ₁ and x ₂ be two points of X such that 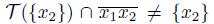and 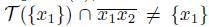. Suppose that T ({x ₁ }) ∩ T ({x ₂ }) # ∅. 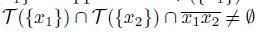Then, since X is hereditarily unicoherent, 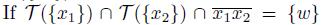, for some element w of X, we have that w ∈ X \ {x ₁ , x ₂ }. 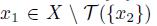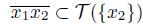Hence, and x ₂ ∈ X \ T ({x ₁ }) (if x ₁ ∈ T ({x ₂ }), then and 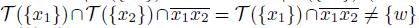, a contradiction; similarly if x ₂ ∈ X \ T ({x ₁ })). Thus, we obtain a contradiction to our assumption. If 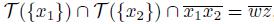, where 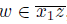, then, since z ∈ T ({x ₁ }), we have that z ∈ T ({w}) (if z ∈ X \ T ({w}), then there exists a subcontinuum Z of X such that z ∈ Int(Z) ⊂ Z ⊂ X \ {w}, since z ∈ T ({x ₁ }), we obtain that x ₁ ∈ Z; thus, w ∈ Z, a contradiction). Also, since w ∈ T ({x ₂ }), we have that w ∈ T ({z}). Hence, by [²², Lemma 2.1.32], X is not semi-aposyndetic. Thus, T ({x ₁ }) ∩ T ({x ₂ }) = ∅. Therefore, by

Theorem 5.4, X is pointwise smooth.

6. Strict Point T -asymmetry on Dendroids

Strict point T -asymmetric continua were defined by David P. Bellamy [¹⁹, p. 392]. We present new results about strict point T - asymmetry.

A continuum X is strictly point T -asymmetric if for any two distinct points p and q of Xwith p ∈ T ({q}), we have that q ∈ X \ T ({p}). David P. Bellamy asked:

Question 6.1. [²², Question 8.1.9] If X is a strictly point T -asymmetric dendroid, then is X smooth?

Leobardo Fernández gave a negative answer to this question [13]. The dendroid presented in Remark 5.2 (Figure 4) is an example of a nonsmooth dendroid that is strictly point T -asymmetric. He proved that the reverse implication is true [¹³, Corollary 3.3]. He also showed that for fans strict point T -asymmetry is equivalent to smoothness [13, Theorem 3.5]. We extend these results to pointwise smooth dendroids (Corollary 6.3).

We present a characterize of strictly point T -asymmetric continua as semi-aposyndetic continua.

Theorem 6.2. Let X be a continuum. Then X is point T -asymmetric if and only if X is semi-aposyndetic.

Proof. Suppose X is strictly point T -asymmetric and let p and q be two points of X. We have that either p ∈ X \ T ({q}) or p ∈ T ( {q}). In the second case, since X is strictly point T -asymmetric, we obtain that q ∈ X \ T ({p}). Therefore, X is semi-aposyndetic [²², Theorem 2.1.32].

Assume that X is semi-aposyndetic and let p and q be two points of X. Suppose p ∈ T ({q}). Since X is semi-aposyndetic and p ∈ T ({q}), we have that q ∈ X \ T ({p}) [²², Theorem 2.1.32]. Therefore, X is strictly point T -asymmetric.

Next, we show that pointwise smooth dendroids are strictly point T -asymmetric.

Corollary 6.3. If X is a pointwise smooth dendroid, then X is strictly point T - asymmetric.

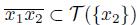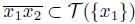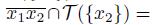
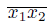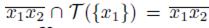Proof. Suppose X is not strictly point T -asymmetric. Then there exist two points x ₁ and x ₂ of X such that x ₁ ∈ T ({x ₂ }) and x ₂ ∈ T ({x ₁ }). Since {x ₁ , x ₂ } ⊂ T ({x ₂ }), we have that . Similarly, we have that . Hence, and Thus, 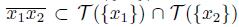Therefore, by Theorem 5.4, X is not pointwise smooth.

As a consequence of Theorem 6.2 and Corollary 6.3, we have:

Corollary 6.4. If X is a pointwise smooth dendroid, then X is semi-aposyndetic.

Remark 6.5. Note that Corollary 6.4 is also a consequence of Theorem 5.24.

Corollary 6.6. Let X be a fan. Then the following are equivalent:

(1) X is strictly point T -asymmetric.

(2) X is a smooth fan.

(3) X is a pointwise smooth fan.

(4) X is semi-aposyndetic.

Proof. By [¹³, Theorem 3.5], (1) and (2) are equivalent. By Theorem 5.3, (2) and (3) are equivalent. By Theorem 6.2, (1) and (4) are equivalent.

We end the paper with another characterization of pointwise smooth dendroids.

Theorem 6.7. A dendroid X is pointwise smooth if and only if X is strictly point T -asymmetric and X does not contain an R ³ -continuum.

Proof. Suppose X is a pointwise smooth dendroid. Then, by Theorem 5.24, X is semi-aposyndetic and X does not contain an R ³-continuum. Since X is semi-aposyndetic, by Theorem 6.2, X is strictly point T -asymmetric.

Assume that X is a strictly point T -asymmetric dendroid such that X does not contain an R ³-continuum. Since X is strictly point T -asymmetric, by Theorem 6.2, X is semiaposyndetic. Hence, by Theorem 5.24, X is pointwise smooth.