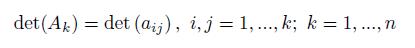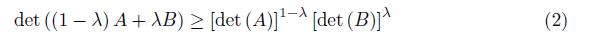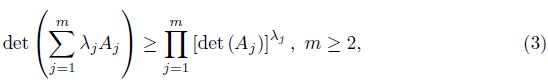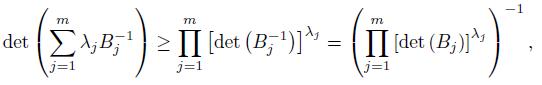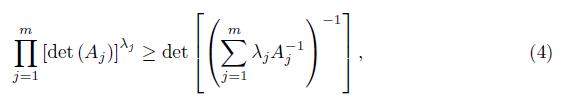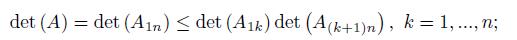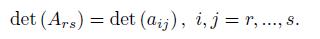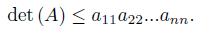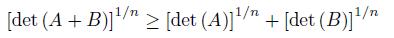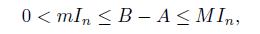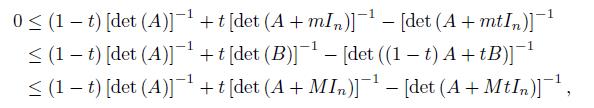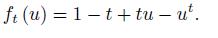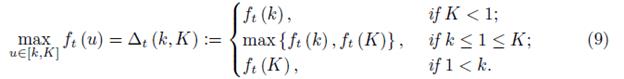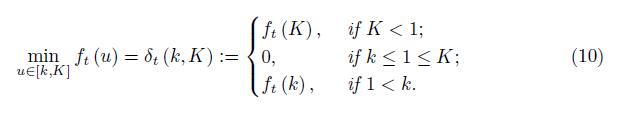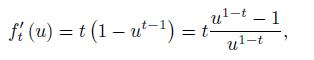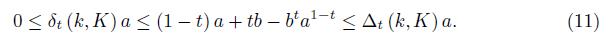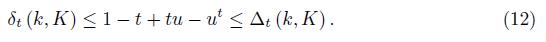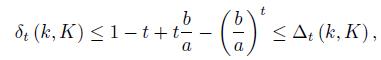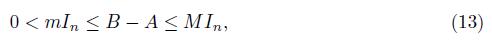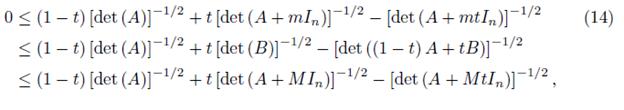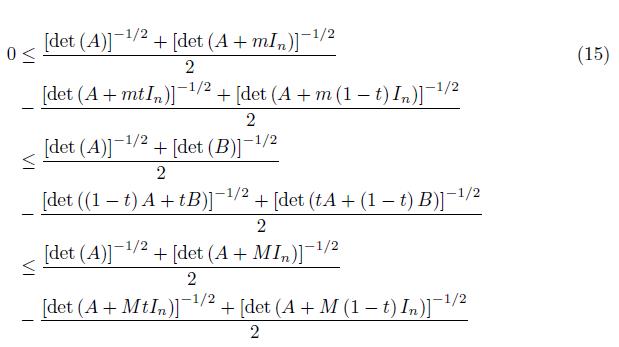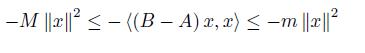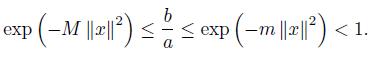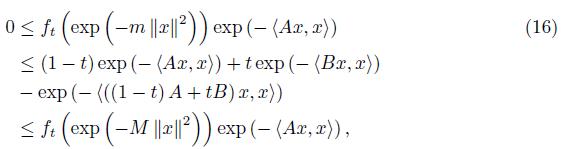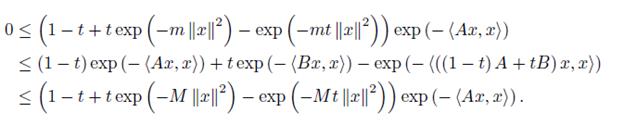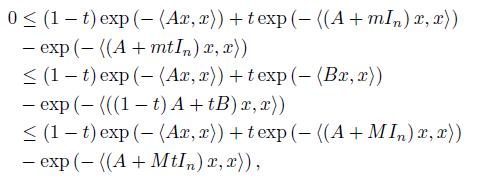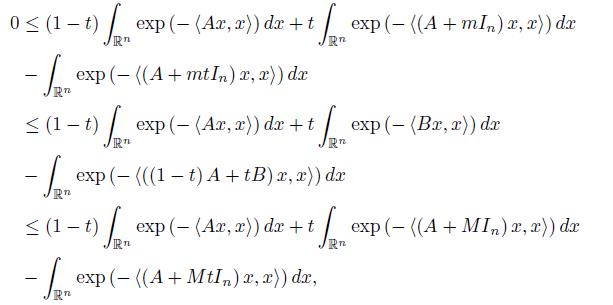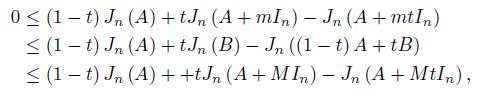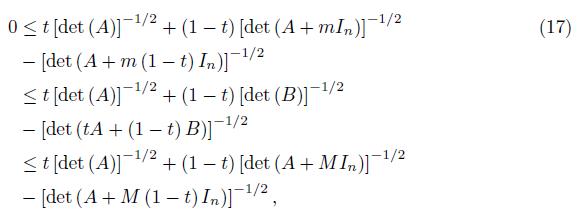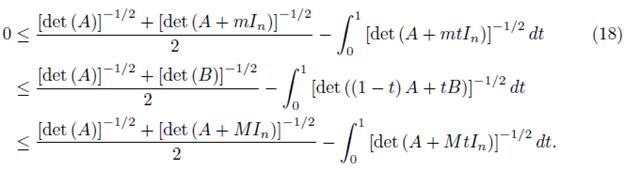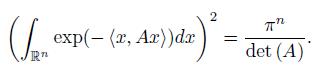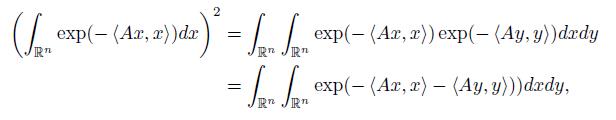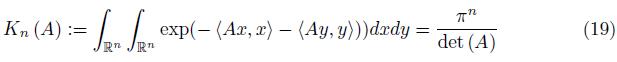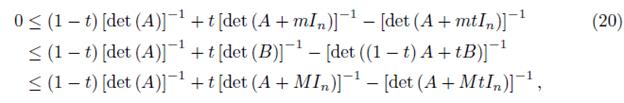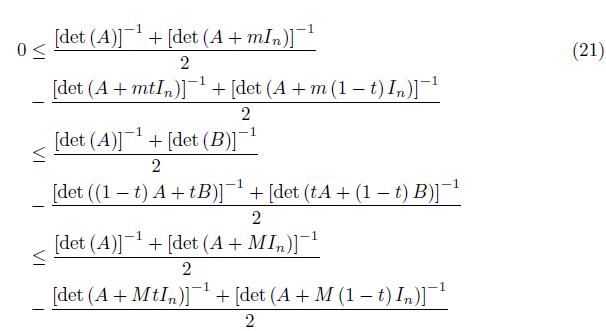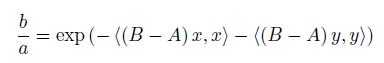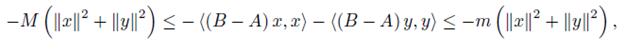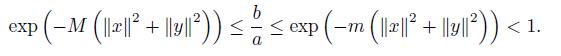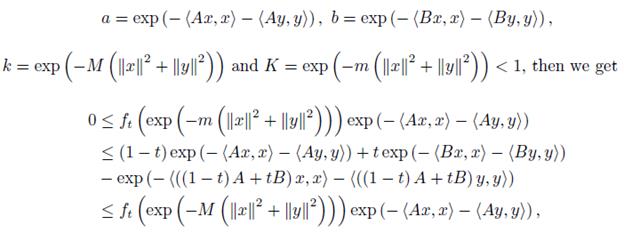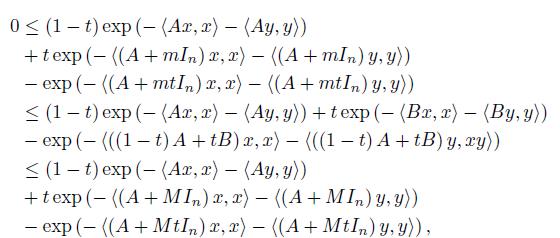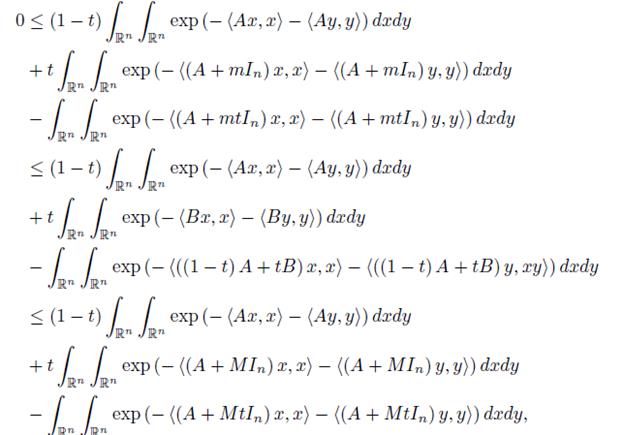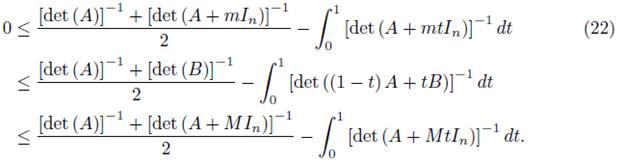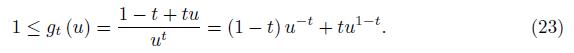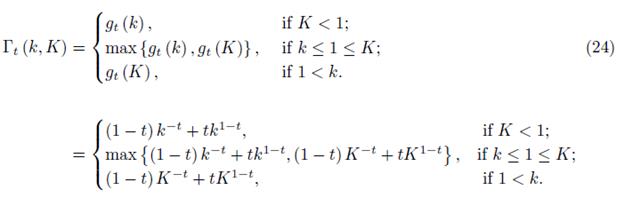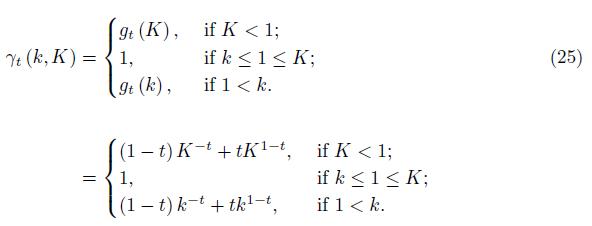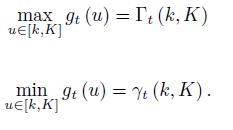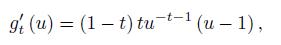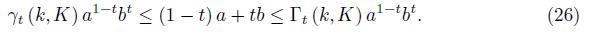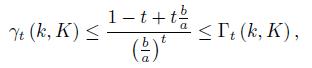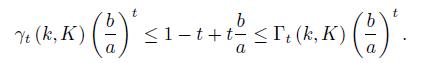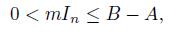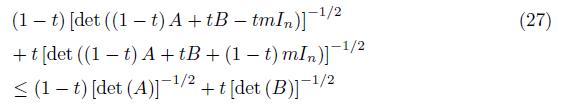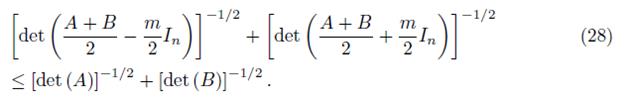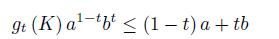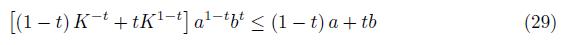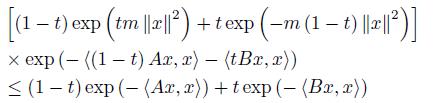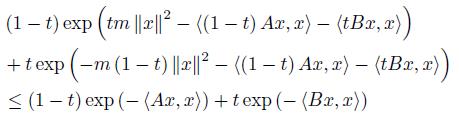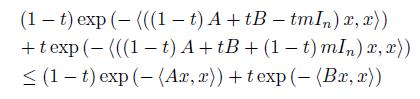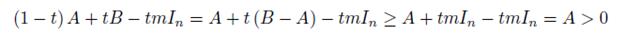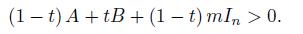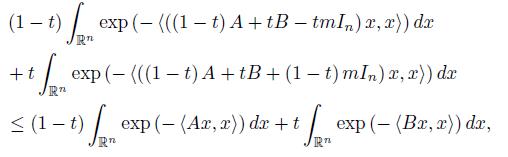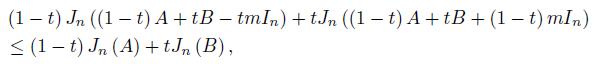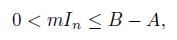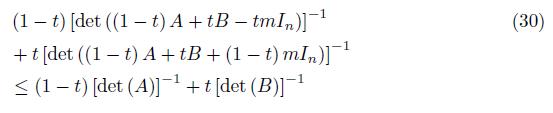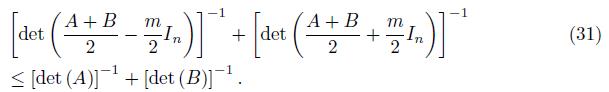1. Introduction

A real square matrix A = (α_ij ) , i, j = 1, ..., n is symmetric provided a_ij = a_ji for all i, j = 1, ..., n. A real symmetric matrix is said to be positive definite provided the quadratic form 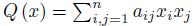is positive for all x = (x₁, ..., x_n) ∈ ℝⁿ \ {0}. It is well known that a necessary and sufficient condition for the symmetric matrix A to be positive definite, and we write A > 0, is that all determinants

are positive.

It is know that the following integral representation is valid, see [¹, pp. 61-62] or [¹¹, pp. 211-212],

where A is a positive definite matrix of order n and 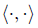· is the usual inner product on ℝⁿ.

By utilizing the representation (1) and Hölder’s integral inequality for multiple integrals one can prove the logarithmic concavity of the determinant that is due to Ky Fan ([¹, pp. 63] or [¹¹, pp. 212]), namely

for any positive definite matrices A, B and λ ∈ [0, 1] .

By mathematical induction we can get a generalization of (2) which was obtained by L. Mirsky in [10], see also [¹¹, pp. 212]

where λ_j > 0, j = 1, ..., m with 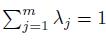and A_j > 0, j = 1, ..., m.

If we write (3) for Aj = B⁻¹ _j we get

which also gives

where λ_j > 0, j = 1, ...,m with 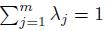and A_j > 0, j = 1, ...,m.

Using the representation (1) one can also prove the result, see [¹¹, pp. 212],

where the determinant det (A_rs) is defined by

In particular,

We recall also the Minkowski’s type inequality,

for A, B positive definite matrices of order n. For other determinant inequalities see Chapter VIII of the classic book [¹¹]. For some recent results see [³]-[⁶].

Motivated by the above results, in this paper we prove among others that, if the positive definite matrices A, B of order n satisfy the condition

for some constants 0 < m < M, where I_n is the identity matrix, then

for all t ∈ [0, 1] .

2. Additive Inequalities

We consider the function f_t: [0, ∞) → [0, ∞) defined for t ∈ (0, 1) by

The following lemma holds.

Lemma 2.1. For 0 ≤ k < K we have

and

Proof. The function f_t is differentiable and

which shows that the function f_t is decreasing on [0, 1] and increasing on [1, ∞), f_t (0) = 1 − t, f_t (1) = 0 and the equation f_t (u) = 1 − t for u > 0 has the unique solution .

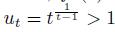Therefore, by considering the 3 possible situations for the location of the interval [k, K] and the number 1 we get the desired bounds (9) and (10).

Lemma 2.2. Assume that a, b > 0 with 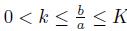, then

Proof. If u ∈ [k, K] , then by Lemma 2.1 we have

If we take 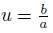in (12), then we get

and by multiplying with a we obtain the desired result (11).

Theorem 2.3. Assume that the positive definite matrices A, B satisfy the condition

for some constants 0 < m < M, then

for all t ∈ [0, 1] .

for all t ∈ [0, 1].

Proof. Let a = exp (− Ax, x ) and b = exp (− Bx, x ) for x ∈ ℝⁿ. Then exp (− (B − A) x, x ) and since 0 < mI_n ≤ B − A ≤ M I_n, hence for x ∈ ℝⁿ,

which gives that

If we apply the inequality (11) for a = exp (− Ax, x ) , b = exp (− Bx, x ) , k = exp (−M ||x||²⁾ and K = exp (−m ||x||² < 1, then we get

Namely

This inequality can be written as

for x ∈ ℝⁿ and t ∈ [0, 1] .

If we take the integral over x ∈ ℝⁿ, then we get

for t ∈ [0, 1] .

By using the representation (1) we get

which, by the second equality in (1) gives (14).

If we replace t with 1 − t in (14), then we have

for t ∈ [0, 1] .

If we add (14) with (17) and divide by 2, then we get (15).

Inequalities for Positive Definite Matrices Via Additive

Corollary 2.4. With the assumptions of Theorem 2.3 we have

The proof follows by taking the integral over t ∈ [0, 1] in (14).

If we take the square in the representation (1), then we get

Since

hence

for A a positive definite matrix of order n and h 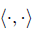i is the usual inner product on ℝⁿ.

We have:

Theorem 2.5. Assume that the positive definite matrices A, B satisfy the condition (13) for some constants 0 < m < M, then

for all t ∈ [0, 1] .

Also,

for all t ∈ [0, 1] .

Proof. Let a = exp (−hAx, xi − hAy, yi) and b = exp (−hBx, xi − hBy, yi) for x, y ∈ ℝn. Then

and since 0 < mIn ≤ B − A ≤ MIn, hence for x, y ∈ ℝn,

which implies that

If we apply the inequality (11) for

Namely

for x, y ∈ ℝⁿ and t ∈ [0, 1] .

If we take the double integral over x, y ∈ ℝⁿ, then we get

and by making use of the representation (19).

Corollary 2.6. With the assumptions of Theorem 2.5 we have

The proof follows by taking the integral over t ∈ [0, 1] in (20).

3. Multiplicative Inequalities

We consider the function g_t: (0, ∞) → (0, ∞) defined for t ∈ (0, 1) by

For [k, K] ⊂ (0, ∞) define the quantities

and

The following lemma holds.

Lemma 3.1. For 0 ≤ k < K we have

Proof. The function g_t is differentiable and

which shows that the function g_t is decreasing on (0, 1) and increasing on [1, ∞) . We have g_t (1) = 1, lim_u→0+g_t (u) = +∞, lim_u→∞g_t (u) = +∞ and g_t ¹ = g_1−t (u) for any u > 0 and t ∈ (0, 1) .

Therefore, by considering the 3 possible situations for the location of the interval [k, K] and the number 1 we get the desired bounds (11) and (12).

Lemma 3.2. Assume that a, b > 0 with 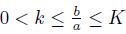then

Proof. From Lemma 3.1 we have

Namely

If we multiply these inequalities by a, then we get (26).

Theorem 3.3. Assume that the positive definite matrices A, B satisfy the condition

for some constant 0 < m, then

for all t ∈ [0, 1] .

In particular, for t = 1/2,

Proof. If 0 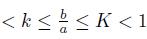, then by (26) we get

Namely

If we apply the inequality (29) for α = exp (− Ax, x ) , b = exp (− Bx, x ) and K = exp (−m ||x|| ² < 1, then we get

This is equivalent to

namely

for all x ∈ ℝⁿ and t ∈ [0, 1]

Observe that

and

By taking the integral on ℝⁿ, we get

namely, by (1)

which gives (27).

By utilizing a similar argument to the one in the proof of Theorem 2.5 we can finally state:

Theorem 3.4. Assume that the positive definite matrices A, B satisfy the condition

for some constant 0 < m, then

for all t ∈ [0, 1] .

In particular, for t = 1/2,

A complex square matrix H = (h_ij ) , i, j = 1, ..., n is said to be Hermitian provided 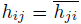for all i, j = 1, ..., n. A Hermitian matrix is said to be positive definite if the Hermitian form 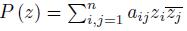is positive for all .

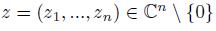It is known that, see for instance [¹¹, pp. 215], for a positive definite Hermitian matrix H, we have

where z = x + iy and dx and dy denote integration over real n-dimensional space ℝⁿ. Here the inner product x, y is understood in the real sense, i.e. .

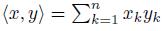On making use of a similar argument to the one in Theorem 2.5 and Theorem 3.4 for the representation K_n (·) we can state the same inequalities for positive definite Hermitian matrices H and K.