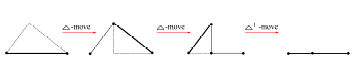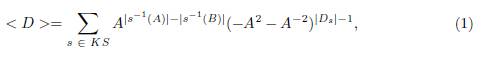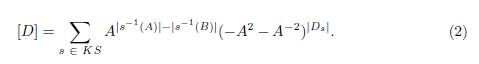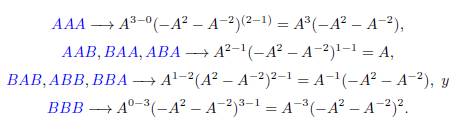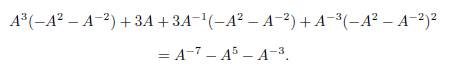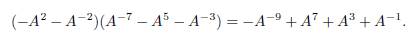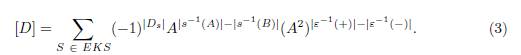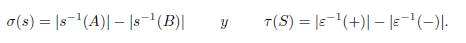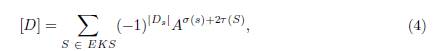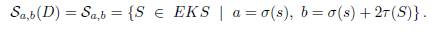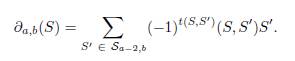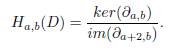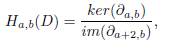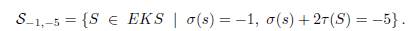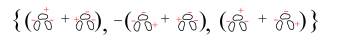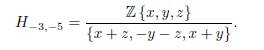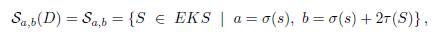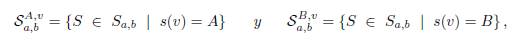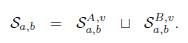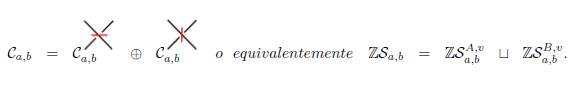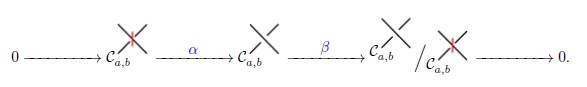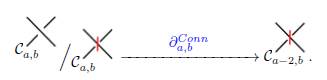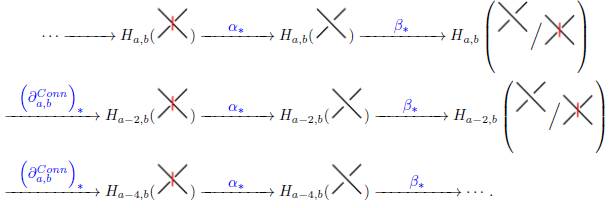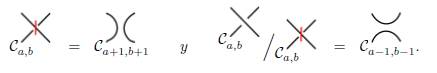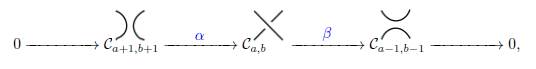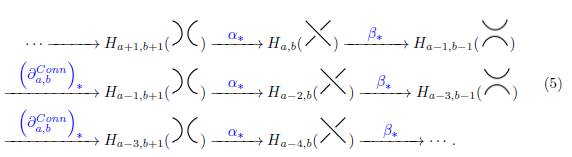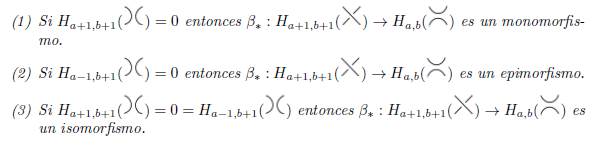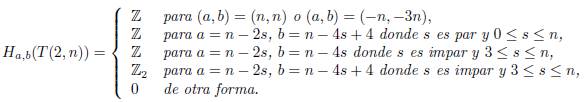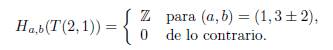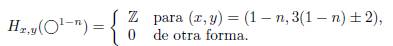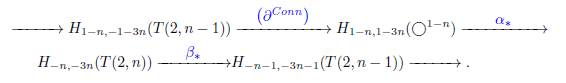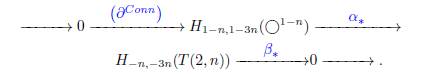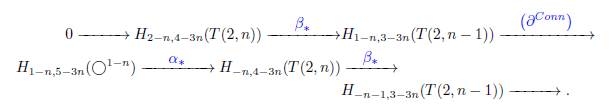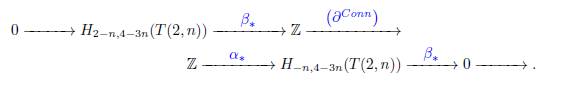1. Introducción
La teoría matemática de nudos es un campo fascinante de investigación que envuelve distintas áreas de la ciencia como la matemática, física, química, entre otras. Una de las motivaciones para publicar este artículo es fomentar la teoría en el Encuentro Internacional de Matemáticas (EIMAT) a realizarse en la Universidad del Atlántico en Barranquilla, Colombia, en noviembre de 2023. El artículo está organizado de la siguiente manera. En la sección 2 se brinda un resumen de la historia temprana de la teoría. En la sección 3 presentamos las primeras definiciones formales, entre ellas los diagramas de nudos y los movimientos de Reidemeister. En la sección 4 se construye la homología de Khovanov partiendo del polinomio bracket siguiendo a [21] y en la sección 5 se construye la sucesión larga de la homología de Khovanov. Finalmente, en la sección 6 se calcula la homología de los nudos toroidales T (2, n) y en la sección 7 se presentan posibles futuras direcciones de investigación.
2. Historia
La teoría de nudos, históricamente considerada como subárea de la topología, es actualmente un campo de investigación matemático que se ha desarrollado intensamente hasta alcanzar una alta independencia. Además de tener una fuerte conexión con otras áreas como el álgebra, la combinatoria y la mecánica estadística, goza de una historia fascinante. Esta historia consiste de un viaje en el tiempo que nos puede llevar incluso hasta el año 2600 a. e. c. pasando por la Italia del siglo XV y por la Escocia del siglo XIX. Existe evidencia clara de que la humanidad ha mostrado interés en los nudos desde tiempos muy tempranos, de hecho podríamos solo especular que llevó a comerciantes en Anatolia (Asia menor) en el año 1700 a. e. c. a usar nudos y trenzas en sus sellos y firmas. Para más información al respecto y gráficas relacionadas, referirse a [3, 15]. Escavaciones hechas en la región de Lerna por la Escuela Americana de Estudios Clásicos, bajo la dirección del Profesor J. L. Caskey, encontraron varias impresiones de sellos en arcilla, muchos de ellos que corresponden al año 2200 a. e. c. contienen nudos y enlaces [5]. Es posible encontrar evidencia aún más temprana (2600-2500 a. e. c.) de sellos conteniendo nudos (véase [23]). Damos un salto en el tiempo hasta el siglo I donde un físico griego llamado Heraklas escribió un ensayo donde daba instrucciones paso a paso de cómo atar 18 cabestrillos ortopédicos. Este trabajo sobrevivió gracias a que Oribasius de Pérgamo (médico del emperador Juliano el Apóstata) lo incluyó a finales del siglo IV en el escrito Sinagogas médicas, el cual incluía todo el saber médico de la época. El escrito más reciente de Sinagogas médicas data del siglo X y fue llevado a Italia por el griego J. Las-caris, un refugiado de Constantinopla. El escrito de Heraklas no contenía ilustraciones y sólo hasta el año 1500 un artista anónimo dibujó uno de sus nudos en el manuscrito de Oribasius de Pérgamo. Una traducción al latín realizada por Vidus Vidius (médico del rey Francisco de Francia I) contiene illustraciones hechas por el artista italiano Francesco Primaticcio; ver por ejemplo [14]. Otros artistas del renacimiento realizaron trabajos que de alguna forma están relacionados con los nudos como Albrecht Dürer y Leonardo da Vinci. Es importante mencionar que la historia de los escritos de Heraklas es importante en la teoría de nudos aunque sean sólo aplicaciones.
Podemos decir que la topología y la teoría de nudos moderna tienen su origen gracias a Gottfried Wilhelm Leibniz. Hay evidencia de una carta de Leibniz enviada a Christiaan Huygens en 1679, en la que habla de la necesidad de un nuevo tipo de análisis. Leibniz lo llamó Analysis situs o Geometría de la posición. En la carta escribió:
No estoy satisfecho con el álgebra, ya que no produce las demostraciones más cortas ni las construcciones más hermosas de la geometría. En consecuencia, en vista de esto, considero que necesitamos otro tipo de análisis, geométrico o lineal, que trate directamente con la posición, como el álgebra trata con la magnitud.
De cualquier manera, no es completamente claro si Leibniz tenía algún ejemplo de un problema que perteneciera al Analysis situs. De hecho, el primer ejemplo conocido es el famoso problema de los puentes de Königsberg. Este problema fue propuesto por Heinrich Kühn en 1735. Kühn comunicó el problema a Leonhard Euler sugiriendo que estaría relacionado con la geometría de la posición. Aunque en primeras instancias podríamos decir que Euler no estaba convencido de la utilidad o importancia de este problema, en 1736 resulta publicando un artículo donde detalla su solución [4]. El artículo titulado Solutio problematis ad geometriam situs pertinentis (Solución de problemas relacionados con la geometría de la posición) da origen a la teoría de grafos y a la topología. El nacimiento de la teoría de nudos se da 35 años después cuando el matemático francés Alexandre-Théophile Vandermonde publica el artículo Remarques sur les problemes de situation (Comentarios sobre problemas de posiciones), en el cual incluye nudos y trenzas como elementos de la geometría de posición [20]. Carl Friedrich Gauss es el siguiente matemático que aporta trabajos de gran importancia para el desarrollo de la teoría. De hecho, en uno de sus apuntes de 1794, titulado Una colección de nudos, incluye 13 dibujos de nudos y métodos para codificarlos. Los trabajos de Gauss fueron los que principalmente motivaron a James Clerk Maxwell quien en su libro A treatise on electricity and magnetism (Un tratado sobre electricidad y magnetismo) incluye dos curvas cerradas que no pueden ser separadas, pero para las cuales el valor de la integral de Gauss es cero. Finalmente, el año 1847 representó grandes avances en el desarrollo de la topología (y por tanto de la teoría de nudos) principalmente debido a que Johan Benedict Listing, un estudiante de Gauss, publicó su monografía Vorstudien zur Topologie (Estudios preliminares en topología), en la cual dedica mucho espacio a los nudos. Listing fue el primero en usar la palabra topología para referirse a la geometría de posición.
En el año 1876, el físico escocés Sir William Thomson (Lord Kelvin) ideó la teoría de los átomos de vórtices. Kelvin creía que los átomos de la materia no eran más que anillos de vórtice que se enlazaban formando distintos nudos en una sustancia llamada éter. La motivación de Kelvin provino del trabajo de su amigo y colega Peter G. Tait, quien había creado un método para producir anillos de humo. Tait, por su parte, llegó a estar interesado en este tipo de estudios gracias a la traducción de un trabajo realizado por el matemático alemán Hermann von Helmholtz Üeber Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen (Sobre integrales de las ecuaciones hidrodinámicas que corresponden a movimientos de vórtice), en el cual aplica hidrodinámica a fenómenos electromagnéticos. En ese momento, crear una tabla de los elementos era de una importancia significante. La teoría de Kelvin implicaba que si se creaban dos anillos de vórtice, enlazados el uno con el otro, entonces esto formaría un átomo indestructible. Tait, queriendo crear un tabla de los elementos, creó una clasificación de estos nudos, en lo que resultó ser uno de los trabajos más importantes en toda la historia de la teoría de nudos. Como es bien sabido, la teoría de Kelvin fue más tarde descartada por la teoría de la relatividad. De cualquier modo, es impresionante ver cómo a partir de una hipótesis refutada se generó un campo formal de investigación alrededor de los nudos.
Como se mencionó al inicio de esta sección, la historia de la teoría de nudos comprende muchos aspectos y sería imposible incluirlos todos en este artículo. El lector es referido a los trabajos de Józef H. Przytycki [15, 16, 18], que contienen gran cantidad de información al respecto. Además, el libro [14] ofrece una extensa discusión histórica de la teoría de nudos y temas actuales de investigación, incluyendo coloraciones de Fox, homología de Yang-Baxter, polinomio de Jones, determinantes de Gram, módulos de madeja, entre otros.
3. Introducción a la teoría de nudos
La teoría clásica de nudos estudia los encajamientos de círculos módulo transformaciones naturales en el espacio ℝ3. Uno de los problemas fundamentales (e históricos) en la teoría es la clasificación. Durante el siglo XIX el estudio y entendimiento de los nudos estaba lejos de ser formal. De hecho, se entendía un nudo como una curva cerrada en el espacio, módulo “deformaciones naturales”. La idea de isotopía ambiente no estaba formalmente definida, por lo que estas deformaciones eran entendidas como “movimientos en el espacio sin cortar ni pegar”. A pesar de la falta de formalidad, con mucha intuición experimental, varios científicos lograron hacer aportes significativos a la teoría, como por ejemplo P. G. Tait, T. P. Kirkman, C. N. Little y M. G. Haseman. En todo caso, métodos precisos para diferenciar nudos no existían al momento. En esta sección introducimos los conceptos de enlace poligonal, movimientos de Reidemeister y ∆-movimientos, los cuales juegan un papel fundamental en la formalización de la teoría de nudos.
Definición 3.1.
(a) Un enlace poligonal es una colección de curvas cerradas poligonales simples disjuntas en ℝ3. Un enlace poligonal que consiste de sólo una curva simple es llamado un nudo poligonal.
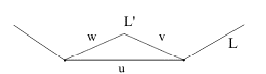
(b) Sea u un segmento o eje en un enlace poligonal L en ℝ3. Sea ∆ un triángulo en ℝ3 cuya frontera consiste de tres segmentos lineales denotados por u, v y w, de tal modo que ∆ ∩ L = u. La curva poligonal L′, definida como L′ = (L − u) ∪ v ∪ w, es un nuevo enlace poligonal en ℝ3. Así, decimos que L′ ha sido obtenido desde L por un ∆-movimiento (∆-move). De forma opuesta, decimos que L se obtiene a partir de L′ por un ∆−1-movimiento (∆−1-move) (ver Figura 1). Además es permitido que el triángulo ∆ sea degenerado de modo que el vértice v ∩ w está en el mismo lado de u. En otras palabras, se permite subdivisión del segmento u como se ilustra en la Figura 2.
(c) Dos enlaces poligonales se dicen ser ∆-equivalentes (o equivalentes combinatorialmente) si uno puede ser obtenido del otro a través de una sucesión finita de ∆-y ∆−1-movimientos.
Los enlaces poligonales son usualmente presentados con diagramas planos. En palabras generales, los diagramas son definidos usando proyecciones del enlace que permiten describir la información local en cada cruce como “sobre” y “bajo”. Con miras a que esta idea esté bien definidia, restringimos la discusión a proyecciones regulares. Sea p : ℝ3 → ℝ2 una proyección y sea L ⊂ ℝ3 un enlace. Un punto P ∈ p(L) se dice un punto múltiple de p si p−1(P ) contiene más de un punto (al número de puntos en p−1(P ) se le denomina la multiplicidad de P ).
Definición 3.2. La proyección p se dice regular si
(1) p tiene sólo un numero finito de puntos múltiples y estos tienen multiplicidad dos,
(2) ningún vértice del enlace poligonal es preimagen de un punto múltiple de p.
Así, en el caso de una proyección regular, las siguientes situaciones ilustradas en la Figura 3 no son permitidas.
Definición 3.3. Un diagrama de un enlace es una proyección regular del enlace con la información de “sobre” y “bajo” en cada cruce.
Es importante observar que por razones prácticas, cuando se dibuja un diagrama se asume que hay un número “bastante grande” de segmentos lineales que componen el nudo o enlace de modo que la traza parece estar “curvada” (ver por ejemplo, la Figura 6). En el año 1927 el matemático alemán Kurt Reidemeister demostró que dos diagramas, posiblemente orientados, son isotópicos si y sólo si están conectados por una sucesión finita de ciertos movimientos e isotopía planar. Actualmente, estos movimientos son conocidos como los movimientos de Reidemeister aunque fueron primeramente ideados por el matemático escocés James Maxwell en el año 1870 y demostrados independientemente por James Alexander y Garland Briggs en 1927 [1].
Teorema 3.4. (Teorema de Reidemeister [19]) Dos diagramas representan enlaces ∆-equivalentes si y sólo si los diagramas están relacionados a través de una sucesión finita de movimientos de Reidemeister Ri, para i = 1, 2, 3 y deformación del plano del diagrama.
La Figura 4 ilustra los movimientos de Reidemeister denotados por R1, R2 y R3. Así, para distinguir nudos se usan los invariantes. En palabras simples, una invariante es una propiedad del enlace que se mantiene intacta bajo isotopía ambiente. Para demostrar que una propiedad P (D) de un diagrama D es una invariante, se verifica que esta propiedad se mantenga intacta bajo los movimientos de Reidemeister. Por ejemplo, las coloraciones de Fox, el polinomio de Alexander y el polinomio de Jones son invariantes [14].
4. Homología de Khovanov desde el polinomio bracket
El matemático estadounidense George David Birkhoff (1884-1944) introdujo el polinomio cromático en el año 1912. En ese momento él estaba tratando de resolver el problema de los cuatro colores. Sin entrar en detalle, el polinomio cromático cuenta el número de coloraciones de los vértices de un grafo, de tal manera que vértices conectados por una arista tienen asignados diferentes colores. El primer polinomio en la teoría de nudos es el polinomio de Alexander. Este importante aporte fue hecho por el matemático estadounidense James Wadell Alexander (1888-1971). Se cree que Alexander sabía del polinomio cromático y esto lo motivó a crear algo similar para nudos. Además de sus grandes aportes en ciencia, Alexander tuvo una vida muy interesante; era millonario y un gran escalador, llegó a completar ascensos populares como los Alpes suizos y las Montañas Rocosas en Colorado. Para más detalles acerca del polinomio de Alexander, ver por ejemplo [14]. En el año 1984, un nuevo polinomio fue anunciado por el matemático neozelandés Vaughan Frederick Randal Jones (1952-2020) [6]. Tan importante fue este descubrimiento que revolucionó la investigación en la teoría de nudos a tal punto que la mayoría de temas hoy en día están relacionados de alguna forma al polinomio. En Agosto del año 1985, Louis H. Kauffman, un matemático estadounidense nacido en 1945 y uno de los más activos actualmente en la investigación en teoría de nudos, anunció un invariante conocido como el polinomio bracket de dos variables. Inicialmente Kauffman creyó que había descubierto o construído un invariante completamente nuevo, pero rápidamente se percató que en realidad había descubierto una forma más sencilla de obtener el polinomio de Jones [7].
Definición 4.1. El polinomio bracket clásico y reducido es una función definida en el conjunto de enlaces no orientados D con imagen en el conjunto de los polinomios de Laurent con coeficientes enteros en la variable A, : D → ℤ[A±1]. Se caracteriza con las condiciones iniciales { ◯} = 1, {D ⊔ ◯} = (−A2 − A−2) {D} y la relación de madeja:
Definición 4.2. Considere D un enlace no orientado y denote por cr(D) el conjunto de sus cruces. Definimos un estado de Kauffman (o simplemente estado), denotado s, del diagrama D, como una función s : cr(D) → {A, B}. Esta función es entendida como una asignación de un marcador A o B a todos los cruces como se indica en la Figura 5Denotamos por KS el conjunto de todos los estados. Además, en la figura se observa cómo cada marcador genera una solución (o suavizamiento) del cruce.
De esta manera, el polinomio bracket del diagrama D está dado por la siguiente fórmula:
donde Ds denota el sistema de círculos obtenidos por la solución de todos los cruces de acuerdo con los marcadores en el estado s y |Ds| denota el número de círculos en el sistema.
El lector pudo haber observado la palabra reducido en la definición 4.1. Esto sugiere correctamente que hay varias versiones de este polinomio. Dado que más adelante usaremos la versión no reducida, la definimos a continuación.
Definición 4.3. El polinomio bracket no reducido es una versión del polinomio bracket en la cual al enlace vacío ∅ le es asignado el polinomio 1. Se denota por [ ] y con esta notación tenemos [∅] = 1, [◯]= (−A2 − A−2) y [D] = (−A2 − A−2) < D >.
Así, la ecuación 1 se convierte en:
Ejemplo 4.4. En este ejemplo presentaremos cómo calcular el polinomio bracket reducido y no reducido del nudo conocido como el trébol derecho. Es claro que, aunque no es la forma óptima, el polinomio puede ser calculado directamente usando la relación de madeja en la definición 4.1. Aquí haremos el cálculo usando los estados de Kauffman.
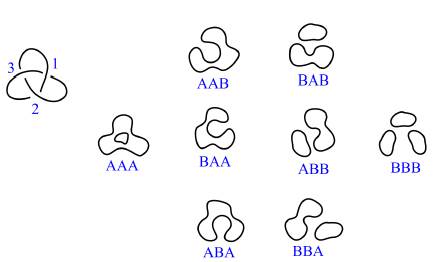
La Figura 6 muestra un diagrama del nudo trébol con sus cruces enumerados 1, 2, 3 y además contiene todos sus estados con los cruces resueltos. Estos estados están nombrados por tres letras que representan el marcador asignado a cada cruce. Por ejemplo, el nombre ABA indica que los cruces 1 y 3 son dados un marcador A y el cruce 2 es dado un marcador B.
Usando las ecuaciones previamente obtenidas, sabemos que aporta cada estado al polinomio:
De esta forma, el polinomio bracket reducido del nudo trébol esta dado por:
Adicionalmente, la versión no reducida está dada por:
Observe que los terminos en la ecuación 2 provienen de los estados del diagrama y por tanto tienen una interpretación geométrica. Además, esta fórmula permite tener una correspondencia 1-1 entre los círculos en Ds y los factores (−A2 − A−2). Esto motiva la siguiente definición.
Definición 4.5. Un estado de Kauffman mejorado S del diagrama D es un estado de Kauffman s junto con una función ε : Ds → {+, −}, la cual asigna a cada círculo de Ds un signo positivo o un signo negativo.
Se denota al conjunto de los estados mejorados de Kauffman por EKS (por sus siglas en inglés Enhanced Kauffman States). Puesto que cada círculo en Ds es dado un signo positivo o negativo, se deduce que para cada estado s existen 2|Ds| estados mejorados. Así, el polinomio bracket puede ser expresado como una suma de monomios, provenientes de los estados mejorados, de la siguiente manera:
Denote por σ(s) la diferencia entre el número de marcadores A (también llamados marcadores positivos) y marcadores B (marcadores negativos) en el estado. Denote por τ(S) la diferencia entre el número de signos positivos y negativos en el estado mejorado. Esto es:
De esta forma, la ecuación 3 se convierte en:
la cual se conoce como la fórmula para el polinomio bracket no reducido en términos de los estados mejorados. Estos estados mejorados forman una base para los grupos de cadena y el complejo de cadena de Khovanov definidos a continuación.
Definición 4.6.
(I) El bigrado en los estados mejorados se define como el siguiente conjunto:
(II) Los grupos de cadena Ca,b(D) = Ca,b se definen como los grupos abelianos libres con base Sa,b(D) = Sa,b, i.e. Ca,b = ℤSa,b. Así,
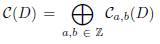 es grupo libre abeliano bigradado.
es grupo libre abeliano bigradado.
(III) Para un diagrama D de un enlace, se define el complejo de cadena C (D) = {(Ca,b, ∂a,b)}, donde el mapa diferencial ∂a,b: Ca,b → Ca−2,b es definido por:
En el item (III) de la definición anterior S ∈ Sa,b y a (S, S ′) se le conoce como el número incidental entre S y S′. Tenemos que (S, S′) = 0 o (S, S′) = 1. Además, sabemos que es igual a 1 si y sólo si las siguientes condiciones se cumplen:
1. S y S′ son idénticos, excepto en un cruce, digamos v. Además, s(v) = A y s′(v) = B, donde S y S′ son estados mejorados de s y s′ respectivamente.
2. τ(S′) = τ(S) + 1 y cada componente de Ds que no pasa por el cruce v mantiene su signo por Ds′.
Note que la condición (1) describe el hecho que el valor de σ decrece en 2, mientras que la condición (2) representa el hecho de que el número de signos negativos decrece o el número de cruces positivos incrementa. Finalmente, el número (−1)t(S,S′) requiere un orden en los cruces del diagrama D. El número t(S, S′) es definido como el número de cruces en D asignados un marcador B en S después del cruce v en el orden estipulado. Este orden es suficiente para que el mapa diferencial cumpla con la condición ∂a−2,b ◦ ∂a,b = 0. De cualquier modo, es importante mencionar que la homología no depende del orden de los cruces [8].
Con la notación dada hasta el momento, podemos presentar en la Figura 7 los posibles escenarios en que los estados mejorados S y S′ son incidentales ( (S, S′) = 1). Por ejemplo, cuando dos círculos con signos diferentes son “unidos”, el resultado debe ser un círculo con un signo positivo.
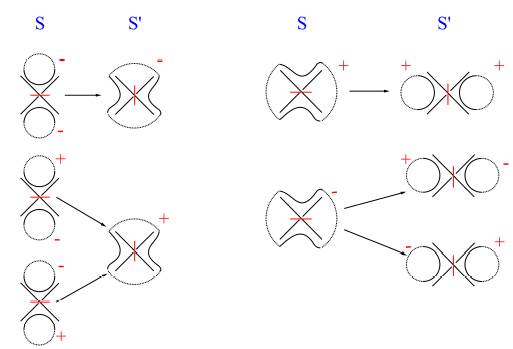
Figura 7 Signos de los círculos después de unión (izquierda) y separación (derecha) de los componentes.
Definición 4.7. La homología de Khovanov del diagrama D se define como la homología del complejo de cadena ℓ C (D):
Por supuesto que la propiedad más importante de la homología de Khovanov es su invarianza bajo los movimientos de Reidemeister de segundo y tercer tipo. El siguiente teorema establece el resultado; ver [21, 22] para una demostración.
Teorema 4.8. Sea D un diagrama de un enlace. Los grupos de homología
son invariantes bajo los movimientos de Reidemeister de segundo y tercer tipo. Por lo tanto, son invariantes de enlaces no orientados enmarcados1. Además, el efecto del movimiento de Reidemeister de primer tipo R1 (positivo o negativo) está dado por Ha,b(R1+(D)) = Ha+1,b+3(D) y Ha,b(R1−(D)) = Ha−1,b−3(D). Estos grupos categorifican el polinomio bracket no reducido y son llamados los grupos homológicos enmarcados de Khovanov.
4.1. Ejemplo: homología del nudo trébol
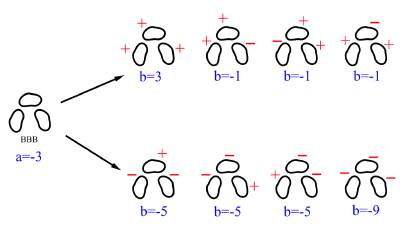
Ahora presentamos a manera de ejemplo el cálculo de la homología de Khovanov para el nudo trébol. Primero se debe asignar un orden a los cruces y obtener todos los estados, tal cual se observa en la Figura 6. Una vez se tienen los estados de Kauffman, es posible determinar los estados mejorados y los valores de α = σ(s) y b = σ(s) + 2τ(S). Por ejemplo, la Figura 8 muestra los estados mejorados que corresponden al estado BBB.
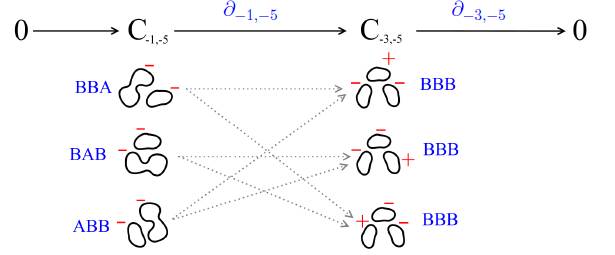
Teniendo los valores del bigrado (a, b) para los estados mejorados del nudo trébol, el próximo paso es construir el complejo de cadena. Recordamos que ∂a,b: Ca,b → Ca−2,b es dado en la definición 4.6. Observe que el valor de b no cambia, lo cual sugiere que para cada valor de b podemos construir un complejo. La Figura 9 ilustra los estados mejorados para los cuales b = σ(s) + 2τ(S) = −5.
De este modo tenemos que: C−1,−5 = ℤS−1,−5, donde
Similarmente, C−3,−5 = ℤS−3,−5, donde
Así, el complejo obtenido para b = −5 es ilustrado en la Figura 10. Además, la figura muestra los pares de estados incidentales.
Se puede observar que
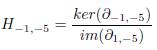 es trivial. Ahora, para obtener H−3,−5 =
es trivial. Ahora, para obtener H−3,−5 =
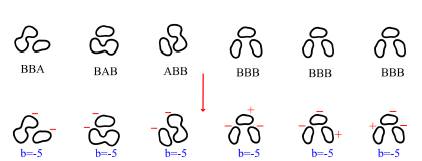
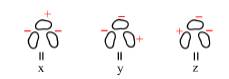
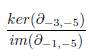 note que ker(∂−3,−5) = C−3,−5 es el grupo abeliano generado por los siguientes estados mejorados, los cuales son denotados por x, y, z para simplificar el procedimiento, como se ilustra en la Figura 11:
note que ker(∂−3,−5) = C−3,−5 es el grupo abeliano generado por los siguientes estados mejorados, los cuales son denotados por x, y, z para simplificar el procedimiento, como se ilustra en la Figura 11:
Por otro lado, note que la imagen de ∂−1,−5 es el grupo abeliano cuya base está dada por el conjunto ilustrado en la Figura 12:
Por lo tanto, el grupo homológico H−3,−5 está dado por
Estas relaciones son equivalentes a tener z = −x = y y 2x = 0. Así, este cociente es Z2, un grupo de torsión. El proceso para los otros grupos homológicos es análogo (ver por ejemplo [10]). El Cuadro 1 contiene la homología de Khovanov completa para el nudo trébol.
5. Sucesión larga de Khovanov
De una forma similar en la que se construye la homología de Khovanov, podemos categorificar la relación de madeja en la definición del polinomio bracket (Definición 4.1). Recuerde que en la definición 4.6 se da el siguiente conjunto:
el cual sirve como base para los grupos abelianos libres Ca,b = ℤSa,b. Sea v un cruce fijo del diagrama D. Considere los conjuntos Sa,b A,v y Sa,b B,v definidos como sigue:
i.e. Sa,b A,v contiene todos los estados mejorados S con bigrado (a, b) que tienen un marcador A en el cruce v; de forma análoga, Sa,b B,v contiene todos los estados mejorados S con bigrado (a, b) que tienen un marcador B en el cruce v. De esta forma, podemos observar que:
Usando la misma notación de la construcción de la homología de Khovanov, denotamos los grupos abelianos generados por estos conjuntos por:
donde
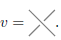 . Así, al nivel de grupos se obtienen las siguientes igualdades:
. Así, al nivel de grupos se obtienen las siguientes igualdades:
Observe que el complejo
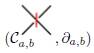 es un sub-complejo de cadena de (Ca,b, ∂a,b), o en otras palabras
es un sub-complejo de cadena de (Ca,b, ∂a,b), o en otras palabras
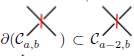 . En contraste, note que esto no es necesariamente cierto para (Ca,b , ∂a,b) puesto que ∂a,b podría cambiar el marcador del cruce de A a B, como fue discutido en la construcción de la homología de Khovanov. La siguiente sucesión exacta corta puede ser escrita:
. En contraste, note que esto no es necesariamente cierto para (Ca,b , ∂a,b) puesto que ∂a,b podría cambiar el marcador del cruce de A a B, como fue discutido en la construcción de la homología de Khovanov. La siguiente sucesión exacta corta puede ser escrita:
En esta sucesión, α toma un estado mejorado del diagrama D con marcador B en el cruce v y lo envía al estado mejorado de D que asigna un marcador B al cruce v y los demás cruces mantienen sus marcadores y los círculos mantienen sus signos. Por otro lado, el mapa β envía a los estados mejorados con marcador B en el cruce v a cero y a cada estado mejorado con marcador A en el cruce v al estado mejorado de D con el cruce v dado un marcador A y los demás cruces y círculos preservan sus marcadores y signos, respectivamente.
Observe que
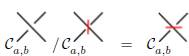 y existe un mapa conector entre los complejos de cadena de la homología de Khovanov:
y existe un mapa conector entre los complejos de cadena de la homología de Khovanov:
Así, obtenemos la siguiente sucesión larga de homologías:
Note las siguientes igualdades obtenidas al solucionar el cruce:
De tal modo que, podemos obtener la siguiente sucesión corta de complejo de cadenas de diagramas:
la cual genera la siguiente sucesión conocida como la sucesión larga de la homología de Khovanov:
El siguiente resultado se obtiene directamente de la construcción previa, por tal motivo omitiremos su demostración.
6. Homología de nudos toroidales T(2,n)
La familia de nudos toroidales T (2, n) ha sido siempre de gran interés para la investigación en teoría de nudos. La homología de Khovanov para estos nudos fue calculada en primera instancia por el creador de esta teoría de homología, el matemático ruso Mikhail Khovanov2 [8]. Luego el matemático polaco Józef Przytycki utilizó un método diferente para calcular esta homología; en particular, en su método usó la conexión que existe entre la homología de Khovanov y la homología de Hochschild [17]. En esta sección presentamos una nueva forma para obtener este resultado usando directamente la sucesión larga previamente construida.
Definición 6.1. Un enlace toroidal del tipo (p,q) (también llamado (p, q)-enlace) es un enlace equivalente a una curva contenida en un toro estándar T 2. Esta curva envuelve p veces alrededor de la longitud y q veces alrededor del meridiano. Si p y q son primos relativos, entonces el enlace tiene un sólo componente y se denomina un nudo toroidal.
Note que un suavizamiento vertical en v produce el nudo trivial con 1 − n “giros”. Ahora construimos la sucesión larga de la homología de Khovanov. Primero, observe que mantener el cruce (trivialmente) no cambia el diagrama de T (2, n), un suavizamiento horizontal resulta en el diagrama T (2, n − 1), y finalmente, un suavizamiento vertical resulta en el nudo trivial con “enmarcado girado” 1 −n veces. Por ejemplo, oberve la Figura 13 la cual ilustra este proceso para el nudo toroidal T (2, 3).

Figura 13 nudo toroidal T (2, n − 1) = T (2, 2) (izquierda), nudo toroidal T (2, n) = T (2, 3) (centro), y el nudo trivial con enmarcado 1 − n = −2 (derecha).
El siguiente teorema establece la homología de Khovanov para nudos toroidales T (2, n) con n > 0.
Teorema 6.2. Sea T (2, n) un nudo toroidal con n > 0. Su homología de Khovanov Ha,b(T (2, n)) es dada por:
Demostración: La herramienta principal que usamos en la prueba de este resultado es la sucesión larga de la homología de Khovanov (5). La demostración procede por inducción sobre n. Para n = 1: El nudo toroidal T (2, 1) es el nudo trivial con un “giro” positivo. Su homología esta dada por:
Observe que H1,1(T(2, 1)) = ℤ y note que (a, b) = (1, 1) = (n, n), lo cual significa que el teorema se cumple. Además, note que H1,5(T(2, 1)) = ℤ y (a, b) = (1, 5) =(n − 2s, n − 4s + 4) = (1 − 2(0), 1 − 4(0) + 4) para s = 0 y el teorema se cumple. Por lo tanto, concluímos que el teorema se cumple para el caso n = 1.
Para n = 2: El nudo toroidal T (2, 2) es llamado el enlace de Hopf. El teorema se cumple como puede ser verificado con el Cuadro 2 3.
Supongamos como hipótesis inductiva que el resultado se cumple para n−1, donde n > 2. Además considere el caso en el que el mapa β∗: Ha,b(T (2, n)) −→ Ha−1,b−1(T (2, n−1)) no es necesariamente un isomorfismo. Así, analizamos la sucesión larga de la homología de Khovanov. Recordamos que, al solucionar un cruce v con un suavizamiento de tipo B, obtenemos el nudo trivial con enmarcado 1 − n, i.e. TB(2, n) ◯ 1−n. Por lo tanto, su homología está dada por:
Esto significa que β∗ no es necesariamente un isomorfismo cuando Hx,y (◯1−n) # 0. Esto es, Hx,y (◯1−n)# 0 cuando (x, y) = (1 − n, 3(1 − n) − 2) = (1 − n, 1 − 3n) o (x, y) = (1 − n, 3(1 − n) + 2)) = (1 − n, 5 − 3n).
Caso (I) Supongamos que (x, y) = (1 − n, 1 − 3n):
En la sucesión larga de homología de Khovanov, en cercanías de H1−n,1−3 n (◯1−n), tenemos:
Por la hipótesis inductiva, H1−n,−1−3n(T (2, n − 1)) y H−n−1,−3n−1(T (2, n − 1)) son triviales. Entonces, la sucesión previa se convierte en:
Así, H1−n,1−3 n (◯1−n) = H−n,−3n(T (2, n)) = ℤ, y por tanto el teorema se cumple, pues (a, b) = (−n, −3n).
Caso (II) Supongamos que (x, y) = (1 − n, 5 − 3n):
En la sucesión larga de homología de Khovanov, en cercanías de H1−n,1−3 n (◯1−n), tenemos:
Por la hipótesis inductiva H−n−1,3−3n(T (2, n − 1)) = 0 y H1−n,3−3n(T (2, n − 1)) =H−(n−1),−3(n−1) = ℤ. Así, la sucesión previa se convierte en:
Las entradas restantes en la sucesión se determinan entendiento el mapa ∂Conn 1−n,3−3n: ℤ → ℤ. En general hay dos posibilidades: el mapa es el mapa cero o es multiplicación por k > 0. Supongamos primero que ∂Conn 1−n,3−3n es el mapa cero. En este caso, H2−n,4−3n(T(2, n)) = H1−n,3−3n(T(2, n − 1)) = Z y H−n,4−3n(T(2, n)) = H1−n,1−3 n (◯1−n) = ℤ. Así, H2−n,4−3n(T(2, n)) = Z y en ese caso tenemos que (a, b) = (2−n, 4−3n) = (n−2n+2, n−4n+4) = (n−2(n−1), n−4(n−1)) = (n−2s, n−4s), para s = n − 1. De forma similar, H−n,4−3n(T(2, n)) = ℤ, donde (a, b) = (−n, 4 − 3n) = (n − 2s, n − 4s + 4), para s = n, y así, el teorema se cumple. Finalmente, suponga que ∂Conn 1−n,3−3n es multiplicación por k > 0. Ese caso particular fue estudiado en 2006 por M. Pabiniak, J. H. Przytycki, y R. Sazdanovć en [13] usando el álgebra Am = Z[x] / (xm), la cual para m = 2 está fuertemente relacionada con la homología de Khovanov [8, 2]. Cuando n es par, ∂Conn 1−n,3−3n es el mapa cero y así H2−n,4−3n(T(2, n)) = ℤ = H−n,4−3n(T(2, n)), como se observó en la parte previa. Cuando n es impar, ∂Conn 1−n,3−3n es multiplicación por k = 2 y obtenemos que H2−n,4−3n(T(2, n)) = 0, H−n,4−3n(T(2, n)) = ℤ2, y así el teoremase cumple.
6.2. Ejemplo: tablas de homología para T(2,11) y T(2,12)
En esta sección presentamos las tablas de homología de Khovanov, en el Cuadro 3 y el Cuadro 4 para T (2, 11) y T (2, 12), respectivamente. Observe que Ha,b(T (2, n)) tiene so-porte en dos diagonales que contienen (n, n) o (n, n+4). En otras palabras, Ha,b(T (2, n)) es no trivial solamente para (a, b) = (n−2s, n−4s) o (a, b) = (n−2s, n −4s+4). Además, Ha,b(T (2, n)) tiene torsión solamente en grupos para los cuales (a, b) = (n−2s, n−4s+4).
Cuadro 3 Homología de Khovanov del nudo toroidal T (2, 11).
| b | a | -11 | -9 | -7 | -5 | -3 | -1 | 1 | 3 | 5 | 7 | 9 | 11 | ||
| 15 | ℤ | |||||||||||||
| 11 | ℤ | |||||||||||||
| 7 | ℤ | |||||||||||||
| 3 | ℤ2 | |||||||||||||
| -1 | ℤ | ℤ | ||||||||||||
| -5 | ℤ2 | |||||||||||||
| -9 | ℤ | ℤ | ||||||||||||
| -13 | ℤ2 | |||||||||||||
| -17 | ℤ | ℤ | ||||||||||||
| -21 | ℤ2 | |||||||||||||
| -25 | ℤ | ℤ | ||||||||||||
| -29 | ℤ 2 | |||||||||||||
| -33 | ℤ |
7. Conclusión
Gran parte de la investigación actual en teoría de nudos está conectada al polinomio de Jones y ahora, además, incluye el concepto de categorificación. En particular, las teorías de homología en contextos topológicos generan estructuras matemáticas que abren muchas posibilidades para próximas investigaciones. Por ejemplo, actualmente hay mucha investigación activa en la homología de Khovanov (par e impar), la homología de Khovanov-Rozansky, la homología de Yang-Baxter, homología de quandles, entre otras. Sin duda la mayor parte de la literatura en teoría de nudos está en inglés, aunque existen algunos trabajos en español como [9, 18]. Con miras a atacar esa brecha del idioma, una traducción parcial al inglés de este trabajo es ofrecida en [11]. El lector es referido a los trabajos de Bar-Natan y Khovanov para una discusión detallada de la homología de Khovanov [2, 8]. Para una introducción completa a distintos temas actuales de investigación en teoría de nudos se recomienda [14]. En cuanto al uso de la sucesión larga de Khovanov, es pertinente decir que existen futuros posibles caminos de investigación. Por ejemplo, se puede considerar la familia de nudos “pretzel” de tres columnas ya que resolver un cruce de forma vertical produciría un nudo trivial con cierto número de “giros”. Se podría también tratar de aplicar una metodología similar para nudos toroidales de tipo T (3, n). Además, se ha verificado que la sucesión larga de Khovanov puede ser muy útil en crear nudos cuya homología contenga tipos específicos de torsión [12].