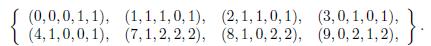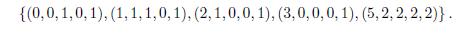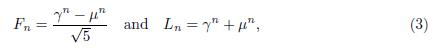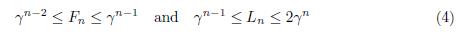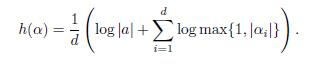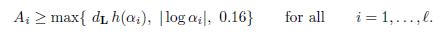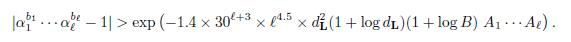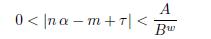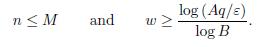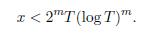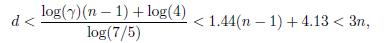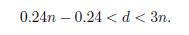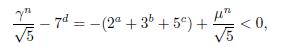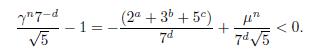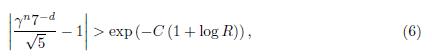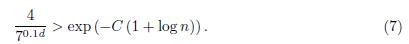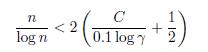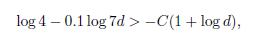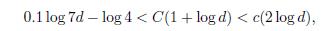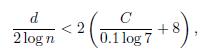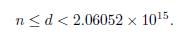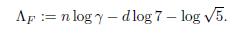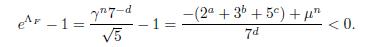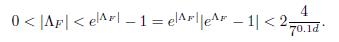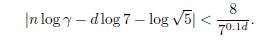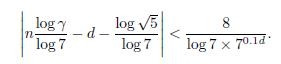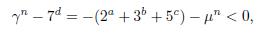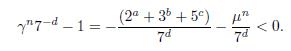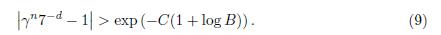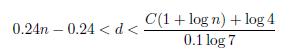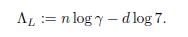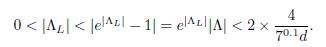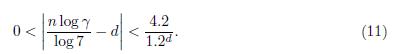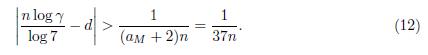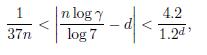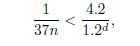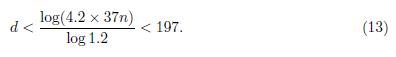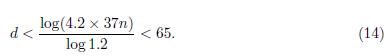1. Introduction

Let (F _n ) _n≥0 be the Fibonacci numbers defined by the recurrence F _n+2 = F _n+1 + F _n with initial conditions F ₀ = 0, F ₁ = 1. Let (L _n ) _n≥0 be the Lucas sequence that has the same recurrence formula as the Fibonacci numbers, but with initial conditions L ₀ = 2 and L ₁ = 1. The study of diophantine equations that involves Fibonacci or Lucas numbers is a very rich area of research and has attracted the attention of many researchers, see, e.g., [³, ⁶, ⁷, ⁹, ¹⁰, ¹¹, ¹³] and the references therein. For example, Luo [¹¹] proved that 1, 2, 21, and 55 are the unique Fibonacci numbers that are also triangular numbers, and some years later he also found all Lucas numbers that are also triangular numbers [¹²]. Marques and Togbé [¹³] found all the Fibonacci and Lucas numbers that are of the form 2 ^a + 3 ^b + 5 ^c , with 0 ≤ max{a, b} ≤ c. Later, Qu, Zeng and Cao [⁸] found all the Fibonacci and Lucas numbers that are of the form 2 ^a + 3 ^b + 5 ^c + 7 ^d , with 0 ≤ max{a, b, c} ≤ d, and posted the problem of finding Fibonacci and Lucas numbers of the form −2 ^a −3 ^b −5 ^c +7 ^d , with 0 ≤ max {a, b, c} ≤ d. In this note we solve this problem. Our main results are the following two theorems:

Theorem 1.1. All non-negative integer solutions (n, a, b, c, d) of the Diophantine equation

with 0 ≤ max{a, b, c} ≤ d belong to the set

Theorem 1.2. All non-negative integer solutions (n, a, b, c, d) of the Diophantine equation

with 0 ≤ max{a, b, c} ≤ d belong to the set

2. Preliminaries and tools

In this section we present several known results that we will use in our proofs. First, let’s remember some properties of Fibonacci and Lucas sequences.

Let 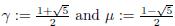. The numbers γ and μ are the roots of the characteristic polynomial x ² − x − 1 = 0. The well-known Binet’s formulas are

which holds for all n ≥ 0. Also, the inequalities

Let α be an algebraic number of degree d. Let a be the leading coefficient of its minimal polynomial (over ℤ) and let α ₁ , . . . , α _d denote the conjugates of α, with α ₁ = α. The logarithmic height of α is defined as

The following result is a lower bound for a linear form in logarithms due to Matveev [14].

Lemma 2.1. Let L be a real number field of degree d _L , α ₁ , . . . , α _ℓ ∈ L and let b ₁ , . . . , b _ℓ be non-zero integers. Let B ≥ max{|b ₁ |, . . . , |b _ℓ |}. Let A ₁ , . . . , A _ℓ be real numbers satisfying

If α ₁ ^b1 · · · α _ℓ ^bℓ ≠ 1. Then

To reduce even more the bounds obtained with Matveev’s result we use a version of Baker-Davenport lemma based on Lemma in [¹]. We shall use the one given by Bravo, Gómez and Luca [²] that is a slightly variation of the one given by Dujella and Petho [⁴]. For a real number x, we write ∥x∥ = min{|x − n|: n ∈ ℤ} for the distance from x to the nearest integer.

Lemma 2.2. Let M be a positive integer. Let α, τ, A > 0, B > 1 be given real numbers. Let p/q be a convergent of α such that q > 6M and ε: = ∥qτ ∥ − M∥qα∥ > 0. Then the inequality

does not have a solution in positive integers n, m and w in the ranges

We also need the following result (Lemma 7 in [¹⁵]).

Lemma 2.3. If m ≥ 1, T > (4m ²) ^m and T > x/(log x) ^m , then

3. Proof of Theorem 1

In order to simplify some calculations, with a Mathematica’s program we have checked all the solutions for equation (1) in the range 0 ≤ d ≤ n ≤ 20 and 0 ≤ n ≤ d ≤ 20, that in fact are the solutions that appear in the statement of Theorem 1.1. So in the rest in the proof we assume that max{n, d} > 20. We start working with equation (1) and the first inequality of (4). From inequality γ ⁿ⁻² ≤ F _n we have that γ ⁿ⁻² ≤ F _n < 7 ^d which implies that 0.24(n − 1) < d. From F _n ≤ γ ⁿ⁻¹ we obtain that 7 ^d ≤ γ ⁿ⁻¹ + 3 · 5 ^d < 4 · 5 ^d · γ ⁿ⁻¹ and this implies that

because n > 2. So we conclude that

By using equation (1) and Binet’s formula we obtain

because |µ| < 1 and 2 ^a ≥ 1. Now

By using that x ^d /7 ^d ≤ 1/7 ^0.1d , for every x ∈ {2, 3, 5}, and that |µ ⁿ /(7 ^d 5|1/7 ^0.1d we obtain

Notice that this inequality is the same obtained by the authors of [8] and we can obtain equation (6) in the same way as they do. For the reader’s convenience we repeated the calculations. We take ℓ: = 3, γ1 := γ, γ2 := 7, γ3 :=5 and b1 := n, b2 := −d, b3 := −1.

Then d _L = [Q (5) :Q)] = 2. Now, h(γ ₁) = 1/2 log γ, h(γ ₃) = log 7, h(γ ₃) = log5, and hence we can take A ₁: = 0.5, A ₂: = 3.9 and A ₃: = 1.7. Let R: = max{|b ₁ |, |b ₂ |, |b ₃ |} = max{n, d, 1}. By Matveev’s result (Lemma 2.1) we have that

where C = 3.22 × 10¹². We have two cases

Case 1. R = n.

From equations (5) and (6) we obtain

Taking logarithms in equation (7) and using that log γ/ log 7(n − 1) < d we obtain, after some straightforward calculations that

Now we use Lemma 2.3 to obtain that max{d, n} < 8.8 × 10¹⁵.

Case 2. R = d, that is n ≤ d.

In this case, after taking logarithms to equation (6) we get

that is

because d ≥ 3. After some straightforward calculations we obtain

and by using Lemma 2.3 we get

Now we will reduce the bounds previously obtained. Let

Note that Λ _F < 0 because

We have that 1 − e ^ΛF = |e ^ΛF − 1| < 1/2 which implies that e ^ΛF < 2. Therefore

Thus

Dividing by log 7 we get

Now we use Lemma 2.2 with 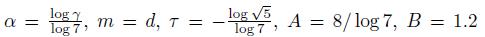(in [⁸] was proved that α is irrational). We take M = 8.8 × 1015, and with the use of Mathematica we observe that q ₃₉ = 119059818885400441 (the denominator of the p ₃₉ /q ₃₉ convergent of α) satisfies q ₃₉ > 6M and ϵ = 0.419601. Therefore, if (n, a, b, c, d) is a solution in positive integers to equation 1, then d < 229 and hence n < 928. Applying again Lemma 2.2, but now with M = 928, we obtain q ₈ = 21064 and ϵ = 0.07494895 which implies that d < 77 and hence n < 314.

Finally, we use a program written in Mathematica to determine all the solutions in the range d < 77 and n < 314 considering both cases n > d and d ≥ n. In both cases all the solutions are given in the statement of Theorem 1.

4. Proof of theorem 2

With a Mathematica’s program we have checked all the solutions for equation (2) in the range 0 ≤ d ≤ n ≤ 20 and 0 ≤ n ≤ d ≤ 20. So, in the rest of the proof we assume that max{n, d} ≥ 20.

From Binet’s formula for the Lucas sequence and equation (2) we obtain

because |µ| < 1 and 2 ^a ≥ 1. Now, dividing by 7 ^d we obtain

From which we deduce that

Now, combining the second inequality of (4) with (2) we obtain γ ⁿ⁻¹ < 7 ^d and (7/5) ^d < 5γ ⁿ , which together implies that 0.24n − 0.24 < d < 2n (for the second inequality we use that n > 9). Equation (8) is the same inequality obtained by Qu, Zeng and Cao [8] and hence we apply Matveev’s result (Lemma 2.1) exactly as in [⁸] by taking ℓ: = 2, γ1 := γ, γ ₂: = 7, and b ₁: = n, b ₂: = −d. Thus d _L = [Q(5) : Q] = 2 and h(γ ₁) = 1/2 log γ, h(γ ₂) = log 7. We can take A ₁: = 0.5, A ₂: = 3.9 and B: = max{n, d}. By using Lemma 2.1 and after some calculations we obtain

where C = 1.02 × 10¹⁰. We use equations (8) and (9) to obtain

Now, we proceed by cases.

Case 1: d ≥ n

To simplify equation (10) we use that 1 + log d < 2 log d (because d > 3). After some calculations we obtain d/ log d < (2C + log 4)/(0.1 log 7) and by using Lemma 2.2 we obtain d < 5.33 × 10¹².

Case 2: n ≥ d.

We have that

After some straightforward calculations (and using that n > 3) we apply Lemma 2.2 to obtain n < 2.27 × 10¹³.

Now we will reduce the bounds. As in [⁸], we define

Notice that Λ _L < 0. For d > 3, |e ^Λ L − 1| < 1/2, which implies that |e ^Λ L | < 2. Let Λ:= e ^Λ L − 1. Then we have

Dividing by log 7 we obtain

Now we proceed in a similar way that in [⁸]. Let [a ₀ , a ₁ , . . . , ] = [0, 4, 22, 1, 5, . . . ] be the continued fraction of log γ/ log 7, and let p _i /q _i be its ith convergent. We have obtained that n < 2.27 × 10¹³ and using Mathematica we observe that q ₂₉ < 2.27 × 10¹³ < q ₃₀. If a _M : = max{a _i : i = 0, 1, . . . , 30}, then a _M = a ₁₄ = 35. Now we use properties of continued fractions similarly as in [⁸] and [5, page 10] to obtain

From equations (11) and (12) we have

and hence

from which, by using n < 2.27 × 10¹³, we obtain

Now we proceed by cases.

Case 1: If n ≤ d, then n < 197, and using that d < 2n we obtain 98 < n < 197.

Case 2: When d ≤ n we use 0.24n − 0.24 < d to obtain n < 822. And using this last inequality we obtain

and hence 136 < n < 272. We write a program in Mathematica to obtain all the solutions in the ranges obtained in Case 1 and Case 2 and the results are showed in the statement of Theorem 2.