Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ensayos sobre POLÍTICA ECONÓMICA
Print version ISSN 0120-4483
Ens. polit. econ. vol.29 no.spe64 Bogotá June 2011
Quantile Regression Model Applied to Artificial Neural Networks. An Approximation of the Structure Caviar for the Colombian Stock Market
Regressão do quantil aplicada ao modelo de redes neuronais artificiais. Uma aproximação da estrutura CAViaR para o mercado de valores colombiano
Charle Augusto Londoño*
*El autor de esta investigación agradece todos los comentarios y sugerencias hechas por los economistas Marithza Hernández, Juan G. Sánchez y Diana M. Vélez. Al profesor Mauricio Lopera, de la Universidad de Antioquia, por su asesoría en la parte econométrica. A los profesionales del Banco de la República, Jair Ojeda por sus sugerencias, y a José E. Gómez y Franz A. Hamann por sus buenos comentarios. Grupo de Macroeconomía Aplicada, Universidad de Antioquia.
Correo electrónico: chlondono@yahoo.es
Documento recibido: 7 de octubre de 2010; versión final aceptada: 14 abril de 2011.
Existen diversas metodologías para calcular el valor en riesgo (VaR) que pretenden capturar principalmente el riesgo de mercado al que están expuestas las instituciones financieras. Siendo el modelo de valor en riesgo condicional autorregresivo (CAViaR) de Engle y Manganelli (1999, 2001, 2004) una buena aproximación empírica para la verdadera medida VaR, tanto para cubrir el riesgo como para el cumplimiento de la regulación bancaria. Por consiguiente, el objetivo de este artículo es realizar una aproximación al modelo CAViaR para el mercado de valores colombiano, empleando diferentes factores de riesgo macroeconómicos y financieros como los esbozados en Chernozhukov y Umantsev (2001); además, se busca establecer qué regla empírica permite una mejor captura del comportamiento del índice general de la Bolsa de Valores de Colombia (IGBC).
Clasificación JEL: C14, C16, C45, E44, G28, G15.
Palabras clave: valor en riesgo condicional autorregresivo, regresión del cuantil, redes neuronales artificiales, variables macroeconómicas y financieras, regulación bancaria, mercado de valores.
There are different methodologies for calculating Value at Risk (VaR) seeking to capture market risk primarily exposed to financial institutions. As the conditional autoregressive Value at Risk (CAViaR) model of Engle y Manganelli (1999, 2001, 2004) a good empirical approximation to the true measure VaR, both to cover the risk, as for compliance with banking regulations. Therefore, the objective of this paper is to approach the model CAViaR for the Colombian stock market using different macroeconomic risk factors and financial as outlined in Chernozhukov and Umantsev (2001), it also seeks to establish empirical rule allows better capture the behavior of the General Index of the Stock Exchange of Colombia (GISEC).
JEL classification: C14, C16, C45, E44, G28, G15.
Keywords: conditional autoregressive Value at Risk, regression quantile, artificial neural networks, macroeconomics and financial variable, banking regulation, financial market.
Existem diferentes metodologias para calcular o valor em risco (VaR) que pretendem capturar principalmente o risco de mercado ao que estão expostas as instituições financeiras. Sendo o modelo de valor em risco condicional auto-regressivo (CAViaR) de Engle e Manganelli (1999, 2001, 2004) uma boa aproximação empírica para a verdadeira medida VaR, tanto para cobrir o risco como para o cumprimento da regulação bancária, o objetivo deste artigo consiste em realizar uma aproximação ao modelo CAViaR para o mercado de valores colombiano, empregando diversos fatores de risco macroeconômicos e financeiros como os esboçados em Chernozhukov e Umantsev (2001); adicionalmente, busca estabelecer qual regra empírica permite uma melhor captura do comportamento do índice geral da Bolsa de Valores da Colômbia (IGBC).
Classificação JEL: C14, C16, C45, E44, G28, G15.
Palavras chave: valor em risco condicional auto-regressivo, regressão de quantil, redes neuronais artificiais, variáveis macroeconômicas y financeiras, regulação bancária, mercado de valores.
I. INTRODUCCIÓN
Una tendencia que se ha presentado en el sector bancario desde 1980, es la ampliación de las líneas de negocio, donde en sus etapas iniciales el ahorro y el crédito fueron las actividades más importantes. Hoy, debido a la internacionalización del sector, el aumento de la competencia y las mejoras tecnológicas, esta línea viene menguándose a favor de otros instrumentos, productos y servicios financieros, tales como trading de monedas, bonos, acciones y derivados; los cuales exigen un mayor monitoreo, información y conocimiento por parte de los administradores. A pesar de que las nuevas líneas generan a los bancos mayores ingresos y grado de diversificación, estas también incrementan la interdependencia y, por consecuencia, el riesgo tomado, a tal punto que han sido partícipes en las principales crisis económicas de las últimas décadas (Greuning y Bratanovic, 2009)1.
En 1996, el Comité de Basilea, buscando aminorar y regular los posibles riesgos que se pudiesen presentar en una institución financiera (riesgo crédito, operacional, de liquidez y de mercado)2, elaboró una medida de riesgo conocida como valor en riesgo (VaR)3, cuyo propósito fue determinar cuánto podría perder un portafolio en un período y a un nivel de confianza dado ante movimientos no esperados del mercado, lo que permite a bancos, firmas comisionistas y entes reguladores administrar, evaluar, y controlar el riesgo de una posición financiera (Engle y Manganelli, 1999, 2001).
Aunque la medida VaR presenta múltiples ventajas para estas instituciones4, su metodología de cálculo como lo muestran Diagne (2002), Engle y Manganelli (1999, 2001) y Taylor (2005) es un desafío estadístico al diferir en sus supuestos e implementación, siendo sus mayores desventajas las de suponer que la distribución condicional es constante cuando varía su volatilidad, la incapacidad de predecir eventos extremos y la forma funcional del modelo que no admite la captura de todos los patrones de la variable bajo estudio.
Para solventar tales deficiencias, se propone modelar el cuantil de manera directa mediante una estructura de valor en riesgo condicional autorregresiva (CAViaR)5, que usando regresión del cuantil introducida por Koenker y Bassett (1978), extendida al modelo de redes neuronales artificiales (ANN)6 por White (1992) y nombrado como red neuronal de regresión del cuantil (QRNN)7, dota de ciertas ventajas, tales como la de no requerir supuestos distribucionales y de independencia; es robusta en la captura de datos atípicos; reacciona directamente al valor objetivo desde el procedimiento de estimación; es un aproximador universal de funciones, entre muchos otros aspectos favorables.
Por tanto, el presente artículo pretende realizar una aproximación del modelo CAViaR usando diversas variables económicas y financieras para esclarecer qué patrones influencian el riesgo de mercado del índice general de la Bolsa de Valores de Colombia (IGBC). Para tal objetivo, por medio de un modelo de QRNN se emplearán los argumentos de las hipótesis de los mercados eficientes, que junto con el modelo de precios de los activos de capital (CAPM)8 y la teoría de precios de arbitraje (APT)9 buscan caracterizar la dinámica del cuantil, como lo proponen Chernozhukov y Umantsev (2001). Así mismo, se hará un análisis de sensibilidad para determinar qué variables exhiben una mayor influencia en la modelación del cuantil.
Con el propósito de esclarecer la robustez o no de una arquitectura de QRNN en la captura del cuantil, se comparará este con el modelo de heterocedasticidad condicional autorregresivo generalizado (GARCH)10 indirecto, propuesta por Engle y Manganelli (1999) y un GARCH (1,1) fusionado con la teoría del valor extremo (EVT)11 sugerido por McNeil y Frey (2000), los cuales presentan resultados sobresalientes para el cálculo del VaR. Así pues, la actual investigación pretende brindar una revisión de algunas metodologías para la cobertura del riesgo aplicadas al mercado de valores colombiano.
Este trabajo se divide en cinco partes, incluida esta introducción. En la segunda se muestra la importancia de los argumentos teórico-empíricos que se pueden esgrimir para comprender los efectos anormales que se presentan en el mercado de valores a causa de una mala valoración de los activos, y de cómo la relajación de algunos supuestos teóricos conllevan a resultados empíricos satisfactorios para predecir el comportamiento esperado del cuantil; del mismo modo, se proporciona una justificación del esquema CAViaR como una buena estrategia de modelación del VaR. En la tercera se explica a grandes rasgos los modelos econométricos empleados. En la cuarta se entregan los resultados, tanto en lo que respecta a los datos y al desempeño de las metodologías usadas, como en la delimitación de las variables más relevantes en la captura del cuantil. Finalmente, se brindan unas breves conclusiones, donde se halla que el modelo GARCH indirecto y APT ampliado son las mejores estrategias en lo que atañe a la captura del cuantil y, por consecuencia, la cobertura del riesgo.
II. UNA APROXIMACIÓN TEÓRICA-EMPÍRICA PARA COMPRENDER EL COMPORTAMIENTO DEL RETORNO DE LOS ACTIVOS
A. MOTIVACIÓN PARA EL USO DE MODELOS DE PRECIOS DE LOS ACTIVOS
El análisis del riesgo en los mercados financieros se halla impregnado de una gran cantidad de factores de riesgo, que en su mayoría se presentan de manera latente. Los administradores del riesgo y los reguladores tienen como desafío la implementación de una serie de políticas que favorezcan la cobertura ante eventos negativos que generen pérdidas de capital, lo que les posibilitaría, además a las instituciones financieras, tener un buen valor de mercado al cumplir con códigos de buen gobierno. Por esta razón, es necesario que tales entes comprendan la naturaleza de esos eventos que se dan, en parte, por el comportamiento de los inversionistas, los cuales pueden modificar las condiciones normales del mercado y, de esta forma, poder establecer un método que permita capturar los riesgos acaecidos por el mercado (Alexander, 2009; Greuning y Bratanovic, 2009).
En el proceso de entender el comportamiento de los inversionistas, Fama (1970, 1991) establece las hipótesis de los mercados eficientes, según las cuales los precios de los activos reflejan toda la información disponible, implicando la imposibilidad de obtener ganancias superiores a las del mercado por medio de la información que este ya ha descontado. Con el objetivo de probar su presunción, Fama realiza una revisión de trabajos aplicados a la valoración de activos y encuentra que a través de modelos lineales con supuestos de normalidad, se puede capturar toda la dinámica contenida en el mercado de valores.
No obstante, se han generado diversas críticas sobre la veracidad de las hipótesis y los supuestos en los que se basan los modelos empleados en esta revisión, donde se incluyen modelos de precios de los activos como el CAPM y el APT (Connor y Linton, 2007; Cao, Leggio y Schniederjans, 2005; Shiller, 2003; Stout, 2003; Singal, 2003; entre otros). Desde esta perspectiva, surgen las preguntas de si los supuestos de los modelos sobre el comportamiento de los agentes y cómo estos toman sus decisiones son adecuados y si el proceso distribucional es apropiado en la captura del retorno de los activos.
Por su parte, el modelo CAPM, que busca explicar el retorno de los activos regresándolo contra un índice de mercado, establece la regla de decisión según la cual para obtener las mayores ganancias se deben comprar los activos con los β más altos, siendo β la pendiente de esta regresión. A partir de esta teoría, se ha generado una extensa literatura que tiene como propósito darle una mayor adaptabilidad al modelo bajo condiciones reales por medio de la relajación de algunos supuestos, tales como la limitación a las ventas en corto (en el mercado de valores se conoce como vender un activo sin poseerlo), no prestar y pedir prestado a la misma tasa libre de riesgo, aplicar impuestos personales a las transacciones bursátiles, expectativas heterogéneas, agentes no tomadores de precios y modelos multiperíodo. Sin embargo, la modificación de tales supuestos no creó ningún cambio al estado de equilibrio general (véanse Elton y Grueber (2002) para un estado del arte y las demostraciones formales e informales de estos resultados).
Por otro lado, el modelo APT que es explicado a través de factores de riesgo macroeconómicos -como las tasas de interés, el tipo de cambio, la inflación, entre otros-, presenta algunas modificaciones que han ofrecido una mejor explicación del comportamiento de los retornos de los activos, como la introducción de variables internacionales (Solnik, 1983), una regla empírica que avala el cumplimiento de la ley de los grandes números (Connor, 1984) y la integración de los modelos CAPM y APT (Connor, 1984; Wei, 1988). Estos cambios, aunque importantes, no han producido una variación drástica al modelo APT tradicional.
En lo que respecta a la distribución de los retornos, una de las principales críticas se puede vislumbrar en Koenker y Bassett (1978). Estos autores muestran qué modelos teóricos y, su respectiva aplicación empírica, están supeditados a varios supuestos que parecen axiomas sobre la distribución de los activos, al no tener en cuenta el verdadero proceso generador de los datos que usualmente no exhibe normalidad o distribución gaussiana. De modo tal que la implementación de las teorías de precios de los activos en sus formas tradicionales (en términos distribucionales), pueden ser poco convenientes en la captura de las regularidades y patrones que presentan los retornos de los activos (colas pesadas, heterocedasticidad, incapacidad de predecir eventos extremos).12
Así mismo, el solo tener en cuenta la modelación del retorno promedio y no la función de distribución como un todo, evita dar mayor luz a los inversionistas en su proceso de toma de decisiones. Al respecto, Singal (2003) y Koenker y Hallock (2001) manifiestan que puede ser difícil determinar la mala valoración de una firma, es decir, si esta obtiene un retorno superior o inferior al retorno normal; no obstante, podría ser más sencillo establecer su anormalidad por medio de la estimación de los cuantiles que exhibe las posibles desviaciones del activo, lo que puede esclarecer hasta qué punto es conveniente abrir una posición financiera y determinar su cuantía, según sea su heterogeneidad.
En definitiva, la eficiencia del mercado es quebrantada por ciertos efectos anormales no previstos (exceso de volatilidad como principal componente, Shiller, 2003)13, donde los inversionistas en su proceso de toma de decisiones no prevén burbujas especulativas que afecten el equilibrio de largo plazo. Lo que hace necesario la introducción de nuevos supuestos distribucionales a los modelos CAPM y APT, que empíricamente han mostrado un buen desempeño en condiciones normales del mercado (véanse, por ejemplo, Chen, Roll y Ross, 1984; Koutulas y Kryzanowski, 1994; Shaharudin y Fun, 2009; Londoño, Lopera y Restrepo, 2010), y que pueden mejorar al relajar sus supuestos distribucionales en su función objetivo, como lo puede brindar la regresión del cuantil 14 y, de esta manera, tener una mayor capacidad predictiva en la captura de eventos extremos.
La importancia de lo anterior, como lo indica Singal (2003), se sustenta en que el fortalecimiento de la asignación óptima de los recursos por medio de precios correctos puede fomentar el bienestar de inversionistas, compañías y consumidores, lo que promovería el crecimiento económico. Desde esta misma perspectiva, Melo y Becerra (2005) arguyen que tener metodologías cada vez más precisas para la predicción de cualquier tipo de riesgo, posibilita que se genere un ambiente de estabilidad y certidumbre en las instituciones financieras y la economía, en términos particulares y generales.
B. JUSTIFICACIÓN DEL MODELO CAViaR COMO UNA BUENA APROXIMACIÓN A LA VERDADERA MEDIDA VaR
Diversas metodologías se han empleado para calcular el VaR, de las cuales dos trabajos han realizado una buena revisión de la literatura de sus estructuras univariadas con sus respectivas aplicaciones: Melo y Becerra (2005) y Engle y Manganelli (1999, 2001). El primer trabajo, clasifica las técnicas en dos grupos: aquellas que no tienen en cuenta las dependencias del primer y segundo momento, tales como metodologías de normalidad, simulación histórica y la EVT; y otras que sí incorporan tales dependencias, como un modelo ARMA-GARCH y ARMA-GARCH-EVT. Con esos métodos, estos autores efectúan una aplicación a la tasa de interés interbancaria (TIB), y usando estadísticos de prueba basados en la distribución binomial dentro y fuera del período de estimación, encuentran que el segundo grupo es el que mejor desempeño ofrece, destacando que la fusión con EVT es una buena aproximación a la verdadera medida VaR.
El segundo trabajo, separa estos métodos en tres categorías: la primera, utiliza técnicas factoriales como RiskMetrics y GARCH. La segunda, usa modelos de portafolio como simulación histórica e híbridos. La tercera, la EVT, el modelo CAViaR y un GARCH estimado con cuasi-máxima verosimilitud15. Estos autores, al estudiar cada una de esas metodologías, encuentran que los dos primeros grupos presentan algunas falencias estadísticas: en lo que respecta a las factoriales, hallan que su forma de estimación supone que los retornos de un portafolio dividido por su desviación estándar se distribuyen de forma independiente e idénticamente distribuido (i.i.d.), cuando realmente se presenta un exceso de curtosis o colas pesadas; igualmente, los agrupamientos de la volatilidad difieren de este supuesto.
En lo que concierne a los modelos de portafolio, aunque no supongan una distribución a priori, se asume que la muestra evaluada es representativa y, ante cambios no esperados, los cuantiles estimados son igualmente probables, independiente de las malas noticias futuras, lo cual es poco verosímil y sesga los resultados dependiendo de los datos bajo estudio (calcula un VaR muy alto si la muestra tiene períodos de alta volatilidad, y viceversa)16. En cambio, la tercera categoría que contiene la estructura CAViaR que calcula el VaR de forma directa empleando regresión del cuantil, presenta resultados más realistas, dada la flexibilidad de sus supuestos teóricos sobre la distribución de los retornos.
Ahora bien, Engle y Manganelli (1999, 2001) aplican estas metodologías a diferentes procesos distribucionales obtenidos mediante simulación de Monte Carlo, y encuentran que los retornos generados con colas pesadas son los que mejor se ajustan al modelo CAViaR, lo que revela su gran habilidad para adaptarse a eventos extremos y condiciones reales, por encima de un modelo GARCH. A partir de esta investigación, se ha suscitado un gran interés por modelar el cuantil de forma directa con la estructura CAViaR. Taylor (2000), por medio de una representación híbrida que integra la regresión del cuantil con ANN, realiza una aplicación para el tipo de cambio de la moneda alemana y japonesa contra la americana y, usando varios períodos de tenencia, descubre que esta técnica es consistente en sus resultados en comparación a su contraparte lineal y modelos GARCH.
Chernozhukov y Umantsev (2001) explican la dinámica del cuantil para una acción de petróleos por medio de las teorías de precios de arbitraje; esto les permite obtener una buena interpretación de cómo los factores de riesgo, tales como los precios spot, un índice accionario y los mismos precios rezagados, afectan el cuantil, alcanzando resultados robustos en el cálculo del VaR. En lo que atañe a Taylor (2005), este encuentra que si bien el modelo CAViaR es una aproximación adecuada para el cálculo del VaR, no es aplicable para otros tipos de riesgos como la valoración de opciones, al no incluir en su estructura el cálculo de la volatilidad; para solventar tal deficiencia, utiliza la desviación estándar de los intervalos de la distribución, así, usando varios activos visualiza que este método se desempeña mejor que un modelo GARCH.
Gourieroux y Jasiak (2008) introducen el modelo de cuantil dinámico adaptativo, y descubren que esta técnica presenta múltiples propiedades deseables para el cálculo del VaR; para demostrarlo efectúan una aplicación para el mercado de valores canadiense y junto con la EVT llegan a resultados satisfactorios. No obstante, ellos revelan los riesgos en los que se podría caer si no se determina debidamente la estimación del cuantil al integrarlo con la EVT.
White, Kim y Manganelli (2008) desarrollan una estructura CAViaR multivariada, la cual tiene en cuenta la modelación del coeficiente de asimetría, la curtosis y varios cuantiles de forma simultánea y dinámica. De este modo, realizan un estudio al índice S&P 500, hallando resultados estadísticos robustos en la captura de datos atípicos. Por su parte, Huang, Yu, Fabozzi y Fukushima (2009) muestran la importancia de tener predicciones exactas del riesgo ante cambios en los precios del petróleo; con este objetivo, implementan el modelo CAViaR con dos modificaciones: un promedio móvil de precios exponenciales y una regresión de datos mixtos. Con estas variaciones llegan a resultados que hacen posible una buena generalización y captura de los factores de riesgo.
III. METODOLOGÍA
Con el objetivo de esclarecer la capacidad predictiva que tiene la estructura CAViaR, según los diferentes trabajos que se han elaborado en función de su técnica de estimación, este trabajo realizará una comparación con el modelo GARCH-EVT. Donde esta última técnica ha mostrado resultados sobresalientes para el cálculo del VaR, como se puede vislumbrar en el trabajo de Melo y Becerra (2005). De la misma manera, hay una adecuada literatura que avala este tipo de metodología, como es la de McNeil y Frey (2000) y McNeil, Frey y Embrechts (2005), entre otros.
A. MODELO GARCH
El ARCH generalizado (GARCH), introducido por Bollerslev (1986), presenta una estructura parsimoniosa en comparación al modelo ARCH, al requerir solo la estimación de unos pocos parámetros, y exhibe ciertas ventajas, como tener que depender solo de su volatilidad y valores al cuadrado del proceso previo. Sea 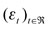 un proceso aleatorio i.i.d. N(0,1). Si at es generado por un GARCH (m,s), se satisfacen las condiciones de que el modelo es estrictamente estacionario y cumple con la restricción de
un proceso aleatorio i.i.d. N(0,1). Si at es generado por un GARCH (m,s), se satisfacen las condiciones de que el modelo es estrictamente estacionario y cumple con la restricción de  , el proceso es positivo (McNeil et al., 2005). El modelo es expresado por la siguiente ecuación:
, el proceso es positivo (McNeil et al., 2005). El modelo es expresado por la siguiente ecuación:
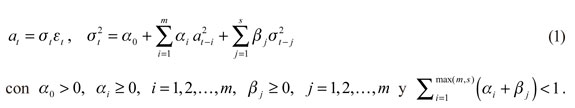
con y . Aquí todos los parámetros deben ser positivos y la última condición avala que la varianza de sea finita (Tsay, 2005). Como lo muestran McNeil et al. (2005), se usa normalmente el GARCH (1,1), el cual admite la captura de los períodos de alta volatilidad, tiene en cuenta los momentos de alto orden como son el coeficiente de asimetría y la curtosis, entre otras ventajas provistas por el método (para más detalles sobre modelos GARCH, remítase a Bollerslev, 1986; Engle y Manganelli, 2001; McNeil et al., 2005; Melo y Becerra, 2005 y Tsay, 2005).
B. MODELO CAViaR
Esta estrategia permite modelar el cuantil empleando un grupo de información de manera directa, y se halla muy vinculado a los métodos que usan momentos centrales de la distribución condicional -media, varianza, curtosis, coeficiente de asimetría- (Chernozhukov y Umantsev, 2001), que presenta múltiples beneficios; como lo explican Engle y Manganelli (2004), al argumentar que el VaR se encuentra estrechamente ligado a la desviación estándar. Es así como bajo la estructura CAViaR se puede capturar el comportamiento de la volatilidad (aglomeraciones, asimetrías, entre otros componentes) y, de esta manera, la autocorrelación que presenta el retorno promedio de los activos. Supóngase que el retorno de un portafolio de activos está denotado como 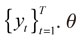 . es la probabilidad asociada al VaR. La especificación del modelo en forma general es como sigue 17:
. es la probabilidad asociada al VaR. La especificación del modelo en forma general es como sigue 17:

siendo el 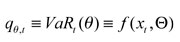 el θ-cuantil en el período t de la distribución de los retornos de un portafolio formado en el período
el θ-cuantil en el período t de la distribución de los retornos de un portafolio formado en el período 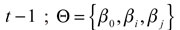 ; es el vector de w -parámetros desconocidos, con w = r + q + 1 , Y I (•) es una función indicador que representa diversas formas funcionales y grupo de variables. Aquí, el término autorregresivo
; es el vector de w -parámetros desconocidos, con w = r + q + 1 , Y I (•) es una función indicador que representa diversas formas funcionales y grupo de variables. Aquí, el término autorregresivo 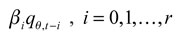 , hace que el cuantil cambie suavemente en el tiempo. El objetivo del grupo de información I (•) es crear un puente de las variables observadas con
, hace que el cuantil cambie suavemente en el tiempo. El objetivo del grupo de información I (•) es crear un puente de las variables observadas con 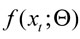 , que se puede visualizar como una curva de impactos de noticias (Engle y Manganelli, 2004). Ahora bien, una de las especificaciones de I (•) que muestra buenos resultados en su aplicabilidad, según Engle y Manganelli (1999), es el GARCH indirecto, definido como18:
, que se puede visualizar como una curva de impactos de noticias (Engle y Manganelli, 2004). Ahora bien, una de las especificaciones de I (•) que muestra buenos resultados en su aplicabilidad, según Engle y Manganelli (1999), es el GARCH indirecto, definido como18:

De la ecuación (3) se puede aseverar que cuando los datos utilizados pertenecen a un proceso GARCH, se puede considerar que el modelo está adecuadamente especificado con el término de perturbación distribuido i.i.d., y arroja mejores resultados que un modelo GARCH estimado con máxima verosimilitud. Además, este esquema es consistente para realizar simulación (Engle y Manganelli, 1999, 2004).
Un caso especial del esquema CAViaR, como lo establecen Engle y Manganelli (2001), se ostenta en el trabajo de Chernozhukov y Umantsev (2001), en el cual el grupo de información I (•) es de suma importancia, ya que integra el modelo estadístico con la teoría económica. Específicamente, el uso de variables macroeconómicas y financieras como es instaurado por los modelos de precios de los activos, son de gran preponderancia al poder integrar los componentes observables y latentes que ligan la economía real y el sector financiero. En este orden de ideas, en la actual investigación se plantea estimar el GARCH indirecto, sugerido por Engle y Manganelli (1999, 2001, 2004), y diferentes especificaciones de los modelos de precios de los activos como el CAPM de Sharpe (1964) y el APT de Ross (1976).
Por otro lado, para estimar los parámetros del modelo CAViaR, Engle y Manganelli (1999, 2001, 2004) utilizan regresión del cuantil, que exhibe múltiples ventajas como las mencionadas anteriormente y es aplicada en diversos campos, como el mercado laboral, la educación, análisis de la demanda, en finanzas, entre otras áreas, presentándose buenos resultados estadísticos. Con la intención de extender los resultados que ofrecen Engle y Manganelli, los modelos de precios de los activos se estimarán con una estructura no lineal en su función objetivo a través de QRNN, como lo propone Taylor (2000). White (1992) muestra que esta fusión tiene buenas propiedades y ventajas, como son su forma de estimación no paramétrica, su proceso de optimización que produce estimadores consistentes, lo que concibe valores de los parámetros exactos tanto para variables aleatorias i.i.d. como para procesos con dependencia estacionaria, entre otras características.
C. RED NEURONAL DE REGRESIÓN DEL CUANTIL
Una QRNN, es una extensión de la metodología de regresión del cuantil lineal al caso no lineal y no paramétrico utilizando ANN, lo que la hace útil para hacer predicción de diferentes cuantiles con un buen desempeño en la captura de patrones y fuerte no linealidad exhibida por variables financieras. Su forma de interconexión y retroalimentación, le permite incorporar dos características: reacción dinámica entre sus unidades que posibilita una conexión bidireccional entre todos sus componentes, y un nivel de generalidad, que por medio de un proceso de falla y error, busca obtener el nivel óptimo de activación (Anderson, 2007; Cannon, 2011; Kuan y White, 1994; Londoño et al., 2010).
Este método de estimación presenta buenos resultados en la obtención de estimadores consistentes no paramétricos aplicados a la función de expectativa condicional, como lo muestran Cheng y Titterington (1994), Diagne (2002), Franses y Dijk (1999), Kuan y White (1994), entre otros. White (1992) extendió estos resultados a la regresión del cuantil, que admite tener en cuenta no solo un pronóstico promedio de la variable de interés, sino también su nivel de variación, lo que consiente la captura completa de la distribución.
Así pues, considérese una muestra de observaciones Y1 ,Y2 ,...,YT generadas por el modelo:
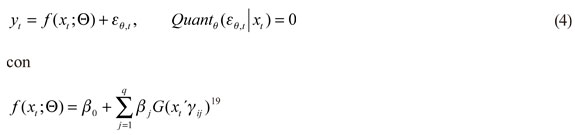
siendo 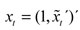 la unidad de sesgo y el vector de variables de entrada (inputs), respectivamente, en esta última hay p rezagos de yt - j, r variables exógenas xj,t con sus consiguientes m rezagos;
la unidad de sesgo y el vector de variables de entrada (inputs), respectivamente, en esta última hay p rezagos de yt - j, r variables exógenas xj,t con sus consiguientes m rezagos;  es el
es el 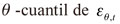 condicionado a Xt . βj son los pesos de conexión (connection strengths) de la capa oculta (hidden layer);
condicionado a Xt . βj son los pesos de conexión (connection strengths) de la capa oculta (hidden layer); 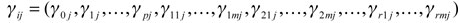 es el vector de pesos con los que ingresa cada variable de entrada en la capa oculta j; G(•)es la función de activación no lineal de la capa oculta, que en este caso es la función tangente hiperbólica operando en el intervalo [-1,1], cuya expresión es la siguiente:
es el vector de pesos con los que ingresa cada variable de entrada en la capa oculta j; G(•)es la función de activación no lineal de la capa oculta, que en este caso es la función tangente hiperbólica operando en el intervalo [-1,1], cuya expresión es la siguiente:

La ecuación (4) puede ser descrita como una arquitectura del perceptrón multicapa (MLP) de una capa o superficie oculta. Ahora, con la intención de obtener los estimadores de  , se minimiza la función objetivo en el θ-ésimo cuantil de la regresión, que es definida como 20:
, se minimiza la función objetivo en el θ-ésimo cuantil de la regresión, que es definida como 20:
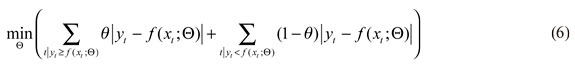
con 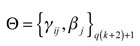 el vector de parámetros. Para evitar que la ecuación (6) tenga altos valores en algunos de sus parámetros estimados, Cannon (2011), Franses y Dijk (1999) y Taylor (2000) sugieren introducir unos parámetros de penalización conocidos como decaimiento de los pesos (weight decay) y un conjunto promedio de agregación vía bootstrap o bagging, quedando la función objetivo de la siguiente forma:
el vector de parámetros. Para evitar que la ecuación (6) tenga altos valores en algunos de sus parámetros estimados, Cannon (2011), Franses y Dijk (1999) y Taylor (2000) sugieren introducir unos parámetros de penalización conocidos como decaimiento de los pesos (weight decay) y un conjunto promedio de agregación vía bootstrap o bagging, quedando la función objetivo de la siguiente forma:
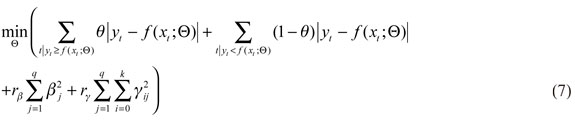
donde rβ y rΥ son los parámetros de decaimiento de los pesos, los cuales le permiten al modelo de QRNN que no se genere en su proceso de estimación un sobreajuste, avalando la minimización de los errores de manera óptima. Mientras el bagging disminuye el componente de la varianza de los errores del modelo, por medio de un método de agrupamiento y muestreo que posibilita la obtención de los parámetros en su valor promedio, lo que es logrado utilizando diferentes conjuntos de entrenamiento de los casos disponibles (Cannon, 2011; Franses y Dijk, 1999; Taylor, 2000).
Como lo exponen Engle y Manganelli (2001, 2004), la regresión del cuantil forma parte del modelo de la desviación absoluta mínima (LAD)21 como un caso especial. Este presenta resultados más robustos que los estimadores OLS, si el proceso distribucional a modelar tiene colas pesadas. Además, este método tiene buenas propiedades estadísticas independientemente de su mala especificación en el proceso generador de los datos del cuantil, ofreciendo resultados satisfactorios en términos de consistencia y eficiencia asintótica (para la demostración de sus propiedades del modelo lineal y de ANN, remítase a Koenker y Bassett, 1978 y White, 1992, respectivamente).
D. INTEGRACIÓN DE LAS METODOLOGÍAS VaR A LA TEORÍA DEL VALOR EXTREMO
El objetivo de introducir la EVT a esta investigación, se debe a la necesidad de combinarla con instrumentos de administración más consistentes para la cobertura del riesgo, que por medio del conocimiento de la distribución del valor máximo faciliten la captura de estados contingentes no lineales en los retornos de un activo o portafolio (Diagne, 2002). Esta metodología presenta dos derivaciones: el método de máximo por bloques y picos sobre un umbral (POT)22.
La primera es construida en función del estimador de Hill, que se obtiene por medio de los máximos extraídos a lo largo de la muestra d que fueron divididos en bloques de tamaño s (Melo y Becerra, 2005). Empero, esta técnica no es adecuada, a causa de que los supuestos de independencia no son satisfechos por los retornos de los activos; así mismo, emplea un período mínimo que no tiene una justificación estadística a priori o una definición clara, pasando por alto los agrupamientos de la volatilidad (Tsay, 2005)23.
La segunda, más empleada en la literatura por ofrecer resultados más robustos estadísticamente, consiste en identificar los excesos que superan un umbral (mínimos o máximos). Sea 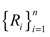 una variable i.i.d. con función de densidad
una variable i.i.d. con función de densidad 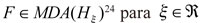 . Con Hξ denotando las formas que puede tomar la distribución del valor extremo generalizada (GEV)25 que depende del valor de ξ26. es un umbral preespecificado27; Nη como el η-ésimo exceso de ocurrencia dado Ri>η.
. Con Hξ denotando las formas que puede tomar la distribución del valor extremo generalizada (GEV)25 que depende del valor de ξ26. es un umbral preespecificado27; Nη como el η-ésimo exceso de ocurrencia dado Ri>η.
Si 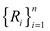 denota el número de veces que se excede el umbral η o las pérdidas que son i.i.d. y Υ1, Υ2,..., ΥNη, es su exceso (Embrechts et al., 1997). Su función de densidad está definida como:
denota el número de veces que se excede el umbral η o las pérdidas que son i.i.d. y Υ1, Υ2,..., ΥNη, es su exceso (Embrechts et al., 1997). Su función de densidad está definida como:

Luego, la distribución Pareto generalizada (GPD)28 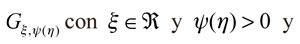 y contiene las colas de la distribución, es establecida:
y contiene las colas de la distribución, es establecida:
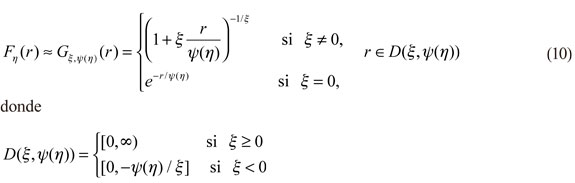
con 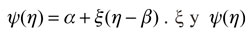 son los parámetros de forma y escala, respectivamente. Una propiedad importante para GPD es el teorema de Fisher-Tippet que instituye la siguiente condición:
son los parámetros de forma y escala, respectivamente. Una propiedad importante para GPD es el teorema de Fisher-Tippet que instituye la siguiente condición:
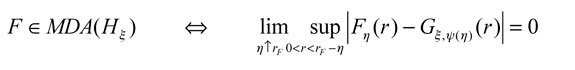
siendo rF el punto extremo derecho de la distribución F. Este resultado determina que si F se encuentra en el MDA de un GPD, cuanto más η se aproxima al punto final F el GPD viene a ser más preciso en Fη (Engle y Manganelli, 2001; Melo y Becerra, 2005). Ahora bien, para obtener el percentil se debe estimar (9), lo cual se realiza de manera separada para 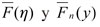 Así, un estimador para
Así, un estimador para 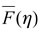 es:
es:

Por tanto, la estimación conjunta de 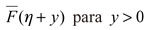 es dada por:
es dada por:

La ecuación (13) solo es aplicable a probabilidades p pequeñas (Engle y Manganelli, 2001) 30.
Gráfico de la media de los excesos
A partir de la función GPD, se puede determinar el umbral η óptimo utilizando el gráfico de la media de los excesos, e(η), que es definido por la siguiente ecuación:
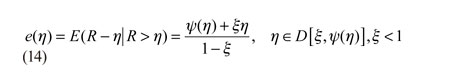
Debido a que e(η) es lineal. Este resultado puede conducir a un método gráfico para establecer el umbral η óptimo para el GPD. Por tal motivo, dado R1, R2,...,Rn su gráfico es determinado por:

De esta manera, la regla de decisión para definir el umbral η es: "Seleccionar η > 0 tal que en(r) es aproximadamente lineal para r ≥ η" (Embrechts et al., 1997, p. 355 31).
IV. RESULTADOS
A. DATOS, ESTIMACIÓN Y COMPARACIÓN DE LAS METODOLOGÍAS USADAS A PARTIR DE CONTRASTES BASADOS EN LA MEDIDA VaR
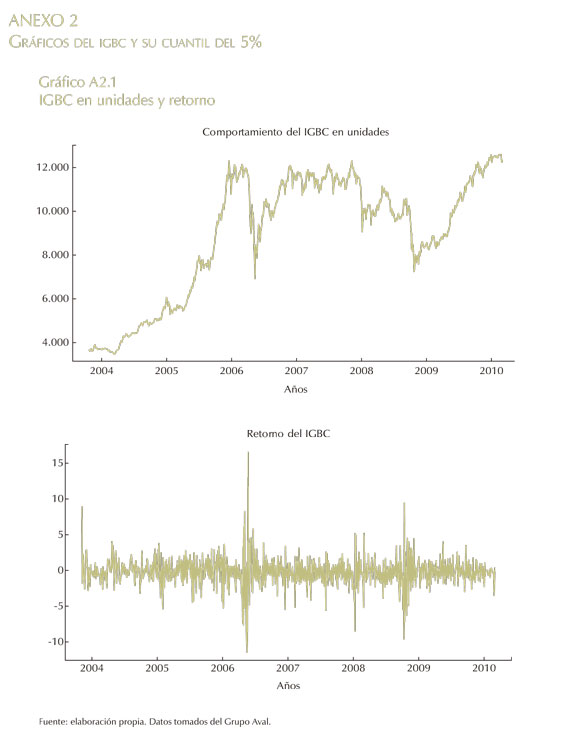
Las series estadísticas utilizadas en esta investigación se obtuvieron de la base de datos de Reuters y de la página web del Grupo Aval. El período considerado comprende desde el 5 de mayo de 2004 al 28 de enero de 2010, para un total de 1.327 observaciones. Dado que la actual investigación tiene como propósito evaluar cómo se desempeña el modelo en condiciones extremas, se hará backtesting en las últimas 300 observaciones, las cuales incluyen un período en el que el retorno del IGBC (que es la variable objetivo de esta investigación) presenta una alta volatilidad a causa de la crisis financiera de los Estados Unidos. Estas series se transformaron por medio de la fórmula 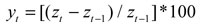 Para luego ser estandarizadas como una normal [0,1]; esto último con el objetivo de "mejorar las propiedades del método numérico de estimación no lineal" (Franses y Dijk, 1999, p. 222). En el Gráfico A2.1 se puede observar el comportamiento del IGBC en unidades y su respectivo retorno para la muestra bajo estudio.
Para luego ser estandarizadas como una normal [0,1]; esto último con el objetivo de "mejorar las propiedades del método numérico de estimación no lineal" (Franses y Dijk, 1999, p. 222). En el Gráfico A2.1 se puede observar el comportamiento del IGBC en unidades y su respectivo retorno para la muestra bajo estudio.
En el Cuadro 1 se hallan resumidas las variables que se van a utilizar en este trabajo, en las cuales se incluyen variables macroeconómicas y financieras, tanto nacionales como internacionales. Ahora bien, dada la relevancia de la mejor especificación en el trabajo de Melo y Becerra (2005), de las estructuras CAViaR de Engle y Manganelli (1999) y las distintas versiones de los modelos de precios de los activos, tales como el modelo CAPM y el APT y sus respectivas derivaciones (Londoño, 2009), se realizarán cinco esquemas de modelación: el primero, es un modelo ARMA-GARCH-EVT. El segundo, es el modelo GARCH indirecto de Engle y Manganelli (1999, 2001, 2004). El tercero, emplea variables macroeconómicas (modelo APT). El cuarto, toma tanto variables macroeconómicas como financieras (modelo APT ampliado). El quinto, usa variables financieras (modelo CAPM). Esta división tiene como intención establecer qué regla empírica siguen los cuantiles del IGBC a través de tales especificaciones, y de esta forma esclarecer la robustez de estos modelos bajo un contexto de estudio de metodologías VaR.
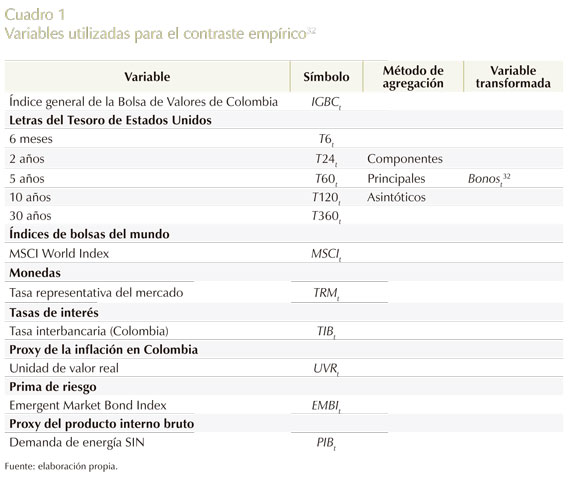
En el Cuadro 2 se puede observar las variables seleccionadas por cada especificación. En lo que respecta al modelo ARMA-GARCH-EVT, se utilizaron los rezagos de la variable dependiente y se aplicó la ecuación (1) para modelar la varianza (véase Anexo 1 para resultados de parámetros y algunas pruebas de especificación). Para luego integrar la EVT por medio de la estrategia de dos pasos propuesta por McNeil y Frey (2000), que a grandes rasgos consiste en estimar la media y la varianza del modelo previo, para después, a través de los residuales estandarizados asumidos como i.i.d., aplicar la EVT a los θ-cuantiles pre-especificados.

Ante la anterior metodología, Engle y Manganelli (2004) argumentan que si bien esta estrategia permite un mejoramiento a los resultados que arroja el modelo GARCH para el cálculo del VaR, esta técnica presenta los mismos problemas que sufren los modelos de volatilidad, como son supuestos inverosímiles sobre la distribución de los retornos como su principal desventaja.
Para el GARCH indirecto se usaron las variables establecidas por Engle y Manganelli (1999, 2001, 2004) (véase Anexo 1 para resultados de los parámetros estimados).
Finalmente, para los modelos de precios de los activos se seleccionaron los seis primeros rezagos de cada variable y se eligieron los mejores rezagos de cada versión a través de tres procedimientos secuenciales de selección de variables (Backward, Forward y Stepwise). Cabe anotar que estos últimos esquemas son justificados por los trabajos de Chen et al. (1984), Koutulas y Kryzanowski (1994), y Shaharudin y Fun (2009)33, donde muestran la relevancia de los factores de riesgo macroeconómicos y financieros nacionales e internacionales para la modelación del retorno promedio de los activos; y Chernozhukov y Umantsev (2001) amplían estos resultados a la modelación del cuantil.
Por tanto, el modelo del cuantil estimado bajo la estructura CAViaR queda como sigue:

donde 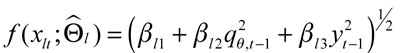 para la especificación del GARCH indirecto, con l = 2.
para la especificación del GARCH indirecto, con l = 2.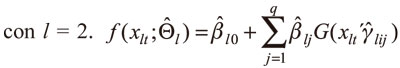 para las versiones de los modelos de precios de los activos, es decir, para l = 3 o 4 o 5. Aquí
para las versiones de los modelos de precios de los activos, es decir, para l = 3 o 4 o 5. Aquí 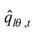 es el vector de cuantiles del IGBC en el período t. xlt es la matriz de variables de entrada, como se ve en el Cuadro 2. Para esta investigación, θ tomará los valores de 0,1%, 1% y 5%. Con respecto a estas probabilidades, Engle y Manganelli (2001) aseveran que el modelo CAViaR funciona bien para niveles de probabilidad comunes (1% y 5%). Sin embargo, presenta ciertos problemas para niveles más bajos, tales como el 0,1%, a causa de que el modelo es estimado con una muestra finita, por lo que se sugiere introducir la EVT dentro de su estructura de modelación por medio de los siguientes pasos: ajustar un modelo CAViaR con el propósito de obtener los cuantiles
es el vector de cuantiles del IGBC en el período t. xlt es la matriz de variables de entrada, como se ve en el Cuadro 2. Para esta investigación, θ tomará los valores de 0,1%, 1% y 5%. Con respecto a estas probabilidades, Engle y Manganelli (2001) aseveran que el modelo CAViaR funciona bien para niveles de probabilidad comunes (1% y 5%). Sin embargo, presenta ciertos problemas para niveles más bajos, tales como el 0,1%, a causa de que el modelo es estimado con una muestra finita, por lo que se sugiere introducir la EVT dentro de su estructura de modelación por medio de los siguientes pasos: ajustar un modelo CAViaR con el propósito de obtener los cuantiles 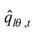 con θ relativamente grande (por ejemplo, el 5% o 10%). Con este modelo se construyen las series de los residuales del cuantil estandarizados.
con θ relativamente grande (por ejemplo, el 5% o 10%). Con este modelo se construyen las series de los residuales del cuantil estandarizados.

Luego, si gt(•) es la función de densidad condicional de los residuales del cuantil estandarizado, entonces se aplica el supuesto:
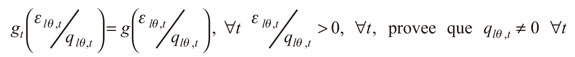
Lo que implica que la distribución de los residuales de la ecuación (17) no son variantes en el tiempo más allá de (1 - θ)-cuantil34. Por consiguiente, con el anterior supuesto de la ecuación precedente, se puede implementar la EVT a los residuales del cuantil estandarizado, y se obtiene una estimación para la cola:
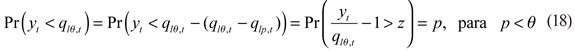
siendo el 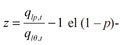 -cuantil de los residuales estandarizados. De esta manera, si zlp es la estimación de z por EVT, su correspondiente p-cuantil para los retornos de un portafolio son dados por
-cuantil de los residuales estandarizados. De esta manera, si zlp es la estimación de z por EVT, su correspondiente p-cuantil para los retornos de un portafolio son dados por 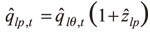 . Así, se introduce la EVT en el modelo CAViaR.
. Así, se introduce la EVT en el modelo CAViaR.
Por otra parte, como se mencionó antes, para estimar la ecuación (16) con las versiones de los modelos de precios de los activos, se usa una arquitectura de QRNN, la cual puede presentar un buen desempeño para el cálculo del cuantil o valor objetivo35. No obstante, esta afirmación no es cierta, si no se exhibe un balance en la elección del número de neuronas, es decir, pocas neuronas pueden conducir a un aprendizaje incompleto de la red; en cambio, muchas neuronas pueden llevar a que el modelo, en lugar de aprender memorice, presentándose un sobreajuste. Por tanto, se sugiere estimar varias arquitecturas cambiando el número de neuronas, con q = 1 hasta q = q*, siendo q* el número de variables de entrada + 1, y se selecciona el mejor modelo por medio de medidas de desempeño (Londoño, 2009).
Del mismo modo, es necesario especificar una minimización óptima de la ecuación (7), debido a que puede arrojar muchos mínimos locales, independientemente de que el modelo converja. En consecuencia, fue necesario aplicar un componente de control que permite inicializar los pesos y sesgos varias veces hasta obtener el mejor resultado; en este caso se realiza diez veces por cada neurona y cuantil estimado (Cannon, 2011; Londoño et al., 2010).
Para determinar que los modelos se encuentran bien especificados, se emplean medidas de desempeño tanto dentro como fuera del período de entrenamiento. Lo cual se realizó con un esquema Rolling de pronósticos (Aristizábal, 2006; Jalil y Misas, 2007), que consiste, en este caso, en elaborar los pronósticos por tramos de cien datos por cada horizonte. La estrategia, como se observa en el Gráfico 1, se lleva a cabo adicionando los cien patrones más alejados (primeros) del período de entrenamiento (pronósticos), empezando en T hasta completar el período de pronósticos en T + i, donde, T = 1.020 e i = 300. Dándose así en cada horizonte un nuevo conjunto de parámetros 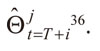 .
.
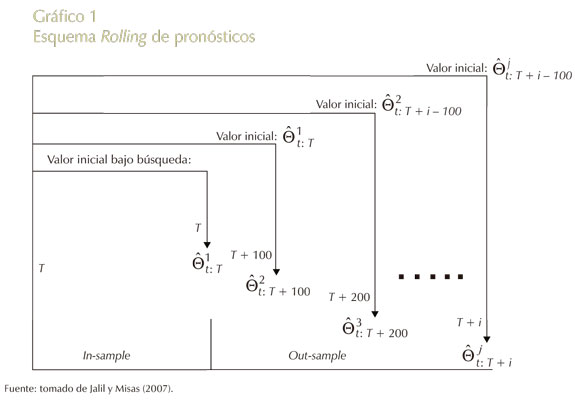
De esta forma, se evalúa la consistencia del modelo en los h horizontes de tiempo, con h = 1, 2 y 3. Produciéndose tres modelos por cada horizonte para las respectivas cinco especificaciones37. Esta segmentación se hace con la intención de establecer cómo se desempeñan los modelos en tres estados contingentes: uno, en el cual el IGBC presenta una alta volatilidad originada por la crisis financiera de los Estados Unidos (aproximadamente a partir de octubre de 2008); otro, después de este período, donde el modelo se halla en un proceso de transición (de alta volatilidad a baja), y por último, uno en el que se exhibe relativa calma en el mercado.
Con esta división en el proceso de estimación, se eligieron las arquitecturas que ostenten el mejor desempeño dentro y fuera del período de entrenamiento, y se usaron estadísticos basados en la medida VaR para una posición larga38. Engle y Manganelli (1999) sugieren dos estadísticos para determinar el desempeño del modelo que calcula el cuantil o el VaR: uno conocido como la proporción de falla o %HIT(θ), que se define como:

Esta prueba establece que un modelo se encuentra bien especificado si la proporción de falla es igual a la probabilidad θ pre-especificada o teórica del cuantil. El otro, es el cuantil dinámico que evalúa la hipótesis nula conjunta de que E(%HIT(θ)) = 0 e incorrelacionada con los factores de riesgo que se localizan en el grupo de información. Su estadístico de prueba es:

donde k son los grados de libertad iguales al número de variables incluidas en la matriz X. 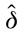 es el vector de parámetros estimados a través de la siguiente regresión artificial,
es el vector de parámetros estimados a través de la siguiente regresión artificial, 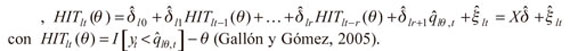 Otra medida empleada fue la proporción de fallas de Kupiec, la cual valora la hipótesis nula de que H0: p = θ, lo que establece la precisión del modelo en la captura de la probabilidad θ a un nivel de confianza pre-especificado 1 - θ. Su estadístico de prueba es una razón de verosimilitud que es definida como:
Otra medida empleada fue la proporción de fallas de Kupiec, la cual valora la hipótesis nula de que H0: p = θ, lo que establece la precisión del modelo en la captura de la probabilidad θ a un nivel de confianza pre-especificado 1 - θ. Su estadístico de prueba es una razón de verosimilitud que es definida como: 
con x el número de fallas, m el número de observaciones usadas para cada período de evaluación y 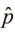 = x / m . El numerador de la ecuación (21) es el valor de máxima verosimilitud bajo la hipótesis nula, y el denominador es la función de verosimilitud evaluada en el estimador de máxima verosimilitud de p,
= x / m . El numerador de la ecuación (21) es el valor de máxima verosimilitud bajo la hipótesis nula, y el denominador es la función de verosimilitud evaluada en el estimador de máxima verosimilitud de p, 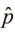 (Melo y Becerra, 2005).
(Melo y Becerra, 2005).
Los anteriores estadísticos producen resultados adecuados para establecer la buena o mala especificación del modelo en el instante de capturar el nivel de probabilidad pre-especificado. No obstante, tales medidas desconocen los costos que acarrearía tener un cuantil por encima (por debajo) del valor observado. Específicamente, los administradores del riesgo cuando implementan una metodología de cálculo del VaR, no solo deben tener en cuenta los costos en los que se incurre al tener un evento extremo no predicho, sino además el costo que se infringe al hacer una cobertura superior al riesgo que se presenta en un período concreto de negociación39.
Por esta razón, se evaluará el modelo con una función de costos asimétrica. Siguiendo a Aristizábal (2006) y Jalil y Misas (2007), se utilizó la función de pérdida LINLIN, cuya forma es lineal a ambos lados del valor objetivo, pero de manera asimétrica determinada por el ratio a/b, su fórmula es:
En este caso, a representa los costos en los que se incurre por realizar una cobertura superior a la requerida, y b el costo de aplicar una cobertura inferior a la que se espera capture la probabilidad θ pre-especificada. Además, a y b son parámetros suavizadores que penalizan en menor medida los valores pronosticados del cuantil más alejados de su origen, obteniéndose una mejor evaluación40.
En el Cuadro 341 se resumen los resultados obtenidos de los estadísticos de prueba dentro del período de estimación para las cinco especificaciones (GARCH-EVT, GARCH indirecto, APT, APT ampliado y CAPM) con sus respectivos tres horizontes de tiempo. En donde se pueden observar pruebas, tales como el porcentaje de veces que el VaR es excedido (%HIT(θ)), y los valores p del cuantil dinámico y la proporción de fallas de Kupiec.
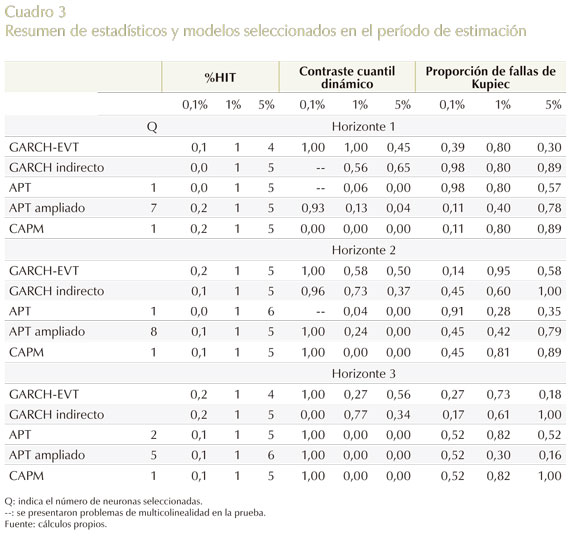
En lo que respecta a la %HIT(θ), se obtuvieron los resultados esperados en términos generales por las diferentes especificaciones; es decir, para los cuantiles teóricos o proporción de pérdidas pre-especificadas que se muestran en la parte superior del Cuadro 3 (0,1%, 1% y 5%). Los valores empíricos de los cuantiles fueron similares a los cuantiles teóricos en los diferentes modelos; no obstante, se presentan resultados muy heterogéneos en el cuantil del 0,1% en lo que respecta a la sobre y subestimación del riesgo en los distintos modelos y horizontes.
En lo que atañe al contraste del cuantil dinámico, para esta prueba se incluyen los diez primeros rezagos de la proporción de fallas (esto se hizo dentro y fuera del período de estimación). Este estadístico mostró buenos resultados para el modelo GARCH-EVT y el GARCH indirecto en la aceptación de la hipótesis nula en casi todos sus cuantiles. Para las especificaciones de los modelos de precios de los activos (APT, APT ampliado y CAPM), en esta prueba se acepta solo la hipótesis nula para el cuantil pre-especificado del 0,1%, presentándose algunas excepciones en otros cuantiles, como es el del 1% y 5% para el modelo APT ampliado en los horizontes 1 y 2, respectivamente; así mismo, para el modelo APT en el cuantil del 1% en el horizonte 1. De lo último se observa que los problemas de autocorrelación que muestran estos esquemas pueden ser causa de la muestra bajo estudio o grupo de datos.
De lo anterior, Engle y Manganelli (1999) advierten que la prueba del cuantil dinámico puede ser usada para determinar la capacidad predictiva en el cálculo del VaR con diversas metodologías, sin que el rechazo de la prueba inhabilite la estabilidad del modelo en el tiempo durante el período de estimación. Sin embargo, si se presenta este caso en el período de pronóstico, esto implicaría la nulidad del modelo y su estabilidad en el tiempo, significando la poca conveniencia del uso de esa metodología para el cálculo del VaR.
Por último, la proporción de fallas de Kupiec es aceptada por todos los modelos a los niveles de significancia convencionales (1% y 5%) para todos sus horizontes de tiempo. Según los anteriores resultados, dos puntos importantes para destacar son: de acuerdo con la prueba del cuantil dinámico, se puede establecer cierto sesgo en los resultados de manera condicional en los modelos de precios de los activos, así se desempeñen correctamente de manera incondicional. Así mismo, se podría afirmar que los modelos que se desempeñan mejor dentro del período de estimación son el GARCH-EVT y GARCH indirecto.
Antes de iniciar la exposición de los estadísticos de desempeño de los modelos fuera del período de estimación (Cuadro 4), es necesario aclarar que el cuantil teórico del 0,1% se usa solo con propósitos expositivos de cómo se comportan las diferentes metodologías en la captura de cuantiles más extremos, mas no como un cuantil cuyo propósito sea la toma de decisiones, debido a que la muestra evaluada para hacer pronósticos es muy pequeña (cien datos por cada horizonte y se necesitarían al menos mil para poder hacer inferencia en este cuantil).
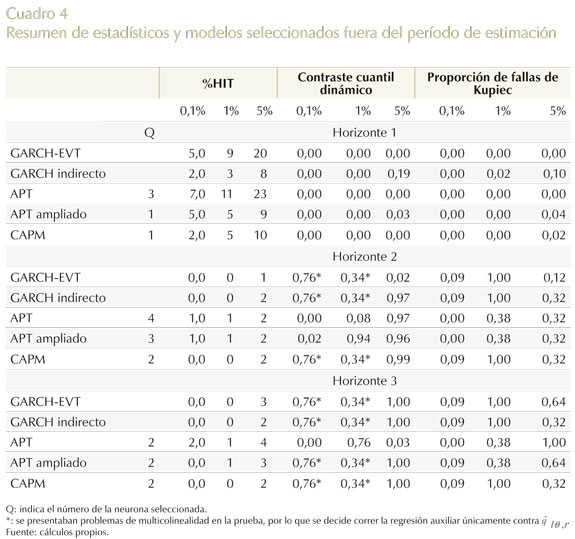
Ahora bien, en el Cuadro 4 se resumen los resultados de las pruebas de desempeño usadas en el Cuadro 3 para los cinco modelos estudiados con sus respectivos cuantiles teóricos y horizontes de tiempo, pero para el período fuera de entrenamiento. En esta situación, debido a que se estudiaron tres períodos contingentes, los valores de los estadísticos en cada horizonte son disímiles, donde esto se distingue en mayor medida en el horizonte 1, que es un período de alta volatilidad.
En este orden de ideas, respecto al horizonte 1, en la prueba de %HIT(θ) se observa que todos los modelos subestiman el riesgo; siendo el GARCH indirecto seguido por el APT ampliado los modelos que presentan menos errores en la captura de la probabilidad pre-especificada. En cuanto a las pruebas del cuantil dinámico y la proporción de fallas de Kupiec, se rechaza la hipótesis nula en general para casi todos los modelos bajo estudio. Claro está, con algunas excepciones, como son el GARCH indirecto en el cuantil del 5% (acepta ambas pruebas a los niveles convencionales de significancia) y el APT ampliado, que acepta estas pruebas al 3% y 4%, respectivamente.
En el horizonte 2, otro es el escenario en comparación con el horizonte 1, donde los modelos al haber sido estimados con un grupo de información que contenía un período de alta volatilidad, presentan una sobrestimación del riesgo en el cuantil del 1% y 5%, con la excepción del APT y APT ampliado, para el cuantil teórico del 1%. Para el 5%, en general se observa una sobrestimación del riesgo para todos los modelos; específicamente, por lo común se equivoca el 2%, cuando su nivel teórico o θ pre-especificada exige hacerlo el 5%.
En cuanto al estadístico del cuantil dinámico, presenta un buen desempeño en todos los modelos a los niveles de significancia convencionales. No obstante, se acepta solo al 2% para el GARCH-EVT en el cuantil del 5%; y en el cuantil del 0,1% para el APT y APT ampliado al 0% y 2%, respectivamente. En lo que atañe a la prueba de proporción de fallas de Kupiec, se presenta el mismo resultado con relación al cuantil dinámico en lo concerniente a la aceptación de la hipótesis nula, y solo se rechaza la hipótesis nula para el APT y APT ampliado al nivel teórico del cuantil del 0,1%.
En el horizonte 3, todos los modelos muestran un buen desempeño, destacándose el modelo APT ampliado como uno de los que mejor desempeño tiene al capturar el nivel de probabilidad pre-especificado en la %HIT(θ). También es de destacar que el modelo APT es el más preciso en la captura de la %HIT(θ) en el cuantil teórico del 5% (4%). En resumen, no se podría extraer una conclusión definitiva sobre cuál es el mejor modelo tanto en condiciones adversas como de relativa calma en el período de pronóstico. Pero sí se puede decir que fusionando estos dos estados contingentes, el modelo GARCH indirecto y APT ampliado son los que presentan el mejor desempeño, donde este último es una estrategia balanceada que avala un universo de opciones más robusto al incorporar variables macroeconómicas y financieras para la captura del riesgo.
Por otro lado, en el Cuadro 5 se puede visualizar los resultados arrojados por la función de pérdida LINLIN; en este caso, los modelos que presentan menores costos son GARCH-EVT seguido por el GARCH indirecto, en todos los horizontes. Ahora bien, al observar el desempeño de los cinco modelos, en lo que respecta a la subestimación del riesgo que es un tema neurálgico para los administradores de riesgo al momento de tomar la decisión de qué metodología VaR emplear, se puede ver que en períodos de alta volatilidad (horizonte 1) el modelo GARCH indirecto es el que ofrece el mejor desempeño; pero en períodos de relativa calma, los modelos de precios de los activos ocupan este lugar. Lo que se destaca con este hallazgo, es que puede ser beneficioso emplear ambos modelos, donde su uso dependería de las condiciones del mercado de valores y de la economía.
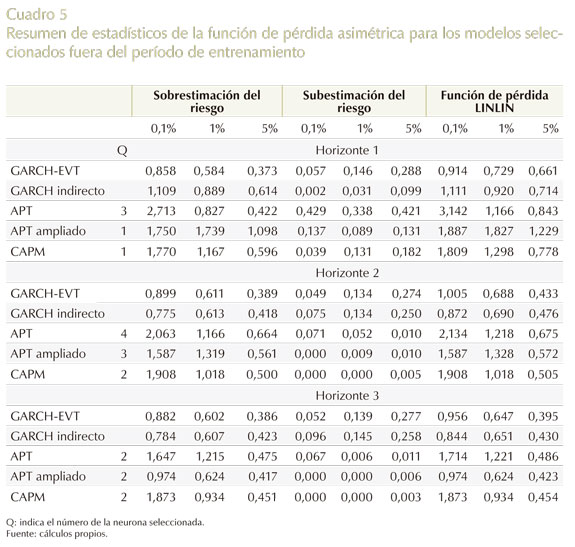
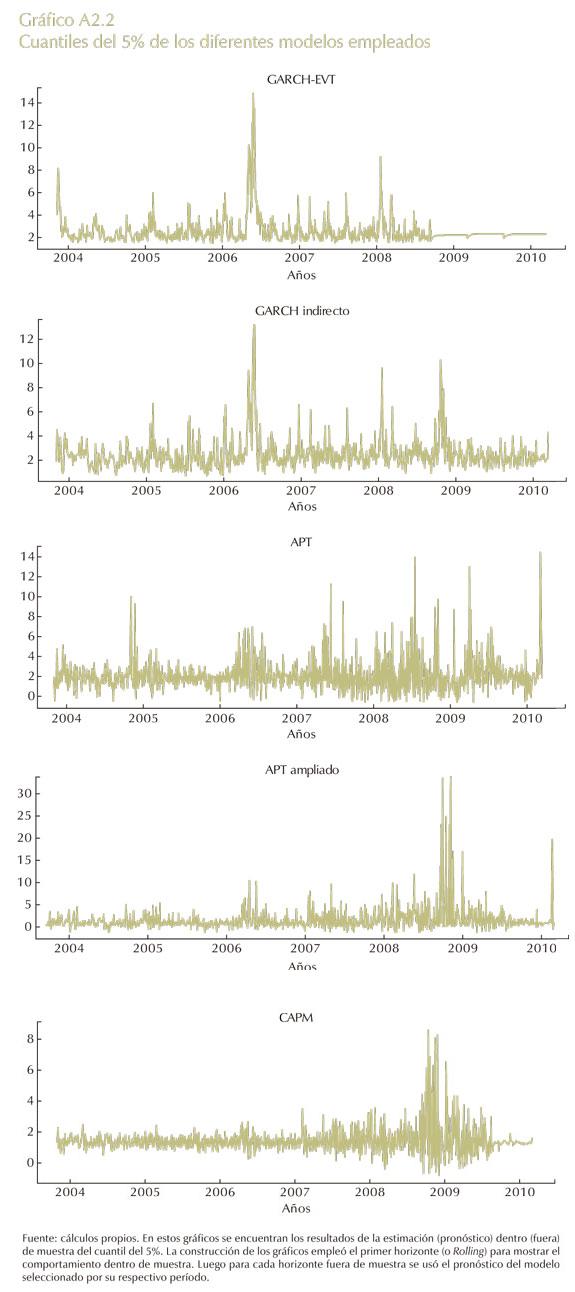
Para finalizar, en el Gráfico A2.2 se encuentra el desempeño de las cinco especificaciones en el cuantil de 5%. Ahí se puede vislumbrar los diferentes patrones como se captura el cuantil dentro y fuera del período de entrenamiento y se destacan varios hechos estilizados:
• El modelo GARCH indirecto se desempeña de forma muy similar al GARCH-EVT en el período de estimación. Pero en el período de pronóstico lo hace mucho mejor el primer modelo, hasta el punto de poder capturar la dinámica del IGBC en su cuantil, lo que destaca la superioridad de la técnica de regresión del cuantil para adaptarse a eventos extremos y condiciones reales.
• Comparando los modelos GARCH-EVT y GARCH indirecto con los modelos de precios de los activos, se puede observar que los primeros buscan adaptarse al cuantil del retorno del IGBC como una banda de confianza. En cambio, los segundos tratan no solo de establecer esta banda, sino que además buscan seguir la tendencia de este índice, y ajustarse a los patrones de la variable subyacente; un modelo que resalta esta situación, es el CAPM en el período de crisis de 2008.
• El modelo CAPM no tiene en cuenta el período de la crisis de 2006. Esto puede ser explicado, porque este evento se presenta por la euforia de los inversionistas que provocaron una burbuja especulativa internamente, que si bien el mercado colombiano de valores estaba muy bien aspectado por los fundamentales de sus empresas, las altas rentabilidades de las acciones no reflejaban cabalmente esta situación en el entorno financiero nacional e internacional.
B. INTERPRETACIÓN ESTADÍSTICA Y ECONÓMICA DE LOS PARÁMETROS DE LOS MODELOS DE QRNN
En este caso, considerando que se usó un modelo de QRNN, los valores de los parámetros de las variables de entrada no son interpretables directamente. Por este motivo, para probar la significancia de las variables al igual que su signo, Qi (1994) y Franses y Dijk (1999) proponen efectuar análisis de sensibilidad basado en la salida de la matriz jacobiana 42, la cual determina la influencia que tiene cada variable de entrada xi,t (suponiéndose continua) sobre la variable de salida yt dadas las variables de entrada X 1,t, X2,t, ..., Xi - 1,t, ..., Xk,t como constantes en su valor promedio. Es decir, se analiza la siguiente derivada43:
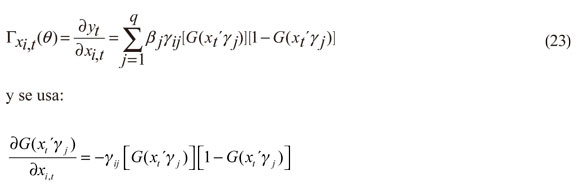
Su interpretación es que entre mayor sea en términos absolutos 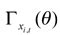 , tendrá una mayor importancia xi,t con relación a yt. No obstante, es necesario adicionar otras características que presenta la estimación del cuantil.
, tendrá una mayor importancia xi,t con relación a yt. No obstante, es necesario adicionar otras características que presenta la estimación del cuantil.
Concretamente, si se tiene el modelo 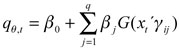 a causa de que su estimación se hace a partir de la inversa de la función de distribución condicional (o función del cuantil condicional), el efecto que se pueda generar en yt dependerá del signo que tome . Si se presenta un cambio positivo, entonces yt se moverá a la derecha; esta modificación obedecerá a la fuerza que tenga un choque de la variable xi,t sobre yt, el coeficiente de asimetría y el nivel de probabilidad θ, donde este último entre más pequeño sea su probabilidad, se dará un efecto más completo. Igualmente, el signo positivo mostrará que puede ser beneficioso tener una posición larga, debido a que la variable yt estipula incentivos de tenencia de un activo. Claro que esta modificación será local, dado que solo se analiza una variable a la vez (este resultado se provee de forma inversa para cambios negativos) (Chernozhukov y Umantsev, 2001).
a causa de que su estimación se hace a partir de la inversa de la función de distribución condicional (o función del cuantil condicional), el efecto que se pueda generar en yt dependerá del signo que tome . Si se presenta un cambio positivo, entonces yt se moverá a la derecha; esta modificación obedecerá a la fuerza que tenga un choque de la variable xi,t sobre yt, el coeficiente de asimetría y el nivel de probabilidad θ, donde este último entre más pequeño sea su probabilidad, se dará un efecto más completo. Igualmente, el signo positivo mostrará que puede ser beneficioso tener una posición larga, debido a que la variable yt estipula incentivos de tenencia de un activo. Claro que esta modificación será local, dado que solo se analiza una variable a la vez (este resultado se provee de forma inversa para cambios negativos) (Chernozhukov y Umantsev, 2001).
Ahora bien, se realizará este análisis para el modelo APT ampliado con tres neuronas que recoge casi todas las variables y, además, en términos absolutos, muestra los valores más altos en comparación tanto de las otras neuronas como de los modelos APT y CAPM. Lo anterior será evaluado para un modelo con un cuantil del 5%. En estos gráficos, se tiene que en el eje de las ordenadas se encuentra como cambia el IGBC ante variaciones en cada variable de entrada, donde entre mayor sea su valor en términos absolutos, más grande será su impacto sobre la variable de salida; en el eje de las abscisas se halla cómo evoluciona el efecto de la variable de interés a medida que su valor cambia (aumenta o disminuye).
Así las cosas, en el Gráfico 2 se observa el MSCI, el cual es un Benchmark creado por Morgan Stanley Capital Investment, que agrupa las empresas más importantes de veintidós países en Norteamérica, Europa y la región pacífica de Asia (www.bloomberg.com). Empíricamente se supone que este factor de riesgo presenta una relación positiva con relación al mercado de valores colombiano; sin embargo, el efecto del MSCI rezagado 1 y 2 períodos sobre el retorno del IGBC es negativo en ambos paneles, lo que invalida esta presunción.
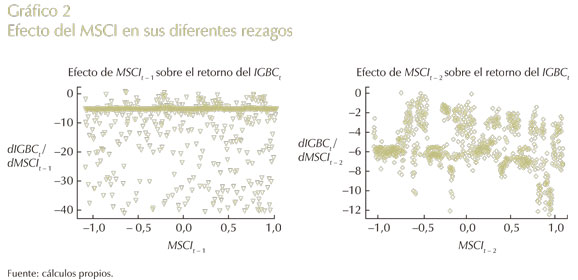
No obstante, si se evalúan las variables que componen esta construcción, se puede decir que el componente determina el costo de oportunidad para los inversionistas y administradores de riesgo al realizar una inversión o abrir una posición larga en activos en una economía desarrollada o subdesarrollada, donde esta última ofrece mayores riesgos, pero no necesariamente mayores ganancias. De este modo, los administradores como minimizadores del riesgo, más que optimizadores de ganancias, estarán incentivados a invertir recursos en mercados que presenten resultados menos volátiles en términos negativos, como se puede presentar en las acciones de las empresas que componen el MSCI.
Ahora, en el panel izquierdo de este gráfico se presenta una dispersión en su efecto en todo su rango hacia abajo, lo que manifiesta incentivos de tenencia corta de un activo; sin embargo, se da una concentración en -5, a través de todo el rango de esta variable. En cambio, para el panel derecho se da un efecto disperso que se puede ubicar en el rango (-2, -8), lo que muestra que con el paso del tiempo el cambio de esta variable es mucho más concentrado en un rango pequeño, pero sin un comportamiento definido; lo que puede vislumbrarse como una regla de tenencia de activos, en la cual entre más tiempo pase aumentando la variable MSCI esto se hará a tasas de retorno más bajas, lo que provocará que los inversionistas tiendan a mantener una mayor cantidad de activos de economías emergentes, dada la posible baja volatilidad de las economías desarrolladas que ofrecerán rentabilidades, que si bien son más seguras serán más bajas.
En el Gráfico 3 se encuentra la variable TIB. Esta puede ser interpretada como una proxy de las decisiones de política monetaria, y se relaciona de manera negativa con el precio de las acciones al representar los costos de endeudamiento a los que están dispuestas las instituciones financieras y, por consecuencia, las empresas en obtener recursos; es decir, si la tasa de interés en un país es muy alta, será más difícil para las empresas hacer inversión de capital, lo que hará que se desplacen los recursos a otras actividades más rentables (Melo y Becerra, 2005; Shaharudin y Fun, 2009).
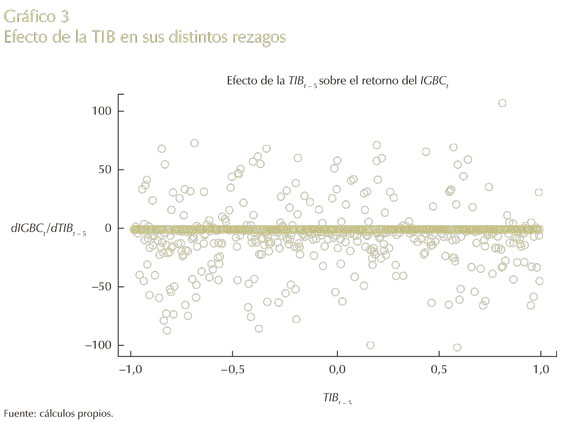
Así pues, en este gráfico se observa el comportamiento de la TIBt - 5, el cual presenta un resultado similar al del MSCIt - 1 al agrupar en una línea recta todos sus valores, pero con la mayor variabilidad en su rango entre todas la variables analizadas en esta investigación; esto se da de forma simétrica arriba y abajo, mostrando valores positivos y negativos que incentivan el tener tanto posiciones largas y cortas.
Esto último contradice el efecto que se presenta en el trabajo de Londoño et al. (2010), donde se muestra un efecto muy pequeño en la predicción del retorno promedio con la TIB. No obstante, se puede decir que para los cuantiles extremos de probabilidad esta variable es de suma relevancia, a causa de que el manejo de la política monetaria puede mostrar los niveles de riesgo a los que una institución financiera podría incurrir si no realiza previsiones y provisiones adecuadas al cambio de esta variable, al ser este factor de riesgo neurálgico para la estabilidad económica de las empresas en el corto y largo plazo y, por consecuencia, del país.
En el Gráfico 4 se presenta la TRM, la cual es un predictor del comportamiento del retorno de los activos determinado por las preferencias de los inversionistas en la tenencia de activos y divisas de un país. Por tanto, las decisiones de inversión estarán influenciadas por cambios en el precio de la divisa. Dejando todo lo demás constante, si estas tienen una tendencia esperada a apreciarse (depreciarse), influirá en la compra (venta) de activos financieros (Londoño et al., 2010).
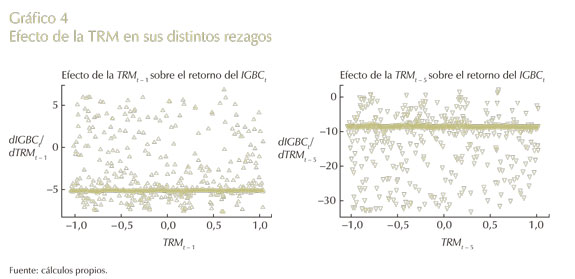
Así, este gráfico en ambos paneles presenta un signo negativo que es lo esperado; indistintamente se proporciona la misma tendencia de las anteriores variables en lo que atañe a centrar la mayoría de su efecto en un solo punto en sus diferentes niveles de variación. Así mismo, se da un efecto de mayor dispersión hacia arriba en el panel izquierdo (propiciando tenencia larga) y lo contrario para el derecho (favoreciendo una posición corta). Del mismo modo, si se observan los gráficos de forma conjunta, se puede ver que ante un aumento del IGBC a medida que van pasando los diferentes períodos (en este caso, TRMt - 1 y TRMt - 5), los inversionistas esperan una corrección del mercado, que si en un principio se generan decisiones de compra, con el paso del tiempo pasa a una posición de venta.
En el Gráfico 5 se halla la UVR que se puede considerar como una proxy del nivel de precios agregado; tiene una relación negativa que contrasta con lo esperado (Chen et al., 1984). Esta se interpreta como un indicador de estabilidad macroeconómica, concretamente si los inversionistas tanto en el sector financiero como en el sector real esperan una inflación alta; esto puede ocasionar volatilidad e incertidumbre en el consumo y la actividad real futura (Edwing, 2002), debido a que la confianza en el manejo macroeconómico por la autoridad monetaria no es creíble, provocando un desplazamiento de la inversión a otro tipo de instrumentos financieros y economías con condiciones más propicias para invertir (Londoño, 2009).
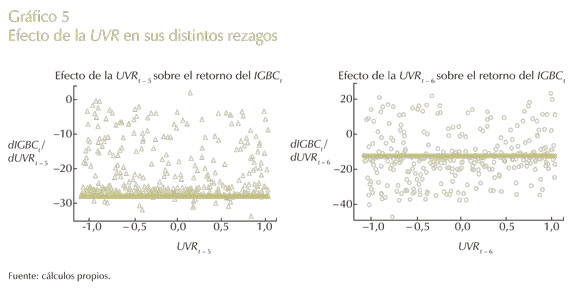
También, en este gráfico, la mayoría de los cambios se ubica en un solo valor a lo largo de su rango, y se da la misma regla de tendencia de la TRM, es decir, pasa de una posición corta a una larga. Con respecto a su signo, también puede ser explicado por la aversión de los inversionistas a mantener activos que son sensibles ante cambios nominales. Lo que influye en las perspectivas de inversión real y, por consecuencia, en el valor futuro de las acciones (Chen et al., 1984).
V. CONCLUSIONES
Este artículo tuvo como propósito investigar las propiedades del modelo CAViaR que estima el cuantil de forma directa, usando varias especificaciones metodológicas y factores de riesgo para el cálculo del VaR. Se encontró que el modelo GARCH indirecto y el APT ampliado, son los que en general presentan mejor desempeño en la captura del riesgo en el período de pronóstico. De ambas estructuras puede señalarse que la primera se desempeña mejor en condiciones extremas y la segunda en condiciones de relativa calma. También, con respecto a la función LINLIN, el GARCH-EVT fue el que menores costos presentó; pero en el instante de observar la subestimación del riesgo, el modelo GARCH indirecto se desempeña mejor en el horizonte 1, pero para los otros horizontes analizados los modelos de precios de los activos hicieron mejor este trabajo.
De lo precedente, la función de pérdida LINLIN posibilitó una mejor comprensión y entendimiento de la sobrevaloración o subvaloración del riesgo por parte del modelo subyacente; lo que puede admitir que esta medida por medio de un estudio más detallado se convierta en un determinante clave de la toma de decisiones de los administradores de riesgo en el momento de seleccionar una metodología para el cálculo del VaR. Por otro lado, aunque la prueba del cuantil dinámico sea interesante e importante para determinar el desempeño de un modelo que busque calcular el VaR, es una prueba que requiere un estudio más concienzudo sobre su veracidad en el establecimiento de su hipótesis, ya que puede ser fácilmente manipulable en sus variables explicativas que dependen de los rezagos de la proporción de fallas, la introducción o no del VaR, unas variables dummies para capturar la estacionalidad, entre otros componentes.
Una precisión que se hizo antes, es que el cuantil 0,1% fuera del período de entrenamiento no se ajusta, porque la muestra evaluada es muy reducida para alcanzar el nivel θ pre-especificado. No obstante, esto se hizo con propósitos expositivos para esclarecer cómo se comportaba el cuantil en condiciones extremas. Para futuras investigaciones, sería interesante con una muestra más amplia establecer cómo se comporta cualquier modelo fuera del período de entrenamiento a este nivel de probabilidad.
Cabe notar que los modelos GARCH-EVT, GARCH indirecto y CAPM presentaron una sobrestimación del riesgo, explicada por la rapidez que tienen las variables financieras en la captura de la información, como es el IGBC y el MSCI que hizo que el modelo sobrerreaccionara a la información (Chen et al., 1984). También es importante mencionar que en el artículo de Chen et al. (1984), la variable índice de mercado puede sesgar los resultados cuando se combina con factores de riesgo macroeconómicos como variables explicativas en un modelo; no obstante, este efecto no se presenta en esta investigación, que puede ser explicado por las características diferentes que tienen los cuantiles extremos en relación a los promedios.
Por último, el análisis de sensibilidad asintió ver cómo las distintas variables macroeconómicas y financieras afectaban al cuantil, mostrando que su efecto aunque señalaba cierta dispersión, en general se ubicaba en un punto específico a través de todo el rango de las distintas variables. Además, que dicha dispersión se podía explicar por algunas divergencias de opciones que hacían que se diera un mejor ajuste de la variable de interés en el momento de ser evaluada por la variable dependiente.
Específicamente, en el trabajo de Chernozhukov y Umantsev (2001) se realiza un modelo de regresión del cuantil lineal, el cual permitió observar los resultados de los parámetros de las variables de forma constante; no obstante, no se podía visualizar cómo las diferentes variables utilizadas afectaban el cuantil a distintos niveles de variación como lo hizo este trabajo, lo que posibilitó capturar de una mejor forma la dinámica contenida en cada variable. Una falla que presentó el análisis de sensibilidad fue la variable MSCI que no arrojó el signo esperado, lo que puede ser explicado en parte por los costos de oportunidad que tienen los inversionistas y administradores de riesgo en el momento de abrir una posición financiera en dos mercados diferentes.
Comentarios
1 Para una revisión completa sobre las principales crisis económicas remítase a Gençay y Selçuk (2004).
2 El riesgo crédito se define como el riesgo de pérdida por default. El riesgo operacional es la posible pérdida resultante por un proceso interno mal elaborado, de personas y sistemas o externo a la institución. El riesgo de liquidez consiste en el análisis de la probable insolvencia de una posición, al no poderse cumplir con una obligación en un período determinado. El riesgo de mercado es establecido como la volatilidad de los ingresos esperados de forma no favorable, que es afectada ante cambios de las variables subyacentes (Greuning y Bratanovic, 2009; Gregoriou, 2009; Engle y Manganelli, 2001).
3 Por sus siglas en inglés, Value at Risk. Esta metodología de control del riesgo es implementada hasta el 2001 en la regulación colombiana (Melo y Becerra, 2005).
4 Ofrece una medida estándar que determina una pérdida de un activo individual o portafolio con una probabilidad dada de manera simple. Esta puede ser comparable entre mercados al ser una medida aplicada de forma universal. Recoge en un solo número (en términos monetarios) las posibles fuentes de riesgo que se pueden presentar en un portafolio, entre otras características (Alexander, 2009).
5 Por sus siglas en inglés, Conditional Autoregressive Value at Risk.
6 Por sus siglas en inglés, Artificial Neural Network.
7 Por sus siglas en inglés, Quantile Regression Neural Networks. Este nombre se le da para distinguir la regresión del cuantil aplicada al modelo de ANN, como es hecho en los trabajos de Cannon (2011) y Taylor (2000).
8 Por sus siglas en inglés, Capital Asset Pricing Model.
9 Por sus siglas en inglés, Arbitrage Pricing Theory.
10 Por sus siglas en inglés, Generalized Autoregressive Conditional Heteroskedastic.
11 Por sus siglas en inglés, Extreme Value Theory.
12 Otro componente que ha venido adquiriendo importancia, es la fuerte no linealidad con la que se ve afectado el retorno de los activos por diversos factores de riesgo de manera asimétrica y a diferentes pesos, lo que depende de su nivel de variación y capacidad explicativa de la variable de entrada (Aristizábal, 2006; Diagne, 2002; Franses y Dijk, 1999; Jalil y Misas, 2007; Londoño, 2009).
13 Según Shiller (2003), la contrariedad más problemática para que se satisfagan las hipótesis de los mercados eficientes es el exceso de volatilidad. Este autor también establece que hay otras anormalidades como el efecto enero y el día de la semana, pero que estos fenómenos no son tan neurálgicos en el cumplimiento de tales hipótesis.
14 Más adelante se explicará esta técnica de estimación.
15 Esta división en Engle y Manganelli (1999, 2001) se conoce como métodos paramétricos, no paramétrico y semiparamétrico, respectivamente.
16 Véanse Engle y Manganelli (1999, 2001) y Melo y Becerra (2005) para una exposición más detallada sobre estas metodologías.
17 En la actual investigación, βi = 0 bajo la especificación de QRNN, como se realiza en Chernozhukov y Umantsev (2001); esto a causa de que esta variable no es directamente observable y operacionalmente no sería viable. Sin embargo, Taylor (2000) asevera que la omisión de esta variable no es un problema, ya que la regresión del cuantil no exige este factor de riesgo para obtener un buen pronóstico de los cuantiles.
18 Otras especificaciones de l(•) que utilizan Engle y Manganelli (1999, 2001, 2004), son un modelo adaptivo, un valor absoluto simétrico y una pendiente asimétrica.
19 Sin pérdida de generalidad en la exposición del método de estimación f(xt;Θ), puede ser de la forma bosquejada en la ecuación (3) y minimiza una función objetivo como la de la ecuación (6).
20 Para los detalles sobre el algoritmo de optimización usado por este modelo, remítase a Cannon (2011).
21 Por sus siglas en inglés, Least Absolute Deviation.
22 Por sus siglas en inglés, Peaks Over Thresholds.
23 Véanse Embrechts, Kluppelberg y Mikosch (1997) para una exposición sobre esta metodología.
24 El MDA es el dominio de atracción máximo (por sus siglas en inglés, Maximun Domain Attraction). Relaciona la distribución de F de una variable aleatoria R con su distribución límite que esta asociada a sus máximos (Embrechts et al., 1997; Melo y Becerra, 2005).
25 Por sus siglas en inglés, Generalized Extreme Value.
26 El parámetro ξ determina la forma de la distribución GEV, si el MDA(Hξ) tiene como valor ξ > 0, esta entonces proviene de distribuciones de colas pesadas (Cauchy, t-Student, Pareto y logGamma). Si ξ = 0 implica que esta procede de distribuciones Gamma, Normal, Lognormal y Exponencial. Si ξ < 0 se ajusta a distribuciones de puntos finitos, como la Uniforme y la Beta (Engle y Manganelli, 2001).
27 Para obtener el valor del umbral óptimo se emplea el gráfico de la media de los excesos que se explicará más adelante.
28 Por sus siglas en inglés, Generalised Pareto Distribution.
29 Para emplear la EVT en el modelo GARCH de Bollerslev (1986) en lugar de emplearse 1 - p en la ecuación (13), se usa 1 - K, siendo K = 1 - p.
30 Para las críticas sobre esta técnica remítase a Embrechts et al. (1997), Melo y Becerra (2005) y Engle y Manganelli (2001).
31 Para instituir el umbral η óptimo, a veces una justificación financiera es suficiente; es decir, el valor de este parámetro puede ser pre-especificado hasta el punto en el cual la institución financiera sea tolerante a una pérdida (Tsay, 2005).
32 El componente principal Bonost explica el 59,24% de la variabilidad de las letras del Tesoro de los Estados Unidos; esta se puede definir como un índice general. Sus respectivos pesos van como siguen: Bonost = 0,3942*T6t + 0,5256*T24t + 0,5283*T60t + 0,4025*T120t + 0,3565*T360t
33 Véase Londoño (2009) para una revisión más detallada.
34 En este punto se supone que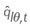 es un número negativo.
es un número negativo.
35 En la literatura de modelos de precios de los activos, tres técnicas diferentes son empleadas para modelar el comportamiento del retorno promedio de los activos; estas son: variables esperadas, análisis factorial y ANN. Las dos primeras metodologías presentan problemas de medición en las variables, tales como fallas de periodicidad, multicolinealidad, poca o nula interpretabilidad económica, entre otros. En cambio, ANN puede solventar tales problemas dada su estructura de estimación no lineal que admite la captura del ruido, ineficiencias del mercado, asimetrías y regularidades de los activos (Londoño et al., 2010).
36 Cabe observar que el administrador de riesgo tiene como principal función la de minimizar las posibles pérdidas. Es así, que en su proceso de administración, luego de un evento extremo negativo, se pueden tomar dos decisiones: una, es la de permanecer con el mismo modelo después de un período de alta volatilidad; otra, es la de actualizar el modelo antes de que se cumpla su período de vigencia para obtener pronósticos más verosímiles que incorporen nueva información de períodos extremos.
37 Para las especificaciones de QRNN, se debe tener en cuenta también que es necesario realizar la estimación y la respectiva evaluación por cada neurona j = 1,2,..., q *.
38 Para hacer más sencilla la exposición, se explicaron todos los estadísticos notacionalmente como si funcionaran dentro del período de estimación.
39 Las políticas de administración del riesgo de mercado determinan los límites y monitoreo de las posiciones (largo, corto, posición neta en el mercado, entre otras). Por tal motivo, es necesario que el capital que se invierta esté restringido al posible riesgo de liquidez en el que podría incurrir la institución financiera, por lo que se debe evaluar el grado de volatilidad, que entre mayor sea en un activo, es necesario un monitoreo más continuo y de esta forma poder prever de manera precisa las posibles contingencias no deseadas (Greuning y Bratanovic, 2009).
40 La función de pérdida LINLIN se debe observar con cuidado, porque más que ser un estadístico de decisión, este es un complemento después de observar otras medidas tales como la %HIT(θ).
41 En los Cuadros 3 y 4 para las arquitecturas de QRNN, no fue necesario aplicar la EVT, debido a la capacidad que presentó este modelo para adaptarse a situaciones extremas o cuantiles muy bajos, como el 0,1%.
42 Específicamente, estos autores proponen este análisis para ANN, pero su extensión es directa al caso de QRNN.
43 Concretamente, para realizar el análisis de sensibilidad, se toma la variable xi,t bajo estudio en un rango pre-especificado; por ejemplo, entre [-1,1] para n observaciones (que pueden ser la cantidad de patrones usados en el horizonte 1) y se evalúa en la ecuación (23) con los coeficientes estimados por el modelo seleccionado, dato por dato de forma ordenada y a pequeñas proporciones de cambio en dicho rango. También, con el propósito de poder delinear mejor el gráfico, las otras variables de entrada x1,t, x2,t, ..., xi - 1,t, ..., xk,t se dejan variar en sus valores reales. Esto último no modifica el resultado general.
REFERENCIAS
1. Alexander, C. Market Risk Análysis. Value-at-Risk Models (vol. IV), England, John Wiley & Sons, Ltd., 2009. [ Links ]
2. Anderson, J. A. Redes neuronales, México, Alfaomega Grupo Editor, 2007. [ Links ]
3. Aristizábal, M. C. "Evaluación asimétrica de una red neuronal artificial: aplicación al caso de la inflación en Colombia", Lecturas de Economía, vol. 65, Universidad de Antioquia, pp. 73-116, 2006. [ Links ]
4. Bollerslev, T. "Generalized Autoregressive Condicional Heteroskedasticity", Journal of Econometrics, vol. 31, Elsevier, pp. 307-327, 1986. [ Links ]
5. Cannon, A. J. "Quantile Regression Neural Networks: Implementation in R and Application to Precipitation Downscaling", Computers & Geosciences, vol, 37, Elsevier, pp. 1277-1284, 2011. [ Links ]
6. Cao, Q.; Leggio, K.; Schniederjans, M. J. "A Comparation Between Fama and French's Model and Artificial Neural Networks in Predicting the Chinese Stock Market", Computers & Operarations Research, vol. 32, Elsevier, pp. 2499-2512, 2005. [ Links ]
7. Chen, N. F.; Roll, R.; Ross, S. A. "Economic Forces and the Stock Market", The Journal of Business, vol. 59, núm. 4, University of Chicago, pp. 383-403, 1986. [ Links ]
8. Cheng, N.; Titterington, D. M. "Neural Network: A Review from a Statistical Perspective", Statistical Science, vol. 9, núm. 1, University of Kent, pp. 2-54, 1994. [ Links ]
9. Chernozhukov, V.; Umantsev, L. "Conditional Value-at-Risk: Aspects of Modelling and Estimation", Empirical Economics, vol. 26, Springer-Verlag, pp. 271-292, 2001. [ Links ]
10.Connor, G. "A Unified Beta Pricing Theory", Journal of Economic Theory, vol. 34, pp. 13-31, 1984. [ Links ]
11. Connor, G.; Linton, O. "Semiparametric Estimation of a Characteristic-Based Factor Model of Common Stock Returns", Journal of Empirical Finance, vol. 14, Elsevier, pp. 694-717, 2007. [ Links ]
12. Diagne, M. "Final Risk Management and Portfolio Optimization Using Artificial Neural Networks and Extreme Value Theory", tesis para optar al grado de PhD, Keiserslautern, University Keiserslautern-Mathematics Departament / Financial Mathematics, 141 pp., 2002. [ Links ]
13. Edwing, B. T. "Macroeconomic News and the Returns of Financial Companies", Managerial and Decision Economics, vol. 23, pp. 439-446, 2002. [ Links ]
14. Elton, E. J.; Grueber, M. J. Modern Portfolio Theory and Investment Analysis, Six Edition, John Wiley & Sons, Ltd, 2002. [ Links ]
15. Embrechts, P.; Kluppelberg, C.; Mikosch, T. Modelling Extremal Events for Insurance and Finance, Springer-Verlag, 1997. [ Links ]
16. Engle, R. F.; Manganelli, S. "CAViaR: Conditional Autoregressive Value at Risk by Regression Quantiles", NBER Working Paper Series, núm. 7341, National Bureau of Economic Research, Massachusetts, 1999. [ Links ]
17. Engle, R. F.; Manganelli, S. "Value at Risk Models in Finance", Working Paper Series, núm. 75, European Central Bank, 2001. [ Links ]
18.Engle, R. F.; Manganelli, S. "CAViaR: Conditional Autoregressive Value at Risk by Regression Quantiles", Journal of Business & Economic Statistics, vol. 22, núm. 4, American Statistical Association, pp. 367-381, 2004. [ Links ]
19. Fama, E. F. "Efficient Capital Markets: A Review of Theory and Empirical Work", Journal of Finance, vol. 25, núm. 2, The America Economic Riview, pp. 383-417, 1970. [ Links ]
20. Fama, E. F. Efficient Capital Markets: II", Journal of Finance, vol. 46, núm. 5, The America Economic Riview, pp. 1575-1617, 1991. [ Links ]
21. Franses, H. P.; Dijk, D. Non-Linear Time Series Models in Empirical Finance, England, Cambrige University Press, 1999. [ Links ]
22. Gallón, S. A.; Gómez, K. "Distribución condicional de los retornos de la tasa de cambio colombiana: un ejercicio empírico a partir de modelos MGARCH", tesis para optar al título de magíster en economía, Medellín, Universidad de Antioquia-Facultad de Ciencias Económicas, 38 pp., 2005. [ Links ]
23. Gençay, R.; Selçuk, F. "Extreme Value Theory and Value-at-Risk: Relative Performance in Emerging Markets", International Journal of Forescasting, vol. 20, Elsevier, pp. 287-303, 2004. [ Links ]
24. Gourieroux, C.; Jasiak, J. "Dynamic Quantile Model", Journal of Econometrics, vol. 147, Elsevier, pp. 198-205, 2008. [ Links ]
25. Greuning, H. V.; Bratanovic, S. B. Analyzing Banking Risk: A Framework for Assessing Corporate Gobernance and Risk Management, Third Edition, Washington, D. C., The World Bank, 2009. [ Links ]
26. Huang, D.; Yu, B.; Fabozzi, F. J.; Fukushima, M. "CAViaR-Based Forescast for Oil Price Risk", Energy Economics, vol. 31, Elsevier, pp. 511-518, 2009. [ Links ]
27. Jalil, M. A.; Misas, M. "Evaluación de pronósticos del tipo de cambio utilizando redes neuronales y funciones de pérdida asimétrica", Revista Colombiana de Estadística, vol. 30, núm. 1, Bogotá, Universidad Nacional, pp. 143-161, 2007. [ Links ]
28. Jang, S. J.; Sun, C. T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Aproach to Learning and Machine Intelligent, Upper Saddle River, Pritice Hall, 1997. [ Links ]
29. Koenker, R.; Bassett, G. "Regression Quantiles", Econometrica, vol. 46, núm. 1, The Econometric Society, pp. 33-50, 1978. [ Links ]
30. Koenker, R.; Hallock, K. "Quantile Regression", The Journal of Economic Perspectives, vol. 15, núm. 4, American Economic Association, pp. 143-156, 2001. [ Links ]
31. Koutulas, G.; Kryzanowski, L. "Integration or Segmentation of the Canadian Stock Market: Evidence Based on the APT", The Canadian Journal of Economics, vol. 27, núm. 2, Canadian Economics Association, pp. 329-351, 1994. [ Links ]
32. Kuan, C. M.; White, H. "Artificial Neural Networks: An Econometric Perspective", Econometric Riviews, vol. 13, núm. 1, pp. 1-91, 1994. [ Links ]
33.Kudryavtsev, A. "Using Quantile Regression for Rate-Making", Insurance Mathematics and Economics, vol. 45, Elsevier, pp. 296-304, 2009. [ Links ]
34. Londoño, C. A. "Teoría de precios de arbitraje. Evidencia empírica para Colombia a través de redes neuronales", tesis para optar al título de economista, Medellín, Universidad de Antioquia-Facultad de Ciencias Económicas, 58 pp., 2009. [ Links ]
35. Londoño, C. A.; Lopera, M.; Restrepo, S. "Teoría de precios de arbitraje. Evidencia empírica para Colombia a través de redes neuronales", Revista de Economía del Rosario, vol. 13, núm. 1, Universidad del Rosario, pp. 41-73, 2010. [ Links ]
36. McNeil, A. J.; Frey, R. "Estimation of Tail-Related Risk Measures for Heteroscedastic Financial Time Series: An Extreme Value Approach", Journal of Empirical Finance, vol. 7, Elsevier, pp. 271-300, 2000. [ Links ]
37. McNeil, A. J.; Frey, R.; Embrechts, P. Quantitative Risk Management. Concepts, Techniques and Tool, United Kingdom, Princenton University Press, 2005. [ Links ]
38. Melo, L. F.; Becerra, O. R. "Medidas de riesgo, características y técnicas de medición: una aplicación del VaR y el ES a la tasa interbancaria de Colombia", Borradores de Economía, núm. 343, Banco de la República, pp. 1-75, 2005. [ Links ]
39. Qi, M. "Financial Application of Artificial Neural Networks", Manddala, G. S.; Rao, C. R. (eds.). Handbook of Statistiscs 14: Statistical Methods in Finance, Elsevier Science B. V., pp. 529-552, 1994. [ Links ]
40. Ross, S. "The Arbitrage Theory of Capital Asset Pricing", Journal of Economic Theory, vol. 13, pp. 341-353, 1976. [ Links ]
41. Shaharudin, R. S.; Fung, H. S. "Does Size Really Matter? A Study of Size Effect and Macroeconomics Factor in Malaysian Stock Returns", International Research Journal of Finance and Economics, núm. 24, EuroJournals Publishing, Inc, pp. 101-116, 2009. [ Links ]
42. Sharpe, W. "Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk", Journal of Finance, vol. 19, núm. 3, American Finance Association, pp. 425-442, 1964. [ Links ]
43. Shiller, R. J. "From Efficient Markets Theory to Behavioral Finance", Journal of Economic Perspectives, vol. 17, núm. 1, pp. 83-104, 2003. [ Links ]
44. Singal, V. Beyond the Random Walk: A Gude to Stock Market Anomalies and Low- Risk Investing, New York, Oxford University Press, 2003. [ Links ]
45. Solnik, B. H. "An International Market Model of Security Price Behavior", The Journal of Financial and Quantitative Analysis, vol. 9, núm. 4, University of Washington School of Business Administration, pp. 537-554, 1974. [ Links ]
46. Stout, L. A. "The Mechanisms of Market inefficeincy: An Introduction to the New Finance", Working Paper Series, NYU Center for Law & Business, pp. 1-40, 2003. [ Links ]
47. Taylor, J. W. "A Quantile Neural Network Approach to Estimating the Conditional Density of Multiperiod Return", Journal of Forescasting, vol. 19, núm. 4, pp. 299-311, 2000. [ Links ]
48. Taylor, J. W. "Generating Volatility Forescasts from Value at Risk Estimate", Management Science, vol. 51, núm. 5, Institute for Operations Research an the Management Sciences, pp. 712-725. 2005. [ Links ]
49. Taylor, J. W. "Using Exponentially Weighted to Estimate Value at Risk Expected Shortfall", Journal of Financial Econometrics, vol. 6, pp. 382-406, 2008. [ Links ]
50. Tsay, R. S. Analysis of Financial Time Series, Second Edition, New Yersey, John Wiley & Sons, Inc., Hoboken, 2005. [ Links ]
51. Wei, J. "An Asset Pricing Theory Unifying the CAPM and APT", The Journal of Finance, vol. 43, núm. 4, American Financial Association, pp. 881-892, 1988. [ Links ]
52. White, H. "Nonparametric Estimation of Conditional Quantiles Using Neural Network", Gallant, A. R. et al. (eds.). Artificial Neural Network: Approximation and Learning Theory, Cambrige and Oxford, Blackwell, pp. 191-205, 1992. [ Links ]
53. White, H.; Kim, T.-H.; Manganelli, S. "Modellling Autoregresive Conditional Skewness and Kurtosis with Multi-Quantile CAViaR", Bollerslev, T.; Russel, J. R.; Watson, M. W (eds.). Volatility and Time Series Econometrics: Enssays in Honor of Robert F. Engle. Oxford University Press, pp. 231-256, 2008. [ Links ]
ANEXO 1
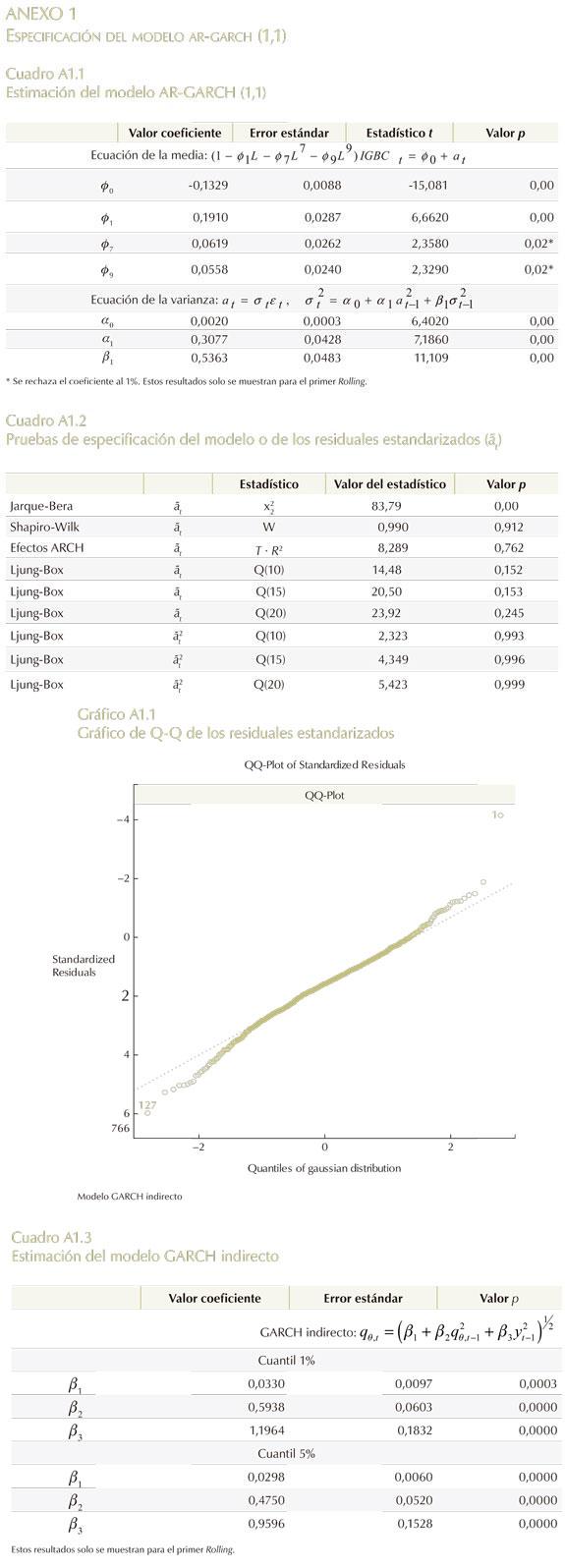
ANEXO 2