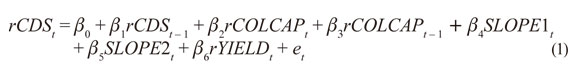Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ensayos sobre POLÍTICA ECONÓMICA
Print version ISSN 0120-4483
Ens. polit. econ. vol.29 no.spe64 Bogotá June 2011
CDS: relación con índices accionarios y medida de riesgo
CDS: Relationship With Stock Indexes and Risk Measure
CDS: relação com índices acionários e medida de risco
Bernardo León
Andrés Mora*
*Los autores agradecen las valiosas sugerencias y recomendaciones de los evaluadores anónimos y los comentarios de Andrés Murcia P. en el VII Seminario de la revista ESPE. Estas contribuciones ayudaron significativamente a mejorar la versión previa de este artículo.
Los autores son en su orden: Investigador asociado al Colegio de Estudios Superiores de Administración. Profesor investigador del Colegio de Estudios Superiores de Administración.
Correos electrónicos: uniandinos2007@gmail.com; amora@cesa.edu.co
Documento recibido: 7 de octubre de 2010; versión final aceptada: 18 de abril de 2011.
Un indicador de la crisis financiera ha sido el comportamiento de los contratos de seguros contra la cesación de pagos (CDS, por sus siglas en inglés). De esta manera, este artículo en primer lugar, toma el caso de Grecia, Italia y España y sus respectivos índices accionarios. En segundo lugar se analiza y muestra evidencia de relación existente entre el spread observado de los CDS de la república de Colombia y el índice accionario COLCAP. Seguidamente se enfoca en el valor en riesgo (VaR, por sus siglas en inglés) condicional de estos CDS en períodos antes y durante la crisis crediticia, y se encuentra que estimados de VaR bajo el supuesto de distribución normal no es adecuado en el análisis de mercado de CDS.
Clasificación JEL: C13, G12, G32.
Palabras clave: contrato de seguro contra la cesación de pago, valor en riesgo, teoría del valor extremo, índices accionarios.
The main driver as a result of the recent financial crisis studies is the CDS behavior. Thus, we study the relationship between CDS and stock indices in countries like Greece, Spain and Italy due to the recent financial turmoil. Secondly, we analyze and show evidence on the link between deal spread on CDS of Republic of Colombia and COLCAP stock index. Then we focus on conditional VaR of these CDS before and during the credit crisis. We found that VaR estimates based on normal distribution assumption fails on CDS market analysis.
JEL classification: C13, G12, G32.
Keywords: CDS, VaR, EVT, stock indices.
Um indicador da crise financeira tem sido o comportamento dos contratos de seguros contra a suspensão de pagos (CDS, por suas siglas em inglês). Desta forma, o artigo toma em primeiro lugar o caso da Grécia, Itália e Espanha e seus respectivos índices acionários. Em segundo lugar analisa e oferece evidência da relação existente entre o spread observado nos CDS da república da Colômbia e o índice acionário COLCAP. Seguidamente focaliza no valor em risco (VaR, por suas siglas em inglês) condicional deste CDS em períodos antes e durante a crise creditícia, e conclui que as estimações de VaR sob o suposto de distribuição normal não são adequadas na análise de mercado de CDS.
Classificação JEL: C13, G12, G32.
Palavras chave: contrato de seguro contra a suspensão de pagos, valor em risco, teoria do valor extremo, índices acionários.
I. INTRODUCCIÓN
Un seguro contra la cesación de pagos (CDS, por sus siglas en inglés) protege al tenedor del CDS cuando se incumple el pago de un bono. Por tanto, el tenedor recibe un pago por parte del vendedor del seguro (quien recibe una prima durante la vida del bono) cuando ocurre el incumplimiento. Pero no es necesario poseer los bonos para comprar estos seguros, volviéndose así una estrategia especulativa, además de ser una estrategia de cobertura para el que posee el bono.
Se ha criticado el uso de los CDS en la crisis financiera del 2008 por la caída de Lehman Brothers y Bear Stearns en ese año, puesto que se cree que los inversores usaron combinación de CDS y venta en corto para provocar su caída. En el 2010, se critica su uso por provocar pánico en los mercados europeos por la reciente crisis de deuda, que afrontan algunos países de la zona euro, al apostar un incumplimiento de sus obligaciones por algunos países europeos.
También se critica la interpretación de los spreads de los CDS como un indicador de probabilidad de incumplimiento. Debido a las inconsistencias que se presentan cuando se comparan los spreads de CDS de países con los de compañías establecidas en el mismo país, además cuando se compara estos spreads y sus calificaciones crediticias. A pesar de estas críticas, también se observa algunas propuestas de medir riesgo/país por medio de los spreads de los CDS, en lugar de usar el tradicional indicador EMBI. Se propone como futura investigación analizar si los spreads de los CDS funcionan bien como un indicador de probabilidad de incumplimiento y a qué se debe estas inconsistencias.
En Colombia ya se ha realizado un estudio de los CDS, pero en el caso de valoración de estos instrumentos mediante una aproximación Monte Carlo, aplicado a bonos corporativos (Arbeláez y Maya, 2008). En el conocimiento de los autores, este es el primer trabajo que analiza los spreads de los CDS del gobierno colombiano y su relación con el índice accionario COLCAP. En primer lugar, el artículo investiga la relación existente entre la evolución de los mercados de los CDS y el mercado accionario. Para ello, se realiza una descripción de la relación entre la reciente crisis de deuda pública en países europeos con la evolución de los CDS soberanos de algunos de estos países. Al observar una relación inversa entre los spreads de los CDS soberanos y los índices accionarios de los países europeos, se plantea un modelo de regresión con datos de Colombia. El resultado es que sí existe una relación negativa entre los spreads de los CDS de Colombia y el índice accionario escogido, COLCAP. Por último, se investiga el riesgo de poseer CDS soberanos de la república de Colombia. Se observa cómo en el período de crisis hipotecaria, estos spreads aumentaron y se muestra que el supuesto de normalidad falla en el mercado de derivados de crédito.
De esta forma, el artículo se divide de la siguiente manera: la sección primera corresponde a la introducción. La segunda resume la reciente crisis de deuda de algunos países europeos y su relación con los CDS. La sección tercera presenta los resultados de una regresión para hallar posible relación entre los spreads de los CDS de Colombia y su índice accionario. La cuarta muestra el cálculo de VaR condicional de las variaciones de los spreads de CDS de Colombia bajo varios métodos, y finalmente, la quinta concluye.
II. Crisis de deuda pública y CDS
Recientemente se habla de la crisis en Grecia y cómo ha afectado el valor de los spreads en los CDS soberanos de este país. Los problemas realmente comienzan en el 2001 cuando Grecia hizo uso de derivados denominados cross-currency swaps con Goldman Sachs para reducir su deuda. Estos derivados son utilizados para transferir activos o pasivos de una moneda a otra. Grecia lo utilizó para intercambiar deuda en dólares y yenes a euros. Debido a que esta fue una operación con monedas, Grecia no tuvo que divulgar la obligación adicional. Pero la tasa de cambio usada en la operación permitió que Grecia reportara una reducción en su deuda, puesto que la tasa empleada no fue la del mercado, sino una en la que el euro era más fuerte. De esta forma, el uso de estos derivados se convirtió en una manera de pedir prestado dinero sin ser clasificado como deuda (Risk, marzo 2010a). Italia siguió unas operaciones similares y están descritas en Piga (2001). En su artículo, Piga critica el uso de derivados para disfrazar el déficit presupuestario y propone procedimientos contables apropiados para eliminar el efecto de tales operaciones, debido a que en la fecha que se realizaron estas operaciones, no era prohibido por las normas contables europeas. Uno de los últimos casos conocidos es el de la ciudad de Riga (Letonia) en el 2005, que después de haberle sido negado un préstamo para construir un puente, acudió al Deutsche Bank para una financiación. La solución incluyó una combinación de derivados en divisas y CDS, sin reportar esta financiación en las cuentas nacionales del país. En el 2007, Eurostat, la Oficina de Estadísticas de la Unión Europea, obligó a Letonia incluir esta transacción como un préstamo. En resumen, lo que se observa es el uso de derivados para beneficiarse de una reducción de costos de préstamos en los períodos iniciales, o para obtener grandes sumas de dinero sin ser registradas como obligaciones, pero tienen que ser pagadas en el futuro.
Las consecuencias se sintieron en los mercados de los CDS y accionarios. En febrero 4 de 2010, los temores de los problemas fiscales de Grecia y de su posible contagio a otros países europeos, provocaron una caída en los principales índices accionarios. Los índices IBEX 35 (Madrid) y PSI-20 (Lisboa) cayeron ese día 5,9% y 5%, respectivamente. El euro cayó más de 1% frente al dólar. El alza de los spreads de los CDS genera miedo en los inversores de acciones y bonos, y por tal razón, los mercados globales se ven afectados. En el Gráfico 1 se aprecia la relación entre los spreads de CDS a cinco años de Grecia y el índice accionario griego ASE (Athex Stock Exchange).
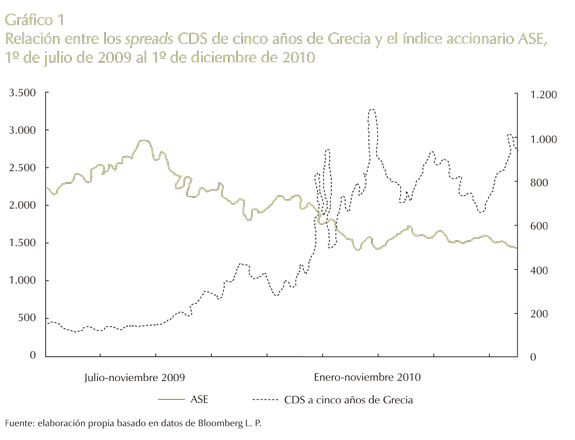
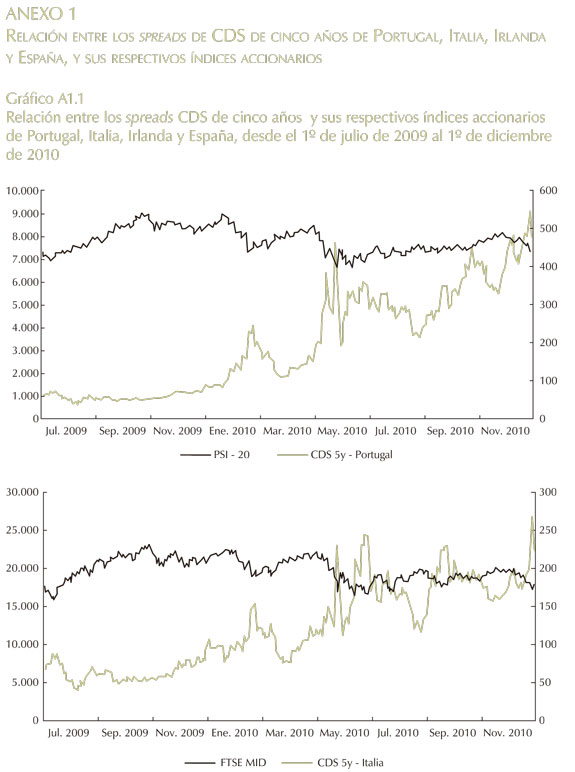
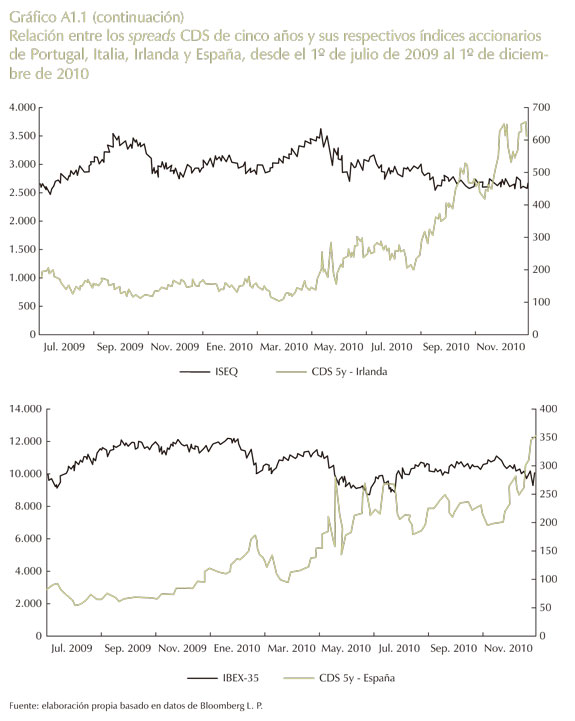
En el Anexo 1 se puede encontrar la relación de los otros cuatro países que conforman el denominado Piigs (Portugal, Italia, Irlanda, Grecia y España por sus siglas en inglés).
En mayo 20 y 21 de 2010, el costo de los CDS de cinco años de la zona euro estuvo relativamente alto comparado con semanas anteriores, debido a un período de volatilidad en los CDS y otros mercados. El índice de volatilidad de activos Vix, un índice calculado por el Chicago Board Option Exchange de la volatilidad implícita de las opciones del S&P500, se ubicó en 45,79, lo más alto después de marzo de 2009. Para mayo 25, estos spreads de los países Piigs incrementaron significativamente. Los de Portugal cerraron en 334, puntos básicos (p.b.), Irlanda en 254,9 p.b., Italia en 207,4 p.b., Grecia en 704,7 p.b. y España en 239,6 p.b., de acuerdo con Bloomberg. Mientras algunos ministros de finanzas de la zona euro exigen más regulación a los mercados de CDS soberanos, los participantes de estos mercados se defienden diciendo que los CDS soberanos han ayudado a esclarecer los problemas fiscales existentes y volverlos más transparentes, además de tener una idea más clara del riesgo soberano. Sin embargo, se podría cuestionar si los spreads de los CDS miden probabilidad de incumplimiento. Por ejemplo, en febrero 5 de 2010, el spread de los CDS del Reino Unido era de 82 p.b. y la de BP era de 46 p.b. Si los spreads de los CDS realmente reflejan probabilidad de incumplimiento, quiere decir que el Reino Unido tiene más probabilidad de incumplimiento que BP. Además, estos spreads de CDS no son consistentes con los fundamentales económicos, puesto que el Reino Unido es calificado AAA, mientras que BP es calificado AA+ por Fitch Rating. Este ejemplo muestra que los spreads pueden verse afectados por factores como liquidez, volatilidad y tasa esperada de recuperación, que finalmente influyen en la valoración de los CDS, más que reflejar enteramente una probabilidad de incumplimiento. Pero estos factores no explicarían la diferencia de 36 p.b. entre los spreads de los CDS del Reino Unido y BP. Para Damiano Brigo (Risk, marzo 2010b), la razón es que los CDS no miden probabilidades reales de incumplimiento, sino que expresan probabilidades de incumplimiento bajo la medida de valoración; esto es, los spreads incorporan una prima al riesgo ocasionado por percepción de los inversores, más que en fundamentales económicos.
Cecchetti, Mohanty y Zampolli (2010) proyectan razones de deuda/PIB alrededor de 200% en el Reino Unido, 150% en Bélgica, Francia, Irlanda, Grecia, Italia y Estados Unidos para el 2020. Estas cifras no son tan irreales, si se observan las publicadas por la Organización para la Cooperación y el Desarrollo Económico (OCDE), donde se muestra que la deuda total del sector público de países industrializados excederá el 100% del PIB en el 2011. Los autores también observan que los niveles elevados de deuda pública conllevan el riesgo de reducir acumulación de capital, crecimiento de la productividad y el crecimiento potencial a largo plazo. Debido a esto, la siguiente sección analiza la relación entre spreads de CDS y un índice accionario, pero en Colombia.
III. RELACIÓN ENTRE CDS Y EL ÍNDICE ACCIONARIO COLOMBIANO
Esta sección aunque no pretende realizar una aplicación de determinantes de los spreads de los CDS, sí realiza una revisión no exhaustiva de la literatura en este aspecto, para luego analizar la relación entre el índice accionario y los spreads de los CDS en Colombia. En el período de la crisis financiera (18 de julio de 2007 al 1º de junio de 2010), el promedio de los spreads de los CDS de la república de Colombia fue de 204,87 puntos básicos; esto quiere decir, que cubrir un millón de dólares de los títulos del gobierno, costaba en promedio 20.487 dólares. Mientras que en el período de precrisis (1º de octubre de 2004 al 17 de julio de 2007), dicho promedio fue de 201,12 puntos básicos, lo que indica que sí hubo un incremento en la percepción de riesgo, y Colombia no fue ajena a la crisis financiera internacional. Según el Depositary Trust and Clearing Corporation, el mercado de CDS corresponde entre 33 y 47 billones de dólares, de los cuales aproximadamente 1,5 billones están relacionados a gobiernos. De estos 1,5 billones, el valor nocional de los CDS de la república de Colombia corresponde alrededor del 2%, es decir, unos 30,5 mil millones de dólares a finales del 2008.
Ericsson, Jacobs y Oviedo (2009) investigan la relación entre los determinantes teóricos de riesgo de incumplimiento y los spreads reales. Los determinantes son el apalancamiento de la firma, la volatilidad de los activos subyacentes y la tasa libre de riesgo. Estas variables explicativas se toman del artículo de Collin-Dufresne, Goidsiein y Martin (2001). Ericsson et al. (2009) encuentran que estas variables son estadísticamente significativas y que su efecto es económicamente importante. Otros artículos similares a este trabajo se pueden encontrar en la sección de introducción del mismo.
Greatrex (2009) usa cambios mensuales en spreads de CDS para 333 firmas entre enero de 2001 y marzo de 2006, y encuentra que las variables apalancamiento de la firma, volatilidad del mercado, clima de negocios (medido como retornos de mercado accionario y un índice basado en calificación de los spreads de CDS) y tasas de interés, explican el 35% de la variación en los cambios de los spreads. Las variables más importantes son apalancamiento y volatilidad, puesto que explican casi la mitad de la variación (del 35%) en estos cambios.
Alexander y Kaeck (2008) investigan la influencia de los determinantes teóricos de spreads de CDS, como tasas de interés, retornos de acciones y volatilidad implícita, a cambios diarios en los índices iTraxx Europe, y encuentran que estos determinantes tienen efectos significativos de los spreads de los CDS. Sin embargo, solo entre el 20% y el 30% de la variación en los spreads puede ser explicado por estas variables. La única variable que no tiene relativa significancia en su estudio es la pendiente de la curva de rendimientos.
Realdon (2008) presenta un modelo para valorar CDS y lo prueba en compañías como Ford, Telefónica, Volkswagen, Bayer y British Airways. Su modelo depende solo del precio de la acción de cada firma. El autor encuentra que en la mayoría de las compañías analizadas (excepto Telefónica), el modelo puede explicar por lo menos un 63% de la variación de las tasas de los CDS.
Fung, Sierra, Yau y Zhang (2008) investigan la relación entre los mercados accionarios y de CDS, y encuentran que el mercado accionario parece influir en los mercados de CDS con alto rendimiento, y que estos pueden contener ciertos componentes de riesgo de incumplimiento de las firmas, que no podrían estar implícitos en los retornos de las acciones. Esta relación sugiere que los inversores estén mirando de cerca ambos mercados para tenerlos en cuenta en sus decisiones de inversión.
Abid y Naifar (2006) usan como variable dependiente precios de CDS y como variables explicativas la calificación crediticia, madurez del contrato, tasa libre de riesgo, pendiente de la curva de rendimientos y volatilidad de las acciones. Estos autores encuentran que las variables mencionadas explican más del 60% del nivel total de los CDS. En su estudio, la variable más importante es la calificación crediticia.
Sin duda, el trabajo inicial que inspira todos estos artículos es el realizado por Merton (1974), puesto que en su trabajo expone que la probabilidad de incumplimiento de un pago de una entidad está directamente relacionada con el mercado accionario y la volatilidad de los retornos de las acciones de la entidad. Por tal razón, se espera una relación negativa entre los spreads de los CDS y los precios de acciones. Pero ¿se puede extender este resultado a países emergentes? El apéndice de Chan-Lau y Kim (2004) muestra cómo esta teoría se puede aplicar al caso de bonos soberanos en este tipo de economías, y es, precisamente, lo que se quiere estudiar en este artículo para el caso colombiano.
En el Gráfico 2 se muestra la relación entre el COLCAP y los spreads de los CDS en Colombia.
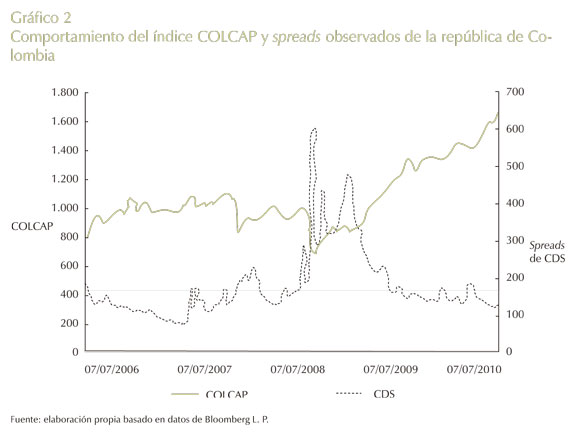
En cuanto al COLCAP, se observa un mínimo de 686,64 puntos, el 27 de octubre de 2008 (con respecto al gráfico). Antes de la fecha, se observaba que los mercados accionarios a escala mundial habían tenido importantes caídas. Debido, principalmente, a expectativas de menores crecimientos en el campo mundial y aumento en las tasas de interés. El mercado accionario de Estados Unidos cerró a la baja en medio de altas variaciones, según informe de Corficolombiana. Mientras que el índice brasilero BOVESPA cayó por debajo de los 30.000 puntos por primera vez en tres años. De esta manera, el índice de mercados emergentes MSCI cayó 4,4% ese día, de acuerdo con Bloomberg.
El modelo de regresión de este artículo está basado inicialmente en Byström (2005), quien evidencia relación entre el iTraxx (de siete índices sectoriales) y el mercado accionario. El autor encuentra que la volatilidad del precio de las acciones está significativamente correlacionada con los spreads de los CDS, y también encuentra autocorrelación positiva de manera significativa en el mercado del iTraxx. Además, se agregaron otras variables explicativas de acuerdo con la revisión de la literatura. El modelo empírico está dado por:
Donde:
rCDSt : es el logretorno diario de la serie de los spreads observados de los CDS de la república de Colombia en el período t.rCDSt - 1 : es el logretorno diario de la serie de los spreads observados de los CDS de la república de Colombia en el período t - 1.
rCOLCAPt : es el logretorno diario de la serie del índice accionario de Colombia, COLCAP, en el período t.
rCOLCAPt - 1 : es el logretorno diario de la serie del índice accionario de Colombia, COLCAP, en el período t - 1.
SLOPE1t : es la pendiente calculada como la diferencia entre el rendimiento de los bonos TES septiembres del 14 y el de los TES noviembres del 10, en el período t.
SLOPE2t : es la pendiente calculada como la diferencia entre el rendimiento de los bonos TES julios del 20 y el de los TES noviembres del 10, en el período t.
rYIELDt: es el logretorno diario de la serie de los rendimientos de los bonos TES de julios del 20, en el período t.
βi: son los coeficientes de la regresión. Con i = 0, 1, 2, 3, 4, 5 y 6.
et: son los errores de la regresión.
La razón de no incluir la tasa libre de riesgo, es que los CDS son exposiciones crediticias puras sin riesgo de tasa de interés (Byström, 2005).
A. RESULTADOS DE LA REGRESIÓN
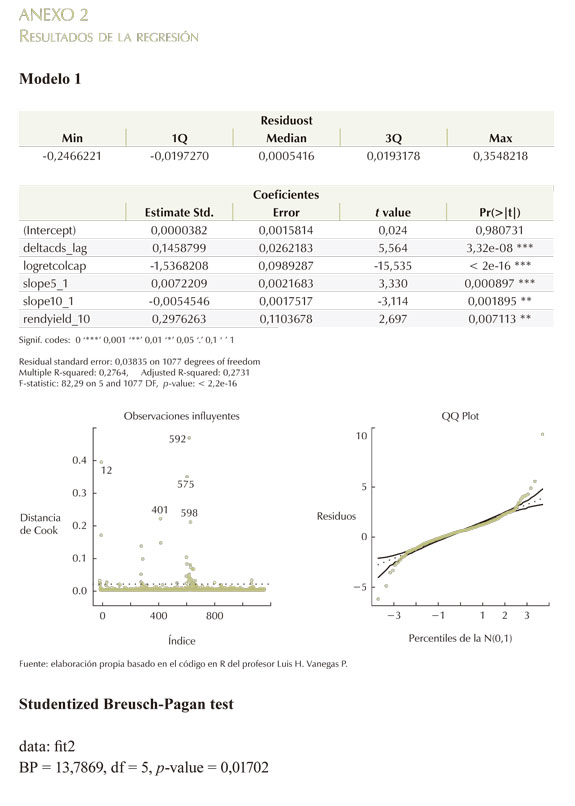
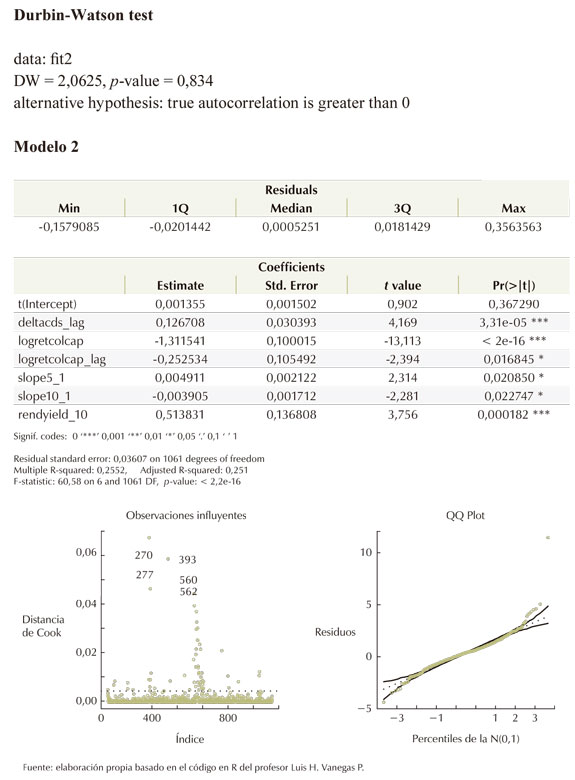
El modelo inicial (Modelo 1), en general, es significativo y cada una de las variables también lo es, excepto la del logretorno del COLCAP rezagado en un día. Sin embargo, al remover algunas de las observaciones influyentes, un segundo modelo (Modelo 2) muestra que esta variable sí es significativa. El R2 de este modelo empírico es de 25,5% (véase Anexo 2). Este resultado es similar al encontrado por Byström (2005). En su estudio, el R2 en la mayoría de los sectores está entre 10% y 20%. Entonces, el 25,5% de la variación en los cambios de los spreads de los CDS de Colombia son explicados por los cambios en las variables explicativas de (1). El supuesto de la varianza constante de los residuales se cumple en el Modelo 2, a diferencia del Modelo 1. El supuesto de no autocorrelación se cumple en los dos modelos; sin embargo, el supuesto de normalidad de los errores no. Una posible solución a este tipo de problemas es usar el método de regresión robusta. Los estimados de este modelo no son tan sensibles en la presencia de datos influyentes (Fox, 2002). El método más común en regresión robusta es la estimación-M, desarrollada por Huber (1964) y es la que se utiliza en este artículo. A continuación se presenta la comparación de los estimados de los parámetros de la regresión mediante el método de mínimos cuadrados ordinarios y la regresión robusta:Cuadro 1
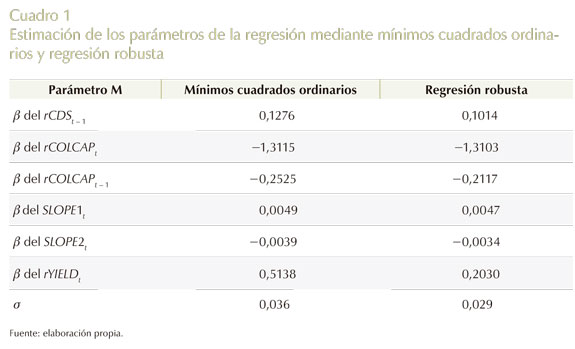
Como era de esperarse, se observa una relación negativa (significativa) entre los cambios de los spreads de los CDS y los logretornos del COLCAP en el período t y t − 1. Esto quiere decir que el índice COLCAP es una variable que sirve para explicar y anticipar el signo de las variaciones de los spreads de los CDS de la república de Colombia. También se encuentra una posible autocorrelación positiva de primer orden en los cambios de los spreads de los CDS, puesto que la variable es altamente significativa. Esto se observa en el Gráfico 5, más adelante (correlograma de los cambios en los spreads), y usado para ajustar la serie de tiempo de los spreads a un modelo ARMA-GARCH. La variación en los cambios de los spreads de los CDS en un día dada una variación en una unidad de estos cambios del día anterior, es menor al encontrado en la mayoría de los casos por Byström (2005). El coeficiente estimado del parámetro de regresión para esta variable es de 0,10, a diferencia del estudio de Byström (2005) quien encuentra un rango entre 0,19 y 0,28 para la mayoría de los sectores. Esta información sería útil para los inversores, ya sea que se utilice con fines especulativos o de cobertura; sin embargo, el R2 es apenas el 25%.
Los fondos de cobertura (hedge funds) han implementado recientemente una estrategia denominada arbitraje de estructura de capital, la cual está basada en el modelo estructural de Merton. La idea es comparar los spreads de los CDS del mercado con el modelo teórico, que está en función del valor de las acciones. Si el valor observado de los CDS es más alto de lo esperado, según el modelo, y si el inversor cree que el mercado accionario es correcto, puede vender protección de crédito. De otra manera, puede vender el índice de las acciones si cree que el valor del CDS es correcto. Usualmente, no es tan seguro cuál de los mercados es el correcto. Por tanto, la estrategia consiste en vender protección de crédito y vender el índice accionario, de tal manera que una de las posiciones cubrirá las pérdidas de la otra en cualquier condición del mercado (Yu, 2006). Para este caso, el valor estimado (del modelo) del spread de los CDS puede estar dado por el modelo de regresión.
Aunque en este tipo de relaciones no es tan claro cuál es la variable endógena, se realiza una prueba de causalidad de Granger (véase Anexo 3), la cual muestra que la relación planteada es la adecuada. Si la relación de causalidad hubiese sido al contrario, es decir, que los retornos del COLCAP son explicados por las variaciones de los spreads de los CDS, se podría afirmar que el mercado accionario colombiano es ineficiente, puesto que el precio del índice reacciona a la información pública disponible. Para soportar la hipótesis de que la relación planteada es la adecuada, la teoría financiera dice que el riesgo crediticio afecta los precios de los bonos y de las acciones. Al observar una caída en los precios de estos títulos, los inversores demandan por protección en contra de un potencial incumplimiento de las entidades referentes, causando así un incremento en el precio de los CDS. Además, el mercado accionario tiene la ventaja de incorporar información de condiciones macroeconómicas más rápidamente (Chan, Fung y Zhang, 2009) que otros mercados.
A continuación se realiza otra comparación de los CDS colombianos, pero desde el punto de vista del riesgo. La siguiente sección muestra cómo la crisis financiera afectó los CDS de Colombia, y cómo nuevamente el supuesto de la distribución normal falla en el análisis financiero, en este caso en el mercado de los CDS.
IV. MEDIDA DE VaR DE LOS CDS DE LA REPÚBLICA DE COLOMBIA
Esta sección se enfoca en el cálculo del VaR condicional para los CDS de la república de Colombia. Desde la publicación del artículo de McNeil y Frey (2000), se han realizado varias investigaciones internacionales y nacionales aplicando la combinación de modelos GARCH, para estimar la volatilidad junto con la teoría del valor extremo (EVT, por sus siglas en inglés), y así calcular el VaR condicional a diferentes series financieras. Quizá la publicación de mayor impacto en nuestro país es el elaborado por Melo y Becerra (2006), quienes aplican modelos ARMA-GARCH y ARMA-GARCH-EVT para estimar medidas de riesgo condicionales a variaciones diarias de la tasa interbancaria. Lo novedoso en el presente artículo, es el uso de innovaciones distribuidas mediante una t-asimétrica en los modelos GARCH, aplicados a las variaciones diarias de la serie de los spreads observados de los CDS, y este se compara mediante backtesting con los modelos más empleados en este tipo de investigaciones.
Una aplicación de estas herramientas a CDS, es el trabajo de Byström (2010) para analizar su relación con la reciente crisis crediticia. El autor utiliza uno de los diferentes índices del iTraxx de cinco años; una de las razones por la cual en este artículo, también se usa el plazo de cinco años para examinar los CDS de Colombia. El índice utilizado por Byström es el iTraxx Europe index, que recopila 125 CDS referenciado a 125 compañías con grado de inversión.
Para realizar el análisis, se toman datos de Bloomberg de spreads observados de CDS de la república de Colombia entre el 1º de octubre de 2004 y el 1º de junio de 2010, para un total de 1.463 datos. Así como en Byström, para el backtesting se define el período de crisis entre el 18 de julio de 2007 y el 1º de junio de 2010, y el período de precrisis entre el 1º de octubre de 2004 y el 17 de julio de 2007. La razón de haber tomado el 18 de julio de 2007 como comienzo de la crisis financiera, se debe a que en ese día Bear Stearns anunció cuantiosas pérdidas en sus dos fondos de cobertura. El comportamiento de los spreads de los CDS y de sus variaciones se muestra en el Gráfico 3.
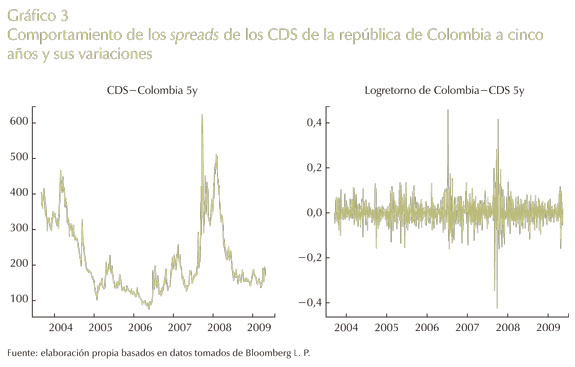
La estadística descriptiva de las variaciones de los spreads de los CDS se muestra en el Cuadro 2.
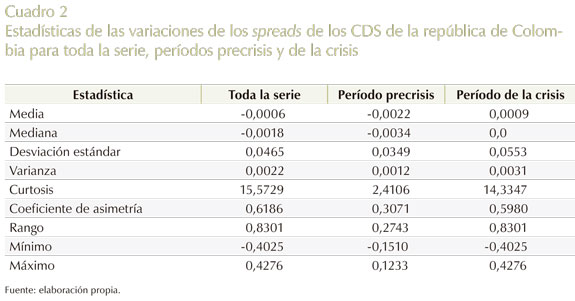
La volatilidad diaria de las variaciones de los spreads de los CDS es mayor en el período de crisis (5,53%) que en el período de precrisis (3,49%). En los períodos de crisis y precrisis, el coeficiente de asimetría es positivo pero mayor en el período de la crisis; lo que muestra mayor probabilidad de obtener variaciones de los spreads más bajos durante este período. Debido a que las distribuciones de pérdidas en riesgo crediticio a menudo no son simétricas y presentan colas pesadas (véanse, por ejemplo, Ramaswamy, 2004; McNeil, Frey y Embrechts, 2005, y Saunders y Allen, 2002), modelos de VaR basados en normalidad, incluso t, fallan en modelar correctamente la cola izquierda y derecha de las distribuciones de pérdida. Para brindar una posible solución a este problema, se introduce la distribución t-asimétrica como se verá más adelante.
El valor de curtosis es más grande durante el período de crisis (14,33), lo que evidencia una distribución de las variaciones en los spreads con colas más pesadas que en el período de precrisis (en este período, la curtosis es de 2,41), y lejos de ser una distribución normal. El Gráfico 4 muestra los cuantiles para toda la serie.
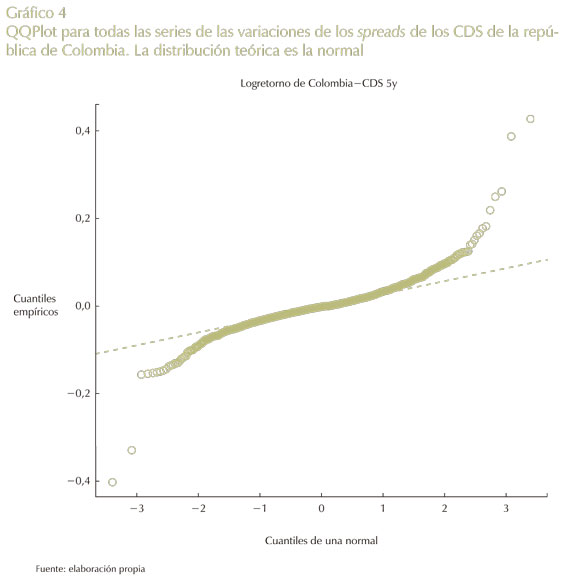
Para este caso, solo se muestra el gráfico de cuantiles para toda la serie de las variaciones de los spreads de los CDS.
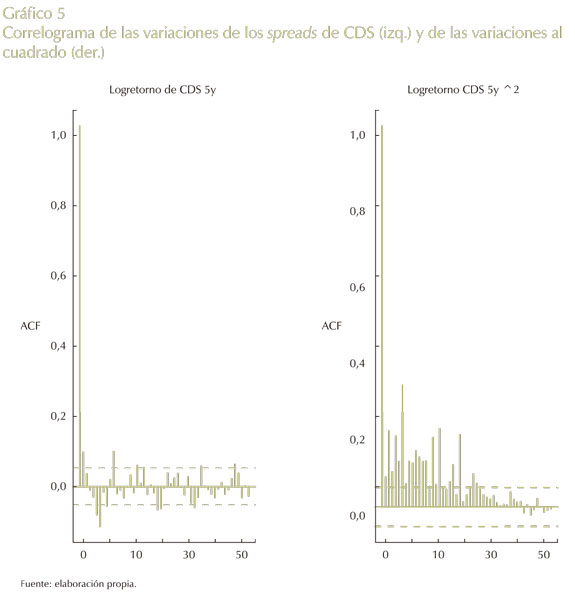
En el Gráfico 5 se presenta el correlograma de las variaciones y variaciones elevadas al cuadrado de los spreads de los CDS. Las variaciones al cuadrado pueden usarse como una aproximación de la varianza de los logretornos de los spreads de los CDS.
Como se observa en el Gráfico 5, se podría utilizar un método autorregresivo para modelar la media de las variaciones y un modelo GARCH para la varianza de estas variaciones.
A. MÉTODOS
Para estimar VaR condicional, se asume que el proceso de variaciones positivas y negativas de los spreads de los CDS es un proceso estacionario y es de la forma Xt = μt + σtZt, y se asume que μt y σt son medibles con respecto a la información disponible del proceso en el tiempo t - 1. Zt son las innovaciones independientes e idénticamente distribuidas (i.i.d.) que siguen una distribución G, con media cero y varianza uno. De esta manera, para estimar VaR condicional se usa la siguiente relación:

Donde Z es una variable aleatoria con distribución G. Para estimar la media y volatilidad condicional μt + 1 y σt + 1, se emplea un proceso ARMA (1,1) con errores GARCH (1,1). También se requiere estimar el cuantil qα(Z), que en el caso de innovaciones distribuidas normal es igual a Φ- 1(α), donde F es la función de distribución de una normal estándar. De otra manera, qα(Z) dependerá de la distribución de las innovaciones que se estén asumiendo. En este documento también se usan innovaciones que se distribuyen mediante t y la t-asimétrica. Para la distribución t,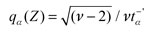 donde t es la función de distribución de una t con ν grados de libertad. Se introduce el factor
donde t es la función de distribución de una t con ν grados de libertad. Se introduce el factor 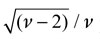 para que la distribución tenga varianza igual a uno, puesto que la varianza de una t es igual a v/(v - 2). Hansen (1994) propuso la distribución t-asimétrica, al introducir una generalización de la distribución t y manteniendo el supuesto de media cero y varianza igual a uno. Giot y Laurent (2003) usan modelos GARCH con innovaciones distribuidas t-asimétrica, y encuentran que las medidas de VaR se desempeñan mejor con este tipo de distribución que asumiendo la distribución t. Lambert y Laurent (2001) también utilizan modelos GARCH con innovaciones t-asimétrica aplicados a NASDAQ. Estos últimos autores emplean el enfoque de la t-asimétrica propuesto por Fernández y Steel (1998), y es la que se usa en este documento. La función de distribución obtenida por Fernández y Steel (1998), está directamente relacionada con la obtenida por Hansen (1994), y está dada por:
para que la distribución tenga varianza igual a uno, puesto que la varianza de una t es igual a v/(v - 2). Hansen (1994) propuso la distribución t-asimétrica, al introducir una generalización de la distribución t y manteniendo el supuesto de media cero y varianza igual a uno. Giot y Laurent (2003) usan modelos GARCH con innovaciones distribuidas t-asimétrica, y encuentran que las medidas de VaR se desempeñan mejor con este tipo de distribución que asumiendo la distribución t. Lambert y Laurent (2001) también utilizan modelos GARCH con innovaciones t-asimétrica aplicados a NASDAQ. Estos últimos autores emplean el enfoque de la t-asimétrica propuesto por Fernández y Steel (1998), y es la que se usa en este documento. La función de distribución obtenida por Fernández y Steel (1998), está directamente relacionada con la obtenida por Hansen (1994), y está dada por:

Donde γ es el parámetro de forma que describe el grado de asimetría y f(x) es la función de densidad de una t. De esta forma qα(Z) = sst-1a donde sst representa la función de distribución de una t-asimétrica estandarizada.
Para el método ARMA-GARCH-EVT, se usa el procedimiento de dos pasos propuesto por McNeil y Frey (2000):
1) Se ajusta el modelo ARMA (1,1)-GARCH (1,1) mediante el enfoque de cuasi-máxima verosimilitud, con el cual no se asume una distribución G específica para las innovaciones, y se estiman μt + 1 y σt + 1 usando el modelo ajustado.
2) En este paso se usan los residuos estandarizados del modelo, los cuales se asumen ser i.i.d., y se usa el método picos sobre el umbral (POT, por sus siglas en inglés), con un umbral del 10% de la cola de la distribución de los datos para estimar el cuantil al nivel α. De esta manera, qα(Z) está dado por:

Donde u es el umbral escogido (o estimado), β y ξ son los parámetros de escala y de forma de una distribución generalizada de Pareto (GPD, por sus siglas en inglés), Nu es la cantidad de datos que exceden el umbral y n el total de datos de la muestra (residuos estandarizados en este caso). Por tanto, Nu /n es un estimador empírico de la cola de los datos que han superado un umbral u. Para más detalles del método POT, véanse Smith (1989), Davison y Smith (1990) y Leadbetter (1991). Teoría y aplicaciones más recientes en finanzas se pueden encontrar en los textos de Embrechts, Klüppelberg y Mikosch (1997), McNeil et al. (2005), Coles (2001) y Reiss y Thomas (1997).
El punto de Aquiles de la teoría del valor extremo es, precisamente, la selección del umbral. Escoger un valor de umbral conlleva a un tradeoff entre sesgo y varianza en la estimación de los parámetros, en especial el parámetro de forma ξ de la distribución GPD. Existen varios métodos para tratar de estimar este parámetro, desde gráficos hasta técnicas de remuestreo; sin embargo, en la actualidad no existe un método óptimo para la selección del umbral. Estudios empíricos han mostrado que una buena aproximación para escoger el umbral, es utilizar el 5% o el 10% de los datos de la cola de la distribución. En este documento se utiliza el 10%, así como en McNeil y Frey (2000).
B. MODELO ARMA-GARCH
El modelo ARMA (1,1)-GARCH (1,1) es de la siguiente forma:
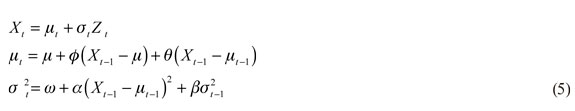
Y los parámetros son estimados mediante máxima verosimilitud utilizando el paquete R. Más detalles de modelos ARMA y GARCH en aplicaciones a la administración del riesgo se pueden encontrar en el capítulo 4 y sección 7.2.6 de McNeil et al. (2005), y capítulos 4 y 8 de Jondeau, Poon y Rockinger (2007).
C. BACKTESTING
Se realiza el backtesting de los cuatro métodos a tres casos: período precrisis, período de crisis y período total. Para hacer el backtesting de la serie histórica x1, …, xm se calcula el VaRαt en los t días del siguiente conjunto: T = {n + 1, …, m }, usando una ventana de n días que varía según el período (si es precrisis, crisis o total).
Luego se compara el VaR estimado con el valor realizado (observado) a dos niveles de confiabilidad: 95% y 99%. Por tanto, cuando se estima el VaR al 95% (99%), se espera que en el 5% (1%) de los días de backtesting las variaciones (positivas y negativas) de los spreads de los CDS hayan superado el nivel del VaR. A estos valores se les denomina comúnmente violaciones o excepciones.
Sea la función indicadora de violaciones It igual a:

Esto quiere decir, que cada vez que haya una violación (xt + 1 > VaRαt), la función toma el valor de 1, de lo contrario el valor de cero. Si el método funciona bien, se espera que la función indicadora de violaciones se comporte como realizaciones de ensayos i.i.d. Bernoulli con probabilidad de éxito 1 - α; por tanto, se espera que 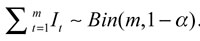 . Esto es, que la suma de m ensayos Bernoulli se distribuya binomial con parámetros m y 1 - α. Así, se realiza una prueba de hipótesis binomial de una cola, donde la hipótesis nula indica que el método utilizado estima correctamente el VaR condicional. La hipótesis alternativa sugiere que el método subestima o sobreestima el cálculo del VaR según sea el caso de número de violaciones esperadas. Un p-valor menor a 0,05 puede indicar evidencia de no aceptar la hipótesis nula. Otras pruebas de backtesting pueden encontrarse, por ejemplo, en Christoffersen (2003). En los siguientes cuadros se muestran las excepciones en cada caso y el p-valor para la prueba binomial.
. Esto es, que la suma de m ensayos Bernoulli se distribuya binomial con parámetros m y 1 - α. Así, se realiza una prueba de hipótesis binomial de una cola, donde la hipótesis nula indica que el método utilizado estima correctamente el VaR condicional. La hipótesis alternativa sugiere que el método subestima o sobreestima el cálculo del VaR según sea el caso de número de violaciones esperadas. Un p-valor menor a 0,05 puede indicar evidencia de no aceptar la hipótesis nula. Otras pruebas de backtesting pueden encontrarse, por ejemplo, en Christoffersen (2003). En los siguientes cuadros se muestran las excepciones en cada caso y el p-valor para la prueba binomial.
1. Backtesting - Precrisis
Se usa una ventana de 500 días (puesto que no se cuentan con más datos). En el período de precrisis, los días de backtesting comprenden desde el 21 de septiembre de 2006 hasta el 17 de julio de 2007, para un total de 211 días. Cuadro 3
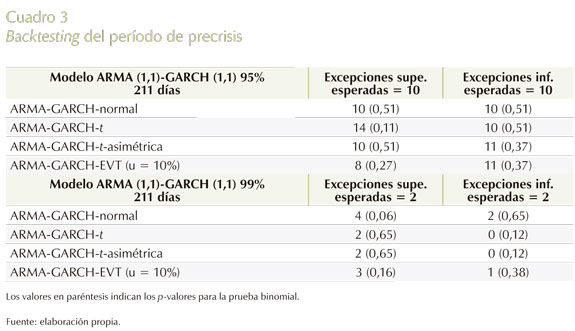
Se observa que en ninguno de los métodos se rechaza la hipótesis nula de que los métodos estiman correctamente el VaR al 95% y 99%.
2. Backtesting - Crisis
Para este caso se usa una ventana de 712 días. En el período de crisis, los días de backtesting comprenden desde el 18 de julio de 2007 hasta el 1º de junio de 2010, para un total de 749 días. Cuadro 4
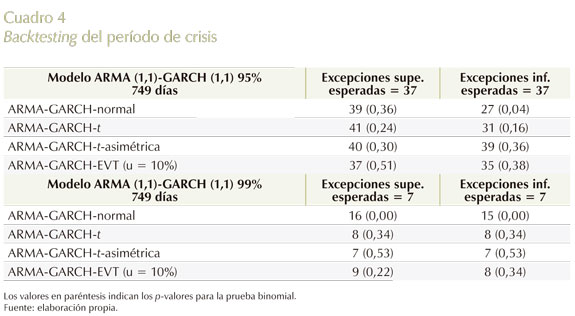
En este período cuando se estima VaR al 99%, el método basado en normalidad falla tanto en variaciones positivas como negativas de los spreads, y también cuando se estima VaR al 95% en las variaciones negativas.
3. Backtesting - Período total
Se usa una ventana de 500 días. El período total de los días de backtesting comprende desde el 21 de septiembre de 2006 hasta el 1º de junio de 2010, para un total de 960 días. Cuadro 5
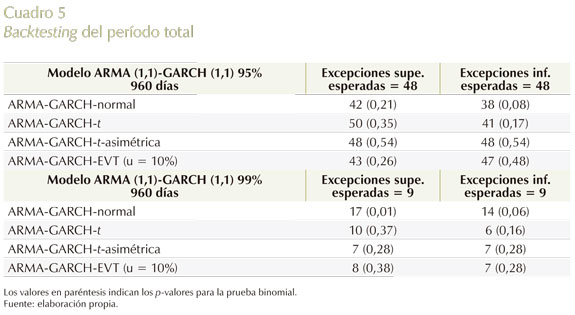
Para el total del período, el método basado en normalidad falla al estimar el VaR al 99% para variaciones positivas en los spreads. En general, el método basado en t-asimétrica se desempeña mejor que el método basado solo en t, recogiendo de mejor manera la asimetría presentada en las variaciones de los spreads de los CDS. Uno de los hechos estilizados de los activos financieros, es que estos presentan coeficiente de asimetría positivo. Esto sucede porque los retornos negativos extremos ocurren más frecuentemente que los positivos. En otras palabras, las malas noticias tienen un mayor efecto en las variaciones de los activos financieros que las buenas noticias. Lo anterior se observa en la estadística descriptiva de las variaciones de los spreads de los CDS (véase Cuadro 2), donde la volatilidad es mayor en el período de crisis (5,53%) que en el período de precrisis (3,49%). En retornos de índices accionarios, es común encontrar que una distribución simétrica con colas pesadas, como por ejemplo la distribución t, puede ajustarse bien. Esto sucede porque los factores de riesgo de un índice accionario son diversos, y dan como resultado este tipo de distribuciones; mientras que el único factor de riesgo de un CDS es el riesgo de incumplimiento. Sin embargo, para el mercado de CDS, pueden existir otras explicaciones aún no descubiertas para la forma de distribución de las variaciones en los spreads, como lo anota O'Neil (2010), y pueden originar futuras investigaciones. De esta manera, el método basado en t-asimétrica puede ser un complemento a modelos de volatilidad asimétrica como el TGARCH, EGARCH, entre otros, en el análisis de riesgo cuando se presentan eventos de cola.
V. CONCLUSIONES
Los seguros contra la cesación de pagos (CDS) son utilizados para cubrir el riesgo de un probable incumplimiento de un bono; sin embargo, muchos inversores lo utilizan como estrategia especulativa al apostar contra la entidad que emite el bono. spreads de CDS de países como Grecia, España, Portugal, Italia e Irlanda se han incrementado a principios del 2010, debido a los problemas de deuda que enfrentan estos países y su contagio. Este incremento ha afectado de manera negativa sus respectivos índices accionarios. Como futura investigación, se propone el análisis de los spreads de los CDS como indicador (o no) de probabilidad de incumplimiento.
Se encuentra una relación negativa y significativa entre las variaciones de los spreads de los CDS de la república de Colombia y el índice accionario COLCAP. También se observa que la variación en las variables independientes de la regresión explica el 25,5% de la variación de los cambios de los spreads de los CDS, resultado similar encontrado en otros estudios aplicados a diferentes mercados. Esta información sería útil para inversores en el mercado de CDS con fines de cobertura o de especulación (como la estrategia de arbitraje de estructura de capital); sin embargo, el R2 es apenas del 25,5%. Además, se presencia una correlación serial en la serie de las variaciones de los spreads CDS visto en la regresión y comprobada con la prueba de autocorrelación (véase Anexo 4).
Se estimó el VaR condicional al 95% y 99% de las variaciones positivas y negativas de los spreads de los CDS de Colombia, y se encontró que en el período de crisis, el método basado en normalidad falla al estimar el VaR al 99% y también VaR al 95% en variaciones negativas de los spreads. El método basado en normalidad tampoco funciona bien al estimar VaR al 99% en variaciones positivas de los spreads en el período total de análisis. En resumen, de los doce casos analizados, el método basado en normalidad falla en cuatro. Los demás métodos funcionan bien en todos los casos. De esta manera se concluye que el supuesto de distribución normal no es adecuado en el análisis de mercado de CDS.
REFERENCIAS
1. Abid, F.; Naifar, N. "The Determinants of Credit Default Swap Rates: An Explanatory Study", International Journal of Theoretical & Applied Finance, vol. 9, núm. 1, pp. 23-42, 2006. [ Links ]
2. Alexander, C.; Kaeck, A. "Regime Dependent Determinants of Credit Default Swap spreads", Journal of Banking & Finance, núm. 32, pp. 1008-1021, 2008. [ Links ]
3. Arbeláez, J. C.; Maya, C. "Valoración de Credit Default Swaps (CDS): una aproximación con el método Monte Carlo", Cuadernos de Administración, vol. 21, núm. 36, pp. 87-111, 2008. [ Links ]
4. Byström, H. N. E. "Credit Default Swaps and Equity Prices: The iTraxx CDS Index Market", Working Papers, núm. 24, Lund University, Department of Economics, 2005. [ Links ]
5. Byström, H. N. E. "The Age of Turbulence - Credit Derivatives Style", Working Paper, núm. 16, Lund University, Department of Economics, 2010. [ Links ]
6. Cecchetti, S. G.; Mohanty, M. S.; Zampolli, F. "The Future of Public Debt: Prospects and Implications", BIS Working Papers, núm. 300, Monetary and Economic Department, 2010. [ Links ]
7. Chan-Lau, J. A.; Kim, Y. S. "Equity Prices, Credit Default Swaps, and Bond spreads in Emerging Markets", Working Papers, International Monetary Fund, Washington, D. C., 2004. [ Links ]
8. Chan, K. C.; Fung, H.-G. G.; Zhang, G. "On the Relationship Between Asian Sovereign Credit Default Swap Markets and Equity Markets", Journal of Asian Business Studies, vol. 4, núm. 1, pp. 3-12, 2009. Available at SSRN: http://ssrn.com/abstract=1497538. [ Links ]
9. Christoffersen, P. Elements of Financial Risk Management, San Diego, CA: Academic Press, 2003. [ Links ]
10. Coles, S. An Introduction to Statistical Modeling of Extreme Values, London, Springer-Verlag, 2001. [ Links ]
11. Collin-Dufresne, P.; Goidsiein, R.; Martin, S. "The Determinanis of Credit spread Changes", Journal of Finance, núm. 56, pp. 2177-2207, 2001. [ Links ]
12. Davison, A. C.; Smith, R. L. "Models for Exceedances Over High Thresholds", Journal of the Royal Statistical Society Series B, núm. 52, pp. 393-442, 1990. [ Links ]
13. Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events for Insurance and Finance, Berlin, Springer, 1997. [ Links ]
14. Ericsson, J.; Jacobs, K.; Oviedo, R. "The Determinants of Credit Default Swap Premia", Journal of Financial & Quantitative Analysis, vol. 44, núm. 1, pp. 109-132, 2009. [ Links ]
15. Fernández, C.; Steel, M. F. J. "On Bayesian Modeling of Fat Tails and Skewness", Journal of the American Statistical Association, núm. 93, pp. 359-371, 1998. [ Links ]
16. Fox, J. An R and S-PLUS Companion to Applied Regression, Sage Publications, 2002. [ Links ]
17. Fung, H.-G.; Sierra, G. E.; Yau, J.; Zhang, G. "Are the U.S. Stock Market and Credit Default Swap Market Related? Evidence from the CDX Indices", Journal of Alternative Investments, vol. 11, núm. 1, pp. 43-61, 2008. [ Links ]
18. Giot, P.; Laurent, S. "Value-at-risk for Long and Short Trading Positions", Journal of Applied Econometrics, núm. 18, pp. 641-663, 2003. [ Links ]
19. Greatrex, C. A. "Credit Default Swap Market Determinants", Journal of Fixed Income, vol. 18, núm. 3, pp. 18-32, 2009. [ Links ]
20. Hansen, B. E. "Autoregressive Conditional Density Estimation", International Economic Review, núm. 35, pp. 705-730, 1994. [ Links ]
21. Huber, P. J. "Robust Estimation of a Location Parameter", Annals of Mathematical Statistics, núm. 35, pp. 73-101, 1964. [ Links ]
22. Jondeau, E.; Poon, S.-H.; Rockinger, M. Financial Modeling Under Non-Gaussian Distributions, London: Springer Verlag, 2007. [ Links ]
23. Lambert, P.; Laurent, S. "Modelling Financial Time Series Using GARCH-Type Models and a Skewed Student Density", Mimeo, Universite de Liège, 2001. [ Links ]
24. Leadbetter, M. R. "On a Basis for 'Peaks Over Thresholds' Modeling", Statistics & Probability Letters, vol. 12, núm. 4, pp. 357-362, 1991. [ Links ]
25. McNeil, A. J.; Frey, R. "Estimation of Tail-related Risk Measures for Heteroscedastic Financial Time Series: An Extreme Value Approach", Journal of Empirical Finance, núm. 7, pp. 271-300, 2000. [ Links ]
26. McNeil, A. J.; Frey, R.; Embrechts, P. Quantitative Risk Management: Concepts, Techniques and Tools, Pricenton, Princeton University Press, 2005. [ Links ]
27. Melo, L. F.; Becerra, O. R. Medidas de riesgo, características y técnicas de medición: una aplicación del VaR y el ES a la tasa interbancaria de Colombia, Bogotá, Centro Editorial Universidad del Rosario, 2006. [ Links ]
28. Merton, R. C. "On the Pricing of Corporate Debt: The Risk Structure of Interest Rates", Journal of Finance, núm. 29, pp. 449-470, 1974. [ Links ]
29. O'Neil, C. "Measuring CDS Value-at-Risk", RiskMetrics Working Papers, 2010. Recuperado de http://www.riskmetrics.com/docs/measuring-cds-var. [ Links ]
30. Piga, G. "Do Governments Use Financial Derivatives Appropriately? Evidence from Sovereign Borrowers in Developed Economies", International Finance, vol. 4, núm. 2, pp. 189-219, 2001. [ Links ]
31. Ramaswamy, S. Managing Credit Risk in Corporate Bond Portfolios: A Practioner's Guide, New Jersey: Wiley, 2004. [ Links ]
32. Realdon, M. "Credit Default Swap Rates and Stock Prices", Applied Financial Economics Letters, vol. 4, núm. 4, pp. 241-248, 2008. [ Links ]
33. Reiss, R.-D.; Thomas, M. Statistical Analysis of Extreme Values, Basel, Brikhäuser, 1997. [ Links ]
34. Risk. "Greek woes focus attention on swap" by Duncan Wood and Alexander Campbell. Risk, March 2010, pp. 8, 2010a. [ Links ]
35. Risk. "Cat or canary?" by Mark Pengelly. Risk, March 2010, pp. 55, 2010b. [ Links ]
36. Saunders, A.; Allen, L. Credit Risk Measurement: New Approaches to Value at Risk and other Paradigms, 2nd Edition, New York: Wiley, 2002. [ Links ]
37. Smith, R. L. "Extreme Value Analysis of Environmental Time Series: An Application to Trend Detection in Ground-Level Ozone", Statistical Science, núm. 4, pp. 367-393, 1989. [ Links ]
38. Yu, F. "How Profitable is Capital Structure Arbitrage?", Financial Analysts Journal, vol. 62, núm. 5, pp. 47-62, 2006. [ Links ]
Anexo 1
Relación entre los spreads de CDS de cinco años de Portugal, Italia, Irlanda y España, y sus respectivos índices accionarios
Anexo 2
Resultados de la regresión

Anexo 3
Resultados de la prueba de causalidad de Granger en R



Anexo 4
Prueba de autocorrelación
Box-Ljung test
data: delta_cds
X-squared = 535,6346, df = 417,25, p-value = 7,63e-05