Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ensayos sobre POLÍTICA ECONÓMICA
Print version ISSN 0120-4483
Ens. polit. econ. vol.30 no.spe67 Bogotá June 2012
La reconstrucción de la reciente historia de la política monetaria colombiana entre 1990 y 2010*
A reconstrução da recente história da política monetária Colombiana entre 1990 e 2010*
Andrés Giraldo
Martha Misas
Edgar Villa
*Pontificia Universidad Javeriana. We thank Banco de la República for generously providing the data used in this study. We would like to thank Adolfo Cobo for his guidance in choosing the series to be used in this project, Andrés González, Franz Hamann, Roberto Junguito, Hernando Vargas, Miguel Urrutia and other participants of the seminar La historia de la banca central, monetaria y bancaria en América Latina (October 27 and 28 of 2011) for their useful comments on a preliminary draft of this article. Finally, we wish to thank an annonymous referee for her comments. Evidently all remaining errors are our own.
E-mail: mmisas@javeriana.edu.co; a.giraldo@javeriana.edu.co; e.villa@javeriana.edu.co.Document received: 27 October 2011; final version accepted: 12 December 2011.
This article presents a reconstruction of the history of Colombia's central bank's (Banco de la Republica) monetary policy between 1990 and 2010, during which explicit inflation targeting was adopted by October of 2000. To do so we developed a theoretical modified Taylor rule with interest rate smoothing for an open and small economy and accordingly estimated a two regime Markov switching model which allowed the switching dates to be endogenously determined. We found that one regime had explicit inflation targeting (from the year 2000 to 2010), whereby the inflation rate became a stationary series consistent with our empirical finding that Banco de la República enforced a monetary policy that satisfied more likely the Taylor principle. This inflation stabilizing regime did present itself in some quarters before the year 2000, but not as the predominant regime. The other regime was more prevalent during the 1990s, but did not satisfy the Taylor principle as it allowed a unit root behavior of the inflation rate. Finally, we found no evidence that Banco de la República changed its behavior in terms of output fluctuations during the period studied.
JEL classification: C24, E42, E52, E58, N16.
Keywords: Taylor rule, Taylor principle, monetary policy rules, monetary history of Colombia, Markov switching model.
Este artículo presenta una reconstrucción de la historia de la política monetaria del Banco Central de Colombia (Banco de la República) en el período 1990 a 2010 durante el cual se implementó una política explícita de metas de inflación en octubre de 2000. Para lograr nuestro objetivo, desarrollamos una regla teórica de Taylor modificada con suavización de tasa de interés para una economía pequeña y abierta; consecuentemente, estimamos un modelo de cambios de régimen (Markov switching) de dos regímenes, el cual admite que las fechas de cambio de régimen sean determinadas de manera endógena. Encontramos que uno de los regímenes, que corresponde al período 2000 a 2010, coincide con fijación explícita de las metas de inflación por parte del Banco de la República, en donde la tasa de inflación tuvo un comportamiento de serie estacionaria, consistente con que el Banco de la República cumplió con el principio de Taylor. Dicho régimen de política monetaria se había presentado en algunos trimestres antes del 2000, pero no como el régimen predominante. El otro régimen prevaleció durante la década de los noventa, pero no cumplió con el principio de Taylor en general debido a que permitió un comportamiento de raíz unitaria de la tasa de inflación. Finalmente, no encontramos evidencia de que el Banco de la República haya cambiado su comportamiento en cuanto a las fluctuaciones del producto durante el período estudiado.
Clasificación JEL: C24, E42, E52, E58, N16.
Palabras clave: regla de Taylor, principio de Taylor, reglas de políticas monetarias, historia de Colombia, modelo de cambios de régimen.
Este artigo apresenta uma reconstrução da história das políticas monetárias do Banco Central da Colômbia (Banco de la República) de 1990 a outubro do ano 2000, quando se adotou uma política explícita que fixava metas para a inflação. Para alcançar o nosso objetivo, desenvolvemos uma regra teórica de Taylor, modificada com versão suavizada da taxa de juros para uma economia pequena e aberta; consequentemente, calculamos um modelo de Markov de mudança de dois regimes, o que permite que as datas de mudança sejam determinadas de maneira endógena. Encontramos que um dos regimes fixava explicitamente as metas de inflação (de 2000 a 2010) onde a taxa de inflação se transformou em uma série estacionária consistente com o nosso achado empírico: que o Banco de la República acatou uma política monetária que cumpriu com o princípio de Taylor. Dito regime de estabilização inflacionária se havia apresentado em alguns trimestres antes do ano 2000, mas não como o regime predominante. O outro regime prevaleceu durante a década dos noventa, mas não cumpriu com o princípio de Taylor, devido a que permitiu uma unidade de comportamento de raiz da taxa de inflação. Além disso, não encontramos evidências de que o Banco de la República haja mudado seu comportamento em quanto à produção de flutuações durante o período estudado.
Classificação JEL: C24, E42, E52, E58, N16.
Palavras chave: regra de Taylor, princípio de Taylor, regras de políticas monetárias, história da Colômbia, modelo Markov de mudança.
I. INTRODUCTION
Since the debate on discretion versus monetary rules (Kydland and Prescott (1977), Barro and Gordon (1983)), there has been an emerging consensus on the convenience for an economy whereby the central bank should pursue price stabilization under a transparent strategy in which credible and systematic information is revealed to the public. This has generated the advancement of a systematic research program to develop strategies to solve the time inconsistency of monetary policy. An emerging theme has been that of generating simple monetary rules that could convey transparent information to the public in an accessible way which, in turn, has spurred research into the operational implementation of a simple strategy for monetary policy. The aim of the first approach was to monitor monetary aggregates following the pioneering idea of M. Friedman (1968) in order to control inflation (monetarism). The purpose of the second approach was to target the exchange rate in order to avoid independent monetary policy and import inflation from the country that was used to anchor the currency of the local economy. The third approach proposed explicit inflation targeting as a way of controlling inflation (Bernanke and Mishkin (1997)). Behind all these approaches there is the intermediate goal of monetary policy that seeks to manage inflation indirectly, through what has been called the nominal anchor. In the first approach, the idea was to use the monetary aggregates as the nominal anchor to control inflation, whereas in the second approach, the nominal anchor is the nominal exchange rate. Finally, explicit inflation targeting focuses on inflation forecasts and the strategy is to affect the intervention interest rate. This is where Taylor rules emerged. Since the publication of John Taylor's seminal paper about the practice of monetary policy (Taylor, 1993), the specification and estimation of a reaction function that characterizes the behavior of a central bank in order to obtain a simple guide regarding how to intervene in the economy has become frequent. The goal of the Taylor rule is to summarize the complex and challenging process of monetary policy decisions into a simple rule. Importantly, most of the Taylor rules in the existing literature have been devised for the United States economy, which has been characterized as a more or less closed economy. In contrast, this article follows the economic history of monetary policy implemented by Banco de la República since 1990 and accordingly develops a modified Taylor rule that incorporates both interest rate smoothing and exchange rate targeting for an open and small economy. It then compares this modified Taylor rule with the original Taylor rule and shows that it too satisfies the Taylor principle under certain restrictions.
We briefly introduce, as our preface and motivation for the theoretical framework, the history of monetary policy in Colombia since 1990, bearing in mind that the independence of Colombia's central bank (Banco de la República) from the government by constitutional mandate occurred in 1991. Importantly, almost a decade later, in October 2000, Banco de la República announced the implementation of explicit inflation targeting. This event presents itself as a potentially exogenous event that could justify splitting the data into two periods: before and after October 2000, and then analyze our modified Taylor rule to study whether the central bank's behavior changed in any way during both periods; for example, through structural break tests. Nonetheless, we refrain from taking such an adhoc position to model a two regime model, and prefer to estimate our modified Taylor rule in a two regime Markov model that endogenously allows switching dates to occur probabilistically as opposed to deterministically as the previous approach would suggest. We also consider a Markov switching unit root test for the inflation rate in order to test whether one could have stationarity in the regime that satisfies the Taylor principle while not having a unit root in the regime that does not. Our results are in line with the monetary history of Colombia's central bank in several ways. We found that one regime had explicit inflation targeting (from the year 2000 to 2010), in which the inflation rate was a stationary series given that, in our view, the central bank enforced a monetary policy that satisfied the Taylor principle. Even though this inflation stabilizing regime presented itself in some quarters before the year 2000 the other regime was, in fact, predominant during the 1990s and did not satisfy the Taylor principle allowing a unit root behavior of the inflation rate. Moreover, our evidence suggests no statistically significant change in the central bank's behavior in the two regimes to output fluctuations.
The article is organized as follows: the second section presents a brief monetary history of the Banco de la República during the twenty year span that we studied, and during which it became independent from the government by constitutional mandate (1991). The third section, is a brief literature review on Taylor rules. The fourth section introduces the model in which we optimally derive the modified Taylor rule with interest rate smoothing for a small and open economy. We analyze the rule theoretically, compare it to the original Taylor rule, and verify whether it satisfies the Taylor principle. The fifth section addresses the empirical framework that we use to estimate the modified Taylor rule, and the sixth, presents the data to be used in our estimations. Section seven reports our results; first for the two regime Markov unit root test for the inflation rate, and then for the two regime Markov switching model for the modified Taylor rule. Finally, section eight concludes this article.
II. MONETARY POLICY IN COLOMBIA DURING THE 1990-2010 PERIOD
The proclamation of the 1991 Constitution was a major event in Colombia's recent history as it led to a mandate for the independence of the Banco de la República from the executive government in order to stabilize output fluctuations and inflation. This historical event brought with it operative changes and different procedures in managing the country's monetary policy1. Before the constitutional change was approved the Bank's monetary policy was highly dependent on the fiscal policy of the government and actually did not impose stringent restrictions on the emission of currency in order to finance public spending (Kalmanovitz, 2003). Moreover, the monetary policy that followed the bank did not contribute to the financial deepening of capital markets, mainly because the intervention interest rate was not really a reflection of market conditions, but rather a response to political pressures (Sanchez, Fernández and Armenta, 2007). The 1991 Constitution granted Banco de la República the mandate to maintain price stability in line with other economic policy objectives, such as stabilizing output fluctuations by conferring monetary, foreign exchange and credit instruments to the bank. To this day, all decisions are made by a board of directors responsibile for making sure the constitutional mandate is adhered to. During the first years after 1991, the bank had the traditional dichotomy of designing the monetary policy strategy: either targeting monetary aggregates or targeting an intervention interest rate (Hernández and Tolosa, 2001). The importance of this decision was related to the choice of an adequate nominal anchor to send the right signals to the markets2.
According to Hernández and Tolosa (2001), the Colombian central bank chose to target monetary aggregates after independence. The main intermediate monetary target chosen was M3 (which includes the bank's monetary and some non-monetary liabilities) because the recommended empirical instruments allowed some adequate monitoring, given their relationship with the final target; that is, the inflation rate. Besides tracking this monetary aggregate, the Banco de la República board set up an exchange rate band during the 1990s, whereby it expected the nominal exchange rate to remain within it3. This policy required Banco de la República to make an intervention when the exchange rate hit the top or the bottom of the established band. In both cases, the monetary policy became dependent on the foreign exchange rate policy and it seemed that the ultimate target –the inflation rate– was moved to a second level of priority.
Also during the nineteen nineties, Banco de la República had a band for its intervention nominal interest rate. The aim was for the money market to understand the strategy in order to achieve the maintained target as well as the procedure to accomplish the ultimate inflation rate. During those years the main monetary policy instruments were open market operations used to increase or reduce the liquidity in the monetary market, using the M3 growth rate as a target. It could be interpreted that the central bank had three (intermediate) objectives in those years: M3, the exchange rate and the interest rate, all of which were used in order to reach the final target, obviously, the inflation rate. Notwithstanding, to manage these three objectives simultaneously was not conflict-free. Monetary policy during the nineteen nineties seemed even more complicated under other structural reforms that were undertaken at the beginning of the decade and which coincided with the independence of Banco de la República. The structural reforms that were generated during those years included greater openness of capital markets, greater liberalization of the financial system and the decentralization of fiscal policy within the departments of Colombia. In fact, the board of directors defined the order of priorities given the case that the three policy objectives were conflicting: the first objective was to drop the interest rate band and the other two were analyzed depending on the current economic shocks (Hernández and Tolosa, 2001, pp. 5)4.
In October 2000, the board of directors announced that Banco de la República would adopt an inflation targeting policy in order to maintain the stability of prices. Since then, the central bank has changed its main instrument for the intervention interest rate and accorded with other countries that also adopted inflation targeting as the main monetary policy. The idea was to make monetary policy more transparent and more easily understood for the public and for the markets alike. According to the literature on inflation targeting, this regime is characterized by three factors: 1) an announcement of the numerical inflation target (or the range where the long run target was to be realized); 2) an increased importance of the role of inflation forecasting5; and 3) a consistent and systematic strategy of public communication to increase policy transparency6.
Although the central bank only adopted inflation targeting in 2000, there was a special feature of the policy that Banco de la República followed since the adoption of the new Constitution in 1991: the explicit announcement of a quantitative inflation target. Even so, the reviewed history of the monetary policy followed by Banco de la República suggests two distinct periods: one from 1991 to 2000, in which the regime used had an implicit inflation target, and another period from 2000 to the present, in which the regime uses an explicit inflation target. Accordingly, the instruments used to implement the monetary policy can be identified in these two periods as follows: the use of monetary aggregates since the independence of the bank through 1998; then, the use of an exchange rate regime7 that lasted until a speculative attack on the currency, which made Banco de la República abandon it by 1999; and finally, the use of an interest rate target since the explicit adoption of inflation targeting by the central bank from 2000 until now. This hypothetically suggests two distinct periods in which monetary policy was undertaken differently by Banco de la República: 1991 to 2000, and 2000 to 2010.
III. BRIEF LITERATURE REVIEW
The subject regarding monetary policy rules emerged out of the debate on rules versus discretion, and the rise of inflationary bias due to the time inconsistency of a central bank8. To reach time consistency, monetary theory has generated a large body of literature in which it states the importance of monetary policy rules. As Woodford (2003a) argues:
-
there is a good reason for a central bank to commit itself to a systematic approach to policy that not only provides an explicit framework for decision making within the bank, but that is also used to explain the bank's decisions to the public
(p. 14).
The literature on inflation targeting argues that if a country's central bank acts without a systematic (strict or flexible9) rule, recurring only to discretion, it is likely that the results of its monetary policy will end up being suboptimal, regardless of whether it has the best human resources and technical tools available. Given this, the proponents of inflation targeting argue in favor of the use of an explicit rule for a central bank in order to guide its monetary policy. Among the proponents, Mishkin (1999) has shown different monetary regimes available to conduct monetary policy where the common denominator of these regimes is the existence of a nominal anchor to control the expectations of the agents in the economy and increase the effectiveness of the policy. Mishkin identifies three anchors depending on the regime: monetary aggregate regimes, exchange rate regimes and inflation targeting regimes10. Each of them is characterized by the use of an intermediate target that allows the expectations to be anchored and, thus, reach the ultimate goal of any monetary policy: the inflation rate.11
Although the central bank can summarize some important issues of its monetary policy into a (simple or complicated) monetary policy rule, the lags of any monetary policy makes the process of taking adequate decisions more difficult. This is one of the reasons why the monetary policy should have a forward looking component (Mishkin, 2007, chapter 2). Since the publication of John Taylor's seminal paper about the practice of monetary policy (Taylor, 1993), the specification and estimation of a reaction function that characterizes the behavior of a central bank in order to obtain a simple guide regarding how to intervene in the economy has become frequent. The aim of the Taylor rule is to summarize the complex and challenging process of monetary policy decisions into a simple rule. The original rule stated by Taylor, for the Federal Reserve of the United States economy, is actually a static or contemporaneous rule which is specified as follows

where 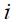 is the federal fund rate,
is the federal fund rate, 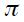 is the inflation rate of the last four quarters, 2 is the inflation rate target and
is the inflation rate of the last four quarters, 2 is the inflation rate target and 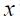 is the output gap (the difference between the logarithm of the observed GDP and the potential GDP). The rationale of the rule is that if the output gap is positive, the Fed responds by increasing the interest rate to contain the inflationary pressures while if the inflation is increasing the federal funds rate is also increased. The rule suggests that if
is the output gap (the difference between the logarithm of the observed GDP and the potential GDP). The rationale of the rule is that if the output gap is positive, the Fed responds by increasing the interest rate to contain the inflationary pressures while if the inflation is increasing the federal funds rate is also increased. The rule suggests that if 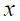 is zero and
is zero and 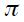 is 2 the implicit real interest rate implied is 4. Taylor showed that this rule is a good decription of the monetary policy of the United States during the late eighties and early nineties.
is 2 the implicit real interest rate implied is 4. Taylor showed that this rule is a good decription of the monetary policy of the United States during the late eighties and early nineties.
Now, since the publication of Taylor's paper, the area of econometric assessment of monetary policy rules was established as a prolific macroeconomic and public policy area of research. The first objective was to make a quantitative evaluation of the Taylor rule to test if this specification described the true path of the intervention interest rate, at least for the United States. The next step in that research program was to evaluate the performance of different specifications of monetary rules into macroeconomic models and assess their optimal conditions12. Taylor's contribution has resulted in normative and positive implications even though some criticisms have appeared13. On the normative side, the rule is in accordance with the main principles for optimal policy described above. In at least an approximate sense, the rule calls for a countercyclical response to demand and accommodation of shocks to potential GDP that do not affect the output gap. On the positive side, Taylor's contribution has shown that, under certain parameter values, the rule that he proposed describes the monetary policy over the period in which he studied the US economy reasonably well (period 1987-92).
There are different Taylor rules that have been evaluated using different empirical strategies. Similarly, from a theoretical perspective the rule has been explained using microfoundations. However, it has been more traditional to formulate Taylor type rules from economic intuition without a structural model. In the literature, it is common to find a great variety of articles either only on the empirical side or to examine the appropriateness of the rule under simulations and then contrast its optimality and robustness in the same context. One important characteristic of the Taylor rules is the concept related to the so called Taylor principle which Woodford (2003a) defines it as follows: " In Taylor's discussions of the rule, he places particular stress upon the importance of responding to inflation above the target rate by raising the nominal interest-rate operating target by more than the amount by which inflation exceeds the target..." (p. 40).
If the rule is expressed as

where 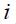 is the policy or intervention interest rate,
is the policy or intervention interest rate, 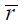 is the real interest rate,
is the real interest rate, 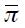 is the inflation target,
is the inflation target, 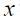 is the output gap,
is the output gap, 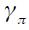 is the inflation aversion,
is the inflation aversion, 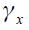 is the business cycles aversion, the Taylor principle is satisfied if
is the business cycles aversion, the Taylor principle is satisfied if 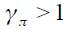 . In the tradition on evaluation of Taylor rules, some authors have tried to reconstruct the monetary history of certain economies, in the same way as Taylor (1993), estimating the inflation aversion
. In the tradition on evaluation of Taylor rules, some authors have tried to reconstruct the monetary history of certain economies, in the same way as Taylor (1993), estimating the inflation aversion 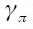 coefficient14. As Orphanides (2008) argues, there are different sorts of Taylor rules that try to describe the way a central bank adjusts its intervention interest rate to changes in economic activity and inflation.
coefficient14. As Orphanides (2008) argues, there are different sorts of Taylor rules that try to describe the way a central bank adjusts its intervention interest rate to changes in economic activity and inflation.
Among the ample literature on Taylor rules, we would like to emphasize two articles that are related to this article. Importantly, when a central bank follows a monetary rule compatible with the Taylor principle it exhibits a high inflation aversion and reacts strongly against inflationary pressures. This has been shown empirically by two articles using a Markov switching model: Kuzin (2004) for the Bundesbank and Murray, Nikolsko-Rzhevskyy and Papell (2008) for the Federal Reserve. Kuzin (2004) estimates a simple backward-looking Taylor rule (with interest rate smoothing) in a time-varying coefficient framework with quarterly German data for the period 1975-1998. The main finding is that the inflation aversion of the Bundesbank was not constant over time and exhibited some sudden and large shifts during the period of monetary targeting. There are phases with low and high inflation aversion; the former is compatible with the Taylor principle and the latter violates it. Kuzin argues that his results provide evidence that the Bundesbank followed the so-called 'opportunistic approach' to disinflation.
Murray et al. (2008) show that a "textbook" macroeconomic model with an IS curve, a Phillips curve, and a Taylor rule, should exhibit a stationary inflation rate if and only if the central bank obeys the Taylor principle, since the real interest rate is increased when inflation rises above the target inflation rate. Moreover, they argue that there is no reason to presume that monetary policy per se is either always stabilizing or always unstabilizing and therefore suggest that the inflation rate might switch from a stationary regime to a unit root behavior regime, depending on whether the policy followed the Taylor principle or not. They estimate a Markov switching model for inflation and show that inflation for the US economy is best characterized by two states, one stationary and the other with a unit root. They find that the unit root state spans most of the period from the 1967 to 1981, while the stationary state appears in the second quarter of 1981 and goes on until 2008. Consistent with this, they also estimate a Markov switching model for various real-time forward looking Taylor rules and find that the considered Taylor rule equation switches between states where the Federal Reserve did and did not try to stabilize inflation by following the Taylor principle. More precisely, they find that even though the pre and post-Volcker subsamples each contain multiple Taylor rule regimes, the Volcker tenure at the Federal Reserve, for most of the time did not follow a Taylor rule, but instead switched to a stabilizing Taylor rule state in 1985:4, which has lasted until 2008.
Furthermore, Murray et al. (2008) contrast their result with Orphanides (2004). Using data from 1965:4-1995:4, Orphanides estimates forward looking Taylor rules and splits the sample into pre and post-Volcker periods, with the change occurring between 1979:2 and 1979:3. He concludes that there was no significant change in the Federal Reserve's response to inflation before and after Volcker: in both regimes the Federal Reserve was estimated to have followed a stabilizing Taylor rule. This is almost exactly the opposite of Murray et al's. (2008) findings. They argue that Orphanides (2004) splits his sample after 1979:2, which is an intuitive break date, chosen exogenously and which he imposes to analyze the corresponding two regimes. Murray et al. (2008) suggest that when the break date is endogenized, via Markov switching, each of Orphanides' "regimes" contains periods where the Federal reserve both did and did not follow the Taylor principle. They argue that not only did the Federal Reserve change its response to inflation throughout the entire sample, but that the timing of these changes is not simply pre and post Volcker. Indeed, for the Volcker years, they conclude that it was not until he had less than two years remaining in his term that monetary policy permanently switched to a stabilizing Taylor rule.
Both Kuzin (2004) and Murray et al. (2008) can be interpreted as warning us against the dangers of exogenously imposing a break date given by economic history. Hence, we do not impose the known date of October 2000 as a break date when Banco de la República explicitly announced inflation targeting as a monetary policy. On the contrary, we endogenize a potential break date in a Markov two regime model and let the empirical model tell us whether there are two separate regimes of monetary policy for Colombia which might or might not coincide with what economic history tells us. Nonetheless, we want to study whether the bank's behavior can be associated with a low inflation aversion before October 2000 and a high inflation aversion afterwards as economic history suggests.
In order to capture different characteristics of the monetary policy rules 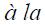 Taylor, it is important to take into account a number of factors that can influence the decision making process: i) The monetary policy rule must capture the desire of stabilizing GDP15, ii) it should include interest rate smoothing16, iii) it might be important to consider the exchange rate as another variable that may be included in a modified Taylor rule, specially for open and small economies17.
Taylor, it is important to take into account a number of factors that can influence the decision making process: i) The monetary policy rule must capture the desire of stabilizing GDP15, ii) it should include interest rate smoothing16, iii) it might be important to consider the exchange rate as another variable that may be included in a modified Taylor rule, specially for open and small economies17.
One way of capturing output stabilization and an interest rate smoothing preference from the central bank is the following modified Taylor rule as in Kuzin (2004) which can be expressed as:
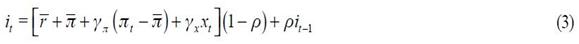
where 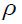 is the parameter that measures the smoothing of the interest rate by the central bank. Furthermore, Woodford (2003a) argues that the reduction of both the interest rate and the inflation variability are appropriate goals of monetary policy and an interest rate smoothing rule allows a greater degree of stabilization of the long-run price level by making inflation fluctuations less persistent (Woodford, 2003a, pp. 98-99). Nonetheless, the functional form in equation (3) is ad hoc and does not come from an optimal program. We will have much to say about this in our structural model developed below which optimally derives the monetary rule with interest rate smoothing.
is the parameter that measures the smoothing of the interest rate by the central bank. Furthermore, Woodford (2003a) argues that the reduction of both the interest rate and the inflation variability are appropriate goals of monetary policy and an interest rate smoothing rule allows a greater degree of stabilization of the long-run price level by making inflation fluctuations less persistent (Woodford, 2003a, pp. 98-99). Nonetheless, the functional form in equation (3) is ad hoc and does not come from an optimal program. We will have much to say about this in our structural model developed below which optimally derives the monetary rule with interest rate smoothing.
IV. MODEL
As the literature on optimal monetary rules argues, a policy of inflation rate targeting implies optimal rules that take into account both changes in the output gap and the inflation rate. The original Taylor rule includes only these changes in a very simple way presumably because it was appropriate for a big closed economy such as the United States. Nonetheless, as mentioned above, interest rate smoothing and exchange rate targeting could be included in a modified Taylor rule specially designed for an open and small economy such as Colombia. The purpose of this section is to theoretically justify the modified Taylor rule that we end up estimating in a two regime Markov switching model. To do this, we developed a structural model that derives the optimal monetary rule for an open economy which yields interest rate smoothing. This was then analyzed and compared to the original Taylor rule for a closed economy as in equation (1).
A. SET UP
Consider a central bank of a small open economy that takes as given an intertemporal IS aggregate curve denoted as
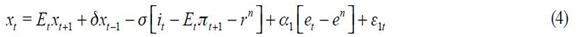
and an aggregate supply curve
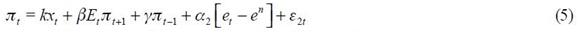
where 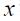 denotes the log of the output gap,
denotes the log of the output gap, 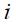 the log of nominal (short run) interest rate,
the log of nominal (short run) interest rate, 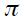 the log of the inflation rate,
the log of the inflation rate, 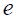 the log of real (short run) exchange rate, while
the log of real (short run) exchange rate, while 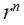 and
and 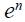 denote respectively the long run levels of the logs of the real interest rate and real exchange rate which are both assumed to be determined by exogenous factors. The term
denote respectively the long run levels of the logs of the real interest rate and real exchange rate which are both assumed to be determined by exogenous factors. The term 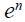 reflects an exchange rate target that the central bank might want to maintain. The parameters are assumed to have the following signs:
reflects an exchange rate target that the central bank might want to maintain. The parameters are assumed to have the following signs: 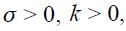
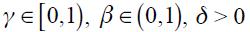 while
while 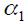 and
and 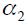 could be positive, but not necessarily so. The terms
could be positive, but not necessarily so. The terms 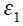 and
and 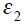 denote respectively the supply and demand disturbances where we assume they are iid normally distributed with mean zero and variances
denote respectively the supply and demand disturbances where we assume they are iid normally distributed with mean zero and variances 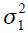 and
and 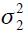 respectively. The operator
respectively. The operator 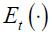 denotes the expected value at time
denotes the expected value at time 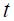 of the variable next period using all observable information up to time
of the variable next period using all observable information up to time 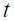 .
.
The central bank is assumed to have a loss function represented by
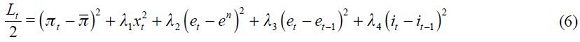
where the lambdas are assumed to be positive. The first two terms are common to all monetary rules where 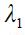 reflects the weight of the output gap in the loss function which is always seen as relative to the weight of one for changes in the inflation rate from a maintained target
reflects the weight of the output gap in the loss function which is always seen as relative to the weight of one for changes in the inflation rate from a maintained target 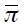 . Now, the term associated with
. Now, the term associated with 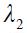 reflects our concern that Colombia's central bank had an explicit exchange rate band during the 1990s and this term reflects a preference for deviations of the real exchange rate from the implicit target denoted as
reflects our concern that Colombia's central bank had an explicit exchange rate band during the 1990s and this term reflects a preference for deviations of the real exchange rate from the implicit target denoted as 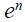 . Moreover, we also consider that the central bank could intervene under strong fluctuations of the real exchange rate from one period to another which is summarized by the term associated with
. Moreover, we also consider that the central bank could intervene under strong fluctuations of the real exchange rate from one period to another which is summarized by the term associated with 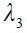 . Finally, the fluctuation of the nominal interest rate is captured by the term associated with
. Finally, the fluctuation of the nominal interest rate is captured by the term associated with 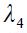 in the same way as in Woodford (2003a).
in the same way as in Woodford (2003a).
We assume that the behavior of the central bank could be understood as the policy that emerges when minimizing (6) subject to (4) and (5). The corresponding Lagrangian is defined by
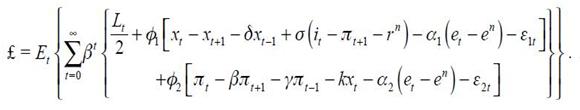
where 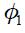 and
and 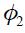 are the Lagrangian multipliers and which we assume constant through time.18 Since the loss function is quadratic, the following first order conditions that solve the optimization program are necessary and sufficient
are the Lagrangian multipliers and which we assume constant through time.18 Since the loss function is quadratic, the following first order conditions that solve the optimization program are necessary and sufficient
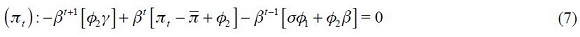
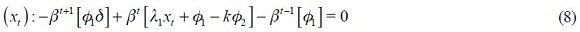
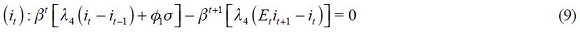
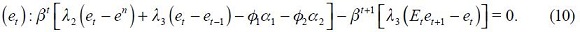
From these four conditions, (4) and (5), we are able to get a modified Taylor rule given by
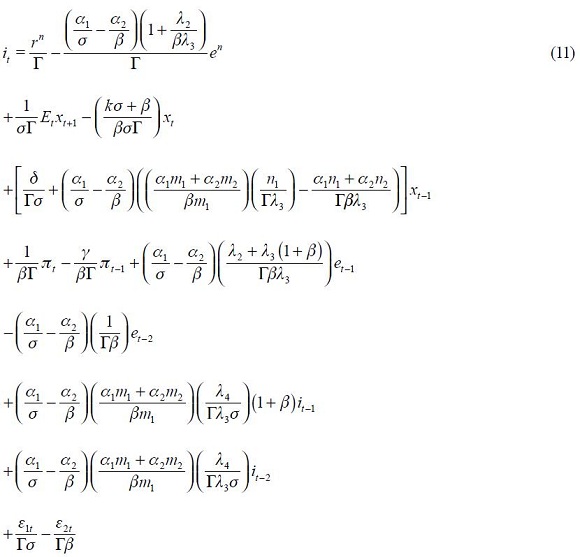
where
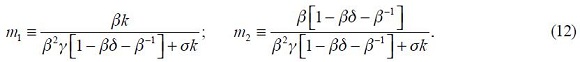
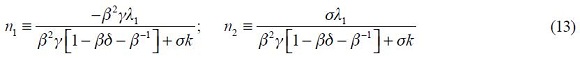
and
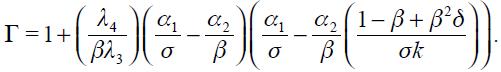
The full derivation of equation (11) is shown in the appendix. Equation (11) is the optimal monetary rule that results from the setup above and which is a modified Taylor rule with interest rate smoothing. Moreover, since a lag of the inflation rate presents itself in equation (11), it means that the inflation rate is persistent. Furthermore, it has a forward looking expectations component associated with the output gap as well as a lagged value of the output gap that also generates persistency of this variable in the rule. The rule also responds to fluctuations of the real exchange rate by incorporating two lags.
B. ANALYZING THE MODIFIED TAYLOR RULE
It is instructive to study some of the theoretical predictions of our model. Note first that this model can generate the simple Taylor rule for a closed economy with naive expectations on the output gap. To see this, note that under naive expectations 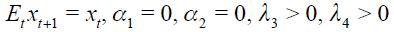 and
and 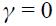 (which together imply
(which together imply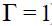 ) equation (11) turns out to be
) equation (11) turns out to be

which is similar to the simple Taylor rule proposed originally by Taylor (1993). As shown above, Taylor proposed a rule for the United States in which the coefficient associated with 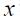 could be around 0.5 while that associated with
could be around 0.5 while that associated with 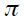 could be 1.5. In this case the Taylor principle requires that
could be 1.5. In this case the Taylor principle requires that 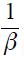 be greater than one for monetary policy in order to be offsetting when inflation rises which is guaranteed under the assumption
be greater than one for monetary policy in order to be offsetting when inflation rises which is guaranteed under the assumption 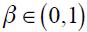 . In fact, the values 0.5 and 1.5 could be replicated in this model with the parameter set values defined as:
. In fact, the values 0.5 and 1.5 could be replicated in this model with the parameter set values defined as: 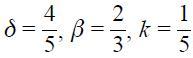 , and
, and 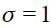 . These parameter values result in
. These parameter values result in 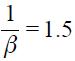 and
and 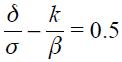 the values proposed by Taylor for the United States viewed as a closed economy as in equation (1). It is important to note that in equation (14), the optimal response to the output gap is not necessarily positive theoretically since it could be the case that
the values proposed by Taylor for the United States viewed as a closed economy as in equation (1). It is important to note that in equation (14), the optimal response to the output gap is not necessarily positive theoretically since it could be the case that 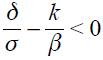 , even though, empirically, this does not seem to be the case. Moreover, note that demand shocks, represented by an increase in
, even though, empirically, this does not seem to be the case. Moreover, note that demand shocks, represented by an increase in 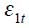 , increase optimally
, increase optimally 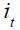 while supply shocks, represented by an increase in
while supply shocks, represented by an increase in 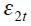 , decrease
, decrease 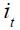 .
.
Let us now study the optimal monetary rule for an open economy (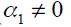 and
and 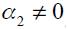 ) where a central bank is interested in real exchange rate targeting, real exchange rate fluctuations as well as nominal interest rate fluctuations
) where a central bank is interested in real exchange rate targeting, real exchange rate fluctuations as well as nominal interest rate fluctuations 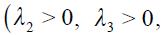
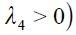 . For this part we specialize equation (11) under two assumptions:
. For this part we specialize equation (11) under two assumptions: 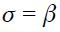 and
and 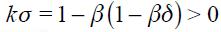 .19 These two conditions simplify the equation substantially allowing us to discuss the sign of most of the terms. Hence equation (11) simplifies to
.19 These two conditions simplify the equation substantially allowing us to discuss the sign of most of the terms. Hence equation (11) simplifies to
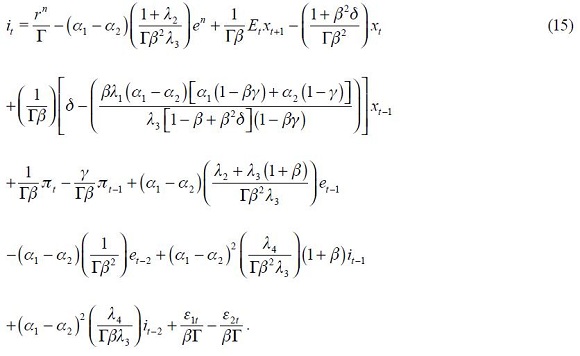
where we have used (12) and (13) as well as
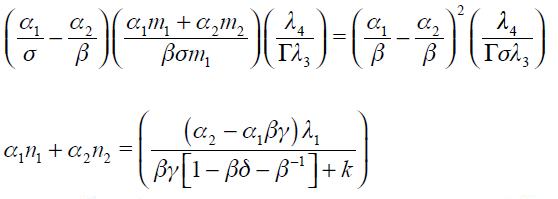
and
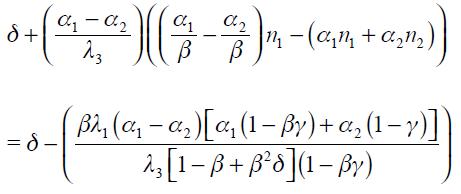
Under the two assumptions that we have imposed 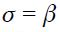 and,
and, 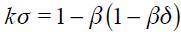 , we get from equation (15) that coefficients associated to
, we get from equation (15) that coefficients associated to 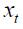 and
and 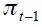 are negative. Moreover, coefficients associated to
are negative. Moreover, coefficients associated to 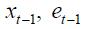 and
and 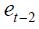 have an ambiguous sign. In the short run an optimal response for an inflation rate change
have an ambiguous sign. In the short run an optimal response for an inflation rate change 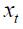 is attenuated with respect to an identical closed economy. To see this, note that the coefficient associated with
is attenuated with respect to an identical closed economy. To see this, note that the coefficient associated with 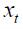 in the modified Taylor rule (15) is
in the modified Taylor rule (15) is 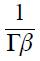 while in the closed economy Taylor rule (14) is
while in the closed economy Taylor rule (14) is 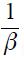 . Hence, under the two stated assumptions above, we have that
. Hence, under the two stated assumptions above, we have that 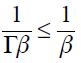 given that
given that 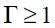 . Moreover, we conclude that interest rate smoothing of the optimal monetary rule is to increase the nominal interest rate during two consecutive periods, given a contemporaneously increase in the interest rate. This is seen in equation (15) since the coefficients on
. Moreover, we conclude that interest rate smoothing of the optimal monetary rule is to increase the nominal interest rate during two consecutive periods, given a contemporaneously increase in the interest rate. This is seen in equation (15) since the coefficients on 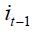 and
and 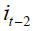 are positive. It is interesting that the coefficient associated with
are positive. It is interesting that the coefficient associated with 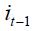 in equation (15) is greater in absolute value than the coefficient associated with
in equation (15) is greater in absolute value than the coefficient associated with 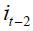 since
since
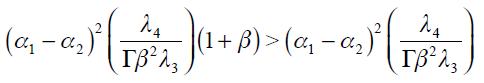
given that 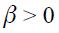 . These conclusions are summarized as propositions.
. These conclusions are summarized as propositions.
Proposition 1. Under 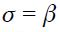 and
and 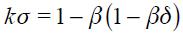 the modified Taylor rule in equation (15) is less responsive in the short run to changes in the inflation rate
the modified Taylor rule in equation (15) is less responsive in the short run to changes in the inflation rate 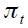 compared to an identical closed economy as in equation (14).
compared to an identical closed economy as in equation (14).
Proposition 2. Moreover, the optimal monetary rule implies that interest rate smoothing has the feature of increasing the nominal interest rate during consecutive periods after a change in the nominal interest rate in period 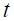 ; the increase being greater in period
; the increase being greater in period 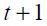 than in
than in 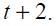
Nevertheless, we need to study the long run effect on the nominal interest rate of changes in 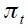 and
and 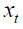 given that the modified Taylor rule in equation (15) has interest rate smoothing captured by the terms
given that the modified Taylor rule in equation (15) has interest rate smoothing captured by the terms 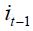 and
and 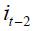 . Consider first the Taylor principle that says that a change in
. Consider first the Taylor principle that says that a change in 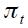 must generate a greater increase in the nominal interest rate to off set the inflation surge. This comes down to studying the long run effect of a unit change in
must generate a greater increase in the nominal interest rate to off set the inflation surge. This comes down to studying the long run effect of a unit change in 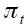 which is given by
which is given by
 .
. If the Taylor principle is to hold, we need to verify that the long run effect satisfies 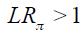 . Under the two simplifying assumptions
. Under the two simplifying assumptions 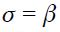 and
and 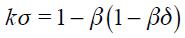 and using
and using 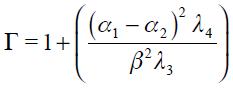 in (16) yields
in (16) yields
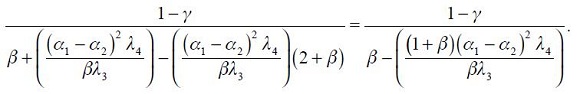 .
. Note that a necessary condition for the Taylor principle to hold is that 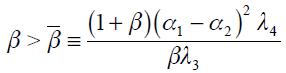 since only if this is true can the long run effect actually be positive given that
since only if this is true can the long run effect actually be positive given that 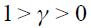 is satisfied by assumption. Nonetheless, the optimal monetary reaction of an open economy to changes in
is satisfied by assumption. Nonetheless, the optimal monetary reaction of an open economy to changes in 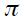 satisfies the Taylor principle only for values of
satisfies the Taylor principle only for values of 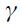 close to zero. To see why this is note first that under
close to zero. To see why this is note first that under 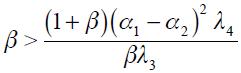 for
for 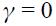 the coefficient on the long run effect of a unit increase in
the coefficient on the long run effect of a unit increase in 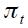 is
is 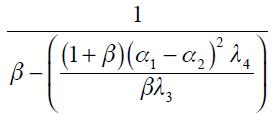 which is strictly greater than one satisfying the Taylor principle if
which is strictly greater than one satisfying the Taylor principle if 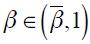 . Now, when
. Now, when  increases towards one the coefficient
increases towards one the coefficient 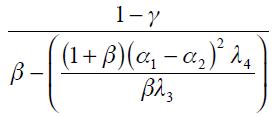 decreases and could eventually become less than one even if
decreases and could eventually become less than one even if 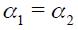 . Hence, the Taylor principle is satisfied only for values of
. Hence, the Taylor principle is satisfied only for values of 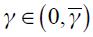 where
where 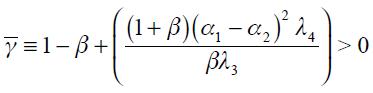 . We summarize this as a proposition.
. We summarize this as a proposition.
Proposition 3. Under 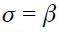 and
and 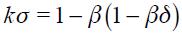 the modified Taylor rule in equation (15) satisfies the Taylor principle in the long run if
the modified Taylor rule in equation (15) satisfies the Taylor principle in the long run if 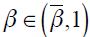 and
and 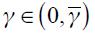 where
where 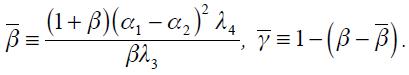
It is theoretically possible for the optimal rule to violate the Taylor principle in an open economy, which would be the case when 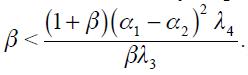 In this case, a unit change effect of
In this case, a unit change effect of 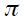 would actually end up reducing the interest rate! This result is more likely to present itself the greater the difference between
would actually end up reducing the interest rate! This result is more likely to present itself the greater the difference between 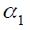 and
and 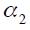 for given values of
for given values of 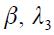 and
and 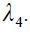
Consider now the long run effect on the nominal interest rate for a unit increase in the output gap. Let us assume that expectations are rational such that  and for the sake of simplicity, assume that
and for the sake of simplicity, assume that 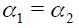 which implies
which implies 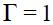 . The long effect according to equation (15) is
. The long effect according to equation (15) is
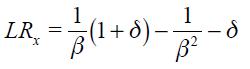
which is not necessarily positive, given that for values of 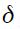 close to zero the expression is negative. Here, we conclude that the optimal reaction to changes in the output gap for an open economy is not necessarily greater or smaller than the reaction of an identical closed economy. We summarize this too as a proposition.
close to zero the expression is negative. Here, we conclude that the optimal reaction to changes in the output gap for an open economy is not necessarily greater or smaller than the reaction of an identical closed economy. We summarize this too as a proposition.
Proposition 4. For an open economy the modified Taylor rule in equation (15) does not necessarily generate a greater or smaller response on the nominal interest rate than what is optimal for an otherwise identical closed economy according to equation (14).
Woodford (2003a) has argued that optimal monetary rules can end up having an interest rate smoothing component which is absent in the original Taylor rule. He has argued this for a closed economy i.e. an economy in which the real exchange rate does not have a role to play. Interestingly in our model we end up having interest rate smoothing only if the economy is actually open i.e. 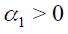 and
and 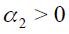 such that
such that 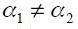 under
under 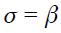 and
and 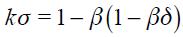 . As can be seen in equation (15), when
. As can be seen in equation (15), when 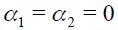 we end up without interest rate smoothing. To be sure, we are not arguing that in a general model a closed economy cannot have an optimal monetary rule with interest rate smoothing. In fact, Woodford (2003a) has shown that interest rate smoothing can present itself in the optimal policy of a closed economy even if interest rate changes is not a social objective in itself for a central bank. What we are arguing is simply and interestingly that in our simple model, we generated interest rate smoothing optimally only for an open economy, not for a closed one.
we end up without interest rate smoothing. To be sure, we are not arguing that in a general model a closed economy cannot have an optimal monetary rule with interest rate smoothing. In fact, Woodford (2003a) has shown that interest rate smoothing can present itself in the optimal policy of a closed economy even if interest rate changes is not a social objective in itself for a central bank. What we are arguing is simply and interestingly that in our simple model, we generated interest rate smoothing optimally only for an open economy, not for a closed one.
The following proposition is detailed in the appendix
Proposition 5. If 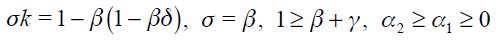 the modified Taylor rule (15) is consistent with an underlying dynamic system that has a unique steady state.
the modified Taylor rule (15) is consistent with an underlying dynamic system that has a unique steady state.
This proposition guarantees the conditions under which the modified Taylor rule developed above is made consistent with an underlying dynamic system that has a unique steady state. It is important to highlight that we do not show the local or global dynamic properties of the implicit dynamic system; we merely assume that it is locally stable in the vicinity of the unique steady state.
V. EMPIRICAL SPECIFICATION
In this section, we link the theoretical with an empirical specification. First, consider the modified Taylor rule derived above given by equation (11), which does not impose any restriction, under rational expectations 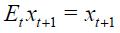 as its reduced form
as its reduced form
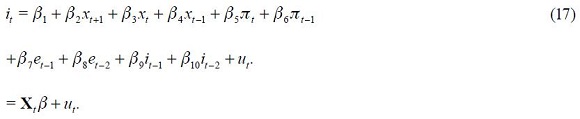
where the fundamental parameters are combined in the reduced form parameters 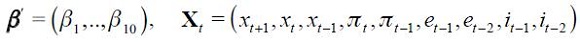 and
and 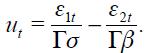 Under the above assumptions that
Under the above assumptions that 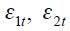 are iid normally distributed with mean zero and variances
are iid normally distributed with mean zero and variances 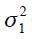 and
and 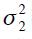 respectively, the result is that
respectively, the result is that 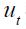 is iid normally distributed with conditional mean given by
is iid normally distributed with conditional mean given by 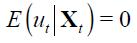 and variance given by
and variance given by 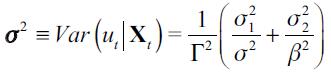 for all
for all 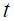 and serially uncorrelated.
and serially uncorrelated.
In view of the above review of economic history about Banco de la República from 1990.I to 2010.IV, we specify a Markov switching regime model that allows the nominal interest rate to be in two different states, each of which is characterized by a different inflation rate behavior related to the monetary policy strategy. We restrict the state space to two regimes denoted as state 0 and state 1 where the former is labeled explicit inflation targeting regime (mainly through an interest rate reaction function) while the latter is labeled non explicit inflation targeting regime (through either monetary aggregates or exchange rate targeting). Denote as 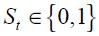 the state space variable which is discrete and unobserved and which is associated to the state of the economy.20 This state variable
the state space variable which is discrete and unobserved and which is associated to the state of the economy.20 This state variable 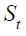 is governed by the transition probabilities given by
is governed by the transition probabilities given by
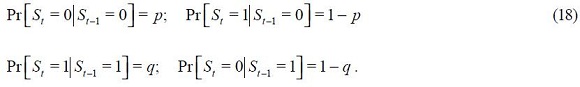
which gives its non linear Markovian nature. The state variable 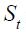 indexes the parameters of the Taylor rule given in (17) such that
indexes the parameters of the Taylor rule given in (17) such that

Where
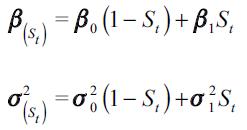
reflects the regime dependency of both the parameters 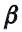 and the variance
and the variance 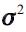 . The empirical model given by (19) was pioneered by Hamilton (1994) and is estimated by a maximum likelihood procedure using Krolzig's (1997) algorithm.
. The empirical model given by (19) was pioneered by Hamilton (1994) and is estimated by a maximum likelihood procedure using Krolzig's (1997) algorithm.
Note that we are making the strong assumption that the behavior of Banco de la República can be understood "as if" it would follow a modified Taylor rule with fundamental parameters that could shift across a two regime environment. A critique to this approach, which we have received from some colleagues, is that this assumption may not be appropriate for the case of a central bank that follows a monetary policy that focuses on monetary aggregates and not on the interest rate. Hence, our modified Taylor rule could be a misspecified model of the true behavior of Banco de la República prior to October 2000. Even though we believe we cannot refute this critique, we are forced to assume that the modified Taylor rule can be a good description of the behavior of Banco de la República "as if" it had been following it even before the explicit announcement of explicit inflation targeting in October 2000. We can point to the case of the United States and the work of John Taylor. It is a well known fact that the United States has never adopted an inflation targeting system, despite the fact that Ben Bernanke was appointed chair of the Federal Reserve in 2006 and his prior academic work seemed to have suggested the possibility of the adoption of this policy for the Federal Reserve21. Nevertheless, the simple Taylor rule has proven to be a good approximation of U.S. monetary policy. It is in this sense that we believe our approach could be defended from this important critique.
VI. DATA
The data was generously provided by Banco de la República. It is important to point out that the interest rate data used in the estimations is the nominal interest interbank rate, whereas the output GAP (its methodology has not been publicly disclosed) was developed by Banco de la República who generously provided us with the data. The inflation rate used in the estimations is annualized quarterly data taken from the Statistical Bureau DANE (Departamento Administrativo Nacional de Estadística) and the log of real exchange rate used was provided by Banco de la República where the real exchange rate uses the consumer price index as deflator and the total weights are taken from twenty countries that are considered by Banco de la República as Colombia's principal commercial partners.
Graphs 1 to 4 summarize the four time series (interest rate, output gap, inflation rate and log of real exchange rate) in quarterly frequency from the first quarter of 1990 up to the last quarter of 2010 used in the empirical specification discussed above. All Graphs display a vertical line that identifies October 2000 as the date in which explicit inflation targeting was implemented by Banco de la República. As illustrated by the Graphs, the nominal interest rate, output gap and inflation rate seem to have changed their behavior after the year 2000, while for the log of the real exchange rate this is not apparent. In particular, one sees that prior to October 2000, the interest interbank rate was at a higher level with much more volatility than after October 2000. The output gap reflects a huge recession of the Colombian economy in 1999, which coincided shortly after with the adoption of inflation targeting by Colombia's central bank. Moreover, the inflation rate prior to October 2000 experienced a steep decrease, which seems to have been attenuated after October 2000.
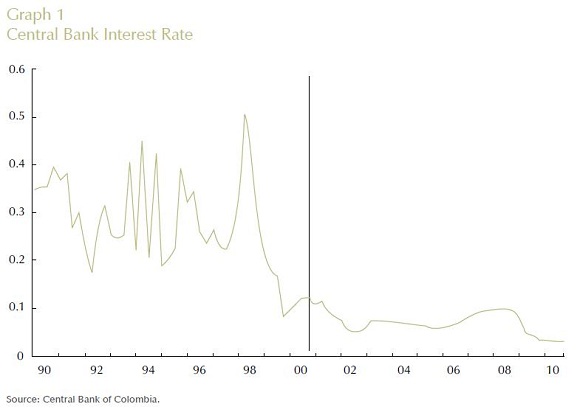
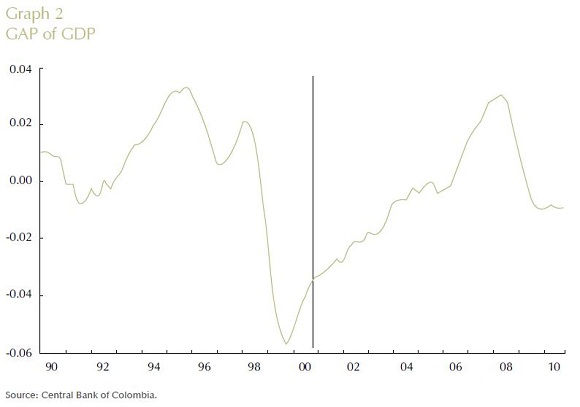
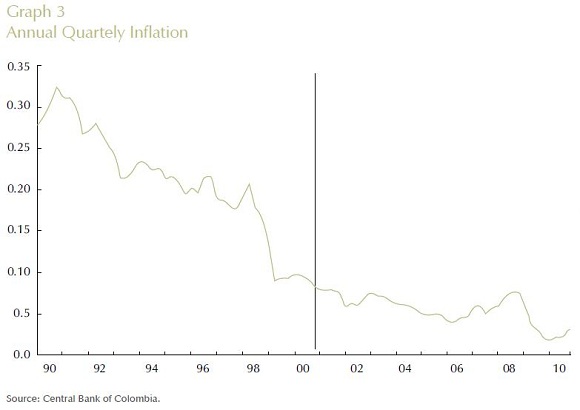
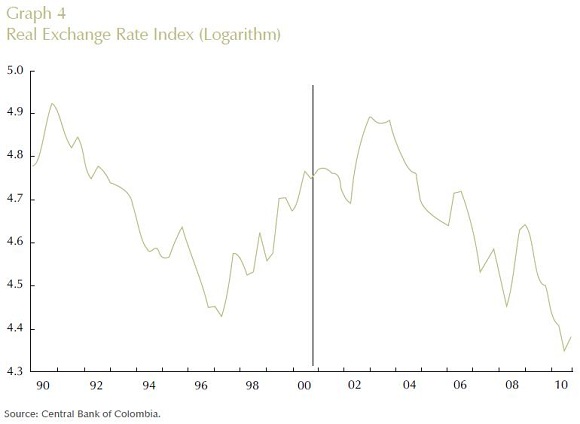
VII. RESULTS
Before reporting the two regime Markov switching model for the modified Taylor rule according to (19), we first present a unit root test for the inflation rate. This was undertaken following the lead of Kuzin (2004) and Murray et al. (2008), which suggest that when the Taylor principle is not violated, a Taylor rule implies that the inflation rate should be a stationary series, whereas when it does not hold, it could become non stationary.
A. MARKOV SWITCHING UNIT ROOT TEST
Let 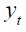 be the annual quarterly inflation rate for the period 1990.I-2010.IV. Consider the following Markov-switching augmented Dickey-Fuller representation, whereby coefficients and variances are driven by an unobservable state variable
be the annual quarterly inflation rate for the period 1990.I-2010.IV. Consider the following Markov-switching augmented Dickey-Fuller representation, whereby coefficients and variances are driven by an unobservable state variable 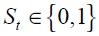
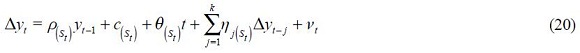
where 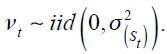 The state variable is governed by a Markov process of order one whose transition probabilities are defined by the following equation
The state variable is governed by a Markov process of order one whose transition probabilities are defined by the following equation
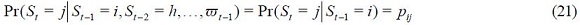
where 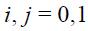 and
and 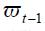 is the information set up to period
is the information set up to period 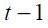 . The unit root tests are based on the t-statistic corresponding to the coefficient of
. The unit root tests are based on the t-statistic corresponding to the coefficient of 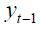 associated with
associated with 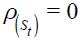 . In particular, the t-statistic is computed as a ratio of the estimated parameter and its standard deviation which is taken from the negative Hessian matrix of the log likelihood function evaluated at the maximum (see Camacho, 2010; Hall, Psaradakis and Sola, 1999). The steps of the bootstrapping Markov-switching unit root test are the following:
. In particular, the t-statistic is computed as a ratio of the estimated parameter and its standard deviation which is taken from the negative Hessian matrix of the log likelihood function evaluated at the maximum (see Camacho, 2010; Hall, Psaradakis and Sola, 1999). The steps of the bootstrapping Markov-switching unit root test are the following:
- Equation (20) is estimated under the null hypothesis and the disturbances are saved and two subsets are formed. The Selection scheme is performed by filtered transition probabilities. - Subset A1 corresponds to the residuals associated to state 0 or explicit inflation targeting regime. - Subset A2 corresponds to the residuals associated to state 1 or non explicit inflation targeting regime.
- Generate a large number B of disturbances with sample size equal to that of the data generating process by bootstrapping the residuals from A1 and A2. It is noted that disturbances are ordered according to the time dimension.
- Generate a dichotomous state variable using filtered transition probabilities.
- Generate B realizations of
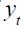 using disturbances obtained through bootstrapping and the estimated parameters where
using disturbances obtained through bootstrapping and the estimated parameters where 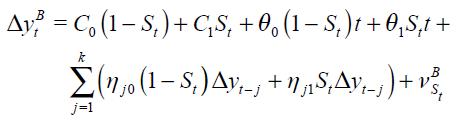
- Equation (20) is estimated for each of
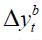 for
for 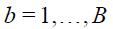 and the t-statistic associated to
and the t-statistic associated to 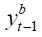 for
for 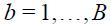 are stored in a vector of size
are stored in a vector of size 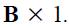
- The p-value of the unit root test for each state is the percentage of the generated t-ratios that are below the original
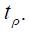
To test whether the inflation is generated by unit root Markov-switching processes, we applied an ADF Markov-switching unit root test. First, equation (20) is estimated for both regimes simultaneously and is reported in Table 1.
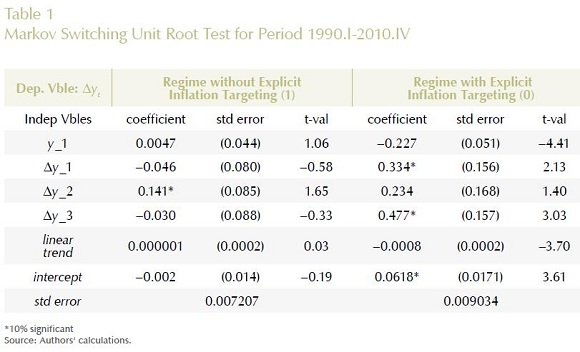
Second, we calculate the p-value for to the t-statistic of the coefficient associated to 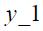 through a bootstrapping procedure for each of the regimes as described above with 1000 replications. The result is reported in Table 2 and shows that the null is rejected because of the presence of a unit root in regime 0 (which coincides mainly with the regime that we identify later as explicit inflation targeting) while it is not rejected in regime 1 (which coincides with the regime that we identify later as the regime without explicit inflation targeting).
through a bootstrapping procedure for each of the regimes as described above with 1000 replications. The result is reported in Table 2 and shows that the null is rejected because of the presence of a unit root in regime 0 (which coincides mainly with the regime that we identify later as explicit inflation targeting) while it is not rejected in regime 1 (which coincides with the regime that we identify later as the regime without explicit inflation targeting).

B. MARKOV SWITCHING FOR THE MODIFIED TAYLOR RULE
A first order two state Markov switching model was estimated for Colombia with quarterly data of the interest rate and its explanatory variables for the period 1990.I-2010.IV. Table 3 reports the maximum likelihood estimates of the reduced form parameters of the modified Taylor Rule using specification (19) where again 0 denotes a regime labeled as explicit inflation targeting and 1 denotes a regime labeled without explicit inflation targeting. The table reveals different signs for some of the coefficients across regimes. Take for instance the coefficient on the forward term of the output gap 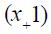 which is negative in regime 1 while positive in regime 0, both being statistically significant at the 10% level using bootstrap standard errors with 2000 replications. In contrast, the coefficient on the contemporaneous term of the output gap
which is negative in regime 1 while positive in regime 0, both being statistically significant at the 10% level using bootstrap standard errors with 2000 replications. In contrast, the coefficient on the contemporaneous term of the output gap 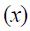 is positive in both regimes, but only statistically significant at the 10% in regime 1. Furthermore, the coefficient on the lag term of the output gap
is positive in both regimes, but only statistically significant at the 10% in regime 1. Furthermore, the coefficient on the lag term of the output gap 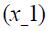 is positive in regime 1 while negative in regime 0, both being statistically significant at the 10%. Similarly, the coefficient on the contemporaneous inflation rate
is positive in regime 1 while negative in regime 0, both being statistically significant at the 10%. Similarly, the coefficient on the contemporaneous inflation rate 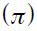 is positive in regime 1 while negative in regime 0, but only the latter is statistically significant at the 10%. The lag of the inflation rate
is positive in regime 1 while negative in regime 0, but only the latter is statistically significant at the 10%. The lag of the inflation rate 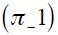 is positive on both regimes, but only statistically significant in regime 0. The coefficients associated to the lags on the interest rate
is positive on both regimes, but only statistically significant in regime 0. The coefficients associated to the lags on the interest rate 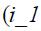 and
and 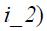 also switch signs across regimes. The first lag is always statistically significant at 10%, while the second lag is only significant in regime 1 when there is no explicit inflation targeting. Finally, the exchange rate lags are not statistically significant at any reasonable level in any regime which suggests that the interest rate is not sensitive in any regime to changes in this variable. In terms of practical significance the magnitudes of the coefficients also contrast from one regime to the other. Note that the coefficients on the output gap are much higher in magnitude in regime 1 than in regime 0.
also switch signs across regimes. The first lag is always statistically significant at 10%, while the second lag is only significant in regime 1 when there is no explicit inflation targeting. Finally, the exchange rate lags are not statistically significant at any reasonable level in any regime which suggests that the interest rate is not sensitive in any regime to changes in this variable. In terms of practical significance the magnitudes of the coefficients also contrast from one regime to the other. Note that the coefficients on the output gap are much higher in magnitude in regime 1 than in regime 0.
In this set up, the most important thing is the magnitude of the long run effects of a unit increase in both the output gap and the inflation rate. First, note that the long run effect of a unit increase in the output gap in period 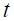 is reported in Table 3 as the coefficient on
is reported in Table 3 as the coefficient on 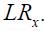 As seen in Table 3, the magnitude is 3.263 for this coefficient in regime 1 and 0.282 in regime 0. These point estimates might suggest that Colombia's central bank targeted the fluctuations on the output gap across regimes in different ways. Nonetheless, this is not true given that with bootstrap standard errors, the 90% confidence interval across both regimes includes zero. In fact, the confidence interval for the parameter in regime 1 includes the confidence interval for regime 0. Even though it may seem that Banco de la República presented a different behavior with respect to output fluctuations in both regimes according to the resulting point estimates, the standard errors show that this conclusion cannot be drawn in this case. Hence, we found no evidence that Banco de la República changed its behavior with respect to output fluctuations during the period studied.
As seen in Table 3, the magnitude is 3.263 for this coefficient in regime 1 and 0.282 in regime 0. These point estimates might suggest that Colombia's central bank targeted the fluctuations on the output gap across regimes in different ways. Nonetheless, this is not true given that with bootstrap standard errors, the 90% confidence interval across both regimes includes zero. In fact, the confidence interval for the parameter in regime 1 includes the confidence interval for regime 0. Even though it may seem that Banco de la República presented a different behavior with respect to output fluctuations in both regimes according to the resulting point estimates, the standard errors show that this conclusion cannot be drawn in this case. Hence, we found no evidence that Banco de la República changed its behavior with respect to output fluctuations during the period studied.
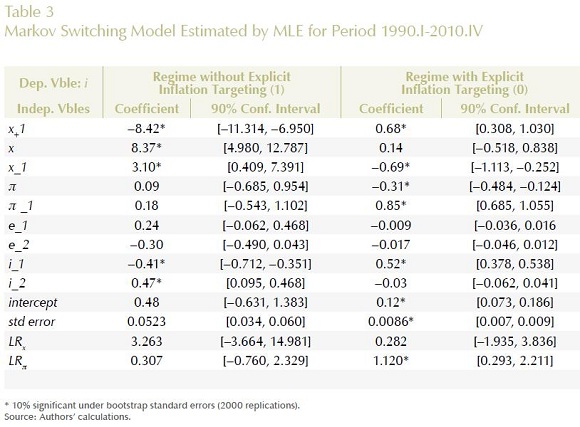
It is striking that the coefficients on the inflation rate are quite small in magnitude in regime 1 and much higher in regime 0. In fact, as the table reports, the long run effect of a unit increase in the inflation rate in period 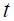 , denoted
, denoted 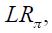 is only 0.307 in regime 1, whereas it is 1.12 in regime 0, which represents an almost four fold increase. Nonetheless, the 90% confidence interval for this parameter with bootstrap standard errors includes one in both regimes. In fact, the confidence interval for regime 1 (without explicit inflation targeting) includes the confidence interval for regime 0 (with explicit inflation targeting). Note that only in regime 0 does the confidence interval exclude the value zero. The sampling distributions for the estimator of parameter
is only 0.307 in regime 1, whereas it is 1.12 in regime 0, which represents an almost four fold increase. Nonetheless, the 90% confidence interval for this parameter with bootstrap standard errors includes one in both regimes. In fact, the confidence interval for regime 1 (without explicit inflation targeting) includes the confidence interval for regime 0 (with explicit inflation targeting). Note that only in regime 0 does the confidence interval exclude the value zero. The sampling distributions for the estimator of parameter 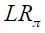 under the bootstrap procedure allowed us to calculate the probability that
under the bootstrap procedure allowed us to calculate the probability that 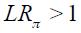 for both regimes. We found that for regime 1, the probability that
for both regimes. We found that for regime 1, the probability that 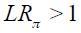 is only 0.26, whereas for regime 0, it increased to 0.55. This suggests that probabilistically, the Taylor principle is more likely satisfied in regime 0 than in regime 1.
is only 0.26, whereas for regime 0, it increased to 0.55. This suggests that probabilistically, the Taylor principle is more likely satisfied in regime 0 than in regime 1.
It is significant to point out that our previous result with the ADF Markov switching unit root test suggested that the inflation rate was stationary (resp. non stationary) in a regime called 0 (resp. regime 1), which coincides mainly with regime 0 (resp. regime 1) of explicit (resp. without explicit) inflation targeting for the Markov switching modified Taylor rule. According to Murray et al. (2008), it seems reasonable to conclude –and this is our main finding– that the Taylor principle was more likely satisfied in the regime with explicit inflation targeting (regime 0) than in the other regime (regime 1) as suggested by the point and interval estimates.
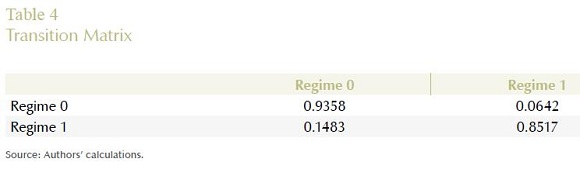
Table 4 reports the transition matrix between regimes of the Markov switching modified Taylor rule estimation which shows high persistency in regimes. As we can see, the probability of switching from regime 1, the non explicit inflation targeting state, to the inflation target regime 0 is equal to 0.1483, while the probability of switching from the inflation targeting regime 0 to the non explicit inflation targeting state 1 is 0.0642. This shows that once the inflation targeting regime state is reached, it is quite unlikely that one can switch.
Given the estimated transition probabilities, the average length of each state can be calculated using the following equations.
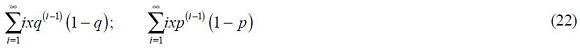
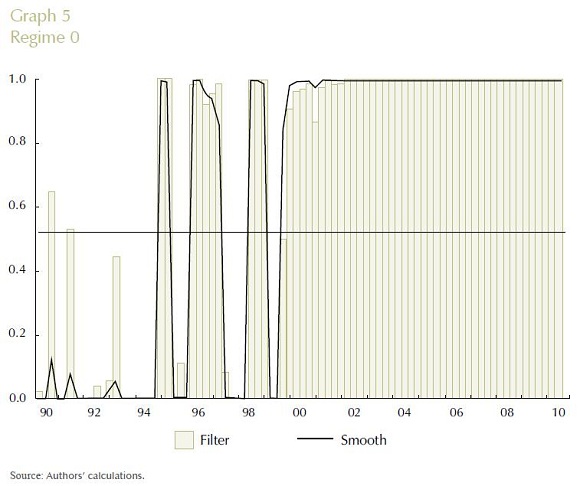
The first equation in (22) gives us the expected duration of state 1 and the second equation, the expected duration of state 0. Table 5 shows the properties of each regime. The average length of being in state 0 is 15.58 quarters, whereas for state 1, it is only 6.74 quarters.
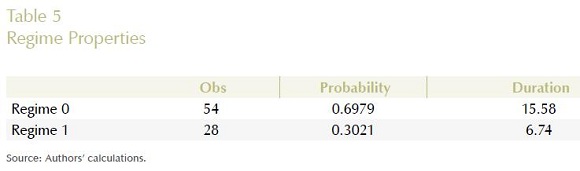
Graph 5 shows the evolution for each quarter from 1990.I to 2010.IV of the filter and smoothed probabilities of regime 0. As Graph 5 reveals, regime 0 of explicit inflation targeting is almost exclusively prevalent after the year 2000 (since it has a probability greater than a half), which approximately coincides with the Bank's announcement that it would be implementing explicit inflation targeting. The figure also reveals that regime 0 became prevalent somewhat before the year 2000 which suggests that the central bank adopted a policy consistent with the Taylor principle even before the announcement of adopting explicit inflation targeting in October of 2000. However, the monetary policy followed by Banco de la República between 1990.I and 2000.IV also had a behavior, in some quarters, consistent with regime 0. One of the reasons that could explain this result is that the Constitutional mandate of 1991 required that the central bank announce to the public a quantitative target of inflation for each year and that the central bank started to implement some elements of an inflation targeting strategy like models to forecast inflation (Gómez, Uribe and Vargas, 2002; Hernández and Tolosa, 2001) using the interest rate as an instrument of monetary policy.22
These results show that we have labeled regime 0 as an explicit inflation targeting regime as it became almost exclusively prevalent after 1999, according to figure 5. Furthermore, these results contrast with Bernal (2002) since she found, for the period 1991 to 1999, a coefficient of less than one on the output gap in a simple Taylor rule with interest rate smoothing, while we found a coefficient greater than one for the same period in which regime 1 was prevalent. Also and for the same period, Bernal (2002) found a coefficient greater than one on the inflation rate, in opposition to our results which suggest that in this period, regime 1 was prevalent and, accordingly, the Taylor principle was more likely violated.
VIII. CONCLUSIONS
This article has reconstructed the history of monetary policy of Colombia's central bank between 1990.I to 2010.IV when explicit inflation targeting was adopted by October of year 2000. We developed a theoretical modified Taylor rule with interest rate smoothing for an open and small economy and accordingly estimated a two regime Markov switching model. We found that one regime had explicit inflation targeting (from the year 2000 up to 2010) in which the inflation rate is a stationary series given that Banco de la República enforced a monetary policy that more likely satisfied the Taylor principle. The prevalent regime before the year 2000 did not satisfy the Taylor principle probabilistically, allowing a unit root behavior of the inflation rate. Moreover, we found no evidence that Banco de la República changed its behavior with respect to output fluctuations during the period studied.
COMMENTS
1 There were more structural changes such as a greater financial liberalization, a different exchange rate system among many others. In this sense the changes were not only institutional.
2 An introductory review about the role of a central bank can be seen in Mishkin (2007, chapter 2).
3 With the exchange rate band, the central bank expected to provide a credible market signal about expectations which were coherent with the inflation target. In its monetary policy strategy, the bank did not have the intention of keeping a fixed exchange rate regime or a highly volatile but flexible exchange rate regime. In practice, this exchange rate band had in some sense the best and worst of both exchange rate regimes. For example, when Colombia was exposed to a speculative attack on its local currency (peso) during the nineteen nineties, the central bank abandoned the interest rate band and aggregate monetary bands in order to maintain the exchange rate band. Nonetheless, the exchange rate band disappeared in September 1999. From that moment on, the exchange rate regime has a controlled flexibility.
4 As is known, monetary policy has a trilemma: when a central bank wishes to achieve three targets related to a target exchange rate, a target interest rate and free mobility of capital it is difficult to achieve the three objectives at the same time. The decision around these objectives and the restrictions involved the procedure to achieve the targets is summarized by Gómez (2006).
5 In order to capture the forward-looking characteristics of monetary policy (Mishkin, 2007, p. 39).
6 For a detailed treatment of the inflation targeting as a monetary policy regime see Svensson (2008, 2011).
7 As Bernal (2002) argues Banco de la República did have some space for changes in the intervention interest rate but only when the exchange rate was close to the two extremes of the exchange rate band.
8 Walsh (2003) presents a detailed discussion about this topic of monetary policy.
9 See (Walsh, 2003, chapter 7) for a detailed discussion.
10 In fact, Mishkin (1999) identifies a fourth regime, which is called "just do it", and argues that it is used in United States. However, this regime has an implicit rather than explicit nominal anchor.
11 Svensson (1997) identifies the forecast of inflation as the appropriate intermediate goal of monetary policy.
12 Taylor (1999) is a good compilation of many works undertaken in that tradition.
13 One criticism of simple interest rate rules is that, under certain circumstances, they may induce instability (Clarida, Gali and Gertler, 2000).
14 Orphanides (2003) and Jalil (2004) estimate it for the US economy while Kuzin (2004) for the German economy. For the Colombian case Bernal (2002), López (2004), Giraldo (2008) and Bernal and Tautiva (2008) can be reviewed.
15 Consider 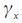 in the equation (2). If there is some mandate for the central bank to stabilize the economy, the way to do it is to include the output gap explicitly into the rule as McCallum (2001) has shown to be desirable. Although it is difficult to observe the gap since potential GDP must be estimated, which makes it difficult to evaluate the performance of the rule. However it is important to make an effort in order to estimate the variable because the central bank should stabilize the business cycles (Mishkin, 2007, chapter 4)
in the equation (2). If there is some mandate for the central bank to stabilize the economy, the way to do it is to include the output gap explicitly into the rule as McCallum (2001) has shown to be desirable. Although it is difficult to observe the gap since potential GDP must be estimated, which makes it difficult to evaluate the performance of the rule. However it is important to make an effort in order to estimate the variable because the central bank should stabilize the business cycles (Mishkin, 2007, chapter 4)
16 Although the interest rate inertia was born as an idea of empirical thought (Clarida, Gali and Gertler, 1998; Woodford, 2003a) Woodford (2003b) shows that under some circumstances it is optimal to include smoothing in the intervention interest rate for a central bank when some economic condition changes. Clarida et al. (1998) state that it is desirable because of the "...fear of disrupting capital markets, loss of credibility from sudden large policy reversals, the need for consensus building to support a policy change, etc" (Clarida, Gali and Gertler, 1998, p. 1038).
17 Svensson (2000), Ball (1999) and Taylor (2001) show that the original Taylor rule performs quite poorly in an open economy context which motivates us to deduce it within our optimal monetary rule.
18 This constancy of the Lagrange multipliers is a restriction since Woodford (2003a) does not impose it. Nonetheless, we do it to make the analysis tractable analytically as otherwise we would have had to resort to numerical simulations.
19 We get that 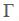 becomes positive and greater than one under the specific parametric value
becomes positive and greater than one under the specific parametric value 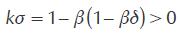 since now
since now 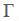 turns out to be
turns out to be 
20 Determining the number of states is crucial in characterizing the underlying Markov process. We considered initially a state space of three versus two regimes as well as two versus one regime. In this paper, the number of states was determined by Davies' test (1977). The existence of a non-linearity behavior was carried out via the classical likelihood ratio test.
21 See Bernanke and Mishkin (1997) and Bernanke, Laubach, Mishkin and Posen (2001).
22 An interesting anecdote comes to our attention which came through a conversation with former staff of Banco de la República. We presented a preliminary version of this paper in Banco de la República (October of 2011) which spurred some reactions and comments. One of the former governors of Banco de la República during the second half of the nineteen nineties tolds us that some characteristics of the explicit inflation targeting system was starting to be implemented in the bank during 1996 through 1998 following the work of Svensson and others. This was not publicly disclosed at that time. He was quite surprised that our Markov switching modified Taylor rule estimation would actually identify a regime consistent with explicit inflation targeting during precisely those years.
23 Let a given matrix be partitioned in a 2x2 blocked matrix 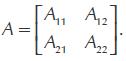 The determinant of A is given by
The determinant of A is given by 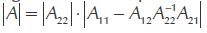
REFERENCES
1. Ball, L. "Policy Rules for Open Economies", in J. B. Taylor (Ed.), Monetary Policy Rules (vol. 31 of NBER Business Cycles Series, chap. 4, pp. 127-144), Chicago, NBER-University of Chicago Press, 1999. [ Links ]
2. Barro, R.; Gordon, D. "A Positive Theory of Monetary Policy in a Natural Rate Model", Journal of Political Economy, num. 91, pp. 589- 610, 1983. [ Links ]
3. Bernal, G.; Tautiva, J. "Relevancia de los datos en tiempo real en la estimación de la regla de taylor para Colombia", Tesis de Maestría en Economía, Bogotá, Pontificia Universidad Javeriana, 2008 [ Links ]
4. Bernal, R. "Monetary Policy Rules in Colombia", Documento CEDE, num. 2002-18, Bogotá, Universidad de los Andes, Centro de Estudios para el Desarrollo Económico, 2002. [ Links ]
5. Bernanke, B.; Mishkin, F. "Inflation Targeting: A New Framework for Monetary Policy", Journal of Economic Perspectives, vol. 11, num. 2, pp. 97-116, 1997. [ Links ]
6. Bernanke, B. S.; Laubach, T.; Mishkin, F. S.; Posen, A. S. Inflation Targeting: Lessons from the International Experience, Princeton, New Jersey, Princeton University Press, 2001. [ Links ]
7. Camacho, M. Markov-Switching Models and the Unit Root Hypothesis in Real U. S. GDP, Departamento de Métodos Cuantitativos para la Economía y la Empresa, Facultad de Economía y Empresa, Universidad de Murcia, http://www. um.es/econometria/Maximo/articulos/MSUR. pdf, 2010. [ Links ]
8. Clarida, R.; Gali, J.; Gertler, M. Monetary Policy Rules in Practice: Some International Evidence", European Economic Review, num. 42, pp. 1033-1067, 1998. [ Links ]
9. Clarida, R.; Gali, J.; Gertler, M. "Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory", Quarterly Journal of Economics, vol. 115, num. 1, pp. 147-180, 2000. [ Links ]
10. Davies, R. B. "Hypothesis Testing when a Nuisance Parameter is Present only under Alternative", Biometrika, num. 64, pp. 247-254, 1977. [ Links ]
11. Friedman, M. "The Role of Monetary Policy", American Economic Review, vol. 58, num. 1, pp. 1-17, 1968. [ Links ]
12. Giraldo, A. "Aversión a la inflación y regla de Taylor en Colombia 1994-2005", Cuadernos de Economía, vol. XXVII, núm. 49, pp. 229-262, Bogotá, Universidad Nacional de Colombia, 2008. [ Links ]
13. Gómez, J. "La política monetaria en Colombia", Borradores de Economía, núm. 394, Bogotá, Banco de la República, 2006. [ Links ]
14. Gómez, J.; Uribe, J.; Vargas, H. "The Implementing of Inflation Targeting in Colombia", Borradores de Economía, num. 202, Bogotá, Banco de la República, 2002. [ Links ]
15. Hamilton, J.D. Time Series Analysis, Princeton, Princeton University Press, 1994. [ Links ]
16. Hall, S. G.; Psaradakis, Z.; Sola, M. "Detecting Periodically Collapsing Bubbles: A Markov- Switching Unit Root Test", Journal of Applied Econometrics, num. 14, pp. 143-154, 1999. [ Links ]
17. Hernández, A.; Tolosa, J. "La política monetaria en Colombia en la segunda mitad de los años noventa", Borradores de Economía, núm. 172, Bogotá, Banco de la República, 2001. [ Links ]
18. Jalil, M. Monetary Policy in Retrospective: A Taylor Rule Inspired Exercise, San Diego, University of California, 2004. [ Links ]
19. Kalmanovitz, S. Ensayos sobre banca central. Comportamiento, independencia e historia, Editorial Norma, Colección Vitral, 2003. [ Links ]
20. Krolzig H. M. Markov-Switching Vector Autoregressive. Modelling, Statistical Inference and Application to Business Cycle Analysis. Lecture Notes in Economics and Mathematical Systems, Berlin, Springer, 1997. [ Links ]
21. Kuzin, V. "The Inflation Aversion of the Bundesbank: A State Space Approach", Journal of Economic Dynamics and Control, vol. 30, num. 2006, pp. 1671-1686, 2004. [ Links ]
22. Kydland, F.; Prescott, E. "Rules Rather than Discretion: The Inconsistency of Optimal Plans", Journal of Political Economy, num. 85, pp. 473- 492, 1977. [ Links ]
23. López, M. "Efficient Policy Rule for Inflation Targeting in Colombia", Ensayos sobre Política Económica, núm. 45, pp. 80-115, 2004. [ Links ]
24. McCallum, B. T. "Should Monetary Policy Respond Strongly to Output Gaps?" The American Economic Review, vol. 91, num. 2, pp. 258-262, 2001. [ Links ]
25. Mishkin, F. "International Experiences with Different Monetary Policy Regimes", Journal of Monetary Economics, vol. 43, num. 3, pp. 579- 605, 1999. [ Links ]
26. Mishkin, F. Monetary Policy Strategies, MIT Press, 2007. [ Links ]
27. Murray, C. J.; Nikolsko-Rzhevskyy, A. Papell, D. H. "Inflation Persistence and the Taylor principle", MPRA Paper, num. 11353, 2008. [ Links ]
28. Orphanides, A. "Historical Monetary Policy Analysis and the Taylor Rules", Journal of Monetary Economics, num. 50, pp. 983-1022, 2003. [ Links ]
29. Orphanides, A. "Monetary Policy Rules, Macroeconomic Stability, and Inflation: A View from the Trenches," Journal of Money, Credit, and Banking, num. 36, pp. 151-175, 2004. [ Links ]
30. Orphanides, A. "Taylor rules", in S. N. Durlauf and L. E. Blume (Eds.), The New Palgrave Dictionary of Economics (2nd ed.), Palgrave Macmillan, 2008. The New Palgrave Dictionary of Economics Online. Palgrave Macmillan. 09 May 2012. http://www.dictionaryofeconomics. com /ar ticle?id=pde2008_T000215 doi:10.1057/9780230226203.1686 [ Links ]
31. Sánchez, F.; Fernández, A.; Armenta, A. J. "Historia monetaria colombiana durante el siglo XX", in J. Robinson and M. Urrutia (Eds.), Economía colombiana del Siglo XX (chap. 7, pp. 313-382), Bogotá, Fondo de Cultura Económica- Banco de la República, 2007. [ Links ]
32. Svensson, L. "Inflation Forecast Targeting: Implementing and Monitoring Inflation Targets", European Economic Review, num. 41, pp. 1111- 1146, 1997. [ Links ]
33. Svensson, L. "Open-Economy Inflation Targeting", Journal of International Economics, vol. 50, num. 1, pp. 155-183, 2000. [ Links ]
34. Svensson, L. "Inflation targeting." The New Palgrave Dictionary of Economics. Second Edition. Eds. Steven N. Durlauf and Lawrence E. Blume. Palgrave Macmillan, 2008. The New Palgrave Dictionary of Economics Online. Palgrave Macmillan. 09 May 2012
35. Svensson, L. "Inflation Targeting", in B. M. Friedman and M. Woodford (Eds.), Handbook of Monetary Economics (vol. 3B, chap. 22, pp. 1237-1302), Elsevier B. V., San Diego, 2011. [ Links ]
36. Taylor, J. B. "Discretion Versus Policy Rules in Practice", Carnegie-Rochester Conference Series on Public Policy, num. 39, pp. 195-214, 1993. [ Links ]
37. Taylor, J. B., (Ed.). "Monetary Policy Rules", Business Cycles Series, vol. 31, National Bureau of Economic Research, 1999. [ Links ]
38. Taylor, J. B. "The Role of the Exchange Rate in Monetary-Policy Rules", The American Economic Review, vol. 91, num. 2, pp. 263-267, 2001. [ Links ]
39. Walsh, C. Monetary Theory and Policy (2nd ed.), MIT Press, 2003. [ Links ]
40. Woodford, M. Interest and Prices. Foundations of a Theory of Monetary Policy, Princeton, New Jersey, Princeton University Press, 2003a. [ Links ] 41. Woodford, M. "Optimal Interest-Rate Smoothing", Review of Economic Studies, num. 70, pp. 861-886, 2003b. [ Links ]
41. Woodford, M. "Optimal Interest-Rate Smoothing", Review of Economic Studies, num. 70, pp. 861-886, 2003b.
APPENDIX
1. MODIFIED TAYLOR RULE WITH INTEREST RATE SMOOTHING
Equation (11) is derived here explicitly. Note that the fundamental problem to be solved is
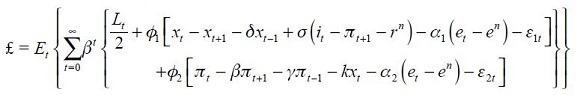
where
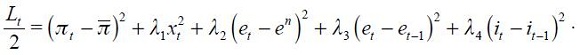
and where we restrict 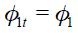 and
and 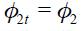 for all
for all 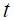 . Since the loss function is quadratic the following first order conditions that solve the optimization program are necessary and sufficient
. Since the loss function is quadratic the following first order conditions that solve the optimization program are necessary and sufficient
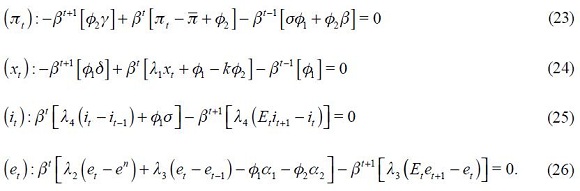
From (23) we get

while from (24) we obtain
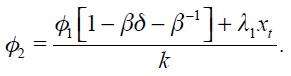
Equalizing these last two equations yields
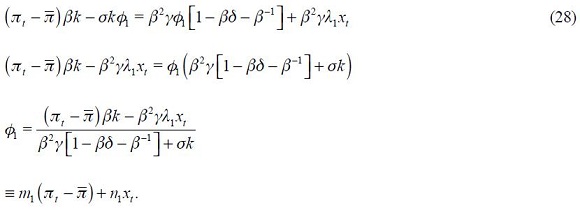
where the  and
and  are functions of parameters given by
are functions of parameters given by
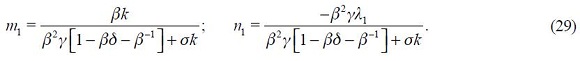
Note that in general 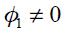 unless
unless 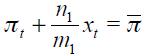 which we rule out by assumption. Equation (28) replaced in (27) gives us
which we rule out by assumption. Equation (28) replaced in (27) gives us
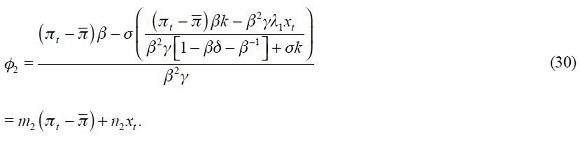
where
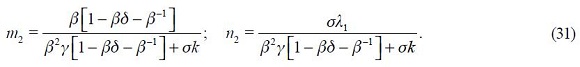
Note again that 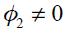 unless
unless 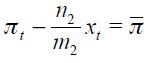 which again we rule out by assumption. Now from equation (25) we get
which again we rule out by assumption. Now from equation (25) we get
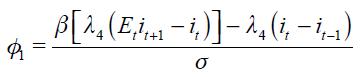
which equalized with (28) yields
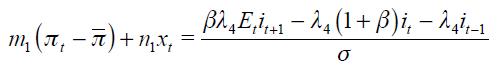
which rearranged and lagged one period gives us
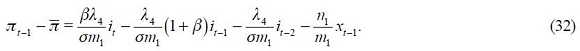
While from equation (26) we get
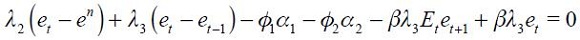
and using (28) and (30) to replace  and
and 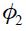 allows us to obtain
allows us to obtain
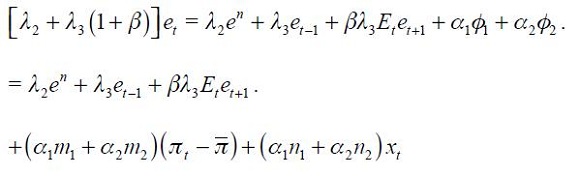
or equivalently when lagged one period and rearranged
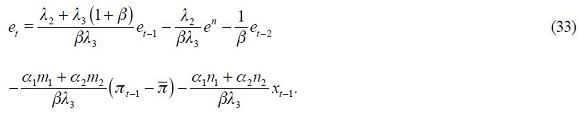
Replacing (33) in (32) one gets a simple expression that allows us to reduce the four FOC (23), (24), (25) and (26) in one single equation without the endogenous variables 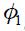 and
and 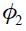 explicitly
explicitly
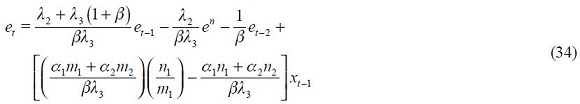
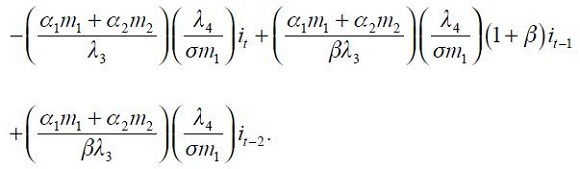
From (4) one has the following expression rearranged such that 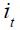 is on the left hand side
is on the left hand side
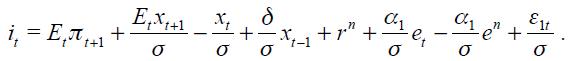
while from (5) we get
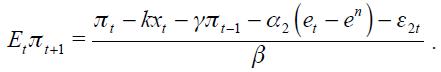
which inserted in the former equation yields
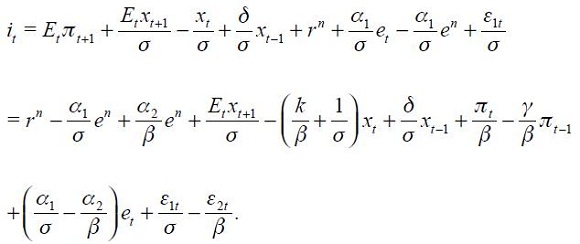
Note that in this last equation we have not made use of the four first order conditions derived in solving the minimization problem. Since equation (34) collapsed all first order conditions in one single equation, where 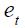 is a function of the other endogenous variables, we can actually insert equation (34) in this last equation to arrive at
is a function of the other endogenous variables, we can actually insert equation (34) in this last equation to arrive at
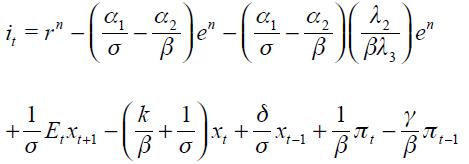
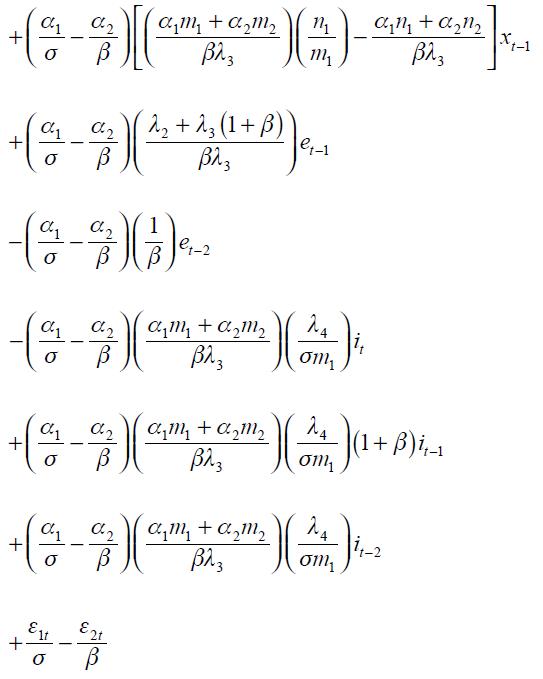
which rearranged leaving  on the left hand side finally gives us
on the left hand side finally gives us
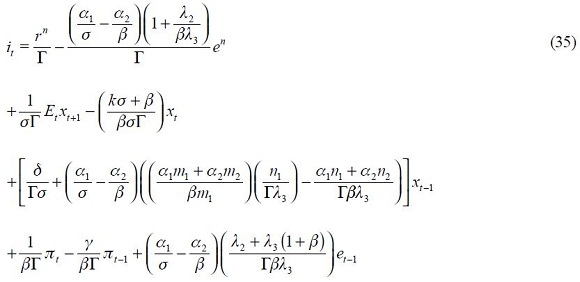
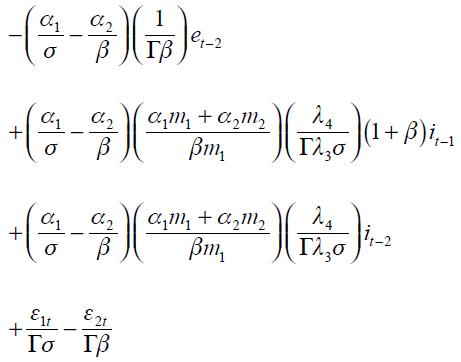
where
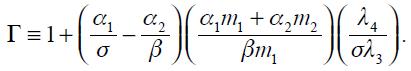
Note that from (29) and (31) we get
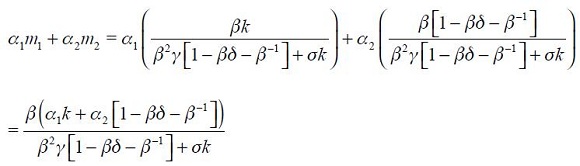
which then implies
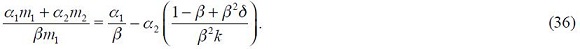
Hence, we can write 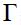 as
as
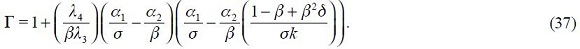
2. LINEAR DYNAMIC SYSTEM
We can rewrite the system (4), (5), (32) and (33) recursively as a discrete linear dynamic system in order to show the existence of a stationary state. Consider first, equation (32) which can be forwarded one period and rearranged to yield
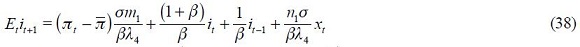
while equation (39) can also be forwarded one period to result in
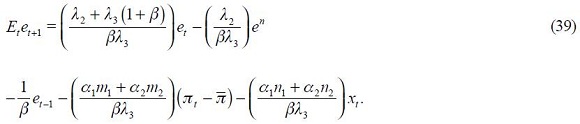
Now, equations (4) and (5) can be rewritten as
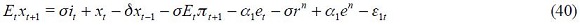
and
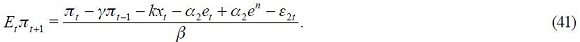
Replace (41) in (40) to get
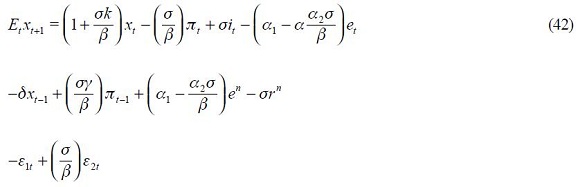
Under  for all
for all 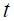 in a steady state we can write equations (38), (39), (41) and (42) as a second order non-homogenous linear system
in a steady state we can write equations (38), (39), (41) and (42) as a second order non-homogenous linear system

where

A convenient way to analyze this system is to transform it into a first order nonhomogenous linear system. To do so define 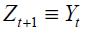 so that
so that 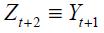 and rewrite (43) as
and rewrite (43) as
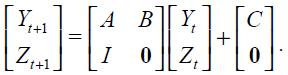
or equivalently as

where 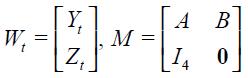 and
and 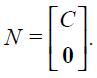 Note that W is a 8x1 vector as well as N while M is an 8x8 matrix.
Note that W is a 8x1 vector as well as N while M is an 8x8 matrix.
3. EXISTENCE AND UNIQUENESS OF A STEADY STATE
Proposition 6. The dynamic system (44) has a unique steady state if 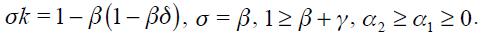
To prove this result note that in a steady state, one should have 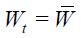 for all
for all 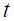 in (44). Hence to prove the existence and uniqueness of a steady state, one should find the conditions that guarantee that
in (44). Hence to prove the existence and uniqueness of a steady state, one should find the conditions that guarantee that 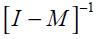 exists so that one can compute
exists so that one can compute
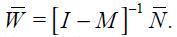
Hence, a necessary condition is that 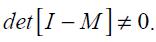 To get the sufficient conditions under which this determinant is non zero note that
To get the sufficient conditions under which this determinant is non zero note that
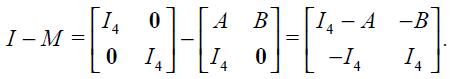
By the formula for the determinant of a partition matrix23 one has
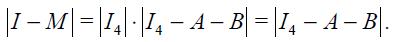
Therefore consider
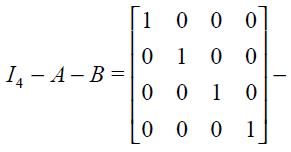

The determinant of 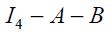 can be obtained easily using cofactors through the third column of the matrix which reduces to
can be obtained easily using cofactors through the third column of the matrix which reduces to
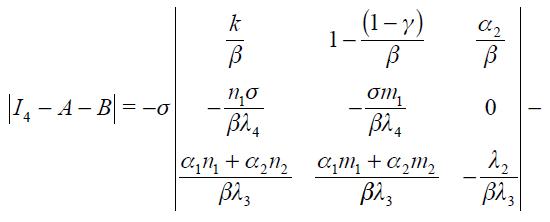

Equivalently the determinant of 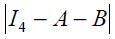 is
is
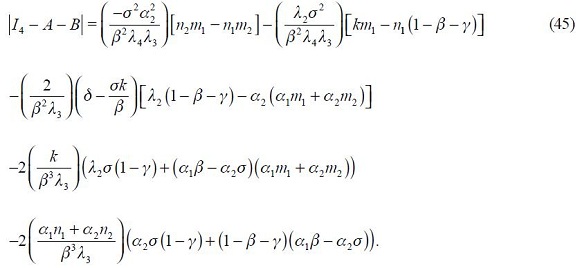
Under 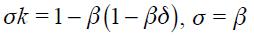 and the definitions of
and the definitions of  we have that
we have that
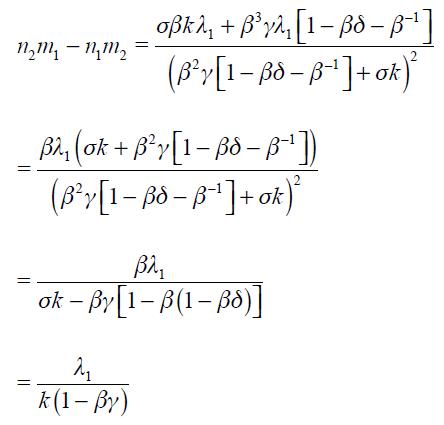
which is positive as well as
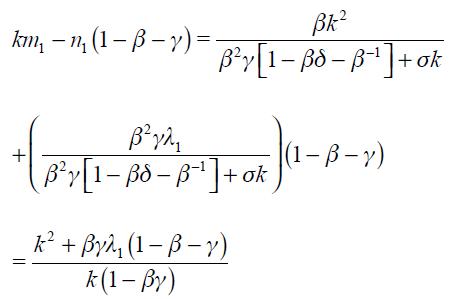
given that 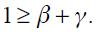 Moreover note that
Moreover note that
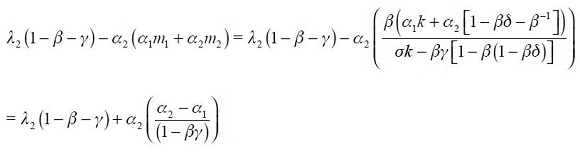
is positive under 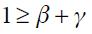 and
and 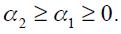 Furthermore, note that
Furthermore, note that
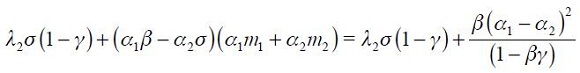
which is always positive. Consider now
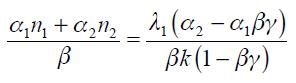
which is positive under 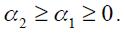 Finally, consider
Finally, consider
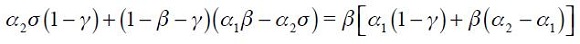
which is also positive under 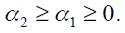 Taking into account all the terms developed above and replacing them in (45) under
Taking into account all the terms developed above and replacing them in (45) under 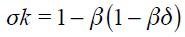 which implies
which implies 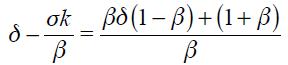 yields
yields
which has a strictly negative sign. Hence, a unique steady state exists.













