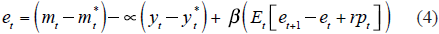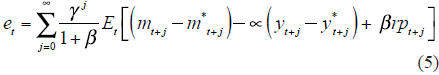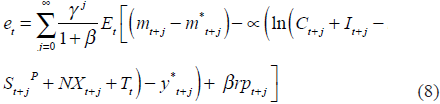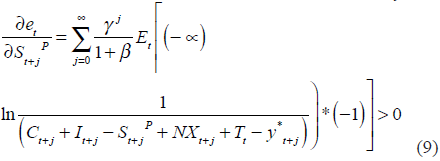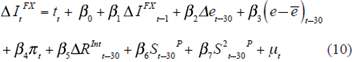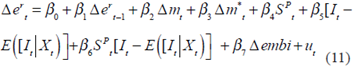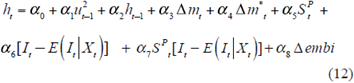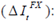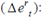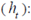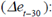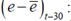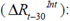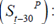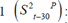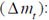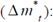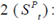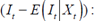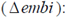1. Introduction
Since the enactment of the new Colombian Political Constitution (PC)1 in 1991, Banco de la República2 (BR) started a process of extreme make over3. Before 1991, BR acted as a development bank that funded the public and private sector alike, with resources coming from inflationary emission4,5. The new PC established a clear mandate for BR of maintaining the purchasing power of the peso, with political independence from the Government, and technical and asset autonomy. BR became the monetary, exchange rate and credit authority. This was the first of two steps in gaining a much higher credibility that would help BR to bring inflation rates down6.
The second step was the implementation of the Inflation Targeting Regime (IT) framework with a floating exchange rate, as a replacement for the exchange rate bands7 used from 1994 to 19998. With the IT framework, BR gained a broader credibility and managed to anchor inflationary expectations9, to the point of using the monetary policy in a countercyclical sense, something never before accomplished in the history of Colombia´s monetary policy10.
The IT framework has been very popular among developed and developing countries because of its main features -including the use of a repo rate as the policy instrument, the announcement of medium-term inflation targets, and a clear and comprehensive communication strategy-, but also because of its evolution over time in response to new economic difficulties11. Plausible changes to the IT framework include: i) additional policy goals other than delivering low and stable inflation, and ii) the use of extra tools apart from the repo rate, such as FXI, reserve requirements on domestic financial liabilities, regulations on foreign capital flows, dynamic provisioning or loan-to-value limits. In various countries of the region, the IT framework practice has expanded through the use of additional instruments, in particular FXI. Barajas et al. (2014) find, in the cases of Brazil, Chile, Colombia and Peru, strong evidence that Central Bank (CB) interventions in foreign exchange markets present systematic response to objectives other than pure inflation stabilization, with special regard for levels of exchange rate misalignments rather than concerns over exchange rate volatility, which is contrary to official bank statements.
This result puts the controversy surrounding the sterilized FXI and its effectiveness on influencing the exchange rate back on the table. How can a CB influence the exchange rate without altering the monetary base? Under which conditions is it plausible? The literature recognizes three theoretical channels through which sterilized FXI might have an effect on the exchange rate: i) the portfolio balance channel; ii) the signaling channel; and iii) the coordinating channel. This paper focuses on a macroeconomic condition that would provide a sound environment for the portfolio balance channel to work properly, thus making sterilized FXI effective. Therefore, three questions arise: i) When is it possible for the portfolio balance channel to work well (which is the key variable)? ii) What are the determinants of the FX preannounced day-to-day interventions done by BR? And iii) is sterilized FXI effective in reducing exchange rate volatility in the presence of public savings?
This paper attempts to give an empirical answer to these questions for the Colombian case over the 2010-2014 period12. First, the paper explains the theoretical macroeconomic condition through which the portfolio balance channel is active, where public savings stand as the key variable. Second, it provides a literature review with a quick overview of the articles written on the effectiveness of the sterilized FXI for the Colombian case and the causes of intervention. Third, preliminary data analysis is undertaken. In the fourth place, the empirical models used to test the different hypotheses are outlined with their corresponding results. Finally, conclusions are drawn.
2. Literature Review
2.1 Portfolio Balance Channel Plausibility and Public Savings
The theory of the portfolio balance channel affirms that when authorities intervene in the exchange rate markets, the relative supply of domestic currency bonds is modified and the exchange rate must change as agents try to rebalance their portfolios. However, this only occurs assuming the following: i) foreign and domestic bonds are imperfect substitutes, in such a way that agents are not indifferent to the relative holding of assets; and ii) the Ricardian equivalence does not hold, given that if investors perceive the increase in the supply of domestic bonds as a rise in future taxation they will not increase their demand for these assets. Therefore, if a CB wants to conduct FXI without jeopardizing the inflation target, finding a condition through which the portfolio channel is active is essential. This condition is nothing more than a macroeconomic situation that can be captured by a single variable: public savings.
In the literature, there are two articles where the authors construct the theoretical framework through which public savings might act as the key variable for enhancing the effectiveness of sterilized FXI. Nevertheless, it is necessary to point out that this conclusion is not made explicit by the authors; instead, it is a construction based on the theoretical foundations provided by them. By using a DSGE model, Kumhof & Nieuwerburgh (2007) and Kumhof (2010) simulate a fiscal exogenous shock, where the Government experiences a major and unexpected income cut13. In this situation, the fiscal policy is exogenous in the sense that the exchange rate adjusts instantaneously, and permanently, to balance the government’s budget. This implies that money is endogenous, and more specifically, that the money supply is adjusted instantaneously to accommodate the exchange rate movement needed by the fiscal balance. However, after this exchange rate jump, fiscal policy is again assumed to be endogenous, or passive, in that it adjusts anticipated or drifted taxation to ensure solvency. The fiscally induced exchange rate shock increases in the volatility of the fiscal shocks but decreases in the amount of nominal government debt held in household’s portfolios. A larger stock of nominal debt can be revalued by nominal exchange rate’s (NER) movements, representing a larger base of inflation tax14.
This exchange rate’s depreciation affects households that hold domestic currency debt in two ways. First, depreciation reduces the realized (ex-post) real return in terms of tradables, therefore, households are going to request higher nominal returns to maintain or increase their asset holdings. Second, according to Jensen’s inequality, larger exchange rate volatility increases the expected (ex-ante) real return, because the real value of nominal assets is convex in the exchange rate. For these reasons, the perfect substitutability between foreign and domestic currency assets no longer holds and the uncovered interest parity is replaced by a portfolio balance equation among interest rates that depends positively on outstanding stock of government debt.
This relationship features an additional term that is the agents’ portfolio´s share of domestic currency assets. A higher portfolio share reduces the currency risk of holding domestic bonds (due to the existence of a larger base for an inflation tax, instead of large jumps in the exchange rate), thereby decreasing the exchange rate’s volatility, reducing the real return and reinforcing the effect of the higher nominal mean return required by households. The result is a monotonically increasing and concave relationship between the interest rate and domestic currency government debt, and a monotonically decreasing relationship between the interest rate and exchange rate risk (smaller exchange rate jumps are needed to rebalance the government’s budgetary constraint).
In this scenario, the sterilized FXI becomes a second and independent monetary policy that affects portfolios, interest rates, consumption and exchange rates. A purchase of FX is sterilized through domestic government bond issuance, increasing the domestic public debt stock and the domestic interest rate, leaving the money supply unchanged and obtaining a depreciated and less volatile nominal exchange rate. An important conclusion gathered from Kumhof & Nieuwerburgh (2007) and Kumhof (2010), is that the smaller the initial stock of debt that is issued, the larger the space for sterilized FXI to depreciate the exchange rate and reduce its volatility. Conversely, the more public savings, the more effective the sterilized the FXI becomes. The objective of the paper is to find out if this holds empirically15.
The next step is to build the economic equation from which the econometric specification will be obtained. To do so, the result must be an equation that explains the NER in terms of nominal and real variables. Following Villamizar & Perez (2015), the starting point is the Uncovered Interest Parity Condition:
Where e is the log exchange rate, i is the domestic interest rate, i* is the foreign interest rate and rp is the risk premium. Equation (1) describes the exchange rate behavior in the short run. In the long run, currencies should have equal purchasing power. Therefore, the “generalized law of one price” is expressed as:
Where e is the log exchange rate, p denotes the log of the price of a representative basket of goods and services in a certain country. The next step is to add the money market equilibrium equation to the model, which is typically expressed as:
Where m is the money supply, y corresponds to real output, and i is the short-term interest rate (all variables expressed as logs). By substituting (1) and (3) into (2), we obtain:
By iterating (4) forward and defining 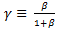 yields:
yields:
Finally, it is necessary to incorporate the key variable of the paper into (5). We know from the basic macroeconomic identity that:
Where y corresponds to the real output, C is the aggregate private consumption, I is the aggregate investment16, G is the Government aggregate expenditure, and NX equals net exports. By adding and subtracting T (taxes) from (6) it is found that:
Where 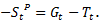 Then equation (7) is introduced into (5):
Then equation (7) is introduced into (5):
Then, to learn how public savings may affect the NER, it is necessary to derive (8) with respect to  :
:
As it turns out, (8) and (9) state that the exchange rate behavior responds to nominal and real variables alike. In this sense, macroeconomic variables complement monetary policy in determining the NER; public savings appear within these macroeconomic variables. As expected, more public savings means a more depreciated NER.
2.2. The Determinants and Effectiveness of Foreign Exchange Intervention in Colombia
There is ample literature on the determinants and the effectiveness of sterilized FXI for the Colombian case. Echavarría et al. (2010) found, by using a Tobit model, that BR´s FX purchases for the 2000-2008 period were done to compensate for the day-to-day revaluation, correcting for excessive deviations from the trend when inflation pressures were low and when BR was a net creditor for private banks. The authors also use an E-GARCH model to show that FX purchases devalued the exchange rate and reduced its volatility in the short- and medium-term. On the other hand, Rincón & Toro (2011), using high frequency data for the 1993-2010 period and a GARCH model, concluded that FXI was not effective in depreciating the NER. Nevertheless, when FXI was used simultaneously with capital controls in the 2008-2010 period, a significant statistical effect was found and daily average depreciation was accomplished. Additionally, Echavarría et al. (2013) compared the effects of the pre-announced day-to-day interventions, carried out between 2008 and 2012, with the discretionary interventions done in the 2004-2007 period by combining a Tobit-GARCH reaction function with an asymmetric power GARCH (APGARCH(1,1)) impact function. The results show that the day-to-day interventions had a much larger impact on the NER than the discretionary or dirty interventions. Echavarría et al. (2014) evaluate the effectiveness of different types of interventions done in the 2000-2012 period. Their methodological approach was a non-parametric model that did not impose assumptions as restrictive as the structural models. They used an event study methodology, finding that all types of interventions were successful according to the Smoothing Criterion. Finally, Durán (2015) analyzed the effectiveness of FXI for the 2008-2013 period following Hansen (2000) and his methodology. Here, the author found that FXI had a considerable and statistically significant effect in depreciating the NER when the spot exchange rate was sufficiently below its fundamental value.
In most of the aforementioned papers (and others), which search for determinants and/ or the impact of sterilized FXI on the volatility or level of the NER, the explanatory variables used by the authors are the different types of sterilized FXI, risk premiums, interest rates’ differential, capital controls, foreign exchange reserves’ stock, and even some real variables, such as the terms of trade mentioned in Rincón & Toro (2011), productivity, stated in Engel et al. (2007), or the relative price of tradable and non-tradable goods, revealed by Chinn (2012). Nonetheless, there are no signs of public savings, or the economy’s total savings for that matter. This is the paper´s most important contribution: public savings as the key determinant of the FXI´s impact on the NER volatility.
3. Preliminary Data Analysis
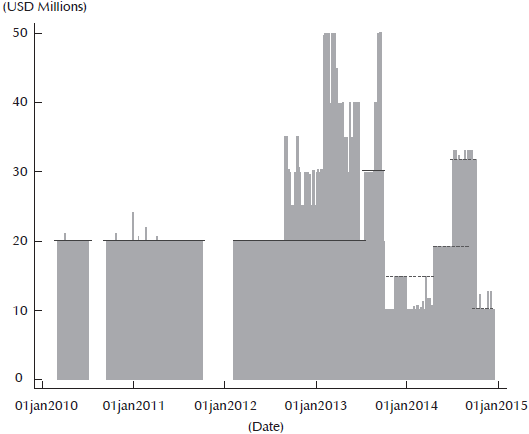
Before BR started using pre-announced day-to-day interventions, it used other kinds of FXI17. However, this study is going to focus on pre-announced day-to-day interventions for the 2010-2014 period. The interventions started in late June 2008 and stopped in the first days of October of the same year. They were used again in March 2010. This large gap in the data of more than one year, would complicate the paper´s analysis, therefore, the 2008 FXI is not included.
From 2010 to 2014, BR intervened in the FX market an average of 205 days per year. The intervention mean throughout the whole period was of USD 21.6 million, per day of intervention. The maximum amount of FX purchased was USD 50 million in 2013; the minimum amount was USD 5 million in 2014 (Table 1). The largest number of USD were purchased in 2013, with a total amount of 6,770 million, while the least USD were purchased in 2010, with a total amount of 3,020 million. Throughout the five years of study, no USD sales were made, and there were no other types of interventions being held at the same time as the pre-announced day-to-day FX purchases.
Table 1 Pre-Announced Day-to-Day FX Purchases 2010-20141
1 All values in millions of USD unless otherwise noted.
Source: Author’s calculations based on Banco de la República.
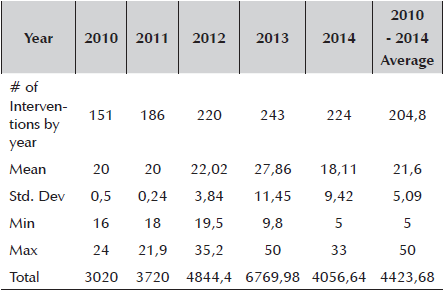
2010-2014 was a period of NER appreciation. The NER average for the last 15 years was of COP/USD 2,214.5, while the average for the 2010-2014 period was of COP/USD 1,882.6. The most depreciated NER occurred in 2014, with an annual average of COP/USD 2000.3, and the most appreciated NER occurred in 2012, with an annual average of COP/USD 1,797.8. As table 2 shows, the years that presented the most depreciated NER are also the ones with the largest standard deviations. From 2010 to 2014, the NER moved between a wide range of COP/USD 1,748.4 as a minimum in 2011, to a maximum of COP/USD 2,446.4 by the end of 2014.
Table 2 NER Descriptive Statistics1: Was 2010-2014 a NER Appreciation Period?
1 All values in COP unless otherwise noted.
Source: Author’s calculations based on Banco de la República.
One of this paper´s main challenges, is the reconciliation of a high frequency variable such as the exchange rate, with a low frequency variable such as the public savings, understood -in a standard macroeconomic model- as the difference between fiscal revenue and expenditure. Because of this, the paper uses one of the highest frequency fiscal variables available, the Central Government’s Balance. While the Non-Financial Public Sector’s Balance data has a quarterly frequency, the Central Government’s Balance data has a monthly frequency, providing much more information and variance. However, it is important to know about this variable´s construction in order to understand if it is a good proxy for the standard macroeconomic definition. The Central Government’s Balance is the monthly difference between the Central Government’s revenue, -which is the monthly tax´s and capital returns’ revenue-, and the Central Government’s expenditure, which is built by summing effective payments and the change in the “budgetary lag” or the “floating debt”18.
As can be seen, the Central Government’s Balance is closely related to the standard macroeconomic definition. Nonetheless, a strong counter that may arise to the use of this variable, is that it reflects only the Central Government’s liquidity position and not public savings. In other words, the Central Government does not make debt issuance decisions on a month-by-month basis; debt issuance decisions are made with a lower frequency. A counterargument is that the debt issuance decision is made by adding the month by month excess or lack of Central Government’s liquidity captured by the Central Government’s fiscal balance.
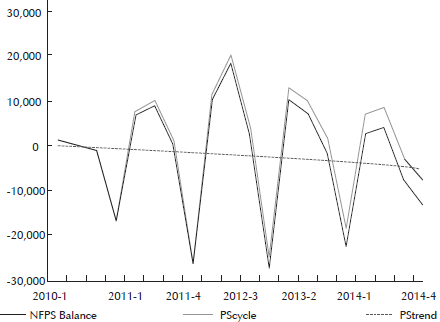
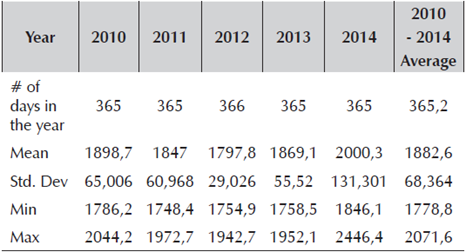
To explore the periods in which there were public savings, the Central Government’s Balance was filtered with a Hodrick-Prescott Filter, separating the trend from the series´ cycle. As shown in Graph 1, the trend of the Central Government’s Balance is negative all through the period of study, meaning that this was mostly a period of dissaving. The periods considered as public saving periods for the preliminary data analysis are the months for which the Central Government’s balance cycle is above the trend. Between the years 2010 and 2014, there was a total of 40 months of public saving.
Source: Author’s Calculations based on MHCP.
Figure 1 Central Government’s Balance Series Components
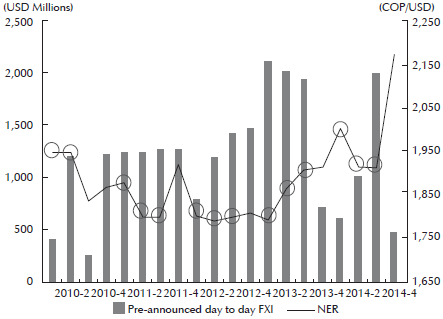
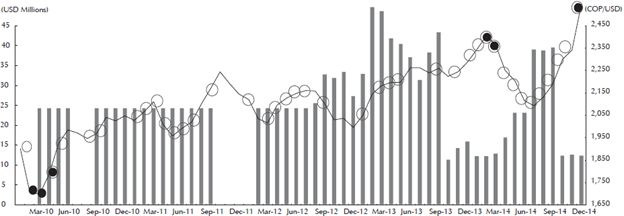
Figure 2 shows the 40 different moments of public saving, the pre-announced day-to-day FX purchases and the NER series. No explicit pattern is exhibited in between the public saving’s periods, the NER or the FXI from January 2010 to September 2011. Since August 2012 until the end of the period of interest, the pre-announced day-to-day FXI series have a symmetrical pattern with the NER series. From this date on, the FX purchases increased and the amounts purchased became much more volatile. The reason for the change in the FXI’s behavior will be explained later on.
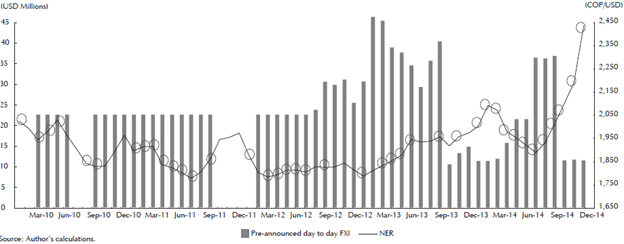
Source: Author’s calculations based on Banco de la República and MHCP.
Figure 2 Public Saving Periods, NER and Pre-Announced Day-to-Day FX Purchases (2010-2014)
As a preliminary exercise, a t-test is used to observe if the NER depreciated or appreciated more in periods of public saving, in comparison to periods of public dissaving (Table 3). The t-test gives evidence of a more depreciated NER in public saving periods, in comparison with public dissaving ones. In periods where internal savings are present, it is less urgent to acquire foreign funds, therefore, the amount of USD present in the economy is smaller, making the exchange of COP per USD more expensive, or, in other words, making the NER more depreciated.
Table 3 T-Test: Was the NER more Depreciated in Public Saving Periods?
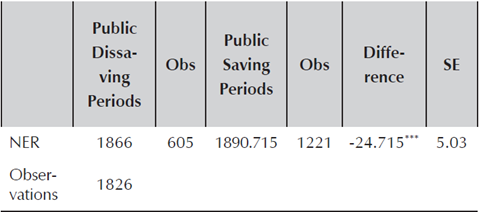
***p<0.01, **p<0.05, *p<0.1
Source: Author’s calculations based on Banco de la República and MHCP.
A t-test is also used to compare the NER growth in periods of public saving with those of public dissaving. The t-test of table 4 supports the idea of a less appreciated NER in public saving periods.
Table 4 T-Test: Was the NER more Depreciated in Public Saving Periods?
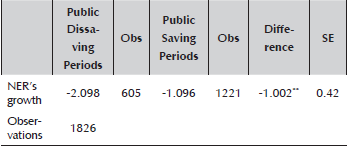
***p<0.01, **p<0.05, *p<0.1
Source: Author’s calculations based on Banco de la República and MHCP.
To continue exploring the relationship between public savings and the NER, it is necessary to delve into the NER’s growth, the NER’s volatility and public savings´ behavior. The liaison between these variables is of special interest to this paper. The result variable chosen to measure the effectiveness of the FXI in the presence of public saving is the NER’s volatility. This variable was selected over others, such as a given exchange rate equilibrium level, because the NER´s volatility is much easier to define, while finding a long run level of exchange rate equilibrium would mean a much larger amount of work and unnecessary controversy19,20.
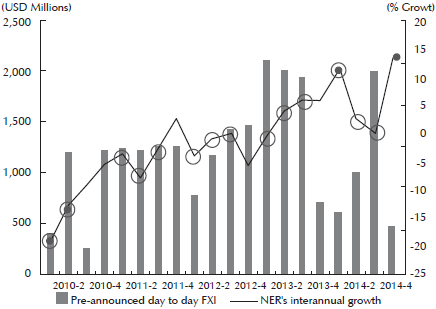
Table 5 exhibits the inter-annual growth of the NER for the 2010-2014 period. In 2010, the NER appreciated the most on average, and it was also the year with the largest standard deviation. In 2014, on the other hand, the NER depreciated the most on average. Graph 3 shows the NER’s growth, along with the FXI’s amounts, and the 40 public saving periods. The red dots represent the six periods in which the NER’s growth showed the largest increases/decreases. 4 of the 6 dots matched the public saving periods. Nevertheless, only 2 of the 6 periods were of actual fiscal surplus. So, an important pattern emerges from graph 3. The periods of public saving match the periods of smaller NER volatility.
Table 5 NER´s Inter-Annual Growth Descriptive Statistics*: Was 2010-2014 a NER Appreciation Period?
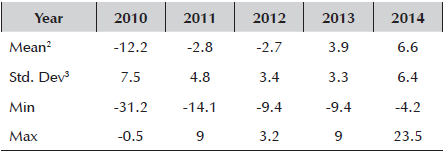
1 All values in percentage growth unless otherwise noted.
2 Is the annual average growth of the NER.
3 Is the annual NER’s average growth standard deviation.
Source: Author’s calculations based on Banco de la República.
Source: Author’s calculations
Figure 3 Public Saving Periods, the NER’s Inter-Annual Growth and the Pre-Announced Day-to-Day FX Purchases (2010-2014)
Returning to the periodicity controversy of the public savings variable, it is important to show evidence of similarities between the Central Government´s Fiscal Balance --the chosen variable- and the Non-Financial Public Sector’s Balance -an alternative, less frequent and broader definition- 21.
First of all, the correlation coefficient between both variables is positive and significant at a 1.0% confidence level. The correlation coefficient is also relatively high (0.71)22. Second, Appendix B shows the same graphic exploratory exercises performed for the Central Government´s Fiscal Balance, for the Non-Financial Public Sector’s Balance. Graph 1 shows the results of applying a Hodrick-Prescott Filter to the time series. The Non-Financial Public Sector’s Balance trend is also negative throughout the period of study. Of the 20 quarters between 2010 and 2014, 14 were periods of public savings (70% of the total number of quarters in the case of the Non-Financial Public Sector´s Balance, very similar to the 66% of the total number of months of the Central Government’s Fiscal Balance exercise). It is also relevant to highlight that both series present the same peaks and valleys at exactly the same periods of time. Graph 2 reveals how the NER and pre-announced day-to-day FXIs have a symmetrical behavior in a quarterly frequency. Also, quarterly public saving periods nearly perfectly match the monthly public saving ones. Finally, Graph 3 shows how public saving periods match the less volatile NER periods (as in the monthly frequency case). Only 3 of the 4 periods with highest volatility match public saving periods, of which only 2 are periods of actual fiscal surplus. These are very similar preliminary results to the ones encountered with the monthly frequency data.
4. Drivers and Effectiveness of the Pre-Announced Day-to-Day FXI in the Presence of Public Savings
4.1 Drivers of the Pre-Announced Day-to-Day FXI in the Presence of Public Savings
In this section, BR’s reaction function for FX purchases will be constructed in order to identify the drivers of the pre-announced day-to-day interventions and to estimate a policy shock of these interventions, which will be used in the next section to test the FXI’s effects on the NER. As will be explained later on, because of endogeneity concerns and following Romer & Romer (2004), the estimated residual will be used as the policy shock instead of the predicted FXI.
The BR has a main purpose: to target a medium-term inflation rate. Therefore, any kind of intervention must be coherent and must not endanger the possibility of achieving the inflation target. Since the implementation of the flexible exchange rate in Colombia in 1999, BR has intervened in the FX market in a sterilized manner, without pretending to fix or achieve any level of the exchange rate. So, what reasons does the Colombian CB give for intervening?
To understand the logic behind these interventions in the FX market we must examine the CB´s means of communication for informing economic agents about its policy decisions, and its perspective on the market and economy. One of the CB´s most important vehicles of communication is the biannual report that the Board of Directors must present to Congress23. In these reports, the CB gives four main reasons to intervene: i) to mitigate excessive trend misalignments that do not correspond to the economy’s fundamental behavior, and which may put the inflation target in danger in the case of an extreme depreciation, or that may negatively affect the exportation productive system in the case of an extreme appreciation; ii) to diminish the exchange rate’s volatility; iii) to accumulate International Reserves (IR) in order to reduce external vulnerability and increase financial facilities´ access to external credit; and iv) to guarantee enough liquidity.
As this paper’s period of interest goes from 2010 to 2014, it was necessary to look into a total of 10 Board of Directors´ Reports to the Congress of Colombia (BDRC) looking for explicit mentions of the four reasons to intervene in the FX market. As table 6 shows, the main reason for the FXI was “to accumulate IR”, followed by “to mitigate excessive trend misalignments”. Another important result is that the four different reasons for intervention are mentioned in at least one of the BDRC.
Table 6 Explicit Mention of the Four Main Reasons for FXI in the BDRC (2010-2014)
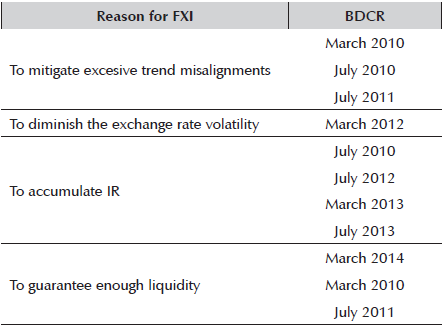
Source: Elaborated by the author based on the Informe de la Junta Directiva al Congreso de la República (2010-2014).
For a well-constructed reaction function, in addition to the explicit drivers given by the CB for FX purchases, it is also necessary to consider other and more operative characteristics inherent to the pre-announced day-to-day interventions. During the Board of Directors´ meetings, the minimum and maximum amounts of FX purchases are pre-established for certain periods of time. The actual amounts of FX purchases are determined by the Monetary and FX Operative Committee, according to the probability of a Real Exchange Rate (RER) misalignment and international liquidity indicators24. Graph 4 presents the FXI’s limits. The red lines show a minimum amount that should have been purchased, while the yellow lines present a maximum amount. As can be seen, from March 2010 to August 2012, the exchange rate’s behavior did not force the CB to exceed the daily minimum amount of FX purchases too often. But this was not the case from September 2012 to September 2013, where the FX purchases exceeded the minimum limit by a lot, to such a point that it was necessary for the Board of Directors to raise the daily minimum limit of FX purchases from USD 20 million to USD 30 million. After September 2013, the Board of Directors changed the minimum FX purchases limits to a maximum limit25. Another important change, made in the communication strategy followed by the Board of Directors is that, when the minimum amount of FX purchases was established, the Board began announcing the total amount that should be purchased for a certain period as well as divulging the minimum daily amount that should be purchased in that period. The latter stopped happening when they changed the minimum limits for the maximum limits. From that point on, they were only explicit about the total maximum amount to be purchased and said nothing about the daily minimum. This lack of information imposes an extra complication on the construction of the CB’s reaction function.
Because of this, it is possible to think that there is some type of censorship in the pre-announced day-to-day FXI. When modelling the policy function of FXIs, the general absence of variance in almost half of the sample may lead to two different interpretations: i) economic conditions were such that it was optimal for the CB to conduct daily purchases of only USD 20 million, or ii) economic conditions were such, that it was optimal for the CB to purchase lower quantities but still carry these purchases because of some external factor or constraint. Based on this evidence, it is now possible to build the equation that was used for the first econometric exercise:
Where 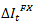 is the difference between the daily amount of FX purchased by the CB and the FX purchases’ limit pre-established by the Board of Directors, the more positive the variable´s value, the higher the CB´s need to purchase FX26,27; t t is the year effects’ dummies;
is the difference between the daily amount of FX purchased by the CB and the FX purchases’ limit pre-established by the Board of Directors, the more positive the variable´s value, the higher the CB´s need to purchase FX26,27; t t is the year effects’ dummies; 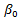 is the constant;
is the constant; 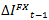 is the lagged difference between the daily amount of FX purchased by the CB and the FX purchases’ limit pre-established by the Board of Directors (included with the intention of controlling for the persistency of the series)28;
is the lagged difference between the daily amount of FX purchased by the CB and the FX purchases’ limit pre-established by the Board of Directors (included with the intention of controlling for the persistency of the series)28; 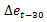 is the inter-annual NER’s depreciation/appreciation;
is the inter-annual NER’s depreciation/appreciation; 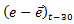 is the RER’s misalignment from a given level (the difference between the observed RER and the RER’s trend29);
is the RER’s misalignment from a given level (the difference between the observed RER and the RER’s trend29);  is the difference between inter-annual inflation and the monetary authority’s target;
is the difference between inter-annual inflation and the monetary authority’s target; 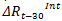 is the inter-annual percentage growth of the monthly stock of IR;
is the inter-annual percentage growth of the monthly stock of IR; 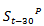 is the Central Government’s Fiscal balance cycle used as a proxy for public savings; and
is the Central Government’s Fiscal balance cycle used as a proxy for public savings; and 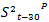 is the squared Central Government’s Fiscal Balance Cycle, which tries to capture public savings´ non-linearity effects on FXIs (all variables are described in detail in Appendix C). All variables were lagged because of endogeneity concerns. An alternative specification was run in which the dependent variable is the FXI instead of the difference between the daily amount of FX purchased by the CB and the FX purchases’ limit. Three dummy variables were included in this specification. They take a value of 1 when the FXI’s limit is equal to a certain quantity of USD (USD 15, 20, or 30 million daily purchases) and zero otherwise. OLS was the econometric model used for estimating both specifications.
is the squared Central Government’s Fiscal Balance Cycle, which tries to capture public savings´ non-linearity effects on FXIs (all variables are described in detail in Appendix C). All variables were lagged because of endogeneity concerns. An alternative specification was run in which the dependent variable is the FXI instead of the difference between the daily amount of FX purchased by the CB and the FX purchases’ limit. Three dummy variables were included in this specification. They take a value of 1 when the FXI’s limit is equal to a certain quantity of USD (USD 15, 20, or 30 million daily purchases) and zero otherwise. OLS was the econometric model used for estimating both specifications.
The public savings variables introduced in both specifications were not explicitly mentioned by BR in any of the BDRC, nor do they appear in FXI literature about reaction functions. Allegedly, the monetary and exchange rate policies are independent from the fiscal policy. Nevertheless, they were included because of the Colombian Minister of Finance´s central participation on the Board of Directors of BR; he is the president30 of the Board, and he may have different interests than the rest of the members31, such as fiscal or governmental financial interests, among others. A more formal reason for including these variables is the following: from 2010 to 2014, BR communicated the Board’s decision to start or extend the FX purchases program in 6 press releases. 5 out of 6 of these press releases matched periods considered as times of public saving.
But most importantly, including these variables helps test if the CB’s FX purchases quantity decisions are influenced by public savings. If public savings enhance the FXI's effectiveness, is it possible to influence the NER with smaller purchases? One might be tempted to answer yes, if the upcoming regressions show that FX purchases decrease when public savings increases.
Table 7 shows the results. Column (5) exhibits the specification described in (1). From columns (1) to (4), public savings variables and year effects variables are progressively included. As shown, the more depreciated the NER is, and the more depreciated the RER is in relation to a long-term trend, the smaller the difference between the actual FXI and the pre-established limit. The larger the growth of IR, the larger the difference between the actual FXI and the pre-established limit. Nevertheless, once year effects are included, the NER’s depreciation/appreciation and the RER’s misalignment variables lose their significance, and the IR’s growth changes its sign. The larger the IR’s growth, the smaller the difference between the actual FXI and the pre-established limit. The IR’s growth variable is significant at a 1 percent confidence level. Public savings’ variables did not have an influence on the difference between the FXI and the FXI pre-established limit.
Table 7 Drivers for the Difference Between FXI and FXI Pre-Established Limit (OLS model)
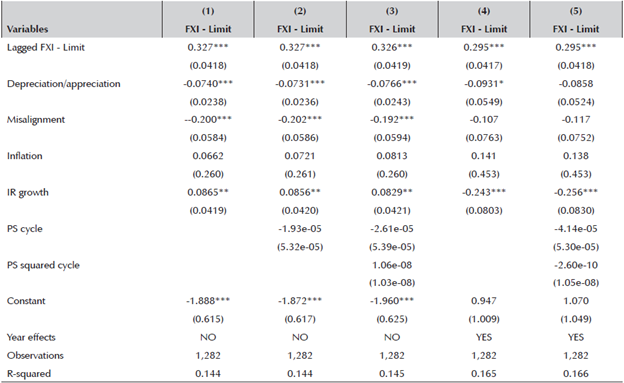
Robust standard errors in parentheses
*** p<0.01, ** p<0.05, * p<0.1
Author’s calculations based on Banco de la República and MHCP.
Table 8 displays the results for the alternative specifications. Column (6) shows the main specification results. From (1) to (5), public savings’ variables, pre-established FXI dummies, and year effects are progressively introduced. All variables exhibit the expected sign when year effects dummies are included. All variables are at least significant at the 10% confidence level. BR decreased the FX purchases when the NER was depreciated, when the RER was depreciated in relation to a long-term trend, when inflation was high, and when IR were high. Only the USD 20 and 30 million FX pre-established dummies variables were significant. This may be explained by the fact that these were the only explicit daily FX’s limits announced by the CB through its means of communication.
Table 8 Drivers of Pre-Announced Day-to-Day FXI (OLS model)
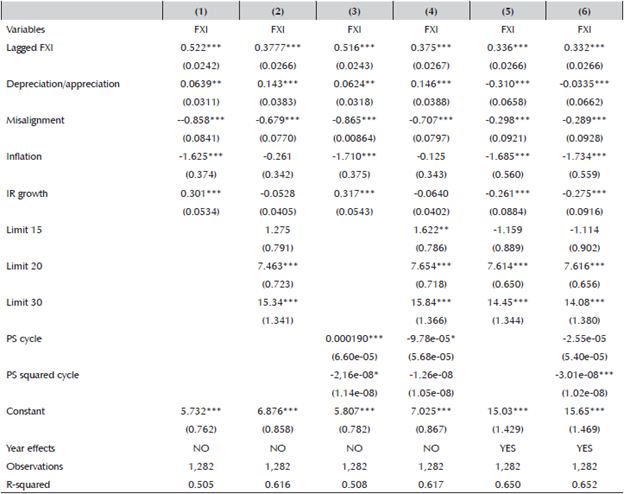
Robust standard errors in parentheses
*** p<0.01, ** p<0.05, * p<0.1
Source: Author’s calculations based on Banco de la República and MHCP.
Regarding the public savings’ variables, only column (3) exhibits non-linearity. The more public savings there are, the higher the FXI is. Nevertheless, the higher the public savings are, the lower the marginal increase in FXI.
The lack of significance of the public savings’ variables throughout the 6 different specifications shows that FXI might not be influenced by the presence of public savings. Therefore, it is impossible to suggest or conclude that even if FXI is enhanced by public savings, a smaller quantity of FXI would be needed to affect the NER’s behavior.
Finally, after getting to know the drivers of FXI and the difference between the FXI and the pre-established limit, it is necessary to finish the policy shock construction. Instead of using the estimated FXI as the policy shock (which is nothing more than the linear combination of the independent variables), this paper follows Romer & Romer´s (2004) methodology, which uses the estimated residual. The advantage of doing so, is that the policy shock would be relatively free from endogeneity and anticipatory movements. In other words, it cleans the effect from the CB’s overseeing action. The preferred policy shock is the one estimated from the difference between the FXI and the pre-established limit (Table 7, column 5). The policy shock that comes from the FXI’s determinants (Table 8, column 6) is estimated and used in the upcoming regressions as a robustness exercise for the main results.
4.2 Effectiveness of Pre-Announced Day-to-Day FXI in the Presence of Public Savings
Now that there is a theoretical model for the NER’s determinants, it is necessary to pose the econometric model as follows:
Where 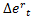 is the NER’s return;
is the NER’s return; 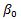 is the long-term return of the NER;
is the long-term return of the NER; 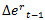 is the lagged NER’s return;
is the lagged NER’s return; 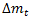 is Colombia´s M1 growth;
is Colombia´s M1 growth; 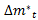 is USA´s M1 growth;
is USA´s M1 growth; 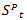 is the Central Government Fiscal Balance’s inter-annual difference expressed as GDP points;
is the Central Government Fiscal Balance’s inter-annual difference expressed as GDP points; 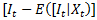 is the policy shock of pre-announced day-to-day FXI (column 5, table 7);
is the policy shock of pre-announced day-to-day FXI (column 5, table 7); 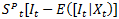 is the interaction between the Central Government Fiscal Balance’s inter-annual difference expressed as GDP points and the policy shock;
is the interaction between the Central Government Fiscal Balance’s inter-annual difference expressed as GDP points and the policy shock; 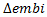 is the Colombia´s EMBI growth; and
is the Colombia´s EMBI growth; and 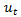 is the unexpected short-term NER’s return. The coefficients of most interest in this exercise are
is the unexpected short-term NER’s return. The coefficients of most interest in this exercise are 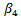 for public savings,
for public savings, 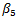 for the policy shock of FXI, and
for the policy shock of FXI, and 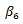 for the interaction between the public savings variable and the FXI´s policy shock.
for the interaction between the public savings variable and the FXI´s policy shock.
Because of the high frequency of the NER and its clustered variance, a GARCH(1,1)32 model is used to estimate equation (11). A very helpful feature of the GARCH model that helps to test this paper´s hypothesis is that it estimates the mean equation given in (11) at the same time that the variance equation of the NER’s return is being estimated. The specification of the variance equation is:
Where 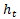 is the short-term conditional variance or volatility of the NER’s return33;
is the short-term conditional variance or volatility of the NER’s return33; 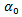 is the long-term conditional variance;
is the long-term conditional variance; 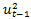 is the unexpected squared return;
is the unexpected squared return; 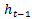 is the lagged short-term conditional variance of the NER’s return. The rest of the variables are defined as in (11).
is the lagged short-term conditional variance of the NER’s return. The rest of the variables are defined as in (11).
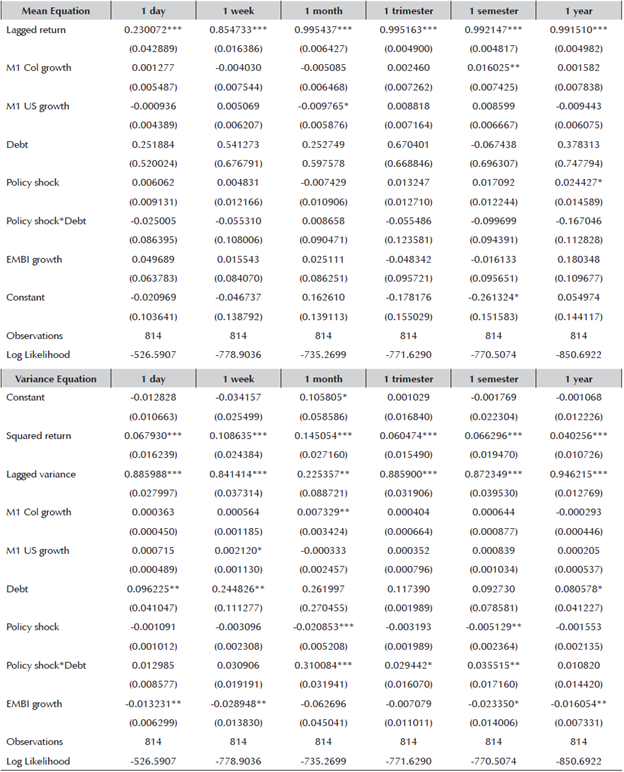
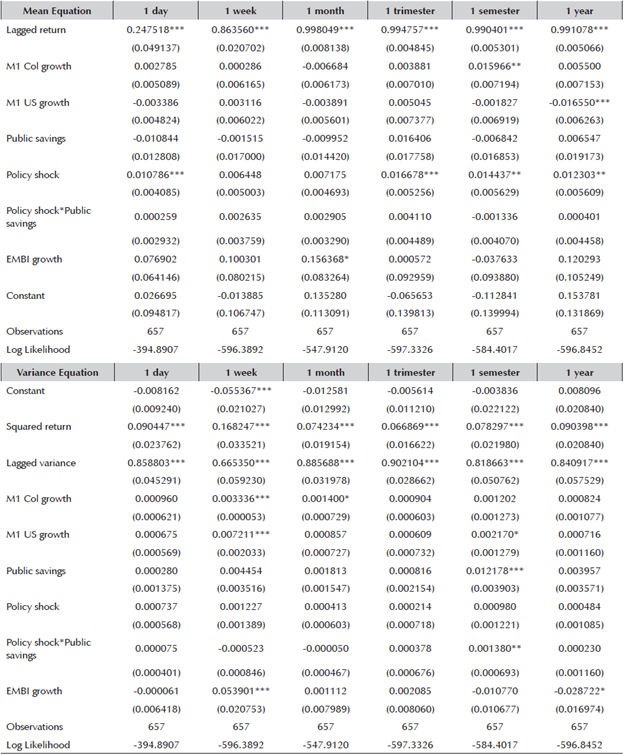
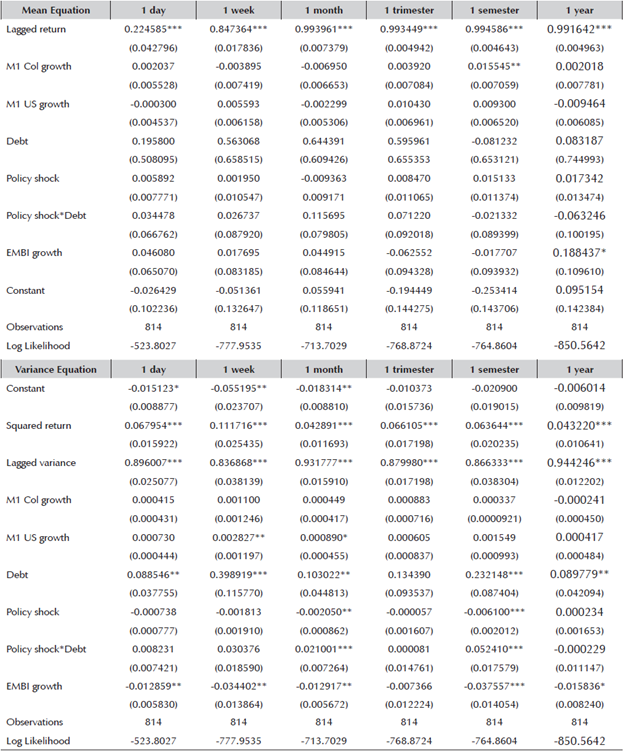
Different versions of (11) and (12) are estimated. Table 9 displays the results for different NER return’s maturities. Appendix D exhibits the results for different NER return’s maturities but with a different definition of public savings. Instead of including the Central Government’s Balance inter-annual difference, it includes the Central Government total debt’s inter-annual difference expressed as GDP points, which is a more financial definition of the variable. Appendix E’s panel A & panel B, report the same exercises but with column 6 of Table 8, policy shock.
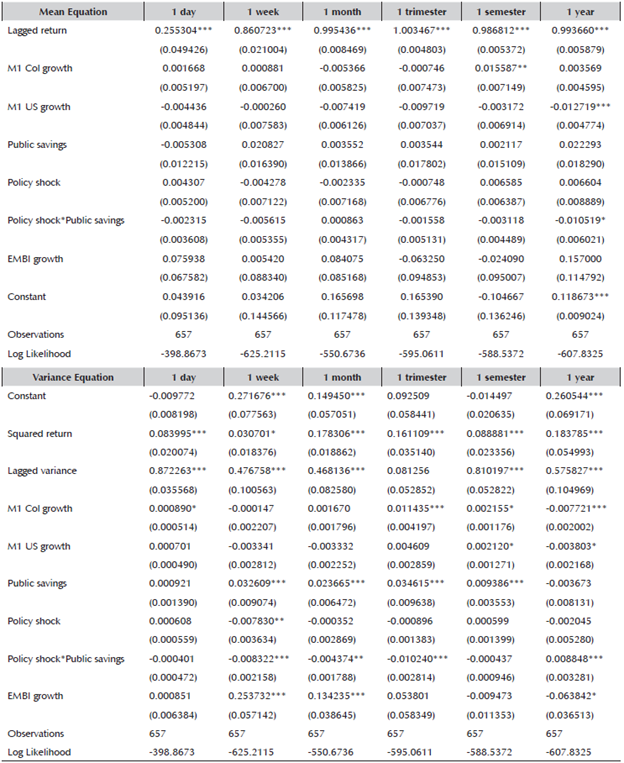
As table 9’s mean equation shows, in most of the different NER return’s maturities, there are no significant control variables except for a few exceptions. Colombia’s M1 growth in the 1 semester maturity column is significant at a 5.0% confidence level and exhibits the expected sign, consistent with equation (10). The faster the growth of Colombia’s M1, the more depreciated the NER becomes. US’ M1 growth in the 1 year maturity column is significant at a 1.0% confidence level and has the expected coefficient’s sign. The faster the M1 growth, the higher the probability of USD entering the economy and appreciating the NER. Nonetheless, the significance of both variables is not a regularity between the different maturity specifications. A highly consistent result among the different specifications is the lagged return variable’s significance. For all six of them, it is significant at a 1% level of confidence and with a positive sign. This provides evidence of high persistence in the NER’s returns regardless of the maturity.
Table 9 NER Determinants: Is FXI Enhanced by Public Savings? (GARCH Model). Central Government’s Balance Public Savings Definition
Robust standard errors in parentheses
*** p<0.01, ** p<0.05, * p<0.1
Source: Author’s calculations based on Banco de la República and MHCP.
In regard to the variables of interest, it is found that public savings do not influence the NER, which may be related to the short-comings of the chosen high frequency public savings’ variable. There is also no evidence that the FXI depreciates or appreciates the NER, not even in the presence of public savings (with the exception of the 1 year NER return’s column in which the NER appreciates).
Regarding the NER’s variance equation, it is found that for all specifications (except for the 1 trimester column), the squared return and the lagged variance were significant at least at a 10% confidence level, providing evidence of a well-chosen GARCH(1,1) model. For the other control variables, there is not an expected sign. The paper did not develop a model to study how Colombia´s or the US’s M1 or EMBI growth would affect the NER’s volatility. Nevertheless, they did not present a consistent behavior among the different maturity specifications. Colombia’s M1 growth was significant at least at a 10% level of confidence and had a positive sign for the 1 day, 1 trimester, 1 semester specifications, and a negative sign for the 1 year specification. US’ M1 growth was significant at a 10% level of confidence and presented a positive sign for the 1 semester specification, and a negative sign for the 1 year specification. The EMBI growth was significant at least at a 10% level of confidence and presented a positive sign for the 1 week and 1 month specification, and a negative sign for the 1 year specification.
With respect to the variables of interest, it is found that public savings are significant at a 1.0% level of confidence and have a consistently positive sign around the 1 week, 1 month, 1 trimester, and 1 semester specifications. The higher the public savings, the higher the NER’s volatility. As mentioned before, this paper did not develop a model to learn about the relation between public savings and the NER’s volatility. Nonetheless, public saving´s behavior did not change among the maturity’s specifications (in contrast with other control variables). The FXI’s policy shock was significant at a 5.0% level of confidence for the 1 week specification, meaning that just the FXI’s effect on the NER does not last. The interaction between public savings and the FXI’s policy shock is significant at least at a 5.0% confidence level, and with a negative sign for the 1 week, 1 month, and 1 trimester specifications. For every USD 10 million purchased by the CB, accompanied by an increase of 0.5 GDP points in the Central Government’s balance, the weekly NER’s variance was reduced in 0.12, the monthly NER’s variance shrunk in 0.022, and the trimester NER’s variance was reduced in 0.051. Meaning that the FXI’s effectiveness in reducing the volatility of the NER is enhanced by the presence of public savings.
As Appendix D shows, when the definition of public savings is changed to the inter-annual difference of the Central Government´s total debt expressed as GDP points, most of the results hold. There is no evidence that the FXI appreciates or depreciates the NER with or without public savings. Nevertheless, FXI’s effectiveness in reducing the NER’s volatility is enhanced by public savings after a month, a trimester or a semester. FXI on its own also diminished the NER’s volatility after a month and a semester. For every USD 10 million purchased by the CB, accompanied by a decrease of 0.1 GDP points in the Central Government’s debt, the monthly NER’s variance was reduced in 0.052, the trimester NER’s variance shrunk in 0.029, and the semester NER’s variance was reduced in 0.087. All the described variables are significant at least at a 10% level of confidence.
Finally, when using the alternative definition of policy shock (column 6 of Table 8) and the Central Government’s Balance definition, as Appendix E, Panel A shows, there is evidence that FXI does depreciate the NER after a day, a trimester, a semester and a year, and reduces the NER’s volatility with and without public savings enhancement after a semester. All the described variables are significant at least at a 5.0% level of confidence. When the Central Government’s total debt definition of public savings is used, there is no evidence of the NER being appreciated or depreciated by the FXI with or without public savings enhancement. Nevertheless, FXI does reduce the NER’s volatility on its own and with public savings enhancement after a month and a semester. All variables are significant at a 5.0% confidence level.
5. Conclusions
This paper deduces a theoretical framework for how public savings may act as the key variable to make the portfolio balance channel active. To prove this empirically, a FXI reaction function was constructed to estimate a FXI’s policy shock, which was introduced as a NER’s determinant. From the FXI’s reaction function it was learned that BR purchases FX when the NER is appreciated, when the RER is appreciated in relation to a long-term trend, when inflation is low, and when IR are low. There is no evidence that public savings affect the CB’s FX purchases quantity decision (despite FXI being more effective in the presence of public savings, there is still the need for purchasing the same quantities, and not more or less). From the NER returns’ mean equation, it was learned that FXI does depreciate the NER, a day, a month, a trimester and a semester after the intervention. Public savings did not play a role in the FXI´s effectiveness in depreciating the NER. From the NER returns’ variance equation, it was learned that the FXI did decrease the NER’s volatility, a week, a month and a semester after the intervention. FXI’s effectiveness in reducing the NER’s volatility was enhanced by public savings after a week, a month, a trimester and a semester. In conclusion, and to answer the questions in the introduction: i) it is possible for the portfolio channel to work powerfully in the presence of public savings; ii) the determinants of the FX pre-announced day-to-day purchases carried out by the CB, match the reasons to intervene stated in the CB’s means of communication; iii) sterilized FXI is more effective in reducing the volatility of the exchange rate in the presence of public savings.
All the results empirically support the idea of considering public savings as the key macroeconomic condition for activating the portfolio channel and making the FXI effective. Therefore, it is imperative to reach a high level of coordination between the country´s monetary and fiscal authorities. As it is known, resources are scarce, and FXIs have a non-negligible cost (on average, the CB bought USD 6770 million per year equivalent to 2.5% of GDP from 2010 to 2014) so the better the coordination, the higher the effectiveness of intervention and the easier it becomes to influence the exchange rate’s behavior, which means a better use of scarce resources. Fortunately for Colombia, because of the way the PC conceived the organization of the Board of Directors of the CB, this coordination might not be that hard to achieve given the fact that the Finance Minister is part of the Board.
Another mechanism that may align the fiscal authority’s incentives -keeping in mind that during the last decade Colombia´s President has suggested to the Board of Directors that they intervene in the FX market despite the CB’s constitutional independence34- with the monetary authority, is to continue with the completion of the fiscal rules’ budgetary objectives, giving a stronger credibility to the fiscal policy, reducing fiscal deficit/increasing public savings, and therefore making the FXI more effective.