Estimadores del índice de cola y el valor en riesgo

Means of estimating the tail index and the value at risk

Estimateurs de l'indice de queue et la valeur en risque

Andrés Mora Valencia
E-mail: amora@cesa.edu.co
Colegio de Estudios Superiores de Administración - CESA. Bogotá-Colombia

Artículo Tipo 2: de reflexión. Según Clasificación Colciencias.
Fecha de recepción: junio 12 2010
Fecha de corrección: septiembre 14 2010
Fecha de aprobación: septiembre 30 2010

Resumen

Este artículo presenta algunas metodologías para cuantificar riesgo cuando la distribución de pérdidas presenta eventos extremos, debido a que los activos financieros generalmente presentan alta curtosis. De esta manera, el principal concepto utilizado en el documento es el valor en riesgo (VaR, por sus siglas en inglés), medida introducida por J. P. Morgan en 1995. Desde el punto de vista estadístico, VaR es un cuantil de una función de distribución; sin embargo, su valor dependerá de la forma de la distribución que se utilice para ajustar los datos de pérdida. Por tal razón, al estimar de manera confiable el parámetro de forma de la distribución de pérdidas, se obtiene un estimador confiable de medida de riesgo. La teoría del valor extremo (EVT, por sus siglas en inglés) es una técnica estadística que ha sido empleada para tal fin. En este documento se utiliza la metodología de EVT, denominada picos sobre el umbral (POT, por sus siglas en inglés), en el cual, se estima el parámetro de forma de la distribución de excesos mediante máxima verosimilitud. Este método de estimación se revisa brevemente en el documento junto con el método de mínimos cuadrados ponderados. Este último se utiliza para cuantificar el estimador de Hill y con este valor se calcula el VaR para distribuciones con colas pesadas. Finalmente, se comparan las metodologías propuestas en el artículo para cuantificar VaR con otras dos metodologías que son simulación histórica y bajo el supuesto de normalidad mediante pruebas de desempeño a dos casos.

Palabras clave: índice de cola, colas de Pareto, VaR, máxima verosimilitud, cuadrados ponderados.

Abstract

This article presents some methodologies to quantify risk when the loss distribution exhibits extreme events because the financial assets generally have high kurtosis. Thus, the main concept utilized in the document is the Value at Risk (VaR), a measure introduced by J. P. Morgan in 1995. From the statistical point of view, VaR is a quantile of a distribution function, but its value depends on the shape of the distribution that is used to fit the data loss. For this reason, in order to obtain a reliable measure of risk it is necessary to obtain a reliable shape parameter of the distribution of losses. The extreme value theory (EVT) is a statistical technique that has been used for this purpose. This document uses the EVT methodology, called peaks over threshold (POT), in which the shape parameter of the distribution of excesses is estimated by maximum likelihood. This estimation method is briefly reviewed in the document along with the weighted least squares method. The latter is used to quantify the Hill estimator and this value is used to calculate VaR for heavy tailed distributions. Finally, we compare the methods proposed in the article to measure VaR with two other methods that are; historical simulation and the assumption of normality through backtesting in two cases.

Keywords: tail index, Pareto tails, VaR, maximum likelihood, weighted squares.

Résumée

Cet article présente quelques méthodologies pour quantifier un risque quand la distribution de pertes présente des événements extrêmes, grâce à ce que les actifs financiers présentent en général une haute kurtosis. De cette façon, le principal concept utilisé dans le document est celui de valeur en risque (VaR, par ses sigles en Anglais), mesure introduite par J. P. Morgan en 1995. Du point de vue statistique, VaR est un quantile d'une fonction de distribution ; cependant, sa valeur dépendra de la forme de la distribution que l 'on utilise pour ajuster les données de pertes. Par telle raison, après avoir estimé d 'une manière de confiance le paramètre de forme de la distribution de pertes, on obtient un estimateur de confiance pour la mesure de risque. La théorie de la valeur extrême (EVT, par ses sigles en Anglais) est une technique statistique qui a été employé pour telle fin. Dans ce document on utilise la méthodologie EVT avec la méthode des dépassements de seuil (POT, par ses sigles en Anglais), dans laquelle, le paramètre de forme de la distribution d'excès est estimé par la probabilité maximale. Cette méthode d'estimation est brièvement repassée dans le document avec la méthode de minimes carrés pondérés. Ce dernier est utilisé pour quantifier l'estimateur de Hill et avec cette valeur on calcule le VaR pour les distributions avec des queues lourdes. Finalement, on compare les méthodologies proposées dans l'article pour quantifier le VaRavecdeuxautres méthodologies qui sont, la simulation historique, et l'hypothèse de normalité au moyen d'essais de dégagement à deux cas.

Mots clef: Indice de queue, queues de Pareto, VaR, vraisemblance maximale, carrés pondérés.

1. Introducción

En administración de riesgos financieros es muy frecuente reportar la máxima pérdida esperada dado un nivel de confiabilidad y en un tiempo determinado. Este concepto es conocido como VaR o elvalor en riesgo, medida introducida por J.P. Morgan en 1995 en su documento de Riskmetrics. Desde el punto de vista estadístico, el VaR no es más que uncuantil de una función de distribución depérdidas dado un nivel de probabilidad. Sin embargo, las primeras aplicacionesde VaR presumían pérdidas distribuidas normales. En riesgo financiero es poco común encontrar un factor de riesgo cuya distribución de pérdidas sea normal; porlo general, en riesgo de mercado estas distribuciones de pérdida presentan valores de curtosis¹ más alto que el de una normal, lo que indica que hay más probabilidad en las colas de estas distribuciones que en la de una normal. Esto quiere decir que la probabilidad de que un evento extremo ocurra es muy baja, pero cuando se da, se incurre en grandes pérdidas. En riesgo crediticio es común tener distribuciones de pérdidas asimétricas, y el coeficiente de asimetría de una normal es cero. Por tal razón no es conveniente utilizar el supuesto de normalidad en la distribución de pérdidas para cuantificar riesgo financiero.

De esta manera, el presente documento se divide de la siguiente forma: en la sección uno se presentan las distribuciones más utilizadas para modelar pérdidas extremas. La sección dos presenta dos métodos de estimación de parámetros de distribuciones para luego ser aplicados en la cuantificación de cuantiles, como medida de riesgo. La sección tres describe brevemente el método de picos sobre el umbral (POT, por sus siglas en inglés), es esta la metodología más utilizada bajo el enfoque de la teoría del valor extremo. En la sección cuatro se muestra cómo estimar VaR para distribuciones de colas pesadas y mediante el método POT. La sección cinco aplica las metodologías expuestas en la sección anterior a datos reales y que han sido analizados por varios investigadores, como también al IGBC. Finalmente la sección seis concluye.

2. Distribuciones de colas pesadas

En finanzas y seguros es de particular interés el estudio de distribuciones con alta probabilidad en las colas comparadas con una normal, las cuales se denominan distribuciones de colas pesadas. Una distribución con un valor alto de curtosis se relaciona con una distribución de colas pesadas. El capital de una compañía financiera puede verse gravemente afectado si la distribución de pérdidas de un activo financiero o de quejas en seguros es bien modelada por una distribución de colas pesadas puesto que existe una probabilidad, muy baja, de que un evento extremo ocurra pero cuando este evento suceda causará grandes pérdidas. Ejemplos de estas distribuciones están la doble exponencial, t, modelos mezclados, Pareto y distribuciones con colas de Pareto. A continuación se describe brevemente algunas de estas funciones utilizadas en finanzas. Para más detalles, ver Ruppert (2004, pág. 28-36).

2.1. Distribución doble exponencial

Esta función también es conocida como distribución de Laplace, que tiene colas un poco más pesadas que las de una normal y su función de densidad está dada por:

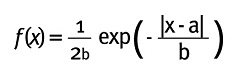
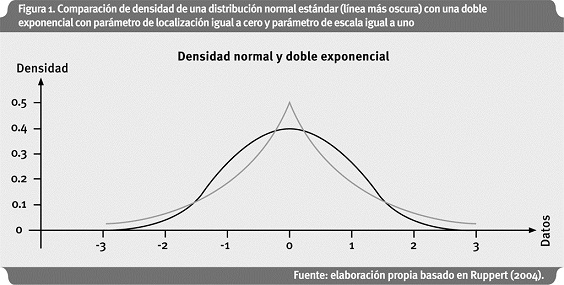
Donde a y b son los parámetros de localización y de escala respectivamente. La Figura 1 compara la función de una normal y una doble exponencial:

Como se puede observar, la función de densidad normal converge a cero mucho más rápido que la de una doble exponencial a valores muy grandes de x. Esto también se puede observar al comparar las dos funciones. Si se asume una normal estándar, esta función es proporcional a exp (-1/2 (x)²) mientras que la de una doble exponencial es proporcional a exp(-|x|) si el parámetro de localización es igual a cero y el parámetro de escala igual a uno. Entonces el término -(x)² converge a -∞ mucho más rápido que -|x| cuando x → ∞

Cuando la función de densidad se comporta como -|x|^-(α+1) para algún α>0 , se obtienen colas más pesadas y éstas se denominan colas polinomiales (o también llamadas colas de Pareto), mientras que las de una Laplace se denominan colas exponenciales. El parámetro α se denomina el índice de cola, el cual se estimará bajo una distribución con colas de Pareto. Para distribuciones con colas polinomiales, las colas son más pesadas entre más pequeño es el valor de α.

2.2. Distribución t

La distribución t ha sido ampliamente usada para modelar retornos de activos financieros. A medida que los grados de libertad (ν) decrecen, la curtosis aumenta. Para valores grandes de |x| la función de distribución es proporcional a - |x |^-(ν+1), por lo tanto la t tiene colas polinomiales con α=ν. Entonces, entre más pequeño es el valor de ν , más pesadas son las colas de una t.

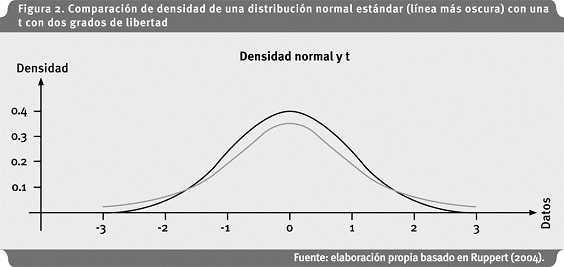
Al igual que el caso anterior, la normal converge a cero mucho más rápido que la t con ν= 2, según puede observarse en la figura 2.

2.3. Distribución Pareto

La función de densidad de una distribución Pareto está dada por:

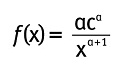
Con x>c. Como se observa, la distribución Pareto tiene colas polinomiales con índice de cola igual a α, también denominada constante de Pareto. La ventaja de usar una distribución Pareto con respecto a la t en finanzas, es que el índice de cola en una Pareto puede tomar cualquier valor positivo mientras que en la t, el índice de cola solo toma valores enteros positivos.

La función de supervivencia de una variable aleatoria X está dada por:

P(X > x) = 1 - F(x),

Donde F es la función de distribución acumulada de X. Por lo tanto, en finanzas, si X representa las pérdidas en una inversión, P(X > x) es la probabilidad de que una pérdida sea mayor que x. La función de supervivencia de una Pareto está dada por:

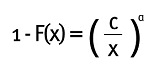
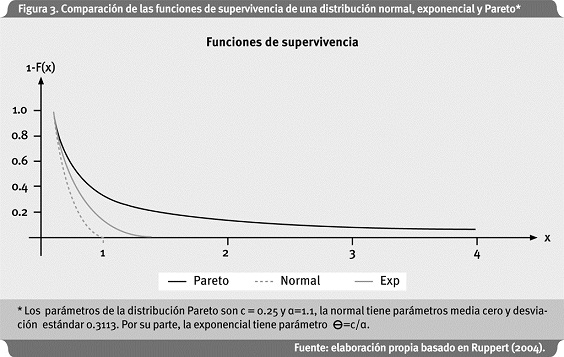
Con x>c. Para valores grandes de x, la función de supervivencia de una distribución Pareto converge a cero a una tasa polinomial más lenta que una exponencial; esto indica que la distribución Pareto tiene una cola a la derecha más pesada. La Figura 3 es una representación de la Figura 2.12 de Ruppert (2004), y compara las funciones de supervivencia de una Pareto, normal y exponencial, de tal manera que las tres distribuciones tienen el mismo valor de 1- F(x) en x = 0.25.

Como se observa en la figura 3, la función de supervivencia de la normal decae mucho más rápido que la de una Pareto, y la de la exponencial está en medio de las dos.

2.4. Distribuciones con colas de Pareto

Una función de distribución tiene cola derechade Pareto si su función de supervivencia satisface la siguiente condición:

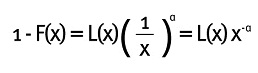
Donde α>0 y L(x) es una función de variación lenta en ∞. x puede representar valores de pérdidas (tomadas positivas). De manera similar se puede definir cola izquierda de Pareto. Ejemplos de estas distribuciones son Pareto, gamma inversa, t-Student, loggamma, F y Burr. Una función L se dice ser de variación lenta en ∞ si:

Para todo 0 <λ. En otras palabras, para valores muy grandes de x, el valor de la función L evaluada en λ x es muy cercano al valor de la función L evaluada en x, para un λ positivo. Distribuciones con colas de Pareto son las más estudiadas en administración de riesgo por ser distribuciones con colas muy pesadas, puesto que como se había mencionado anteriormente, la probabilidad de que un evento extremo ocurra es muy baja, pero cuando este evento sucede, causa grandes pérdidas.

2.4.1. Distribución Burr

Este es un caso de distribuciones con colas de Pareto y será utilizado más adelante para mostrar un ejemplo de gráfico de cuantiles de Pareto.

La función de densidad Burr tiene la siguiente forma (tomada de Klugman et al., 2008):

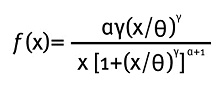
Para valores de x, α, γ, Θ > 0. Θ es el parámetro de escala y α, γ son parámetros de forma. La distribución Burr es muy usada en el campo de seguros para simular pérdidas extremas y tiene los siguientes casos especiales:

* Distribución Loglogística cuando α = 1

* Distribución Paralogística cuando γ = α

* Distribución Pareto cuando γ = 1

A continuación se presentan algunos métodos de estimación de parámetros de distribuciones más comunes y se estimará el índice de cola.

3. Métodos de estimación

Se verán los métodos de estimación mediante máxima verosimilitud y de mínimos cuadrados. Se comienza con la definición del método de máxima verosimilitud, tomada de Canavos (1988, p. 265).

3.1. Máxima verosimilitud

Sea X1, X2,…, Xn una muestra aleatoria (es decir, una colección de variables aleatorias independientes e idénticamente distribuidas, iid) de una distribución con función de densidad ƒ(x,Θ) y sea L(x1, x2,…,xn, Θ), la función de verosimilitud de la muestra en función del parámetro Θ. Si t = u(x1, x2,…,xn) es el valor de Θ para el cual el valor de la función de verosimilitud es máxima, entonces T = u(X1, X2,…, Xn) es el estimador de máxima verosimilitud de Θ.

Dada una función de densidad ƒ(x,Θ), se define la función de verosimilitud como:

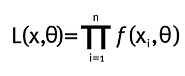
Entonces, la función de verosimilitud para el índice de cola de una distribución Pareto está dada por:

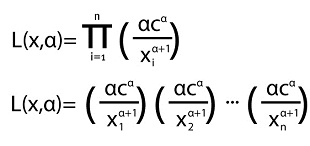
Aplicando logaritmo a la función de verosimilitud y aprovechando las propiedades de los logaritmos, se obtiene:

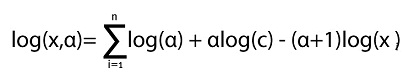
Derivando esta expresión con respecto al parámetro α, e igualando a cero:

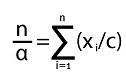
De esta manera se obtiene el estimador de máxima verosimilitud para α como:

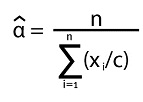
Esto es cierto si se supone que la muestra aleatoria proviene de una distribución Pareto. Pero si se supone que la distribución tiene colas de Pareto (como la mayoría de las distribuciones de pérdidas en finanzas y seguros), interesa más utilizar los datos de la cola de la distribución que todos los datos en sí, de otra manera se incurriría en un alto sesgo en la estimación. Por lo tanto, se escoge un dato c de los xi y se usan los datos que superen este valor de c llámese n(c). Así se obtiene el conocido estimador de Hill:

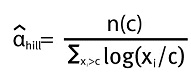
El estimador de Hill para 1/α se define formalmente de la siguiente manera:

Dado unos estadísticos de orden de n observaciones X1, X2, …, Xn, el estimador de Hill está dado por:

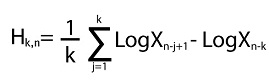
Al comparar esta ecuación con la anterior, se obtiene la siguiente igualdad: H_k,n=1/α. El valor de c es X_n-k. Los datos x_i que superan el valor de c que anteriormente se denominaba n(c), son ahora k. A continuación se utilizará el método de mínimos cuadrados ponderados para estimar α, pero antes se verá la utilidad del gráfico de cuantiles de Pareto.

3.1.1. Gráfico de cuantiles de Pareto

Por lo general, para saber si una distribución se puede ajustar a una serie de datos se usa el gráfico de cuantiles, y el más usado es el gráfico de cuantiles de una normal. Pero para este estudio el interés es utilizar la distribución exponencial y Pareto, en lugar de la normal para ajustar datos empíricos, puesto que en riesgo se estudian distribuciones para pérdidas como la lognormal, Weibull entre otras.

Para el gráfico de cuantil cuantil Pareto (también conocido como el gráfico de Zipf) se toma F(x) = 1 - x^-α, la función de distribución acumulada de una Pareto, entonces la función cuantil tiene la forma, tomando la inversa de F(x):

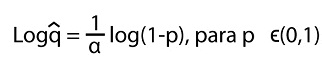
Y se obtendría un gráfico para varios valores de α:

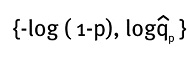
La pendiente de esta línea recta sería un buen aproximado de 1/α. Siguiendo la notación formal de la definición del estimador de Hill, el gráfico corresponde a:

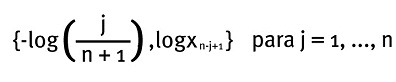
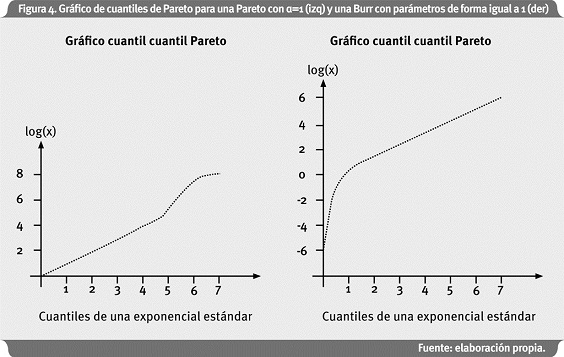
La Figura 4 muestra el gráfico de cuantil cuantil Pareto de 1,000 datos simulados de una Pareto con parámetro de forma igual a 1, y de una distribución Burr con parámetros de forma igual a 1.

Por lo tanto, el gráfico de cuantil cuantil Pareto sirve como prueba de bondad de ajuste para verificar si los datos se distribuyen Pareto, así como la versión clásica del QQ-plot para una distribución normal. Sin embargo, los datos (financieros en general) exhiben distribuciones con colas de Pareto donde la linealidad se observa en la parte superior del gráfico de cuantil cuantil Pareto. Esto último se puede ver en el lado derecho de la Figura 4; los datos siguen una distribución Burr. Para este caso un estimador de α se puede obtener de la pendiente del gráfico de cuantil cuantil Pareto, pero desde un punto donde se comienza a observar linealidad, y luego se resuelve mediante un método de mínimos cuadrados ponderados. El problema se convierte en decidir desde qué punto se comienza a observar linealidad en el gráfico de cuantiles.

3.2. Mínimos cuadrados ponderados (WLS)

En algunas regresiones no es válido aceptar que todos los errores provienen de una misma población. Se supone que los errores son independientes pero tienen varianzas desiguales, que son proporcionales a una de las variables explicatorias (o independientes). De forma más general se supone que var (ei) = σ2vi, para cantidades positivas vi. Entonces el estimador de mínimos cuadrados ponderados es el valor de β que minimiza σ (yi - β'xi)2/vi. Cuando todos los vi son iguales, éste se convierte en el caso de mínimos cuadrados ordinarios. Una ventaja de los estimadores de mínimos cuadrados ponderados (comparado al de mínimos cuadrados ordinarios) es que no son tan sensibles a valores atípicos. En ausencia de valores atípicos, un estimador de mínimos cuadrados ordinarios puede ser más confiable (Birkes y Dodge, 1993).

La solución de los coeficientes de una regresión, en términos matriciales, de un modelo de mínimos cuadrados ordinarios está dada por:

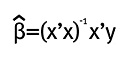
Donde X es la matriz de regresores y contiene las observaciones de las variables explicativas, Y es la matriz de la variable dependiente y contiene las observaciones de la variable explicada. X' es la traspuesta de la matriz X. Pero para un modelo de mínimos cuadrados ponderados la solución está dada por:

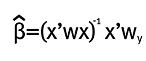
Donde W es una matriz diagonal con valores wi (wi = 1/νi). Para más detalles del estimador de mínimos cuadrados ponderados se puede consultar la sección 11.5 de Greene (2002).

Beirlant et al. (1996) proponen un estimador del índice de cola como la pendiente de un gráfico de cuantil cuantil Pareto a partir de un punto donde comience a notarse linealidad en el gráfico de cuantiles. Este punto es:

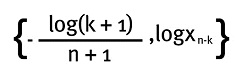
El problema es, como se mencionó anteriormente, identificar el punto X_{n - k} a partir del cual el gráfico de cuantiles muestra linealidad, como se observa en la Figura 5:

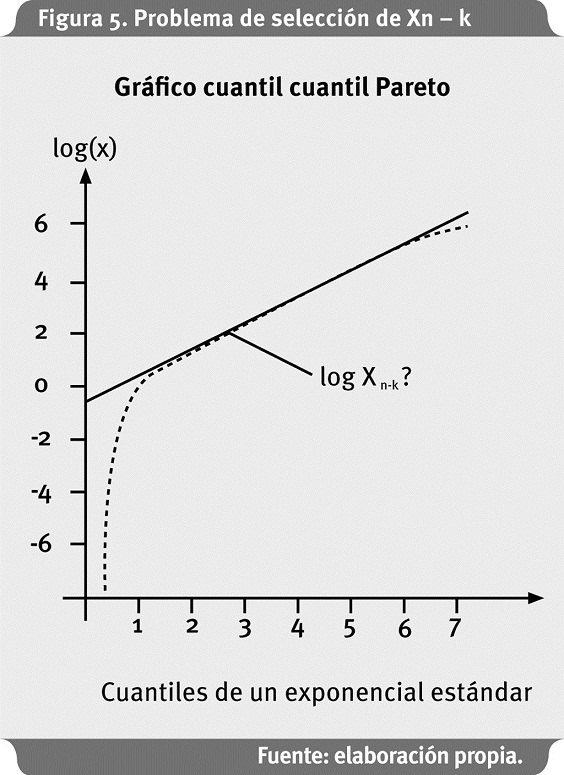
Este problema es equivalente a escoger el valor de k, el número de datos que superan a X_n-k en el Gráfico de Hill. Una vez solucionado el problema de selección de X_n-k, se aplica el método de mínimos cuadrados ponderados a la ecuación con pendiente m:

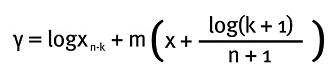
que conlleva a solucionar la minimización de la siguiente expresión con respecto a m:

De esta manera, se ha obtenido el estimador de Hill mediante un método de mínimos cuadrados y, anteriormente, mediante máxima verosimilitud. Otros estimadores más avanzados basados en regresión de los últimos datos en el gráfico de cuantiles de Pareto han sido obtenidos, por ejemplo ver Shultze y Steinebach (1996), Kratz y Resnick (1996) y Csörgõ y Viharos (1998). Estos y otros estimadores son discutidos en Beirlant et al. (2004). Este texto presenta una revisión de estimadores que mitigan el problema de sesgo en la estimación del índice de cola, como también el problema de varianza. Otro método muy usado para estimar α ó ξ (= 1/α) es mediante la estimación del parámetro de forma de una distribución de Pareto generalizada (GPD, por sus siglas en inglés), que se describe brevemente a continuación.

4. Método de picos sobre el umbral

La teoría del valor extremo (EVT, por sus siglas en inglés) es una técnica que estudia la importancia de los eventos atípicos. Esta técnica se basa en métodos para estimar probabilidades condicionales concernientes a eventos de cola y recientemente ha sido aplicada a riesgo financiero. En otras palabras, EVT es el estudio de las colas de las distribuciones.

La teoría del valor extremo dice que el valor más grande o más pequeño de un conjunto de valores tomados de la misma distribución original tiende a una distribución asintótica que sólo depende de la cola de la distribución original (Vose, 2002). EVT ha sido probado útilmente para modelar eventos catastróficos en seguros y otros eventos financieros, como pérdidas inesperadas en crédito (Embrechts et al., 1998).

Un administrador de riesgos está interesado en las pérdidas que exceden un umbral u. Este enfoque es denominado el método picos sobre el umbral (POT, por sus siglas en inglés), y ha sido estudiado por Smith (1989), Davison y Smith (1990) y Leadbetter (1991)². Existe una amplia literatura en EVT y entre ellos están: Embrechts et al. (1997), Resnick (1987), de Haan y Ferreira (2006), Coles (2001), Falk et al. (2004), Reiss y Thomas (1997). McNeil et al. (2005), Malevergne y Sornette (2006), Moix (2001) y Balkema y Embrechts (2007).

4.1. Distribución de los excesos (F(u))

Se define como:

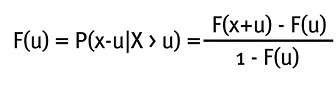
Esto es, la probabilidad de que una pérdida muy grande menos un umbral u sea menor que x dado que esa pérdida excedió el umbral.

El método tradicional usado en la teoría del valor extremo es el block-maxima; sin embargo, el método POT usa datos de manera más eficiente y por tal razón ha sido empleado recientemente (Gilli y Kellezi, 2003, p. 4).

4.2. Teorema del límite para las distribuciones de exceso

En la teoría del valor extremo, el siguiente resultado es de gran importancia para el cálculo de medidas de riesgo:

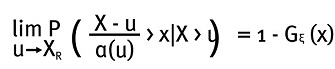
Donde α(u) es una función positiva tal que 1 + ξx > 0 y G es la función de distribución de Pareto generalizada, XR es el punto final a la derecha de la distribución de datos. Lo que es equivalente a:

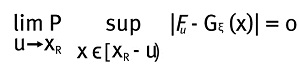
Que es el teorema de Pickands, Balkema y de Haan. En otras palabras, lo que dice el teorema es que la función de distribución de excesos F_u se aproxima a una función GPD cuando u tiende a X_R.

4.3. GPD (Distribución de Pareto Generalizada)

Donde ξ es el parámetro de forma y caracteriza la cola de la distribución, β es el parámetro de escala de la distribución. ξ = 1/α, donde α es el índice de cola. A continuación se verán los métodos de  cuantificación de cuantiles como medida de riesgo.

5. Estimación del VaR

Valor en riesgo o VaR es la medida de riesgo financiero más comúnmente usada. Esta medida fue introducida por J.P. Morgan y sus documentos técnicos pueden ser consultados en Internet. VaR mide la máxima pérdida esperada dado un nivel de confiabilidad en un tiempo determinado. Para más detalles³, ver por ejemplo J.P. Morgan (1995) y el texto de Jorion (2001). Otra definición de VaR es la mínima pérdida esperada en el p% de los peores casos: xp = inf{x : F(x) ≥ p}, es decir, un cuantil de la función de distribución de pérdidas.

5.1. Estimación de VaR con colas de Pareto

Suponga que las pérdidas (positivas) X tienen distribución con colas de Pareto:

5.2. VaR bajo el método POT

Asumiendo que la cola de la distribución de pérdidas se aproxima a una GPD, VaR(p) está dado por:

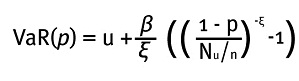
Donde u es el umbral escogido (o estimado), β y ξ son los parámetros de escala y de forma de una distribución de Pareto generalizada, N_u es la cantidad de datos que exceden el umbral y n el total de datos de la muestra. Por lo tanto N_u/n es un estimador empírico de la cola de los datos que han superado un umbral u. Este estimador de cola de distribución se debe a Smith (1987).

6. Aplicación

En esta sección se muestra una aplicación a datos de seguros (constantemente revisado bajo el enfoque de la teoría del valor extremo ver por ejemplo Degen et al., 2007) y a un caso nacional, IGBC.

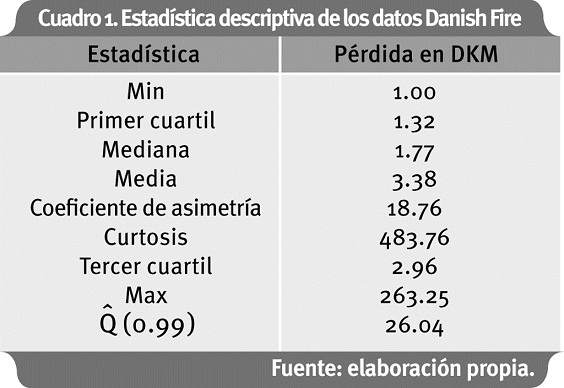
6.1. Caso Danish Fire

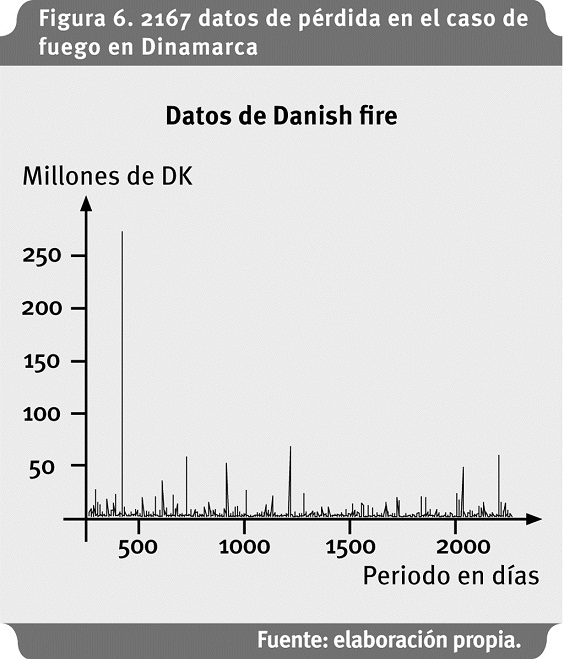
En el primer caso⁴, los datos comprenden 2,167 reclamos en seguro contra fuego en Dinamarca, donde las pérdidas se expresan en millones de Coronas Danesas (DKM), desde marzo 1 de 1980 hasta diciembre 12 de 1990. Estas pérdidas corresponden a eventos que incluyen daños a edificaciones, mobiliario y propiedad personal. Los datos han sido ajustados por inflación para reflejar precios a 1985 (McNeil, 1997). Se inicia con un análisis exploratorio de los datos (Figura 6).

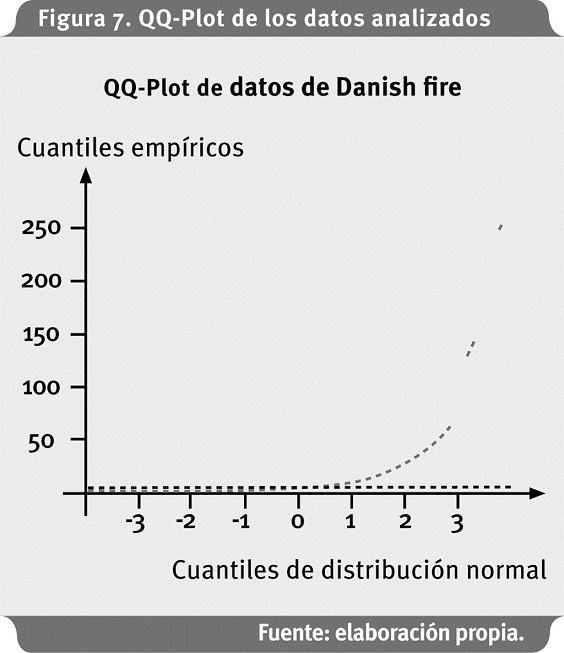
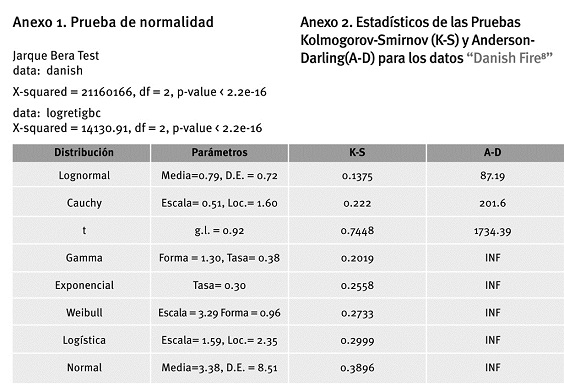
La estadística descriptiva muestra que los datos de pérdida para analizar se alejan de una distribución normal, como se observa en el gráfico de cuantiles y corroborado por el test de Jarque Bera⁵ (Figura 7), (Anexo 1).

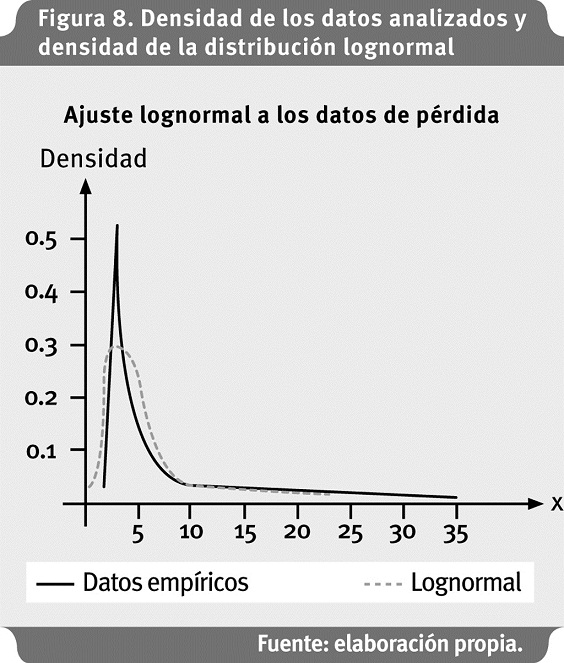
De acuerdo con las pruebas de bondad de ajuste, la distribución que más se adecua a los datos es una lognormal. En la Figura 8 se muestran las densidades de los datos empíricos y la lognormal con los parámetros que se encuentran en el Anexo 2.

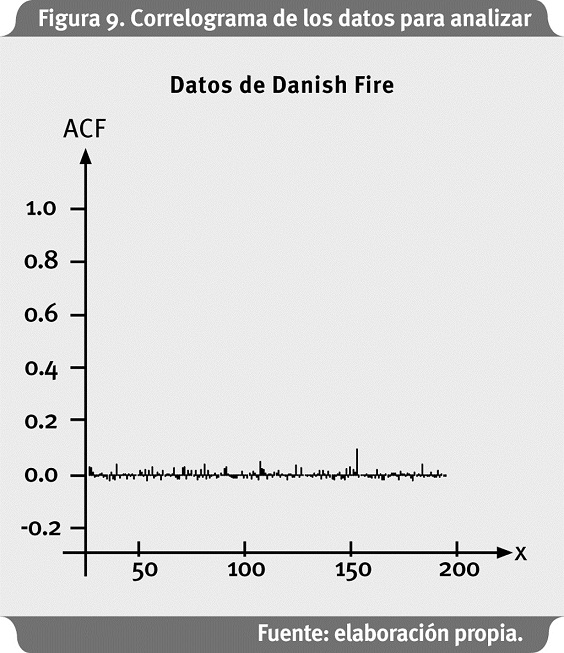
Anteriormente se muestra el gráfico de función de autocorrelación.

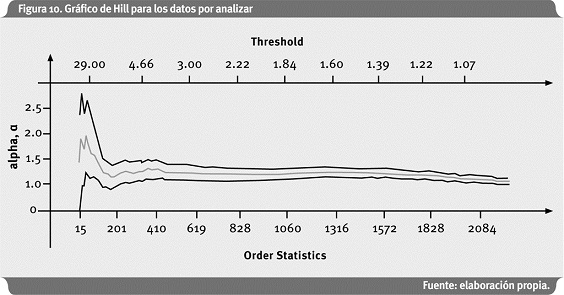
Como se observa en La Figura 9, los datos no exhiben correlación serial. Esto sucede a menudo con datos del sector seguros (y pérdidas por riesgo operativo) y se puede presumir que son observaciones iid; sin embargo, esto no es muy común con los datos financieros. Ver Resnick (1997) para pruebas adicionales de independencia aplicadas a este caso. A continuación, en la Figura 10, se presenta el Gráfico de Hill.

Pareciera que el Gráfico de Hill se estabiliza en un α alrededor de 1.5, es decir un ξ de 0.67.

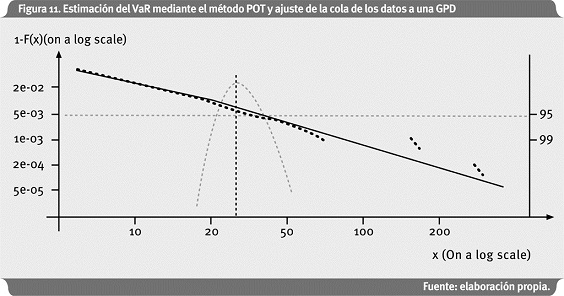
La Figura 11 muestra el resultado de aplicar el método POT al caso analizado.

Los puntos representan los datos de la cola de la distribución en escala logarítmica y la diagonal que atraviesa estos puntos es el ajuste de la distribución GPD. La línea punteada vertical presenta el VaR al 99% estimado mediante la metodología POT, y es de DKM 27.28. La parábola punteada representa el intervalo de confianza del cálculo del VaR, que al nivel de confianza del 95%, se tiene como límite inferior DKM 23.36 y límite superior de DKM 33.16. Estos resultados son obtenidos escogiendo un umbral de 10 DKM; de esta forma, el ξ (1/α) estimado es de 0.497 con un error estándar de 0.136, como se observa en el Anexo 3.

6.1.1. Método de mínimos cuadrados ponderados

Se seleccionaron los 109 datos extremos como en el método POT y se estima un ξ = 0.3406 (1/α) mediante este método, con un error estándar de 0.0185 y un R² ajustado del 75.65% (ver Anexo 4). El VaR usando la aproximación de colas de Pareto sería estimado en:

Si se escoge un α alrededor de 1.5 se observa una estabilidad en el Gráfico de Hill. El VaR, usando la aproximación de colas de Pareto, sería estimado en⁶:

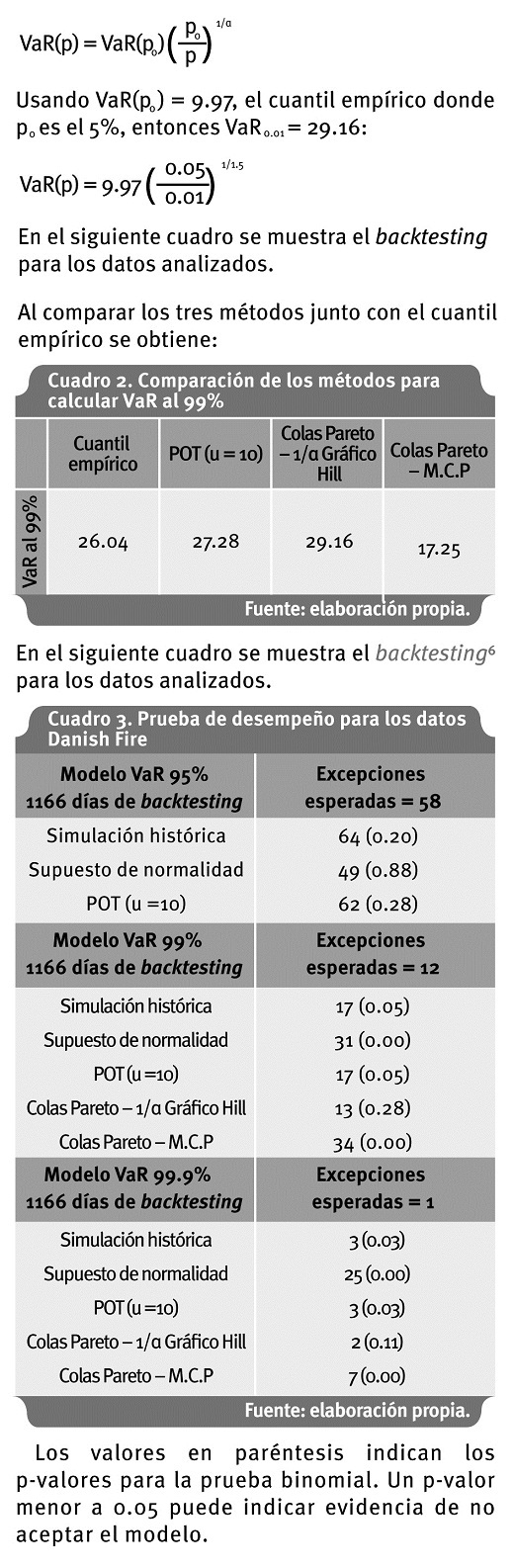
Al nivel del 90%, el supuesto de normalidad funciona bien, pero al aumentar el nivel de confiabilidad este supuesto falla. Para cuantiles altos el método basado en colas de Pareto funciona bien.

6.2. Caso IGBC

En esta sección se probarán los mismos métodos aplicados al IGBC, el tradicional índice accionario colombiano. A continuación se presenta la estadística descriptiva más importante del IGBC entre el 29 de junio de 2001 y el 30 de junio de 2010.

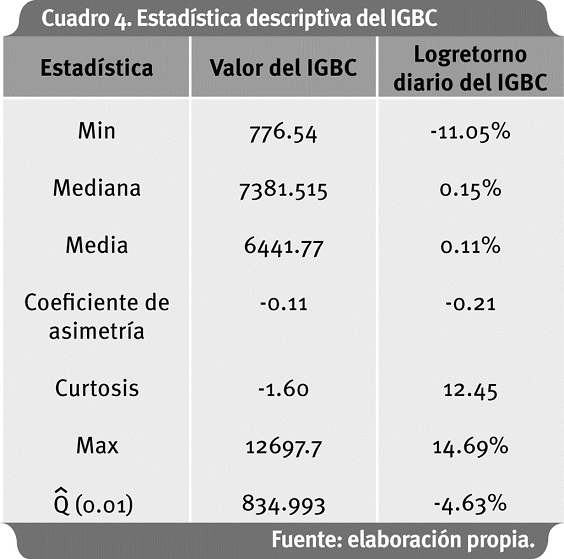
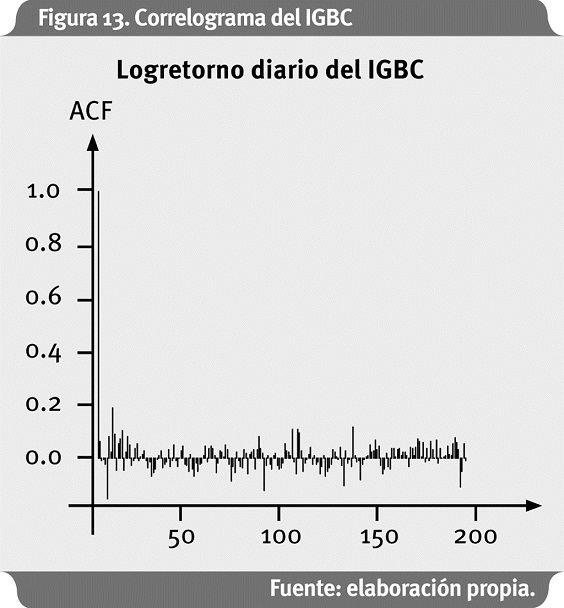
Como se observa en el Cuadro 4, los logretornos diarios del IGBC presentan una alta curtosis, no tan grande como el caso de los datos de Danish Fire, pero es un buen ejemplo por analizar para el propósito de este artículo. No hay evidencia estadística que permita aceptar la hipótesis nula de normalidad de los logretornos del IGBC en el periodo de análisis basado en la prueba Jarque-Bera (Anexo 1).

El correlograma muestra que hay cierta autocorrelación en los logretornos diarios del IGBC, lo cual es natural que suceda en la mayoría de series financieras de este tipo. Esto no ocurre con datos de pérdida por riesgo operativo o en seguros como se observó en la aplicación anterior. Esto puede conllevar problemas en la estimación de parámetros mediante el método POT, puesto que este método asume que la serie es iid. La Figura 14 presenta el Gráfico de Hill para los logretornos negativos del IGBC, y con el valor de ξ en el eje de las ordenadas.

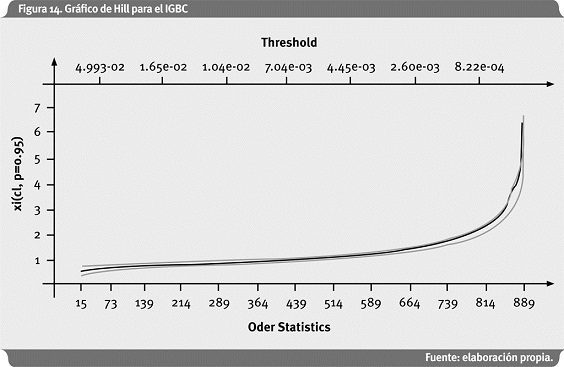
En este caso se observa el problema de alto sesgo al lado derecho del Gráfico de Hill. Embrechts et al. (1997, pág. 194) denominan este tipo de casos como "Hill horror plot". Pero al inicio del gráfico se observa cierta estabilidad alrededor de ξ = 0.5. Al seguir los mismos pasos aplicados a los datos Danish Fire, se obtiene el resultado del backtesting⁷ para los datos del IGBC:

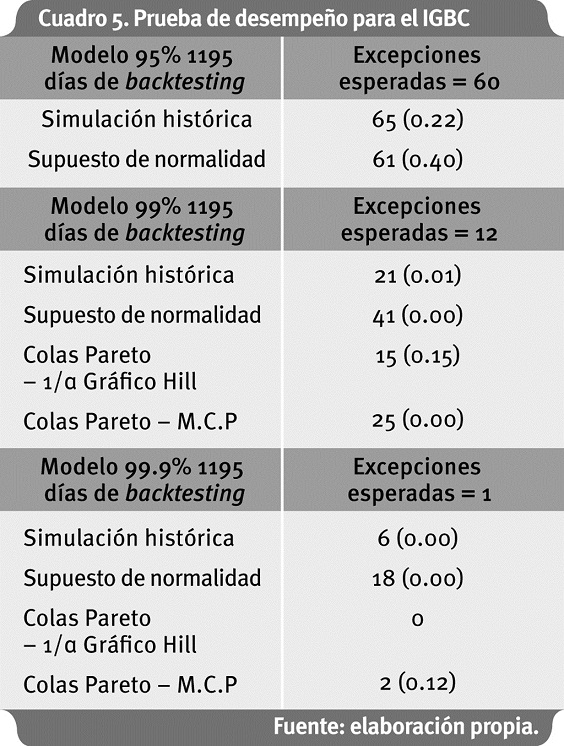
Nuevamente el supuesto de normalidad falla en los cuantiles más altos. La combinación de métodos de colas de Pareto funciona bien en tales casos.

Estas medidas de riesgo calculadas en el backtesting son medidas incondicionales de riesgo. Una aplicación de medidas condicionales de riesgo a la tasa interbancaria es realizada por Melo y Becerra (2006).

7. Conclusiones

En este documento se aplicaron algunos métodos para estimar el índice de cola de distribuciones con cola de Pareto, para estimar VaR a tres niveles diferentes de confiabilidad. Estos métodos se aplicaron a un caso en particular analizado por investigadores bajo el marco de la teoría del valor extremo y al IGBC. El método que más se aleja del valor de VaR empírico al 99%, en el primer caso, es el que se usa calculando el estimador de Hill mediante mínimos cuadrados ponderados. Esto se puede deber a la escogencia del punto en donde se comienza a observar linealidad en el gráfico de cuantiles de Pareto. El método basado en colas de Pareto con observación directa del índice de cola en el Gráfico de Hill, arroja valores aproximados al cuantil empírico de los datos.

El backtesting en los dos casos de aplicación muestra que el VaR bajo el supuesto de normalidad funciona bien a un nivel de confiabilidad del 95%; sin embargo, cuando el nivel de confianza es del 99% y 99.9% este método falla. En riesgo operativo, Basilea sugiere estimar el capital regulatorio como el VaR al 99.9%. Por lo tanto, los administradores de riesgo deberían utilizar medidas basadas en colas de Pareto puesto que los hechos estilizados en riesgo operativo muestran que las distribuciones de pérdida presentan colas pesadas y son asimétricas. Algo similar ocurre con riesgo crediticio y de mercado. En los dos casos de aplicación se observa que los métodos basados en colas de Pareto, en general, se desempeñan mejor que el método de simulación histórica y bajo el supuesto de normalidad. Sin embargo, la estimación "óptima" del índice de cola es un problema aún no resuelto debido al tradeoff que hay entre sesgo y varianza en la estimación. Existen otras técnicas de estimación como por ejemplo el de momentos, remuestreo y métodos robustos, que quedan para una futura investigación.

De esta manera, si el administrador de riesgos trata con distribuciones de pérdidas que exhiben colas pesadas, se recomienda tener en cuenta las diversas formas de estimar el índice de cola de estas distribuciones y así obtener un estimado de VaR mediante los métodos sugeridos en este artículo.

8. Agradecimientos

El autor agradece las valiosas sugerencias y recomendaciones de los evaluadores anónimos que ayudaron significativamente a mejorar la versión previa de este artículo.

Citas de pie de página

1. La curtosis mide qué tan elongada es una función de distribución. Si este valor es mayor a tres, la distribución presenta un pico alto y colas alargadas (pesadas), pero si es menor que tres, la distribución es relativamente plana. Si es igual a tres la distribución no es tan elongada ni tan plana (Canavos, 1988). La distribución normal tiene una curtosis igual a tres.(volver)

2. Extreme value analysis of environmental time series: an application to trend detection in ground-level ozone (with discussion), Models for exceedances over high thresholds (with discussion) y On a basis for "peaks over thresholds" modeling.(volver)

3. Los avances más recientes acerca de VaR pueden consultarse en: www.gloriamundi.org (volver)

4. Estos datos están disponibles en: http://www.ma.hw.ac.uk/~mcneil/ (volver)

5. La hipótesis nula es normalidad de los datos. (volver)

6. Se usa una ventana de 1,000 días y el periodo de backtesting comprende desde 12 de octubre de 1985 hasta 31 de diciembre de 1990, para un total de 1,166 días. El método de simulación histórica consiste en calcular la medida de riesgo como el percentil de las pérdidas históricas al nivel solicitado. El método de normalidad asume que las pérdidas se distribuyen normal con media y desviación de las pérdidas históricas y cuantiles 1.65, 2.33 y 3.09 para el 95%, 99% y 99.9%. (volver)

7. Se decide no adicionar el método POT puesto que se necesitan sólo pérdidas y éstas son 932. El estimador de ξ mediante el método de M.C.P. es 0.4 al escoger 220 datos extremos (10% de la cola). (volver)

Anexos

9. Referencias

Balkema, G. y Embrechts, P. (2007). High Risk Scenarios and Extremes. A Geometric Approach. Zürich Lectures in Advanced Mathematics. Zürich: European Mathematical Society Publishing House.        [ Links ]

Beirlant, J., Vynckier, P. y Teugels, J. (1996). Tail index estimation, Pareto quantile plots and regression diagnostics. Journal of the American Statistical Association, 91: 1659-1667.        [ Links ]

Beirlant, J., Goegebeur, Y., Segers, J. y Teugels, J. (2004). Statistics of Extremes: Theory and Applications. John Wiley Sons.        [ Links ]

Birkes, D. y Dodge, Y. (1993). Alternative Methods of Regression. New York: Wiley.        [ Links ]

Canavos, G.C. (1988). Probabilidad y Estadística: Aplicaciones y Métodos, McGraw-Hill.        [ Links ]

Coles, S. (2001). An introduction to statistical modeling of extreme values. London: Springer-Verlag.        [ Links ]

Csörgo, S. y Viharos, L. (1998). Estimating the tail index. En: B. Szyszkowicz (Ed.), Asymptotic Methods in Probability and Statistics (833881). Amsterdam: North-Holland.        [ Links ]

Degen, M., Embrechts, P. y Lambrigger, D. (2007). The quantitative modeling of operational risk: between g-and-h and EVT. ASTIN Bulletin, 37: 265-291.        [ Links ]

Embrechts, P., Resnick, S. y Samorodnitsky, G. (1998). Living on the Edge. RISK, 11(1), 96-100.        [ Links ]

Embrechts, P., Klüppelberg, C. y Mikosch, T. (1997). Modelling Extremal Events for Insurance and Finance. Berlin: Springer.        [ Links ]

Falk, M., Hüssler, J. y Reiss, R.D. (2004). Laws of small numbers: extremes and rare events (2nd ed.). Basel: Birkhäuser.        [ Links ]

Gilli, M. y Kellezi, E. (2003). An application of extreme value theory for measuring risk. Gene-va: Dept. of Economics and FAME, University of Geneva, 23.        [ Links ]

Greene, W.H. (2002). Econometric Analysis (5th ed.). Prentice Hall.        [ Links ]

Haan, L. y Ferreira, A. (2006). Extreme value theory. An introduction. Springer Series in Operational Research and Financial Engineering, New York: Springer-Verlag.        [ Links ]

Morgan, J.P. (2005). Riskmetrics Technical Manual, New York: J.P. Morgan.        [ Links ]

Jorion, P. (2001). Value at Risk: The New Benchmark for Measuring Financial Risk (2nd ed.). McGraw-Hill.        [ Links ]

Klugman, S.A., Panjer, H.H. y Willmot, G.E. (2008). Loss Models, From Data to Decisions (3rd ed.). Wiley.        [ Links ]

Kratz, M. y Resnick, S.I. (1996). The qq-estimator and heavy tails. Stochastic Models, 12: 699-724.        [ Links ]

Malevergne, Y. y Sornette, D. (2006). Extreme financial risks. Berlin: Springer-Verlag.        [ Links ]

McNeil, A.J. (1997). Estimating The Tails of Loss Severity Distributions Using Extreme Value Theory. ASTIN Bulletin, 27: 1117 -1137.        [ Links ]

McNeil, A. J., Frey, R. y Embrechts, P. (2005). Quantitative Risk Management: Concepts, Techniques and Tools. Pricenton: Princeton University Press.        [ Links ]

Melo, L.F. y Becerra, O.R. (2006). Medidas de riesgo, características y técnicas de medición: Una aplicación del VaR y el ES a la tasa interbancaria de Colombia. Bogotá: Centro Editorial Universidad del Rosario, 86.        [ Links ]

Moix, P.Y. (2001). The measurement of market risk. Lecture Notes in Economics and Mathematical Systems 504. Berlin: Springer-Verlag.        [ Links ]

Reiss, R.D. y Thomas, M. (1997). Statistical Analysis of Extreme Values. Basel: Brikhäuser.        [ Links ]

Resnick, S.I. (1987). Extreme Values, Regular Variation and Point Processes. New York: Springer.        [ Links ]

__ (1997). Discussion of the Danish data on large fire insurance losses. Astin Bulletin, 27: 139-151.        [ Links ]

Ruppert, D. (2004). Statistics and Finance: an Introduction. Springer.        [ Links ]

Smith, R.L. (1987). Estimating tails of probability distributions. Annals of Statistics 15:1174-1207.        [ Links ]

Vose, D. (2002). Risk Analysis. John Wiley & Sons.        [ Links ]