Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Praxis Filosófica
Print version ISSN 0120-4688On-line version ISSN 2389-9387
Prax. filos. no.31 Cali July/Dec. 2010
LA NOCIÓN DE MODELO EN EL ENFOQUE SEMÁNTICO DE LAS TEORÍAS*†
The Notion of Model within the Semantic Approach of Theories
Universidad del Valle
† Las ideas centrales de este artículo las expuse en la XII Jornada Rolando Chuaqui Kettlun, realizada en la Universidad de Valparaíso, Chile, los días 10, 11 y 12 de noviembre de 2010, y también en la Tercera Escuela de Historia y Educación Matemática (ENHEM3), realizada en la Universidad del Valle, Cali - Colombia, del 27 al 29 de octubre de 2010.
* Recibido Septiembre de 2010; aprobado Noviembre de 2010.
Una cosa es el mundo físico externo, otra es el mundo
matemático, y otra el mundo físico interno, ideal, abstracto
y modelizado que tenemos en nuestra cabeza... Los objetos
físicos sensibles, de estructura más o menos complicada, se
simplifican asintóticamente para buscarles analogías con
los modelos matemáticos; esta es la base del principio del
conocimiento voluntariamente incompleto y modelizado de
la física.
R. Martínez-Chavanz, Álgebra multilineal (2006)
RESUMEN
El artículo busca clarificar la noción de modelo involucrada en el enfoque semántico de las teorías (EST). Se muestra que en el contexto del EST el término 'modelo' tiene dos funciones: en un caso se presenta como una estructura que satisface una descripción y en el otro como una estructura matemática que representa aspectos de ciertos sistemas reales. Así, el término 'modelo' posee dos sentidos, pero la función relevante de los modelos para el EST es la de representación y no la de satisfacción. Esto nos permitirá concluir, entre otras cosas, que los partidarios de la concepción estructuralista de las teorías, una de las versiones del EST, colocan el acento en forma inadecuada al concebir los modelos en el sentido de la semántica formal, en tanto que las versiones últimas de van Fraassen y Giere son más apropiadas al privilegiar los modelos como estructuras matemáticas, el primero, y como representaciones, el segundo.
Palabras clave: teoría, estructura matemática, representación, enfoque semántico y concepción estructuralista.
SUMMARY
The article aims to clarify the notion of model involved in the semantic approach of theories (SAT). It is shown that in the context of the SAT, the term 'model' has two functions: in one case, it is featured as a structure that satisfies one description and in another it is featured as a mathematical structure that represents aspects from some actual systems. Thus, the term "model" has two senses, however for the SAT the relevant function of models is representation and not satisfaction. This will allow us to conclude, among other things, that proponents of the structuralist conception of theories, one of the SAT's versions, put the accent in an inappropriate way when conceiving the models in the formal semantic sense, whereas the latter versions by van Fraassen and Giere are more appropriate because they conceive the models as mathematical structures (van Fraassen) and as representations (Giere).
Key words: Theory, Mathematical Structure, Representation, Semantic Approach and Structuralist Conception.
1. Introducción
El presente artículo busca clarificar la noción de modelo involucrada en el enfoque semántico de las teorías (EST) recogiendo, contrastando y complementando los planteamientos hechos al respecto por van Fraassen (1989), Giere (1999) y Thomson-Jones (2006), principalmente. Se muestra que en el contexto del EST el término 'modelo' tiene dos funciones: en un caso se presenta como una estructura que satisface1 una descripción y en el otro como una estructura matemática que representa aspectos de ciertos sistemas reales. Así, el término 'modelo' posee dos sentidos, pero la función relevante de los modelos para el EST es la de representación y no la de satisfacción. Esto nos permitirá concluir, entre otras cosas, que los partidarios de la concepción estructuralista de las teorías, una de las versiones del EST, colocan el acento en forma inadecuada al concebir los modelos en el sentido de la semántica formal, en tanto que las versiones últimas de van Fraassen y Giere son más apropiadas al privilegiar los modelos como estructuras matemáticas, el primero, y como representaciones, el segundo.
Para ello se procede del siguiente modo, en primer lugar se traza la distinción general entre modelos hacedores de verdad y modelos representacionales. En segundo lugar, y de acuerdo con Thomson-Jones (2006), se establece la distinción entre dos tipos de modelos hacedores de verdad: modelo semántico2 y modelo ajustado a (que satisface) una descripción (o conjunto de descripciones). En tercer lugar, y de acuerdo con Giere (1999), se presentan los aspectos sustantivos de un modelo representacional, y después se explican distintos tipos de modelos de esta clase (diagramas y modelos a escala). En cuarto lugar, se define estructura matemática con el objetivo de presentar los modelos matemático puro y matemático aplicado. Finalmente, se muestra que los modelos de las teorías empíricas de principio (llamados por Giere modelos teóricos) son estructuras matemáticas (tal y como lo plantea van Fraassen) que guardan relación tanto con la descripción o caracterización de la teoría como con los sistemas del dominio de aplicación de la teoría. De tal manera que en el primer caso dichas estructuras (matemáticas) son modelos en el sentido de ajustarse a una descripción, mientras que en el segundo caso son modelos en el sentido representacional. Esto permite concluir que la función relevante de las estructuras matemáticas de una teoría, bajo el espíritu del EST, es la de representación. Para todo esto último se analiza, bajo el trasfondo de los distintos tipos de modelos, la presentación de una teoría empírica a través de su axiomatización mediante un predicado conjuntista.
El EST surge como alternativa al enfoque sintáctico-axiomático (lingüístico o concepción heredada, la expresión introducida por Putnam3) de las teorías, según el cual una teoría es, básicamente, un conjunto de enunciados en un lenguaje especificado, esto es, los principios o leyes de la teoría más los enunciados que se derivan lógicamente de ellos. Así, por ejemplo, la mecánica newtoniana consiste, básicamente, en sus tres leyes de movimiento más la ley de gravedad, y todo lo demás que de ellas se deduce.
Mientras que de acuerdo con los partidarios del EST una teoría empírica hay que identificarla con un conjunto de modelos (criterio de identificación) o, metodológicamente (criterio metodológico4), una teoría queda mejor comprendida como un conjunto de modelos. Así, en el caso de la mecánica newtoniana el énfasis no hay que hacerlo en sus leyes sino en los modelos (o sistemas idealizados) que estas (las leyes o principios) describen, caracterizan o definen; modelos como el siguiente: tenemos partículas puntuales con masa que interactúan entre sí mediante fuerzas de diversos tipos, de modo que cada una de estas fuerzas produce una aceleración sobre la partícula que actúa, de acuerdo con la ecuación de movimiento (segunda ley de Newton).
En cuanto al origen del EST, vale la pena comenzar observando que la distinción sintaxis / semántica, que supuestamente permite caracterizar dicho enfoque y también establecer su principal diferencia con el lingüístico, se recogió de la lógica y filosofía del lenguaje (de manera más precisa, de la teoría de modelos o semántica formal), en donde el significado de cada uno de estos términos es relativamente preciso, para aplicarse en la filosofía de la ciencia.
La distinción entre sintaxis y semántica se puede trazar en los siguientes términos. Si se parte de considerar un lenguaje como un conjunto de expresiones, como es usual en estos estudios, las propiedades sintácticas de una expresión de un lenguaje sólo tienen que ver con sus relaciones con otras expresiones, dejando de lado cualquier consideración sobre el significado o la interpretación de las mismas. Por la otra parte, una propiedad semántica de una expresión concierne a la relación de la expresión con el mundo, con el universo de discurso. La semántica estudia el significado de las palabras y la verdad o falsedad de los enunciados. Estas relaciones semánticas, gracias a los trabajos de Tarski, pueden expresarse en términos de lo que se llama interpretación o modelo de un lenguaje formal, de modo que la noción de modelo hace parte de la semántica.
Pero, por otra parte, en realidad nos encontramos con que actualmente no hay un conceso entre los partidarios del EST respecto a la noción de modelo, si bien en un comienzo las distintas versiones del EST entendían los modelos en el sentido de la teoría de modelos. Veamos algunos casos. Tenemos la interpretación ya clásica de P. Suppes en su artículo fundador del enfoque, "A Comparison of the Meaning and Use of Models in Mathematics and the Empirical Sciences" (1961), en donde plantea:
- Pretendo que el concepto de modelo en el sentido de Tarski puede usarse sin distorsión y como un concepto fundamental en todas las disciplinas... En este sentido, aseveraré que el significado del concepto de modelo es el mismo en matemáticas y en las ciencias empíricas. La diferencia que se encuentra en esas disciplinas se encuentra en sus usos del concepto.
El mismo van Fraassen, quien posteriormente criticará el identificar los modelos del EST con los de la teoría de modelos, en uno de sus artículos fundacionales del enfoque establece tal identidad y, lo que es más grave, defiende que en principio el EST y el lingüístico son equivalentes:
- En el estudio formal del lenguaje corrientemente encontramos dos enfoques generales: uno es de orientación sintáctica y axiomática, y el otro de orientación semántica... Entre estos dos enfoques se presentan interrelaciones naturales: una teoría axiomática puede caracterizarse por la clase de interpretaciones que la satisfacen y una interpretación puede caracterizarse por el conjunto de oraciones que son satisfechas en esta... Estas interrelaciones,... harían implausible cualquier afirmación sobre una superioridad filosófica de un enfoque sobre el otro5.
Un cambio de parecer semejante encontramos también en Giere, pues en su destacado libro Explaining Science (1988, 79) hace tal equivalencia: "sugiero llamar "modelos teóricos" a los sistemas idealizados de que tratan los textos de mecánica... Esta terminología incluso coincide convenientemente con el uso de los lógicos para quien un modelo de un conjunto de axiomas es un objeto o conjunto de objetos que satisfacen los axiomas".
En cuanto a la versión estructuralista, tenemos que Sneed, Balzer y Moulines dicen, por ejemplo, en uno de sus últimos artículos colectivo: "De acuerdo con el estructuralismo, los modelos (en el sentido de la semántica formal) son las unidades estructurales más simples de que consta una teoría"6. Pero Moulines es un poco más preciso al plantear que "en un primer paso..., esos complejos que son las teorías científicas consisten en modelos en el sentido de la semántica formal, esto es, en estructuras que satisfacen determinados axiomas"7.
Los estructuralistas se han mantenido en este punto, en el de identificar los modelos del EST con los de la teoría de modelos, pero van Fraassen y Giere han hecho cambios importantes al respecto. Así, por ejemplo, van Fraassen diez años después, en su importante libro The Scientific Image (1980), plantea que, por contraste con el sintáctico, en el EST se presenta "una teoría por medio de la identificación de una clase de estructuras como sus modelos" y que, además, en este enfoque "el lenguaje utilizado para expresar la teoría no es único ni básico; la misma clase de estructuras podrían muy bien describirse de maneras radicalmente distintas, cada una con sus limitaciones propias. Los modelos son el centro de atención [no los enunciados]"8. Por otra parte, Giere, también casi diez años después, plantea: contrario a la afirmación de Suppes, pienso que esta forma [la concepción instancial de los modelos] no es la mejor concepción de los modelos para comprender los modelos tal y como son empleados en la práctica de las ciencias empíricas... Por contraste, llamo representacional a la forma como entiendo los modelos, porque no los considero como proporcionando un medio para interpretar sistemas formales, sino más bien como herramientas para representar el mundo9. Tenemos, entonces, que ahora van Fraassen enfatiza en el hecho de que los modelos son estructuras matemáticas y Giere en su carácter representacional.
2. Modelo semántico
Siguiendo la terminología de Thomson-Jones (2006), se tienen dos tipos de modelos hacedores de verdad, los que podemos llamar modelos semánticos y los modelos que se ajustan a descripciones10. Un modelo semántico es un modelo de acuerdo a la teoría de modelos o semántica formal, esto es, una estructura no lingüística que proporciona una interpretación a un conjunto de enunciados y los hace verdaderos, los satisface en el sentido técnico de Tarski. Así, un modelo semántico es un modelo hacedor de verdad que adicionalmente proporciona una interpretación de un enunciado o conjunto de enunciados; en este sentido, un modelo semántico es realmente un modelo interpretativo.
De acuerdo con la teoría de modelos, una estructura (o sistema)  es una entidad abstracta compleja, compuesta por un conjunto no vacío A -llamado universo de la estructura- y una serie de individuos a, de funciones f y de relaciones R -definidas sobre el universo- destacados o considerados
es una entidad abstracta compleja, compuesta por un conjunto no vacío A -llamado universo de la estructura- y una serie de individuos a, de funciones f y de relaciones R -definidas sobre el universo- destacados o considerados
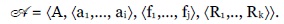
Ahora bien, dado un lenguaje de primer orden L, adecuado a la estructura  , y una función de interpretación I tal que hace que los nombres de L denoten individuos de A, que los predicados de L se correspondan con relaciones de A y que los enunciados de L adquieran un valor de verdad, esto es, que se conviertan en verdaderos o falsos en A; se dice, entonces, que la estructura
, y una función de interpretación I tal que hace que los nombres de L denoten individuos de A, que los predicados de L se correspondan con relaciones de A y que los enunciados de L adquieran un valor de verdad, esto es, que se conviertan en verdaderos o falsos en A; se dice, entonces, que la estructura  es un modelo de los enunciados del lenguaje L. Esto es, si se trata de un enunciado φ de L, simplemente decimos que
es un modelo de los enunciados del lenguaje L. Esto es, si se trata de un enunciado φ de L, simplemente decimos que 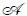 es un modelo de φ o
es un modelo de φ o 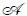 satisface a φ o φ es verdadero en
satisface a φ o φ es verdadero en 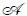 o φ es satisfecho en
o φ es satisfecho en 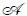 11.
11.
En el presente contexto diremos que bajo estas condiciones A es un modelo semántico. Obsérvese que un modelo semántico siempre está vinculado a un lenguaje particular porque proporciona una interpretación a dicho lenguaje.
Veamos una ilustración, las interpretaciones dualistas del primer postulado de la geometría euclídea. Se tiene la expresión desinterpretada "por dos puntos pasa una recta" (o "dos α se relacionan mediante Φ con una β"). En la interpretación usual tenemos que los términos del enunciado significan lo que corrientemente se entiende por ellos; es decir, en sentido literal: por los puntos X y Y pasa la recta Z. En tanto que en la interpretación dual los significados se intercambian; es decir, en sentido literal: las rectas X y Y contienen el punto Z. Por otra parte, a continuación aparecen dos estructuras y cada una consta de ciertos objetos (puntos y rectas) y de determinada relación entre estos (pasar y contener).
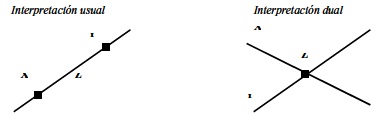
Así que cada una de estas estructuras proporciona una interpretación de la expresión original y la hacen verdadera, la satisfacen. En definitiva, estas dos estructuras son modelos del enunciado "por dos puntos pasa una recta".
3. Modelo que se ajusta a descripciones
Siguiendo a Thomson-Jones (2006), un modelo de este tipo es un sistema que hace verdaderos a los miembros de un conjunto de enunciados completamente interpretados, como los del lenguaje científico. Así, un modelo de este tipo no es, en sentido estricto, un modelo interpretativo como el semántico. Veamos el ejemplo que propone Thomson-Jones. Consideremos el siguiente enunciado E de la física,
E: Toda resistencia se calienta cuando pasa una corriente por ella.
Este enunciado está completamente interpretado. Así que no se trata del caso anterior. Pero, dados dos sistemas o circuitos eléctricos particulares (R1, I1) y (R2, I2), con resistencia R1 y R2, y por lo que pasan las corrientes I1 y I2, respectivamente; tenemos que estos dos circuitos satisfacen, hacen verdadero el enunciado E o, si se quiere, la descripción E. De ahí que se acostumbre a decir que estos sistemas o circuitos son modelos del enunciado E, son modelos que se ajustan a la descripción E.
4. Modelo representacional
De acuerdo con Giere (1999), la noción de modelo del EST no equivale a la de modelo semántico, sino que más bien la principal peculiaridad de estos modelos es su función representacional; una vez más: contrario a la afirmación de Suppes, pienso que esta forma [la concepción instancial de los modelos] no es la mejor concepción de los modelos para comprender los modelos tal y como son empleados en la práctica de las ciencias empíricas... Por contraste, llamo representacional a la forma como entiendo los modelos, porque no los considero como proporcionando un medio para interpretar sistemas formales, sino más bien como herramientas para representar el mundo12.
Aún más, de acuerdo con Giere, este aspecto representacional de los modelos del EST se puede comprender mejor a través de la función representacional que le asignamos a un mapa, por ejemplo, a un mapa de una ciudad. Respecto a la función representacional de los mapas podemos subrayar las siguientes características.
- El mapa no es una entidad lingüística, es un objeto físico.
- Usualmente los mapas no son pensados como instanciando (o hacedores de verdad de) una forma lingüística o ajustadores a una descripción.
- La relación de representación es tríadica: se utiliza (los usuarios) un objeto (el mapa) para representar otro objeto (la ciudad). En otras palabras, hay una relación de representación entre el objeto representado (la ciudad) y el objeto que representa (el mapa), establecida y utilizada por los usuarios. Es en este sentido que se acostumbra a decir que el mapa es un modelo de la ciudad.
- El mapa representa a la ciudad en ciertos aspectos (no en todos) y con cierto grado (aproximación y no de igualdad).
Lo anterior puede expresarse del siguiente modo en términos de teorías empíricas.
- Las teorías no son entidades lingüísticas, son objetos abstractos, estructuras matemáticas.
- Las teorías no son modelos semánticos que proporcionen una interpretación de un lenguaje y hagan verdaderos o falsos a sus enunciados.
- Los científicos (para quien representa) emplean una teoría (lo que representa) para representar ciertos aspectos del dominio de investigación (lo representado). Una teoría modela el dominio de investigación en cuestión.
- Una teoría representa al dominio de investigación correspondiente en algunos aspectos y con cierto grado de aproximación.
Por otra parte, la función de los diagramas y los modelos a escala es similar a la de los mapas. Un diagrama en papel de un circuito eléctrico, por ejemplo, busca representar ciertas relaciones del circuito físico real y con cierta aproximación. La simulación del comportamiento de un avión en un túnel de viento es un modelo a escala de (representa) lo que le podría suceder a un verdadero avión bajo condiciones reales.
Una observación final, en este tipo de modelos no tiene sentido preguntarse si son semánticos o se ajustan a una descripción, bajo la relación que se está privilegiando.
5. Modelo matemático
Como se advirtió desde un comienzo, la idea que se quiere defender aquí es que en EST los modelos hay que entenderlos como estructuras matemáticas que representan aspectos de cierta parcela de la realidad. En el apartado anterior se ha expuesto en qué consiste la función representacional y en éste se precisará el que sean estructuras matemáticas. Este segundo aspecto es el que van Fraassen viene enfatizando últimamente, tal como se mencionó más arriba: "se perdería el impacto de la innovación de Suppes si los modelos se definen, como en muchos textos corrientes de lógica, como parcialmente entidades lingüísticas cada una bajo el yugo de una sintaxis particular... Los modelos son estructuras matemáticas llamadas modelos de una teoría sólo en virtud de pertenecer a la clase definida de los modelos de esa teoría"a href="#num13">13. Esto es, en los términos que Thomson-Jones interpreta esta idea de van Fraassen, "un modelo es simplemente una estructura matemática usada para representar la estructura y/o la conducta de un sistema, o clase de sistemas, del dominio de investigación de una disciplinada dada - esta es la noción de modelo matemático"14.
De manera más precisa, la estructura 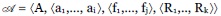 es una estructura matemática cuando el universo A son objetos matemáticos y las funciones f y las relaciones R también son matemáticas15. El hecho que estas estructuras tengan que ver con entidades matemáticas, con una interpretación particular, hace que estas estructuras no puedan ser modelos semánticos en sentido estricto, pero sí pueden ser modelos que satisfacen descripciones o modelos representacionales.
es una estructura matemática cuando el universo A son objetos matemáticos y las funciones f y las relaciones R también son matemáticas15. El hecho que estas estructuras tengan que ver con entidades matemáticas, con una interpretación particular, hace que estas estructuras no puedan ser modelos semánticos en sentido estricto, pero sí pueden ser modelos que satisfacen descripciones o modelos representacionales.
Para explicar estas dos funciones recurro, entonces, a las nociones de modelo matemático puro y modelo matemático aplicado introducidas por Giere (1999). Consideremos la relación lineal entre las variables X y Y. Así, tenemos la relación propiamente, la ecuación correspondiente y la gráfica correspondiente, tal y como aparece a continuación.

Ahora bien, y a la luz de Giere (1999), podemos afirmar lo que sigue.
- La ecuación es un objeto lingüístico y un objeto físico (letras sobre el papel), pero aquí sólo nos fijaremos en su aspecto lingüístico.
- La relación lineal descrita por la ecuación es un tipo de objeto abstracto, una estructura matemática, que es mucho más abstracto que la ecuación escrita. Giere llama a este tipo de objetos modelos matemáticos puros y son modelos en el sentido que son estructuras que satisfacen la ecuación lineal, la expresión lingüística. Así, como advertíamos arriba, no son modelos semánticos que proporcionan una interpretación, sino modelos que satisfacen la descripción proporcionada por la ecuación.
- La gráfica como tal es un objeto físico, y es la contraparte física de la relación lineal, que es un objeto abstracto, una estructura matemática. Así que podemos decir que la gráfica lineal representa (es un modelo de) la relación lineal, pero por ser un modelo físico es imperfecto y sólo similar o aproximado a la relación lineal abstracta.
Nótese que el tipo de relación entre el par ecuación y relación lineal no es la misma que entre el par gráfica y relación lineal: la primera es de ajuste16 y la segunda de representación.
De acuerdo con Giere, un modelo matemático aplicado, o simplemente modelo matemático, se obtiene a partir de un modelo matemático puro remplazando sus distintos elementos por sistemas conformados por objetos reales y sus relaciones. Así, por ejemplo, son aplicaciones de la función lineal Y = aX + b: la ecuación x (t) = vt + x0, que representa el cambio de la posición x de un cuerpo respecto al tiempo t, donde x0 es la posición en t = 0 y v es la velocidad constante del cuerpo; y la ecuación P (t) = rt + P0 que representa el comportamiento de una población en el tiempo t (o, si se quiere, en un intervalo de tiempo determinado), siendo P el número de personas en el tiempo t, P0 las personas en t = 0 y r la rata de crecimiento constante de la población. En este caso tenemos tres elementos que vale la pena distinguir bien: la función lineal, los modelos matemáticos (aplicados) y los sistemas reales.
La función lineal, que hemos llamado modelo matemático puro, es modelo en el sentido que satisface la ecuación. Los dos modelos matemáticos aplicados, el cinemático y el de crecimiento poblacional, son estructuras matemáticas que buscan aplicarse a determinado ámbito de la realidad; para el presente caso, cuerpos en movimiento o crecimiento de poblaciones. Aunque es claro que los sistemas reales, a los cuales pretende aplicarse los respectivos modelos matemáticos, no cumplen estrictamente la ecuación correspondiente. En este sentido, los modelos matemáticos son idealizaciones de cuerpos y poblaciones que satisfacen las respectivas ecuaciones y, a la vez, son modelos que pueden aplicarse de menara aproximada a sistemas reales; por ejemplo, el movimiento de un automóvil concreto o el crecimiento de una población bacteriana particular.
En síntesis tenemos que la ecuación de movimiento es verdadera en el modelo particular idealizado, pero propiamente no podemos decir que esta ecuación es verdadera respecto a las distintas posiciones ocupadas por un automóvil real en movimiento o, en general, respecto a un sistema real. Además, la relación importante en este último caso es la que existe entre el modelo matemático (aplicado) y los sistemas reales que busca describir, que es una relación representacional y no de ajuste.
A partir de lo que es un modelo matemático podemos precisar lo que se quiere decir con analogía o con modelo analógico en ciencia. Utilizando el ejemplo anterior, podemos decir que el tipo de movimiento anterior es análogo al tipo crecimiento de ciertas poblaciones o, con otro ejemplo más familiar, se suele hablar de la analogía presente entre un circuito eléctrico y un circuito hidráulico, el comportamiento del último, que nos es más familiar, nos permite comprender ciertos aspectos del primero. En ambos casos tenemos que los pares de situaciones satisfacen el mismo tipo de ecuación, esto es, tienen estructuras isomorfas. Sus estructuras son isomorfas porque es posible establecer una relación biunívoca entre los respectivos elementos seleccionados de las estructuras. Así, en el primer caso, ambos tipos de sistemas (tanto el movimiento del cuerpo como el crecimiento de la población) se comportan linealmente, tienen la misma estructura matemática. En el segundo caso decimos que la corriente eléctrica en un circuito es un flujo de electrones a través del material conductor, y que este se comporta de manera análoga al flujo de agua en una tubería, que es un sistema mecánico. De tal manera que la relación matemática entre potencia de la bomba, velocidad del agua y resistencia dentro de la tubería (la cual nos es más familiar) es la misma que existe entre voltaje, corriente eléctrica y resistencia en el circuito eléctrico (que es la que queremos comprender); ambos sistemas cumplen el mismo tipo de ecuación, poseen la misma estructura matemática, y esto es lo que permite emplear a uno de ellos como modelo (analógico) del otro.
Ahora bien, es cierto que cada uno de los circuitos (hidráulico y eléctrico) satisface su respectiva ecuación, de modo que son modelos que se ajustan a una descripción; pero la relación relevante aquí es la de representación, el que el circuito hidráulico permite entender (representa) parte del funcionamiento del circuito eléctrico.
6. Modelo teórico
En este aparto se aplican las ideas precisadas en los anteriores apartados al caso de las teorías de principios (principios matemáticos), teorías que contienen leyes o principios teóricos, como: las leyes de Newton, la ecuación de Schröedinger, el principio de relatividad, el principio de selección natural y las leyes de la genética mendeliana. Giere llama modelos teóricos17 a los modelos de este tipo de teorías y, si bien precisa muchas de sus características, no dice explícitamente que sean estructuras matemáticas; en tanto que esta es una idea persistente en los planteamientos de van Fraassen. En definitiva, a continuación se mostrará que los modelos teóricos (recogiendo la terminología de Giere que me parece bastante sugerente) son estructuras matemáticas que son utilizadas por los científicos para representar aspectos del dominio de investigación de su interés.
Por tanto, para determinar qué tipo de modelos se emplean en el EST, esto es, para precisar si son semánticos o ajustadores a una descripción o representacionales, analicemos una teoría particular como la mecánica newtoniana de partículas, la cual se presenta mediante la definición de un predicado conjuntista, que es una de las formas más recurrente entre los partidarios del enfoque semántico18. El análisis que viene se recoge básicamente de Thomson-Jones (2006).
En la axiomatización de McKinsey, Sugar y Suppes19, se llama sistema mecánico clásico newtoniano de partículas a un sistema que cumple la segunda ley de Newton (la ley de movimiento), y por tanto la primera (la ley de inercia), y además la tercera ley (la ley de acción-reacción); y su reconstrucción axiomática es como sigue.
Definición: X es un sistema mecánico clásico newtoniano de partículas si y solo si existen P, T, m, s, ƒ tales que:

Es claro que X no es simplemente una estructura, es una estructura matemática. Así que la pregunta, entonces, es: ¿las estructuras matemáticas seleccionados mediante el predicado conjuntista funcionan como modelos semánticos o modelos que se ajustan a una descripción o modelos representacionales? La respuesta en concreto es como sigue.
a) No son modelos semánticos porque las cláusulas del predicado conjuntista están interpretadas, hablan de entidades matemáticas y de sus propiedades20. Esto es, hace parte de la axiomatización conjuntista la explicación de ciertos símbolos y determinados conceptos, por ejemplo: N denota el conjunto de los números naturales, y R+ y R3 denotan, respectivamente, el conjunto de los números reales positivos y el espacio euclídeo tridimensional proporcionado por los productos escalar y vectorial 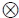 , normales; el conjunto P es un conjunto de cuerpos o partículas, T es el conjunto de instantes de tiempo; s(p,t) es el vector posición de la partícula en el instante t; m(p) es la masa de la partícula p, etc.
, normales; el conjunto P es un conjunto de cuerpos o partículas, T es el conjunto de instantes de tiempo; s(p,t) es el vector posición de la partícula en el instante t; m(p) es la masa de la partícula p, etc.
b) Son modelos en el sentido trivial de ajustarse a la descripción del predicado conjuntista, satisfacen los distintos enunciados empleados para presentar la teoría, esto es, las distintas cláusulas del predicado conjuntista.
c) También son modelos en el sentido (incluso débil) de estructuras hacedoras de verdad de una formulación lingüística de la teoría presentada, esto es, de la mecánica clásica newtoniana de partículas. Puesto que, si bien las distintas cláusulas del predicado conjuntistas están formuladas en un lenguaje matemático, estas además están interpretadas (tal y como se mostró en a.) dentro de un lenguaje de la física que habla de partículas, tiempo, masa de partículas, fuerza y cosas por el estilo21. En otras palabras, las estructuras del predicado conjuntista son modelos matemáticos (aplicados), en la terminología de Giere. En definitiva, los axiomas, en el sentido de la axiomatización conjuntista, son componentes de una caracterización (descripción) de una clase de estructuras matemáticas interpretadas en términos físicos.
Esto en cuanto a la relación que guardan las estructuras matemáticas con el predicado conjuntista.
d) Pero también existe la relación que guardan estas estructuras (definidas mediante el predicado conjuntista) con los sistemas del dominio de investigación, con los fenómenos, con los sistemas reales. Esto es, tal como muestra la figura 2, las estructuras matemáticas seleccionadas por el predicado conjuntista se relacionan de dos modos: con los enunciados del predicado conjuntista y con los sistemas reales. Esta última relación es la importante para el EST, en cuanto estamos hablando de teorías acerca de la realidad (teorías empíricas), y este tipo de relación es la que hemos calificado de representacional. Por tanto, de acuerdo con la teoría, la clase de estructuras matemáticas definidas mediante el predicado conjuntista es la adecuada para representar, de un modo parcial y aproximado, cierto tipo de sistemas reales; en el caso de la mecánica, aquellos conjuntos de partículas que tienen masa e interactúan entre sí por medio de distintas fuerzas, etc.
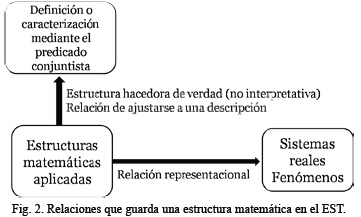
En síntesis, la novedad del EST está en concebir un modelo como una estructura matemática cuya función es la de representar los fenómenos de cierta parcela de la realidad. Con las palabras de Thomson-Jones, "la noción de modelo matemático - esto es, la de una estructura matemática cuya función es la de representar los sistemas del dominio de investigación- es todo lo que necesitamos para obtener la versión más atractiva y útil del enfoque semántico"22. Pero esta conclusión nos permite ver que el calificativo semántico es inapropiado porque no refleja en realidad las dos novedades del EST23, tal vez podríamos decir mejor enfoque estructuralista representacional.
Lo anterior nos permite concluir, en particular, que los estructuralistas colocan el énfasis de los modelos de manera inadecuada. Al afirmar que "son modelos en el sentido de la semántica formal"24, dan a entender que las estructuras son modelos semánticos que proporcionan una interpretación; lo cual es incorrecto a la luz del análisis de arriba. Pero, por otra parte, al afirmar que "son modelo que satisfacen unos axiomas"25, y no decir nada respecto a su función de interpretación, dan a entender que las estructuras no son modelos semánticos sino modelos que se ajustan al conjunto de descripciones dadas por las cláusulas del predicado conjuntista; pero esto también es incorrecto, también a la luz de las reflexiones de arriba. En ambos casos ponen el acento en la relación que tienen las estructuras con la formulación lingüística y no en la que estás tienen con los sistemas reales, con las aplicaciones intencionales.
A manera de conclusión.
- La noción apropiada de modelo (la novedad) en el EST es: una estructura matemática que tiene como función representar sistemas reales de un dominio de investigación particular.
- Es secundario que estos modelos se ajusten a las descripciones de un predicado conjuntista o a cualquier otra forma de caracterizar las estructuras matemáticas que contiene la teoría.
- No tiene sentido aquí hablar de modelos semánticos, pues las estructuras matemáticas corresponden a una interpretación matemática particular, así que en sentido estricto no están proporcionando ninguna interpretación, no son estructuras interpretativas.
Pie de página
1Este término no se emplea aquí en el sentido técnico de la teoría semántica de la verdad de Tarski.2Otros adjetivos apropiados podrían ser tarskiano (que emplea Thomson-Jones) o instancial o intepretativo (que emplea Giere), pero he preferido utilizar semántico por ser la terminología que introduje en Guerrero (2003) y que también emplea Suárez (2005), p. 34.
3Para las características principales de los enfoques lingüístico y semántico, así como para las distintas versiones del último, remito a mi escrito Guerrero (2008).
4Estas expresiones las recojo de Thomson-Jones (2006).
5Van Fraassen (1970), p. 326. Aún en 1980, van Fraassen es partidario de este punto de vista, pues en su importante libro The Scientific Image (1980, p. 43), escribe: "un modelo de una teoría es cualquier estructura que satisfaga sus axiomas".
6Véase la introducción de Balzer, Sneed y Moulines (2000), p. 11.
7Moulines (2002), p. 71. Suppes (2002, 21) también se expresa en estos mismos términos.
8Van Fraassen (1980), p. 44. Lo del paréntesis es mío. En Laws and Symmetry (1989), p. 366, se expresa en el mismo tono: "se perdería el impacto de la innovación de Suppes si los modelos se definen, como en muchos textos corrientes de lógica, como parcialmente entidades lingüísticas cada una bajo el yugo de una sintaxis particular... Los modelos son estructuras matemáticas, llamadas modelos de una teoría sólo en virtud de pertenecer a la clase definida de los modelos de esa teoría".
9Giere (1999). Lo del paréntesis es mío, pero recoge la terminología de Giere.
10Giere (1999) no diferencia entre estos dos tipos de modelos, así que podríamos decir que para él ambos son semánticos (en nuestra terminología). Pero como veremos más adelante, es un error considerar a un modelo que se ajusta a descripciones como modelo semántico o interpretativo. Así que es más adecuada la clasificación de Thomson-Jones, y precisamente por esto he preferido implementarla.
11Véase Manzano (1989).
12Giere (1999).
13Van Fraassen (1989), p. 366.
14Thomson-Jones (2006), p. 528.
15Suárez defiende, en términos generales, esta idea cuando dice que una estructura matemática es aquella que se define bajo un dominio de objetos matemáticos, véase Suárez (2005), p. 35.
16Como se advirtió más arriba, Giere llama también modelos instanciales (semánticos) a los modelos que satisfacen una descripción, así que en este caso, para él, la relación lineal abstracta es un modelo semántico, en sentido estricto.
17Véase Giere (1988) y Giere (1999).
18El análisis que aquí se hace también puede hacerse de forma semejante cuando la teoría se presenta a través de espacios de estados, que es el enfoque preferido por van Fraassen (1980) y Giere (1988).
19Véase McKinsey et al. (1953).
20Esta conclusión es contraria a lo que plantea Giere (1999), pues él considera que los modelos que cumplen el predicado conjuntista son modelos interpretativos o instanciales, que equivalen a lo que aquí llamamos modelos semánticos.
21Esta conclusión es contraría a lo que plantea Thomson-Jones (2006), p. 351.
22Thomson-Jones (2006), p. 534.
23En esto coincido con Suárez (2005), p. 35, y Thomson-Jones (2006), p. 532.
24Véase la introducción de Balzer, Sneed y Moulines (2000), p. 11.
25Moulines (2002), p. 71. Considero que esta segunda interpretación de los modelos es la más acorde con los distintos planteamientos y reflexiones de los estructuralistas, pues hay afirmaciones donde dejan claro que las teorías empíricas no pueden axiomatizarse sin pérdidas dentro de un lenguaje formal, de modo que los modelos determinados mediante una axiomatización de un predicado conjuntista no son modelos semánticos o, como dice Moulines (1982), modelos en el sentido de los estudios metamatemáticos. Así, por ejemplo, Moulines dice: "afortunadamente disponemos de otro procedimiento para definir el concepto de modelo, mucho más práctico, y que, aunque no es completamente formal, es suficientemente exacto [mediante la axiomatización de un predicado conjuntista]" [Molines (1982), 78, lo del paréntesis es mío].
Referencias Bibliográficas
Balzer, W.; Moulines, C.U.; y Sneed, J.D. (eds.) (2000): Structuralist Knowledge Representation. Paradigmatic Examples, Amsterdam, Rodopi. [ Links ]
Giere, R. (1988): Explaining Science. The Cognitive Approach, Chicago, University of Chicago Press. [ Links ]
_ (1999): "Using Models to Represent Reality", L. Magnani et al. Edits, Model-Based Reasoning in Scientific Discovery, N.York/Dordrecht, Kluwer, pp 41-57. [ Links ]
Guerrero, G. (2003): Enfoque semántico de las teorías. Estructuralismo y espacio de estados: coincidencias y divergencias, Tesis doctoral, Madrid, Universidad Complutense de Madrid, (publicada en cd-rom). [ Links ]
_ (2008): "Individuación de las teorías en el enfoque semántico", Principia, 12(1), pp. 97-119. [ Links ]
Manzano, M. (1989): Teoría de Modelos, Madrid, Alianza. [ Links ]
Martínez-Chavanz, R. (2006): Álgebra multilineal, Medellín, Editorial Universidad de Antioquia. [ Links ]
McKinsey, J; Sugar, A.; y Suppes, P. (1953): "Axiomatic Foundation of Classical Particle Mechanics", Journal of Rational Mechanics and Analysis 2, pp. 253-272. [ Links ]
Moulines, C.U. (1982): Exploraciones metacientíficas, Madrid, Alianza. [ Links ]
_ (2002): "La concepción estructuralista de la ciencia", Revista de Filosofía, Universidad de Chile, vol. 58, pp. 69-77. [ Links ]
Suárez, M. (2005): "The Semantic View, Empirical Adequacy, and Application", Crítica, vol. 37, No 109, pp. 29-63. [ Links ]
Suppes, P. (1960): "A Comparison of the Meaning and Use of Models in Mathematics and the Empirical Sciences", Synthese 12, pp. 287-301; v.e. "Una comparación del significado y los usos de los modelos en las matemáticas y las ciencias empíricas", en P. Suppes, Estudios de filosofía y metodología de la ciencia, Madrid, Alianza, 1988. [ Links ]
_ (1970): Set-Theoretical Structures in Science, Tech. Report, Institute for Mathematical Studie in the Social Sciences, Stanford University. (Reimpreso en Suppes, 2002). [ Links ]
_ (2002): Representation and Invariance of Scientific Structure, Stanford, CLSI. [ Links ]
Thomson-Jones, M. (2006): Models and the Semantic View", Philosophy of Science, 73, pp. 524-535. [ Links ]
Van Fraassen, Bas C. (1970): "On the extension of Beth's Semantics of Physical Theories", Philosophy of Science, pp. 325-339. [ Links ]
_ (1980): The Scientific Image, Oxford, Clarendon Press; v.e. La imagen científica, México, Paidós-UNAM, 1996. [ Links ]
_ (1989): Laws and Symmetry, Oxford, Clarendon Press. [ Links ]














