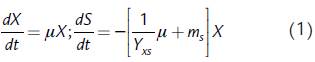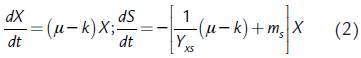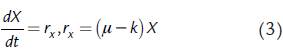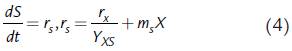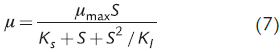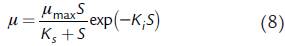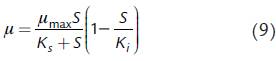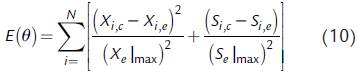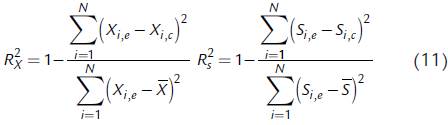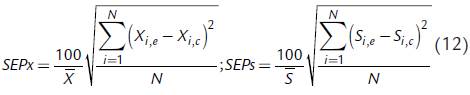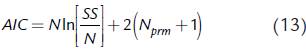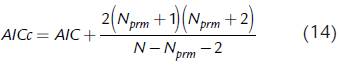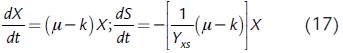INTRODUCCIÓN
Gluconacetobacter diazotrophicus es una bacteria endófita que presenta importantes propiedades de promoción del crecimiento vegetal como fijación de nitrógeno gracias a su actividad nitrogenasa, síntesis de compuestos indólicos considerados como fitohormonas (en especial el ácido indolacético) y solubilización de fosfatos (Restrepo et al., 2017), por lo que se ha venido utilizando como inoculante microbiano en diferentes cultivos de importancia agrícola (Cocking, 2012). Originalmente fue aislada a partir de la caña de azúcar, y se considera que es responsable de la fijación biológica de nitrógeno en este cultivo (Tejera et al., 2004). En particular, este microorganismo tiene la capacidad de fijar nitrógeno atmosférico, y disponer parte de este en forma utilizable por las plantas (Boniolo et al., 2009).
En la literatura disponible se han reportado diferentes estudios sobre el crecimiento de G. diazotrophicus utilizando diferentes fuentes de carbono y de nitrógeno, pero no se han publicado trabajos en donde se empleen fuentes de carbono de bajo costo como las melazas. Específicamente, la melaza de caña tiene una concentración de azúcares totales de aproximadamente el 50 % (Vega-Baudrit et al., 2008) y contiene elementos traza y vitaminas como tiamina, riboflavina, piridoxina y niacinamida, por lo que es un material muy atractivo para el cultivo de esta bacteria.
Uno de los principales enfoques para el estudio del comportamiento microbiano es el modelamiento matemático de su crecimiento celular. En particular, a través de los modelos cinéticos, se puede estudiar el efecto del consumo del sustrato limitante sobre la formación de biomasa, sobre todo cuando se evalúan diferentes fuentes de carbono. Adicionalmente, los modelos de crecimiento microbiano permiten evaluar y representar el crecimiento de biomasa, así como ofrecer información valiosa para diseñar, optimizar y controlar el proceso de cultivo celular ya sea a escala piloto o a nivel industrial (Belfares et al., 1995; Montoya et al., 2015; Rolling et al., 2015).
Para el caso del cultivo de G. diazotrophicus, se requiere la evaluación de diferentes expresiones cinéticas que consideren la inhibición por sustrato, ya que se ha reportado que el crecimiento celular y el rendimiento de biomasa son menores para altas concentraciones de la fuente de carbono (Molinari, 2011). En el cultivo de G. diazotrophicus, cuando se tienen altas concentraciones de sacarosa (mayores a 20 g/L), ésta deja de ser el nutriente limitante para el crecimiento; así se obtiene un menor rendimiento de biomasa, lo cual se debe a que se utiliza gran parte del azúcar para producción de energía y subproductos carbonados. G. diazotrophicus alcanza mayor crecimiento en medios de cultivo con 10 % de sacarosa, pH de 5,5 y temperatura de 30 °C, pero puede crecer en concentraciones de sacarosa de hasta 30 % y puede fijar nitrógeno en concentraciones de oxígeno del 4 % (Gillis et al., 1989; Tejera et al., 2004; Rios y Dibut, 2007). En los cultivos de G. diazotrophicus en medio sumergido se ha usado sacarosa en el rango de 10 a 150 g/L, y más comúnmente 100 g/L (Tejera et al., 2004; Videira et al., 2007; Molinari y Boiardi, 2013).
El propósito del presente trabajo fue realizar un estudio cinético del crecimiento de G. diazotrophicus en cultivo sumergido por lotes en un biorreactor a nivel de banco en un medio con melazas de caña y sacarosa como fuente de energía y de carbono. Este estudio cinético comprendió la medición en el tiempo de la biomasa celular, los azúcares totales y el pH, y la evaluación de los datos experimentales obtenidos, la aplicación de diferentes modelos matemáticos no estructurados y no segregados a fin de describir el comportamiento de estos datos experimentales y la comparación de los modelos aplicados en cuanto a la calidad de ajuste y la determinación de la precisión de los parámetros cinéticos mediante el análisis de sensibilidad paramétrica. Se usó melaza como fuente de carbono (medio mixto o complejo) considerando su bajo costo, así como su contenido de vitaminas y otros factores de crecimiento que favorecen el incremento de la biomasa de la bacteria. Adicionalmente, se realizó un ensayo utilizando sacarosa en lugar de melazas con el fin de comparar la formación de biomasa celular en un medio definido (sintético).
MATERIALES Y MÉTODOS
Material biológico y preparación del inóculo
Se utilizó la cepa nativa G. diazotrophicus GIBI029 que fue obtenida a partir de caña de azúcar en un estudio previo (Restrepo et al., 2017). El inóculo del cultivo con una concentración de 1,6x108 UFC/ml de G. diazotrophicus se obtuvo de la siguiente forma. Se tomaron viales con la cepa bacteriana, que estaban bajo congelación a -80 °C, y se sometieron a reactivación a 30 °C durante 30 minutos en thermomixer. En cámara de flujo laminar, se transfirió 1,0 mL de los viales a tubos falcon con 9 mL de medio líquido DYGS (Dextrose Yeast Glutamate Sulfate). Se incubó a 30 °C con un pH inicial de 5,5 a 150 rpm durante cuatro días aproximadamente, hasta alcanzar una densidad óptica de 1,0 a una longitud de onda de 600 nm. Posteriormente, 5 mL del cultivo se depositaron en 45 mL de caldo DYGS hasta completar 50 mL y se incubó bajo las mismas condiciones de pH, temperatura y agitación durante aproximadamente 6 días hasta alcanzar de nuevo una densidad óptica de 1,0 a 600 nm obteniéndose de esta manera el preinóculo. Luego, 26 mL del preinóculo se depositaron en 234 mL de caldo LGI-P con melazas de caña o sacarosa según sea al caso hasta completar 260 mL en un erlenmeyer de 1000 mL y se incubaron bajo las mismas condiciones durante aproximadamente 6 días hasta que el inóculo alcanzara una concentración de 1,6x108 UFC/ml de G. diazotrophicus. El caldo DYGS usado tiene la siguiente composición (Rodrigues Neto et al., 1986) en g/L: glucosa 2,0, peptona bacteriológica 1,5, extracto de levadura 2,0, K2HPO4 0,5, MgSO4-7H2O 0,5 y ácido glutámico 1,5.
Condiciones de cultivo
Los cultivos sumergidos se realizaron empleando un medio líquido cuya composición se basó en el medio semisólido LGI-P (por los nombres de sus creadores y el lugar de la última modificación reportada: Lipman Goodale Ivo-Pernambuco), el cual es utilizado para el aislamiento de G. diazotrophicus (Cavalcante y Dobereiner, 1988). La composición del medio sólido o semi-sólido LGI-P reportada por Videira et al., (2007) fue modificada a fin de obtener un medio líquido considerando el empleo de melaza de caña como una fuente de energía y de carbono alternativa, así como la adición de una fuente de nitrógeno (extracto de carnaza) y la exclusión del agar; igualmente, mediante ensayos preliminares (no reportados en este trabajo), se modificaron las concentraciones de los restantes componentes del medio LGI-P y se obtuvieron los valores con mayor producción de biomasa celular de G. diazotrophicus. De esta manera, el medio líquido basado en melaza de caña y empleado para los cultivos en el biorreactor fue el siguiente (en g/L): melaza de caña 130; K2HPO4 0,05; KH2PO4 0,75; MgSO4-7H2O 0,35; CaCl2-2H2O 0,035; Na2MoO4-2H2O 0,0035; FeCl3 6H2O 0,019; extracto de carnaza 0,1. También se realizaron cultivos en este medio modificado, pero utilizando sacarosa en lugar de melaza de caña a una concentración de 95 g/L; los restantes componentes tuvieron las mismas concentraciones del medio basado en melaza.
Se realizó un cultivo sumergido a nivel de banco, por lotes, en un biorreactor agitado de 3 L con un volumen de trabajo de 2,6 L sin control de pH. El pH inicial fue cercano a 5,6. La temperatura de incubación fue de 30 °C y el medio se mantuvo agitado a una velocidad de 150 rpm (Luna et al., 2006; Restrepo et al., 2017) con una tasa de aireación de 0,57 vvm (volúmenes de aire por volúmenes de caldo en un minuto) regulada con una bomba de aire (Elite, EUA). En el biorreactor se mezclaron 2340 mL de medio LGI-P modificado con melaza o sacarosa y 260 mL de caldo de cultivo LGI-P con una concentración de 1,6x108 UFC/m L de G. diazotrophicus. El biorreactor se operó durante 384 horas (16 días).
Toma de muestras
Para identificar el momento adecuado para el paso del cultivo en erlenmeyer (inóculo) al cultivo en el biorreactor, se hizo un seguimiento mediante la técnica de recuento viable que arroja la concentración celular en UFC/m L ante la imposibilidad de aplicar el método de densidad óptica ya que el uso de melazas genera un color oscuro. Se usó una muestra control, que consistió de medio LGI-P con melaza pero sin bacterias a fin de establecer la influencia de los sólidos en la medición de peso seco. Se tomaron tres muestras de 10 mL cada una, y se les aplicó el procedimiento de medición de peso seco. Se promedió el peso de sólidos de las tres muestras, y este valor fue posteriormente restado del peso seco obtenido. Del biorreactor se tomaron muestras para medir la viabilidad y pureza de la población microbiana, así como la concentración de biomasa, nitrógeno y azúcares totales en el volumen evaluado. Se colectó 0,1 mL de muestra para la prueba de viabilidad y pureza. De otro lado, se tomaron 15 mL de muestra por triplicado, que fueron centrifugadas; luego se separaron las dos fases, obteniéndose el sedimento y el sobrenadante. Del sedimento de cada muestra, se tomaron 10 mL para la medición de peso seco. El sobrenadante se llevó a congelación para su preservación a fin de determinar posteriormente los azúcares totales y el nitrógeno total.
Para el cultivo en el medio basado en melaza, se tomaron un total de 19 muestras por triplicado, lo cual generó 19 datos de concentración de sustrato y 19 datos de concentración de biomasa celular donde cada dato es un promedio de tres repeticiones. El tiempo de muestreo correspondió al tiempo de operación del biorreactor que fue de 384 horas (16 días). Para el cultivo en el medio basado en sacarosa, se realizó un muestreo similar al del medio basado en melaza con un tiempo de operación de 324 horas (13,5 días) para un total de 15 muestras por triplicado.
Análisis químicos
A la melaza de caña se le realizaron los siguientes análisis: azúcares totales por espectrofotometría UV-VIS (Browne y Zerban, 1948); calcio, hierro, magnesio y potasio por espectrometría de absorción atómica según la Norma Técnica Colombiana (NTC) 5151 (ICONTEC, 2003); cenizas por incineración directa a 600 °C según el método AOAC 942.05 (AOAC, 2016); y nitrógeno por el método Kjeldahl de acuerdo con la NTC 4657 (ICONTEC, 1999).
La viabilidad y pureza de las muestras se midieron por el método de siembra por agotamiento en medio de cultivo PDA (Madigan et al., 2015).
La concentración de biomasa fue determinada usando el método del peso seco (Herbert y Phipps, 1971), centrifugando las muestras por 30 min a 10 000 rpm y secando el centrifugado a 100 °C hasta peso constante considerando el promedio de sólidos obtenidos de las muestras de control. A las muestras de sobrenadante tomadas del biorreactor, se les realizaron análisis de azúcares totales y nitrógeno, por los métodos indicados anteriormente para la muestra de melaza.
Modelamiento matemático
Durante el modelamiento matemático se asumió temperatura constante durante el cultivo, así como procesos homogéneos teniendo en cuenta que se aplicó agitación mecánica mediante el impulsor del biorreactor y bombeo de aire; igualmente, se asumió un volumen constante durante el cultivo. Los diferentes modelos matemáticos aplicados a los datos experimentales de las curvas cinéticas obtenidas a nivel de banco están indicados en la Tabla 1. Cada modelo incluyó una expresión para la velocidad de formación de biomasa celular (dX/dt), una expresión para la velocidad de consumo de sustrato (dS/dt) y una expresión de velocidad específica de crecimiento celular (μ).
Tabla 1 Modelos de velocidad de crecimiento microbiano y consumo de sustrato aplicados al cultivo sumergido de G diazaotrophicus, y valores de los parámetros cinéticos y estadísticos respectivos.

Observaciones: N prm -número de parámetros del modelo; R 2 x -coeficiente de determinación para la biomasa; R 2 s -coeficiente de determinación para el sustrato.
Las primeras expresiones para analizar de formación de biomasa celular y consumo de sustrato corresponden al modelo de Pirt, el cual tiene en cuenta la utilización del sustrato para el mantenimiento celular (Pirt, 1965; Wang y Post, 2012):
donde X representa la concentración de biomasa, S representa la concentración de la fuente de carbono y j es la velocidad específica de crecimiento; los parámetros de este modelo incluyen el coeficiente de rendimiento celular a partir de sustrato (Y xs ) que representa la cantidad de biomasa celular formada por unidad de masa de sustrato consumido, y el coeficiente de mantenimiento (m s ), los cuales se deben ajustar a partir de los datos experimentales. Esta expresión se ha empleado ampliamente para el modelamiento del crecimiento microbiano (Belfares et al., 1995; He et al., 2008; De Andrade et al., 2013). En la ecuación de velocidad de consumo de sustrato (dS/dt), el término -μX/Y xs describe la utilización de parte del sustrato para formación de biomasa celular, mientras que el término -m s X describe la utilización de parte del sustrato para proveer energía para mantenimiento celular y no para crecimiento de biomasa (Pirt, 1965). Las actividades celulares de mantenimiento incluyen regulación osmótica, reparación de las estructuras celulares, re-síntesis de componentes macromoleculares (RNA y proteínas), y mantenimiento de la movilidad (Dawes y Ribbons, 1964).
La segunda expresión de formación de biomasa celular y consumo de sustrato es la de Seer y Nandong, (2015):
donde k es el coeficiente de metabolismo endógeno y m s es el coeficiente de mantenimiento. La expresión de velocidad de formación de biomasa (r x ) se compone de un término que corresponde a las biosíntesis de células nuevas empleando las fuentes de energía y de carbono del medio (en este caso, estas fuentes coinciden) y de otro término que representa el proceso mediante el cual la biomasa misma se emplea como fuente de energía y carbono para su superviviencia (metabolismo endógeno); cuando el sustrato se agota, el componente de destrucción de las células (-kX) excede al de su síntesis (μX) lo que conlleva a una disminución de la concentración de biomasa (Herbert, 1959; Dawes y Ribbons, 1964):
La segunda ecuación de las expresiones (3) se puede presentar de tal forma que se visualice el consumo de sustrato tanto para la formación de nueva biomasa, como para el mantenimiento celular (Pirt, 1965; Wang y Post, 2012; De Andrade et al., 2013):
donde r s es la expresión de velocidad de consumo de sustrato.
Para la velocidad específica de crecimiento (μ), la ecuación más empleada es la de Monod (Monod, 1949; Han y Levenspiel, 1988):
donde μ max es la máxima velocidad de crecimiento específico y K s es el parámetro de saturación por sustrato, también definido como la concentración de sustrato a la cual la velocidad j es igual a la mitad de μ max .Por su parte, la ecuación de Contois (Contois, 1959; Birol et al., 2002; Vatcheva et al., 2006) tiene en cuenta el efecto de inhibición debido a la biomasa:
donde μ max es la máxima velocidad de crecimiento específico y B el coeficiente de crecimiento de la expresión de Contois. La ecuación de Contois es una variante del modelo de Monod, en la cual la velocidad específica de crecimiento es inhibida por la concentración de biomasa X (Vatcheva et al., 2006).
Para considerar el efecto inhibitorio causado por altas concentraciones de sustrato se ha empleado la ecuación de Andrews (Andrews, 1968; Dutta et al., 2015):
donde K l es la constante de inhibición relacionada con el sustrato S. Para estos fines también se ha aplicado la siguiente expresión (Aiba et al., 1968; Luong, 1987; Niu et al., 2016):
donde Ki es la constante de inhibición por sustrato. Finalmente, la expresión de Aiba-Taylor (Luong, 1987) considera el efecto inhibitorio del sustrato como un factor que incluye la constante de inhibición por sustrato:
Cada uno de los modelos aplicados incluyó una expresión para la velocidad de formación de biomasa celular (dX/dt) y una expresión para la velocidad de consumo de sustrato (dS/ dt), es decir, las ecuaciones (1) o las ecuaciones (2); asimismo, los modelos contemplaron una expresión de velocidad específica de crecimiento celular (μ), es decir, una de las expresiones (5-9). En la Tabla 1 se indica qué expresiones incluye cada modelo para el análisis cinético de los cultivos estudiados. Cada uno de los modelos de la Tabla 1 fue ajustado por regresión no lineal a los datos experimentales del cultivo sumergido por lotes de G. diazotrophicus. Para ello, se utilizó una rutina de minimización, siendo la función objetivo la suma normalizada del cuadrado de los errores o residuos para ambas variables estudiadas (De Andrade et al., 2013):
donde N es el número de puntos experimentales, es decir, el número de muestras (N = 19 para los modelos que describen los cultivos empleando el medio basado en melaza, y N = 6 para el medio basado en sacarosa considerando solo los puntos experimentales representados por los modelos propuestos). Para el caso de sacarosa como fuente de carbono, se usaron solo las primeras seis muestras, puesto que los modelos usados no presentan la capacidad de representar toda la curva de crecimiento incluyendo la fase de muerte celular. Adicionalmente, i es el índice correspondiente a cada muestra, X i,e y S i,e son la concentración experimental de biomasa y de la fuente de carbono, respectivamente, X i c y S i c corresponden a la concentración de biomasa y de la fuente de carbono calculadas por los modelos de la Tabla 1, respectivamente, X e | max es el máximo valor de las concentraciones medidas de biomasa, y S e | max es el máximo valor de las concentraciones medidas de la fuente de carbono, y θ es el vector de parámetros del modelo.
Se empleó la función fmincon de Matlab versión R2014a para minimización con restricciones a fin de obtener los valores de los parámetros de los modelos, y la función ode 113 para la resolución del sistema de ecuaciones diferenciales de cada modelo. La función fmincon encuentra el mínimo de una función multivariable no-lineal con restricciones, lo que se conoce como optimización no lineal con restricciones; para ello, emplea un método de aproximaciones sucesivas que parte de un punto inicial, y realiza iteraciones hasta converger a un mínimo local sujeto a restricciones. En cada iteración se genera un nuevo punto para el cual la función a minimizar presenta un valor menor, y más cercano al mínimo. Para problemas de optimización de gran escala, como método iterativo esta función utiliza el procedimiento de región de confianza, y para problemas de optimización de escala media, usa un método de Programación Cuadrática Secuencial (SQP, por sus siglas en inglés). El método de región de confianza, en cada iteración comprende las siguientes acciones: i) utiliza una función q que aproxima la función a minimizar en una región de confianza denominada vecindad; ii) minimiza la función q para encontrar el punto siguiente de la iteración; iii) evalúa la función a minimizar en este nuevo punto; iv) si la función evaluada en este nuevo punto disminuye, entonces acepta el nuevo punto, de lo contrario disminuye el tamaño de la región de confianza y repite el procedimiento hasta que la función evaluada en el nuevo punto disminuya. El método de SQP, en cada iteración, utiliza la ecuación QP que representa el problema original de minimización de función no lineal con restricciones, y la resuelve para obtener la dirección de búsqueda y el punto subsiguiente de la iteración (Novac etal., 2009; Sreeraj etal., 2013). Las funciones ode de Matlab son programas de integración de ecuaciones diferenciales ordinarias. En particular, la función ode113 se usa para ecuaciones diferenciales no rígidas, y es especialmente útil para casos con tolerancias de error estrictas o para casos intensivos computacionalmente. Esta función presenta un nivel de exactitud en el rango de bajo a alto y es una implementación de los métodos de Adams-Bashforth-Moulton, realizando extrapolación local (Shampine y Reichelt, 1997).
Evaluación de la calidad de ajuste
Los parámetros usados para cuantificar la efectividad de los cálculos realizados por los modelos fueron el coeficiente de determinación (R 2) y el error estándar de predicción (SEP)
donde R
2
x
corresponde al coeficiente de determinación para la biomasa, R
2
s
corresponde al coeficiente de determinación para el sustrato, i es el índice correspondiente a cada muestra, N es el número de puntos experimentales, y 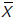 y
y 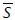 son el promedio de los datos medidos de biomasa y sustrato, respectivamente. El coeficiente de determinación, que toma valores desde 0 a 1, indica las variaciones tenidas en cuenta por el modelo; entre mayor sea su valor, hay una mayor correspondencia entre los valores calculados por los modelos y los observados.
son el promedio de los datos medidos de biomasa y sustrato, respectivamente. El coeficiente de determinación, que toma valores desde 0 a 1, indica las variaciones tenidas en cuenta por el modelo; entre mayor sea su valor, hay una mayor correspondencia entre los valores calculados por los modelos y los observados.
Generalmente, se logra una mayor calidad de ajuste al utilizar modelos con mayor complejidad, es decir, con mayor número de parámetros. Para comparar modelos teniendo en cuenta la calidad de ajuste y al mismo tiempo el número de parámetros del modelo, se puede utilizar el criterio de Akaike (Dutta etal., 2015), cuya forma básica es la siguiente (Akaike, 1974):
donde N es el número de datos experimentales, N prm es el número de parámetros a ser ajustados y SS es la suma de los cuadrados de las diferencias entre los datos experimentales y los datos obtenidos con el modelo. El modelo con menor AIC tiene una mejor combinación entre calidad de ajuste y complejidad. Cuando la muestra es pequeña, de modo que N es pequeño en comparación con N prm , el valor de AIC es muy pequeño, dando como resultado que el criterio AIC sugiere como más apropiados los modelos que tienen muchos parámetros, lo cual implica sobreajuste (Mutolsky y Christopoulos, 2003). Con el fin de corregir este fenómeno fue desarrollado el criterio AICc, que es una versión corregida del criterio de Akaike (Hurvich y Tsai, 1989):
donde AIC está dado por la ecuación (13). El modelo con menor AICc tiene una mejor combinación entre calidad de ajuste y complejidad. En el presente trabajo se decidió usar el criterio AICc en lugar del criterio AIC, considerando que los valores de N son relativamente pequeños. Para aplicar el criterio de Akaike se toman los modelos con mayor calidad de ajuste: dos modelos de cuatro parámetros y dos modelos de cinco parámetros. Los términos SS, AIC y AICc se calcularon por separado para biomasa (AICc ) y para la fuente de carbono (AICcs). Adicionalmente, se aplicó un criterio AICc combinado, el cual emplea la función objetivo de minimización de los residuos E(θ) dado por la ecuación (10) en lugar del término SS. De esta forma, se evita tener AICc por separado para biomasa y para la fuente de carbono.
Análisis de sensibilidad
Se realizó el análisis de sensibilidad aplicando el método desarrollado por Sobie, (2009) y empleado por Dutta et al., (2015). Este método evalúa el efecto del valor de cada parámetro sobre el coeficiente de determinación (R 2 ) con variación de un solo parámetro a la vez; de este modo, el método indica el nivel de sensibilidad del coeficiente de determinación con respecto a cambios en cada parámetro del modelo. Adicionalmente, este procedimiento indica los parámetros de mayor efecto sobre el coeficiente de determinación; para un parámetro dado, un alto nivel de sensibilidad indica que el valor del parámetro debe ser calculado con mayor exactitud. En términos generales, el procedimiento comprende los siguientes pasos: i) para cada parámetro se define un rango de variación, y se definen varios puntos o valores dentro de dicho rango; ii) para cada parámetro tomado individualmente y para cada valor dentro del rango, se realiza nuevamente la simulación; iii) se calcula el valor de R 2 , correspondiente a cada valor; y iv) se grafica R 2 como función de cada valor del parámetro. En el presente trabajo, se usó la función de costo E(θ) en lugar de R 2 , puesto que este criterio está particionado en R 2 x y R 2 s. El fin fue evaluar la precisión de los valores estimados de los parámetros de los modelos con base en el efecto del cambio de los parámetros sobre la función de costo E(θ). Para este análisis se consideró el modelo que obtuvo mayor calidad de ajuste. Los parámetros varían de -50 % a +50 % con respecto a los estimados obtenidos por minimización; se varía un solo parámetro a la vez. Para los cálculos de la evaluación de la calidad de ajuste y de sensibilidad se utilizó también el software Matlab 2014.
RESULTADOS
Crecimiento de G. diazotrophicus en cultivo por lotes
La melaza de caña empleada tuvo la siguiente composición de acuerdo con los análisis realizados: azúcares totales 40,47 % (p/v), cenizas 8,71 % (p/v), calcio 1,83 % (p/v), nitrógeno total 0,7 % (p/v), potasio 0,65 % (p/v), hierro 12 mg/kg y magnesio 950 mg/kg. Durante los cultivos, la concentración de nitrógeno en el caldo fue menor a 0,4 % (p/v). Las pruebas de viabilidad y pureza indicaron que no hubo contaminación del medio en el biorreactor. Los valores experimentales de concentración de biomasa, azúcares totales y pH se muestran en la Fig. 1. En el caso del cultivo con melaza (Fig. 1a), se puede observar un período de latencia en la curva de formación de biomasa celular durante las primeras 20 horas aproximadamente, durante el cual el crecimiento de G. diazotrophicus no sufre mayores variaciones; este período de latencia no se aprecia para el caso del cultivo con sacarosa. Posteriormente, se evidencia un crecimiento logarítmico hasta el final del seguimiento (384 horas). Se puede observar que, en el medio con melaza, el crecimiento es mucho más lento en comparación con el medio con sacarosa, alcanzándose una concentración de 1,41 g/L a las 384 horas aproximadamente. En el caso del medio con sacarosa (Fig. 1b), a las 100 horas aproximadamente se alcanza la máxima concentración de biomasa celular: 1,83 g/L. A las 150 horas aproximadamente, se logra estabilidad en la formación de la biomasa, pero con una significativa disminución respecto al valor máximo alcanzado.
Figura 1 Perfil temporal de las concentraciones de biomasa (X) y azúcares totales (S), y del pH durante el cultivo sumergido por lotes de G. diazotrophicus en un biorreactor de3L agitado y aireado. Las desviaciones estándar de las tres réplicas se muestran como barras verticales. (a) Cultivo en un medio basado en melaza de caña. (b) Cultivo en un medio basado en sacarosa.
La concentración de azúcares totales en el caldo para el cultivo con melaza disminuyó desde 50,0 g/L hasta 40,5 g/L, de modo que se consumió el 18,9 % de azúcares totales. En contraste, el cambio total de azúcares totales fue de cerca de un 86,7 % para el cultivo con sacarosa.
De acuerdo con la definición de rendimiento global de biomasa a partir de sustrato (Y xs ) reportada por Doran, (2013), el valor de este parámetro se puede calcular como el cociente entre la diferencia de concentración de biomasa y la diferencia de consumo de sustrato:
Los rendimientos calculados de esta manera son aparentes u observados. Para el caso de melaza como fuente de carbono, Y xs = 0,2874 g biomasa/g azúcares si se consideran las concentraciones obtenidas de las pruebas de cultivo en el biorreactor correspondientes al momento inicial (concentración inicial de sustrato de 47 g/L) y al momento de pico máximo de biomasa. Para el caso de sacarosa como fuente de carbono y energía, el valor de este parámetro es de 0,1325 g biomasa/g sacarosa, considerando como momento final el correspondiente al pico máximo de biomasa. De otro lado, en el caso del cultivo con melazas, el pH presenta un cambio desde 5,6 a 4,85, mientras que para el caso de sacarosa el pH cambia desde 5,15 hasta 2,63.
Modelamiento cinético del cultivo de G. diazotrophicus
La aplicación de los modelos cinéticos propuestos para el cultivo sumergido a nivel de banco de G. diazotrophicus en un medio basado en melaza de caña permitió obtener las curvas de biomasa celular y de sustrato mostradas en la Fig. 2 en donde también se presentan los datos experimentales respectivos como referencia. En esta figura, se representan los resultados de los modelos de Pirt-Contois, Herbert-Pirt-Monod, Herbert-Pirt Contois, y Herbert-Pirt-Contois con m s =0. Los valores de los parámetros de todos los modelos aplicados, y los parámetros de calidad de ajuste se muestran en la Tabla 1.
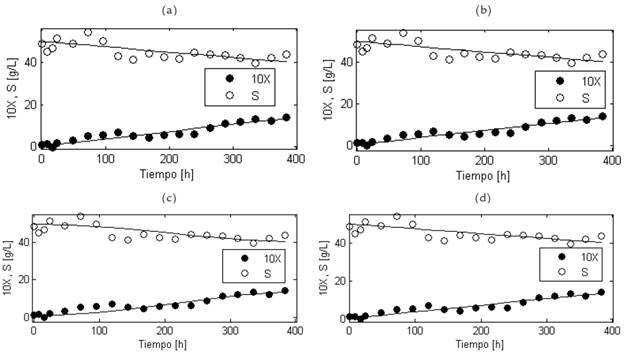
Figura 2 Resultados del modelamiento matemático de las concentraciones de biomasa celular (X) y sustrato (S) para el cultivo sumergido a nivel de banco de G. diazotrophicus en un medio a base de melaza de caña. Las curvas de crecimiento celular y de azúcares totales calculadas por cada modelo se muestran en líneas continuas; las mediciones de concentración de biomasa y de sustrato se representan con círculos. Los valores de concentración de biomasa celular están multiplicados por 10. (a) Modelo de Pirt-Contois. (b) Modelo de Herbert-Pirt-Contois con m s = 0. (c) Modelo de Herbert-Pirt-Monod. (d) Modelo de Herbert-Pirt-Contois.
Para el caso de melazas como fuente de carbono y energía, se observa en la Fig. 2 la correspondencia entre los valores calculados por los modelos y los valores experimentales. Para los datos de biomasa hay una correspondencia relativamente alta, lo cual es confirmado por los valores de R 2 x en el rango de 0,828 a 0,888 (ver Tabla 1). Para sustrato hay una menor correspondencia entre los datos experimentales y los calculados por los modelos, lo cual es confirmado por los valores de R 2 s en el rango 0,352 a 0,425. Visualmente es difícil distinguir cuáles modelos logran mejor calidad de ajuste. Aunque no se muestran, los resultados para los modelos de Pirt-Monod, Pirt-Andrews y Pirt-Aiba-Taylor son muy similares al caso del modelo de Pirt-Aiba; para estos cuatro modelos es evidente una concavidad de la curva de biomasa hacia arriba, y una concavidad de la curva de sustrato hacia abajo. En contraste, los modelos de Pirt-Contois, Herbert-Pirt-Contois y Herbert-Pirt-Monod no exhiben esta concavidad. El modelo de Herbert-Pirt-Monod al principio presenta concavidad hacia arriba para biomasa y hacia abajo para sustrato, pero luego de 300 h presenta estabilización en el tiempo.
De las expresiones con cinco parámetros aplicadas a los cultivos con melaza, los modelos de Herbert-Pirt-Monod y Herbert-Pirt-Contois lograron mayor R 2 (ver Tabla 1), siendo mayor para el modelo de Herbert-Pirt-Contois. En contraste, los modelos de Pirt-Andrews, Pirt-Aiba-Taylor y Pirt-Aiba obtuvieron menores valores de R 2 y a su vez, mayores valores de SEP x y SEP s , con resultados muy similares entre ellos. De las expresiones con cuatro parámetros, los modelos de Pirt-Contois y Herbert-Pirt-Contois con m s =0 lograron coeficientes de determinación más altos, siendo mayor para Herbert-Pirt-Contois con m s =0. De lo anterior, se observa que los tres modelos con mayor R 2 involucran la expresión de Contois para la biomasa y que los datos generados por los tres modelos son muy similares. En contraste, el valor de R 2 de los modelos que incluyen efecto de inhibición por sustrato (Pirt-Andrews, Pirt-Aiba-Taylor y Pirt-Aiba), fue menor comparado con los tres modelos con mayor valor de este parámetro.
Los modelos de cuatro y cinco parámetros que mostraron mayor R2 (modelo de Herbert-Pirt-Contois con ms=0 y modelo de Herbert-Pirt-Contois), presentaron valores muy similares de sus parámetros μmax , B, Yxs y k; pero también de R2. Estos modelos exhibieron valores de μmax de 0,1178 h-1 y 0,1214 h-1, que son relativamente cercanos. En contraste, de entre todos los modelos, la mayor velocidad específica de crecimiento (μmax = 0,9994 h-1) fue obtenida para el modelo de Herbert-Pirt-Monod con ms=0, seguido por el modelo de Herbert-Pirt-Monod que obtuvo un valor de μmax =0,9868 h-1. El coeficiente de rendimiento de biomasa Yxs presentó valores muy similares para el modelo de Herbert-Pirt-Contois con ms=0 y el modelo de Herbert-Pirt-Contois: 0,1341 y 0,1342 g biomasa/g azúcares respectivamente. En el modelo de Pirt-Andrews, el parámetro Kl tomó un valor muy grande, de modo que el termino S2/Kl es despreciable con respecto al término Ks+S.
Los resultados del modelamiento matemático aplicado al cultivo de G. diazotrophicus en un medio basado en sacarosa se muestran en la Fig. 3 y en la Tabla 1. Se observa que los valores calculados por los modelos son muy cercanos a los valores experimentales, pero visualmente se puede notar una mejor representación en los modelos de Herbert-Pirt-Contois y Herbert-Pirt-Contois con ms=0. En general, los modelos de cinco parámetros utilizados presentaron mayor R2 x y R2 s en comparación con los modelos de cuatro parámetros. El modelo que obtuvo mayores valores de los coeficientes de determinación fue el modelo de Herbert-Pirt-Contois, seguido por el modelo de Herbert-Pirt-Contois con ms=0, mientras que el modelo que obtuvo menores valores fue el modelo de Pirt-Contois.
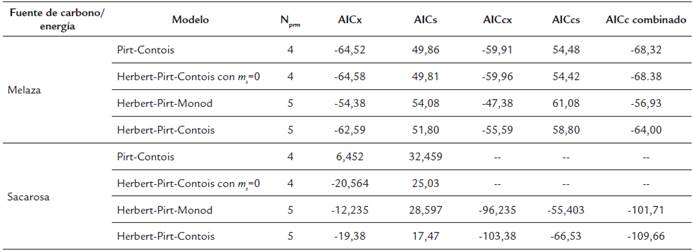
En la Tabla 2 se muestran los valores de los parámetros del criterio de Akaike para los modelos analizados. Para el caso de melaza como fuente de carbono, el modelo de Herbert-Pirt-Contois con ms=0 presentó menores valores de AICcx, AICcs y AICc combinado; por tanto, presenta una mejor combinación de calidad de ajuste y complejidad. Los dos modelos de cuatro parámetros presentaron menores valores de AICcx, AICcs y AICc combinado, en comparación con los dos modelos de cinco parámetros.
Tabla 2 Resumen de parámetros del criterio de Akaike para cuatro modelos cinéticos aplicados al cultivo sumergido por lotes de G. diazotrophicus.
Se puede plantear un modelo más simplificado, teniendo en cuenta los resultados del ajuste de los modelos y de la aplicación del criterio de Akaike. En este sentido, el modelo de Herbert-Pirt-Contois con ms=0 presentó la mejor combinación de calidad de ajuste y complejidad. De hecho, en los modelos que involucran la expresión de Contois, el parámetro B tomó valores altos, entre 1300 y 1550 (g azúcares)/(g biomasa), de modo que en el denominador de la esta expresión (ecuación 6), el término S es despreciable en comparación con el término BX. Esto indica que se puede omitir el término S en el denominador de la expresión cinética de Contois, de modo que el efecto de la concentración de sustrato sobre la velocidad específica de crecimiento es representado por una expresión de primer orden con respecto al sustrato, de acuerdo con la siguiente simplificación:
Por tanto, se propone el modelo de Herbert-Pirt-Contois con m s =0 y simplificación de la ecuación de Contois, es decir, considerando la expresión (15):
Este modelo comprende tres parámetros a estimar, que son: k, μmax , y Y xs . En este caso, el parámetro μ max incluye el valor del parámetro B de la expresión original de Contois. La estimación da como resultados μ max =0,00007285 h-1, Y xs =0,1356 (g biomasa)/(g azucares) y k=0,00007485 h-1. Además, se obtiene un R 2 x de 0,8898 y R 2 s de 0,433.
Aplicando el criterio corregido de Akaike, se obtiene un AICcx de -63,99, un AICcs de 50,40 y un AICc combinado de -72,33. Así, según el criterio de Akaike este modelo presenta la mejor combinación de calidad de ajuste y complejidad (ver Tabla 2).
Para los modelos aplicados al medio con sacarosa de Herbert-Pirt-Contois con m s=0 y de Pirt-Contois, que son ambos de cuatro parámetros, no fue posible calcular los valores de AICcx ni AICcs ni AICc combinado debido a que el factor N-N prm -2 se hace cero, generando una indeterminación.
Para los modelos de Herbert-Pirt-Monod y de Herbert-Pirt-Contois, que son ambos de cinco parámetros, los valores de AICcx, AICcs, y AICc combinado indican que este último modelo presenta la mejor combinación de calidad de ajuste y complejidad.
Se desarrolló un análisis de sensibilidad para la aplicación al cultivo sumergido en un medio con melaza, del modelo de Herbert-Pirt-Contois con m s =0, el cual se muestra en la Fig. 4. Se observa que el orden de los parámetros de mayor a menor efecto sobre la función de costo E(θ) es el siguiente: B, μ max , Y xs , y k. El parámetro B generó un aumento significativo de la función objetivo E(θ) para bajos valores de B, pero para altos valores su efecto sobre E(6) es bajo. También μmax generó aumentos de E(θ) para bajos valores de Μmax. La función objetivo E(θ) es menos sensible con respecto a Y xs , y su sensibilidad con respecto a k es despreciable. En general, las curvas de los parámetros son asimétricas. El análisis de sensibilidad realizado a los modelos de Herbert-Pirt-Contois y de Pirt-Contois (no se muestran), son muy similares al del modelo de Herbert-Pirt-Contois con m s =0.
DISCUSIÓN
Crecimiento de G. diazotrophicus en cultivo por lotes
Según la literatura disponible, G. diazotrophicus es una bacteria poco eficiente en la utilización de fuentes de carbono para la producción de biomasa, lo cual ha sido reportado para el caso de la sacarosa y la glucosa como fuentes de carbono (Molinari y Boiardi, 2013); inclusive, los rendimientos de biomasa de esta bacteria son mucho menores a los rendimientos de 0,4-0,5 g biomasa/g azúcar consumido que presentan los microorganismos heterótrofos. En el estudio de Molinari, (2011) se cultivó G. diazotrophicus con sacarosa como fuente de carbono y se reportó que el carbono aportado por la sacarosa genera polisacáridos, ácido glucónico, ceto-ácidos y CO2 (producto de la respiración celular). A medida que se aumenta la concentración de sacarosa aumenta la producción de subproductos, generando un descenso del rendimiento celular debido a que esta fuente de carbono es usada para producir otros metabolitos que contienen carbono en lugar de usarse para producir biomasa. En el estudio de Molinari y Boiardi, (2013) también con sacarosa como fuente de carbono, se utilizó pH controlado a 6,0 con concentraciones iniciales de sacarosa en el medio de cultivo en el rango entre 10 y 150 g/L. El mayor rendimiento de biomasa alcanzado fue de 0,18 g biomasa/g sacarosa para una concentración inicial de sacarosa de 20 g/L. Adicionalmente, se observó que a medida que aumentaba la concentración inicial de sacarosa por encima de 20 g/L, disminuía el rendimiento de biomasa desde 0,18 hasta 0,02 g biomasa/g sacarosa. En el presente trabajo, se obtuvieron bajos valores del rendimiento de biomasa, lo cual confirma esta característica de los cultivos con G. diazotrophicus. Los valores obtenidos de Y xs de 0,2874 y 0,1325 g biomasa/g azúcares totales para los medios con melaza (384 h) y sacarosa (88 h), respectivamente, son aproximadamente similares a los obtenidos en el estudio de Molinari y Boiardi, (2013) y menores a los rendimientos que presentan los microorganismos heterótrofos. El hecho de que el rendimiento en sacarosa sea menor que en melaza es coherente con los resultados del estudio de Molinari y Boiardi, (2013) y confirma la baja eficiencia de G. diazotrophicus en la utilización de fuentes de carbono para la producción de biomasa, considerando que el medio con melaza contiene menor cantidad de sacarosa y de otros azúcares como glucosa y fructosa.
El perfil temporal de concentraciones de biomasa obtenido indica que G. diazotrophicus puede utilizar melaza de caña como fuente de carbono y energía, alcanzando concentraciones mayores a 1,3 g/L. Sin embargo, su crecimiento es muy lento presumiblemente debido al contenido de varias sustancias en las melazas de caña que potencialmente pudieran ser inhibitorias para el crecimiento. Lo anterior puede evidenciarse en la concentración máxima alcanzada cuando se empleó un medio definido con sacarosa (cerca de 2 g/L).
El cultivo de G. diazotrophicus en el medio basado en melaza mostró un crecimiento de biomasa celular menos rápido y una disminución más lenta del pH y del consumo de la fuente de carbono (medido como azúcares totales) en comparación con el medio basado en sacarosa (ver Figura 1). En el caso del cultivo con melaza, el cambio total en el consumo de azúcares totales fue de 18,9 %, mientras que con sacarosa el cambio total en la concentración de sacarosa fue de 86,7 %. La menor velocidad en el crecimiento microbiano en el primer caso es atribuible al contenido de varias sustancias en las melazas de caña que inhiben el crecimiento. La melaza de caña representa el licor madre resultante de la cristalización final de las soluciones concentradas de jugo de caña de azúcar (mieles). La composición de la melaza es muy variable ya que depende de factores como el tipo de suelo en donde se cultiva la caña, la temperatura ambiental, la humedad, la temporada de producción de caña, la variedad de esta, el tipo de procesamiento de la caña en el ingenio y las condiciones de almacenamiento (Sánchez y Cardona, 2007). Además de sacarosa (35-65 %), glucosa (7 %), fructosa (9 %), otros carbohidratos (rafinosa y gomas), proteínas, aminoácidos, otros compuestos nitrogenados, cenizas (entre el 9 y el 12 %), vitaminas y otros compuestos no nitrogenados (ceras, esteroides, fosfolípidos) (Vega-Baudrit et al., 2008), la melaza puede contener restos de suelo y de otras sustancias empleadas para la clarificación del jugo de caña. Lo anterior, hace difícil identificar qué compuestos pueden exhibir propiedades inhibitorias para el crecimiento de G. diazotrophicus, teniendo en cuenta que no se han reportado estudios dirigidos exclusivamente a elucidar la relación entre los componentes de la melaza de caña y el crecimiento de esta bacteria.
La adición de melazas al medio de cultivo proporciona azúcares, pero también aumenta la viscosidad del medio, disminuyendo la transferencia de oxígeno (Page, 1992). En particular, se ha reportado la disminución en la velocidad específica de crecimiento celular para otras especies de bacterias como Alcaligenes eutrophus (Beaulieu et al., 1995) y Bradyrhizobium elkanii (Gómez, 2008) cultivadas en medios con concentraciones iniciales de melaza superiores a 10 g/L. Al respecto, muchos géneros bacterianos presentan inhibición del crecimiento para altas concentraciones de carbohidratos, lo cual puede deberse a la saturación en los complejos enzimáticos responsables del transporte de estos al interior de la célula. De otro lado, la concentración relativamente alta de sales en la melaza hace que los medios basados en ella presenten alta presión osmótica, lo que también afecta negativamente el crecimiento celular como se ha reportado ampliamente para el caso de las levaduras durante la producción de etanol (Sánchez y Cardona, 2007). Este efecto también podría afectar a la bacteria G. diazotrophicus de acuerdo con lo que los datos experimentales sugieren; en este sentido, es evidente que en el medio basado en sacarosa, se puede alcanzar en menor tiempo una concentración mayor de biomasa celular comparado con el medio basado en melaza de caña (ver Figura 1).
En el caso del cultivo con melazas, el pH presentó un cambio desde 5,60 hasta 4,85. Para cultivos por lotes de G. diazotrophicus usando sacarosa como fuente de carbono sin control de pH, se ha encontrado que se produce una cantidad considerable de ácidos orgánicos, generando un descenso notable del pH y una disminución significativa de la producción y rendimiento de biomasa, en comparación con cultivos con pH controlado (Molinari, 2011). De hecho, para el caso de pH no controlado, con concentraciones iniciales de sacarosa de 20 g/L y pH inicial de 6,0, el pH desciende hasta valores comprendidos en el rango de 2,4 a 3,5, mientras que para concentraciones iniciales de sacarosa de 100 g/L, el pH desciende hasta valores en el rango de 1,4 a 2,0, siendo el ácido glucónico el principal responsable de la disminución del pH. Para el caso de pH no controlado, la disminución en la producción y rendimiento de biomasa se debe a que los bajos pH implican un consumo de energía mayor, que se requiere para la homeóstasis citoplasmática y para mantener el pH constante dentro de la célula (Molinari, 2011). Considerando el perfil de pH en el tiempo obtenido en el presente estudio empleando melaza como fuente de carbono, se concluye que la disminución del pH es menor en comparación con los experimentos realizados en el trabajo de Molinari, (2011) siendo el pH final (4,85) mucho mayor a los reportados por Molinari, (2011). Esta reducción en el pH también es menor en comparación con los datos obtenidos por Attwood et al., (1991) en donde el pH disminuyó desde 5,6 a 3,0 aproximadamente. La menor disminución del pH encontrada en este trabajo pudo haber conducido a concentraciones de biomasa celular mayores (1,41 g/L) que las obtenidas en el trabajo de Molinari (2011) quien reportó 1,23 g/L de biomasa para un medio con 20 g/L de sacarosa y 0,65 g/L de biomasa para un medio con 100 g/L de sacarosa bajo condiciones de pH no controlado. Adicionalmente, en la Fig. 1 se puede ver que la evolución de biomasa presenta un comportamiento aproximadamente simétrico a la evolución del pH, lo que sugiere que los ácidos orgánicos producidos son metabolitos primarios.
Para el caso del cultivo con sacarosa como fuente de carbono, se evidenció que la disminución del pH desde 5,15 hasta 2,63 es comparable a la disminución reportada por Molinari, (2011) y Attwood et al., (1991). Esto es atribuible a una mayor concentración de sacarosa, lo cual genera una mayor producción de ácido glucónico, que es el principal responsable de la disminución del pH. La máxima concentración de biomasa celular alcanzada en este caso fue de 1,83 g/L que, sin embargo, fue menor a los 3,2 g/L de biomasa alcanzada por Molinari, (2011) cuando se controló el pH en un nivel de 6,0 para concentraciones iniciales de sacarosa de 100 g/L. Estos resultados indican la conveniencia de introducir en los modelos matemáticos expresiones que vinculen el pH del caldo de cultivo con la producción de biomasa o el consumo de la fuente de energía. Sin embargo, el desarrollo de tales expresiones es una tarea compleja considerando la necesidad de establecer modelos estructurados que permitan relacionar diferentes metabolitos intracelulares clave (como los ácidos orgánicos que interviene en el ciclo de Krebs y vías metabólicas derivadas) con la concentración global de biomasa y de la fuente de energía. Una vía alternativa consiste en desarrollar expresiones empíricas que vinculen el pH con las variables biomasa y sustrato. Por ello, uno de los trabajos futuros derivados de los resultados del presente artículo se orientará al desarrollo de estas expresiones, las cuales tendrán una utilidad evidente para el estudio cinético del crecimiento de G. diazotrophicus y su modelamiento matemático. Asimismo, se requiere profundizar en la evaluación de cultivos celulares sumergidos de esta bacteria en condiciones de pH controlado obteniendo un valor óptimo de esta variable mediante un adecuado diseño experimental que, a su vez, pueda facilitar el modelamiento cinético de este tipo de cultivos.
En el caso de melaza, en la curva de concentración de sustrato se observa una tendencia creciente de azucares en las primeras 80 horas del cultivo con melaza, como se puede ver en la Fig. 1. Se debe tener en cuenta que en los cultivos de G. diazotrophicus se ha observado la producción de polisacáridos, ácido glucónico y ceto-ácidos. De hecho, la hidrólisis de la sacarosa genera glucosa que luego es oxidada generando ácido glucónico que, a su vez, puede ser metabolizado produciendo ceto-ácidos. Tanto la glucosa como el ácido glucónico son utilizados por la bacteria para las necesidades de crecimiento y de mantenimiento celular. Molinari, (2011) reportó que se produce ácido glucónico durante la fase de latencia y la fase exponencial temprana, aunque en menor cantidad que en el momento de cambio de pendiente. Adicionalmente, este autor indica que esta producción temprana de ácido glucónico presenta un pico que generalmente coincide con el momento de cambio de pendiente, aunque depende de las condiciones de cultivo. Por ejemplo, para pH controlado y 100 g/L de sacarosa como fuente de carbono y energía y 3 g/l de (NH4)2SO4 como fuente de nitrógeno, dicho pido se presenta para la fase exponencial tardía.
La curva de crecimiento celular para el cultivo en un medio basado en melaza de caña presenta dos fases de crecimiento con una etapa intermedia como se puede ver en la Fig. 1. Este comportamiento ha sido reportado en otros trabajos para cultivos por lotes de G. diazotrophicus empleando diferentes fuentes de energía. Attwood et al., (1991) observaron que la curva de crecimiento de esta bacteria empleando un medio con glucosa es bifásica, caracterizada por dos etapas de distinta pendiente. Estos autores atribuyen este fenómeno a que en la fase de latencia y la fase exponencial temprana se consume glucosa y se genera la mayor parte del ácido glucónico producido; posteriormente, en la fase exponencial tardía, se presenta consumo del ácido producido en la etapa anterior y, bajo algunas condiciones, se observa producción de ceto-ácidos. Molinari, (2011), por su parte y para cultivos en medios basados en sacarosa, indica que estas dos etapas solo se presentan en condiciones muy particulares, por ejemplo, cuando la sacarosa está en exceso (100 g/L, como la concentración utilizada en el presente trabajo) y sin control de pH. De las curvas de crecimiento se puede observar que después de la primera fase exponencial, sigue una etapa intermedia caracterizada por un comportamiento aproximadamente estacionario de la biomasa que, en la mayoría de los casos, coincide con el momento de mayor concentración de ácido glucónico. Esta etapa intermedia puede considerarse como una segunda etapa de latencia, que se debe al reacondicionamiento metabólico con el fin de posibilitar el consumo de ácido glucónico que es producido en la etapa inicial de crecimiento. En la segunda fase exponencial, la pendiente de la curva de crecimiento no es necesariamente distinta de la pendiente de la primera fase y el ácido glucónico comienza a ser consumido por la bacteria. Lo anterior indica que, en este trabajo, el comportamiento en la fase de latencia y la primera parte de la fase de crecimiento es atribuible a la hidrólisis de la sacarosa y el consumo de la glucosa y fructosa formadas acompañados de la síntesis de ácido glucónico; en la etapa intermedia ocurre el reacondicionamiento metabólico para posibilitar el consumo de ácido glucónico, el cual se consume durante la segunda parte de la fase de crecimiento. En el caso del medio basado en sacarosa, la curva de crecimiento celular no presenta este comportamiento bifásico como se puede ver para las primeras 100 h de cultivo en la Fig. 1b. La disminución brusca en la concentración de células luego de las primeras 100 h se puede explicar porque el cultivo entra rápidamente en fase estacionaria a un nivel menor que la máxima concentración celular alcanzada (1,83 g/L); lo anterior se comprueba por el consumo sostenido de los azúcares totales presentes en el medio hasta el final del proceso indicando que el sustrato es asimilado principalmente con fines de mantenimiento celular.
Ajuste de modelos cinéticos para la descripción del crecimiento de G. diazotrophicus
Como se comentó anteriormente, el crecimiento de biomasa para el caso de melaza como fuente de carbono presenta un comportamiento bifásico con un período intermedio que corresponde a una segunda etapa de latencia. Los modelos usados no representan estos comportamientos; en su lugar, proporcionan una representación suavizada del crecimiento exponencial (ver Fig. 2). El crecimiento de biomasa para el caso de sacarosa como fuente de carbono no presenta este comportamiento bifásico, y como consecuencia, como se puede observar en la Fig. 3, los modelos presentan una mejor representación de los datos. De hecho, para el caso de sacarosa como fuente de carbono, los mayores valores de R 2 x y R 2 s son de 0,984 y 0,9403, respectivamente; mientras que para el caso de melaza los mayores valores de R 2 x y R 2 s son de 0,8898 y 0,433, respectivamente. Estos datos indican que para el caso de sacarosa se logró una mejor representación de los datos, en comparación con el caso de melaza. Cabe anotar, sin embargo, que el modelamiento de la cinética del cultivo para el medio basado en sacarosa solo se tuvo en cuenta hasta las 120 h, ya que no fue posible representar la abrupta caída de la concentración de biomasa luego de este tiempo con los modelos aplicados en este trabajo. De hecho, dentro de los modelos matemáticos no estructurados y no segregados comúnmente empleados para describir las cinéticas de fermentación, este pico de biomasa, con la subsiguiente estabilización a valores sensiblemente más bajos de concentración celular en la fase estacionaria, es imposible de representar a menos que se incluyan más términos y parámetros en los modelos lo que aumentaría la complejidad del tratamiento matemático y conduciría a la formulación de constantes cinéticas sin mayor sentido físico o biológico.
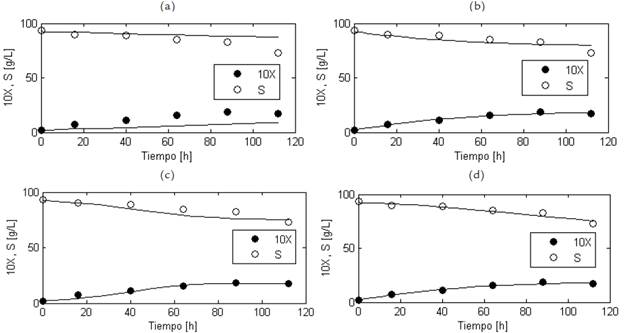
Figura 3 Resultados del modelamiento matemático de las concentraciones de biomasa celular (X) y sustrato (S) para el cultivo sumergido a nivel de banco de G. diazotrophicus en un medio a base de sacarosa. Las curvas de crecimiento celular y de azúcares totales calculadas por cada modelo se muestran en líneas continuas; las mediciones de concentración de biomasa y de sustrato se representan con círculos. Los valores de concentración de biomasa celular están multiplicados por 10. (a) Modelo de Pirt-Contois. (b) Modelo de Herbert-Pirt-Contois con m s = 0. (c) Modelo de Herbert-Pirt-Monod. (d) Modelo de Herbert-Pirt-Contois.
Para el caso de melaza como fuente de carbono, se puede observar que los modelos de cuatro y cinco parámetros con mayor calidad de ajuste, es decir, los modelos de Herbert-Pirt-Contois con m s =0 y de Herbert-Pirt-Contois, presentan el mismo R 2 ; lo anterior implica que pasar de cuatro a cinco parámetros no genera una mejora significativa en la calidad de ajuste. Además, teniendo en cuenta que la diferencia entre los dos modelos es el coeficiente ms, se concluye que el parámetro m s puede omitirse, pues no genera aumento alguno en el R 2 . En contraste, cuando se modeló el cultivo en un medio basado en sacarosa, se pudo observar que, de los dos modelos de cuatro parámetros, el modelo de Herbert-Pirt-Contois con m s =0 presenta coeficientes de determinación mucho mayores que el de Pirt-Contois. Por otro lado, pasar de cuatro a cinco parámetros (del modelo de Herbert-Pirt-Contois con m =0 al modelo de Herberts Pirt-Contois) implica una mejora significativa del R 2 s de 0,71 a 0,94. Lo anterior sugiere que las mayores concentraciones de sacarosa hacen que la bacteria dirija, en una proporción importante, el consumo de este azúcar a la formación de otros metabolitos carbonados que no necesariamente hacen aumentar la concentración celular, comportamiento que es representado por el modelo de Herbert-Pirt-Contois con un valor del coeficiente de mantenimiento de 0,1078 h-1 (ver Tabla 1); para el medio con melaza (que tiene menor concentración de azúcares), este efecto no es apreciable por lo que el valor de este coeficiente es cero. Estos resultados demuestran la gran utilidad de este modelo y su versatilidad para describir la cinética de cultivo de G. diazotrophicus en medios con diferentes concentraciones de sacarosa como fuente de carbono y energía.
Para los experimentos realizados en el presente trabajo, la expresión cinética de Contois para la velocidad específica de crecimiento celular de las bacterias permitió un mejor ajuste en comparación con las otras expresiones cinéticas. Lo anterior se basa en que los tres modelos con mayor calidad de ajuste involucraron la expresión de Contois y en que la calidad de ajuste fue menor para los modelos con efecto de inhibición por sustrato (modelos de Pirt-Andrews, Pirt-Aiba-Taylor y Pirt-Aiba) y los modelos basados en la ecuación de Monod. La expresión de Contois comprende el efecto inhibitorio o de reducción sobre la velocidad específica de crecimiento celular que ejerce la concentración de biomasa conforme la misma se acumula en el medio líquido mediante el término BX, así como también un efecto de saturación por sustrato mediante el término S en el denominador de la ecuación (6). En este sentido, el término BX representa la disminución de la velocidad de formación de biomasa microbiana a medida que aumenta la concentración de células (Zhang et al., 2015). De hecho, en el presente estudio, la expresión de Contois fue la única que involucró el efecto de la concentración de biomasa sobre la velocidad específica de crecimiento celular. De otro lado, en el denominador de la expresión de Contois el término S fue mucho menor que el término BX, lo que sugiere que la inhibición de la velocidad de crecimiento de G. diazotrophicus se debe en mayor medida al aumento de la concentración de biomasa que a la saturación por sustrato (este efecto se comprobó para ambos medios de cultivo). Desde el punto de vista biológico, la ecuación de Contois refleja el efecto de la acumulación de biomasa celular en el caldo de cultivo. Cuando la concentración celular aumenta en un sistema de cultivo sumergido por lotes, también se empiezan a acumular sustancias de desecho en el caldo o antimetabolitos como inhibidores de enzimas de rutas del metabolismo primario, los cuales desaceleran la velocidad con que las células se multiplican; este efecto es diferente al de disminución de esta misma velocidad por el metabolismo endógeno (explicado por el agotamiento de los sustratos nutritivos). De esta manera, la ecuación de Contois permite tener en cuenta, mediante el término BX, un efecto de hacinamiento celular durante el proceso de cultivo o, como lo expresa el mismo Contois, (1959) la influencia de la densidad de la población bacteriana sobre la velocidad específica de crecimiento. Teniendo en cuenta los resultados obtenidos, la inhibición de la velocidad de crecimiento específico (μ) puede ser causada por altas concentraciones de biomasa o de productos inhibitorios en lugar de altas concentraciones de sustrato, lo cual se confirma si las concentraciones de las fuentes nutricionales están lejos de los valores de inhibición o limitación (Belfares et al., 1995). En el caso del cultivo de G. diazotrophicus utilizando sacarosa, se ha observado la producción de polisacáridos, acido glucónico y ceto-ácidos. A su vez, la producción de ácido glucónico genera reducción del pH, lo cual afecta la producción de biomasa. En estos cultivos, la hidrólisis de la sacarosa genera glucosa que luego es oxidada generando ácido glucónico, y este a su vez puede ser metabolizado produciendo ceto-ácidos (Molinari, 2011). De lo anterior se infiere que, en el presente trabajo, la inhibición por biomasa en el cultivo de G. diazotrophicus es atribuible a estos productos, aunque se requiere desarrollar investigaciones tendientes a identificar de manera particular cuál es la estructura de estos compuestos inhibitorios y sus umbrales de inhibición.
Aunque la ecuación de Contois se desarrolló como un modelo empírico para describir el crecimiento microbiano en sustratos solubles, esta expresión se ha empleado ampliamente para modelar la cinética de degradación microbiana de sustratos insolubles. Precisamente, se considera que el parámetro B caracteriza la afinidad de los microorganismos por el sustrato insoluble, es decir, cuando las células rápidamente cubren la superficie del sustrato en una monocapa para alcanzar un alto valor de ocupación de la superficie del sustrato por los microorganismos (saturación por biomasa), lo que resulta en valores pequeños de B, es decir, en una velocidad específica de crecimiento más rápida (Wang y Li, 2014). Si por el contrario B tiene valores muy altos, la afinidad por la superficie del sustrato es menor y las células se desarrollan en forma suspendida en el caldo de cultivo en donde tienen acceso al sustrato en forma soluble; en este último caso, el término BX se aproxima a la constante de semisaturación del sustrato K S de la ecuación de Monod. Los valores altos de B obtenidos en este trabajo indican que la bacteria se desarrolla mayoritariamente en forma suspendida, pero ello no implica que el efecto de hacinamiento celular previsto por la ecuación de Contois no ocurra, lo que se evidencia en la mejor calidad de ajuste para este modelo comparado con el de Monod. De otro lado, en el modelo de Pirt-Andrews, el término S 2 /K l es despreciable con respecto al término Ks+S, debido al alto valor del parámetro K l . A su vez, esto es otro indicio de que el efecto de limitación por biomasa de la velocidad de crecimiento de G. diazotrophicus es más importante que el efecto de inhibición por sustrato.
Para el caso de sacarosa como fuente de carbono y energía, de los cuatro modelos considerados, el de Pirt-Contois es el único que no incluye el coeficiente de metabolismo endógeno (k), y fue siendo el modelo que obtuvo menores valores de R 2 x y R2 s. Este hecho confirma la importancia del parámetro k para representar el comportamiento del experimento realizado. De otro lado y considerando que en el denominador de la expresión de Contois el término S fue mucho menor que el término BX, es decir, S << BX, se pudo obtener un modelo simplificado para el medio con melaza teniendo en cuenta, además, el criterio corregido de Akaike y el hecho de que en el denominador de la expresión de Contois el término BX es mucho mayor que el término S (Tabla 1).
Para el caso de la melaza, el hecho de que los dos modelos de cuatro parámetros presentaran menores valores de AICcx, AICcs y AlCc combinado, que los dos modelos de cinco parámetros, indica que el aumento en el número de parámetros no genera una mejora significativa en la suma de los cuadrados (SS). Asimismo, el hecho de que el parámetro B generó mayor efecto sobre la función de costo E(θ) (ver Figura 4b), implica que es fácil obtener un estimado significativo del mismo, mientras que la baja sensibilidad de E(θ) con respecto a k (Figura 4d), indica que es difícil obtener un estimado significativo de este parámetro. Para el caso de sacarosa como fuente de carbono y energía, se debe tener en cuenta que el criterio AIC es inexacto para muestras pequeñas con valores bajos de N en comparación con N prm.
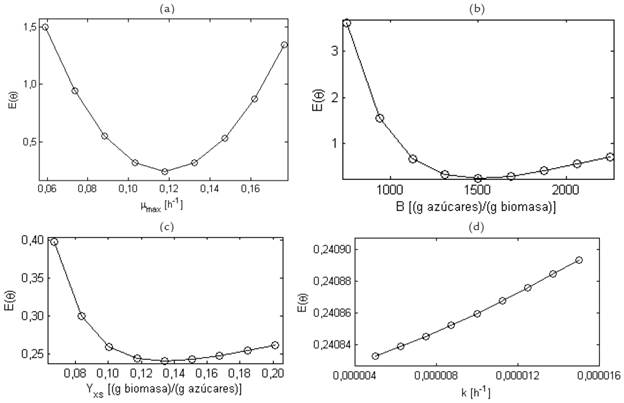
Figura 4 Análisis de sensibilidad de la función de costo E(θ) con respecto a los parámetros del modelo de Herbert-Pirt-Contois con m =0 aplicado al cultivo en un medio basado en melaza de caña. (a) E(θ) en función de la velocidad específica máxima de crecimiento celular (μmax ). (b) E(θ) en función del coeficiente de crecimiento de la ecuación de Contois (B). (c) E(θ) en función del rendimiento de biomasa a partir de sustrato (Y xs ). (d). E(θ) en función del coeficiente de metabolismo endógeno (k).
En estos casos, es más adecuado utilizar el criterio AlCc y no el AIC. Desde este punto de vista, lo más correcto es utilizar sólo los modelos de cinco parámetros. Ya que el modelo de Herbert-Pirt-Contois presentó un menor valor de AICcx, AICcs, y AICc combinado, este modelo puede considerarse como el de mejor combinación de calidad de ajuste y complejidad, entre los cuatro modelos evaluados.
Aunque el modelo de Pirt es comúnmente usado, y el uso de la combinación de expresiones de Herbert y de Pirt es muy escasa, en el presente trabajo se obtuvo una mayor calidad de ajuste con la segunda que con la primera para ambas fuentes de carbono y energía. Esto indica la importancia del parámetro k. Cabe resaltar que el término -kX corresponde a la disminución de la velocidad de crecimiento de biomasa microbiana debido al uso de la biomasa misma como fuente de energía y carbono para su supervivencia (metabolismo endógeno).
Como se había mencionado en la sección de RESULTADOS, sólo cuando m s =0 el parámetro Y corresponde al rendimiento global de biomasa. Esto explica por qué cuando m s ≠0 se obtienen estimados de Y x que son muy distintos de los rendimientos globales de biomasa obtenidos por la ecuación (15). Este es el caso del modelo Herbert-Pirt-Contois aplicado al caso de sacarosa como fuente de carbono, para el cual se obtuvo Yxs=0,996 g biomasa/g sacarosa, que es un valor muy alto en comparación con los rendimientos de biomasa resultantes cuando se empleó el modelo de Herbert-Pirt-Contois con ms=0 para G. diazotrophicus: Y XS =0,1341 g biomasa/g azúcares para melaza y Y XS =0,1296 g biomasa/g azúcares para el caso de sacarosa. Compárense estos datos de rendimiento con los valores obtenidos del rendimiento global observado calculado a partir de los datos experimentales: 0,2874 y 0,1325 g biomasa/g azúcares, para melaza y sacarosa, respectivamente. Cabe recordar que el modelo de Herbert-Pirt-Contois con m s=0 obtuvo una buena calidad de ajuste. Para el caso de melaza fue el más adecuado según el criterio de Akaike, mientras que para el caso de sacarosa ocupó el segundo lugar en cuanto a valores de R 2 x y R 2 s se refiere. Por tanto, el valor de Y x¡ estimado para dicho modelo es un valor apropiado del rendimiento de biomasa. De los valores de Y xs mencionados se observa que estos valores son menores pero cercanos a los valores obtenidos con la ecuación (15) y que el rendimiento de biomasa para el caso de sacarosa es menor, lo cual concuerda con los valores observados de este parámetro. Como ya se había discutido anteriormente, esto confirma la baja eficiencia de G. diazotrophicus en la utilización de fuentes de carbono para la producción de biomasa, y que a altas concentraciones iniciales de sacarosa la fuente de carbono es utilizada para producción de otros metabolitos en lugar de producir una mayor cantidad de células.
En general, la calidad del ajuste de los modelos estudiados fue mejor para la representación del comportamiento de la biomasa celular que para la descripción del comportamiento del sustrato. En el caso del medio basado en melaza, se observa una dispersión de los datos experimentales para la curva de sustrato vs. tiempo que incluye, además, un aumento de la concentración de azúcares totales durante las primeras 80 horas del cultivo con una posterior disminución hasta niveles de 40-45 g/L (ver Figura 1a). Esta dificultad en capturar el comportamiento del consumo del sustrato está relacionada, en primer lugar, con la dispersión de los datos experimentales de sustrato obtenidos mediante la determinación de azúcares totales, el cual presentó niveles de ruido significativos asociados con el hecho de que el método empleado no discrimina los azúcares fermentables de los no fermentables y con la heterogénea composición de la melaza de caña como se discutió anteriormente. En segundo lugar, los modelos matemáticos propuestos no consideran la dinámica de hidrólisis de la sacarosa o de glucanos presentes en el medio basado en melaza ni su utilización como sustratos solubles por parte de los microorganismos. De hecho, los modelos aplicados no consideran la formación de exopolisacáridos que son liberados al medio por G. diazotrophicus para procesos de adhesión celular, adsorción de nutrientes, protección mecánica, química y biológica, y como reserva de energía ya que estos biopolímeros pueden ser hidrolizados posteriormente conforme las células lo requieran (Carreño et al., 2012; Restrepo, 2014). Como el método empleado detecta no solo mono y disacáridos, sino también exopolisacáridos, los modelos aplicados no alcanzan a reflejar esta dinámica por lo que la simplifican mediante una curva descendente de concentración de sustrato. Para efectos de desarrollar y aplicar modelos matemáticos que describan este complejo comportamiento, se requiere, en primer lugar, utilizar otros métodos instrumentales (como cromatográficos) que posibiliten la cuantificación no solo de la sacarosa, la glucosa y la fructosa presentes en la melaza, sino también de los exopolisacáridos que se van formando en el caldo; de esta manera, los modelos que se propongan se deben centrar exclusivamente en el consumo y formación de los azúcares que G. diazotrophicus asimila verdaderamente como fuente de carbono y energía para la formación de biomasa celular.
Los modelos usados tienen la capacidad de representar un bajo o un alto consumo de la fuente de carbono y energía, asociado a un bajo o un alto nivel de producción de biomasa. Para esto la expresión de velocidad volumétrica de formación de biomasa celular (dX/dt) incluye los términos μX y -kX donde el término -kX representa la disminución de la velocidad de crecimiento de biomasa microbiana debido al uso de la biomasa misma como fuente de energía y carbono para su supervivencia (metabolismo endógeno). Asimismo, la expresión de velocidad de consumo de sustrato (dS/dt) incluye los términos -(1/Y xs)μX y -m s X donde el término -(1/Y xs)μxX representa la utilización de parte del sustrato para formación de biomasa y el término -msX representa la utilización de parte del sustrato para mantenimiento celular (Dawes y Ribbons, 1964; Pirt, 1965;). Los parámetros de la velocidad de formación de biomasa y de la velocidad de consumo de sustrato deben ser estimados para cada caso particular, de tal forma que los datos calculados por los modelos representen adecuadamente los datos experimentales. Se pueden comparar los parámetros obtenidos para el modelo de Herbert-Pirt-Contois con m s=0, el cual obtuvo una buena calidad de ajuste: para el caso de melaza como fue el más adecuado según el criterio de Akaike, mientras que para el caso de sacarosa ocupó el segundo lugar en cuanto a valores de R 2 x y R2 s. Para este modelo, se obtuvieron valores de μ max de 0,1178 h-1 (melaza) y 0,6058 h-1 (sacarosa), y de Y s de 0,1341 g biomasa/g azucares (en melaza) y 0,1296 g biomasa/g azucares (en sacarosa). Consiguientemente, se obtuvo mayor valor de μ max para el caso de sacarosa, lo cual está relacionado con una mayor velocidad de producción de biomasa, y mayor valor de Y xs para el caso de melaza lo cual pudo haber estado relacionado con menores concentraciones iniciales de sacarosa como se discutió anteriormente.
Los resultados obtenidos en el presente trabajo permitieron definir los modelos matemáticos que describen de la manera más adecuada el conjunto de datos experimentales de la cinética de crecimiento de G. diazotrophicus en cultivos sumergidos por lotes en medios basados en sacarosa y melaza de caña. La utilidad de estos modelos está representada en su aplicación durante el diseño de procesos de producción de inoculantes microbianos a base de esta bacteria. En este sentido, los modelos cinéticos estudiados son la base para desarrollar los modelos de los biorreactores que incluyen, además, expresiones para describir sus características hidrodinámicas, ecuaciones de balance de calor y materia, modelos de transferencia de masas (como las ecuaciones para determinar el coeficiente volumétrico de transferencia de oxígeno, las cuales se relacionan directamente con las variables del modelo cinético) y relaciones geométricas de los fermentadores. Asimismo, el modelo cinético tiene una potencial aplicación en el diseño de los sistemas de control automático para el funcionamiento de los biorreactores, así como para la operación y programación de la producción. Finalmente, estos modelos cinéticos se pueden afinar durante la experimentación desde el nivel de banco (como los ensayos que se realizaron en el presente trabajo), pasando por la escala piloto, hasta la escala semi-industrial e industrial, lo que se constituye en una herramienta de apoyo para el escalamiento del proceso de producción de inoculantes microbianos basados en la bacteria G. diazotrophicus.
CONCLUSIONES
El coeficiente de determinación permitió identificar los modelos de cuatro y de cinco parámetros con mayor calidad de ajuste. Igualmente, se identificó que la expresión cinética de Contois dio lugar a una mejor calidad de ajuste de los modelos en comparación con las otras expresiones cinéticas evaluadas. En particular, se evidenció que la concentración de biomasa tiene un efecto de inhibición sobre la velocidad específica de crecimiento de G. diazotrophicus más importante que el efecto de la concentración de azúcares totales. El criterio de Akaike permitió seleccionar el modelo con mejor balance entre calidad de ajuste y número de parámetros que resultó ser el modelo de Herbert-Pirt-Contois con m s =0. El análisis de sensibilidad para este modelo permitió establecer el orden de los parámetros de mayor a menor efecto sobre la función de costo E(θ). Los datos derivados del estudio cinético realizado permitieron seleccionar un modelo cinético adecuado para el cultivo por lotes de G. diazotrophicus en un medio mixto a base de melazas de caña. Este tipo de medios es el más empleado a nivel industrial, por lo que los resultados obtenidos permiten ofrecer una descripción matemática valiosa para el diseño, escalamiento y operación de un futuro proceso de producción de un inoculante microbiano con propiedades promotoras del crecimiento vegetal a base de la bacteria G. diazotrophicus.