Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.25 no.2 Bogotá May/Aug. 2005
María Alejandra Guzmán,1 Alberto Delgado2
1 Ingeniera mecánica, Especialista en Automatización Industrial, Magíster en Automatización Industrial, Universidad Nacional de Colombia. Especialista en Gerencia de Proyectos en Ingeniería, Universidad de La Salle - 1999. Profesora Asociada - Universidad Nacional de Colombia. e-mail: maguzmanp@unal.edu.co
2 Ingeniero electricista, Magíster en Ingeniería Eléctrica, Universidad de Los Andes. PhD en Cibernética - University of Reading - Inglaterra. Profesor Titular - Universidad Nacional de Colombia. e-mail: adelgado@ieee.org
RESUMEN
Muchos problemas de diseño de ingeniería, involucran la maximización o minimización de más de una función objetivo. Para la solución de este tipo de problemas conocidos como problemas de optimización multiobjetivo (POM), en la última década, las técnicas evolutivas han demostrado ser una herramienta efectiva y eficiente. Particularmente, varios algoritmos genéticos han sido propuestos por diversos autores los cuales permiten hallar en un tiempo corto, soluciones óptimas a problemas multiobjetivo. En este artículo, se desarrolla una aplicación del algoritmo NSGA (Non-dominated Sorting Genetic Algorithm) que permite obtener geometrías óptimas para el eje de una máquina herramienta sometido a cargas cíclicas, para el cual se busca minimizar simultáneamente su peso y su deflexión lateral máxima.
Palabras clave: optimización multiobjetivo, algoritmos genéticos, diseño mecánico, ejes.
ABSTRACT
Many engineering design tasks involve optimising several conflicting goals; these types of problem are known as multiobjective optimisation problems (MOPs). Evolutionary techniques have proved to be an effective tool for finding solutions to these MOPs during the last decade. Variations on the basic genetic algorithm have been particularly proposed by different researchers for finding rapid optimal solutions to MOPs. The NSGA (non-dominated sorting genetic algorithm) has been implemented in this paper for finding an optimal design for a shaft subjected to cyclic loads, the conflicting goals being minimum weight and minimum lateral deflection.
Keywords: multiobjective optimisation, genetic algorithms, mechanical design, shafts
Recibido: diciembre 3 de 2004
Aceptado: abril 3 de 2005
Introducción
El diseño de un producto de ingeniería es una tarea compleja. Muchos de los problemas de diseño de ingeniería involucran optimización, esto significa que unas funciones objetivo deben ser maximizadas o minimizadas con el fin de encontrar las soluciones óptimas. Los problemas de optimización del mundo real frecuentemente tienen dos o más funciones objetivo, las cuales son contradictorias entre sí, este tipo de problemas se conocen como Problemas de Optimización Multiobjetivo (PMO). Aunque existen varias técnicas clásicas de optimización multiobjetivo, la aplicación de técnicas evolutivas como los algoritmos genéticos han ganado en las últimas décadas gran aceptación entre la comunidad académica en su aplicación a la solución de diferentes tipos de problemas de ingeniería (Goldberg, 1989), (Zydallis, 2003), (Gen y Cheng, 1997), (Knowles, 2002).
Los algoritmos genéticos (AGs) son técnicas de optimización y búsqueda inspiradas por los principios de la evolución natural. Fueron propuestos por Holland, 1975. Basados en la teoría de la evolución de Darwin, estos algoritmos empiezan con una población de individuos, cada uno de ellos representando una posible solución al problema planteado. Cada individuo de la población transporta información genética, así los mejores individuos son aquellos que poseen mejores genes, de esta forma el algoritmo explota el principio de supervivencia del más apto. Mediante el cruce y reproducción de los mejores individuos, las posibles soluciones son combinadas con otras de manera que puedan formar nuevas soluciones que posean mejores genes que sus antecesoras. Estas nuevas soluciones conforman una nueva población de individuos que reemplaza a la anterior para nuevamente poner en marcha los mecanismos de selección, cruce y reproducción.
Un problema de optimización y búsqueda con múltiples objetivos en conflicto genera un conjunto de soluciones óptimas conocidas como las soluciones óptimas Pareto. Muchos de los Algoritmos Genéticos Multiobjetivo (AGMO) están basados en la obtención de este conjunto de soluciones (Sánchez, 2002), (Andersson, 2002). La idea es que un problema cuyo objetivo sea la minimización o maximización de un conjunto de funciones, las cuales a su vez son dependientes de un número finito de variables puede optimizarse mediante la aplicación de estas técnicas que permiten explorar y explotar el espacio de búsqueda a través de un proceso selectivo de acuerdo con el cual sobreviven los individuos más aptos. Cada individuo del espacio de búsqueda representa una posible solución al problema planteado, siendo más aptos aquellos individuos que más se acercan a la consecución del objetivo. La tarea de los AGMO es identificar el conjunto de soluciones óptimas Pareto y mantener una buena distribución de las soluciones del conjunto.
En el campo del diseño de elementos de máquinas, en los últimos diez años han surgido interesantes desarrollos que aplican AGMO. Por ejemplo en Osyczka y otros, 1998, las dimensiones de las pinzas de un robot son optimizadas aplicando un AG. En este caso las funciones objetivo son la diferencia entre la fuerza máxima y mínima para un rango asumido de desplazamiento de los extremos de las pinzas y la relación entre la fuerza transmitida por el actuador y la fuerza en los extremos de las pinzas. En Deb, 1999, se optimizan algunos parámetros de una viga soldada en voladizo. Las funciones objetivo en este caso, son la deflexión máxima en el extremo y el costo de la viga. En Deb y Goel, 2000, son optimizadas la forma de una viga simplemente apoyada, una viga en voladizo y el marco de una bicicleta. En este trabajo se demuestra la eficacia del algoritmo propuesto. Un problema similar es propuesto en Woon y Querin, 1999, aquí el elemento de máquina optimizado es una viga cargada en un extremo con una fuerza estática. En Missoum, 2000, el problema en consideración consiste en minimizar el peso de una caja de engranajes sujeta a cargas estáticas y dinámicas, el AGMO es utilizado para optimizar la ubicación de unos refuerzos a lo largo de la caja. En Andersson, 2001, se propone un nuevo AGMO y es aplicado en el diseño de un sistema de actuador hidráulico. En Deb y Chaudjuri, 2004, se aplica un AGMO para hallar la forma óptima de una serie de vigas con diferentes cargas. No obstante todos estos resultados, en este importante campo de investigación hay muchas aplicaciones nuevas e interesantes que abordar. En este trabajo, se propone una aproximación práctica que permite aplicar el algoritmo NSGA (Non-dominated Sorting Genetic Algorithm) (Deb, 1999) a la optimización del peso y la deflexión lateral máxima de un eje que pertenece a una máquina herramienta y por lo tanto está sometido a cargas cíclicas.
Problemas de Optimización Multiobjetivo
Un problema de optimización multiobjetivo (POM) se define como aquel problema que involucra la obtención de un vector n-dimensional de variables de decisión que satisface las restricciones del problema y optimiza el vector función cuyos elementos representan las funciones objetivo (Sánchez, 2002). En general un POM se define como (Zydallis, 2003):
minimizar o maximizar
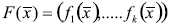
sujeto a:
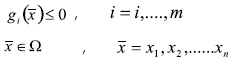
donde 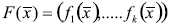 es el vector función,
es el vector función, 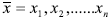 es el vector n-dimensional de variables de decisión y Ω es el espacio de búsqueda.
es el vector n-dimensional de variables de decisión y Ω es el espacio de búsqueda.
Una característica importante de los POM como ya se mencionó, es que tienen más de una solución óptima. No es posible decir que una solución óptima es mejor que otra con respecto a las funciones objetivo, por ello corresponde al diseñador considerar toda la experiencia e información disponible para decidir cuál de las soluciones óptimas satisface de mejor forma las necesidades del problema.
El frente óptimo Pareto y las condiciones de dominación
Vilfredo Pareto (1848-1923) fue un brillante economista italiano, quien planteó por primera vez las comparaciones interpersonales de utilidad. Sus planteamientos generaron los conceptos de soluciones óptimas Pareto y los criterios de no dominación, los cuales pueden ser aplicados a la solución de POM. Una solución A es no dominada si no existe otra solución que sea evaluada de la misma forma que A con respecto a las funciones objetivo y mejor evaluada que A en por lo menos una función objetivo. Esta definición se ilustra en la Figura 1.
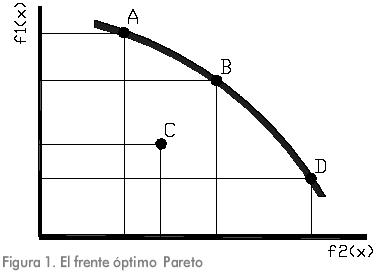
En el caso de la Figura 1, el problema de optimización consiste en maximizar las funciones objetivo f1(x) y f2(x). Existe un número considerable de soluciones para este problema, muchas de ellas son soluciones adecuadas pero solo algunas soluciones son óptimas y por lo tanto pertenecen al conjunto de soluciones óptimas Pareto. La Figura 1 muestra un sistema coordenado en el cual se grafica f1(x) vs. f2(x); se han representado cuatro soluciones del problema designadas con las letras A, B, C y D. Las soluciones óptimas se localizan en la frontera definida por la línea gruesa. Esta frontera es conocida como el frente óptimo Pareto. Las soluciones que representan el mejor balance entre las funciones objetivo, pertenecen a este frente.
De acuerdo con las funciones objetivo, la solución C es mejor que a solución D con respecto a la función objetivo f1(x), sin embargo la solución C no es mejor que la solución D con respecto a la función objetivo f2(x). Se puede concluir que la solución D no es dominada por la solución C. Por otro lado, la solución B es mejor que la solución C en las dos funciones objetivo, por lo tanto la solución C es dominada por la solución B. Las soluciones A, B y D son soluciones óptimas Pareto, en cuanto a la solución C aunque cumple con las restricciones del problema, no es una solución óptima.
Condiciones de dominación
Las condiciones de dominación de una solución pueden definirse así (Deb, 1999):
Se dice que una solución x1 domina a la solución x2 si las siguientes dos condiciones se cumplen:
- La solución x1 no es peor que la solución x2 en la satisfacción de todos los objetivos.
- La solución x1 es estrictamente mejor que la solución x2 en la satisfacción de al menos un objetivo.
Una solución hace parte del frente óptimo Pareto si es una solución no dominada. En la mayoría de los casos no es una tarea fácil encontrar las expresiones analíticas que representan las líneas o curvas que contienen el frente óptimo Pareto, de manera que usualmente se calculan los puntos que corresponden a soluciones óptimas Pareto y sus correspondientes funciones objetivo (Sánchez, 2002).
Algoritmos Genéticos
Ya se mencionó que los algoritmos genéticos son técnicas de optimización y búsqueda en espacios complejos que utilizan algoritmos matemáticos basados en los procesos naturales de selección y transmisión de información genética. El propósito es emular los procesos evolutivos de selección natural para aplicarlos a problemas de optimización que involucran un gran número de parámetros (Goldberg, 1989). Los AGs son aplicables en problemas de optimización que tienen algunas de las características mencionadas a continuación (Mitchell, 1995):
- El espacio de búsqueda es muy grande
- No se sabe si la solución óptima a ser encontrada se encuentra en un pico o en un valle
- Una solución de buena calidad debe ser encontrada rápidamente
- La función de evaluación contiene perturbaciones o ruido
- El problema no es bien entendido
- No se conoce el método de optimización que mejor resuelve el problema
Algunas de estas características son inherentes a los POM.
Aplicación de algoritmos genéticos a la solución de POM
El algoritmo genético simple tiene limitaciones en su aplicación a la solución de POM. La primera limitación radica en que los operadores de selección, cruce y mutación del algoritmo genético simple se refieren a problemas donde solo una función objetivo debe ser optimizada. La integración de los conceptos de frente óptimo Pareto y las condiciones de no dominación con la operación básica del algoritmo genético simple, permite la aplicación de estas técnicas evolutivas a la solución de problemas de optimización multiobjetivo.
Para conseguir la integración efectiva de estos conceptos en el desarrollo de algoritmos genéticos multiobjetivo, deben tenerse en cuenta las siguientes consideraciones (Andersson, 2001):
- Como no es posible afirmar que de dos soluciones pertenecientes al frente óptimo Pareto una es mejor que otra, una función del AGMO es encontrar el mayor número posible de soluciones óptimas Pareto.
- Cualquier sesgo debe ser eliminado hasta donde sea posible, por ello el algoritmo debe encontrar soluciones óptimas Pareto que sean diferentes unas de las otras, de manera que se mantenga la diversidad en el frente óptimo Pareto.
Actualmente existen varias propuestas de diferentes autores en las que presentan operadores y algoritmos para la solución de POM (Sánchez, 2002). En este trabajo se desarrolla una aplicación del algoritmo NSGA propuesto por Deb, 1999. Este algoritmo fue uno de los primeros aplicados a la solución de problemas de diseño mecánico y continua siendo uno de los más populares y aplicados exitosamente a la solución de POM (Knowles, 2002).
Algoritmo NSGA
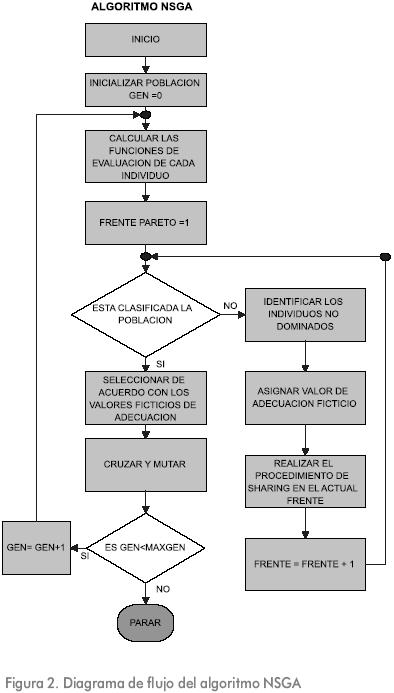
El NSGA se diferencia del algoritmo genético simple en la forma en que usa el operador de selección. Antes de que la selección sea hecha la población es clasificada en frentes óptimos Pareto sobre la base de la determinación de la no dominación de cada individuo y de acuerdo con el frente en el cual quede clasificada una solución se le asigna un valor ficticio de adecuación, siendo mayor este valor para las soluciones clasificadas en el primer frente Pareto y menor para las soluciones clasificadas en el último frente Pareto. Para mantener la diversidad de la población, se utiliza un procedimiento denominado sharing; de acuerdo con el cual, el valor ficticio de adecuación de cada individuo es dividido por una cantidad que depende del número de individuos que tenga en sus cercanías, de esta forma si un individuo está rodeado por muchos otros similares, su valor de adecuación ficticio es disminuido, lo cual favorece la diversidad en los frentes óptimos Pareto. La Figura 2 muestra el diagrama de flujo del algoritmo NSGA, la explicación detallada del NSGA se encuentra en Deb, K., 1999.
Implementación del NSGA
El NSGA fue implementado a través de un módulo desarrollado para este propósito, basado en una modificación del programa UN-Genético (Vélez y otros, 2004). El UN-Genético original permite el desarrollo de algoritmos genéticos con una sola función objetivo, por ello para implementar el NSGA, fue necesario desarrollar un modulo adicional. Para la solución del problema planteado se usaron los operadores mencionados a continuación (Sánchez, 2002 y Lozano, 1996):
- Selección: Operador selección estocástica con reemplazamiento.
- Cruce: Operador BLX-α (Sánchez, 2002). Dados dos individuos i y j con cromosomas bti=(bti1......btin) y btj=(btj1......btjn) seleccionados como padres para la operación de cruce, se genera el descendiente con cromosoma btk=(btk1......btkn) donde btkl se genera aleatoria y uniformemente en el intervalo [mintkl - αItkl, maxtkl + αItkl],siendo mintkl=min(btil,btjl), maxtkl=max(btil,btjl), Itkl=maxtkl-mintkl para l=1,....,n
- Mutación: el módulo adicional del NSGA permite variar la probabilidad de mutación, en la aplicación presentada en este trabajo, se realizaron pruebas del proceso evolutivo con diferentes valores de probabilidad, como se muestra más adelante.
- Restricciones: para el manejo de las restricciones se utilizó una constante que se multiplica por la magnitud de la infracción, este valor resultante se resta al valor ficticio de adecuación y de esta manera se penaliza al individuo infractor.
Aplicación del NSGA a la optimización del peso y la deflexión lateral máxima de un eje
El problema consiste en minimizar simultáneamente el peso y la deflexión lateral máxima de un eje. En este caso los objetivos son contradictorios ya que si el peso del eje disminuye, es porque su volumen también disminuye, así su sección transversal será más pequeña disminuyendo la rigidez y por tanto aumentando la deflexión lateral máxima.
Diseño mecánico de un eje
Un eje es un componente mecánico rotacional cuya función principal es la transmisión de movimiento, potencia y momento torsor. La importancia de estos componentes mecánicos radica en que su presencia es necesaria en la mayoría de las máquinas. Todo diseñador de máquinas debe estar al tanto de los conocimientos y técnicas necesarias para el diseño y fabricación de estos elementos.
El diseño de ejes es una tarea sistemática y compleja para la cual deben considerarse al menos dos tipos de aproximaciones:
- Criterios de resistencia de materiales: incluye el análisis de la resistencia del material bajo cargas estáticas, el comportamiento de los elementos bajo cargas cíclicas considerando los concentradores de esfuerzo. Se busca prevenir las fallas del elemento generadas por la presencia de las cargas estáticas y dinámicas.
- Criterios de rigidez: se refieren a las deformaciones sufridas por la geometría del elemento sometido a cargas externas. El objetivo es mantener las deformaciones del elemento dentro de los rangos permitidos.
El problema
El eje que se muestra en la Figura 3 está sometido a las cargas típicas de un problema real de ingeniería, generadas por los elementos de máquina montados sobre él. Sobre el eje está montada una polea para correa trapezoidal en el punto A de diámetro = 20 pulgadas (0.508 m), peso 60 libras (266.88 N) y un engranaje recto en C de diámetro = 10 pulgadas (0.254 m), ángulo de presión α = 20º y peso = 25 libras (111.2 N). El eje está apoyado en rodamientos de bolas en los puntos B y D. La potencia proporcionada por el motor varía de 20 hp (14.91 kW) a 5 hp (3.72 kW) en cada revolución. La velocidad del motor es de 1200 rpm. El eje está hecho de Acero AISI 1040 CD, se requiere un factor de seguridad contra falla por fatiga Nf = 2.2. La deflexión lateral máxima no puede superar 0.005 pulgadas (0.000127 m).
Aplicando las ecuaciones de equilibrio, hallando las reacciones en los apoyos, los diagramas de fuerzas cortantes, momentos flectores y momentos torsores, aplicando integración numérica para encontrar la deflexión lateral del eje (Shigley y Mischke, 2002) y considerando las teorías de falla estática y falla por fatiga de materiales (Norton, 1999), el problema de optimización multiobjetivo puede plantearse así:
minimizar
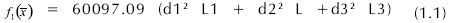
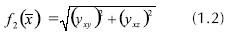
sujeto a :
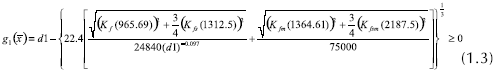
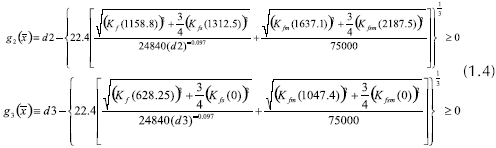
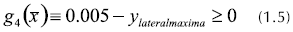
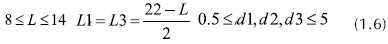
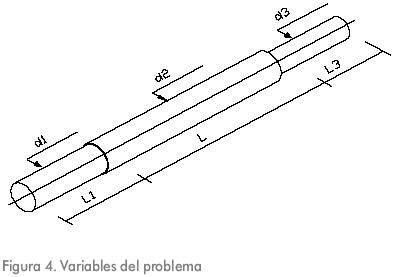
La Figura 4 muestra el significado de las variables d1, d2, d3, L1, L3 y L.
kf es el factor de concentración de esfuerzos para el componente alternante del esfuerzo normal, kfs es el factor de concentración de esfuerzos para el componente alternante del esfuerzo medio, kfm es el factor de concentración de esfuerzos para el componente medio del esfuerzo normal y kfsm es el factor de concentración de esfuerzos para el componente medio del esfuerzo cortante.
La función 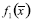 representa el peso del eje y la función
representa el peso del eje y la función 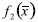 es la deflexión lateral máxima, la cual puede ser expresada como se muestra en la ecuación 1.7:
es la deflexión lateral máxima, la cual puede ser expresada como se muestra en la ecuación 1.7:
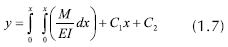
siendo yxy la deflexión lateral en el plano xy y yxz la deflexión lateral en el plano xz, M es el momento flector aplicado, E es el módulo de elasticidad del material e I es el primer momento de área de la sección transversal.
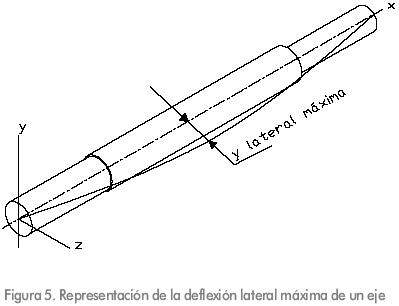
La Figura 5 muestra el significado físico de la deflexión lateral máxima, por criterios de conveniencia en diseño mecánico, esta deflexión no debe ser superior a 0.005 pulgadas (0.12 mm).
Las restricciones 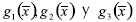 se obtienen de la aplicación de la teoría de falla por fatiga de Goodman modificada. La ecuación general para el diseño de un eje a prueba de fallas por fatiga, de acuerdo con la teoría de Goodman modificada se expresa con la ecuación 1.8 (Norton, 1999):
se obtienen de la aplicación de la teoría de falla por fatiga de Goodman modificada. La ecuación general para el diseño de un eje a prueba de fallas por fatiga, de acuerdo con la teoría de Goodman modificada se expresa con la ecuación 1.8 (Norton, 1999):
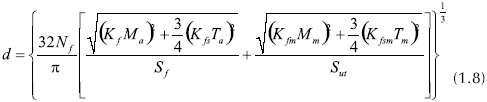
Discusión
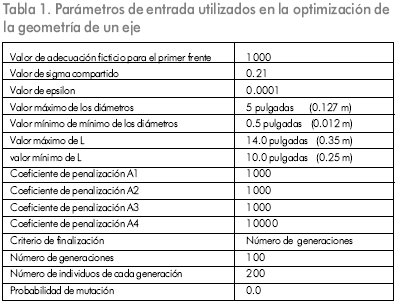
El módulo para el NSGA basado en el programa UN-Genético, permite a los usuarios seleccionar los parámetros de entrada que se listan en la Tabla 1, la columna de la derecha indica los valores de estos parámetros utilizados en la optimización de la geometría del eje.
El valor inicial de sigma compartido se tomó de acuerdo con Deb, 1999, donde se sugiere que se establezca este valor según la fórmula 1.9:
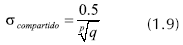
Donde P es el número de variables, en este caso 4 y q es el número de soluciones óptimas diferentes deseadas, en este caso 10.
En este caso la probabilidad de mutación se mantuvo en cero para probar la efectividad del NSGA por sí mismo en esta aplicación en particular (Deb, 1999).
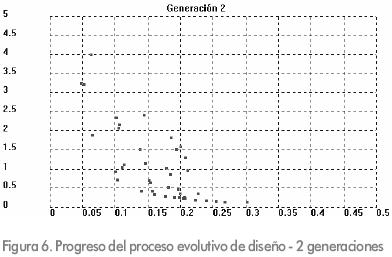
Las Figuras 6, 7 y 8 ilustran el progreso del proceso evolutivo. En estas figuras, el eje y representa los valores de la función objetivo 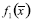 es decir, el peso del elemento, el eje x representa los valores de la función objetivo
es decir, el peso del elemento, el eje x representa los valores de la función objetivo 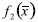 que es la deflexión lateral máxima, los valores de las dos funciones objetivo están representados en una escala apropiada.
que es la deflexión lateral máxima, los valores de las dos funciones objetivo están representados en una escala apropiada.
La Figura 6 muestra el aspecto del proceso evolutivo cuando han transcurrido dos generaciones. Cada uno de los puntos de la gráfica representa una posible solución del problema; algunas de estas soluciones son adecuadas y otras son soluciones óptimas.
En la Figura 7 se observa que luego de transcurridas 20 generaciones, las posibles soluciones que aparecen graficadas se van agrupando en la cercanía del frente óptimo Pareto.
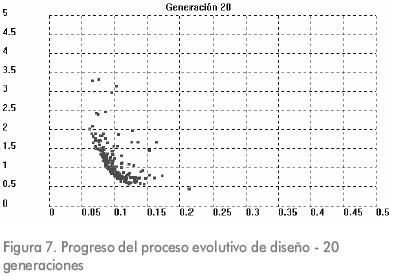
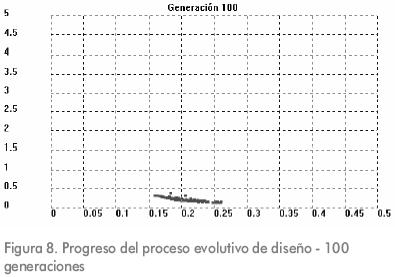
La Figura 8 muestra que 100 generaciones son suficientes para encontrar el frente óptimo Pareto para este problema. Como resultado de la aplicación del proceso evolutivo, más de diez soluciones óptimas Pareto diferentes son halladas.
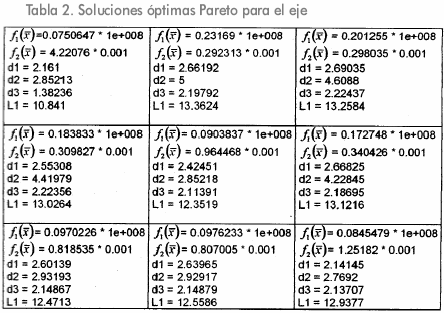
La Tabla 2 muestra algunas de las geometrías óptimas del eje obtenidas con la implementación del algoritmo NSGA. El valor de la función objetivo representa el peso del eje en Newtons, el valor de la función objetivo representa el valor de la deflexión lateral máxima en pulgadas, las variables d1, d2, d3 y L1 están en pulgadas.
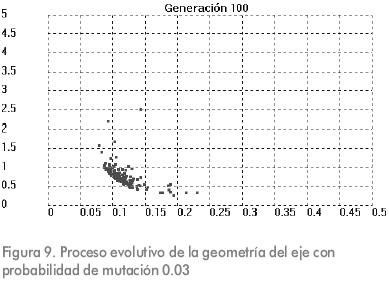
Las Figuras 9, 10 y 11 muestran el resultado del proceso evolutivo luego de 100 generaciones para diferentes valores de probabilidad de mutación. Los parámetros de entrada restantes se mantuvieron iguales.
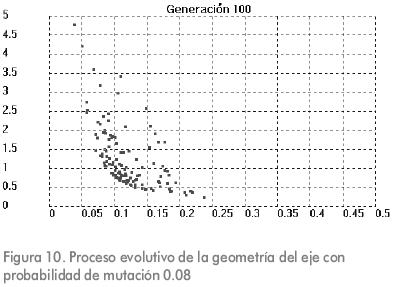
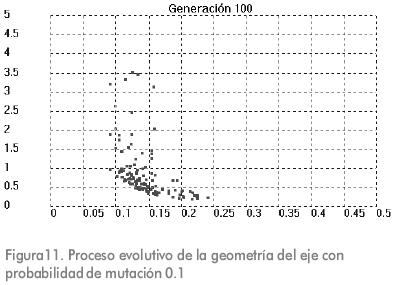
Conclusiones
En este trabajo se desarrolla la implementación del algoritmo NSGA a la solución de problemas de optimización multiobjetivo con dos funciones objetivo, cuatro variables y cuatro restricciones. Se demuestra mediante esta aplicación que este algoritmo constituye una estrategia eficiente que permite hallar el frente óptimo Pareto para esta aplicación.
El método tradicional de diseño de ejes, luego de un trabajo arduo de iteración, permite hallar una única configuración geométrica para un diseño adecuado del eje. La aplicación desarrollada permite hallar rápidamente al menos nueve configuraciones geométricas distintas para las mismas condiciones iniciales de carga, todas ellas son configuraciones óptimas.
Con los resultados del proceso evolutivo de optimización de la geometría del eje el diseñador puede seleccionar la configuración que mejor satisfaga sus requerimientos de diseño a partir de diez geometrías óptimas diferentes. Para la aplicación con probabilidad de mutación igual a cero, las geometrías óptimas halladas para el eje analizado varían desde una con un peso de 23.169 MN y una deflexión lateral máxima de 0,29 milésimas de pulgada, hasta un eje con un peso de 7.50647 MN y una deflexión máxima de 4.22 milésimas de pulgada.
Los desarrollos con diferentes valores de probabilidad de mutación muestran que también en estos casos se encuentran individuos que pertenecen al frente óptimo Pareto. Para la aplicación de que trata este trabajo el efecto de considerar la probabilidad de mutación diferente de cero no es relevante, ya que aún sin mutación, las soluciones halladas son óptimas y lo suficientemente diferentes unas de otras para ofrecer opciones muy variadas al diseñador mecánico.
El diseño de elementos de máquinas es un extenso campo en el cual las técnicas evolutivas presentadas en este trabajo junto con la implementación desarrollada, pueden ser aplicadas en trabajos futuros, como por ejemplo la optimización de la geometría de resortes, uniones soldadas, uniones atornilladas, engranajes, entre otros.
Agradecimientos
Los autores desean expresar sus agradecimientos al ingeniero Jorge Vélez por su colaboración en algunos aspectos de programación, necesarios para este trabajo.
Bibliografía
Andersson, J., Multiobjective Optimization in Engineering Design, Tesis presentada al Institute of Technology - Linkopings Universitet, para optar al grado de Doctor of Philosophy, Suiza, 2001. [ Links ]
Goldberg, D, Genetic Algorithms in Search, Optimization and Machine Learning, Reading, Massachusetts: Addison-Wesley Publishing Company (ed.), Estados Unidos de Norteamérica, 1989. [ Links ]
Gen, M., Cheng, R., Genetic algorithms and engineering design, John Wiley and Sons (ed.), Estados Unidos de Norteamérica, 1997. [ Links ]
Knowles, J., Local-search and hybrid evolutionary algorithms for Pareto optimization, Tesis presentada a la University of Reading para optar al grado de Doctor of Philosophy, Reino Unido, 2002. [ Links ]
List of references on evolutionary multiobjective optimization http://www.lania.mx/~ccoello/EMOO/EMOObib.html. Consultada el 6 de junio de 2004. [ Links ]
Holland, J., Adaptation in Natural Artificial Systems, Ann Arbor: University of Michigan Press (ed.), Estados Unidos de Norteamérica, 1975. [ Links ]
Osyczka,A., Krenich,S., Karás, J., Optimum Design of Robot Grippers Using Genetic Algorithms, Department of Mechanical Engineering, Cracow University of Technology, Polonia, 1998. [ Links ]
Deb, K., Evolutionary Algorithms for Multi-Criterion Optimization in Engineering Design, Proceedings of evolutionary algorithms in engineering and computer science (EUROGEN-99), 1999. [ Links ]
Deb, K., Chaudjuri, S. Automated Discovery of innovative designs of mechanical components using evolutionary multiobjective algorithms, Indian institute of technology Kanpur, KanGal technical report number 2004006, India, 2004. [ Links ]
Deb, K., Goel, T., Multi-objective evolutionary algorithms for engineering shape design, Indian Institute of Technology Kanpur, KanGal technical report number 200003, India, 2000. [ Links ]
Lozano, M., Aplicación de técnicas basadas en lógica difusa para la mejora del comportamiento de los algoritmos genéticos con codificación real, Tesis presentada a la Universidad de Granada para optar al grado de Doctor of Philosophy, España, 1996. [ Links ]
Missoum, S., Optimization of a Gearbox using Mathematical Programming and genetic algorithms, Laboratoire de Génie Mécanique de Tolouse, Francia, 2000. [ Links ]
Mitchell, M., An Introduction to Genetic Algorithms, MA: MIT Press (ed.), Estados Unidos de Norteamérica, 1995. [ Links ]
Norton, R., Diseño de Máquinas, Prentice Hall (ed.), México, 1999. [ Links ]
Sánchez, G., Diseño y evaluación de algoritmos genéticos multiobjetivo en optimización y modelización difusa, Tesis presentada a la Universidad de Murcia para optar al grado de Doctor of Philosophy, España, 2002. [ Links ]
Shigley, J., Mischke, C., Diseño en ingeniería mecánica, McGraw Hill (ed.), Sexta Edición, México, 2002. [ Links ]
Vélez, J., Delgadillo, A., Madrid, J., Ampliación de UN-Genético: una librería en C++ de algoritmos genéticos con codificación híbrida, Trabajo de grado presentado a la Universidad Nacional de Colombia para optar al grado de Ingeniero Electricista, Colombia, 2004. [ Links ]
Woon, S., Querin, Y., Shape Optimization Using Genetic Algorithms, Department of Aeronautical Engineering, University of Sydney, Australia, 1999. [ Links ]
Zydallis, J., Explicit building-block multiobjective genetic algorithms: theory, analysis and development, Tesis presentada al Air Force Institute of Technology para optar al grado de Doctor of Philosophy, Estados Unidos de Norteamérica, 2003. [ Links ]
Apéndice
E: módulo de elasticidad de material
d1: diámetro sección izquierda del eje
d2: diámetro sección central del eje
d3: diámetro sección derecha del eje
L: longitud de la sección central del eje
I: primer momento de área de la sección transversal del eje
Kf es el factor de concentración de esfuerzos para el componente alternante del esfuerzo normal
Kfs es el factor de concentración de esfuerzos para el componente alternante del esfuerzo medio
Kfm es el factor de concentración de esfuerzos para el componente medio del esfuerzo normal
Kfsm es el factor de concentración de esfuerzos para el componente medio del esfuerzo cortante.














