Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.25 no.2 Bogotá May/Aug. 2005
Eduardo Rodriguez Sandoval,1 Alejandro Fernández Quintero,2 Alfredo Ayala Aponte3
1 Ingeniero químico, aspirante a doctor en ingeniería, Universidad del Valle, e-mail: edurosa@univalle.edu.co
2 Ph.D en ciencia de alimentos, profesor Universidad del Valle, e-mail: alfernan@univalle.edu.co
3 Ph.D. en ingeniería de alimentos, profesor Universidad del Valle, e-mail: alfayala@univalle.edu.co
RESUMEN
Los modelos reológicos de un alimento procesado permiten simular la respuesta del material a un esfuerzo o deformación aplicada, al igual que predecir el comportamiento del material de acuerdo a su composición y su forma de preparación. Su aplicación se puede llevar a cabo cuando se tienen datos experimentales expresados en unidades fundamentales. Este artículo describe dos modelos reológicos empleados en el estudio de masas de trigo y maíz, el modelo extensional biaxial y el modelo dinámico oscilatorio. Además, muestra los resultados de algunas investigaciones sobre este tema
Palabras clave: masa, trigo, maíz, modelos reológicos, reología
ABSTRACT
Rheological models of a food system are useful for simulating a material’s response to an applied stress or strain and for predicting the effect of composition and processing conditions. Rheological models can be applied when experimental data is expressed in fundamental units. This article describes two rheological models used for studying wheat and corn dough: the biaxial extensional model and the oscillatory dynamic model. The results of research related to this topic are also reported.
Keywords: dough, rheology, rheological model, wheat, corn.
Recibido: marzo 16 de 2004
Aceptado: marzo 14 de 2005
Introducción
Las propiedades reológicas de un alimento pueden expresarse en términos de funciones viscosas, elásticas y viscoelásticas que relacionan el esfuerzo con la deformación. El esfuerzo, definido como una fuerza sobre unidad de área y expresado generalmente en Pa (N/m2), puede producirse por tensión, compresión o corte, mientras que, la deformación, medida adimensional, es la razón del cambio de longitud de deformación con la longitud original del material cuando se aplica un esfuerzo. La derivada de la deformación con respecto al tiempo da la velocidad de deformación expresado en s-1. Las funciones de viscosidad se utilizan generalmente para relacionar el esfuerzo con la velocidad de corte en sistemas líquidos, mientras que las funciones de elasticidad relacionan el esfuerzo con la deformación en materiales sólidos (Rao, 1999; Steffe, 1996).
Las ecuaciones que muestran la relación entre el esfuerzo y la deformación se denominan ecuaciones reológicas de estado o ecuaciones constitutivas. Una ecuación constitutiva es útil para predecir el movimiento o flujo de un material y estimar los fenómenos e interacciones físicas de sus componentes (Bagley, 1992).
Las masas de trigo y maíz son materiales viscoelásticos, sus propiedades reológicas dependen de su composición y de las condiciones de proceso utilizados en su elaboración. El comportamiento reológico de las masas se puede conocer seleccionando técnicas de medición apropiadas, estas pueden ser de tipo fundamental o empírico. Los métodos empíricos, como el farinógrafo, mixógrafo, extensógrafo, ofrecen información útil y práctica para la industria de la panadería y la molinería; sin embargo, no dan suficiente información para interpretar el comportamiento fundamental de la reología de la masa de trigo porque utilizan medidas arbitrarias propias de cada equipo (Rao y Rao, 1993; Wang y Sun, 2002).
El conocimiento del comportamiento reológico de las masas se puede profundizar si se desarrollan ecuaciones fundamentales que relacionen la composición, la estructura y el comportamiento del material con su procesamiento. La aplicación de las ecuaciones constitutivas requiere de datos reológicos (esfuerzo, deformación y/o velocidad de corte) que estén disponibles en unidades fundamentales. En el caso de las masas, datos apropiados para el análisis por ecuaciones constitutivas o modelos reológicos son relativamente escasos (Bagley, 1992). El objetivo de este artículo es presentar los modelos de flujo extensional biaxial y dinámico oscilatorio, los cuales se han aplicado en el estudio del comportamiento reológico de las masas de maíz y trigo.
Modelos reológicos
Modelo de flujo extensional biaxial
Muchas operaciones de procesamiento en alimentos involucran deformación extensional que puede producir comportamientos únicos en los alimentos. El flujo extensional se toma a veces como un flujo libre de corte. El flujo de corte y el flujo extensional tienen un efecto diferente sobre el comportamiento de los materiales debido a la forma como el flujo genera la orientación de los constituyentes. En el flujo de corte, la orientación corresponde a la dirección del flujo; sin embargo, la presencia de un gradiente de velocidad a través del flujo desarrollado fomenta la rotación de las moléculas reduciendo su normal desplazamiento. En el flujo extensional, la situación es muy diferente, la orientación molecular se dirige en la dirección del flujo debido a que no hay competencia de fuerzas que causen la rotación. Hay tres tipos de flujo extensional: uniaxial, planar y biaxial. Si se considera un material cúbico, durante la extensión uniaxial el material se extiende en una dirección con una correspondiente reducción de tamaño en las otras dos direcciones. En la extensión planar, un material en forma de lámina plana se estira en la dirección horizontal, el ancho permanece constante, mientras que la altura decrece. La extensión biaxial parece una compresión uniaxial, pero se toma usualmente como un flujo que produce un esfuerzo de tensión radial (Steffe, 1996).
La deformación extensional se presenta durante el prensado de masas para formar láminas, el crecimiento de la masa de trigo por la producción de dióxido de carbono durante su fermentación; la expansión de los extruídos por la evaporación del agua y la compresión para obtener productos alargados, entre otros (Steffe, 1996).
El flujo extensional biaxial producido por la compresión de un material en forma cilíndrica entre dos platos paralelos se ha empleado en la evaluación de quesos, masas, geles y mantequilla. La viscosidad extensional, que se define como el resultado de la razón entre el esfuerzo biaxial y la velocidad de deformación biaxial, es un parámetro reológico que se ha empleado en la evaluación de la calidad de productos intermedios y terminados, y en el diseño de procesos y equipos; sin embargo, su aplicación todavía es deficiente por la falta de datos expresados en unidades fundamentales para diferentes tipos de alimentos (Steffe, 1996).
El modelo extensional biaxial se puede desarrollar a partir de las ecuaciones de deformación y esfuerzo, por consiguiente, si se considera una barra regular levemente elongada en ΔL por una fuerza de tensión (Figura 1), su longitud se representa como se muestra en la Ecuación 1.

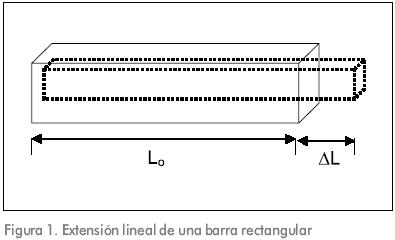
ΔL puede expresarse en términos de la deformación de Cauchy (εc, deformación de ingeniería, Ecuación 2) o la deformación de Hencky (εh, deformación verdadera, Ecuación 3):

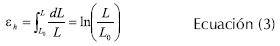
La selección del tipo de deformación a utilizar se determina por la conveniencia del método, εh se prefiere para cálculos con productos que presentan grandes deformaciones (Steffe, 1996).
Cuando se aplica un esfuerzo de compresión en dirección vertical como en la Figura 2, la deformación de Hencky se representa como en la Ecuación 4.

Donde h es función del tiempo y representa la altura que separa los platos (Figura 2). La velocidad de deformación se representa en la Ecuación 5.
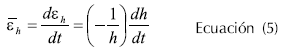
Si se aplica un esfuerzo de deformación por compresión a una muestra utilizando un plato plano con velocidad constante en dirección descendente y una base fija plana (Figura 2), que es la forma usual como se realiza una prueba en una máquina universal de ensayos, la altura de la muestra decrece linealmente como se describe en la Ecuación 6 (Steffe, 1996).
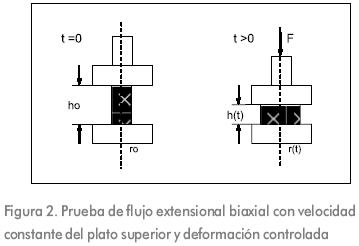
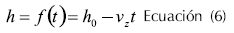
Donde vz representa la velocidad constante del plato superior en dirección descendente. Para el caso de masas, se han utilizado ensayos de extensión biaxial deformando por compresión muestras cilíndricas colocadas entre platos paralelos (Wikström, 1997; Limanond et al. 1999). Durante la compresión, la forma cilíndrica se mantiene mientras que el área en contacto con el plato se incrementa cuando la altura de la muestra decrece. La superficie de contacto de la muestra se lubrica con líquidos de viscosidad baja para evitar fuerzas fricciónales que afecte el resultado, esta lubricación no se puede sobreestimar debido a que pruebas perfectamente lubricadas experimentan solamente deformaciones extensionales (Steffe, 1996).
La velocidad de deformación extensional biaxial (también llamada velocidad de extensión radial) es igual a la mitad de la velocidad de deformación de Hencky como se muestra en la Ecuación 7 (Steffe, 1996).
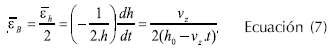
El esfuerzo biaxial depende de la fuerza de compresión y del espacio radial que ocupa la muestra entre los platos durante la prueba como se verifica en las Ecuaciones 8 y 9.


La viscosidad extensional biaxial se calcula por medio de la relación entre el esfuerzo biaxial y la velocidad de deformación biaxial (Ecuación 10).
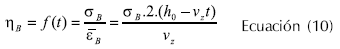
Modelo dinámico oscilatorio
Si un material sólido responde a una carga aplicada deformándose levemente y recuperando su forma original cuando se remueve la carga, este tipo de comportamiento se denomina elástico. Los materiales elásticos ideales se comportan de acuerdo a la ley de Hooke, la cual describe la proporcionalidad directa entre el esfuerzo normal y la deformación como se representa en la Ecuación 11, (Gunasekaran y Ak, 2000).
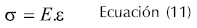
Un fluido se deforma si se aplica una carga y no recupera su forma original cuando la carga se remueve, este comportamiento pertenece a un sistema viscoso. El flujo de un sistema viscoso simple se describe con la ley de Newton de acuerdo a la Ecuación 12, (Gunasekaran y Ak, 2000).
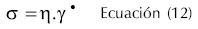
La mayoría de los sistemas alimenticios, entre ellos las masas, se denominan viscoelásticos por su carácter combinado de viscosidad y elásticidad. Las funciones de los materiales viscoelásticos se pueden determinar utilizando experimentos que involucran la aplicación de deformaciones en estado no estacionario (Steffe, 1996).
Los fluidos viscoelásticos exhiben un esfuerzo normal aplicando una fuerza de corte estable. Las diferencias de esfuerzos normales pueden medirse en reómetros producidos por diferentes compañías de instrumentación. Las medidas de corte en estado no estacionario suministran resultados dinámicos que se utilizan para evaluar la viscoelásticidad de los materiales (Steffe, 1996).
Generalmente las técnicas dinámicas se han dividido en dos categorías: transcientes y oscilatorias. Los métodos transcientes incluyen pruebas de fluencia y esfuerzo de relajación. En una prueba de fluencia, el material se somete instantáneamente a un esfuerzo constante y la correspondiente deformación se mide como una función del tiempo. En una prueba de esfuerzo de relajación, la muestra se somete instantáneamente a una deformación constante y se registra el cambio del esfuerzo en función del tiempo. La viscosidad extensional se determina en estado estable, mientras que en los experimentos dinámicos, al efectuarse en estado no estacionario, los datos generados reflejan el comportamiento viscoelástico de un material (Steffe, 1996).
Las pruebas dinámicas oscilatorias se realizan aplicando una pequeña deformación (o esfuerzo) sinusoidal, midiendo el esfuerzo (o deformación) resultante. Las pruebas oscilatorias pueden conducirse en tensión, compresión o corte. Los instrumentos comerciales operan generalmente en el modo de deformación de corte, siendo el método predominante utilizado para la evaluación del comportamiento viscoelástico de los alimentos. La deformación de corte puede generase empleando configuración de platos paralelos, cono y plato o cilindros concéntricos. Los ensayos con pequeñas amplitudes oscilatorias se utilizan en las pruebas dinámicas viscoelásticas. Es importante enfatizar que las deformaciones utilizadas en las pruebas oscilatorias frecuentemente están por el orden del 1 al 3%, para asegurar que la respuesta del material esté en el rango lineal, es decir, intervalo en el cual el esfuerzo es proporcional linealmente a la deformación aplicada (Gunasekaran y Ak, 2000). Si se supone que la muestra se localiza en un reómetro de platos con velocidad controlada y se somete a una pequeña amplitud oscilatoria, la deformación en el material es función del tiempo como se representa en la Ecuación 13. (Steffe, 1996).

La deformación aplicada genera dos componentes del esfuerzo en el material: un componente elástico en línea con la deformación y un componente viscoso 90º fuera de fase. Al derivar la Ecuación 13 con respecto al tiempo se obtiene la velocidad de corte periódica (Ecuación 14), utilizada para evaluar el componente viscoso del material. (Limanond et al.,1999; Steffe, 1996).
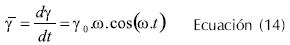
El esfuerzo producido por la aplicación de una fuerza sinusoidal a un material viscoelástico dentro de la región lineal se puede representar como se muestra en la Ecuación 15.
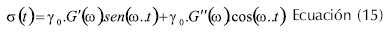
G' es una medida de la energía almacenada y liberada por cada ciclo, y relaciona los eventos moleculares de naturaleza elástica. G'' es una medida de la energía disipada como calor por ciclo y relaciona los eventos moleculares de naturaleza viscosa (Gunasekaran y Ak, 2000). Adicionalmente, se pueden utilizar el modulo complejo (G' , Ecuación 16), la viscosidad compleja (η* , Ecuación 17), la viscosidad dinámica (η' , Ecuación 18), la viscosidad compleja fuera de fase (η'' , Ecuación 19) para describir el comportamiento dinámico de los alimentos.
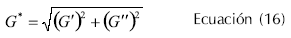
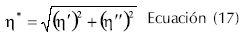


Otra propiedad viscoelástica comúnmente usada es la tangente del ángulo de fase o tangente de pérdida (Ecuación 20), la cual describe los efectos de los componentes viscosos y elásticos en el comportamiento viscoelástico, y es también función de la frecuencia angular (Gunasekaran y Ak, 2000).

Investigaciones en propiedades reológicas de soluciones poliméricas han mostrado que hay correlación entre las funciones que describen las propiedades dinámicas, tal como la viscosidad compleja (η*), y las que caracterizan las propiedades de flujo, como la viscosidad aparente (η , relación entre el esfuerzo y la velocidad de corte). Se ha determinado una regla empírica denominada Cox-Merz para correlacionar las propiedades reológicas dinámicas y las obtenidas bajo condiciones estables de esfuerzo y velocidad de corte. De acuerdo a esta regla, la viscosidad compleja es casi igual a la viscosidad determinada por un esfuerzo de corte estable cuando la velocidad de corte y la frecuencia son iguales como se presenta en la Ecuación 21, ( Rao, 1999; Gunasekaran y Ak, 2000).

(Berland y Launay,1995) estudiaron las propiedades de flujo de la masa de harina de trigo mediante el uso de un reómetro de cono y plato con esfuerzo controlado, a velocidades de corte entre 10-4 y 6.10-2 s-1, con frecuencias entre 0,2 a 20 π.s-1, a una amplitud de deformación de 0,2%. Aplicaron la regla de Cox-Merz con una modificación (Ecuación 22 a Ecuación 26) para que se ajustara a las condiciones de experimentación así:



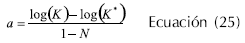
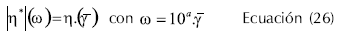
Investigaciones sobre la aplicación de modelos reológicos de masas
La primera evaluación sistemática para determinar las propiedades reológicas fundamentales de la masa de trigo fue realizada por Schofield y Scott Blair durante los años treintas (Létang et al., 1999; Wikström, 1997). Las investigaciones de las propiedades viscoelásticas de los alimentos han cambiado gradualmente por los distintos métodos empleados, desde pruebas en estado estable con aplicación de un esfuerzo normal hasta técnicas reológicas dinámicas a comienzos de los años cincuentas (Rao, 1999). Los métodos dinámicos desarrollados para el estudio de la reología en polímeros han ayudado en la evaluación viscoelástica de los alimentos, incluyendo las masas (Berland y Launay, 1995).
Masas de trigo
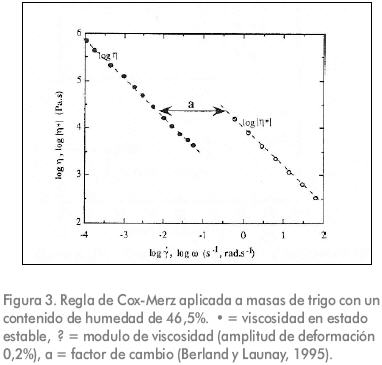
Las propiedades reológicas de la masa de trigo y su relación con la composición fue estudiado por Berland y Launay (1995) utilizando la regla de Cox-Merz modificada por medio de un factor reológico a. Los resultados de la experimentación demostraron que en una masa con un contenido de humedad de 44-49% el agua tiene efectos plastificantes, cambiando los valores de los parámetros reológicos pero sin modificar su estructura, además, plantearon que el factor a refleja el nivel estructural de la masa. La Figura 3 muestra que las propiedades de flujo de las masas de trigo obedecen la ley de potencia para velocidades de corte entre 10-4 y 6.10-2 s-1. La regla de Cox-Merz no se pudo aplicar bajo las condiciones propuestas en los ensayos; sin embargo, fue posible superponer las líneas rectas de η(γ) y |η*|(ω) utilizando el factor de cambio a en el eje de la frecuencia.
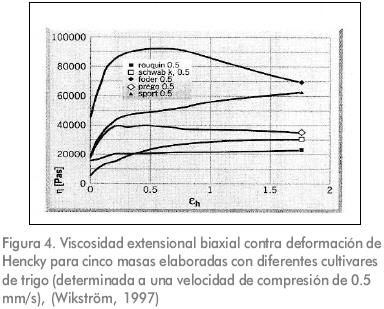
Wikström (1997) estudió el flujo extensional biaxial de masas de trigo para relacionar las propiedades reológicas de la masa y el gluten con su procesamiento y concluyó que las propiedades de flujo de la masa de trigo dependen de la deformación y la velocidad de deformación, además, encontró que existe una amplia variación en los resultados de la viscosidad extensional biaxial de las masas elaboradas con diferentes cultivares de trigo. La Figura 4 muestra un ejemplo representativo de la variación de la viscosidad extensional biaxial con la deformación entre masas de cultivares de trigo de diferentes orígenes. Los trigos con bajo contenido de proteína, como el del cultivar Prego, alcanzaron un máximo seguido por un decrecimiento en la viscosidad, mientras que las viscosidades de las masas procedentes de cultivares con alto contenido de proteína, como Sport y Schwab, se incrementaron continuamente en el rango de la deformación estudiado. La masa preparada con trigo Rouquie presentó una viscosidad constante después de una elevación inicial.
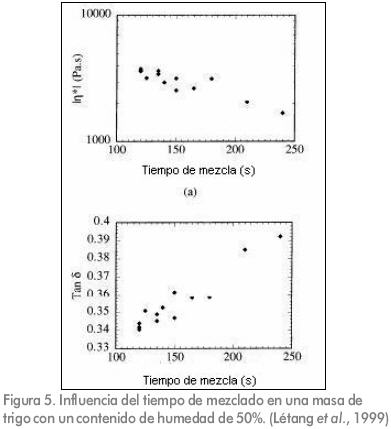
La influencia de los parámetros de mezcla (cantidad de agua y tiempo) en las propiedades reológicas de las masas de trigo y su relación con las propiedades micro y macroestructurales fue investigado por Létang et al. (1999) empleando medidas reológicas dinámicas y observaciones en un microscopio electrónico. Cuando aplicaron pruebas dinámicas a una frecuencia de 1 Hz, verificaron que el almidón presente en la masa incrementa la rigidez del material. Asimismo, un incremento del contenido de agua en un rango de 40 a 45% disminuyó los módulos dinámicos de la masa sin afectar la tangente de perdida (Tan δ, la cual se tomó como un indicador de la organización estructural del material. En la Figura 5 se observa que a tiempos de mezcla prolongados causaron un decrecimiento en |η*| y un incremento en la Tan δ. Tiempos de mezcla entre 120 y 150 s. corresponden a masas óptimamente mezcladas, mientras que masas sobre-mezcladas se obtienen con tiempos superiores a 150 s.
Masas de maíz
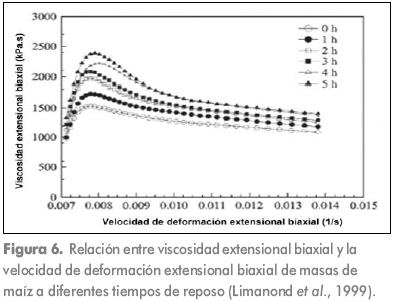
Limanond et al. (1999) estudiaron la aplicación de la viscosidad extensional biaxial para evaluar el efecto del empaque y el tiempo de reposo a temperatura ambiente (tiempos de reposo: 0, 1, 2, 3, 4, 5, 6 h y empaque: polietileno) sobre la estabilidad de las masas de maíz utilizadas en la elaboración de tortillas. Las masas de maíz empacadas y las testigos (sin empaque) mostraron un comportamiento reológico de tipo adelgazante extensional (disminución de la viscosidad con la velocidad de deformación extensional). La viscosidad extensional biaxial de la masa testigo se incrementó significativamente con el tiempo de reposo. Al empacar la masa se disminuyó la pérdida de humedad y la viscosidad permaneció constante durante el período de reposo (6 h). La Figura 6 presenta la viscosidad extensional biaxial de la masa testigo como una función del tiempo de reposo (0 a 5 h) para una velocidad de compresión de 0,3 mm/s, todas las muestras presentaron un ascenso marcado inicial con un declive gradual, la viscosidad extensional biaxial se incrementó significativamente con el período de reposo debido probablemente a la cantidad de agua evaporada en las muestras.
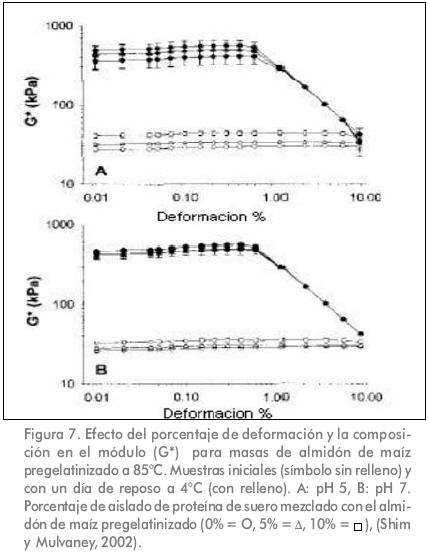
Shim y Mulvaney (2002) determinaron las propiedades reológicas dinámicas de una masa elaborada a partir de almidón de maíz pregelatinizado a diferentes temperaturas de calentamiento (75, 85 y 95 °C), condiciones de pH (5, 7 y 9) y cantidades de aislado de proteína de suero (0, 5 y 10%). Los valores del módulo de almacenamiento (G') más bajos se observaron para masas elaboradas con almidón pregelatinizado a altas temperaturas. El módulo complejo (G*) de masas que contenían aislado de proteína fue más alto que las masas elaboradas solo con almidón de maíz para todos los tratamientos. En la Figura 7 se muestra el efecto de la deformación, el tiempo de reposo y el contenido de aislado de proteína de suero sobre el de masas preparadas con almidón de maíz pregelatinizado a diferentes pH. Se observó que después de un día de reposo a 4 °C el módulo se incrementó sensiblemente.
Conclusiones
Los modelos reológicos extensional biaxial y dinámico oscilatorio aplicados al estudio de masas de trigo y maíz han demostrado ser de utilidad para conocer la influencia de sus constituyentes, determinar su carácter viscoelástico y predecir cambios de la estructura del material durante su procesamiento y almacenamiento, entre otros.
Nomenclatura
L = longitud extendida de la barra (m)
L0 = longitud inicial de la barra (m)
ΔL = incremento en longitud (m)
εc = deformación de Cauchy (adimensional)
εh = deformación de Hencky (adimensional)
h = altura que separa los platos (m)
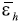 = velocidad de deformación de Hencky (s-1)
= velocidad de deformación de Hencky (s-1)
vz = velocidad constante del plato superior en dirección descendente (m/s)
h0 = altura inicial de la muestra (m)
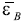 = velocidad de deformación extensional biaxial (s-1)
= velocidad de deformación extensional biaxial (s-1)
σB = esfuerzo biaxial (Pa)
F = fuerza determinada experimentalmente del plato superior (N)
r = radio de la muestra (m)
R = radio del plato (m)
ηB = viscosidad extensional (Pa.s)
σ = esfuerzo de deformación (Pa) (Ecuación 11 y 12)
ε = velocidad de deformación (s-1) (Ecuación 11)
E = modulo de deformación (Pa.s) (Ecuación 11)
γ* = velocidad de corte (s-1)
η = viscosidad aparente (Pa.s) (Ecuación 12)
γ0 = amplitud de la deformación (adimensional)
ω = frecuencia angular dinámica (rad.s-1)
γ = deformación del material (adimensional)
t = tiempo de prueba (s)
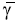 = velocidad de corte periódica (s-1)
= velocidad de corte periódica (s-1)
G' = Modulo de corte elástico o de almacenamiento (Pa)
G'' = Modulo de corte viscoso o de perdida (Pa)
G* = modulo complejo (Pa)
η* = viscosidad compleja (Pa.s)
η' = viscosidad dinámica (Pa.s)
η'' = viscosidad compleja fuera de fase (Pa.s)
δ = ángulo de fase relativo a la deformación (rad)
|η*| = amplitud de viscosidad compleja (adimensional)
K = índice de consistencia (Pa.sn)
K* = índice de consistencia (Pa.sn)
n = índices de comportamiento de flujo (adimensional)
n* = índices de comportamiento de flujo (adimensional)
N = promedio de los índices de comportamiento de flujo (adimensional)
a = factor de cambio (adimensional)
Bibliografía
Bagley, E. B., Constitutive models for doughs, En: Food Extrusion Science and Technology; ed. Kokini, J. L., Ho, C. y Karwe, M. New York: Marcel Dekker Inc., 1992, pp. 203 – 211. [ Links ]
Berland, S. y Launay, B., Rheological properties of wheat flour dough in steady and dynamic shear: Effect of water content and some additives, En: Cereal Chemistry, Vol. 72, No. 1, 1995, pp. 48 –52. [ Links ]
Gunasekaran, S. y Ak, M. M., Dynamic oscillatory shear testing of foods-selected applications, En: Trends in Food Science & Technology, Vol. 11, 2000, pp. 115-127. [ Links ]
Létang, C., Piau, M. y Verdier, C., Characterization of wheat flour-water dough. Part I. Rheometry and microstructure, En: Journal of Food Engineering, Vol. 41, 1999, pp. 121-132. [ Links ]
Limanond, B., Castell-Perez, E. y Moreira, R. G., Effect of time and storage conditions on the rheological properties of masa for corn tortillas, En: Lebensmittel Wissenshaft und Technologie, Vol. 32, 1999, pp. 344-348. [ Links ]
Rao, M. A., .Rheology of fluid and semisolid foods: principles and applications, Maryland: Aspen publications, 1999, pp.100-105. [ Links ]
Rao, V. G. y Rao, H. P., Methods for determining rheological characteristics of doughs: A critical evaluation, En: Journal of Food Science, Vol. 30, No. 2, 1993, pp. 77-87. [ Links ]
Shim, J. y Mulvaney S. J., Effects of pregelatinization conditions and added whey protein isolate on corn starch dough properties, En: Cereal Foods World, Vol. 47, No. 9, 2002, pp. 440 – 446. [ Links ]
Steffe, J., Rheological methods in food process engineering. Michigan: Freeman, 1996, pp.1-10, pp. 258-262, pp. 295-317. [ Links ]
Wang, F. C. y Sun, X. S., Creep-recovery of wheat flour doughs and relationship to other physical dough tests and breadmaking performance, En: Cereal Chemistry, Vol. 79, No. 4, 2002, pp. 567 –571. [ Links ]
Wikström, K., Rheology of wheat flour dough at large deformations and the relation to baking quality and physical structure. Tesis Doctoral presentada a la Universidad de Lund, Lund, Suecia 1997. [ Links ]














