Wilson Rodríguez Calderón,¹ Myriam Rocío Pallares Muñoz²

¹ Ingeniero civil, UIS, Bucaramanga. Magíster en Métodos Numéricos para Ingeniería, Universidad Politécnica de Cataluña. Profesor Investigador del departamento de ingeniería civil, Pontificia Universidad Javeriana, e-mail: wilroca@javeriana.edu.co
² Ingeniera civil, UIS, Bucaramanga. Magíster en Métodos Numéricos para Ingeniería, Universidad Politécnica de Cataluña, e-mail: mrocio03@hotmail.com

RESUMEN

Con el presente trabajo se desarrolla una alternativa para determinar el nivel de abatimiento de agua en acuíferos inconfinados, empleando las técnicas de optimización que están disponibles en el programa comercial de elementos finitos ANSYS³. Las variables de diseño se definen paramétricamente por medio de las coordenadas verticales o cotas de unos puntos clave, que se interconectan por medio de splines para aproximar la superficie libre. Las variables de estado son los valores de temperatura en los puntos clave, que por analogía térmica son análogos a la cabeza de fluido. La función objetivo es el valor absoluto de la diferencia entre las coordenadas verticales y los valores de temperatura calculados en los puntos clave. Con la verificación de estas técnicas en la determinación de la posición de la tabla de agua en el problema de acuíferos libres, se está dando solución al problema de la superficie libre en presas de materiales sueltos y por qué no, a otro tipo de problemas, como los de mecánica de fluidos (por ejemplo, el de flujo en canales o el de oleaje), que aunque son problemas bien diferentes al de medio poroso, la solución sí que es altamente no lineal, y se requiere de técnicas robustas para aproximarse suficientemente al comportamiento real del fenómeno.

Palabras clave: optimización, variables de diseño, variables de estado, función objetivo

ABSTRACT

The present work presents an alternative for determining free surface in free aquifers using the optimisation techniques available in ANSYS (commercial finite elements’ software). This is able to handle variable meshes through optimisation algorithm iterations. This represents an advantage in terms of precision re methods using a constant mesh. Design variables were parametrically defined by means of vertical coordinates, or key point levels, which were interconnected by means of splines for estimating the free surface. State variables were the values of temperature at key points which were analogous at the top of the water by thermal analogy. The objective function is the absolute value of the difference between the vertical coordinates or levels and the calculated values of temperature at key points. These techniques may be used for determining the position of the water table re free aquifers, resolving the problem of free surface in loose material reservoirs and other types of problems such as fluid mechanics (e.g. flow in canals or swell). Even though these are problems which are very different to those of a porous medium, resolving them is highly non-lineal and requires robust techniques for approaching the phenomena’s real behaviour.

Keywords: optimization, spline, design variable, state variable, objective function

Recibido: abril 18 de 2005
Aceptado: octubre 26 de 2005

Marco teórico

El problema de filtración en un medio poroso en condiciones estacionarias se puede plantear matemáticamente mediante la ecuación de Laplace o la de Poisson, usando como variable de trabajo la altura piezométrica:

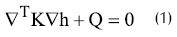
donde h es la altura piezométrica y Q es una función que representa una fuente o un sumidero (una entrada o salida puntual de agua), y que en la mayoría de los problemas suele ser cero. K es la permeabilidad del medio, que en muchos casos se considera un escalar constante. Por otra parte, ∇h representa el operador divergencia, y ∇ el operador gradiente. En el caso de permeabilidad constante (suelo homogéneo e isótropo a efectos de flujo), y en ausencia de fuentes y/o sumideros, la expresión (1) da lugar a la conocida ecuación de Laplace en coordenadas cartesianas:

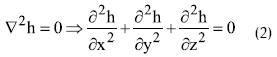
Esta ecuación se puede resolver directamente con algunos de los programas comerciales que resuelven la ecuación de Laplace (2), o la de Poisson (1). En ambos casos será necesario definir las condiciones de contorno apropiadas, que normalmente son de tipo Dirichlet (altura piezométrica impuesta) o de tipo Neumann (derivada de la altura piezométrica impuesta), o en algunos casos puede ser una combinación de ambas.

Sistema de ecuaciones resultantes

El problema matemático planteado se puede expresar mediante la siguiente ecuación diferencial en derivadas parciales y las siguientes condiciones de contorno:

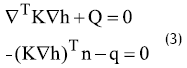
donde n es un vector unitario normal a un contorno por el que sale o entra agua. La condición de contorno segunda expresión de (3) representa que el caudal en la dirección definida por el vector n, vale q. Si se aplica residuos ponderados a (3), utilizando Galerkin, y luego se aplica el teorema de Green (es decir, se usa la forma débil), con la discretización típica del método de los elementos finitos sustituyendo la variable altura piezométrica por sus valores en los nodos, resulta finalmente:

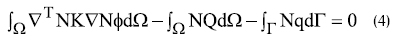
donde Ω es el dominio en el que se aplica la ecuación diferencial, y Γ el contorno. N son las funciones de forma que permiten obtener la altura piezométrica en cualquier punto del interior, y φ es el vector de alturas piezométricas en los nodos (también llamadas potenciales). Es decir, la altura piezométrica en un punto del interior del elemento finito se puede expresar en función de las alturas piezométricas en los nodos mediante: h = Nφ. En (4), la primera integral sobre el dominio puede escribirse separando el vector de alturas piezométricas o potenciales nodales del resto, ya que son valores numéricos y pueden salir fuera de la integral. Las dos integrales siguientes, por su parte, dan lugar a vectores que pueden escribirse como un término independiente. Finalmente (4) se puede expresar en forma de un sistema de ecuaciones algebraico como:

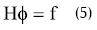
donde H es la matriz de permeabilidad, y representa la primera integral de (4) salvo el término φ, que es el vector de alturas piezométricas en los nodos (unidades de longitud). f es un vector de caudales en los nodos (tiene unidades de m³/s).

Tratamiento de la superficie libre

La expresión (5) permite resolver problemas de filtración en un medio poroso. El problema de los acuíferos no confinados es algo más complicado debido a la presencia de una superficie libre. Si bien la expresión es válida en las regiones completamente saturadas del flujo (por debajo de la superficie libre), esta debe ser resuelta en un dominio con una frontera desconocida: la forma de la superficie freática. La condición de contorno en la interfase aire-agua es de presión constante e igual a la presión atmosférica. También debe incluir el eventual ingreso de agua debido a la recarga del acuífero por infiltración. Una aproximación alternativa a este problema es integrar las ecuaciones en la dirección vertical y tratar sólo con un sistema bidimensional, asumiendo un flujo básicamente horizontal.

Las condiciones que debe satisfacer la superficie libre son:

1. La cabeza de potencial (φ) en cualquier punto de la superficie es equivalente a la cabeza de elevación z en estos puntos, desde alguna superficie de referencia (desde este punto de vista la presión atmosférica actúa en cualquier lugar de la superficie).

2. El flujo a través de la superficie libre en la dirección normal es igual a cero.

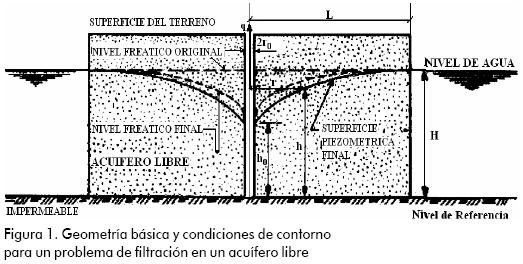
Como consecuencia del pozo de bombeo, es necesario imponer una condición de caudal prescrito en el sitio de extracción ubicado exactamente en el eje de simetría del acuífero. La condición de energía constante prescrita se encuentra localizada a una distancia L a partir del eje de simetría. Por otra parte, en la base del acuífero la condición es de impermeabilidad, y utilizando la ley de Darcy, eso es equivalente a anular la derivada de la altura piezométrica en la dirección perpendicular al contorno impermeable. Finalmente el problema aparece en el nivel de abatimiento, ya que esta línea no es conocida a priori. En realidad este problema es muy complejo desde un punto de vista matemático, porque el dominio Ω de suelo por donde circula el agua no está definido inicialmente. Es decir, tenemos una ecuación diferencial en derivadas parciales definida en un dominio que no conocemos. De aquí que sea necesario adoptar un procedimiento iterativo en la localización de la superficie libre cuando se usan métodos computacionales. El procedimiento comienza con un cálculo inicial acerca de la localización de la superficie libre. Sobre los valores de cabeza del fluido (φ) básicos computados en cada iteración, se modifica la localización de la superficie libre. La condición de borde a lo largo de la superficie libre (φ=z y δφ/δn=0) se verifica al final de cada iteración. El procedimiento se lleva a cabo hasta que el movimiento de la superficie libre durante una y otra iteración consecutiva comience a hacerse despreciable.

Solución del problema por analogía térmica

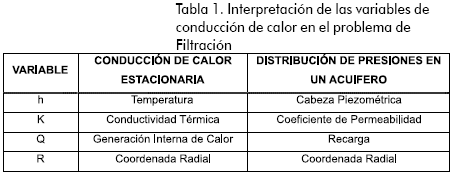
La solución a un problema que involucra el régimen estacionario de flujo de calor bajo condiciones de borde dadas, producirá un campo térmico consistente de líneas de igual temperatura o isotérmicas interceptadas con ángulos rectos por líneas de flujo de calor. Existe una correspondencia directa entre la temperatura y la cabeza total del fluido, la conductividad térmica y la permeabilidad, y el flujo de calor con el flujo de fluidos. De esta manera, un modelo de flujo térmico idéntico al de flujo de agua se puede desarrollar si se conoce una región de flujo bajo condiciones de borde establecidas. A continuación se presenta la relación que existe entre estas variables a través de la Tabla 1.

Optimización del diseño en ANSYS⁴

La optimización del diseño es una técnica que pretende determinar el mejor diseño o el diseño óptimo. Un "diseño óptimo", es aquel que reúne toda una serie de requisitos específicos, pero con un costo mínimo de ciertos factores, tales como el peso, el área, el volumen, los esfuerzos, etc. En otras palabras, el diseño óptimo es normalmente aquel que logra “ser lo más eficaz posible”.

El programa ANSYS ofrece dos métodos de optimización que son adaptables a una amplia gama de problemas. El método de aproximación del subproblema, que es un método de orden cero avanzado que se puede aplicar eficazmente a la mayoría de problemas de ingeniería; y el método de primer orden, que se basa en la sensibilidad del diseño y está recomendado para problemas que requieren gran exactitud, como el caso que nos ocupa. Para los dos métodos, el programa ejecuta una serie de ciclos de: análisis – evaluación – modificación. Es decir, se desarrolla un análisis inicial del diseño, se evalúan los resultados contra los criterios de diseño especificados en el modelo (p. Ej., las condiciones de borde que debe satisfacer la superficie libre), y se modifica el diseño si es necesario. Este proceso se repite hasta que se satisfagan todos los criterios especificados. Así las cosas, este problema será desarrollado utilizando el método de primer orden.

Definiciones básicas en optimización

Antes de describir el procedimiento de optimización, es necesario definir la terminología básica empleada en estos tipos de análisis, como son, variables de diseño, variables de estado y función objetivo (que colectivamente son llamadas variables de optimización), diseño factible y diseño no factible, archivo de análisis, iteraciones, ciclos, conjunto de diseño, etc.

- Variables de diseño (VD) son cantidades independientes que se modifican para alcanzar el diseño óptimo (son las variables independientes del problema). Es necesario especificar límites superiores e inferiores como "restricciones" en las variables de diseño. Estos límites definen su rango de variación. Las VD son normalmente los parámetros geométricos como la longitud, el espesor, el diámetro, o las coordenadas del modelo, y están restringidas con valores positivos.

- Variables de estado (VE) son cantidades que condicionan o restringen el diseño. Se conocen también como "variables dependientes", y son típicamente cantidades de respuesta que son funciones de las variables de diseño [VE = f (VD)]. Algunos ejemplos de VE pueden ser las tensiones, las temperaturas, las tasas de flujo de calor, , las deflexiones o el tiempo. Una variable de estado no necesariamente es una cantidad calculada por ANSYS; virtualmente cualquier parámetro puede definirse como una variable de estado.

- Función objetivo (F) es la variable dependiente que se intenta minimizar. Debe ser función de las VD [F = f (VD)], es decir, si los valores de las VD cambian, el valor de la función debe variar.

- Un conjunto de diseño (o diseño) es simplemente un conjunto único de valores de los parámetros que representan una configuración particular del modelo. Típicamente, se caracteriza por los valores de las variables de optimización.

- Un diseño factible es aquel que satisface todas las restricciones o condiciones especificadas tanto para las VE como para las VD. Si una de las restricciones no se satisface, el diseño se considera como no factible. El mejor diseño es aquel que satisface todas las restricciones impuestas y produce el mínimo valor en la función objetivo. (Si todos los conjuntos de diseño son no factibles, el mejor conjunto de diseño será aquel que más se acerca a la factibilidad, independiente del valor que produzca en la función objetivo).

- El archivo de análisis en ANSYS, es el de entrada, el cual contiene una secuencia de análisis completa (preproceso, solución, posproceso). Este archivo debe contener un modelo definido paramétricamente, lo cual significa que se deben usar parámetros para representar todas las entradas y las salidas, los cuales serán usados como VD, VE, y como función objetivo.

- Un ciclo es un paso a través del análisis (como un paso a través del archivo de análisis).

- Una iteración de optimización (o simplemente una iteración) es uno o más ciclos de análisis que resultan en un nuevo conjunto de diseño. Normalmente, una iteración equivale a un ciclo. Sin embargo, para el método de primer orden, una iteración representa más de un ciclo.

- La base de datos de optimización contiene el último entorno de optimización, e incluye las definiciones de las variables de optimización, los parámetros, todas las especificaciones de optimización y los conjuntos de diseño acumulados.

Métodos de optimización

Los métodos de optimización son técnicas tradicionales que se esfuerzan por la minimización de una función (la función objetivo) que está sujeta a unas restricciones. En el programa ANSYS están disponibles dos métodos de optimización, el de aproximación del subproblema y el de primer orden, y para utilizar uno u otro, necesariamente se debe tener definida una función objetivo.

El método de aproximación del subproblema es de orden cero avanzado que usa aproximaciones (ajuste de curvas) para todas las variables dependientes (VE y la función objetivo). Es un método general que puede aplicarse eficazmente a una gama amplia de problemas de ingeniería.

El método de primer orden es aquel que usa la información de la derivada, es decir, los gradientes de las variables dependientes con respecto a las de diseño. Es un método muy exacto y trabaja bien para problemas que tienen variables dependientes que varían ampliamente en un rango grande del espacio de diseño. Sin embargo, este método puede ser computacionalmente costoso.

Aspectos generales de las técnicas de optimización en ANSYS

Entender el algoritmo usado por un programa de computador es siempre útil, particularmente en el caso de optimización. A continuación se presentan detalles de las técnicas de aproximación del subproblema y primer orden.

Método de aproximación del subproblema

El método de aproximación del subproblema es aquel de orden cero en el que se requiere sólo de los valores de las variables dependientes, y no de sus derivadas. Hay dos conceptos que juegan un papel importante en el método de aproximación del subproblema: el uso de aproximaciones para la función objetivo y las variables de estado, y la conversión de un problema de optimización inicialmente restringido o condicionado a un problema sin restricciones (como ya se había comentado anteriormente).

Aproximaciones

Para este método, el programa establece una relación entre la función objetivo y las VD por medio de ajustes de curvas. Esto se hace calculando los valores de la función objetivo para varios conjuntos de valores de VD (es decir, para varios diseños) y realizando un ajuste por mínimos cuadrados entre los datos. La curva resultante (o superficie) se llama aproximación. Cada ciclo de optimización genera un nuevo dato, y la aproximación de la función objetivo se actualiza. Es esta aproximación la que se minimiza en lugar de la función objetivo real. Las variables de estado son manejadas de la misma manera, es decir, se genera una aproximación para cada variable de estado y se actualiza al final de cada ciclo.

El método de ajuste de las curvas para las aproximaciones se puede controlar, ya sea empleando un ajuste lineal, uno cuadrático, o una combinación entre uno cuadrático y otro ajuste de términos cruzados. Por defecto el programa emplea este último ajuste para la función objetivo, y uno cuadrático para las VE.

Conversión a un problema sin restricciones

Las variables de estado y los límites sobre las variables de diseño hacen que el problema de optimización sea restringido. Este aspecto introduce una complicación para la optimización, da tal manera que el programa ANSYS lo transforma a un problema de optimización sin restricciones, dado que las técnicas de minimización para este último son más eficaces. La conversión se hace agregando penalidades a la aproximación de la función objetivo de acuerdo a las restricciones impuestas. La búsqueda de un mínimo de la aproximación de la función objetivo sin restricciones se lleva a cabo aplicando una técnica de minimización secuencial sin restricciones en cada iteración.

Verificación de la convergencia

Al final de cada ciclo se hace un chequeo de la convergencia. Se dice que el problema es convergente si el actual, el anterior, o el mejor diseño, son factibles. La convergencia no indica necesariamente que se ha obtenido un mínimo global verdadero (puede llegarse a un mínimo local). Por consiguiente, se debe tener especial cuidado para determinar si el diseño se ha optimizado suficientemente. De no ser así, es necesario realizar análisis de optimización adicionales.

Método de primer orden

Al igual que el método de aproximación del subproblema, el método de primer orden convierte el problema inicialmente restringido a un problema sin restricciones agregando funciones de penalización a la función objetivo. Sin embargo, a diferencia del método de aproximación del subproblema, la que se minimiza es la representación del elemento finito real y no una aproximación.

El método de primer orden usa los gradientes de las variables dependientes con respecto a las variables de diseño. Se realizan cálculos del gradiente para cada iteración (a través de técnicas de máximo descenso o del método de dirección conjugada) con el fin de determinar una dirección de búsqueda. La estrategia de búsqueda que se adopta para minimizar el problema sin restricciones es el de búsqueda de línea (LINE SEARCH).

Bajo estas consideraciones, cada iteración está compuesta de varias subiteraciones que incluyen cálculos de la dirección de búsqueda y del gradiente. Por eso una iteración de optimización para el método de primer orden realiza varios ciclos de análisis.

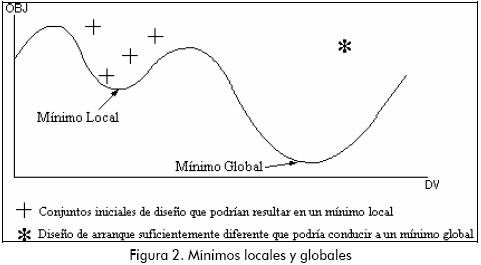
Mínimos locales y mínimos globales

En ocasiones la solución puede desembocar en un mínimo local en lugar del verdadero mínimo global (ver Figura 2). Para verificar que esta situación no haya ocurrido, se debe recalcular nuevamente el problema con un diseño de arranque diferente (es decir, un valor inicial diferente de la VD).

Descripción del problema de optimización en ANSYS

Como se había expresado anteriormente, las variables independientes en un análisis de optimización son las variables de diseño. El vector de variables de diseño está indicado por:

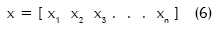
Las variables de diseño están sujetas a n restricciones con límites superiores e inferiores, esto es,

donde: n = número de variables de diseño

Las restricciones de las variables de diseño son denominadas frecuentemente restricciones laterales y definen lo que es llamado el “espacio de diseño factible”.

Se intenta es minimizar una función:

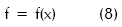
sujeta a las siguientes restricciones:

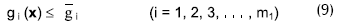
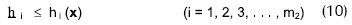
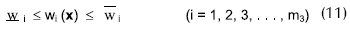
donde: f = es la función objetivo

g_i, h_i, w_i = son las variables de estado que contiene el diseño, con barras superiores e inferiores 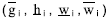que representan los límites mínimo y máximo, respectivamente.

m₁ + m₂ + m₃ = es el número de restricciones de las variables de estado con varios valores límites superior e inferior.

Las variables de estado son también llamadas variables dependientes, ya que ellas varían con el vector x de variables de diseño. Las expresiones (8) a (11) representan un problema típico de minimización restringido, el cual apunta, como es lógico, a la minimización de la función objetivo f bajo las restricciones impuestas por las ecuaciones (7), (9), (10) y (11).

Las configuraciones del diseño que satisfacen todas las restricciones son llamadas diseños factibles, y las configuraciones con una o más violaciones a dichas restricciones se consideran diseños no factibles. En definición, en un espacio de diseño factible se adiciona una tolerancia a cada límite de la variable de estado, de manera que si x* es un conjunto de diseño dado definido como:

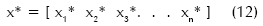
el diseño es considerado factible sólo si:

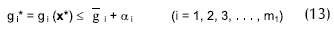
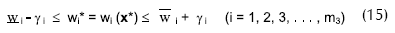
donde α_i, β_i, y γ_i = son las tolerancias, y:

(puesto que no se agregan tolerancias a las restricciones de la variable de diseño)

Las expresiones (13) a (16) son las que definen las instrucciones de un conjunto de diseño factible en las rutinas de optimización de ANSYS.

Planteamiento del problema

Descripción del problema

El problema consiste fundamentalmente en determinar la solución de flujo bidimensional en un acuífero libre, por medio de un modelo 2D de elementos finitos utilizando analogía de flujo de calor por conducción con el programa comercial de elementos finitos ANSYS. Por supuesto, dicha solución incluye la determinación de la posición de la superficie libre mediante técnicas de optimización, que es el objetivo de este trabajo, y para ello, se hace uso del módulo de optimización –OPT– del programa.

La validación se lleva a cabo comparando la solución analítica y numérica del problema de distribución de presiones. Así las cosas, cualquier ejemplo de este tipo es útil para efectuar la validación. Se supone entonces, un pozo que penetra un acuífero, en el que se realiza un bombeo a una tasa de 150 m³/h. En el acuífero existe una simetría radial en el campo de flujo (el lugar de bombeo está ubicado en el origen de coordenadas radiales) de tal manera que a una distancia radial de 200 m se encuentra ubicada una cabeza de 50 m. La permeabilidad del acuífero es de 25 m³/(hm²) y se requiere determinar la distribución de cabezas piezométricas. A continuación se presenta un esquema del problema.

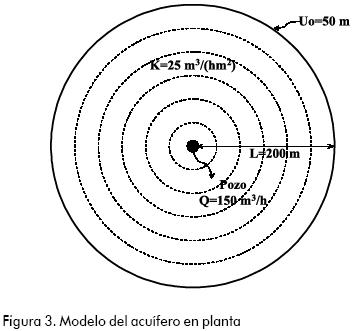
La Figura 3 ilustra un modelo plano. Este es especialmente útil para visualizar los contornos de cabezas piezométricas, los cuales están concentrados en círculos.

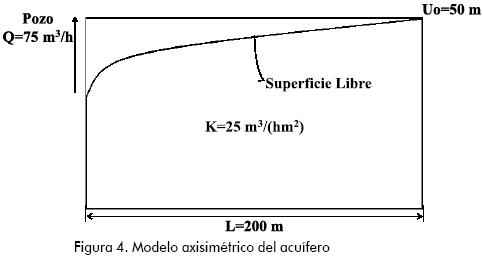
La Figura 4 muestra un modelo axisimétrico (implementado en este trabajo). La axisimetría se usa para simplificar los modelos y además permite contemplar problemas de materiales heterogéneos donde existen variaciones de la permeabilidad.

Solución analítica

La ecuación de gobierno para un acuífero inconfinado con flujo en la dirección radial está descrita por:

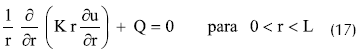
donde r es la coordenada radial, Q es la recarga (el bombeo es considerado como una recarga negativa), K es el coeficiente de permeabilidad y u es la cabeza piezométrica.

Las condiciones de borde asociadas a este problema son:

r = 0, Q = recarga

r = L, u = u₀

La solución de la ecuación diferencial está dada por:

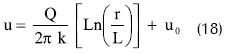
Esta expresión significa que la distribución de presiones en un acuífero en la dirección radial es una función del logaritmo de la coordenada radial. Esta ecuación es análoga a la de conducción de calor estacionaria en dirección radial.

Entonces, dado: Q = 150 m³/h, k = 25 m³/(hm²), u₀ = 50 m y L = 200 m, se encuentra que:

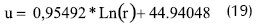
Eespecificaciones del problema

Propiedades geométricas y condiciones de contorno

La aproximación de la curva en el modelo axisimétrico se realiza a través de unos puntos claves que se conectan por medio de splines. Estos puntos se ubican de manera arbitraria y sobre ellos se realizan las iteraciones del algoritmo de optimización, para finalmente determinar las cotas correctas (que son iguales a las cabezas de presión para un acuífero libre). La frontera libre está constituida entonces por nueve puntos claves (del punto 3 al 11 en la figura 5, dado que los puntos 2 y 12 definen condiciones de contorno) ubicados arbitrariamente y sobre los cuales se realizan las iteraciones del algoritmo de optimización, para finalmente determinar las cotas correctas.

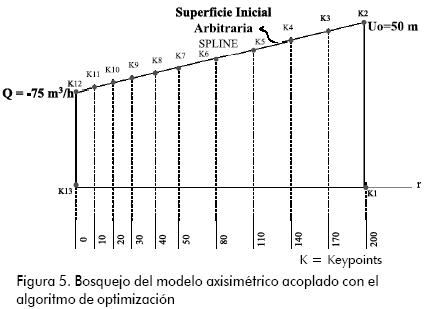
Las condiciones de borde para el problema axisimétrico son de:

Caudal prescrito: r = 0 (K12 – K13), Q = - 75 m³/h

Cabeza de presión prescrita: r = 200 (K1 – K2), u = 50 m

Variables de optimización

Función objetivo

La función a minimizar es el valor absoluto de la diferencia entre la cota y la temperatura (análoga a la cabeza del fluido) de los puntos claves utilizados en la aproximación por splines de la curva de la superficie libre, mostrada en la Figura 5. Para evitar problemas de error por redondeo se suma a la función objetivo un valor arbitrario (se asumió uno de 10.00). La función objetivo tal y como está definida debe tender al valor arbitrario señalado o a cero en caso de no utilizarlo; en otras palabras, la temperatura y la cota de cada punto deben tender a ser iguales.

Variables de diseño

Las variables de diseño son las cotas de los puntos claves utilizados para la aproximación de la superficie libre. Estas coordenadas se encuentran restringidas entre dos límites. Un valor mínimo que corresponde a la cota del punto vecino inmediatamente anterior con menor cota, el cual siempre va a ser correcto si se tiene en cuenta que ya ha sido iterado (físicamente el punto en estudio no podrá estar por debajo de su vecino de menor cota dado que no hay succiones en el modelo), y un valor máximo de 50m correspondiente a la cabeza máxima en el modelo ubicada a un radio de 200 m.

Variables de estado

Las variables de estado son las temperaturas (cabeza de fluido) de los puntos de la superficie libre. Físicamente y de manera flexible se pueden establecer como restricciones mínima y máxima, 0 y 50 m respectivamente. El valor de 50 m corresponde a la cabeza máxima de fluido en el acuífero.

Solución del problema y discusión

El desarrollo del problema en el programa ANSYS requiere de la elaboración de un archivo de análisis empleando los tres niveles de procesamiento básicos, preproceso, solución y posproceso. Con la ejecución de este algoritmo se obtienen finalmente los valores de las variables de estado (temperaturas de los puntos de la superficie libre) actualizadas, de acuerdo a las variables de diseño (cotas de los puntos claves utilizados en la aproximación de la superficie libre) obtenidas utilizando el módulo de optimización.

La optimización del diseño se constituye en un cuarto módulo y a través de él se plantea todo el escenario de optimización, en cuanto a variables de estado y de diseño, función objetivo, tolerancias, método de solución y número máximo de iteraciones. El archivo de datos de optimización contiene el último entorno de optimización e incluye las definiciones de las variables de optimización, los parámetros, todas las especificaciones de optimización y los conjuntos de diseño acumulados. Con él es posible hacer un análisis del comportamiento del método en aspectos tales como convergencia y costo computacional en términos de tiempo CPU, como los más importantes.

Solución del algoritmo por el método de primer orden

La aproximación de la curva se realiza a través de puntos claves que se conectan por medio de splines. Estos puntos se ubican de manera arbitraria y sobre ellos se realizan las iteraciones del algoritmo de optimización, para finalmente determinar las cotas correctas (que son iguales a las cabezas de presión para un acuífero libre).

A continuación se presentan las gráficas de convergencia de la función objetivo (sobre los Keypoints 3, 4, 5, 6, 7, 8, 9, 10, 11 y 12). El Keypoint 2 no se itera porque en él se encuentra aplicada la condición de contorno de cabeza de presión. Con este método es común hacer uso del máximo número de iteraciones, y pese a ello se obtienen resultados más precisos (mayor exactitud), obviamente con mayor esfuerzo computacional, dado que cada iteración consta de varios ciclos. Las curvas realizadas por el programa ilustran muy bien este comportamiento (ver Figura 6).

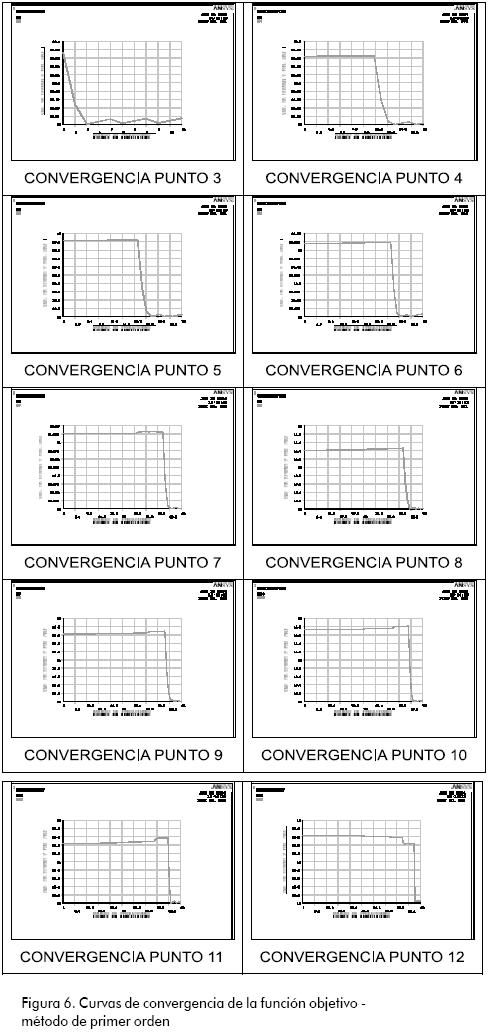
En la Figura 7 se ilustra el comportamiento (movimiento) de la superficie libre en el modelo axisimétrico a los largo de las iteraciones de optimización.

Comparación de resultados

En la Tabla 2 se reúnen los resultados obtenidos del modelo axisimétrico optimizado y los de la solución analítica. Al comparar, se puede observar la validez del algoritmo de optimización implementado para resolver el problema.

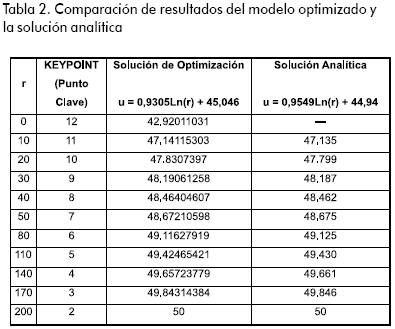
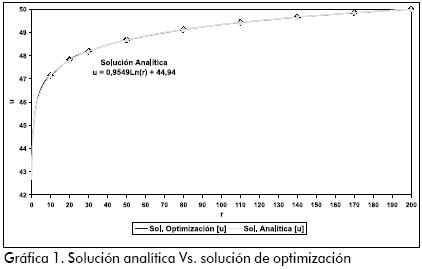
La validez se hace evidente al observar la Gráfica 1. En ella se encuentran dibujadas las curvas para las dos soluciones. En la Gráfica 2 se realiza un ajuste logarítmico con el fin de determinar la ecuación del problema optimizado.

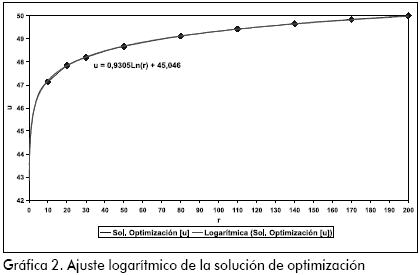
Conclusiones y recomendaciones

El problema de flujo inconfinado está revestido de una complejidad importante que radica en el desconocimiento de la frontera constituida por la superficie libre. Con este trabajo se logra dar solución al problema a través del empleo de técnicas avanzadas de optimización, dejando de lado las técnicas de malla constante (que son menos precisas que las de malla variable), suficientemente referenciadas en gran parte de la literatura que trata el problema de flujo en medio poroso o flujo subterráneo.

La alternativa de utilizar análisis de optimización para determinar la posición de la frontera desconocida en el problema de flujo en medio poroso, abre la posibilidad de emplear también técnicas de optimización como una alternativa para solucionar otros tipos de problemas, como los de mecánica de fluidos (por ejemplo, el de flujo en canales o el de oleaje), que aunque son problemas bien diferentes al de medio poroso, la solución sí que es altamente no lineal, y se requiere de técnicas robustas para aproximarse suficientemente al comportamiento real del fenómeno.

La comparación entre la superficie libre determinada a partir de esta técnica de optimización y por medio de la solución analítica del problema, indica que los resultados son ampliamente satisfactorios. Esto muestra la validez del método de optimización en cuestión para obtener la ubicación de la superficie en problemas de flujo en medio poroso con suficiente confiabilidad.

Bibliografía

ANSYS user manual         [ Links ]

Desai, Chandrakant S. y Christian, John T., Numerical Methods in Geotechnical Engineering., Edit. Mc Graw-Hill Book Company, USA, 1997, pp. 1 - 65, 458 - 506.         [ Links ]

Lambe, T., William y Whitman, Robert V., Mecánica de suelos., Edit. Limusa – Wiley, México, 1963, pp. 225 - 441.         [ Links ]

Ledesma, A., Problemas geotécnicos, apuntes., Centro Internacional de Métodos Numéricos, Barcelona, 2003.         [ Links ]

Olivella, S., Carrera, J., Hidrología subterránea, apuntes., Centro Internacional de Métodos Numéricos, Barcelona, 2003.         [ Links ]

Rao, S. S., The Finite Element Method in Engineering., Edit. Pergamon Press, New York, 1989, pp. 432 - 518, 521 - 592.         [ Links ]

Reddy, J. N., An introduction to the finite element method., McGraw-Hill Book Company, 1984, p. 103.         [ Links ]

Rodríguez, W. y Pallares, M., Determinación de la superficie libre en presas de tierra mediante técnicas de optimización., en revista Ternura, 2004, pp. 33 - 44.         [ Links ]

Streeter, Victor L. y Wylie, Benjamin E., Mecánica de los fluidos., Edit. Mc Graw-Hill, Mexico, 1988, pp. 84 - 162, 323 - 340.         [ Links ]

Willey, John & Sons, Finite Elements in Geomechanics., Interscience Publication, New York, 1979, pp. 496 - 537.         [ Links ]

Zienkiewicz, O. C. y Taylor, R. L., El método de los elementos finitos., Edit. Mc. Graw-Hill, Barcelona, 1994, pp. 1 - 44, 271 - 298.        [ Links ]

3 Este trabajo se ha desarrollado bajo las restricciones propias de la capacidad del paquete en su versión educativa.
4 ANSYS es un programa comercial de elementos finitos. La información que se presenta en este artículo referente al proceso de optimización con el programa, fue tomada de los manuales de usuario del software.