Deisy Corredor¹, Luis Alfonso Caicedo²

¹ Ingeniera química, M.Sc. en ingeniería química, Universidad Nacional de Colombia, Bogotá, e-mail: dycorredorg@unal.edu.co
² Ingeniero químico, M.Sc. en ingeniería química, Ph.D. en tecnología de procesos bioquímicos, Departamento de ingeniería química, Universidad Nacional de Colombia, Bogotá, e-mail: lacaicedom@unal.edu.co

RESUMEN

El modelo matemático y análisis teórico de reactores biológicos de lecho empacado (PBR) ha sido estudiado por diferentes autores, quienes tuvieron en cuenta variedad de cinéticas de reacción, modelos unidimensionales, homogéneos, pseudohomogéneos y heterogéneos. Las ecuaciones resultantes del modelo fueron solucionadas, en su gran mayoría, por sistemas de métodos numéricos. Se ha analizado en estos el efecto de variables de proceso de importancia física con respecto a parámetros de diseño y operación, como tiempos de residencia, flujos de operación, conversiones de sustrato, área y superficie del biofilm, entre otros.

Palabras clave: reactor empacado, biorreactor, células inmovilizadas, modelamiento, simulación.

ABSTRACT

Several authors have subjected packed-bed biological reactors to mathematical and theoretical analysis. They have taken reaction kinetics and single-dimensional, homogeneous, pseudo-homogeneous and heterogeneous models into account. Numerical methods have provided the set of equations so developed. The effect of physically important process variables in terms of design and operation have been investigated (i.e. residence time, operating-flow, substrate conversion, bio-film area and film thickness).

Keywords: packed-bed reactor, bioreactor, immobilised cells, modelling, simulation.

Recibido: agosto de 2004
Aceptado: septiembre 14 de 2005

Introducción

Se ha demostrado la gran variedad de aplicaciones de los reactores de lecho empacado (PBR) en procesos biológicos, gracias a sus ventajas en tiempo en retención, reutilización del sistema biocatalítico, alta eficiencia y conversiones, fácil operación y bajos costos (Klesser, 1990). Los trabajos realizados en tratamiento de aguas residuales (Young y McCarty, 1969), remoción de amoniaco por Haug y McCarty, 1972, y más recientemente los estudios presentados por Beg y Hassan, 1985 y 1987, son algunos de los ejemplos exitosos de su aplicación.

A pesar del amplio uso que han tenido estos reactores en los procesos biológicos, son relativamente pocos los trabajos que se presentan en cuanto a desarrollo de modelos matemáticos que caractericen el comportamiento de los mismos (Elmaleh et al., 1980; Jennings et al., 1976; Mulcahy et al., 1978).

El análisis matemático y los modelos de simulación ayudan a entender el comportamiento cuantitativo del sistema biológico y a predecir el desarrollo general del biorreactor. Adicionalmente, estos pueden ayudar en la puesta en marcha y finalización de la operación del reactor, a describir la dinámica y las características de control del mismo o estimar los tiempos requeridos para alcanzar nuevos estados estables cuando se presenta una perturbación (Hassam et al., 1995).

Los modelos pueden ser agrupados en “empíricos” (Rittman, 1982), ”semiempiricos” (modelos que incorporan aproximaciones empíricas a las ecuaciones fenomenológicas), o fenomenológicos, que se basan completamente en los fenómenos de transporte y leyes de conservación de masa y energía (Rittman et al., 1982).

Con excepción de los modelos matemáticos para reactores en el área de catálisis química (Carberry y Wendel, 1963), que se originaron décadas antes que aquellos del área de bioprocesos, los modelos matemáticos iniciales presentados para reactores bioquímicos anteriores a la década de los 90 consideraban difusión y velocidades de reacción de cero y primer orden, debido a la simplicidad que se obtenía en la solución del problema matemático. Estos modelos pueden ser resueltos analíticamente, pero son válidos sólo para altas o muy baja concentraciones de sustrato (Skowlun y Kimse, 1989).

Dentro de los autores que más han trabajado en modelos de este tipo se encuentran Hassan y Beg, 1995; Hassan y Beg, 1987, 1985, 1993 y 1995; Caicedo, 1996, quienes introdujeron el modelo de dispersión axial para reactores de biofilm operando a flujo pistón. Sin embargo, en los últimos años un gran número de autores han retomado el modelamiento de estos reactores, intentando hacerlos más generales (Bales y Acai, 1999).

El siguiente artículo pretende hacer una revisión de los más recientes modelos desarrollados para el reactor (PBR), y una conclusión de las simplificaciones supuestas por cada uno de los autores, los mecanismos de reacción asumidos, las cinéticas estudiadas, las diferentes clases de modelos aplicados y la evaluación que se ha hecho hasta la fecha de parámetros de interés prácticos según los resultados obtenidos.

Modelos matemáticos

Modelos matemáticos que consideran biofilm homogéneo

Como se dijo anteriormente, los primeros modelos se desarrollaron bajo consideraciones de reactor de flujo pistón (Elmaleh et al., 1980), reactores CSTR (Jennings et al., 1976) y cinéticas de reacción de orden cero y primero (Mulcahy et al., 1978). Sin embargo, la cinética de reacción en muchas situaciones prácticas sigue la ecuación de velocidad tipo Michaelis Mentem, con o sin inhibición por sustrato.

El trabajo que se desarrolla para tres clases de cinética con mecánicos de inhibición se atribuye a Hassan y Beg, 1987, quienes estudian los siguientes mecanismos de inhibición:

1) Inhibición no competitiva: el grado de inhibición no se ve afectado por las concentraciones de sustrato.

2) Inhibición competitiva: el grado de Inhibición va a depender de la cantidad de sustrato presente. Usualmente el grado de inhibición se reduce a medida que la concertación de sustrato aumenta.

3) Inhibición anti-competitiva: el grado de inhibición puede verse incrementado.

Para obtener las matemáticas apropiadas, usaron las siguientes consideraciones:

- La biomasa es homogénea, es decir, que el lecho empacado de microorganismos actúa conjuntamente para formar un biopelícula en la cual el sustrato se difunde.

- La biopelícula está adherida a una superficie.

- Solamente se tiene un sustrato limitante.

- El sustrato es transferido dentro de la biopelícula por difusión.

Realizan el balance de masa alrededor de un elemento diferencial dentro y fuera de la biopelícula, de acuerdo con las anteriores consideraciones. La ecuación resultante para la biopelícula es:

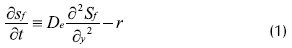
Con las siguientes condiciones límite:

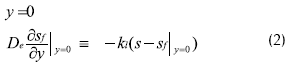
Donde S: concentración de sustrato dentro de la biopelícula (mg L^-1), t: tiempo de reacción (s); D_e: coeficiente de dispersión (cm² s^-1); y: coordenada para la biopelícula (cm); K_L: coeficiente de transferencia de masa (cm s^-1).

Para la fase externa del fluido, el comportamiento se caracteriza por dispersión axial a través de un modelo de reflujo pistón (Bird et al., 1960). Así, presenta la siguiente ecuación:

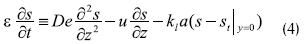
Con las condiciones límite:

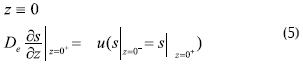
Donde ε: fracción vacía del reactor, z: coordenada axial para el reactor (cm), u: velocidad (cm s^-1), α: área superficial de la biopelícula por unidad de volumen de lecho (cm^-1), L: longitud del reactor (cm).

El sistema de ecuaciones diferenciales con las diferentes expresiones de velocidad de reacción utilizadas se resuelve por medio de un método de colocación ortogonal, para condiciones de estado estable y transiente. Se utilizan ocho puntos de colocación para la fase externa y cuatro para la fase de biopelícula. Los autores aproximan los perfiles de concentración tanto en la fase externa de fluido como en la base de la biopelícula a polinomios no simétricos del tipo:

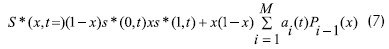
Skowlund y Kirmse, 1989, proponen dos tipos diferentes de modelos de reactor. En el primero consideran, igualmente, que la biomasa es homogénea, es decir, que el lecho empacado de microorganismos actúa conjuntamente para una biopelícula, el cual tiene un espesor constante, y desprecian el efecto difusión dentro del mismo. El segundo modelo supone que el espesor de la capa de biopelícula es dependiente de la concentración de sustrato dentro de é. Esto con el fin de solucionar el problema del perfil de concentraciones de sustrato dentro del reactor.

Para estos casos, los autores proponen innecesario el uso de modelos limitados por difusión, basados en el hecho de que:

- La biopelícula es activa en un intervalo pequeño de espesor (70-100 µm).

- La mayoría de las reacciones biológicas tienen velocidades bajas de reacción.

Para concentraciones bajas de sustrato se demostró que la capa activa de la biopelícula es mucho mejor que la máxima alcanzada y que es dependiente de la concentración de sustrato en el lecho del fluido. Adicionalmente, por debajo de una concentración mínima de sustrato no ocurre crecimiento de la biopelícula, por lo que este se tiene en cuenta para el desarrollo del modelo matemático (Rittman y McCarty, 1980 y 1981).

En coordenadas rectangulares el balance de masa propuesto en la biopelícula es:

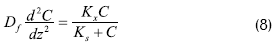
Donde:

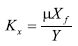
D_f: difusividad del sustrato en la biopelícula

C: concentración de sustrato

Z: coordenada de longitud en el bio-pelet

L: espesor medio del medio de soporte de la biopelícula

δ: espesor activo de la biopelícula

K_s: constante de velocidad de Monod

µ: velocidad máxima de crecimiento

X_f: Concentración de microorganismos en la biopelícula

Y: factor de rendimiento (sustrato-producto)

Las condiciones límite para la ecuación:

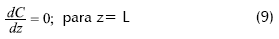
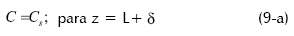
La geometría del pellet homogéneo formador de la biopelícula se toma en cuenta al colocar en forma adimensional la ecuación de balance, ya que se hace necesario minimizar el efecto de la velocidad de reacción de acuerdo a la geometría. Para su cálculo se emplea una longitud característica Vs (Petersen, 1965; Aris Routherform, 1969), la cual va a variar dependiendo si el pellet se considera plano, cilíndrico o esférico de acuerdo a:

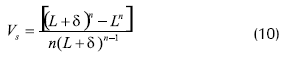
Donde V_s, es el volumen de biopelícula activo por unidad de área superficial de bio-pellet y n es 1, 2, 3 para geometrías planas, cilíndricas y esféricas respectivamente.

Los autores suponen conocida la concentración de sustrato en la superficie, con lo que obtiene la velocidad de reacción para los caso de bio-pellet limitado por difusión de acuerdo a cinética tipo Monod, cinéticas de cero y primer orden, concentraciones bajas y altas de sustrato.

Adicionalmente, en una sección posterior, consideran resistencia difusional entre la fase de lecho y la biopelícula, esto suponiendo concentración de sustrato en la superficie desconocida.

Por último, desarrollan el modelo para una aproximación homogénea, es decir, caso en el cual se supone constante el espesor de la biopelícula, con valor de 100µm. Las soluciones numéricas para las diferentes ecuaciones obtenidas se resuelven por el método Runge Kutta.

Modelos matemáticos para crecimiento celular en pellets

Dos modelos de crecimiento y de fermentación para Saccharomyces cerevisiae inmovilizada en alginato se presentaron en 1990. En el primero de ellos Hannoun y Stephanopoulos, 1990, aplican la teoría de la reacción y difusión a los datos de crecimiento y fermentación obtenidos para Saccharomyces cerevisiae inmovilizada en una membrana de alginato.

Bajo la suposición de velocidad y de metabolismo constantes, obtiene expresiones analíticas y valores que determinan los flujos de glucosa y etanol a través de la membrana. Sin embargo, estos se compararon con datos medios para células en suspensión y se encontraron diferencias importantes.

Los autores, con el fin de satisfacer la suposición de velocidad constante, trabajaron bajo condiciones anaeróbicas y altas concentraciones de glucosa. Sin embargo, notaron que bajo condiciones aeróbicas debido a baja solubilidad del oxígeno y alto consumo del mismo, los gradientes de oxígeno a través de la membrana y la simplificación de velocidad constante, no eran del todo válidas.

Para resolver este problema plantearon entonces un modelo metabólico que tiene en cuenta ecuaciones de velocidad de crecimiento, producción de etanol, consumo de glucosa y oxígeno (Hannoun y Stephanopoulos, 1990). Este modelo se aplicó para simular la fermentación del microorganismo inmovilizado en alginato y en el análisis del microorganismo inmovilizado en un reactor de lecho empacado en operación de estado estable y transiente.

Las suposiciones de los autores para el modelo son:

- Se adiciona al modelo un término para la inhibición por etanol de tipo lineal, debido a que las limitaciones de transporte difusional logran una acumulación significante de etanol en la parte interna de la matriz de alginato.

- La producción de etanol se toma proporcional a la velocidad de consumo de glucosa.

- La utilización de oxígeno se toma idéntica a la velocidad para células suspendidas, haciendo la salvedad de que para las células inmovilizadas el consumo de glucosa es más rápido que para células libres.

- Por datos experimentales obtenidos bajo condiciones aeróbicas se demuestra que la velocidad de consumo de glucosa decrece con la concentración de oxígeno disuelto y asintóticamente se aproxima a la velocidad mínima a altas concentraciones de oxígeno disuelto.

La expresión que describe el consumo de glucosa en el modelo es:

El modelo obtenido es de la forma:

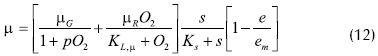
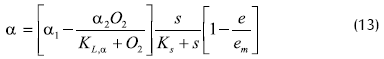
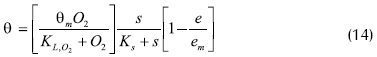
Donde:

α: velocidad específica de consumo de glucosa (h^-1)

K_s: constante de Michaelis para sustrato

K_L: constante de Michaellis para oxígeno

O₂: concentración de oxígeno disuelto

% aire saturado

s: concentración de glucosa (g/L),

e: concentración de etanol

e_m: concentración de etanol límite para crecimiento celular

θ: velocidad específica de consumo de oxígeno (L/g.h)

µ: velocidad específica de crecimiento (h^-1)

p: medida del efecto Pasteur en el modelo.

Las ecuaciones diferenciales parciales para el estado inestable describen la relación y difusión en la membrana de alginato de calcio, utilizando las correspondientes condiciones límite. Se resuelven utilizando el método de Crack-Nicholson (Gerald, 1970) de diferencias finitas.

Aplicaron adicionalmente al análisis en un biorreactor (PBR) empacado con células inmovilizadas, obteniendo resultados acerca del diseño y operación de dichos sistemas para transformaciones bioquímicas. Obviando difusión axial y radial, en una operación con número de Peclet elevado, el balance de masa para cualquiera de los tres componentes se puede escribir como:

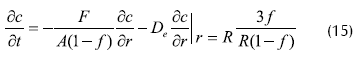
Donde:

F: velocidad de flujo volumétrico

f: fracción de volumen ocupada por los pellets

D_e: coeficientes de difusión (g, glucosa; e, etanol; o, oxígeno)

R: radio de biocatalizador.

Con condiciones límite y de inicio, definidas por las concentraciones de las corrientes límite:

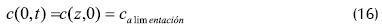
Esta ecuación se usó acoplada a la de reacción y difusión a través de la membrana y se evaluó de acuerdo al método de diferencias finitas de Séller (Keller y Bramble, 1972). El comportamiento del reactor se evaluó sobre la base de productividad de etanol, concentración final de etanol y etanol remanente, obteniendo resultados satisfactorios con el modelo empleado.

El trabajo realizado por Beg et al., 1995, incluye en el modelo el efecto de activadores en la tecnología de catalizador-enzima que pueden alterar la velocidad de reacción de diferentes maneras. Estudiaron siete casos para la activación de la enzima y sus respectivas expresiones para la velocidad de reacción. Las ecuaciones que describen el comportamiento en un reactor de lecho empacado para la biopelícula y la fase externa de fluido son las mismas que las expuestas en su anterior trabajo (Hassam y Beg, 1987), con la salvedad de que el término (r) de la ecuación (1), son las diferentes formas de cinética de reacción dependiendo del mecanismo de activación de la enzima.

Modelos matemáticos considerando bio-pellet esférico

Uno de los primeros trabajos que no considera la biopelícula homogénea, sino los soportes de pellets como un empaque heterogéneo, es el de Gencer y Mutharasan, 1980. Los autores, con el fin de simular la velocidad de cambio en el peso de las células inmovilizadas por unidad de volumen del fermentador y la capacidad de retención para diferentes soportes de inmovilización, realizaron los balances de masa en un reactor tubular empacado, a través de una sección transversal de una columna empacada, obteniendo la siguiente ecuación:

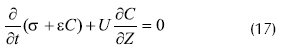
Donde ε: es la porosidad del lecho, C: concentración de células en la suspensión, σ: peso de células entrampadas por unidad de volumen del fermentador, U: velocidad superficial de la solución de células, Z: distancia desde la entrada hasta un determinado tiempo. Reemplazado por variables adimensionales y suponiendo porosidad constante:

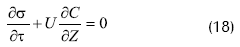
Se atribuye a Hassan et al., 1995, el análisis de un reactor no isométrico en el cual se llevan a cabo los siguientes fenomenitos de transporte:

- Transferencia de sustrato y calor desde el lecho del fluido hasta la superficie del biocatalizador inmovilizado.

- Transferencia de calor de la fuente a la pared del reactor.

- Difusión simultánea y reacción del sustrato dentro del biocatalizador.

Estos investigadores analizaron un reactor empacado con enzima encapsulada de forma esférica. El modelamiento se hizo en términos de parámetros adimensionales de cinética y transporte. El estudio demostró que las partículas de biocatalizador pueden ser consideradas isotérmicas.

Para realizar el modelo matemático, supusieron las siguientes simplificaciones:

- La temperatura del reactor es constante.

- La resistencia de la membrana a cualquier proceso de transporte es insignificante.

- La temperatura del alimento es constante.

- La reacción entre sustrato y la enzima sigue la cinética de Michaellis-Menten sin inhibición de producto y sustrato.

- La actividad enzimática es uniforme a través de la partícula.

- La distribución de las partículas del biocatalizador es uniforme a lo largo del birreactor.

- La caída de presión a través del reactor, el gradiente de concentración radial en el lecho del fluido y otros efectos mecánicos, son insignificantes.

- Todas las propiedades físicas y de transporte se hacen constantes, excepto las constantes de velocidad.

Con las simplificaciones asumidas, el balance diferencial de masa para sustrato en estado inestable, tanto en la partícula de enzima inmovilizada como en el lecho de fluido (Bird et al., 1960), es:

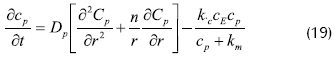
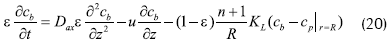
El balance de energía en estado inestable para la partícula de enzima inmovilizada daría la siguiente ecuación:

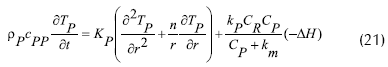
Donde c_p: concentración de sustrato dentro de la partícula, c_b:concentración de sustrato en el lecho del fluido, c_pp: capacidad calorífica para la solución de enzima, C: concentración adimensional (E, enzima; P, sustrato), D_P: coeficiente de difusión en la partícula de biocatalizador, D_ax:coeficiente de dispersión axial, r: coordenada adimensional de la partícula esférica, R: radio de la partícula esférica, ε: fracción vacía de lecho (0.4), T_p: temperatura adimensional para la solución de enzima, ρ_P: densidad solución de enzima, K_L: coeficiente de transferencia de masa externa, K_P: conductividad térmica intraparticular, k_m: constante de Michaellis-Menten, k_P: constante de velocidad de reacción de enzima.

De igual forma, presentan el balance de energía en estado inestable para el lecho del fluido.

El modelo se soluciona por el método de colocación ortogonal, y el procedimiento de solución se describe por Hassan y Beg, 1987 y por Finlayson, 1972. El modelo se solucionó con ecuaciones de Michaellis-Mentem convertida a orden cero y primer orden, haciendo K << C_P, y K >> C_p respectivamente.

En estos trabajos anteriores se ha tenido en cuenta para la elaboración del modelo el crecimiento celular y la utilización del sustrato, combinados con los procesos de reacción y difusión involucrados. Sin embargo, son pocos los trabajos que consideran el posible “escape” de biomasa del soporte y se ha demostrado experimentalmente que se presentan casos en los cuales esta decrece debido a este fenómeno de escape (Wijffels et al., 1998).

Laca et al., 1988, en su modelo, consideraron para sustrato, producto y células, procesos de difusión, reacción, crecimiento celular y posible escape de las células del soporte. En este trabajo, tuvieron en cuenta con dos tipos de modelos, el de difusión de poros y el homogéneo, con el fin de simular la evolución del sustrato y las células, incluyendo su difusión interna y externa.

El concepto de “difusividad celular” (Quirós et al., 1995), que considera el cambio de posición de las células, ajustado a una ley de tipo Fick, incluye un amplio número de fenómenos como convención, sedimentación, efectos inerciales y movilidad celular. Debido a esto, los modelos desarrollados no solo tienen en cuenta el consumo de sustrato y formación de biomasa sino que también la difusión de sustrato de la fase líquida a la esfera y la difusión de biomasa de la esfera a la fase liquida. El modelo se puede aplicar a métodos de inmovilización como entrampamiento, agregación y contención.

Con el fin de estudiar la evolución de la concentración de sustrato y biomasa dentro del soporte se usan dos formas de modelamiento: “modelo de difusión de poro (Froment y Bischoff, 1990; Caicedo et al., 1987; Bird et al., 1960)” y “modelo homogéneo” (Froment y Bischoff, 1990; Conde y Boyacá, 1994). La diferencia básica entre los dos es que el primero considera que el soporte es una estructura heterogénea en la que los poros están distribuidos, siendo la parte interna de estos poros donde el soluto se localiza. Existe difusión tanto de sustrato como biomasa desde la parte exterior a la interior del soporte, a través del líquido contenido en los poros. El segundo modelo supone que el soporte es un medio continuo a través del cual existe el proceso de difusión.

Las ecuaciones correspondientes a los dos modelos se presentan a continuación:

• Modelo de difusión de poro

- Balance de masa dentro del soporte

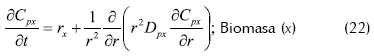
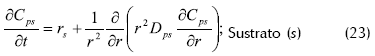
Donde r_j es la velocidad de reacción del componente x o s dentro de los poros, C_pj la difusividad del componente j dentro de los poros y r las coordenadas radiales del soporte que se supone como esférico.

- Balance de masa dentro del reactor

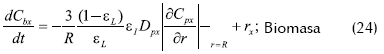
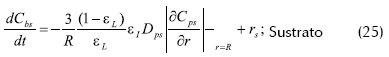
Donde R es el radio promedio de las partículas esféricas, C_bj la concentración del componente j en el medio líquido, ε_L La porosidad del lecho, la porosidad de la partícula y r_j, la velocidad de reacción el componente j en el medio líquido.

• Modelo homogéneo

- Balance de masa dentro del soporte

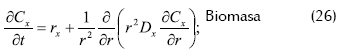
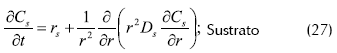
Donde r_j es la velocidad de reacción del componente j dentro del soporte, C_j la concentración del componente j en el soporte y D_j la difusividad efectiva del componente j en el soporte.

- Balance de masa en el reactor

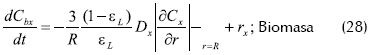
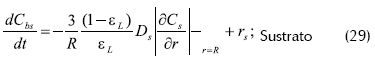
La condición inicial es:

Mientras que la condición límite dentro del soporte, aplicando la simetría:

En r = R, las condiciones límite para el sustrato pueden depender de la existencia o no de agitación externa alrededor de la partícula como función de una turbulencia externa local.

Así, de esta manera, se tiene como condiciones límite para el caso de no presentar resistencia, es decir, cuando la concertación de sustrato en los poros en la superficie del soporte es la misma que en el medio líquido:

Con resistencia, cuando la concentración de sustrato no es la misma en la superficie del soporte que en el medio líquido:

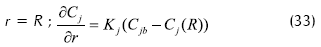
Donde:

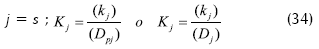
Dependiendo del modelo a usar, donde k_j es el coeficiente de transferencia en la parte externa de la película.

El artículo presenta diferentes formas de aplicar el modelo en las vías de inmovilización conocidas (Webb, 1989). Lo resuelven considerando cinética de Monod:

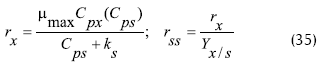
Entre los últimos modelos trabajados se puede hablar del desarrollado por Bales y Acai, 1999, quienes logran la simulación de un reactor empacado con células de Saccharomyces cerevisiae, inmovilizadas en alginato de calcio, teniendo en cuenta como sistema de modelamiento la hidrólisis de la sacarosa y presencia de actividad de la invertasa.

El objetivo fundamental fue desarrollar y aportar un modelo matemático que describiera el funcionamiento de reactores de células inmovilizadas (ICR), en los cuales se consideró la cinética de reacción y la influencia en la resistencia debida a la transferencia de masa, es decir, la influencia del coeficiente de difusión tanto interna como externa y la dispersión axial.

El modelo matemático se basó en el balance de materia para el sustrato en la corriente de fluido y el balance de materia para el sustrato en la partícula. La ecuación escogida para la velocidad de reacción expresa inhibición por sustrato. El conjunto de ecuaciones diferenciales parciales se resolvió a partir de un método de colocación ortogonal y se analizaron los efectos de los coeficientes de difusión interna y externa con respecto a la concentración adimensional de sustrato.

Para lo anterior, los autores supusieron una serie de simplificaciones desarrollando un modelo básico. Estas simplificaciones son las siguientes:

- Se considera la presencia de un único sustrato en la corriente de fluido.

- Velocidad de flujo constante a través del reactor.

- Las partículas del lecho empacado se suponen pseudoshomogéneas, de forma esférica y el coeficiente de difusión efectiva constante.

- Se considera actividad de la enzima invertasa.

- La sección transversal del reactor y el espacio vacío del lecho son constantes.

- No se considera dispersión radial.

- Temperatura constante a lo largo del reactor.

Con lo anterior, el balance de masa para el sustrato en el fluido y en la partícula se expresa de acuerdo a las dos siguientes ecuaciones (Froment y Bischoff, 1990):

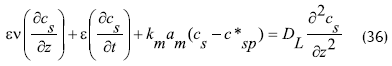
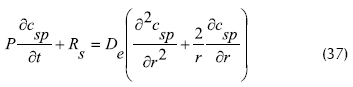
Donde:

ν: velocidad intersticial

k_m: coeficiente de transferencia de masa externo (difusión externa)

a_m: área especifica del biocatalizador

C_s: concentración de sustrato en el líquido

C*_sp: concentración de sustrato en la superficie de la partícula

C_sp: concentración de sustrato en el seno de la partícula

P: porosidad de la partícula

D_L: coeficiente de dispersión axial

R_s: es la velocidad de reacción de la forma:

El siguiente es el análisis de condiciones límites e iniciales para el lecho y la partícula:

Condiciones iniciales para el lecho

Condiciones límite para el lecho

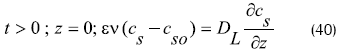
Condiciones iniciales para la partícula:

Condiciones límite para la partícula:

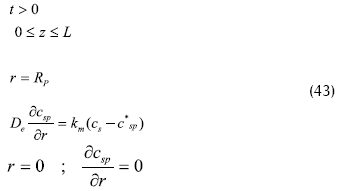
La solución de las ecuaciones parciales se aproximó a un polinomio ortogonal de Legrange, con funciones de peso en puntos de colocación ortogonal redujo el sistema a un modelo de ecuaciones diferenciales de primer orden integrado por la modificación de Merson del método de Runge-Kutta. Para evaluar el desarrollo del reactor se dieron valores numéricos a los parámetros.

Análisis dinámico y de perturbación

Debido a que los procesos industriales no están exentos de perturbaciones en los parámetros de procesos industriales, Gupta y Chand, 1990, iniciaron estudios de análisis dinámicos en este tipo de reactores. Para describir la respuesta dinámica del sistema, los autores suponen:

- No existe influencia del lecho empacado en la reacción a excepción de su contribución en el mezclado axial.

- No existen gradientes de temperatura (radiales o longitudinales).

- Existe un equilibrio dinámico entre las células que crecen y aquellas que se consideran salen, es decir, las concentraciones de las células activas permanecen constantes.

A través de la resolución de las ecuaciones de balance obtenidas por estas simplificaciones, los autores lograron determinar los cambios que experimentan la concentración de salida de azúcar y la productividad, debido a perturbaciones o alteraciones en la concentración de azúcar inicial y en la velocidad de flujo de alimentación.

Un análisis hidrodinámico de un reactor de lecho empacado de uso industrial en la industria cervecera se realizó en 1994, a cargo de Sarraut et al., quienes hicieron aproximaciones clásicas en el bio-rreactor y se enfocaron en el análisis de la distribución de tiempos de residencia (RTD) con el fin de aplicarlo desde un punto de vista de control del proceso.

Aunque el análisis RTD se usa ampliamente en el estudio de reactores químicos, es muy poco lo que se ha aplicado en sistemas biológicos. En este tipo de sistemas se deben considerar modelos de flujo no-ideales debido a la existencia de mezclado radial incompleto y presencia de regiones estancadas. Se utiliza el RTD como impulso de respuesta del sistema y a través de este encontrar el modelo lineal del sistema dinámico.

El análisis de perturbación triangular debido a concentración y temperatura en un reactor de lecho empacado biológico fue realizado igualmente por Hassan et al., 1995. Este análisis se efectúa para cinéticas de cero y primer orden, así como para Michaelis-Menten. Las ecuaciones se resuelven por el método de colocación ortogonal. Para este análisis se tuvieron en cuenta los fenómenos de transporte de agua y sustancias dentro del reactor y el transporte de gases que toma parte en el proceso biológico.

Sin embargo, común para todos los reactores es lo que ocurre dentro del lecho. El sustrato es llevado hacia la biopelícula de diferentes formas, pero dentro de él, debe ser transportado en forma soluble hacia los microorganismos, donde se lleva a cabo la reacción, y los productos de la reacción ser conducidos hacia fuera nuevamente.

En el modelo que los autores plantean, el sustrato se transporta desde el lecho del fluido hasta la capa externa y de esta hacia el interior de la biopelícula por difusión, seguida de reacción dentro del mismo.

Las simplificaciones que se hicieron al respecto fueron:

- La biopelícula es homogénea y de geometría plana.

- Solo existe presencia de un solo sustrato.

- El flujo dentro del lecho se aproxima al modelo de dispersión axial.

Las ecuaciones de balance trabajadas tanto para el lecho de fluido como para la fase de la biopelícula, son las mismas que trabajaron en su anterior trabajo (Hassam y Beg, 1987), con la modificación de que la concentración de sustrato para análisis de perturbación varía de manera triangular de la forma:

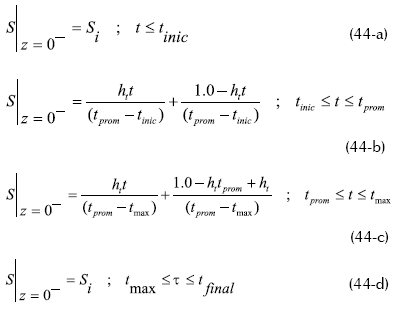
De igual manera, realizaron la consecuente variación para la perturbación triangular de la temperatura, describiéndola a través de las apropiadas relaciones matemáticas.

Conclusiones

En la literatura se presenta variedad de modelos matemáticos que intentan caracterizar el comportamiento de las células inmovilizadas en matrices de alginato de calcio para diferentes procesos.

Estos modelos han tenido en cuenta desde sus inicios, fenómenos tales como dispersión, difusión y convección, entre otros. Se han analizado biorreactores a través de modelos clásicos como son el de “difusión de poro” y el “homogéneo”, considerando reactor de flujo pistón, hasta más complicados, como son los “modelos heterogéneos”.

Todos ellos difieren entre sí, ya que dependen de la geometría del reactor a analizar, las variables de operación que se trabajen, el microorganismo inmovilizado, la cinética y simplificaciones escogidas para el proceso en sí. Es por esto que se hace necesario para un diferente proceso o biorreactor a modelar, generar un nuevo modelo, dependiendo de la complejidad y acercamiento a la realidad que se requiera para la simulación del proceso.

De igual forma, se han aplicado al crecimiento celular cinéticas de cero y primer orden, así como otros más elaboradas como son los modelos tipo Michaellis-Menten y de Monod, y esquemas de modelo no solo de balances de masa y sustrato sino también para reactores no isotérmicos, aplicando balances de energía y de momentum. La resolución es casi siempre de tipo numérico, empleando para ello métodos familiares como colocación ortogonal, Runge-Kutta y Kéller.

Bibliografía

Aris, Routherform, Elementary chemical reaction analysis., Prentice-Hall, N.J., 1969.        [ Links ]

Bales, V., Acai, P., Mathematical analysis of the performance of a packed bioreactor with immobilised cells., Recents Progress en Genierdes Procedes, 13, 71, pp. 335-342, 1999.        [ Links ]

Beg, S.A., Hassam, M., Effects of inhibitors on nitrification in a packed bed biological flow reactor., Water Res., 21, pp. 191-198, 1987.        [ Links ]

Beg, S.A., Hassam, M., Nitrification studies in Bubble aerated packed bed reactor., J. Environ. Sci. Health, Part A, 20, pp. 315-336, 1985.        [ Links ]

Beg, S.A., Hassam, M.M., A Bio-film model for packed-bed reactors considering diffusion resistance and back-mixing effects., Chem. Engineer Journal, 30, pp. B1-B8, 1985.        [ Links ]

Beg, S.A., Hassam, M.M., Jamal, N.A., Modelling the effects of enzyme activation on the performance of a packed bed biological reactor., J. Environm. Sci. Health, A28, 7, pp. 1519-1543, 1993.        [ Links ]

Beg, S.A., Hassam, M.M., Chaudry, S.A., Response of a packed bed biological reactor to perturbation feed concentration and temperature., Intern. J. Envirom. Studies, 49, pp. 31-52, 1995.        [ Links ]

Bird, R.B., Stewart, W.E., Lightfoot, E.N., Transport Phenomena., Wiley and sons, N.Y, 1960.        [ Links ]

Caicedo, L.A., Estudio comparativo de generación de CO² en fermentaciones con células libres e inmovilizadas de Zymomonas mobilis., Ingeniería e Investigación, 34, pp. 23-26, 1996.        [ Links ]

Caicedo, L.A., Torres, J., Vargas, G., Principios para el diseño de reactores bioquímicos de células inmovilizadas., Universidad Nacional de Colombia, chapter 4, 1987.        [ Links ]

Carberry, J.J., Wendel, M.M., Computer model of the fixed catalytic reactor., A.I.Ch.E. Journal, 9, pp. 129-133, 1963.        [ Links ]

Conde, A., Boyacá A., Reactores trifásicos de lecho fijo., Universidad Nacional de Colombia, 1994.        [ Links ]

Elmaleh, S., Labaquere Y Ben Aim, R., Title., Water Res., 12, 41, 1980.        [ Links ]

Finlayson, B.A., The method of weighted residuals and variation principles., Academic Press, N.Y., 1972.        [ Links ]

Froment, G., Bischoff, K., Chemical Reactor Analysis and Design., John Wiley and Sons, chapter 3, 1990.        [ Links ]

Gencer, M., Mutharasan, R., Ethanol fermentation in a yeast immobilised column fermentor., Advances in Biotechnology Proc. Int. Ferm. Symp., 97, pp. 627-633, 1980.        [ Links ]

Gerald, C.F., Applied numerical analysis., Addison Wesley, N.Y., 1970.        [ Links ]

Guota, S.K., Chand, S., Bioconversion of sugars in an immobilised cell packed bed bioreactor; dynamic response to perturbations in process parameters., The Chem. Eng. Journal, 43, pp. B1-B12, 1990.        [ Links ]

Hassam, M.M., Atiqullah, M., Beg, S.A., Analysis of non-isothermal tubular reactor packed with immobilized enzyme systems., The Chem. Enginner Journal, 58, pp. 275-283, 1995.        [ Links ]

Hassam, M.M., Beg, S.A., Theoretical analysis of a packed-bed biological reactor for various reaction kinetics., The Chem. Engineer Journal, 36, pp. B15-B27, 1987.        [ Links ]

Hannoun, B.J., Stephanopoulos, G., Title., Biotechnol. Prog., 6, pp. 349-356, 1990.        [ Links ]

Hannoun, B.J., Stephanopoulos, G., Growth and fermentation model for alginate-entrapped Sacharomyces cervisiae., Biotechnol. Prog., 6, pp. 349-356 1990.        [ Links ]

Haug, R.T., McCarty, P.L., Nitrification with the submerged filter., J. Water Poll. Control Fed., 41, pp. 2086- 2098, 1972.        [ Links ]

Jennings, P., Snoeyink, V. y Chain, S., Theoretical model for a submerged biological filter., Biotechnol. Bioeng., 18, pp. 1249-1273, 1976.        [ Links ]

Keller, H.B.A., Bramble, J., Numerical solutions of partial differential equations., Academic Press, N.Y., 1972.        [ Links ]

Klesser, T., Oertzen, G.A. y Bauer, W., Title., Chem. Eng. Technol, 13, 20, 1990.        [ Links ]

Krishna, R., Ramachandran, P.A., Title., J. Appl. Chem. Biotechnol., 25, pp. 623-640, 1975.        [ Links ]

Laca, A., Quirós, C., García, L., Díaz, M., Modelling and description of internal profiles in immobilised cell systems., Biochemical Engineering Journal, 1, pp. 225-232, 1988.        [ Links ]

Mulcahy, L., Shieih, W. y La Motta, E., Title., Prog. Water Technol., 12, 41, 1978.        [ Links ]

Petersen, E.E., Chemical reaction analysis., Prentice-Hall, N.J, 1965.        [ Links ]

Quirós, C., Rendueles, M., García, L.A., Diffusion of micro-organism in calcium alginate beads., Biotechnol. Tech., 9, 11, pp. 809-814, 1995.        [ Links ]

Rittman, B.E., Comparative performance of bio-film reactor types., Biotechnol. Bioeng., 24, pp. 1341-1370, 1982.        [ Links ]

Rittman, B.E., Strubler, C.E., Ruzicka, T., Anaerobic filter pre-treatment kinetics., J. Environ. Eng. Div, Am. Soc. Civ. Eng., 108, pp. 900-912, 1982.        [ Links ]

Rittman, B.E., McCarty, P.L., Model of steady state bio-film kinetics., Biotechnol. Bioeng., 22, pp. 2343-2357, 1980.        [ Links ]

Rittman, B.E., McCarty, P.L., Substrate flux into bio-film of any thickness., J. Environ. Eng. Div., A.S.C.E., 107, pp. 831-849, 1981.        [ Links ]

Sarraut, P., Cheruy, A., Lenoel, M., Shingleton, M., Ruhaut, L., Hydrodynamic modelling of a packed bed bioreactor used in brewing industry with a view to process control., Automatic Control of Food and Biological Process Development in Food Science, 36, pp. 243-249, 1994.        [ Links ]

Skowlun, C.C.T., Kimse,D.W., The simplified models for packed-bed bio-film reactors., Biotechnol. Bioeng., 33, pp. 164-172, 1989.        [ Links ]

Webb C., The role of cell immobilisation un fermentation technology., Aust. J. Biotechnol., 3, pp. 50-62, 1989.        [ Links ]

Wijffels, R.H., Gooijer, C.D., Scheper, A.W., Beuling, E.E., Maleé, L.F., Dynamic modelling of immobilised Nitrosomonas europea: implementation of diffusion limitation over expanding micro-colonies., Enzyme Microb. Technol., 17, pp. 225-232, 1998.        [ Links ]

Young J.C., McCarty, P.L., The anaerobic filter for waste treatment., J. Water Poll. Control Fed., 41, pp. R160-173, 1969.        [ Links ]