Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.26 no.1 Bogotá Jan./Apr. 2006
Hector Armando Durán Peralta1 y Luis A. Caicedo Mesa2
1 M.Sc. en ingeniería química, profesor del Departamento de Ingeniería Química, Universidad Nacional de Colombia, Bogotá. haduranp@unal.edu.co
2 Ph.D. en procesos bioquímicos. M.Sc. en procesos químicos. Profesor del Departamento de Ingeniería Química, Universidad Nacional de Colombia, Bogotá. lacaicedom@unal.edu.co
RESUMEN
En el diseño de hornos y dispositivos que calientan o enfrían sistemas mediante radiación se necesita calcular el factor de forma, el cual permite determinar la transferencia de calor por radiación entre superficies que estén a diferente temperatura. Generalmente los textos de transferencia de calor deducen y muestran la ecuación para obtener el factor de forma entre dos superficies que intercambian calor por radiación para configuraciones muy sencillas, pero no muestran cómo se hace el cálculo para geometrías y configuraciones un poco más complejas. Muchos de los estudiantes que han cursado la asignatura o asignaturas de transferencia de calor quedan con la impresión de que los factores de forma se calculan sin ningún problema. Otros preguntan por qué en los textos no muestran cómo se calcula el factor de forma para configuraciones un poco más complejas o más reales. Este documento pretende responder esa inquietud, además de presentar como objetivo una estrategia de cálculo con fines netamente pedagógicos que puede ser aplicada a otras configuraciones más complejas.
Palabras clave: factor de forma, transferencia de calor, emisión, Montecarlo
ABSTRACT
The form factor must be calculated when designing ovens and mechanisms heating or cooling systems by radiation, leading to determining heat transfer by radiation between surfaces which are at different temperatures. Heat transfer texts generally deduce and show the equation for obtaining the form factor between two surfaces which exchange heat by radiation for very simple configurations, but do not show how slightly more complex geometries and configurations are calculated. Many students who have studied heat transfer have the impression that form factors are calculated without any difficulty. Other students ask why the texts do not show how to calculate the form factor for slightly more complex configurations or for those which are more real. This document tries to answer these disquietudes as well as presenting a calculation strategy for purely pedagogical ends which can be applied to more complex configurations.
Keywords: form factor, heat exchange, emission, Montecarlo.
Recibido: agosto 12 de 2005
Aceptado: enero 23 de 2006
Introducción
La transferencia de calor es un fenómeno que presenta gran aplicación en la industria y que ha recibido suma atención desde el punto de vista teórico-práctico. En el diseño de hornos y dispositivos que calientan o enfrían sistemas mediante radiación se necesita calcular el factor de forma, el cual permite determinar la transferencia de calor por radiación entre superficies que estén a diferente temperatura. Generalmente los textos de transferencia de calor deducen y muestran la ecuación para obtener el factor de forma entre dos superficies que intercambian calor por radiación para configuraciones muy sencillas, pero no muestran cómo se hace el cálculo para geometrías y configuraciones un poco más complejas. Muchos de los estudiantes que han cursado la asignatura o asignaturas de transferencia de calor quedan con la impresión de que los factores de forma se calculan sin ningún problema. Otros preguntan por qué en los textos no muestran cómo se calcula el factor de forma para configuraciones un poco más reales o complejas. Este documento, a través de la solución de un caso particular aparentemente sencillo (cálculo del factor de forma de la configuración plano-esfera) pretende responder en parte a esta inquietud, y propone lineamientos generales sobre una estrategia de cálculo con fines netamente académicos.
Dentro de los mecanismos de transferencia se tienen: conducción, convección y radiación, siendo este último el que ha merecido, relativamente, menor atención en la literatura, a pesar de sus importantes aplicaciones industriales como hornos de arco, colectores y hornos solares, enfriamiento de cuerpos incandescentes (tuberías, piezas de fundición, etc.) y cálculo de barreras de protección, entre otras.
La radiación es un fenómeno que sucede en todos los cuerpos sólidos y corresponde a la emisión espontánea de ondas electromagnéticas, en todas las longitudes de onda, pero que presenta un intervalo de emisión (de longitudes de onda) preferencial, que depende de la temperatura del cuerpo. Es por esto que un cuerpo a temperatura ambiente emite principalmente radiaciones en el espectro no visible, mientras que a altas temperaturas (500°C a 2.000°C) predomina el espectro visible.
Cuando se tienen dos superficies, cada una emite energía radiante (según su nivel de temperatura) hacia los alrededores, y parte de ella es interceptada por la otra. La relación entre la energía interceptada por una superficie y la total emitida por la otra, es lo que se conoce como factor de visión o factor de forma. Por esta razón, los factores de forma dependen de la geometría y configuración entre las superficies (Holman, 1998 y Mills, 1995) y de los ángulos, respecto de la normal de la superficie, conque son emitidas las radiaciones en cada punto. Estos ángulos en el presente documento se denominarán ángulos de visión.
El cálculo del flujo de calor por radiación, en estos casos, se realiza mediante ecuaciones de balance de energía que incluyen el factor de forma, el cual puede calcularse a partir de la ecuación 1 (Mills, 1995).
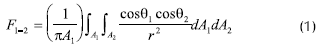
El presente artículo tiene como objetivo mostrar una estrategia para calcular el factor de forma ilustrado con un caso particular (plano-esfera), y como objetivo secundario solucionar la ecuación del factor de forma para el caso del calentamiento de la pared de un horno mediante un arco esférico, aplicando el método de Montecarlo.
Desarrollo del modelo
Como modelo de análisis para calcular el factor de forma se ha escogido el sistema compuesto por una superficie esférica y un plano, el cual se esquematiza en la Figura 1.
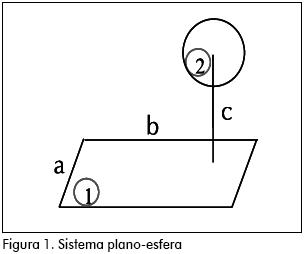
En este esquema, la superficie plana-1 de dimensiones axb, representa la pared del horno, la superficie esférica-2, radio R representa el arco voltaico, y la separación entre ellas se designa por -c-.
Para la solución de la ecuación 1, se requiere en cada caso particular determinar los límites y la relación entre las variables que intervienen. La estrategia a seguir para calcular el factor de forma se puede resumir en tres pasos:
1) Determinar los límites de las integrales.
2) Determinar los cósenos de los ángulos de visión en términos de las variables de integración.
3) Solución de la integral múltiple mediante un método matemático adecuado, que para nuestro caso será el método de Montecarlo.
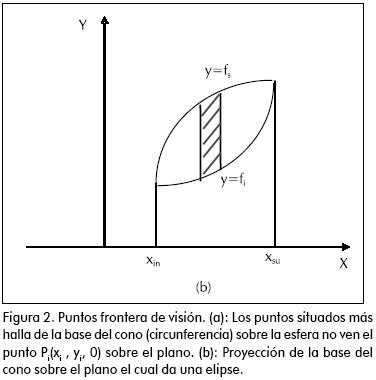
Para la solución nos basaremos en el esquema presentado en la Figura 2, donde: un punto sobre la esfera se denota como p(x,y,z) y uno sobre el plano como pi(xi,yi,0); r es la distancia recorrida por el rayo emitido desde el punto emisor pi(xi,yi,0) hasta el receptor p(x,y,z) o viceversa; θ1 es el ángulo de visión formado entre la normal a la superficie del plano en el punto p(x,y,z) y r; θ2 es el ángulo de visión formado entre la normal a la superficie esférica en el punto (x,y,z) y la línea r.
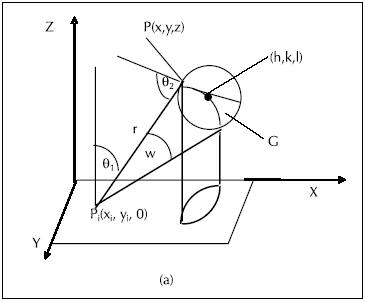
Las coordenadas (x,y,z) corresponden al dominio sobre la esfera G de radio R y centro (h,k,l) cuya ecuación es:
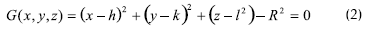
Un elemento de área en el plano calculado en términos de xi,yi viene dado por:
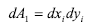
y un elemento de área en la superficie esférica calculado en términos de x,y viene dado por:
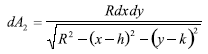
Sustituyendo los elementos de área dA1,dA2 en la integral, resulta en definitiva una integral cuádruple evaluada sobre una región R:
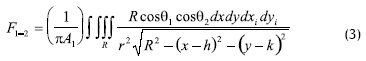
Determinación de los límites de las integrales
Si se toma un punto pi(xi,yi,0) del plano este emite energía radiante en todas las direcciones, con la misma intensidad, es decir, en forma difusa ideal. La primera integral de derecha a izquierda de la ecuación 1 representa la parte de esta energía que emite el punto pi y que es interceptada por la esfera. En la Figura 2 el ángulo sólido (w) abarca la energía emitida desde el punto pi, y forma un cono generado por los rayos emitidos desde pi y llegan a la esfera quedando el cono tangente a la esfera, es decir, el ángulo sólido abarca el espacio limitado por el cono tangente a la esfera y cuyo vértice es el punto pi(xi,yi,0) situado en el plano. Los límites geométricos para la primera integral en la ecuación 1 estarán dados de acuerdo con la ecuación para dA2, siendo esta la elipse resultante de la proyección de la base del cono tangente (circunferencia) sobre el plano. La ecuación rectangular de la base del cono en el espacio R3, es la resultante de la intersección de la esfera (ecuación 2) y el cono tangente (ecuación 4):
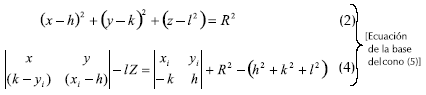
De las dos ecuaciones anteriores es posible eliminar z para obtener la ecuación de la proyección de la circunferencia sobre el plano, resultando:
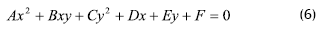
Para resolver la ecuación 3 se integra inicialmente con respecto de y, que corresponde a la ordenada de los puntos sobre la superficie de la esfera, y en consecuencia los límites quedan en función de (xi,yi,x). Partiendo de la ecuación 6, se establecen los límites de integración superior e inferior para y, que corresponden a las funciones fi(x,xi,yi) y fs(x,xi,yi), definidas como:
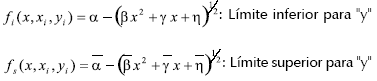
Donde: α,β,γ,η y 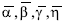 dependen de xi,yi
dependen de xi,yi
Para resolver la segunda integral se deben establecer los límites de x, los cuales corresponden al máximo y mínimo valor de x en la proyección de la base del cono con vértices en pi(x,xi,0) sobre la del plano. El tamaño del intervalo de integración para x depende de la proyección de la circunferencia sobre el plano. En la Figura 2b puede verse que los límites para x son xin,xsulos cuales dependen de la posición del punto pi(xi,yi,0). Los demás límites de las integrales no presentan problema. Reemplazando en la ecuación 3 resulta:
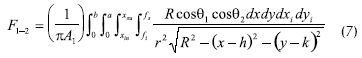
Donde
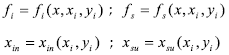
Establecidos los límites de la integral múltiple, el paso siguiente es determinar el coseno de los ángulos de visión.
Determinación de los cósenos de los ángulos de visión (Cos θ1 y Cos θ2)
Con base en la Figura 3 se establecen geométricamente las siguientes expresiones para los cosenos de los ángulos de visión en función de x,y,xi,yi
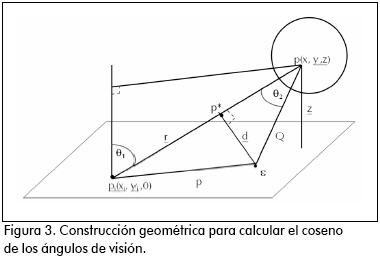

Donde
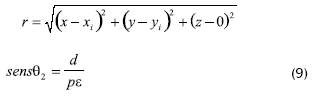
Donde pε es la distancia entre los puntos p y ε que corresponde a la intercepción normal a la esfera en el punto p con el plano. Por lo tanto,
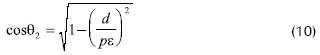
Y la distancia entre los dos puntos será
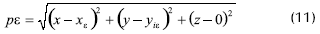
Si se designa como d la distancia entre p*, que es el pie de la perpendicular a r que pasa por ε y aplicamos la fórmula de distancia entre dos puntos (Lehman, 1997) se tendrá:
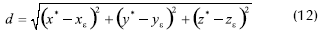
Según lo muestra la Figura 3, zε está en el plano horizontal coordenado, el cual tiene posición z=0, y por lo tanto zε=0
Es importante observar que los ángulos θ1 y θ2 mostrados en la Figura 3 no están en un mismo plano.
El cálculo de las coordenadas del punto ε y p* puede realizarse utilizando conceptos de geometría analítica en el espacio, y ellos están consignados en el Apéndice. Estas coordenadas son:
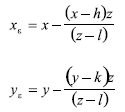
Y zε anteriormente se dijo cómo se determinó, dando el valor
Al calcular las coordenadas del punto p*(x*,y*,z*) estas quedan expresadas implícitamente con el siguiente sistema de ecuaciones:
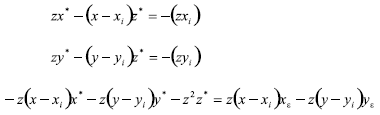
La solución analítica de estas tres ecuaciones dará expresiones voluminosas para x*,y*,z*, por lo cual se solucionan numéricamente dentro del desarrollo del programa.
Determinados los puntos ε(xε,yε,0), p*(x*,y*,z*), y las distancias pε y d, que corresponden al segmento pε*, se pueden calcular los cosenos de los ángulos de visión mediante las expresiones 8 y 9. Estos cosenos se determinan numéricamente en el programa del cálculo del factor de visión (FVIS).
Una vez expresados los cosenos de los ángulos θ1 y θ2 en función de las variables x,y,xi,yi, se reemplazan en la ecuación 7, la cual queda lista para ser integrada, y su solución dará el factor de forma plano-esfera. Si se efectúan las sustituciones indicadas en la ecuación 7 la expresión bajo la integral múltiple resultaría muy voluminosa, por ello la integral 7 se resuelve con el programa numéricamente y utilizando el método de Montecarlo.
Cálculo del factor de visión mediante la integral F1-2 empleando el método de Montecarlo (algoritmo del programa FVIS)
Normalmente, para evaluar integrales múltiples en dimensiones hasta dos e incluso tres se utilizan métodos como el de Simpsom, cuadratura Gaussiana, integración de Romberg, etc, (Carnahan, 1969). La experiencia muestra que para evaluar integrales múltiples en dimensiones mayores a tres los métodos tradicionales se vuelven muy lentos debido a la gran cantidad de cálculos a efectuar (Burden, 1996). En estos casos se recurre a los métodos probabilísticos, como por ejemplo, el método de Montecarlo.
La integral del factor de visión es una integral múltiple en dimensión 4, por ello su evaluación se efectuará mediante el método de Montecarlo. Para este caso se utilizará la versión de Montecarlo del disparo aleatorio hacia un blanco fijo (Sobol, 1983).
La Figura 4 muestra el algoritmo de cálculo para determinar el factor de visión del arreglo plano-esfera. En términos generales, el algoritmo permite calcular los límites variables de la integral múltiple, como son: fi(x,xi,yi), fs(x,xi,yi), xin(xi,yi), xsu(xi,yi); calcula también los puntos p,ε* que permiten evaluar el coseno de los ángulos de visión. Y finalmente evalúa la integral F1-2, la cual determina el factor de visión.
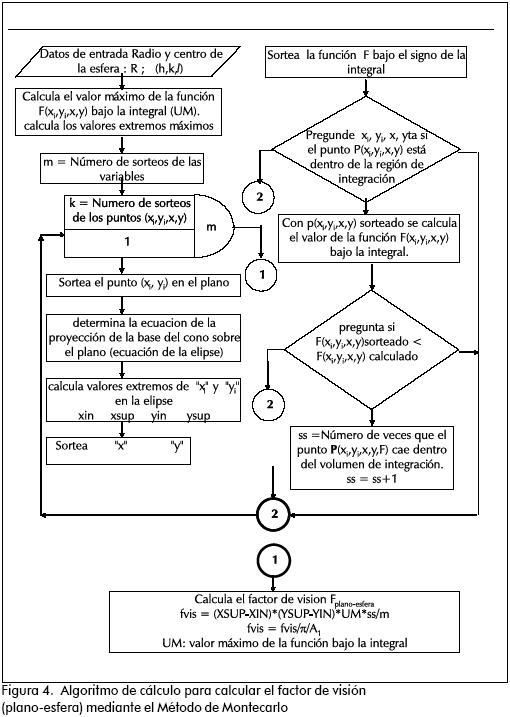
Este algoritmo corresponde al programa FVIS, que permite calcular el factor de visión de la configuración plano-esfera. Las instrucciones del programa están escritas en MATLAB versión 4.0 para Windows*. El programa FVIS fue ejecutado para calcular F1-2 en los parámetros geométricos mostrados en la Figura 1. Resultados para diferentes valores de estos parámetros se encuentran en la Tabla 1. En el método de Montecarlo se realizan sorteos para calcular la integral, cuyo número se puede fijar en el programa; para los cálculos del factor de visión de acuerdo con los parámetros seleccionados se fijaron 200 sorteos. De acuerdo con el factor de visión se calculó con el número de sorteos "ss" que quedaron dentro de la región del espacio R4, limitada por la función F (el integrando de la integral F1-2). La expresión para calcular fue:
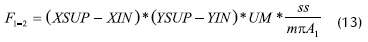
En la Figura 5 se graficó el factor de visión F1-2 VS b/c con los demás parámetros constantes
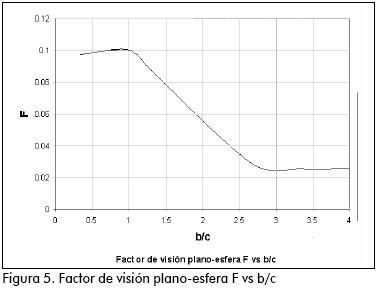
Análisis de resultados
El método desarrollado permite calcular el factor de visión de la configuración "superficie plana hacia una superficie esférica", siempre y cuando la proyección ortogonal de la esfera quede contenida en el plano.
Los valores obtenidos muestran que la exactitud depende del número de sorteos realizados, ya que entre menor sea el número de éstos el intervalo de confianza se hace mayor y por lo tanto diferencias entre tamaños distintos no van a ser tan evidentes. Esto se aprecia en la Tabla 1, donde para las dos primeras corridas el primer valor da menor que el segundo, cosa que no debe ocurrir, pero en realidad ambos se encuentran dentro del mismo intervalo de confianza.
La convergencia del método con el número de sorteos empleado es lenta, mas se espera que mejore aumentando el número de sorteos, como lo plantea el método.
Nomenclatura
F1-2 : Factor de forma de radiación desde la superficie-1 hacia la superficie-2
A1 : Área de superficie de emisión difusa o receptora de radiación (m2)
A2 : Área de superficie receptora de radiación (m2)
θ1 : Ángulo de visión formado entre la normal a la superficie del plano y el vector 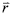
θ2 : Ángulo de visión formado entre la normal a la superficie de la esfera y el vector 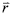
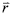 : Vector formado al unir el punto (xi, yi, 0) del plano y el punto (x,y,z) en la esfera
: Vector formado al unir el punto (xi, yi, 0) del plano y el punto (x,y,z) en la esfera
x : Abcisa coordenada sobre un punto genérico de la esfera (m)
y : Ordenada sobre un punto genérico de la esfera (m)
z : Traza coordenada sobre un punto genérico de la esfera (m)
xi : Abcisa coordenada sobre un punto genérico del plano (m)
yi : Ordenada sobre un punto genérico del plano (m)
R : Radio de la esfera (m)
h : Abcisa correspondiente al centro de la esfera (m)
k : Coordenada correspondiente al centro de la esfera (m)
l : Traza coordenada correspondiente al centro de la esfera (m)
fi : Límite inferior para y sobre la superficie esférica (m)
fs : Límite superior para y sobre la superficie esférica
xin : Límite inferior para x sobre la esfera (m)
xsu : Límite superior para x sobre la esfera (m)
a : Límite superior para xi sobre el plano (m)
0 : Límite inferior para xi sobre el plano (m)
b : Límite superior para yi sobre el plano (m)
0 : Límite inferior para yi sobre el plano (m)
Bibliografía
Carnahan, B., Luther Applied Numerical Methods., John Wiley and Sons, 1969. [ Links ]
Burden, R., Análisis numérico, México: grupo Editorial Iberoamericano, 1996. [ Links ]
Halliday, D, Física, Compañía Editorial Continental, México, Volumen 2, 1970. [ Links ]
Colman, J. P., Transferencia de calor, McGraw-Hill, España, 1998. [ Links ]
Lehman, C. H., Geometría Analítica, Limusa, México, 1997. [ Links ]
Mills, A. F., Transferencia de Calor, McGraw-Hill, Colombia, 1995. [ Links ]
Sobol, I. M., Método de Montecarlo, Mir, Moscu, 1983. [ Links ]
Determinación de los puntos ε(xε,yε,0) y p*(x*,y*,z*)
Mediante el procedimiento dado en seguida se determinaron los puntos ε(xε,yε,0) y p*(x*,y*,z*)
Determinación del punto ε: La forma simétrica de la ecuación de la recta que pasa por p y ε es:
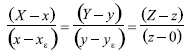
La línea que une p y ε (Figura 3) es normal a la esfera, y el vector que coincide con esta línea es el vector gradiente calculado en p:
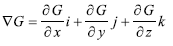
por lo tanto los cosenos directores de la recta normal a la esfera son:
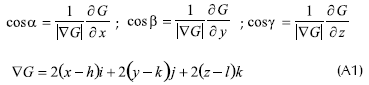
Conocido G (ecuación A1) y los puntos por los que pasa la recta pε, se determinan sus cosenos directores como:
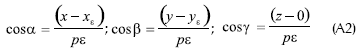
pε : Distancia entre los dos puntos p y ε
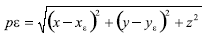
Igualando los cosenos directores entre las ecuaciones (A1) y (A2), se obtienen las coordenadas del punto ε (Figura 3):
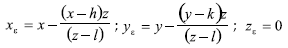
Determinado el punto ε, se calcula la distancia pε.
Determinación del punto p*: Para calcular esta distancia es necesario resolver el siguiente problema geométrico en R3:
Dada la recta ppi (Figura 3):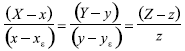 y el punto exterior a ella ε(xε,yε,0), se necesita calcular la distancia del punto ε a la recta ppi. El problema se reduce a hallar el punto p*(x*,y*,z*) (pie de la perpendicular a ppi desde ε (ver Figura 3) y después por la fórmula de distancia euclidiana entre dos puntos se calcula d. Utilizando métodos vectoriales se determinó el siguiente sistema de ecuaciones para hallar p*:
y el punto exterior a ella ε(xε,yε,0), se necesita calcular la distancia del punto ε a la recta ppi. El problema se reduce a hallar el punto p*(x*,y*,z*) (pie de la perpendicular a ppi desde ε (ver Figura 3) y después por la fórmula de distancia euclidiana entre dos puntos se calcula d. Utilizando métodos vectoriales se determinó el siguiente sistema de ecuaciones para hallar p*:
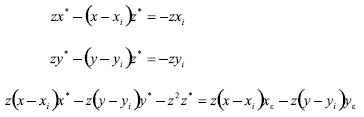
Determinado p*(x*,y*,z*) de la solución del sistema anterior se calcula d