Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.26 no.1 Bogotá Jan./Apr. 2006
Daniel Alfonso Giraldo Giraldo1, Dolly Santos Barbosa2 y Carlos Cotrino Badillo3
1 Ingeniero químico, Universidad Nacional de Colombia, Bogotá; ingeniero de procesos, Abocol, Cartagena.
2 MSc. Automatización Industrial. Ingeniera química, Universidad Nacional de Colombia, Bogotá. Profesor asistente, Universidad Nacional de Colombia, Bogotá. dsantosb318@yahoo.com, dsantosb@unal.edu.co
3 MSc State University of New York. Ingeniero electrónico. Pontificia Universidad Javeriana, Bogotá. Profesor asistente, Pontificia Universidad Javeriana, Bogotá.
RESUMEN
Se presenta el diseño de una estrategia de control predictivo, sobre un modelo matemático, de un evaporador de película descendente con recompresión mecánica de vapor, usado en la industria láctea. Para diseñar el controlador se utiliza el programa ConnoisseurTM, a partir de datos recolectados de la simulación de un modelo no lineal. Se emplea una ley de control obtenida de la minimización de una función de costo, sujeta a restricciones del proceso, empleando un algoritmo de programación cuadrático (QP). Finalmente, se ejecuta un algoritmo de programación lineal (LP) que encuentra un punto de operación subóptimo para el proceso en estado estacionario.
Palabras clave: control predictivo basado en modelos, evaporador de película descendente, funciones de costo, control óptimo, programación lineal.
ABSTRACT
This paper outlines designing a predictive control model (PCM) applied to a mathematical model of a falling film evaporator with mechanical steam compression like those used in the dairy industry. The controller was designed using the ConnoisseurTM software package and data gathered from the simulation of a non-linear mathematical model. A control law was obtained from minimising a cost function subject to dynamic system constraints, using a quadratic programme (QP) algorithm. A linear programming (LP) algorithm was used for finding a sub-optimal operation point for the process in stationary state.
Keywords: predictive control model, falling film evaporator, cost function, optimal control, linear programming.
Recibido: agosto 12 de 2005
Aceptado: enero 24 de 2006
Introducción
Los procesos químicos se caracterizan por ser sistemas multivariables no lineales con interacciones fuertes entre las variables, por lo que la aplicación de una estrategia de control clásico puede, en ocasiones, ser inadecuada. Con el avance en los sistemas de computación se ha facilitado el análisis y la simulación de modelos matemáticos más complejos, lo cual ha impulsado el desarrollo de nuevas técnicas de control avanzado para procesos multivariables (Giraldo, 2002). Una de estas técnicas es el control predictivo, el cual emplea un modelo para prever el comportamiento dinámico de las variables controladas del proceso y poder obtener, a partir de la minimización de una función de costo sujeta a las restricciones de las variables del proceso, una ley de control (Camacho y Bordons, 2000).
Modelo matemático del proceso
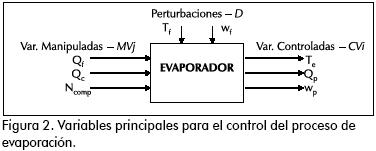
El modelo matemático del evaporador fue desarrollado en la Universidad de Massey, Nueva Zelanda, con el fin de examinar la interacción y la controlabilidad de los tres lazos de control principales: la temperatura en el efecto del evaporador (Te), el porcentaje de sólidos disueltos en el producto (wp) y el flujo del producto (Qp) (Winchester y Marsh, 1999). El modelo representa un evaporador tubular de película descendente de simple efecto con recompresión mecánica de vapor (Mechanical Vapor Recompression – MVR), que consiste en hacer pasar a través de un compresor centrífugo, una fracción del vapor retirado en el efecto e inyectarlo a la coraza del intercambiador de calor (Figura 1). Al efecto se alimentan 50.000 L/h de leche (Qf) que son concentrados desde un 12,5% de sólidos disueltos en el alimento (wf) hasta un 32,1% de sólidos disueltos en el producto (wp).
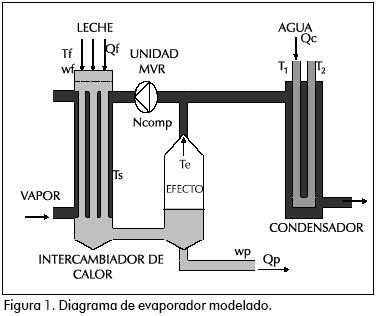
El modelo, desarrollado por Winchester y Marsh, 1999, se obtuvo a partir de los balances de masa y energía del proceso, de las ecuaciones del compresor y de ecuaciones hidrodinámicas:

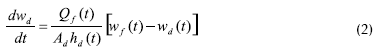
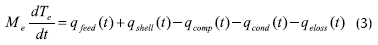
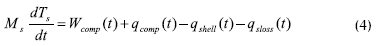
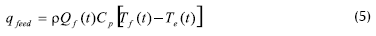



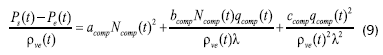
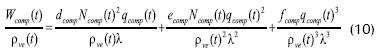
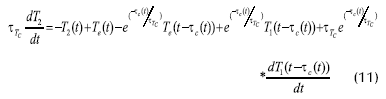
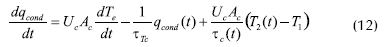
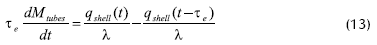
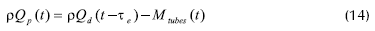
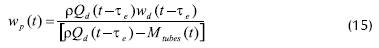
Las variables de entrada: flujo de alimento (Qf), flujo de agua en el condensador (Qc), velocidad de giro del compresor en la unidad de recompresión mecánica de vapor (Ncomp) y la temperatura del alimento (Tf) tienen efecto sobre todas las variables de salida. La variable de entrada, porcentaje de sólidos disueltos en el alimento (wf) sólo tiene efecto sobre la variable de salida porcentaje de sólidos disueltos en el producto (wp) (Winchester y Marsh, 1999).
Estrategia de control
Los objetivos de control que debe cumplir la estrategia son:
1. Mantener wp por debajo de 50% con el fin de evitar el taponamiento del equipo por la cristalización del producto. El modelo en estado estacionario establece 32,1%
2. Te puede variar entre 65,4°C y 69,5°C. Se debe mantener por debajo de 70°C como límite de seguridad (restricción dura), para evitar la degradación térmica del producto.
3. Mantener las fluctuaciones de wp por debajo de un 1%: entre 32,0% y 32,4%.
4. Garantizar que se cumplan los anteriores objetivos de control para fluctuaciones de Qp entre 19.000 y 25.000 L/h (requerimiento del proceso de secado por aspersión que sigue al proceso de evaporación de la leche). Se dejará fluctuar entre 19.420 L/h y 19.900 L/h.
El proceso representado como un sistema multivariable se aprecia en la Figura 2:
Utilizando el modelo en hoja electrónica (Giraldo, et al., 2005), se hace una recolección de datos del comportamiento dinámico del proceso (Figura 3), empleando una secuencia binaria seudo aleatoria (Pseudo-Random Binary Sequence – PRBS (Norton, 1986), para introducirlos al programa Connoisseur.
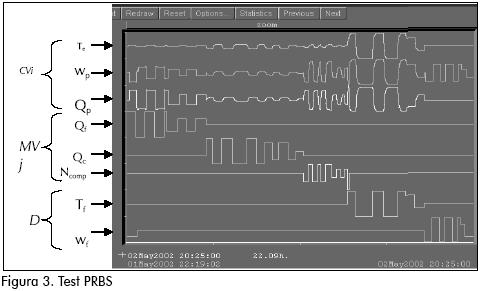
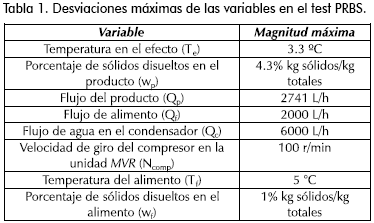
En la Figura 3 se aprecia que la variable wf, sólo tiene efecto sobre la variable wp, mientras que las demás variables de entrada tienen efecto sobre todas las variables de salida en diferentes magnitudes (Giraldo, 2002). La Tabla 1 presenta las desviaciones máximas de las variables.
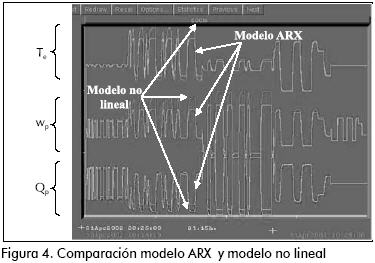
Con estos datos se identifica un modelo lineal de tipo ARX (Auto-Regressive with eXogenous Input) (Norton, 1986). En la Figura 4 se observan los resultados del modelo lineal ARX, comparados con los del modelo no lineal del proceso. A pesar de las diferencias entre el modelo no lineal y ARX, se empleará este último procedimiento por ser la herramienta existente dentro del Model Builder de Connosseiur
En la recolección de datos se aplicó la señal PRBS para cada variable de entrada por separado4, lo cual puede resultar en una excitación pobre de las dinámicas del proceso5. Se plantea una ley de control a partir de la minimización de una función de costo Jc, de la forma:
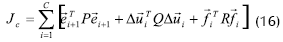
En la anterior ecuación:
- C es el horizonte de control.
- 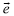 es el vector de magnitud c que contiene las desviaciones de las variables controladas.
es el vector de magnitud c que contiene las desviaciones de las variables controladas.
- 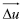 es el vector de magnitud m que contiene los cambios en las variables manipuladas.
es el vector de magnitud m que contiene los cambios en las variables manipuladas.
- 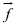 es el vector de magnitud m que contiene las desviaciones de las variables manipuladas respecto de los valores de las variables manipuladas en estado estacionario (MVss)6 (Brosilow, 2002).
es el vector de magnitud m que contiene las desviaciones de las variables manipuladas respecto de los valores de las variables manipuladas en estado estacionario (MVss)6 (Brosilow, 2002).
- P es la matriz [c x c] que agrupa los factores de costo que penalizan el vector 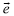 .
.
- Q es la matriz [m x m] que agrupa los factores de costo que penalizan el vector 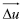 .
.
- R es la matriz [m x m] que agrupa los factores de costo que penalizan el vector 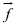 .
.
La ecuación 16 se encuentra sujeta a restricciones establecidas en los objetivos de control y en cuanto a la rapidez de cambio de las variables del proceso, según la Tabla 2.

Para minimizar la ecuación 16 se emplea un algoritmo de programación cuadrático (QP) que arroja una ley de control óptima para el proceso, satisfaciendo los objetivos de control (Predictive Control Ltd., 1998). A manera de ejemplo, se observan los resultados del desempeño de la estrategia de control introduciendo un cambio tipo paso +5ºC en la variable Tf (Figura 5).
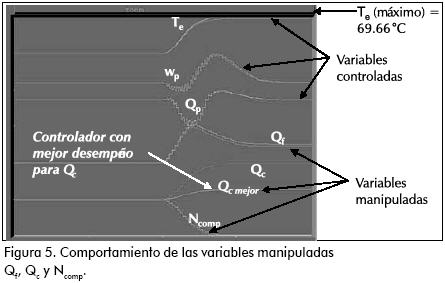
Se aprecia cómo se modifican las variables manipuladas Qf, Qc y Ncomp para mantener controladas las variables Te, wp y Qp al ocurrir un cambio en la perturbación Tf y se presenta la respuesta de un controlador con mejor desempeño en la manipulación de Qc. Este valor se obtiene por iteración de los parámetros de la matriz Q (Giraldo, 2002). Luego de ajustar los parámetros de la ley de control (matrices P, Q y R,)7 se logran los siguientes valores de operación:
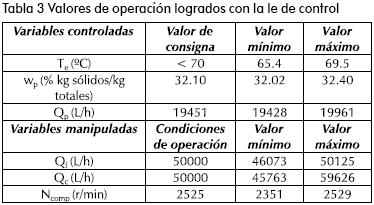
Para comparar el desempeño de la estrategia de control se diseñan lazos de control PID sencillos, cuya función de transferencia es de la siguiente forma:

Donde Kc es la ganancia del controlador, τi es la constante de tiempo integral y τd es la constante de tiempo derivativa. Dado el acople existente entre las variables, para poder seleccionar los pares [controlada-manipulada] se realiza el análisis de ganancias relativas (Relative Gain Array – RGA) (Skogestad, et al., 1996; Zhu, 2001) y se obtiene la siguiente matriz:

Esta matriz indica que los lazos sencillos de control deben ser:
- wp se debe controlar con Ncomp. (único valor positivo)
- Te se debe controlar con Qc. (valor positivo cercano a uno)
- Qp se debe controlar con Qf.
La Tabla 4 presenta los valores de los parámetros de los controladores PID, calculados por Connoisseur, para los lazos {Qc-Te}, {Ncomp-wp} y {Qf-Qp}. La ganancia proporcional Kc está en %/% y los tiempos de integración y derivación en segundos.
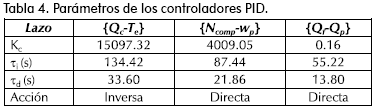
En la Tabla 5 se comparan los resultados sobre el modelo lineal aproximado, del controlador predictivo contra lazos PID individuales:
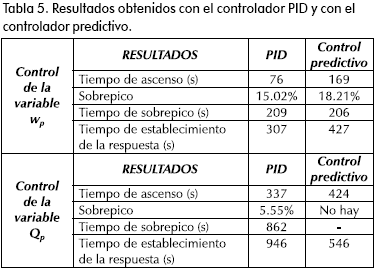
Tanto el sobrepico (overshoot) como el tiempo para el cual ocurre (peak time) se emplean como una indicación de la agresividad del ajuste de la variable. El tiempo de ascenso (rise time) para una respuesta sobreamortiguada es el que toma el sistema para llegar a un valor cercano al nuevo punto de ajuste (Frankiln et al., 2003). Comparando las respuestas del proceso con el controlador predictivo y con los lazos PID, se aprecia que la variable wp se controla mejor con el lazo PID y la variable Qp con el controlador predictivo. Hay que resaltar que el control predictivo controla wp simultáneamente con Te y Qp, mientras que el análisis de los lazos PID se realizó considerando los lazos independientes. De acuerdo con el objetivo 2 de la estrategia de control, solamente se define que se cumpla con la restricción Te < 70ºC, lo cual permite relajar la estrategia. Si el proceso lo requiere, se puede diseñar una estrategia que mejore el desempeño de wp, sacrificando un poco el desempeño de Te y Qp.
Optimización del proceso en estado estacionario con Connoisseur9
La herramienta ConnoisseurTM incluye el algoritmo de optimización del proceso en estado estacionario, que no necesariamente hace parte del control predictivo, y además trae herramientas para el análisis de sistemas multivariables y para la identificación de modelos empleando redes neuronales.
Una vez que se tiene controlado el proceso se busca un nuevo punto de operación en estado estacionario que cumpla con los objetivos de control y brinde un beneficio económico en la operación (Predictive Control Ltd., 1998). Para calcular dicho punto, se ejecuta un algoritmo LP que minimiza una función de costo Jo.
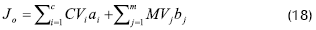
Donde:
- CVi es el vector de variables controladas.
- ai es el vector de los factores de costo para cada variable controlada.
- MVj es el vector de variables manipuladas.
- bj es el vector de los factores de costo para cada variable manipulada.
La Tabla 6 contiene los valores del nuevo punto de operación al ejecutarse el algoritmo LP:
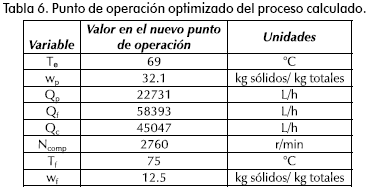
Mientras que las variables controladas Te, wp y Qp conservan los valores logrados bajo la estrategia MPC, las variables manipuladas están por fuera de los intervalos de la Tabla 3, esto significa que el algoritmo de optimización LP calcula las variables por fuera de la región del modelo ARX identificado. En la Figura 6 se aprecia la ejecución del algoritmo LP, y comparando los resultados con los obtenidos sin el optimizador, se deduce que el desempeño de la estrategia no afecta significativamente, razón por la cual se ajustan los parámetros del modelo ARX y de la ley de control sin volver a identificar un modelo lineal ARX. Un análisis más detallado de los resultados del optimizador y la evaluación de matrices de peso diferentes puede conducir a una nueva identificación y otro punto de operación.
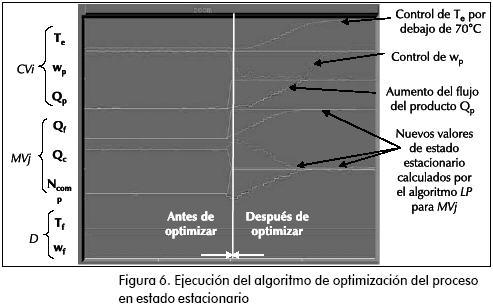
En el nuevo punto de operación se aumentan el flujo de producto y la temperatura en el efecto al límite de control (Te < 70°C). Para lograr esto, es necesario aumentar los flujos de alimento de agua en el condensador y la velocidad de giro del compresor de la unidad MVR (Giraldo, 2002). La estrategia ajusta los parámetros del modelo ARX y la ley de control en este nuevo punto de operación.
Conclusiones
El control predictivo basado en modelo es una estrategia capaz de manejar sistemas multivariables de comportamiento dinámico complejo con buen desempeño. Al comparar los controladores PID diseñados contra el control predictivo, se aprecia que este control sacrifica el desempeño en algunas variables para lograr un excelente desempeño en otras. Cabe anotar que el control predictivo es una estrategia de control lineal válida solamente en un pequeño intervalo de operación, por lo que se requiere identificar nuevamente un modelo lineal en el nuevo punto de operación del proceso. En el control de un evaporador para concentrar leche hay que tener cuidado especial con el control del porcentaje de sólidos disueltos en el producto y la temperatura del efecto, ya que un ajuste errado en la estrategia puede conducir a la violación de los objetivos de control para una de estas dos variables.
Una virtud del control predictivo aplicado a este caso y presente en la herramienta ConnoisseurTM es que se puede controlar Te sin necesidad de definir un valor de consigna, sólo hay que definir un límite superior de seguridad a la variable Te.
Agradecimientos
Los autores expresan sus agradecimientos a Invensys Systems L.A. Colombia por facilitar el uso de la licencia del software ConnoisseurTM, propiedad del grupo Invensys Process Systems plc.
Nomenclatura
acomp: Coeficiente para las ecuaciones del compresor [m2/s2 (r/min)2]
Ac: Área superficial de los tubos del condensador [m2]
Ad: Área de la sección transversal del plato de distribución [m2]
Ael: Área superficial del efecto del evaporador [m2]
Ah: Área de la sección transversal de los agujeros del plato de distribución [m2]
ai: Vector de los factores de costo para cada variable controlada
ARX: Auto-regressive with exogenous input
As: Área superficial de los tubos del evaporador [m2]
Asl: Área superficial de la coraza del evaporador [m2]
bcomp: Coeficiente para las ecuaciones del compresor [m2/s2 (r/min)2]
bj: Vector de los factores de costo para cada variable manipulada
c: Número de variables controladas
C: Horizonte de control
ccomp: Coeficiente para las ecuaciones del compresor [m-4]
Cd: Coeficiente de descarga de orificio del plato de distribución
Cp: Calor específico de la leche [J/kg K]
Cpc: Calor específico del agua del condensador [J/kg K]
CVi: Vector de variables controladas
dcomp: Coeficiente para las ecuaciones del compresor [m2/s2 (r/min)2]
d: Diámetro de los tubos del evaporador [m]
D: Perturbaciones (Disturbances)
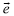 : Vector de magnitud c que contiene las desviaciones de las variables controladas
: Vector de magnitud c que contiene las desviaciones de las variables controladas
ecomp: Coeficiente para las ecuaciones del compresor [(m s (r/min))-1]
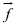 : Vector de magnitud m que contiene las desviaciones de las variables manipuladas respecto de los valores de las variables manipuladas en estado estacionario (MVss)
: Vector de magnitud m que contiene las desviaciones de las variables manipuladas respecto de los valores de las variables manipuladas en estado estacionario (MVss)
fcomp: Coeficiente para las ecuaciones del compresor [m-4]
g: Constante de gravedad [m/s2]
Gc(s): Función de transferencia del controlador PID
hd(t): Altura del líquido sobre el plato de distribución [m]
Jc: Función de costo del algoritmo de control
Jo: Función de costo del algoritmo de optimización
Kc: Ganancia del controlador PID
LP: Linear Programming
m: Número de variables manipuladas
Magua: Peso molecular del agua [g/mol]
Me: Capacidad térmica del efecto incluyendo líquido, vapor y metal [J/K]
MPC: Model Predictive Control
Ms: Capacidad térmica de la coraza incluyendo líquido, vapor y metal [J/K]
Mtubes(t): Masa de evaporación durante el tiempo de residencia de un efecto [kg]
MVj: Vector de variables manipuladas
MVR: Mechanical vapor recompression
n: Número de tubos del evaporador
Ncomp(t): Velocidad de giro del compresor en la unidad MVR [r/min]
P: Matriz [c x c] que agrupa los factores de costo que penalizan el vector 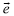
Pe(t) = Presión en el efecto del evaporador [Pa]
PID: Proporcional-Integral-Derivativo (controlador)
PRBS: Pseudo-random binary sequence
Ps(t) = Presión en la coraza del evaporador [Pa]
qcomp(t) = Entalpía latente en el vapor que pasa por el compresor [J/s]
qcond(t) = Flujo de calor a través de los tubos del condensador [J/s]
qeloss(t) = Flujo de calor debido a las pérdidas a través de la superficie del efecto del evaporador [J/s]
qfeed(t): Entalpía neta del alimento que entra al evaporador [J/s]
qsloss(t): Flujo de calor debido a las pérdidas a través de la superficie de la coraza del evaporador [J/s]
qshell(t): Flujo de calor a través de los tubos del evaporador [J/s]
Q: Matriz [m x m] que agrupa los factores de costo que penalizan el vector 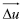
Qc: Flujo de agua del condensador [L/h]
Qd(t): Flujo de alimento a través del plato de distribución [L/h]
Qf: Flujo del alimento [L/h]
Qp: Flujo del producto [L/h]
R: Matriz [m x m] que agrupa los factores de costo que penalizan el vector 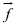
T(t,x): Temperatura del agua del condensador [K]
T1(t): Temperatura del agua que entra al condensador [K]
T2(t): Temperatura del agua que sale del condensador [K]
Ta: Temperatura de los alrededores [K]
Te: Temperatura del efecto [°C]
Tf: Temperatura del alimento [°C]
Ts(t): Temperatura del vapor en la coraza [K]
t: Tiempo
Uc: Coeficiente global de transferencia de calor para el flujo de calor en el condensador [W/m2 K]
Uel: Coeficiente global de transferencia de calor para las pérdidas de calor en el efecto [W/m2 K]
Us: Coeficiente global de transferencia de calor para el flujo de calor en los tubos del evaporador [W/m2 K]
Usl: Coeficiente global de transferencia de calor para las pérdidas de calor en la coraza [W/m2 K]
Vc: Volumen interno de los tubos del evaporador [m3]
vc(t): Velocidad del agua de enfriamiento en el condensador [m/s]
v: Velocidad de caída de la película descendente por los tubos rumbo al efecto [m/s]
wd(t): Porcentaje de sólidos disueltos en el flujo a través del plato de distribución
[kg sólidos/kg totales]
wf: Porcentaje de sólidos disueltos en el alimento [% kg sólidos/kg totales]
wp: Porcentaje de sólidos disueltos en el producto [% kg sólidos/kg totales]
Wcomp(t): Potencia que consume el compresor [W]
Y(t): Variable de salida del proceso
Yss: Variable de salida del proceso en estado estacionario
Δt: paso de integración [s]
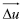 : Vector de magnitud m que contiene los cambios en las variables manipuladas
: Vector de magnitud m que contiene los cambios en las variables manipuladas
λ: Calor latente de vaporización [J/kg]
Λ: ?Matriz de ganancias relativas
ρc: Densidad de la leche [kg/m3]
ρc: Densidad del agua del condensador [kg/m3]
ρve(t): Densidad del vapor en el efecto [kg/m3]
τc(t): Tiempo de residencia del agua en los tubos del condensador [s]
τd: Constante de tiempo derivativa del controlador PID [s]
τe: Tiempo de residencia del alimento a través de la película descendente [s]
τi: Constante de tiempo integral del controlador PID [s]
τTc: Constante de tiempo para los tubos del condensador [s]
Bibliografía
Brosilow, C. and Joseph, B., Techniques of Model-Based Control., Upper Saddle River NJ, Prentice Hall, PTR., 2002. [ Links ]
Camacho, J. E. and Bordons, C., Model Predictive Control: Springer-Verlag,, 2000. [ Links ]
Franklin, G. et al., Feedback control of dynamic systems, 4th edition, Upper Saddle River, NJ, Prentice Hall, 2002. [ Links ]
Giraldo, D., Estrategia de control avanzado para un evaporador, Proyecto de grado presentado en la Universidad Nacional de Colombia, Bogotá, para optar al grado de Ingeniero Químico, 2002. [ Links ]
Giraldo, D., Santos, D. y Cotrino, C. Cálculo numérico de un modelo de evaporador con recompresión mecánica de vapor, En revista Ingeniería Javeriana., No. 40, Julio 2005. [ Links ]
Norton, J.P., An introduction to identification, London, Academic Press, 1986. [ Links ]
Predictive Control Ltd., Connoisseur technology primer, Issue 1.0., 1998. [ Links ]
Skogestad, S. et al., Multivariable feedback control: Analysis and design, Chichester, UK: John Wiley & Sons, 1996. [ Links ]
Winchester, J. A. and Marsh C., Dynamics and control of falling film evaporators with mechanical vapour recompression, Chemical Engineering Research and Design, Vol. 77, Part A., July 1999. [ Links ]
Zhu Y., Multivariable System Identification for Process Control, Amsterdam, Pergamon, 2001. [ Links ]
4 La metodología de prueba más usada actualmente en la identificación de procesos es la de variable sencilla en malla abierta o cerrada. Métodos de prueba multivariable ya han sido desarrollados y probados (Zhu, 2001), pero no están disponibles en la versión del controlador empleado.
5 Para asegurar la mayor fidelidad del modelo, la señal de excitación debe ser persistente, de alta relación señal a ruido, y no llevar el proceso a la región de operación no lineal (Zhu, 2001).
6 Desde el trabajo original sobre MPC (Cutler y Ramaker, 1980) se han incluido las variables manipuladas como parte de la función de costo. Los efectos de offset en el estado estable que esto produce se deben corregir en la estrategia completa.
7 Los parámetros se obtuvieron minimizando una función con la sumatoria del cuadrado del error para las variables de salida F = f [∑ε(Te)2, ∑ε(wp)2, ∑ε(Qp)2]
8 No se comparan valores correspondientes al control de Te, porque para esta variable no hay valor de consigna fijo.
9 La optimización de Connoisseur calcula un punto de operación "suboptimo" en estado estacionario.














