Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.26 no.1 Bogotá Jan./Apr. 2006
Jorge Eduardo Ortiz Triviño1 y Luz Ángela Serrano Rivera2
1 Profesor asistente, Departamento de Ingeniería de Sistemas e Industrial, Universidad Nacional de Colombia, Bogotá, Colombia. jeortizt@unal.edu.co
2 Departamento de Ingeniería de Sistemas e Industrial, Universidad Nacional de Colombia, Bogotá, Colombia. laserranor@unal.edu.co
RESUMEN
En este artículo se presenta un modelo de simulación para la evaluación del desempeño de un sistema de transporte público masivo (STPM). El prototipo resultante es flexible, tanto en la construcción del esqueleto de un STPM, como para el modelamiento de los eventos aleatorios característicos de este tipo de sistemas. El modelo final es una red de colas complementada con elementos adicionales como matrices origen-destino y grafos, que permiten considerar fenómenos propios de un STPM. El modelo de simulación responde, como es esperado, ante los cambios en los parámetros, y permite definir y evaluar medidas de desempeño típicas de las líneas de espera, como por ejemplo, tiempos de permanencia promedio en el sistema y en cola, longitudes esperadas de las colas, junto con otras medidas características de este tipo de sistemas.
Palabras clave: simulación, sistemas de transporte público masivo, redes de colas abiertas, matriz origen-destino, desempeño.
ABSTRACT
A simulation model for evaluating the performance of a mass public-transport system (MPTS) is presented in this report. The final prototype was flexible both for constructing an MPTS skeleton and modelling random events characteristic of this type of system. The final model was a queuing network with other elements such as origin-destination matrices and graphs allowing typical MPTS phenomena to be considered. The simulation model reacted as expected to changes in the parameters and allowed defining and evaluating typical performance measurement for queues (e.g. mean time spent in the system and queue, expected queue length) as well as others representative of these systems.
Keywords: simulation, mass public-transport system, open queuing network, origin-destination matrix, performance.
Recibido: marzo 3 de 2005
Aceptado: enero 10 de 2006
Introducción
El auge actual de la implantación de sistemas de transporte público masivo estructurados (como el Metro, en el caso de Medellín, y Transmilenio, en Bogotá y próximamente en otras ciudades), que buscan, con un costo similar para el usuario, prestar un servicio de mejor calidad al que prestan los sistemas tradicionales, evidencia la conveniencia del diseño y construcción de herramientas que permitan evaluar su desempeño.
La construcción de una herramienta de simulación que permita obtener medidas de desempeño que reflejen la calidad del servicio prestado a los usuarios, de acuerdo con las facilidades ofrecidas por el sistema, constituye una alternativa, hasta cierto punto económica, para la evaluación de la calidad del servicio; y en una herramienta eficaz de apoyo a la toma de decisiones respecto a la viabilidad de posibles cambios.
Además, gracias a la simulación es posible construir modelos que consideren de forma integral los fenómenos que se presentan dentro del sistema, y no como un conjunto de elementos aislados, lo cual no constituye una alternativa lo suficientemente buena como para apoyar tareas de diagnóstico de problemas y evaluación de alternativas de solución, pues evidentemente, en el objeto de estudio (el sistema) existe sinergia3.
El artículo describe las principales características del STPM a partir del cual se elaboró el modelo propuesto, y se dan algunos detalles sobre su implementación. Al final, se encuentran los resultados y las conclusiones y recomendaciones correspondientes.
Esquema general del STPM
La Figura 1 muestra una representación del esquema general sobre el cual opera el STPM a simular. Sistemas como este son comúnmente llamados BRT (Bus Rapad Transit), y se encuentran en operación en ciudades latinoamericanas, siendo tal vez el más reciente Transmilenio en Bogotá.
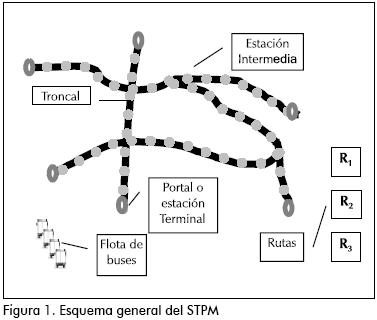
Los elementos más importantes, a nivel estructural, en este tipo de sistemas son:
• Estaciones intermedias, en donde se presentan procesos de arribo de usuarios, los cuales pueden tener ya un tiquete, o pasar a comprarlo en la taquilla antes de ingresar a la estación. Para entrar a la estación, los usuarios deben cruzar un torniquete, y así, adentro esperar el arribo de la ruta que los conduzca a su estación de destino. Allí los usuarios también pueden hacer trasbordos, de ser necesario, para llegar a su destino final.
• Estaciones terminales, en donde además de presentarse los mismos eventos en las estaciones normales, se despachan buses para surtir las rutas que le corresponden.
• Rutas de buses, las cuales tienen una estación terminal origen y otra de destino; recorren las troncales en los dos sentidos y se detienen en estaciones específicas durante su trayecto. Para la prestación del servicio de ruta, se dispone de una flota de buses, y son establecidas frecuencias de despacho para cada ruta.
• Troncales (vías exclusivas), sobre las cuales transitan los buses y están ubicadas las estaciones.
• Flota de buses, de la cual se asignará cierto número para cubrir la demanda de cada ruta.
Modelo para el STPM
Redes de colas abiertas en los STPM
Es evidente la facilidad para evaluar el desempeño de uno solo de los componentes que están presentes en el STPM (taquillas, torniquetes), como modelos de colas sencillos como el M/M/1, en el que el cálculo analítico de los resultados (longitud de la cola, tiempo de permanencia, etc.) bajo condiciones de estado estable, es relativamente trivial. Sin embargo, el tratamiento de dichos componentes como colas simples aisladas no ofrece un modelo significativo para su estudio. En cambio, si son considerados en conjunto, se podrá observar cómo su interacción se ajusta a otros modelos más interesantes, para los cuales su evaluación mediante herramientas de simulación brinda un aporte más apreciable.
Tal es el caso de las redes de Jackson, las cuales constituyen sistemas de colas finitas en serie, en donde los usuarios pueden visitarlas o no en un orden no necesariamente igual (Robertazzi, 2000), y en donde se asumen tiempos entre arribos y de servicio con una distribución exponencial4.
Pero el modelo puede ser aún más interesante si es considerado como una red de colas abierta, en donde se liberan las suposiciones de modelos de redes de colas típicos como el de Jackson y se hace posible el empleo de distribuciones de probabilidad más adecuadas, tanto teóricas como empíricas.
Como se puede observar en la Figura 2, la red de colas cuenta con múltiples fuentes, ya que, para cada estación (la figura sólo muestra la representación de una sola estación, que en el caso de tener varios costados de acceso requeriría varias fuentes), los eventos de arribo de pasajeros constituyen casos aleatorios que pueden comportarse de acuerdo con distribuciones distintas, o por lo menos con diferentes parámetros. También podría hablarse de múltiples destinos; sin embargo, lo que representan estos, en últimas, son los diversos momentos en los que se puede producir una salida del sistema.
Así, cuando un usuario llega a una estación (intermedia o terminal), puede darse alguna de estas situaciones:
• Si el usuario ya tiene un tiquete, seleccionará inmediatamente un torniquete para ingresar a la estación (típicamente será en el que halla una menor cola).
• Entrará a la cola de la taquilla (pueden haber varias) para, luego de ser servido allí y obtener su tiquete, pasar a los torniquetes de ingreso a la estación.
• Entrará a la cola de la taquilla y luego de ser atendido y obtener su tiquete abandonará el sistema, pues su único fin puede ser comprar uno o varios tiquetes para viajes posteriores.
En todo caso, si el usuario finalmente entra a la estación a esperar el arribo de un bus de alguna ruta que lo conduzca a su destino, primero se deben tener en cuenta los elementos del modelo expuestos más adelante, los cuales se refieren a la selección de la ruta y posibles trasbordos a realizar, lo que añade una situación a las mencionadas arriba, ya que pueden llegar usuarios directamente a la estación en espera de la ruta que los conduzca a su destino final. Cuando los usuarios ya saben qué ruta deben esperar, naturalmente buscarán la línea de espera de dicha ruta; el tiempo que tardan en ello representa una variable aleatoria que dependerá tanto de las características físicas de la estación como de ciertos rasgos del usuario.
En las estaciones terminales, dada su naturaleza, sólo se presenta abordaje para tomar los buses hacia un solo sentido (hacia las estaciones que se encuentran antes), y descenso desde rutas que viene en sentido contrario (desde las estaciones que se encuentran antes). Además, tienen la característica de que despachan buses para determinadas rutas (las que le corresponden), con una frecuencia específica, la cual puede ser parámetro para una distribución de probabilidad particular que determinará la longitud del intervalo de tiempo que hay entre el despacho de dos buses consecutivos de la misma ruta. Después de haber sido despachados los buses siguen su flujo normal, pero con un comportamiento no determinístico (tal como se plantea en la sección tiempos de viaje entre estaciones), cumpliendo con su ruta en el STPM, hasta que se termine la jornada.
Modelo para el arribo de buses a las estaciones
Si bien los buses actúan como servidores dentro del sistema, estos cuentan con un ingrediente adicional, cual es el de que no se encuentran en un punto fijo, sino que fluyen a través del sistema, viajando de estación a estación de acuerdo a un fenómeno no determinístico.
En la Figura 2 este fenómeno es representado dibujando los servidores de las líneas de espera para cada ruta mediante líneas punteadas, lo que significa que en realidad no se encuentran en el mismo sitio en donde se genera la línea de espera, sino que en un momento dado aparecerán para atenderla (recoger a los pasajeros que esperan para abordar).
Los otros servidores, que se encuentran a un lado de las líneas de espera para el abordaje, representan el descenso de los usuarios de los buses de cada ruta, pudiendo así (como se ve representado en los conectores), ingresar a la línea de espera para el abordaje de otro bus (en el caso de que le sea necesario realizar un trasbordo) o pasar a los torniquetes que conducen a la salida de la estación y del sistema.
Tiempos de viaje entre estaciones
Si bien existen varios factores que inciden en los tiempos de viaje, en el modelo sólo se tiene en cuenta la relación volumen-capacidad de los segmentos de red por los que deben transitar los buses para realizar el viaje entre dos estaciones. De este modo, los tiempos de viaje entre ellas estarán determinados por la siguiente función:
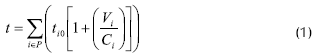
en donde:
t Tiempo de viaje entre las estaciones dadas.
P Es el conjunto de segmentos que conectan a las estaciones dadas.
ti0 Es el tiempo a velocidad de flujo libre para el segmento i.
Vi Es el volumen de vehículos que se encuentran en el segmento i, justo en el instante en que el bus va a entrar al segmento.
Ci Es la capacidad expresada en vehículos equivalentes para el segmento i.
Respecto a la capacidad, esta puede ser vista como número de vehículos que encontraríamos en el segmento si se tomara una instantánea en el momento en el que transita por él el máximo posible de vehículos.
Modelo para los trasbordos
Para manejar el problema de los destinos de los usuarios en el sistema es conveniente el uso de una matriz origen-destino que esté compuesta por probabilidades (Figura 3a), que de algún modo se refieran a la proporción de los usuarios que ingresan a la estación i, cuyo destino es la estación j.

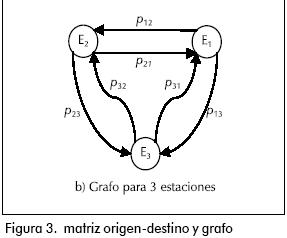
Para la matriz se tiene i = 1, 2,…, n y j = 1, 2,…, n, en donde n es el número de estaciones del STPM, incluyendo los portales. Además se tiene que pij=0, pues es apenas natural que el destino nunca será el mismo origen, y se debe cumplir que ,  i = 1, 2,…, n. De cierto modo, la matriz proporciona probabilidades para la transición entre estaciones (Figura 3b), teniendo en cuenta una relación origen-destino pero no los trasbordos que puedan ser necesarios.
i = 1, 2,…, n. De cierto modo, la matriz proporciona probabilidades para la transición entre estaciones (Figura 3b), teniendo en cuenta una relación origen-destino pero no los trasbordos que puedan ser necesarios.
Por otro lado, para resolver el problema de la selección de la(s) ruta(s) para ir del origen al destino, se cuenta con una matriz de cobertura, la cual tendrá un 1 en la posición k,i, si la ruta k se detiene en la estación i, y 0 en caso contrario. Por supuesto, se tienen en cuenta las estaciones terminales, aunque con la restricción de que una ruta puede pasar (detenerse) por lo menos en dos de ellas (origen y destino), además de otras restricciones de localización.
Así, para una pequeña configuración con cinco estaciones y tres rutas, como la que se ve en la Figura 4a, la matriz será como la mostrada en la Figura 4b).
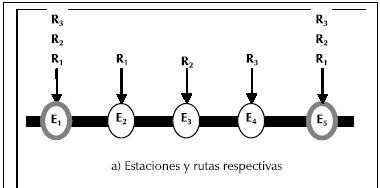

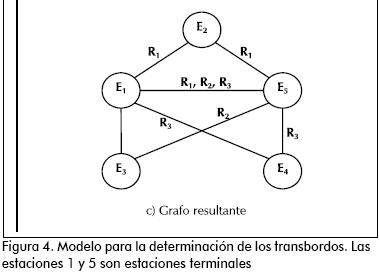
Si adicionalmente se utiliza la información de la matriz para construir un grafo en el cual los nodos sean las estaciones y los arcos entre estaciones existan si hay por lo menos una ruta que se detenga en las dos estaciones, se obtendrá un grafo como el de la Figura 4c, mediante el cual, al asignarle adecuadamente los pesos5, se puede aplicar el algoritmo de la ruta más corta (Hillier et al., 1989) (asumiendo que los pasajeros en verdad eligen siempre una estrategia de minimización) mediante el cual se obtendrán tanto las estaciones en las cuales es necesario detenerse, como la ruta o rutas que se deben tomar para completar el recorrido.
Implementación del modelo
La integración de los modelos expuestos en las secciones anteriores, en una herramienta prototipo de simulación, requiere de la realización de un registro y seguimiento de los eventos de los cuales dependen las medidas de desempeño a determinar, como lo son, el tiempo de llegada al sistema (a una estación intermedia o terminal), tiempo en las colas para ingreso (taquilla y torniquetes), tiempo en espera antes de abordar el bus correspondiente, tiempo invertido en los trasbordos (si estos son necesarios), tiempo de viaje en el bus (el cual en últimas representa un tiempo de servicio), tiempo en cola para salir del sistema, etc. Si bien la cantidad de eventos, y por ende, de información a manejar, es considerable, la capacidad actual de los computadores es suficiente para manejarla de manera eficiente, permitiendo así, finalmente, con base en dicha información, obtener las estimaciones de las medidas de desempeño de interés.
La herramienta prototipo fue implementada usando Java como lenguaje de programación. El IDE usado fue JBuilder 8 Personal edition. Se usaron varias librerías para Java que sirvieron de apoyo durante el proceso de implementación. La más importante fue SimJava, que proporcionó el ambiente y algunas facilidades para el proceso de simulación.
Luego de establecer el esqueleto del STPM (red vial, estaciones, rutas), el prototipo debe recibir la configuración de las entidades (taquillas, torniquetes, etc). Dicha información consiste en:
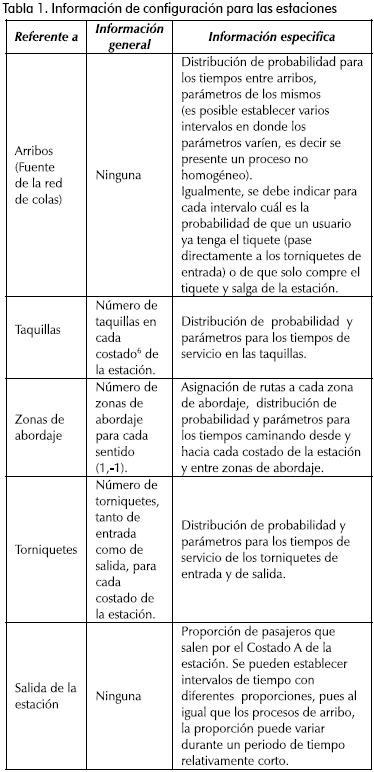
1. Para las estaciones, información tanto general como detallada en cuanto al proceso de arribo de los pasajeros, dispositivos como torniquetes de entrada y de salida, comportamiento de las facilidades de servicio en las taquillas, detalles relacionados con la estructura física de la estación como tiempos caminando, disposición y asignación de zonas de espera para las rutas y capacidad de la estación (Tabla 1).
2. La matriz origen-destino tal y como es descrita en la sección anterior: modelo para los trasbordos
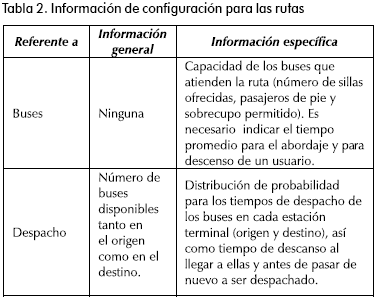
3. Características de las rutas como comportamiento del despacho, flota disponible, capacidad de los vehículos, tiempos de descanso, tiempos de ascenso y descenso, etc. (ver Tabla 2).
Una vez obtenida esta información se puede iniciar la simulación, cuyo tiempo de ejecución dependerá tanto de la longitud de la corrida (tiempo a simular) y del número de entidades (taquillas, torniquetes, zonas de abordaje, rutas).
Durante el proceso de simulación se calculan las medidas de desempeño dependiendo de la entidad. Las siguientes medidas estándar fueron aplicadas a todas aquellas entidades que presentan fenómenos de espera y ofrecen facilidades de servicio:
• Arrival Rate: la tasa de arribo de usuarios a la línea de espera de la entidad (número esperado de llegadas por unidad de tiempo). No se debe confundir con los tiempos de arribo entre usuarios.
• Throughput: la tasa de atención de usuarios.
• Service time: los tiempos de servicio.
• Utilization: la probabilidad de que la cola no esté vacía y el servidor se encuentre ocupado.
• Queue Length: la longitud de la cola.
• Residence Time: tiempo de permanencia en el sistema (incluye el tiempo de servicio).
• Waiting Time: tiempo de espera (permanencia en la cola).
También se usaron las siguientes medidas particulares:
• Para las estaciones: el número de usuarios que se encuentran dentro de la estación, el número de usuarios perdidos por haber excedido la capacidad de la estación.
• Para las fuentes de usuarios: el intervalo de tiempo entre arribos.
• Para las rutas: el nivel de ocupación de los buses. Cantidad de pasajeros sentados, de pie, y el nivel de sobrecarga. Tiempo total de viaje entre las estaciones de origen y destino.
• Para las zonas de abordaje: tiempo entre arribos de buses. Tiempos de espera, de servicio y de permanencia de los buses.
Resultados
El modelo teórico y su implementación en la herramienta prototipo permiten representar de manera adecuada tanto STPM sencillos como complejos; esto dado a gran cantidad de detalles de este tipo de sistemas que se encuentran representados en el modelo. Se obtuvieron de manera satisfactoria las medidas propuestas, quedando además abierta la posibilidad de añadir otras de acuerdo a requerimientos posteriores.
Con la ayuda de SimJava (Simatos, 2000), fue posible ofrecer la opción de usar dos métodos de análisis de datos de salida, y la generación de reportes tanto escritos como gráficos. Los métodos de análisis de datos ofrecidos son réplicas independientes (Independent Replications) y medias por lote (Batch Means). Mediante su aplicación es posible determinar la media para cada medida y un intervalo de confianza con el nivel especificado por el usuario.
La Figura 5 muestra el reporte gráfico obtenido para el tiempo total de los usuarios en el sistema. La línea roja indica el comportamiento de la media muestra a través del tiempo. Las líneas verdes verticales dividen los lotes (o batches) en los que fue dividida la corrida, mientras que las horizontales representan la media muestral para cada uno de los intervalos. La zona amarilla representa el intervalo de confianza obtenido para la media, la línea en el centro de esta zona es la media total.
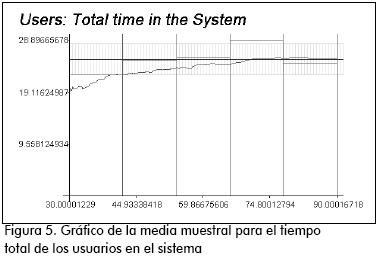
Se realizaron pruebas para comprobar la validez y sensibilidad del modelo ante el cambio de los parámetros. Las reacciones fueron las esperadas.
Aunque los tiempos de ejecución de la simulación son altos (dependen directamente del número de entidades), aún son admisibles y es posible realizar corridas sin grandes requerimientos de hardware (en Serrano, 2004, se encuentra información más completa sobre el desempeño del prototipo).
Conclusiones y recomendaciones
Como se ha mencionado a lo largo del artículo, la posibilidad de reemplazar las suposiciones de los modelos teóricos tradicionales para el estudio de sistemas de líneas de espera, mediante el empleo de un modelo de simulación flexible, facilita notablemente el estudio de un STPM, y más aún, la realización de análisis de sensibilidad que brinden soporte a la toma de decisiones. Además, el esquema general del STPM a partir del cual fue desarrollado el modelo, es fácilmente adaptable a varios sistemas de transporte masivo estructurado, como por ejemplo, un sistema férreo, el Metro, etc. Indudablemente, modelos como este contribuyen notablemente al desarrollo urbano de nuestras ciudades, no quedando solo como la realización de un ejercicio académico.
Por otra parte, una de las posibles mejoras para el modelo, ya que este se centra en principalmente en los fenómenos del sistema directamente relacionados con los usuarios, sería el considerar de manera más completa los fenómenos referentes al tránsito de los buses a lo largo del sistema. Otro de los campos en donde se cree es oportuno introducir mejoras es el de los trasbordos, en particular, en el proceso de selección de la ruta o rutas por parte de los usuarios, pues en la realidad no siempre cuentan con información perfecta (sobre la estructura de las rutas y las distancias), ni no siempre actúan usando criterios de optimización como el de modelo expuesto.
Bibliografía
Hillier, F. S. y Lieberman, G. J., Introducción a la investigación de operaciones, sexta edición, McGraw-Hill, México, 1997. [ Links ]
Johansen, O., Introducción a la teoría general de sistemas, Limada, México, 1994. [ Links ]
Kleinrock, L., Queueing Systems, John Wiley & Sons, New York, Vol 1., Theory; Vol 2., Computer Applications, 1976 [ Links ]
Law, A. M. and Kelton, W. D., Simulation Modeling and Analysis, Tercera Edición, McGraw-Hill, New York, 2000. [ Links ]
Pérez, L., Teoría de colas, Universidad Nacional de Colombia-Medellín, Facultad de ciencias, posgrado en matemáticas, 1985. [ Links ]
Robertazzi, T. G., Computer Networks and Systems. Queueing theory and performance evaluation, Springer, 2000. [ Links ]
Ross, S.M., Simulación, segunda edición, Prentice - Hall, México, 1997. [ Links ]
Saaty, T. L.., Elements of queueing theory with applications, McGraw-Hill, New York, 1961. [ Links ]
Serrano, A., Desarrollo de un prototipo para la simulación de un sistema de transporte público masivo mediante modelamiento estocástico, tesis de pregrado, Departamento de Ingeniería de Sistemas e Industrial, Universidad Nacional de Colombia, 2004. [ Links ]
Simatos, C., Making simjava count, MSc. project report, School of Informatics, University of Edinburgh, 2002. [ Links ]
Wolff, R. W., Stochastic Modeling and the Theory of Queues, Prentice-Hall, New York, 1989. [ Links ]
3 "
un objeto posee sinergia cuando el examen de una alguna de sus partes (incluso cada una de sus partes) en forma aislada, no puede explicar o predecir la conducta del todo." (Johansen, 1994).
4 Cuando los procesos de llegada de usuarios son representados mediante un proceso de Poisson, los tiempos entre arribos, se comportan de acuerdo a una distribución exponencial (Pérez, 1985).
5 En el modelo final se usó una combinación de la distancia entre las estaciones, el número que paradas que hace la ruta, y una constante que ayuda a penalizar el exceso de trasbordos (Serrano, 2004).
6 En el modelo de simulación implementado se asume que todas las estaciones tienen dos costados para el ingreso y salida de los usuarios.














