Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.26 no.3 Bogotá Sep./Dec. 2006
Maritzabel Molina Herrera1 y Javier Alberto Ortiz Porras2
1 Ingeniera civil, Universidad Nacional de Colombia. M.Sc. en Estructuras, Universidad Nacional de Colombia. Profesora, Departamento de Ingeniería Civil y Agrícola, Facultad de Ingeniería, Universidad Nacional de Colombia, Bogotá. mmolinah@unal.edu.co
2 Ingeniero civil, Universidad Industrial de Santander, Colombia. M.Sc. en Estructuras Universidad Nacional de Colombia, Bogotá. jaortizp@unal.edu.co
RESUMEN
En el campo de la lámina delgada continuamente aparecen nuevos tipos de perfiles que son desarrollados con el objeto de mejorar los ya existentes. Un ejemplo de esto es la aparición del perfil M, elaborado para mejorar la eficiencia a corte del perfil C y su resistencia al arrugamiento del alma por efecto de cargas concentradas. Teóricamente, se logra el objetivo de mejorar la resistencia a corte del perfil C y de algún modo su resistencia al arrugamiento del alma, pero debido a los dobleces generados en el alma (rigidizadores intermedios) para acortar la longitud de pandeo, se producen comportamientos que desde el punto de vista de esfuerzos por flexión y deflexiones no pueden ser analizados con los fundamentos teóricos de la mecánica tradicional. Este comportamiento se ve acentuado con la presencia de cargas concentradas. Por la razón expuesta anteriormente, a parte de la determinación de la resistencia teórica del perfil M (basada en el AISI 1996), se desarrollan pruebas sobre cuatro modelos de los que se obtienen tópicos como: carga máxima resistida, identificación visual del posible tipo de falla, deflexiones (centro de la luz) y deformaciones unitarias (εx, εy, εxy), y adicionalmente se elaboran modelos matemáticos simplificados y por elementos finitos (en el programa COSMOS/M), con el fin de hacer una revisión detallada del comportamiento de los esfuerzos y deformaciones en el perfil. La calibración de estos modelos se lleva a cabo con base en los resultados obtenidos de los ensayos. De otra parte, se hacen pruebas cíclicas bajo cargas pseudoestáticas, con el objeto de estudiar el comportamiento histerético del perfil MM, con y sin rigidizadores.
Palabras clave: acero laminado en frío, arrugamiento del alma, rigidizadores, histéresis, elementos finitos, perfil MM.
ABSTRACT
New sections are continually being developed in the cold-formed steel world to improve the performance of existing sections. M-section development provides an example of improving C-sections' shear resistance and web crippling resistance against C-sections' concentrated loads. C-sections' shear nominal strength can be achieved through locating tow web intermediate stiffeners (M-sections) even though web crippling resistance cannot be increased in the same way. Such intermediate stiffeners mean that M-section stresses and deflections cannot be analysed with traditional material mechanics. Concentrated loads cause this behaviour to become increased; 4 different models and 3 tests for each of then were thus developed, as well as determining M-sections' theoretical resistance (based on 1996 AISI). The values obtained corresponded to maximum resistance load, visual identification of any possible type of failure, deflections (at middle span) and deformations (εx, εy, εxy). Mathematical models were also used for comparing the finite element method and simplified mathematical models' test results for a detailed review of MM-section stress and deformation. These models were calibrated on the test results. After the failure mode was identified for each model, MM-section maximum resistance load was compared to nominal load (according to AISI formulation, also aiding formulating nominal strength calculation). The information obtained from tests and mathematical models was analysed to observe parameter (Δ, σ y τ) tendencies respecting applied load (P). Cyclic tests under pseudo-static loads were performed to study MM-sections' hysteretic behaviour.
Keywords: cold-formed steel, web crippling, stiffeners, hysteresis, finite elements, MM section, concentrated loads.
Recibido: febrero 16 de 2006
Aceptado: octubre 10 de 2006
Introducción
Los elementos estructurales de lámina delgada han sido aceptados en el mundo debido a las ventajas que suponen su bajo peso, fácil colocación y economía frente a otros. Sin embargo, para su uso se requiere de un diseño meticuloso por los inconvenientes que acarrean sus reducidos espesores.
Los primeros países en utilizar la lámina delgada como solución a problemas estructurales fueron Estados Unidos y Gran Bretaña, por el año de 1850. También fueron ellos los que dieron muestras de grandes progresos en las investigaciones sobre el comportamiento de elementos estructurales elaborados con este material, alrededor de los años 1960 y 1970, con los trabajos realizados por George Winter y posteriormente por Wei Wen Yu.
Actualmente la mayor parte de las investigaciones sobre la lámina delgada son realizadas en Estados Unidos, Canadá, Europa y Asia, ya sea por universidades u otro tipo de instituciones. La mayoría de estas son realizadas con el propósito de mejorar las normas existentes y ampliar sus alcances; como ejemplo se puede nombrar la tesis doctoral Combined Web Crippling and Bending Moment Failure of First- Generation Trapezoidal Steel Sheeting Experiments, Finite Element Models, Mechanical Models (Hofmeyer, 2000), en la cual se hace un estudio teórico y experimental del problema de pandeo local bajo cargas concentradas y se comparan los resultados con modelos matemáticos calibrados.
Algunas de las instituciones que han dedicado tiempo a la investigación de la lámina delgada son el AISI, la AISC, el ASCE, la Universidad de Cornell, el Centro para Estructuras de Acero Laminado en Frío de la Universidad de Missouri – Rolla, entre otras.
En la actualidad el desarrollo en el campo de la lámina delgada a nivel mundial es avanzado. En nuestro país, específicamente en la Universidad Nacional de Colombia, se ha desarrollado una línea de investigación en este tema teniendo en cuenta que el diseño de estos elementos no debe limitarse a cumplir una norma extranjera, sino que ha de dedicarse tiempo al entendimiento del comportamiento estructural de sus componentes. Esto último toma gran importancia debido a que las empresas que producen estos perfiles en el país introducen en el mercado formas no convencionales que trascienden los alcances de las normas actuales.
Por lo anterior, desde hace algunos años la Universidad Nacional de Colombia, en conjunto con la empresa privada, han venido realizando investigaciones en el campo de la lámina delgada. En el año 1998, debido al interés despertado por las ventajas que traía la utilización de ciertos perfiles como elementos estructurales para placas de entrepiso, se llevaron a cabo las investigaciones Diseño de placas en sección compuesta empleando perfiles C en lámina delgada, formados en frío como viguetas de soporte lámina colaborante – Steel Deck como tablero de refuerzo de la torta superior (Andrade, 1998) y Comportamiento a flexión del sistema conformado por un perfil MM y una losa aligerada compuesta por concreto, perfil Omega y bloque de arcilla (Caro-Muñoz, 2003). En esta última se advirtieron algunos problemas de pandeos locales sobre el perfil MM en los sitios de apoyos y en los puntos de aplicación de cargas concentradas, que dieron origen al presente estudio.
El objetivo principal de esta investigación es la evaluación del comportamiento del perfil MM bajo cargas concentradas, y el análisis de su comportamiento histerético. En la búsqueda de este objetivo, se plantean objetivos secundarios como:
-Determinar la resistencia teórica y experimental del perfil MM.
-Realizar una modelación numérica calibrada del perfil MM para el estudio de la distribución de esfuerzos y deflexiones.
-Establecer el comportamiento del perfil MM (conectado a una viga de concreto), solicitado a ciclos de carga reversibles.
Determinación teórica de la resistencia del perfil MM
La propuesta para la determinación de la resistencia teórica del perfil MM se basa en la utilización de las ecuaciones propuestas por el AISI 1996 (American Iron and Stell Institute, 1996; Yu, 1991), sujetas a algunas suposiciones (Ortiz, 2006).
Los cálculos se hicieron para el perfil M 30x10x2 mm producido por la empresa Tubos Colmena S.A.
Resistencia a flexión
Resistencia nominal a flexión
A la Primera Fluencia:

Fy = esfuerzo fluencia del acero
Se =módulo de sección efectivo
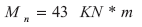
Capacidad inelástica de la sección
Como la aleta en compresión está constituida por un elemento con rigidizadores de borde, se toma Cy = 1, es decir, que la capacidad inelástica de la sección no se tiene en cuenta (Ortiz, 2006).
Resistencia a flexión debida a pandeo lateral
Resultados de investigaciones hechas por Winter (Winter, 1947) y posteriormente por Wei Wen Yu (Yu, 1991), indican que las secciones cajón generalmente no presentan reducción de su resistencia a flexión por pandeo lateral.
El AISI 96 realiza el siguiente chequeo para determinar si la sección cajón se ve afectada por pandeos laterales:
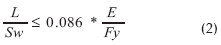
L = longitud del elemento
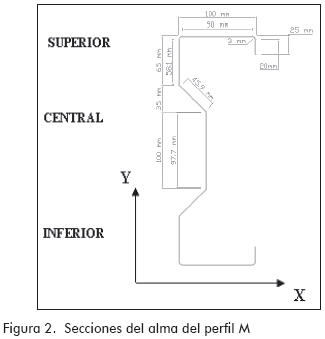
Sw = separación entre almas (Figura 1)
E = módulo elasticidad del acero
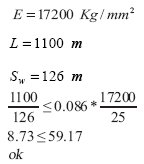
Este resultado indica que la capacidad a flexión del perfil MM no se ve afectada por pandeo flexotorsional.
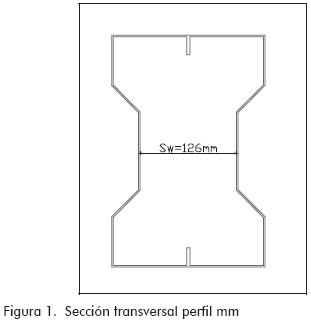
Resistencia a cortante
La resistencia nominal al corte Vn, en una sección puede desarrollarse de diferentes maneras, dependiendo de la relación de esbeltez del alma. Esta relación de la longitud del segmento vs. su espesor marca el estado bajo el cual se presenta la falla (pandeo en rango elástico, pandeo en rango inelástico o plastificación) (LaBoube, 1978; Gaylord, 1992; Valencia, 1997).
Suponiendo que el alma del perfil M está constituida por tres elementos (inferior, central y superior) separados por dos segmentos inclinados (que son considerados rigidizadores intermedios), como se puede ver en la Figura 2, se hace el análisis de cada una de ellas para establecer su comportamiento a corte y así establecer la posibilidad de falla por pandeo o plastificación.
Se tiene la siguiente información:

h = altura del elemento
t = espesor del elemento
Calculando el límite inferior de la relación (h/t) para el perfil sin rigidizadores intermedios (Kv = 5.34), se tiene:
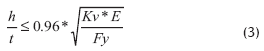
Kv = Coeficiente de pandeo de placas
El segmento plastifica por corte bajo un τ igual a:

τ = esfuerzo cortante
Hecha la verificación de las relaciones h/t de los elementos del alma y el chequeo de la inercia mínima de los rigidizadores intermedios (segmentos inclinados), se tiene que el alma del perfil M plastifica bajo solicitaciones de corte y que se cuenta con una altura de 294 mm para resistirlas, por lo que su resistencia nominal corresponde a:

Vn = cortante nominal
La resistencia nominal a cortante del perfil M es de 88.20 KN, por tanto la resistencia del perfil MM será de 176 KN.
Arrugamiento del alma
El problema de platinas con cargas localmente distribuidas fue estudiado por Sommerfeld en 1906, Timoshenko en 1910, Legget en 1937, entre otros.
Para vigas de acero que tienen el alma conectada a aletas se han llevado a cabo investigaciones por Lyse y Godfrey en el año de 1935, Jockey en 1970, Bagchi (Bagchi, 1968) y otros.
Las provisiones de diseño de AISI para arrugamiento del alma están basadas en extensas investigaciones realizadas en la Universidad de Cornell por Winter y Pian, y por Zetlin, en las décadas de los cuarenta y cincuenta y más recientemente por la Universidad de Missouri-Rolla por Hetrakul (Hetrakul, 1978) y Yu (Yu, 1981).
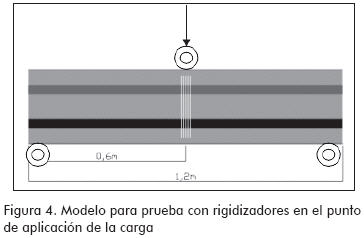
Las pruebas para determinar la resistencia al arrugamiento del alma del perfil MM están divididas en dos etapas. En la primera se utilizan probetas sin rigidizadores de apoyo en el punto de aplicación de carga induciendo la falla en este sitio (Figura 3). Para la segunda, se suministran rigidizadores bajo el punto de aplicación de carga, con lo que la falla se traslada a las zonas de apoyo (Figura 4).
Los cálculos teóricos se hacen teniendo en cuenta que las porciones del alma que sufren el arrugamiento son: la inferior cuando la falla es en los apoyos, y la superior cuando la falla es en el punto de aplicación de carga, en los dos casos h=65 mm.
Cálculo de resistencia al arrugamiento del alma en el punto de aplicación de la carga (Figura 3).
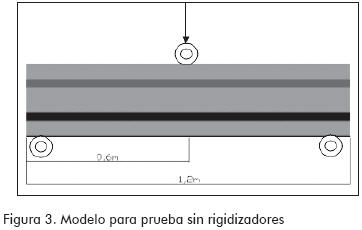

N = longitud de apoyo
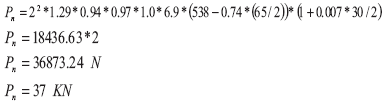
Pn = carga nominal resistida
Cálculo de resistencia al arrugamiento del alma en los puntos de apoyo (Figura 4)
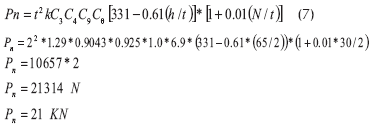
Diseño de los rigidizadores de apoyo (Figura 5)
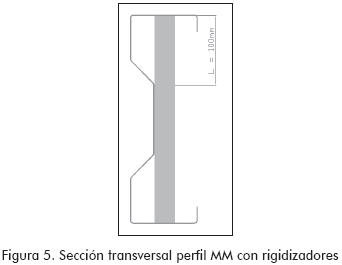
Los rigidizadores se deben diseñar para que sean capaces de soportar toda la solicitación impuesta, acorde con lo especificado por el AISI 96.
Plastificación
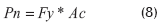
Ac = área sección transversal platina
Debido a que en la zona considerada como crítica (parte superior e inferior del perfil), el rigidizador no se encuentra conectado al alma del perfil, se toma como Ac, el resultado de multiplicar el espesor del perfil por su ancho (Figura 6).
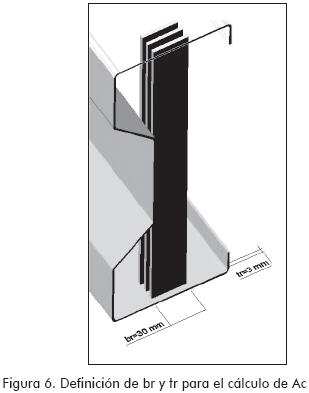
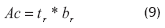
tr = espesor rigidizador
br = ancho rigidizador
Pn = 18 KN
Carga crítica de pandeo
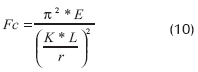
Fc = esfuerzo pandeo Euler
Pandea en rango inelástico
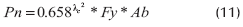
Pn = 8.5 KN
Determinación experimental de la resistencia del perfil MM
Para la primera etapa del proyecto se utilizan cuatro tipos de modelos diferentes y se realizan tres ensayos por tipo. Con cada uno de estos modelos se busca definir: tipo de falla, carga máxima y comportamiento del perfil en diferentes condiciones.
Descripción de los modelos
En los cuatro modelos se emplearon perfiles MM de 1,20 m de longitud con rigidizadores distribuidos de la siguiente manera: en el primero no se colocaron rigidizadores en el perfil, para el segundo se dispusieron rigidizadores en el punto de aplicación de carga; en el tercero y en el cuarto, además de los rigidizadores colocados en el punto de aplicación de carga, se agregaron otros en los puntos de apoyo (Figuras 7 a 10).
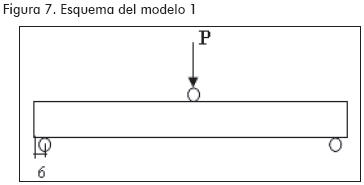
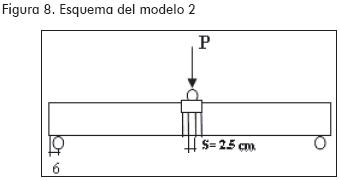
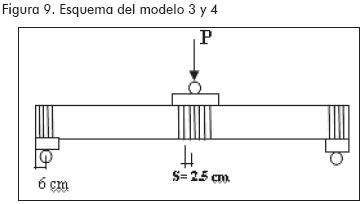
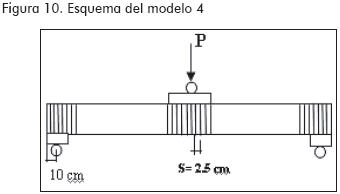
La toma de datos se realizó mediante los siguientes dispositivos (Figura 11):
-Deflexiones: deformímetro mecánico centro de la luz.
-Esfuerzos por flexión: deformímetro eléctrico de una dirección centro de la luz.
-Esfuerzos por corte: deformímetro de tres direcciones en el cuarto de la luz (ubicado sobre el alma).
Resultados experimentales
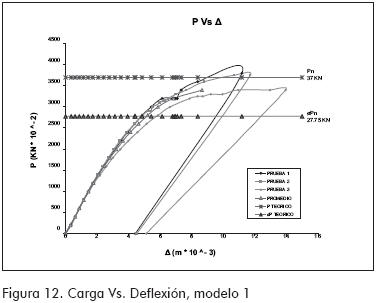
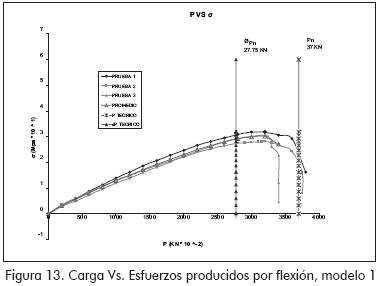
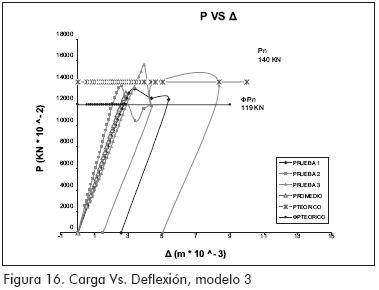
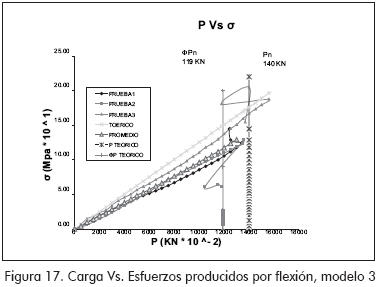
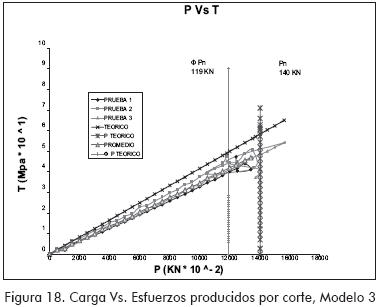
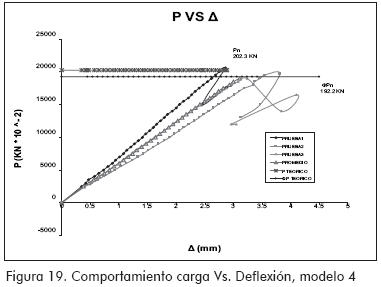
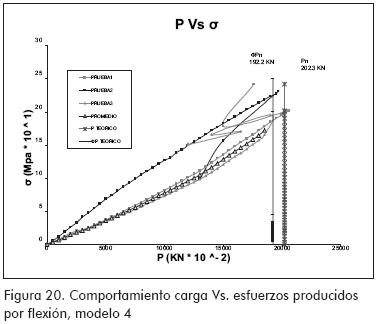
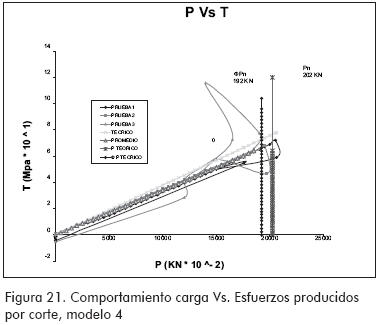
Los resultados obtenidos fueron representados a través de gráficas P-Δ, P-σ y P-τ (P, carga aplicada; Δ, deflexiones; σ, esfuerzos por flexión; τ, esfuerzos por corte).
MODELO 1 (Figuras 12 y 13)
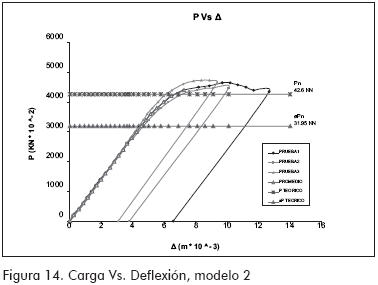
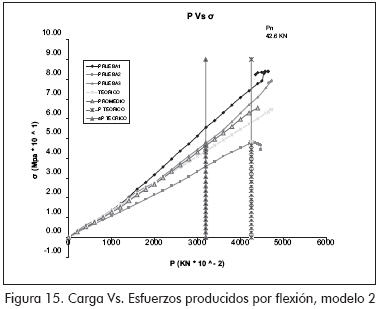
MODELO 2 (Figuras 14 y 15)
MODELO 3 (Figuras 16 a 18)
MODELO 4 (Figuras 19 a 21)
Modelos matemáticos
Modelo matemático simplificado
Este método se basa en la determinación de cortantes, momentos y deflexiones, haciendo uso de la estática y de la integración de la ecuación del momento flexionante (Timoshenko, 1986).
Deflexiones
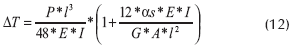
l = Longitud libre entre centros de apoyo.
G = Módulo de cortante.
αs = Coeficiente de cortante.
A = Área sección transversal del perfil.
I = Momento de inercia efectivo.
Cortante a ¼ de la luz

Momento en el centro de la luz

Esfuerzo cortante promedio

Esfuerzo por flexión

c = distancia fibra extrema en tensión o en compresión respecto al eje neutro de la sección
Modelo matemático utilizando el método de los elementos finitos
La realización del modelo matemático basado en el método de los elementos finitos fue llevada a cabo mediante la utilización del programa COSMOS/M.
Los modelos están constituidos básicamente por elementos laminares (shell).
Además de hacer un análisis numérico de tipo lineal, para los modelos 1 y 2 se realizaron análisis no lineales (no linealidad del material y no linealidad geométrica) con el objeto de estudiar con más detalle el comportamiento de esfuerzos y deformaciones que se presentan en el perfil.
Resultados de los modelos matemáticos por el método de los elementos finitos
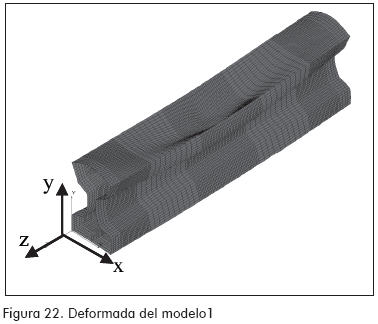
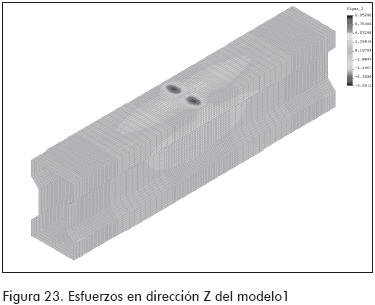
MODELO 1 (Figuras 22 a 24)

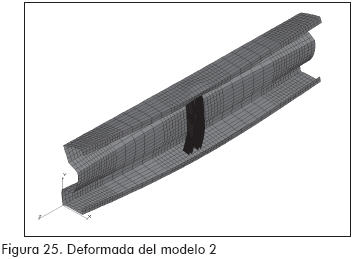
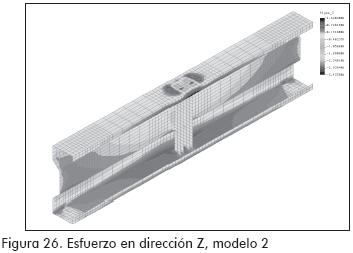
MODELO 2 (Figuras 25 a 27)

MODELO 3 y 4 (Figuras 28 a 30)



En las Figuras 24 y 27 se pueden apreciar zonas de concentración de esfuerzos, que en los ensayos correspondieron a los sitios donde se presentaron las fallas para los modelos 1 y 2, respectivamente.
6. Comportamiento histerético del perfil MM
6.1 Descripción de los modelos
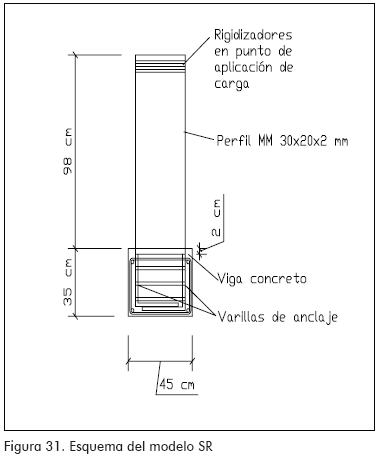
En esta etapa fueron utilizados perfiles MM de 1,0 m de longitud unidos a una viga de concreto. Se analizaron tres condiciones diferentes que fueron: modelo SR perfil sin concreto o rigidizadores en el punto de unión con la viga, modelo CR con rigidizadores en el punto de unión, y modelo CC con concreto reemplazando a los rigidizadores en el punto de unión (Figuras 31 a 33).
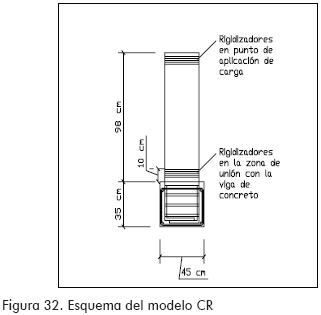
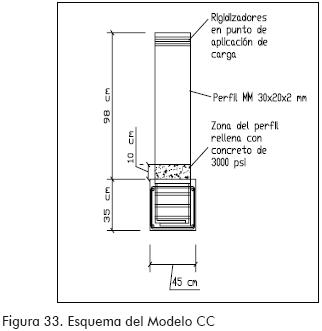
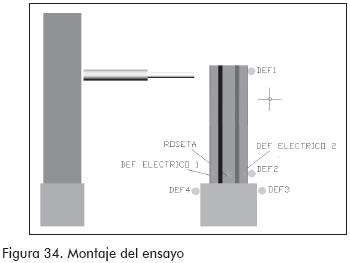
En el montaje se utilizaron cuatro deformímetros mecánicos, dos deformímetros eléctricos de una dirección y una roseta (deformímetro de tres direcciones). El mecánico número 1, colocado en la parte superior del perfil, se utilizó para calcular las deflexiones en el perfil; el número 2, colocado en la parte inferior del perfil, cercano a la zona de falla, fue usado como control (especialmente para estimar tendencias), el 3 y el 4 se destinaron para hacer correcciones debidas a posibles rotaciones de la viga de concreto; adicionalmente, los deformímetros eléctricos 1 y 2, y la roseta, para determinar los niveles de esfuerzos alcanzados en la zona de falla, hasta la aparición de la misma (Figuras 34 y 35).

Resultados de los ensayos cíclicos
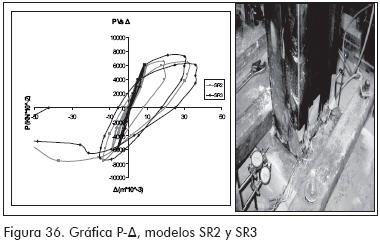
Los resultados de los ensayos cíclicos son presentados como gráficas P Vs Δ (Figuras 36 a 38).

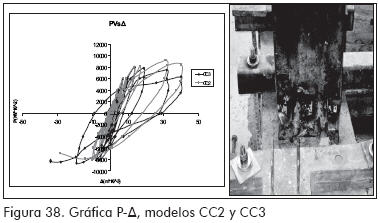
Análisis de resultados y conclusiones
Los pandeos locales que se presentan en los puntos donde existen solicitaciones concentradas hacen que no se aproveche eficientemente la resistencia a corte y a flexión que puede ofrecer el perfil.
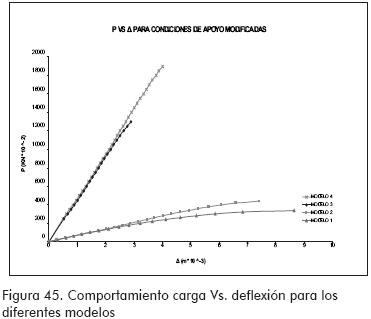
La resistencia del perfil MM se mejora en gran medida al colocar rigidizadores en las zonas donde existen solicitaciones puntuales, pasando de 36 KN en el modelo 1 a 193 KN en el modelo 4 (Figura 45).
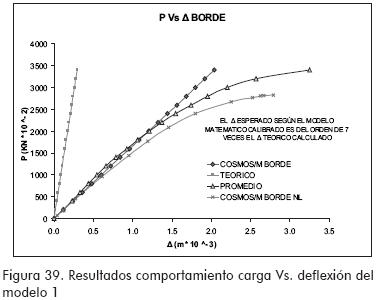
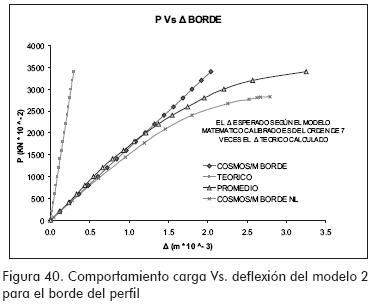
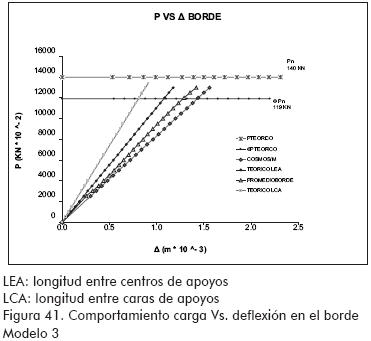
Los valores de cargas máximas alcanzadas en los ensayos estuvieron entre el 75 y 100 % de los valores teóricos esperados (ver Figuras 40 a 44).
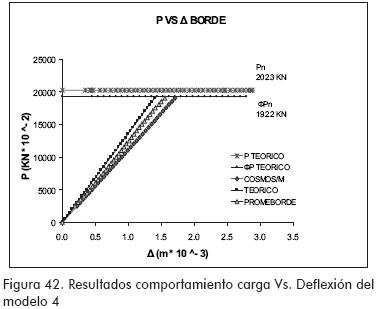
Se encontró que la sección M presenta deflexiones mayores que las teóricas esperadas, debidas a la tendencia a la deformación de su sección, este efecto se atenúa a medida que se colocan rigidizadores (Figuras 39, 40, 41, 42 y 45).
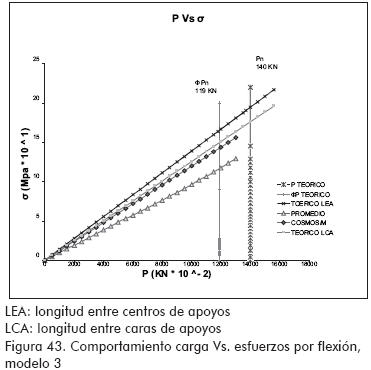
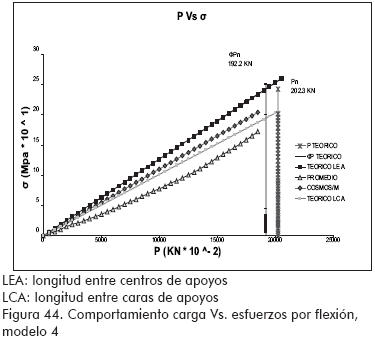
Las tendencias de esfuerzos y deflexiones encontradas haciendo uso de la modelación numérica por elementos finitos mostraron una buena correlación con los resultados experimentales (Figuras 39 a 42).
La distribución de esfuerzos por flexión encontrada en el perfil (haciendo uso de los modelos matemáticos), dista notoriamente de la teórica esperada. Este efecto disminuye a medida que se colocan los rigidizadores en el perfil (Figuras 46 a 48).
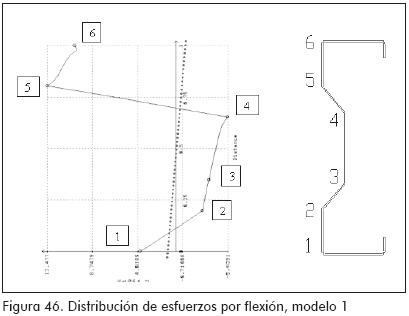
La tendencia a la deformación de la sección del Perfil M afecta tanto el comportamiento de deflexiones como la distribución de los esfuerzos por flexión. Este efecto se reduce de forma apreciable al colocar rigidizadores.
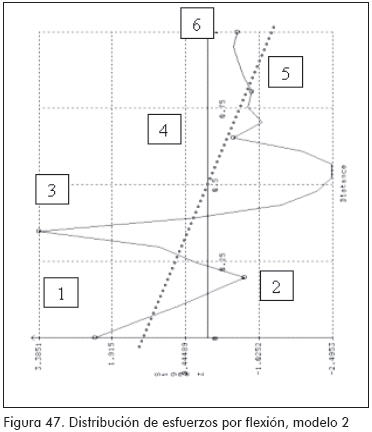
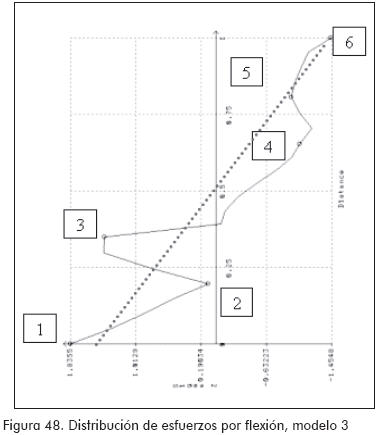
El tipo de falla observado en los ensayos cíclicos corresponde a pandeos locales cercanos al punto de unión entre el perfil MM y la viga de concreto (Figuras 36 a 38).
En los ensayos cíclicos se encontró que el colocar concreto o rigidizadores en el punto de unión entre el perfil y la viga mejora la resistencia del perfil pero no afecta en una forma apreciable su comportamiento histerético (Figura 49).
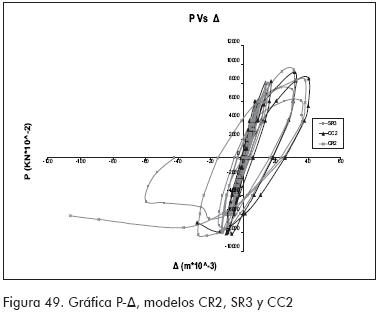
Las cargas máximas obtenidas para los modelos fueron: 66 KN para SR, 89.9 KN para CR y 83 KN para CC y rotaciones de alrededor de 0.035 radianes (Figura 49).
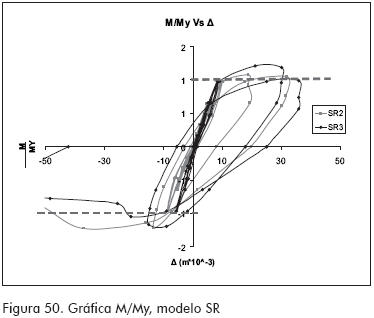
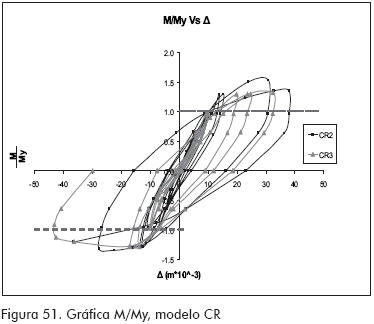
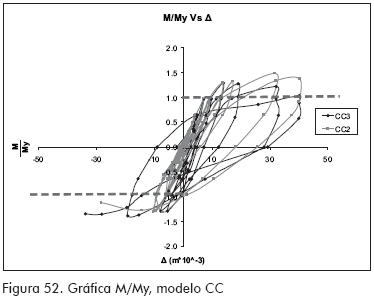
En teoría los modelos alcanzan a trabajar en el rango inelástico del material, obteniéndose valores de M/My de 1.2 para SR y valores hasta de 1.5 para CR y CC (ver Figuras 50 a 52).
Agradecimientos
A la empresa Tubos Colmena S. A. por el apoyo y la confianza que pusieron en esta investigación.
A los laboratorios del Instituto de Extensión e Investigación - IEI de la Facultad de Ingeniería de la Universidad Nacional de Colombia, sede Bogotá.
Nomenclatura
A = área sección transversal del perfil
Ac = área sección transversal platina
br = ancho rigidizador
c = distancia fibra extrema en tensión o en compresión
Respecto al eje neutro de la sección.
E = módulo elasticidad del acero
Fc = esfuerzo pandeo Euler
Fy = esfuerzo fluencia del acero
G = módulo de cortante
h = altura del elemento
I = momento de inercia efectivo.
Kv = coeficiente de pandeo de placas
L = longitud del elemento
l = longitud libre entre centros de apoyo
N = longitud de apoyo
P = carga aplicada
Pn = carga nominal resistida
Se = módulo de sección efectivo
Sw = separación entre almas
t = espesor del elemento
tr = espesor rigidizador
Vn = cortante nominal
αs = coeficiente de cortante
τ = esfuerzo cortante
Bibliografía
American Iron and Steel Instituye (AISI)., Cold Formed Steel Design Manual, 1996. [ Links ]
Andrade Ordoñez, V. M., Diseño de Placas en Sección Compuesta Empleando Perfiles C en Lámina Delgada, Formados en Frío como Viguetas de Soporte Lámina Colaborante – Steel Deck como Tablero de Refuerzo de la Torta Superior., Universidad Nacional de Colombia. Colombia, 1998. [ Links ]
Caro, G. J. y Muñoz, G. D., Comportamiento a flexión del sistema conformado por un perfil MM y una losa aligerada compuesta por concreto, perfil omega y bloque de arcilla., Universidad Nacional de Colombia, Colombia, 2003. [ Links ]
Gaylord Jr, E. H., Steel Structures., Third Edition, Mc Graw Hill, 1992. [ Links ]
Hetrakul, N. and Yu, W. W., Structural Behaviour of Beam Webs Subjected to Web Crippling and a Combination of Web Crippling and Bending., Final Report, Civil Engineering Study 78-4, University of Missouri –Rolla, Rolla, MO, June, 1978. [ Links ]
Hofmeyer, H., Combined web crippling and bending moment failure of first-generation trapezoidal steel sheeting., Universidad de Eindhoven, 2000. [ Links ]
LaBoube, R. A. and Yu, W. W., Structural Behaviour of Beam Webs Subjected Primarily to Shear Stress., Final Report, Civil Engineering Study 78-2, University of Missouri-Rolla, Rolla, MO, June, 1978. [ Links ]
Ortiz Porras, J. A., Determinacion del comportamiento bajo cargas concetradas de perfiles de lamina delgada (MM)., Tesis de Maestría, para optar al título de Msc en Estructuras, Universidad Nacional de Colombia, Facultad de Ingeniería Civil y Agrícola, 2006. [ Links ]
Timoshenko, G., Mecánica de Materiales., Segunda Edición, Grupo Editorial Ibero América, California, 1986. [ Links ]
Valencia Clement, G., Estructuras de Acero. Diseño con factores de carga y de resistencia., Editorial Escuela Colombiana de Ingeniería, Bogotá, 1997. [ Links ]
Winter, G., Discusión of Strength of Beams as Determined by Lateral Buckling, by Karl de Vries., Transactions, ASCE, Vol. 112, 1947. [ Links ]
Yu, W. W., Cold Formed Steel Design., Segunda Edición, John Wiley and Sons, INC. 1991. [ Links ]














