Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.26 no.3 Bogotá Sep./Dec. 2006
Myriam Rocío Pallares Muñoz1 y Wilson Rodríguez Calderón2
1 Ingeniera civil, especialista, UIS, Bucaramanga. M.Sc. en Métodos Numéricos para Ingeniería, Universidad Politécnica de Cataluña. mrocio03@hotmail.com
2 Ingeniero civil. Especialista, UIS, Bucaramanga. M.Sc. en Métodos Numéricos para Ingeniería, Universidad Politécnica de Cataluña. Profesor Investigador, Departamento de Ingeniería Civil, Pontificia Universidad Javeriana. wilroca@javeriana.edu.co
RESUMEN
Las nuevas tecnologías informáticas abren un mundo inagotable de posibilidades en el ámbito de la docencia. En el caso particular de las enseñanzas técnicas, el uso de estas tecnologías se convierte en indispensable por la propia naturaleza de los recursos actuales de diseño y producción industrial. El trabajo que se presenta a continuación consiste en la elaboración de un material didáctico (software educativo) destinado a la enseñanza de la mecánica de los fluidos, particularmente al análisis de sistemas de tuberías, tanques y bombas,3 dirigido en principio a los estudiantes de ingeniería civil de la Universidad Santo Tomás de Bogotá. Este tipo de materiales, han sido desarrollados y utilizados con éxito por varias universidades a nivel mundial,4 a lo largo de los últimos años, dentro de los nuevos planes de estudio. El software didáctico objeto de este trabajo se ha construido utilizando el lenguaje de programación Visual Basic.5 El resultado es una herramienta educativa muy útil que permite una efectiva comunicación profesor-alumno, adecuada tanto para las clases presenciales en el aula de clase como para el trabajo personal del estudiante (Ángel y Bautista, 2001; Aguilar, 2002).
Palabras clave: desarrollo de software, software educativo, Método de Cross
ABSTRACT
New information technologies have opened up a world of inexhaustible possibilities in teaching. Using such technologies in technical teaching has become indispensable due to the nature of current resources in industrial design and production. This work consists of preparing didactic material (educational software) aimed at teaching fluid mechanics, particularly analysing tube, tank and pumping systems, initially aimed at civil engineering students from the Universidad Santo Tomás in Bogotá. Such materials have been successfully developed and used in their formal programmes by several universities around the world during the last few years. The didactic software mentioned in this work was constructed using Visual Basic programming language. This has resulted in a very useful educational tool, leading to effective teacher–student communication which is suitable for both the classroom and students’ personal work (Angel y Bautista, 2001; Aguiar, 2002).
Keywords: software development, educational software, Cross’s method.
Recibido: marzo 30 de 2006
Aceptado: agosto 10 de 2006
Introducción
Cuando se intenta resolver un problema de redes de tubería no es conveniente utilizar la vía analítica, dado que el sistema resultante es de carácter no lineal debido a la naturaleza potencial de las ecuaciones de pérdida en tuberías, bien sea a través de la fórmula de Hazen-Williams para flujo en tuberías comerciales, o de la ecuación de Darcy-Weisbach utilizada en aplicaciones particulares, donde es posible calcular el factor f por medio de la formulación de Coolebrook u otra empírica dependiendo del régimen al que se encuentre sometido el flujo (laminar o turbulento) (Aho y Hopcroft, 1974; Franzini y Finnemore, 1999; Burden y Faires, 1998; Zienkiewicz y Taylor, 1994).
En problemas reales de flujo es necesario emplear métodos de aproximaciones sucesivas comúnmente llamados iterativos. Quizá el más conocido sea el de Hardy-Cross, el cual utiliza la ecuación de continuidad para determinar los flujos de partida y calcula una corrección en cada circuito (se usa para mejorar el balance en ellos). Este procedimiento se realiza de manera repetitiva hasta que la corrección calculada alcanza valores muy pequeños que no modifican la solución. Tal situación conlleva al cálculo definitivo del flujo en cada uno de los elementos componentes del sistema (Gear, 1971; Mathews, 2000).
En redes pequeñas es posible resolver el problema implementando el método de Hardy-Cross en calculadoras programables; sin embargo, en redes mayores o que contienen varios depósitos de suministro (tanques), bombas y una buena cantidad de elementos, es conveniente contar con un programa de computador que pueda solucionar el problema utilizando el mismo método de Hardy-Cross o cualquier otro numérico iterativo disponible (Giles et al., 1994; Mott, 1996).
El software educativo Poseidón 1.0 es un modelador computacional de sistemas hidráulicos de n tuberías, n tanques y n bombas que tiene implementada la clásica ecuación de pérdidas de Darcy-Weisbach y el método de balance de Cross para la solución numérica de los circuitos hidráulicos. Sus características de manejo sencillo hacen de él una herramienta eficiente para la docencia en temas de análisis y diseño de sistemas hidráulicos o redes a presión.
El programa fue desarrollado dentro de un proyecto de investigación adelantado en el año 2005 como parte de la producción investigativa del grupo en simulación y control numérico SICON.6 La herramienta es un producto de la línea de investigación en modelación numérica que contempla el desarrollo de software pedagógico como un área estratégica de la investigación del grupo en la actualidad. Se espera que la comunidad académica y estudiantil pueda aprovechar y emplear este software en las actividades de docencia e investigación.
Motivación y objetivos
Con la introducción de los nuevos planes de estudio en la titulación de las ingenierías y, en general, de la gran mayoría de las carreras en Colombia, las asignaturas técnicas de ingeniería sufren una importante reestructuración. La apuesta por el sistema de créditos conlleva una reubicación de los contenidos en el currículo y una disminución en el número de horas lectivas globales. Además, se hace necesario introducir un carácter experimental en algunas de ellas con la asignación de prácticas en un laboratorio de informática (La enseñanza superior en el siglo XXI: Estrategias de futuro, 1998).
El diseño de estas herramientas educativas se constituye en un reto para cambiar el modo de enseñar, de manera que vaya más acorde con los instrumentos que las nuevas tecnologías ponen a nuestra disposición y, sobre todo, que permita realizar una educación ingenieril para la vida profesional, facilitando al alumno adaptarse a los distintos cambios que, sin duda, tendrá que acometer a lo largo de su carrera.
Por otro lado, los objetivos pedagógicos que se pretenden lograr son muy amplios, y entre ellos se pueden destacar:
Objetivos generales
- Familiarizar al alumno con las nuevas tecnologías informáticas en el campo de la ingeniería, intentando mostrar su utilidad tanto en la formación como en el posterior desarrollo profesional.
- Poner en práctica los conocimientos adquiridos en las clases teóricas, lo que hace más atractivo el aprendizaje de los distintos conceptos estudiados a través de la experimentación, ya sea esta guiada o autónoma.
- Inculcar el sentido del autoaprendizaje en los alumnos como método de trabajo habitual.
- Implicar al alumno en el estudio diario de la asignatura, lo que le permite seguir las clases teóricas con mayor interés.
Objetivo específico
- Proporcionar al alumno una herramienta para obtener la solución de un sistema de tuberías, tanques y bombas, sin la dependencia del profesor, capacitándolo para su autoevaluación en la resolución de ejercicios.
Nomenclatura
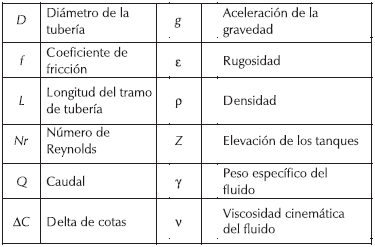
Marco teórico de la solución de sistemas hidráulicos a presión
Descripción del método de Cross
El de Cross es un método iterativo en el que se parte de unos caudales supuestos que cumplen la ecuación de continuidad en cada uno de los nodos de una malla hidráulica. Hecha esta suposición, se realizan ajustes que generalmente convergen a valores estables en pocas iteraciones. La convergencia se controla comparando la norma de las correcciones con un valor de tolerancia determinado (Munson et al., 2002; Potter y Wiggert, 2002).
El método se resume en los siguientes pasos:
1. Se supone inicialmente una cierta distribución de valores de caudal para el sistema en estudio;
2. Se calcula para cada tramo de la malla la pérdida de carga hf tomando en consideración el signo. La pérdida de carga a lo largo de un tramo puede ser expresada por la siguiente fórmula general:

3. Se determina la pérdida de carga total en cada circuito cerrado:

4. Se obtiene en cada circuito cerrado una suma de las cantidades: n r Qn-1;
5. Estas cantidades se designan por R, esto es:

6. Se ajusta el valor en cada circuito sumándose o restándose de los valores admitidos, la corrección Δ calculada por la expresión:

La expresión para Δ se obtiene del siguiente análisis:
Si la distribución de valores adoptados al iniciar fuera exacta, la corrección por hacer en cada circuito sería nula. Esto es: r Qn = 0. En caso contrario el valor debe ser ajustado o corregido en el circuito, pudiéndose escribir para cada tramo que Q = Q0 +Δ, donde Q0 es el valor de caudal adoptado inicialmente
Reemplazando e igualando, se obtiene:
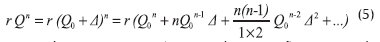
Teniendo en cuenta que Δ es un valor pequeño comparado con Q0, todos los términos que contienen Δ elevado a una potencia igual o superior a 2, son despreciables. Esto es,
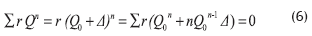
Es decir,

En la expresión (7), el numerador es la pérdida de carga para los caudales supuestos a lo largo del circuito, y el denominador es la resistencia total del circuito, o sea, la suma de lo que podrían ser las resistencias de cada uno de los tramos.
La expresión (7) puede escribirse como:

Si el valor obtenido de Δ es muy grande frente al de Q0, siendo n mayor que la unidad, evidentemente la aproximación no será buena. Con todo, esto no perjudicará al proceso una vez que las correcciones se hagan; el error irá disminuyendo progresivamente en una convergencia relativamente rápida.
7. Se recalculan las pérdidas de carga de cada circuito y se determina la nueva corrección para estos caudales.
8. Se repite el proceso hasta que se obtenga la precisión deseada.
Descripción de la ecuación de Darcy–Weisbash
Para aplicar el método de Hardy Cross al análisis de caudal en un sistema de tuberías ramificadas, es necesario el empleo de una fórmula de pérdidas. A continuación se desarrolla el procedimiento con la ecuación de Darcy–Weisbash:

En la expresión (9), V es la velocidad del fluido en [m/seg]; D el diámetro de la tubería en [m]; g el valor de la gravedad en [m/seg2], L la longitud de la tubería en [m]; f7 un coeficiente de fricción que depende del número de Reynolds y de la rugosidad relativa, y hf la pérdida de carga unitaria (Saldarriaga, 1998; Smits, 2003; Sotelo, 1999; Streeter y Wylie, 2000; White, 1994).
Y la ecuación de continuidad (ecuación fundamental de flujo permanente), es:
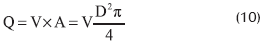
En la expresión (10), A es el área de la sección transversal expresada en m2 y Q el caudal expresado en m3/seg. Sustituyendo (9) en (10), se obtiene:
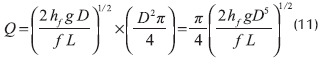
La pérdida de carga total hf en toda la longitud de la tubería L es:
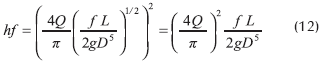
Teniendo en cuenta que: hf = r Qn

donde:
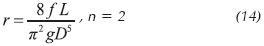
Simplificaciones introducidas
Sabiendo que hf = r Q0n; y:
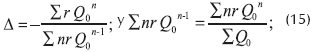
se obtiene:

Siendo n constante, la expresión para Δ se convierte en:
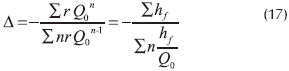
Reemplazando valores en la fórmula de Darcy–Weisbash, para la cual n = 2, la corrección se traduce en:

Diseño del software
La herramienta computacional Poseidón 1.0 resuelve de manera didáctica uno de los problemas más complejos de la mecánica de los fluidos para los estudiantes de ingeniería civil, como es el análisis de sistemas compuestos de tuberías, tanques y bombas. En los apartados siguientes se presentan la estructura y el uso de la herramienta.
Estructura de la herramienta
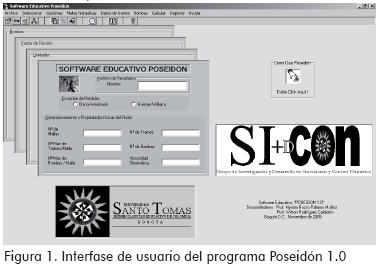
El software educativo se estructura en tres partes: preproceso, solución y posproceso. En el preproceso se cargan los datos de entrada del problema, en la solución se lanza el motor de cálculo que resuelve el problema, y en el posproceso se presentan los resultados del análisis. Cada uno de ellos está compuesto por módulos. En la Figura 1 se muestra la interfase de usuario del programa.
I. Preproceso: entrada de datos 
A. Módulo uno: cargar los datos generales del sistema 
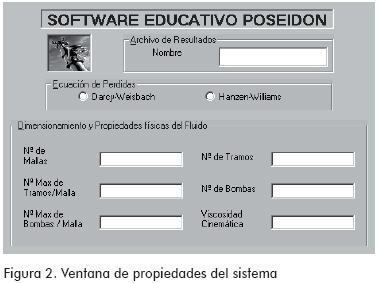
 Propiedades del sistema: En términos generales en esta ventana están contenidos los datos que dimensionan el problema y permiten establecer con qué tipo de formulación de pérdidas será resuelto.
Propiedades del sistema: En términos generales en esta ventana están contenidos los datos que dimensionan el problema y permiten establecer con qué tipo de formulación de pérdidas será resuelto.
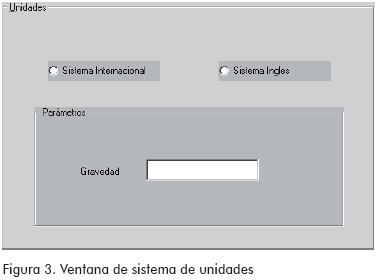
 Sistema de unidades: En esta ventana se define el sistema de unidades, ya que muchos parámetros de las ecuaciones de pérdidas dependen de él.
Sistema de unidades: En esta ventana se define el sistema de unidades, ya que muchos parámetros de las ecuaciones de pérdidas dependen de él.
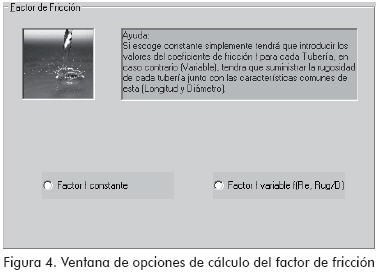
 Factor de fricción: El caso de factor constante simplifica el problema estableciendo una independencia de f tomando como hipótesis que el sistema funciona bajo turbulencia completa.
Factor de fricción: El caso de factor constante simplifica el problema estableciendo una independencia de f tomando como hipótesis que el sistema funciona bajo turbulencia completa.
El caso de factor variable busca simular la realidad teniendo en cuenta que f varía de acuerdo a las condiciones de flujo y a la rugosidad relativa. En este sentido, el programa recalcula este factor para cada iteración de acuerdo a las condiciones de flujo presentes.
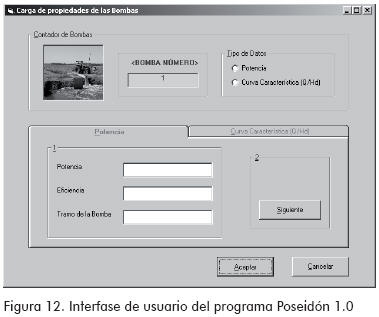
 Bombas: En esta ventana se especifica el grado máximo de la ecuación de ajuste de los datos de la bomba y el peso específico del agua. El grado de la ecuación se utiliza para dimensionar la cantidad de coeficientes del polinomio de ajuste y el peso específico para realizar los cálculos relacionados con la potencia de la bomba.
Bombas: En esta ventana se especifica el grado máximo de la ecuación de ajuste de los datos de la bomba y el peso específico del agua. El grado de la ecuación se utiliza para dimensionar la cantidad de coeficientes del polinomio de ajuste y el peso específico para realizar los cálculos relacionados con la potencia de la bomba.

B. Módulo dos: cargar los datos de los circuitos 
(1) Dimensionamiento de las mallas:
Dimensiona cada circuito del sistema en cuanto a cantidad de tramos y bombas.

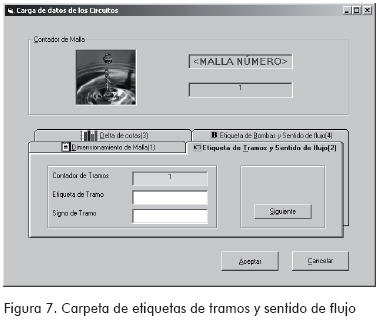
(2) Etiqueta de tramos y sentido de flujo:
Las etiquetas de los tramos deben ser números enteros y el signo se identifica como 1 ó -1 de acuerdo al sentido del flujo.
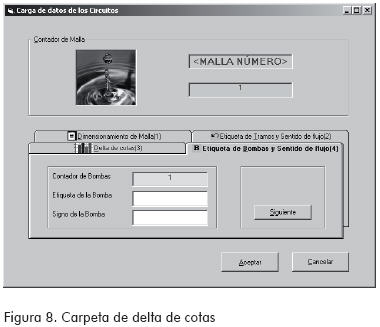
(3) Delta de cotas:
Permite tener en cuenta caídas constantes generadas por tanques presentes en el circuito. En el caso de que no existan, este valor es cero.
(4) Etiqueta de bombas y sentido de flujo:
Las etiquetas de las bombas deben ser números enteros y el signo se identifica como 1 ó -1 de acuerdo al sentido del flujo del tramo al que pertenece la bomba.
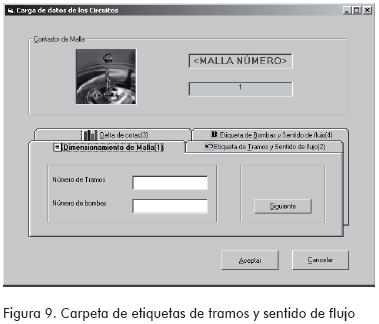
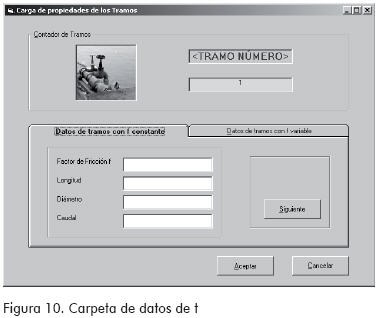
C. Módulo tres: cargar los datos de los tramos 
Este módulo permite cargar los datos característicos de los tramos para el cálculo de pérdidas, de acuerdo a la selección que se realiza en la ventana del factor de fricción (ver Figura 4).
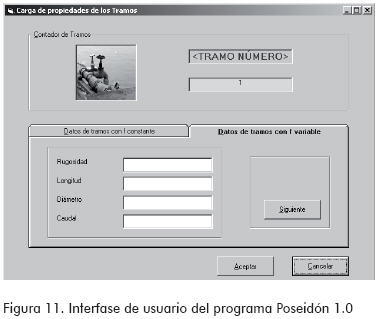
D. Módulo cuatro: cargar las propiedades de la bomba 
En este módulo se cargan los datos característicos de las bombas, ya sea por potencia o por curva característica.
Es necesario especificar el tramo donde se encuentra instalada cada bomba.
II. Solución: motor de cálculo
E. Módulo cinco: calcular 
En este módulo se lanza el motor de cálculo basado en el método de Cross. En él se contabiliza el error total acumulado que engloba todos los errores calculados de cada circuito (corrección de caudal).
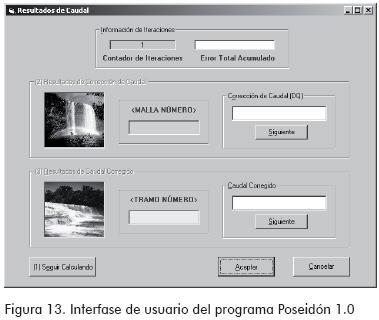
III. Posproceso: presentación de resultados
F. Módulo seis: reporte de cálculos 
El link Reporte permite abrir el archivo de resultados en formato de texto. En este documento queda consignado para cada iteración el factor de fricción, el número de Reynolds, la corrección de caudal de cada malla, así como los caudales corregidos para cada tramo.
Uso de la herramienta
Lo primero que se debe conseguir es la familiarización del alumno con la interfaz de usuario del programa, es decir, el estudiante debe aprender a iniciar una sesión de trabajo, crear un nuevo proyecto y distinguir entre los diferentes módulos que lo componen. Una vez conseguido este primer objetivo se introduce al alumno en el uso del programa, esto es, los pasos previos que se deben realizar y la convención de signos que utiliza el programa. Estas consideraciones se ilustran en el ejemplo siguiente.
Ejemplo
Título: Determinación de caudales en un sistema hidráulico (Problema 11.40)
Referencia: V. L. Streeter, Mecánica de los fluidos, McGraw-Hill Book Company, 1988, pág. 471.
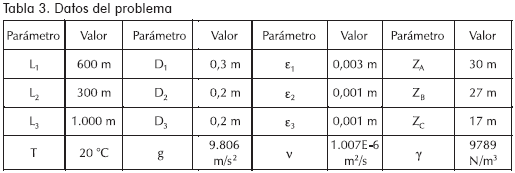
Problema: Con los datos de la bomba colocada en el sistema de la Figura 14, encuéntrese el flujo en el tanque B (temperatura del agua: 20°C).
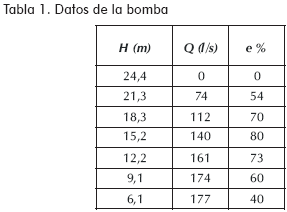
Pasos previos antes de trabajar con Poseidón 1.0
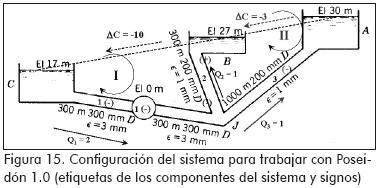
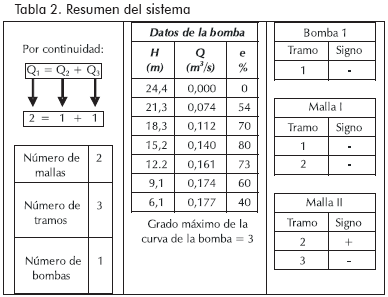
Primero: cerrar el sistema. Esto es, unir los tanques por medio de tramos ficticios. Estos tramos son útiles para determinar el signo del delta de cotas (ΔC en la Figura 15).
Segundo: etiquetar con números los componentes del sistema, o sea, mallas, tramos y bombas.
Tercero: suponer los caudales en el sistema:
-Caudal en los tramos reales: deben cumplir la ecuación de continuidad (Q1 = Q2 + Q3, en la Figura 15).
-Caudal en los tramos ficticios: no existe. Sin embargo, para efectos de determinar el signo del delta de cotas se supone un flujo ficticio que va siempre del tanque de mayor al de menor altura.
Cuarto: determinar los signos de las mallas, los tramos reales y los tramos ficticios.
Quinto: elaborar un cuadro de resumen del sistema (número de mallas, de tramos, de bombas y etiquetas de las mismas con signo). (Ver Tabla 2).
Convención de signos para trabajar con Poseidón 1.0
Primero: Mallas: siempre en el sentido de las agujas del reloj (mallas I y II en la Figura 15).
Segundo: Tramos reales:
-Positivos: cuando coinciden con el sentido de la malla.
-Negativos: cuando van en sentido contrario a la malla.
Tercero: Tramos ficticios: siguen la misma convención de los tramos reales.
Cuarto: Para las bombas: siempre llevan el signo del tramo en el que se encuentran.
Comparación de resultados
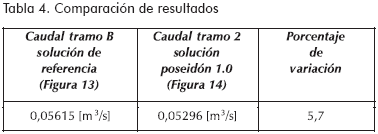
En la Tabla 4 se presenta la comparación entre la solución de referencia (Streeter, 2000) y el software educativo Poseidón 1.0. La variación es mínima y puede ser atribuida a la diferencia que existe entre los grados de precisión en los dos algoritmos.
Conclusiones
La enseñanza en ingeniería debe adaptarse a la sociedad en la que se desarrolla y para ello debe utilizar todas las herramientas a su alcance; hoy en día la utilización del computador en las aulas de clase es algo ineludible y necesario para formar técnicos capaces de afrontar con seguridad su vida profesional. Además, las capacidades multimedia del computador permiten envolver las clases en un entorno que las haga atractivas para el alumno.
Por otra parte, la creación de buenos materiales multimedia requiere de gran trabajo y dedicación por parte del docente, la mayor parte de las veces poco reconocido y menos recompensado, así como de un proceso de ajuste basado en la experiencia y que ha de ser constante como lo son los cambios en nuestros estudiantes.
Los materiales desarrollados con las nuevas tecnologías van a permitir modificar la concepción de las clases tradicionales de ingeniería, dejando de lado la llamada clase magistral y tratando de seducir al alumno para que aporte más trabajo personal en el proceso de aprendizaje. Esto representa una de las bases ideológicas de la reforma educativa. Además, aumenta la participación en la clase, tan difícil de conseguir hoy en día.
El uso del software educativo es un acierto, ya que permite al estudiante profundizar en los conceptos dejando de lado el esfuerzo que suponen cálculos tediosos. Esto, junto a cierto método deductivo de trabajo, le motiva para seguir aprendiendo. De hecho, los alumnos pueden utilizar el programa como ayuda en otras materias (ejemplo hidráulica, acueductos y alcantarillados).
La utilización del computador como medio docente debe llevar aparejados algunos cambios en los contenidos a impartir. Ya no es necesario dedicar excesivo tiempo a los métodos de cálculo tradicionales, sino que se puede emplear en que el alumno comprenda mejor los conceptos. Para tal fin, las capacidades software educativo son importantes.
El software educativo permite obtener resultados de forma ágil y segura, en contraposición al uso de calculadoras tradicionales; la experimentación autónoma del alumno constituye un ejercicio estructurador de la mente que debe ser considerado como de gran importancia en la formación de un técnico.
Agradecimientos
Este trabajo ha sido financiado por la Universidad Santo Tomás de Bogotá.
Bibliografía
Angel, A. J. y Bautista, G., Didáctica de las Matemáticas en enseñanza superior: la utilización de software especializado., disponible en http://www.uoc.edu/web/esp/art/uoc/0107030/mates_imp.html, 2001. [ Links ]
Aguilar, M. E., El diálogo en el aula: ¿Una alternativa al tradicional método de selección natural en la enseñanza de las Matemáticas?.,Tesis doctoral, Universidad de Valladolid, 2002. [ Links ]
Aho, A. V. E., Hopcroft, J. D. and Ullman., The Design and Analysis of Computer Algorithms., Editorial Addison Wesley, 1974. [ Links ]
Ansys User Manual / Revision 5.0., Swanson Analysis Systems, Inc. Houston. [ Links ]
Franzini, J. B. y Finnemore, E. J., Mecánica de fluidos con aplicaciones en ingeniería., Editorial McGraw-Hill Interamericana, Madrid, 1999. [ Links ]
Gear, C. W., Numeric initial value problems in ordinary differential equations., Editorial Prentice Hall, New York, 1971. [ Links ]
Giles, R. V., Evett, J. B. y Liu, Ch., Mecánica de los fluidos e hidráulica., Editorial McGraw-Hill Interamericana, Madrid, 1994. [ Links ]
La enseñanza superior en el siglo XXI: Estrategias de futuro., Texto de la declaración de la World Conference on Higher Education, París, 1998. [ Links ]
Mathews., Métodos Numéricos con Matlab., Editorial Pearson, México, 2000. [ Links ]
Mott, R. L., Mecánica de fluidos aplicada., Editorial Prentice-Hall Hispanoamericana, México, 1996. [ Links ]
Munson, B. R., Young, D. F. y Okiishi, T. H., Fundamentos de Mecánica de Fluidos., Editorial Limusa., México, 2002. [ Links ]
Potter, M. C., Wiggert, D. C., Mecánica de fluidos., Editorial Thomson, México, 2002. [ Links ]
Burden, R., y Faires., Análisis Numérico., Editorial Thompson Internacional, México, 1998. [ Links ]
Saldarriaga, J. G., Hidráulica de tuberías., Editorial McGraw-Hill Interamericana, México, 1998. [ Links ]
Smits, A. J., Mecánica de fluidos, Una introducción física., Editorial Alfaomega, México, 2003. [ Links ]
Sotelo Ávila, G., Hidráulica general., México: Editorial Limusa, 1999. [ Links ]
Streeter, V. L., Wylie, E. B., Mecánica de fluidos., Editorial McGraw-Hill Interamericana, México, 2000. [ Links ]
White, F. M., Fluid mechanics., Editorial McGraw Hill, Inc. New York, 1994. [ Links ]
Zienkiewicz, O. C. y Taylor, R. L., El Método de los Elementos Finitos., Editorial Mc. Graw – Hill, Barcelona, 1994. [ Links ]
3 El análisis de estos sistemas representa uno de los problemas más complejos de solucionar en la mecánica de los fluidos.
4 Las universidades españolas se constituyen en líderes a nivel mundial en estos avances pedagógicos.
5 Visual Basic, es un lenguaje de programación orientado a objetos comercial. La licencia empleada en este trabajo, es propiedad de la Universidad Santo Tomás de Bogotá.
6 SICON es un grupo de investigación y desarrollo de la facultad de ingeniería de la Universidad Santo Tomás reconocido por COLCIENCIAS en el año 2002 que cuenta con sendas líneas de investigación multidisciplinarias como son la simulación y el control numérico de las cuales deriva su nombre.
7 El factor de fricción f puede definirse como un "valor constante" o ser calculado, ya sea utilizando la ecuación explícita de "Swamee y Jain" o la expresión implícita de "Colebrook".














