Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.27 no.1 Bogotá Jan./Apr. 2007
Enrique Eduardo Tarifa1 y Sergio Luis Martínez2
1 Ph.D., en ingeniería química. Profesor asociado, Facultad de Ingeniería, Universidad Nacional de Jujuy, Argentina. Investigador, Consejo Nacional de Investigaciones Científicas y Técnicas – CONICET. eetarifa@arnet.com.ar
2 Ingeniero electrónico. Profesor adjunto, Facultad de Ingeniería, Universidad Nacional de Jujuy, Argentina. smartinez@imagine.com.ar
RESUMEN
La investigación realizada tuvo como objetivo la formulación de un método para el diseño de un sistema de diagnóstico de fallas para plantas químicas utilizando redes neuronales artificiales. El diagnóstico de fallas tiene como misión identificar la falla que está afectando a un proceso dado a través del análisis de las señales suministradas por los sensores del proceso. Las redes neuronales son modelos matemáticos que intentan reproducir la actividad cognoscitiva del cerebro humano. Éstas se caracterizan por su estructura y el método de aprendizaje utilizado. El problema del diagnóstico de fallas se aborda a partir de la perspectiva de la identificación de las trayectorias (secuencias temporales de datos) que describen las variables del proceso al ser afectado por una falla. De esta forma, reconocidas las trayectorias, se habrá identificado la falla asociada. El desarrollo teórico realizado recomienda una estructura y un método de entrenamiento optimizado para las redes neuronales a emplear. Tanto la estructura como el método de entrenamiento propuesto fueron evaluados realizando estudios comparativos con estructuras y un método de entrenamiento tradicionales. Los resultados así obtenidos mostraron la superioridad de las redes neuronales diseñadas y entrenadas con el método propuesto en este trabajo. Salvo en procesos simples, el diagnóstico de fallas es más complejo que el reconocimiento de trayectorias porque cada falla puede provocar un conjunto infinito de trayectorias (flujo). Por ese motivo, los fundamentos establecidos en el trabajo son utilizados en la parte II, donde el análisis se extiende al reconocimiento de flujos.
Palabras clave: diagnóstico de fallas, redes neuronales, reconocimiento de trayectorias, optimización, tolerancia al ruido.
ABSTRACT
The present investigation was focused on formulating a method for designing a fault diagnosis system for chemical plants by using artificial neural networks. Fault diagnosis is aimed at identifying a fault which affects a given process by analysing the signs supplied by process sensors. Neuronal networks are mathematical models which try to imitate the functioning of the human brain. A neural network is defined by its structure and the learning method used. The difficulty with diagnosing faults lies in recognising the trajectories (temporal series of data) followed by process variables when a fault affects the process; when trajectories are recognised, the associated fault is also identified. The theory so developed recommended an optimised structure and training method for the neural networks to use. Both the proposed structure and the training method were tested by carrying out comparative studies between traditional structures and a training method. The results showed the superiority of the neural networks designed and trained with the method proposed in this work. Except for simple processes, fault diagnosis is a more complex problem than simply identifying trajectories, because a fault may cause an infinite set of trajectories (i.e. flow). The fundaments established in this work are thus used in Part II, where the analysis is extended to recognise flows.
Keywords: fault diagnosis, artificial neural network, trajectory recognition, optimisation, noise tolerance.
Recibido: diciembre 7 de 2006
Aceptado: marzo 5 de 2007
Introducción
Desde hace tiempo las redes neuronales, también llamadas ANN (Artificial Neural Networks), son empleadas en una variedad de aplicaciones (Fan et al., 1993; Chen et al., 1999; Rengaswamy y Venkatasubramanian, 2000; Persina y Tovornik, 2005). La capacidad de aprender y la tolerancia al ruido las destacan sobre cualquier otra herramienta. Sin embargo, para que la aplicación sea exitosa se debe elegir cuidadosamente tanto la estructura de la red como el método de entrenamiento. Esta selección es muy dependiente del problema a tratar. El presente trabajo formula un método para realizar una adecuada selección en el marco del problema del diagnóstico de fallas en plantas químicas.
Un sistema de diagnóstico de fallas tiene la misión de analizar el estado del proceso bajo supervisión -por ejemplo: una planta química- a fin de determinar si está desarrollándose en forma normal o anormal. En este último caso, determina la causa de la anormalidad, la cual podrá ser: avería en algún equipo, error de operación, cambios en las corrientes de entrada de la planta, etc.; esta causa se denomina falla. La identificación temprana de la falla es de suma importancia a fin de iniciar las acciones necesarias para atenuar o evitar las consecuencias: lesiones en los operadores, daño en los equipos, pérdidas de producción, explosiones, liberación de contaminantes, etc. Las técnicas a utilizar para tal identificación pueden ser muy variadas (Wang et al., 1997; Persina y Tovornik, 2005; Witczaka et al., 2006; Zhang, 2006). En forma general, se las pueden clasificar como técnicas basadas en modelos y en datos. Dado que las primeras requieren información precisa y consistente del proceso o su modelo, se prefiere el uso de las técnicas del segundo grupo. De esta forma, sólo se necesita un conjunto de datos históricos del proceso, los cuales pueden obtenerse de los sensores instalados para realizar la supervisión y control del proceso (Venkatasubramanian et al., 2003).
Cuando un proceso es afectado por una falla, las variables del proceso evolucionan siguiendo trayectorias (secuencias temporales de datos) que pueden ser utilizadas para identificar la falla que las originan (Wang et al., 1997; Wah y Qian, 2002). Por este motivo, en las secciones siguientes se plantea formalmente el problema a resolver: el diagnóstico de fallas; luego, adoptando un enfoque basado en datos, dicho problema es tratado como si fuera uno de reconocimiento de trayectorias. Con este tratamiento, al reconocer las trayectorias observadas, se identifica la falla asociada. Para ello se formula un método que recomienda la estructura y otro de entrenamiento adecuados para las redes neuronales que componen el sistema de diagnóstico y que estarán a cargo del reconocimiento de trayectorias. Tanto la estructura como el método de entrenamiento propuestos fueron comparados con estructuras y un método de entrenamiento tradicionales. Los resultados obtenidos respaldaron la utilización del método propuesto aquí.
Con excepción de procesos simples, el diagnóstico de fallas es más complejo que el reconocimiento de trayectorias porque cada falla puede provocar un conjunto infinito de trayectorias (flujo). Por ese motivo, los fundamentos establecidos en este trabajo son utilizados en la parte II (Tarifa y Martínez, 2007), donde el análisis se extiende al reconocimiento de flujos.
Diagnóstico de fallas
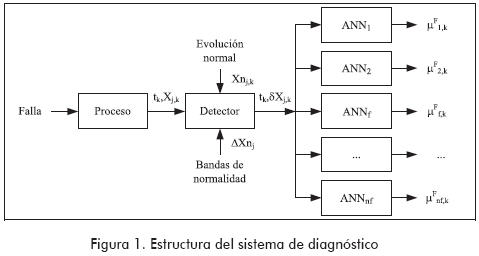
Cuando una falla ocurre en una planta química (por ejemplo: una bomba se detiene), inicialmente afecta a un parámetro o a una variable del proceso (la presión en la tubería decae). Luego, esta perturbación original se propaga a lo largo de la planta, afectando a las variables que encuentra en su camino (presiones, caudales, temperaturas, concentraciones, etc.), alejándolas de sus valores normales. La forma en que las variables afectadas evolucionan es función de las características de la falla presente. Habrá diferentes evoluciones dependiendo de cuál es el parámetro o variable inicialmente afectado por la falla, y de la forma en que se efectúa dicha perturbación original. Tarifa et al. (2002) proponen realizar la identificación de la falla que está afectando a la planta mediante el estudio de la forma en que evolucionan las variables cuando el estado del proceso es anormal. Para lograr este fin, en el citado trabajo, el sistema de diagnóstico adopta la estructura que se muestra en la Figura 1. En este sistema, cada intervalo de tiempo Δt, el detector recibe del sistema de adquisición de datos el vector X, que contiene los valores de las variables del proceso. Luego compara estos valores con los valores normales Xn considerando una cierta tolerancia fijada por la banda de normalidad ΔXn. Como resultado de esta comparación se obtiene el vector de desviaciones tipificadas δX. Este vector es enviado posteriormente a un banco de ANN, el cual está conformado por una ANN por cada falla potencial de la planta; cada ANN está especializada únicamente en el reconocimiento de la falla que se le asignó. Las ANN analizan los datos provenientes del detector buscando síntomas o pruebas para sus respectivas fallas. El resultado de este análisis es el grado de certeza µF que soporta a cada falla, el cual es un número real entre 0 y 1. De esta forma, en un tiempo dado t, la certeza que reporta cada ANN indica el grado de concordancia entre la evolución observada de las variables con respecto a la evolución esperada para la correspondiente falla hasta ese momento. Un valor nulo significa que no existe concordancia alguna y, por lo tanto, no existen pruebas a favor de la falla correspondiente. Por el contrario, un valor igual a la unidad implica una concordancia total entre lo observado y lo esperado y, por lo tanto, todas las pruebas están a favor de la falla considerada. Valores intermedios significan respaldo intermedio para las fallas.
Modelado de fallas con trayectorias
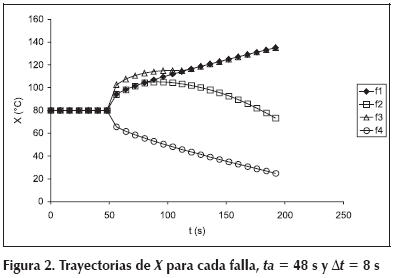
En este primer estudio la evolución de las variables de un proceso afectado por una falla será modelada utilizando trayectorias (secuencia temporal de datos provistos por los sensores). Además, se considerará que el proceso tiene una única variable para supervisar. Ambas simplificaciones permiten explicar con mayor claridad el trabajo realizado sin que por ello se vea afectado el valor de las conclusiones alcanzadas, como queda demostrado en el trabajo presentado por Tarifa y Martínez (2007). Continuando con la descripción del proceso ficticio adoptado como ejemplo, supóngase que la única variable medida es una temperatura. En condiciones normales, el proceso opera en estado estacionario; y por lo tanto, la temperatura mantiene su valor normal Xn = 80 ºC. Considere, además, que existen cuatro fallas potenciales que amenazan al proceso, ellas son: f1, f2, f3 y f4. Cada vez que una de ellas lo afecten, la temperatura evolucionará con una trayectoria característica tal como se muestra en la Figura 2, la cual se obtuvo con un intervalo de muestreo Δt = 8 s. Como puede apreciarse, la variable permanece en su valor normal hasta que ocurre una de las fallas en el tiempo de activación ta = 48 s. Tomando como referencia a la falla f1, la f2 es indistinguible en un principio, pero a partir de t = 88 s comienza a diferenciarse. En cambio, f3 es en principio distinta de la f1, pero a partir de t = 112 s, se confunde con ella. Finalmente, la f4 es en todo momento distinguible de la f1. Las trayectorias descritas son representativas de las trayectorias que pueden observarse en un proceso real, de allí la importancia del proceso ficticio adoptado como ejemplo.
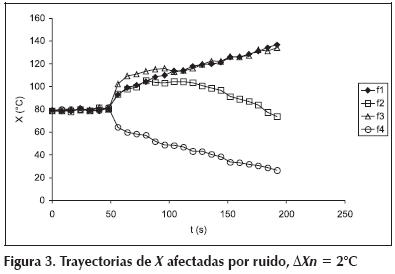
En la práctica, los datos obtenidos del proceso están afectados por ruido, y lo que en realidad observa el operador es lo que se muestra en la Figura 3. La incertidumbre generada por el ruido hace necesario que el sistema de diagnóstico permita cierta variación alrededor del valor normal, esta tolerancia está fijada por la banda de normalidad ΔXn. El valor de la variable se considerará normal mientras permanezca en el intervalo (Xn - ΔXn, Xn + ΔXn). La banda debe ser dimensionada en función del ruido que afecta a la variable; si es demasiada estrecha, se producirán falsas alarmas; y si es demasiada amplia, el sistema perderá sensibilidad y detectará tardíamente las fallas. Si el ruido obedece una distribución normal con media nula y desviación estándar σ, el riesgo de falsas alarmas es de 32% para ΔXn = σ, 5% para ΔXn = 2σ y 0,3% para ΔXn = 3σ. Para este ejemplo se tomó ΔXn = 2°C. Entonces, para este caso en particular, el problema de diagnóstico de fallas puede plantearse como: 1) mientras X esté dentro de la banda de normalidad, no realizar acción alguna; 2) desde que se observe el primer valor anormal, determinar, por comparación con las trayectorias mostradas en la Figura 2, cuál es la falla que mejor explica la evolución observada. Esta tarea es realizada automáticamente por el sistema mostrado en la Figura 1; en las secciones siguientes se explica más detalladamente su funcionamiento.
El detector
Para el ejemplo bajo estudio el sistema detector propuesto por Tarifa et al. (2002) se simplifica de la forma que se explica a continuación. La misión del bloque detector es analizar los valores de X que recibe del sistema de adquisición de datos, en busca de algún valor anormal o síntoma que indique la presencia de una falla. Detectado el mismo, activará el bloque de diagnóstico, y le suministrará la diferencia tipificada δX. Para poder cumplir con su función, cada Δt, el detector recibe del sistema de adquisición de datos el valor de X, siendo la muestra k tomada en el tiempo tk = kxΔt. Por otra parte, el detector también conoce el valor normal Xn, y lo utiliza para calcular la desviación ΔX = X - Xn. Calculada la desviación, el detector emplea la banda normal ΔXn para calcular la desviación tipificada como sigue:
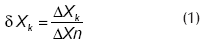
Entonces, la desviación tipificada es un número adimensional que está escalado tomando como referencia la banda de normalidad de la variable.
El detector calcula δX para cada tiempo de muestreo. Por definición, mientras el proceso opere normalmente, el valor absoluto de la desviación tipificada será menor que la unidad, porque los valores de la variable estarán dentro de la banda de normalidad. Cuando el valor de la variable escape de la banda de normalidad el proceso dejará de operar normalmente, y se habrá detectado un estado dinámico provocado por una falla. El tiempo de detección o de observación to es definido como aquel en que se observa por primera vez un valor anormal, formalmente:
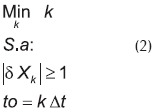
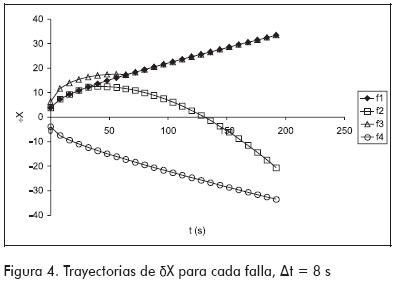
En el tiempo to del proceso, el sistema de diagnóstico es encendido para iniciar la búsqueda de la falla que origina los síntomas observados. El reloj del sistema de diagnóstico arranca en cero esto es, el tiempo to del proceso corresponde al cero en el sistema de diagnóstico. La Figura 4 presenta las trayectorias del vector δX para cada falla. Cuando una de las cuatro fallas potenciales ocurra, el bloque detector entregará gradualmente la correspondiente trayectoria observada de δX al bloque de diagnóstico. Por lo explicado anteriormente, dichas trayectorias nacen en el tiempo cero y con valores absolutos mayores o iguales a la unidad. Debido a que los tiempos de observación to pueden ser distintos para cada falla, las trayectorias de δX (Figura 4) pueden estar desplazadas respecto de las trayectorias de X (Figura 2), y con mucho más razón, respecto a las trayectorias afectadas por ruido (Figura 3).
El sistema de diagnóstico
Para el caso particular del ejemplo bajo análisis, el sistema de diagnóstico propuesto por Tarifa et al. (2002) se simplifica como se explica a continuación. El grado de certeza µF que soporta a la falla f en el tiempo tk es definido como:
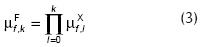
donde µX representa la certeza que soporta a la variable X, y se calcula como:
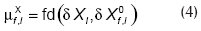
donde fd(δX, δX0) es la función de evaluación que se utiliza para evaluar la diferencia entre el valor observado δX, originado por una falla desconocida, y el valor esperado δX0 para el caso en el que la falla f fuera la que está afectando al proceso; ambos valores se obtienen de la Figura 4. La citada función describe el grado de pertenencia a un conjunto borroso (Russell y Norvig, 1995), y se define de la siguiente forma:
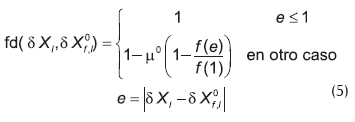
donde µ0 pertenece al intervalo [0, 1], y es utilizado para ajustar la rigurosidad de la evaluación; a mayor valor, mayor rigurosidad. En este trabajo se tomó µ0 = 1.
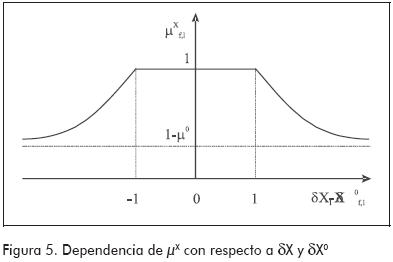
De acuerdo a las definiciones precedentes, la Figura 5 muestra la dependencia de µX con respecto a δX y δX0. La zona plana con µX igual a la unidad, para el intervalo [-1, 1] de la abscisa, implica que se toleran diferencias entre lo observado y lo esperado mientras el valor absoluto de las mismas sea menor que uno. Esta tolerancia es necesaria para que el diagnóstico no se vea afectado por el ruido, por ese motivo la de tolerancia para la comparación es del mismo tamaño que la banda de normalidad.
Dada la forma de la ecuación (3), se la puede reescribir de manera recursiva:
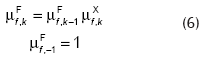
Finalmente, el procedimiento para realizar el diagnóstico es: 1) recibir la muestra k de δX; 2) para cada falla f, obtener de la Figura 4 el valor δX0; 3) para cada falla f, calcular µX utilizando la ecuación (4); 4) para cada falla f, calcular µF utilizando la ecuación (6). Como resultado, se obtendrán las trayectorias de los µF para todas las fallas. Si se grafican estas trayectorias en función del tiempo de diagnóstico, se observará que todas se inician con valor unidad, pues no existen pruebas suficientes para descartar a ninguna falla; pero a medida que pasa el tiempo, los µF de las fallas que no son la causa del estado anormal observado, irán tendiendo a cero, mientras que el µF de la falla que sí afecta al proceso mantendrá su valor igual a uno.
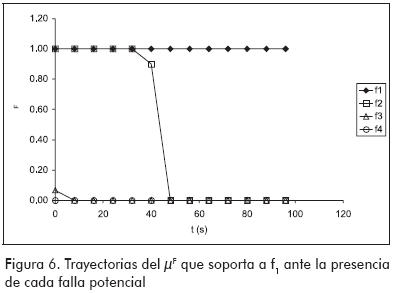
La Figura 6 presenta las trayectorias de los µF obtenidas al comparar las trayectorias δX de la Figura 4 con la que se originaría si f1 fuera la falla que realmente está afectando al proceso. Como puede apreciarse, cuando se ingresa la trayectoria originada por f1, µF se mantiene en 1 respaldando en todo momento a dicha falla. En cambio, cuando se ingresa la trayectoria originada por f2, el sistema no descarta f1 debido a que las trayectorias que ambas fallas originan son similares hasta los 32 s (Figura 4). A partir de los 40 s, el sistema descarta a la falla f1 disminuyendo µF. Cuando se presentan las trayectorias de f3 y f4, la falla f1 es descartada en forma temprana.
Redes neuronales
El bloque de diagnóstico descrito en la sección anterior demanda un gran esfuerzo computacional que siempre debe tratar de evitarse, sobre todo en una aplicación que funcionará on-line. Por este motivo, es necesario encontrar la forma de realizar la misma tarea pero con un menor requerimiento computacional (Tarifa et al., 2002). La alternativa seleccionada para resolver el problema es la que se muestra en la Figura 1, donde el bloque de diagnóstico se implementa utilizando ANN. Esta solución, además de cumplir con el requisito de baja demanda computacional, agrega la propiedad de tolerancia al ruido –característica notable de las ANN-, mejorando así la robustez del sistema (Wah y Quian, 2002).
Las ANN se caracterizan por su estructura y el método de entrenamiento (Russell y Norvig, 1995; Looney, 1997). Trabajos anteriores aplicaron ANN al diagnóstico de fallas, pero lo hicieron en una forma que sólo es eficaz para los casos particulares descritos (Garcés Castro y Miranda, 2005; Zhang, 2006; Witczaka et al., 2006). En esta sección se realizará un análisis de las estructuras y un método de entrenamiento propuestos en trabajos anteriores, se plantearán sus ventajas y desventajas, y finalmente se describirá una nueva estructura novedosa y un nuevo método de entrenamiento adecuados para la gran mayoría de los casos. La nueva estructura y el nuevo método de entrenamiento son el resultado directo del desarrollo presentado en las secciones anteriores.
La unidad fundamental de una ANN es la neurona. Las neuronas se agrupan en capas. De acuerdo a la forma en que se agrupan y se conectan, se tienen diferentes tipos de estructuras. En este trabajo se analizaron tres de ellas (Figura 7): feedforward estándar, feedforward con ventana móvil y feedforward parcialmente recurrente (con retroalimentación). Las dos primeras arquitecturas fueron utilizadas en trabajos anteriores (Fan et al., 1993; Cheng et al., 1999; Rengaswamy y Venkatasubramanian, 2000), y la última está basada en la ecuación (6); todas ellas tienen una capa de entrada, otra oculta y otra de salida. Para el ejemplo bajo estudio, la entrada de cada ANN estará asociada al estado del proceso, mientras que la salida de la red será µF.
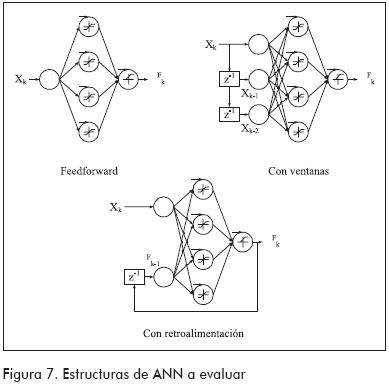
Una vez elegida la estructura, es necesario que la ANN aprenda a realizar la tarea asignada; esto se logra en la etapa de aprendizaje, donde el método de entrenamiento ajusta los pesos de las conexiones entre neuronas. En este trabajo se emplearon métodos de entrenamiento supervisados, en los cuales, al tiempo que se presentan diferentes entradas a la ANN, se presentan también las salidas deseadas correspondientes; entonces, a través del algoritmo backpropagation (Demuth y Beale, 2000), el método de entrenamiento ajusta los pesos para minimizar el error entre los resultados reportados por la ANN y los deseados. Las estructuras contenidas en la Figura 7 fueron entrenadas con dos métodos: el tradicional y el optimizado, empleando como entradas las trayectorias δX exhibidas en la Figura 4, mientras que las salidas deseadas dependen del método de entrenamiento empleado. En el método de entrenamiento tradicional, a la red se le exige salida igual a 1 cada vez que se le ingresa la trayectoria δX de la falla correspondiente a la ANN (recuerde que existe una red por cada falla potencial); por el contrario, se le exige salida igual a 0 cada vez que se le ingresan las trayectorias δX de otras fallas. En el método optimizado (Tarifa et al., 2002) se cambia significativamente esta última parte de la siguiente forma: cada vez que se le ingresan trayectorias δX de otras fallas, a la red se le exige que la salida sea igual a lo indicado por la Ecuación (6). Por ejemplo, para la red correspondiente a la f1, las entradas son los δX mostrados en la Figura 4, mientras las salidas deseadas correspondientes son los µF presentados en la Figura 6.
La diferencia entre los dos métodos es profunda y determinante. En efecto, en el método tradicional el valor de µF se fija por la concordancia entre la falla que origina la trayectoria δX observada y la correspondiente a la ANN entrenada, esto es, µF será 1 cuando se ingrese la trayectoria δX de la falla correspondiente a la ANN entrenada, y será 0 cuando se ingrese la trayectoria δX de una falla distinta de la correspondiente a la ANN entrenada sin considerar la forma de la trayectoria observada; esto último constituye la principal debilidad del método. Si la trayectoria δX provocada por una falla distinta de la correspondiente a la ANN entrenada es similar a la provocada por esta última falla, la ANN recibirá un entrenamiento contradictorio y será incapaz de aprender. Por ejemplo, en el entrenamiento de la ANN correspondiente a la falla f1, cuando se le alimenta la trayectoria δX provocada por la f1, se le enseña a la ANN que produzca una salida µF igual a 1; por el contrario, cuando se le alimenta la trayectoria δX provocada por la f2, se le enseña que produzca una salida µF igual a 0; sin embargo, debido a que durante los primeros 32 s ambas trayectorias son indistinguibles (Figura 4), la ANN no podrá decidir si µF debe ser 0 ó 1 durante el tiempo en que ambas trayectorias son iguales, ya que para entradas δX similares se le piden salidas µF disímiles. Este problema se soluciona en el método optimizado al fijar el valor de µF en función de la concordancia entre la trayectoria δX observada y la esperada para la falla de la ANN, y no en la concordancia de las fallas que causan las trayectorias observadas y esperadas como lo hace el método tradicional.
Retornando al ejemplo anterior del entrenamiento de la ANN correspondiente a la f1, cuando se le alimenta la trayectoria δX provocada por f1 se le enseña a la ANN que produzca una salida µF igual a 1 porque la trayectoria observada es igual a la esperada; cuando se le alimenta la trayectoria δX provocada por la f2, se le enseña que produzca una salida µF igual a 1 durante los primeros 32 s ya que durante ese tiempo la trayectoria observada es igual a la esperada (Figura 4); pero a partir de ese momento, la trayectoria observada comienza a diferir de la esperada, y el valor µF refleja este hecho disminuyendo proporcionalmente su valor (Figura 6). De esta manera, la ANN no tiene ningún conflicto durante el aprendizaje porque para entradas δX similares se le piden salidas similares. No obstante estos resultados, el método tradicional puede ser útil en los caso en que las trayectorias δX provocadas por las fallas no se superpongan en ningún intervalo; si esta condición se cumple, la ANN no tendrá ningún conflicto durante el aprendizaje; sin embargo, la tolerancia al ruido será menor que la que puede obtenerse con el método optimizado debido a la naturaleza discreta de los valores de µF que se utilizan para el entrenamiento.
Estructura feedforward
La primera ANN estudiada fue del tipo feedforward. Luego de varias pruebas se fijó una capa interna de cuatro neuronas y una capa de salida de una única neurona (Figura 7). La señal de excitación net de cada neurona está definida por la función de excitación, que en este trabajo se tomó como igual a la suma ponderada de todas las señales que llegan a la neurona:
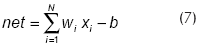
donde xi es la salida de la neurona i de la capa anterior formada por N neuronas, wi es el peso de la conexión entre dicha neurona y la que recibe la señal, y b es el bias de la neurona que está siendo evaluada.
La señal de salida x de cada neurona está definida por la función de activación, que en este trabajo se tomó como igual a la función sigmoide bivaluada para las neuronas de la capa interna:
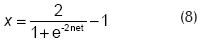
y como la función sigmoide positiva para la neurona de la capa de salida:
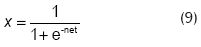
El comportamiento de esta ANN para identificar las trayectorias de la Figura 4 fue deficiente, tanto cuando se la entrenó con el método tradicional como cuando este se la hizo con el método optimizado. Por ejemplo, la ANN que fue entrenada para reconocer la f1 reportó un µF cercano a 0,5 sin importar la trayectoria δX que se le ingresara, cuando lo deseado era que reportara un µF cercano a 1 cuando se le ingresara la trayectoria δX correspondiente a la f1, y cercano a 0 cuando se le ingresaran trayectorias de otras fallas.
Para esta experiencia se utilizó una arquitectura neuronal 1+4+1 completamente interconectada (Figura 7), especializando una ANN para el reconocimiento de la trayectoria de falla f1. Como conjunto de entrenamiento se emplearon las cuatro trayectorias mostradas en la Figura 4. Durante el proceso de entrenamiento se aplicaron 500 iteraciones, produciéndose un error cuadrático medio (MSE) de 0,158 para el método de entrenamiento tradicional y un MSE de 0,152 para el de entrenamiento optimizado. En la fase de comprobación, la ANN que fue entrenada para reconocer la f1 reportó en todo momento un µF cercano a 0,5 sin importar la trayectoria δX que se le ingresara, a excepción de la falla f4, para la cual el µF reportado fue 0. Este resultado difiere mucho de la conducta deseada (µF cercano a 1 cuando se le ingresa la trayectoria δX correspondiente a la f1, y cercano a 0 cuando se le ingresan trayectorias de otras fallas).
Esto demuestra que la ANN no puede aprender las trayectorias generadas por las fallas, ni por lo tanto, identificarlas en forma adecuada. La incapacidad de aprender de esta ANN se origina en su misma estructura. En efecto, al tener que decidir el valor de µF (salida) en función de un único valor δX (entrada), la ANN no cuenta con la información necesaria para discriminar entre varias trayectorias, ya que un valor dado puede ser alcanzado por varias de ellas. Por ejemplo, el valor δX = 10 es alcanzado en algún momento por las trayectorias de f1, f2 y f3 (Figura 4); y ambos métodos de entrenamiento piden en algún momento valores de salida µF diferentes para dicha entrada, lo cual confunde a la ANN. Una forma de resolver este problema es aumentando la cantidad de información disponible para la ANN; a continuación se exploran dos alternativas en este sentido.
Estructura con ventanas
Para incrementar la información enviada a la ANN, se amplió la ANN descrita en la sección anterior por medio de la incorporación de dos entradas adicionales. Estas se obtienen de conservar, mediante retardos, los dos últimos valores observados de δX; es decir, se construyó una red con ventana temporal, también denominada TDNN -Time Delay Neural Network- (Figura 7). En principio esta estructura es más apropiada que la feedforward en el modelado y reconocimiento de secuencias dinámicas (Principe, 2002), pero su desempeño fue igualmente pobre para los dos métodos de entrenamiento empleados.
Para esta experiencia se utilizó una arquitectura neuronal 3+4+1 completamente interconectada (Figura 7), especializando una ANN para el reconocimiento de la trayectoria de falla f1. Como conjunto de entrenamiento se emplearon nuevamente las cuatro trayectorias mostradas en la Figura 4. Durante el proceso de entrenamiento se aplicaron 500 iteraciones, produciéndose un MSE de 0,048 para el método de entrenamiento tradicional y un MSE de 0,028 para el de entrenamiento optimizado. En la fase de comprobación se determinó que la ANN no reconocía apropiadamente las trayectorias utilizadas en el entrenamiento, tanto para la falla de especialización como para las restantes. Esto ocurrió con ambos métodos, aunque se observó una sensible mejora con respecto al modelo anterior, reflejado en la reducción del error entre la salida reportada y la deseada.
El fracaso con el método tradicional es debido a la debilidad intrínseca del mismo y a la superposición de las δX, mas el fracaso con el método optimizado delata una limitación de la estructura probada. Esta limitación podría estar originada en la reducida cantidad de neuronas de la capa interna o por el limitado ancho de la ventana temporal. No obstante, aquí se detiene el análisis de este tipo de red a favor de la estructura, que se explica en la sección siguiente debido a que demostró ser más simple y a la vez más eficaz.
Estructura con reciclo
La estructura con reciclo presentada en la Figura 7 está inspirada en la ecuación (6), la cual le brinda respaldo teórico. Al tener una retroalimentación, la información que recibe la ANN combina el estado presente y la historia total del proceso, lo que le da una gran ventaja sobre la estructura feedforward. Esta misma ventaja la mantiene frente a la estructura con ventanas, la cual sólo ve una porción de la historia del proceso (en el ejemplo estudiado, solo se tomaron dos muestras hacia atrás); pero además mantiene la simplicidad al permitir conservar toda la historia del proceso por el agregado de una única entrada escalar adicional: el µF reciclado. Esto último es de gran importancia cuando se supervisan procesos con gran cantidad de variables. Así, si el proceso tiene 20 variables, la estructura feedforward tendrá 20 entradas, la estructura con ventanas con dos retardos tendrá 3⋅20 = 60 entradas; en cambio, la estructura con reciclo tendrá 20+1 = 21 entradas. A esta simplicidad de estructura, la ANN con reciclo agrega un excelente comportamiento en las pruebas realizadas con el método optimizado. En efecto, cuando la ANN correspondiente a la falla f1 fue entrenada utilizando el método optimizado, fue capaz de producir exactamente las salidas µF deseadas reproduciendo fielmente las curvas de la Figura 6. En cambio, su conducta fue deficiente cuando se la entrenó con el método tradicional debido a las falencias del método empleado y no de la estructura propuesta en sí.
Para esta experiencia se utilizó una arquitectura neuronal 2+4+1 completamente interconectada (Figura 7), especializando una ANN para el reconocimiento de la trayectoria de falla f1. Como conjunto de entrenamiento se emplearon nuevamente las cuatro trayectorias mostradas en la Figura 4. Durante el proceso de entrenamiento se aplicaron 500 iteraciones, produciéndose un MSE de 0,192x10-3 para el método de entrenamiento tradicional y un MSE de 0,128x10-3 para el de entrenamiento optimizado. Como ya se comentó, en la fase de comprobación la ANN entrenada utilizando el método optimizado fue capaz de producir exactamente las salidas µF deseadas. En cambio, su conducta no fue tan eficiente cuando se la entrenó con el método tradicional.
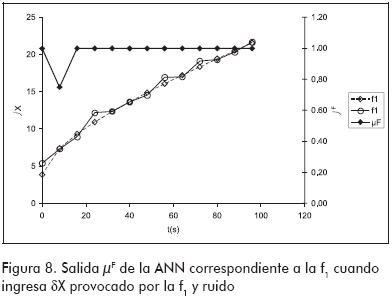
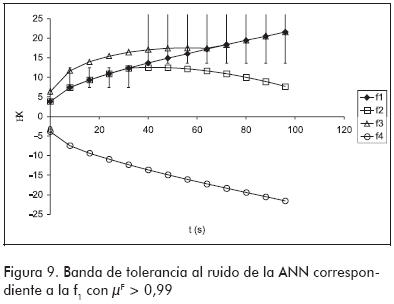
Las pruebas realizadas hasta aquí estuvieron dirigidas al reconocimiento de trayectorias que fueron empleadas durante el entrenamiento, es decir, hasta ahora sólo se evaluó la capacidad de aprendizaje de las ANN. Sin embargo, para que el sistema de diagnóstico sea eficaz las redes deben ser capaces de reconocer trayectorias afectadas por ruido. Esto podría lograrse incorporando trayectorias con ruido en la fase de entrenamiento, o aprovechando la tolerancia al ruido que presentan las ANN. La primera alternativa exige que se determinen los µF con la ecuación (3) para todas las trayectorias con ruido que se vayan a utilizar en el entrenamiento; mientras más trayectorias se utilicen, mejor será el entrenamiento, pero mayor será el esfuerzo para calcular los µF. Por otra parte, la segunda alternativa no requiere que se entrene la ANN con trayectorias con ruido, sino que confía en su capacidad intrínseca para tolerarlos. A fin de probar este punto, en el entrenamiento se utilizaron exclusivamente las trayectorias sin ruido para observar la eficacia de la ANN en reconocer trayectorias con ruidos a pesar de no haberlas utilizado en el entrenamiento. De esta manera, ahora no solo se emplea la capacidad de aprendizaje de la ANN sino que también se acude a su capacidad de generalización. En esta situación, la ANN correspondiente a la f1 reprodujo de nuevo las curvas de µF mostradas en la Figura 6, con una única excepción: esta se presentó en el valor de µF perteneciente a la segunda muestra cuando se ingresó el δX de la falla f1 afectado por ruido. En la Figura 8 puede verse que dicho valor es menor que el correcto, el cual es 1. La explicación de este error es la particular manera en que la ANN ajustó sus pesos para aprender la trayectoria causada por f1. Para tener una idea de la forma en que la ANN ve a dicha trayectoria, la Figura 9 muestra el entorno de cada valor δX dentro del cual la ANN reporta un µF > 0,99. Como puede verse, en la segunda muestra la ANN no tolera valores δX menores que el esperado, y de allí el valor incorrecto de µF para dicha muestra. También en la citada figura queda claro por qué la ANN puede distinguir la trayectoria de la f1 de las trayectorias causadas por las restantes fallas.
Conclusiones
En el trabajo se ha presentado un desarrollo teórico para aproximar el problema de diagnóstico de fallas al de reconocimiento de trayectorias. Como fruto de él, se determinaron la estructura y el método más adecuados de entrenamiento para las ANN que conforman el sistema de diagnóstico de fallas de la Figura 1. El rendimiento de las ANN así obtenidas fue comparado con el de dos estructuras tradicionales (la red feedforward y la red con ventana móvil) entrenadas con el método tradicional y el optimizado. Del estudio surgió que la combinación propuesta (una estructura con reciclo y el método de entrenamiento optimizado) es la más adecuada ya que logra producir las salidas deseadas sin recurrir a una arquitectura mucho más compleja que las empleadas tradicionalmente. En efecto, en las experiencias realizadas para comparar diferentes estructuras y métodos de entrenamiento se mantuvo constante la cantidad de neuronas (Figura 7). El logro de las salidas deseadas sin recurrir a una estructura mucho más compleja es una gran ventaja del método propuesto sobre todo si se considera que, en igualdad de condiciones, las arquitecturas tradicionales fueron incapaces de producir las salidas deseadas. Otra ventaja es la tolerancia al ruido que demostró la estructura propuesta. Queda por perfeccionar el método de entrenamiento para que la ANN aumente su tolerancia inherente al ruido, lo cual podría lograrse incorporando trayectorias con ruido en la fase de entrenamiento, o considerando explícitamente las bandas de normalidad durante la citada fase. Finalmente, las conclusiones de este estudio son extendidas al reconocimiento de flujos en la parte II de este trabajo (Tarifa y Martínez, 2007).
Nomenclatura
δX: vector de desviaciones tipificadas.
δX0: vector de desviaciones tipificadas esperadas.
µF: vector de certeza de fallas.
µX: vector de certeza de variables medidas.
σ: desviación estándar.
Δt: intervalo de muestreo.
ΔX: vector de desviaciones cuantitativas.
ΔXn: vector de bandas de normalidad.
f: fallas.
net: señal de excitación en una neurona.
nf: cantidad de fallas potenciales.
t: tiempo de muestreo.
ta: tiempo de activación.
to: tiempo de observación del primer síntoma.
x: salida de la neurona.
w: vector de pesos de conexión en una ANN.
N: número de neuronas en la capa de una ANN.
X: vector de variables medidas.
Xn: vector de valores normales.
Bibliografía
Chen, B. H., Wang, X. Z., Yang, S. H. and Mcgreavy, C., Application of wavelets and neural networks to diagnostic system development., I. Feature extraction, Computers and Chemical Engineering, 23 (7), 1999, pp. 899-906. [ Links ]
Demuth, H. and Beale, M., Neural Network Toolbox for Use with MATLAB, The MathWorks, Inc. USA, 2000. [ Links ]
Garcez-Castro, A. R. and Miranda, V., An interpretation of neural networks as inference engines with application to transformer failure diagnosis., Electrical Power and Energy Systems, 27, 2005, pp. 620–626. [ Links ]
Fan J., Nikolaou, M. and White, R., An approach to fault diagnosis of chemical processes via neural networks., American Institute of Chemical Engineers Journal, 39 (1), 1993, pp. 82-88. [ Links ]
Looney, C.G., Pattern Recognition Using Neural Networks: Theory and Algorithms for Engineers and Scientists., Oxford University Press, New York, 1997. [ Links ]
Persina, S. and Tovornik, B., Real-time implementation of fault diagnosis to a heat exchanger., Control Engineering Practice 13, 2005, pp. 1061–1069. [ Links ]
Principe, J., Dynamic Neural Networks and Optimal Signal Processing,, Capítulo 6 en Handbook of Neural Network Signal Processing, CRC Press, USA, 2002. [ Links ]
Rengaswamy, R. and Venkatasubramanian, V., A fast training neural network and its updation for incipient fault detection and diagnosis., Computers and Chemical Engineering, 24, (2-7), 2000, pp. 431- 437. [ Links ]
Russell, S.J. and Norvig, P., Artificial Intelligence - A Modern approach., Prentice Hall, New Jersey, 1995. [ Links ]
Tarifa, E.E. y Martínez, S.L., Diagnóstico de fallas con redes neuronales. Parte II: Reconocimiento de flujos, Ingeniería e Investigación, In press, 2007. [ Links ]
Tarifa, E.E., Humana, D., Franco, S., Martínez, S., Nuñez, A. and Scenna, N., Fault diagnosis for a MSF using neural networks., Desalination, 152, 2002, pp. 215-222. [ Links ]
Venkatasubramanian, V., Rengaswamy, R., Kavuri, S. and Yin, K., A review of process fault detection and diagnosis. Part III: Process history based methods., Computers and Chemical Engineering, 27, 2003, pp. 327-346. [ Links ]
Wah, B. and Qian, M., Constraint-Based Neural Network Learning for Time Series Predictions., Department of Electrical and Computer Engineering and the Coordinated Science Laboratory University of Illinois, Urbana-Champaign, USA, 2002. [ Links ]
Wang, Z., Zhang, Y., Li, C. and Liu, Y, ANN-Based Transformer Fault Diagnosis., 59th American Power Conference, Chicago, Vol. 59-I, 1997, pp. 428-432. [ Links ]
Witczaka, M., Korbicza, J., Mrugalskia, M. and Patton, R.J., A GMDH neural network-based approach to robust fault diagnosis: Application to the DAMADICS benchmark problem., Control Engineering Practice, 14, 2006, pp. 671–683. [ Links ]
Zhang, J., Improved on-line process fault diagnosis through information fusion in multiple neural networks., Computers and Chemical Engineering, 30, 2006, pp. 558–571. [ Links ]














