Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.27 no.2 Bogotá May/Aug. 2007
Enrique Eduardo Tarifa1 y Sergio Luis Martínez2
1 Ph.D., en ingeniería química. Profesor asociado, Facultad de Ingeniería, Universidad Nacional de Jujuy, Argentina. Investigador, Consejo Nacional de Investigaciones Científicas y Técnicas - CONICET. eetarifa@arnet.com.ar
2 Ingeniero electrónico. Profesor adjunto, Facultad de Ingeniería, Universidad Nacional de Jujuy, Argentina. smartinez@imagine.com.ar
RESUMEN
En el presente trabajo el sistema de diagnóstico presentado en la parte I es modificado para supervisar procesos que evolucionan en forma compleja ante la presencia de fallas. Al igual que en la Parte I, se considera que cuando una falla afecta a un proceso, cada variable evoluciona siguiendo una trayectoria. Sin embargo, esta vez dicha trayectoria no es única, sino que pertenece a un conjunto de infinitas trayectorias posibles denominado flujo. Cada falla tiene asociado un flujo particular para cada variable. Entonces, en un proceso afectado por una falla, el problema del diagnóstico de fallas se traduce a reconocer, para todas las variables, a cuál flujo pertenece la trayectoria que está siendo observada. Al identificar los flujos se habrá identificado la falla que los provoca. Modelado el diagnóstico de fallas como un problema de reconocimiento de flujos, se realizó un desarrollo teórico que culminó con la definición tanto de la estructura como del método de entrenamiento de las redes neuronales empleadas por el nuevo sistema de diagnóstico. En las pruebas hechas, el nuevo sistema de diagnóstico presentó muy buen comportamiento, siendo el diagnóstico exacto, de alta resolución y estable frente al ruido. Finalmente, la teoría desarrollada también indica cómo deben ser escaladas las redes para supervisar procesos de mayor complejidad.
Palabras clave: diagnóstico de fallas, redes neuronales, reconocimiento de flujos, optimización, tolerancia al ruido.
ABSTRACT
The diagnostic system introduced in Part I is modified in this work for supervising complex processes when faults present themselves. As in Part I, it is supposed that when a fault affects a process, then each variable evolves following a trajectory. However, this time the aforementioned trajectory is not unique but belongs to a set of infinite possible trajectories named flow. Each fault in a particular flow is associated with each variable. Faults affecting a process can then be diagnosed by recognising which flow the trajectory being observed belongs to for every variable in turn. Once flows have been identified, then the fault causing them is also identified. Theory was developed after modelling fault diagnosis as being a flow recognition problem, definitions being yielded for both structure and training method for the artificial neural networks used by the new diagnostic system. The diagnostic system performed well in tests, diagnosis being exact, having high, stable resolution in the presence of noise. The theory so developed recommends networks being scaled-up for supervising more complex processes.
Keywords: fault diagnosis, artificial neural network, flow recognition, optimisation, noise tolerance.
Recibido: diciembre 7 de 2006
Aceptado: marzo 5 de 2007
Introducción
En la primera parte de este trabajo (Tarifa y Martínez, 2007), se revela un completo estudio sobre el comportamiento de distintas estructuras de redes neuronales, también llamadas ANN (Artificial Neural Networks), combinadas con diferentes métodos de entrenamiento, a fin de obtener criterios que permitieran recomendar la combinación más apropiada para el problema del diagnóstico de fallas en una planta química. En dicho trabajo el problema original fue asimilado a un reconocimiento de trayectorias. Ello permitió exponer en forma clara los inconvenientes de las estructuras de redes y métodos de entrenamiento propuestos en trabajos anteriores, a la vez que presentar las ventajas de la estructura y método de entrenamiento propuestos en el citado trabajo.
En la mayoría de los procesos que se llevan a cabo en una planta química, cuando una falla dada ocurre, cada variable evoluciona siguiendo una trayectoria, tal como se planteó en la parte I. Sin embargo, a diferencia de lo allí planteado, esta trayectoria no es única, sino que pertenece a un conjunto de infinitas trayectorias posibles; este conjunto se denomina flujo. Cada falla tiene asociado un flujo para cada variable, y los flujos pueden ser determinados por medio de simulación; de esta forma, para una planta química dada, es posible conocer los asociados a cada falla de interés. Cuando la planta sea afectada por una falla, el diagnóstico implicará reconocer, para cada variable, a cuál flujo pertenece la trayectoria que está siendo observada. Identificados todos los flujos, y utilizando la información obtenida por simulación, se habrá identificado también la falla que los origina. En este trabajo se utilizan ANN para el reconocimiento de flujos, una por cada falla de interés. Para construir una ANN es necesario definir su estructura (cantidad de neuronas, capas, conexiones) y el método de entrenamiento para lograr el comportamiento deseado (Russell y Norvig, 1995; Looney, 1997).
En resumen, la estrategia planteada aquí requiere primero elaborar una lista de fallas de interés que pueden afectar al proceso en estudio. Luego, es necesario simular cada una de esas fallas a fin de obtener los flujos correspondientes a cada variable del proceso. Determinados estos, por cada falla se construye y entrena una ANN especializada en el reconocimiento de los flujos correspondientes.
Las ANN fueron aplicadas desde sus inicios al diagnóstico de fallas en plantas químicas, y aún continúan las investigaciones en esta materia (Ferrer-Nadal et al., 2007). Por lo general, los trabajos previos en ese campo aplicaron las ANN en forma empírica para resolver problemas diversos, como: el reconocimiento de patrones para un elevado número de variables (Srinivasan et al., 2005a), la supervisión del conjunto de sectores que componen una planta química (Power, Bahri, 2004) y la utilización del contexto (historia del proceso) para refinar el diagnóstico (Srinivasan et al., 2005b).
A diferencia de los trabajos anteriores, acá se realiza un esfuerzo por justificar teóricamente tanto la estructura como el método de entrenamiento empleados para las ANN que componen el sistema de diagnóstico propuesto. Gracias a ello las redes así formuladas mostraron un buen comportamiento en las pruebas, produciendo diagnósticos exactos, de alta resolución y estables frente al ruido. Más aún, se obtuvieron criterios generales que permiten adaptar las redes a procesos distintos del tomado como caso de estudio.
Diagnóstico de fallas
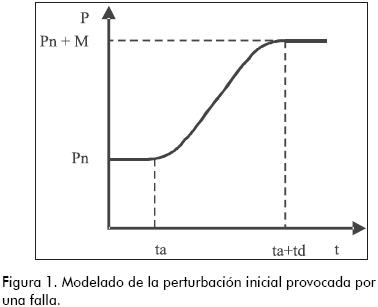
Cuando una falla ocurre en una planta química (por ejemplo: una bomba se detiene), inicialmente afecta a un parámetro o a una variable del proceso (la presión en la tubería decae). Luego, esta perturbación original se propaga a lo largo de la planta, afectando las variables que encuentra en su camino (presiones, caudales, temperaturas, concentraciones, etc.), alejándolas de sus valores normales. La forma en que las variables afectadas evolucionan es función de las características de la falla presente. Habrá diferentes evoluciones dependiendo de cuál es el parámetro o variable inicialmente afectado por la falla, y de la forma en que se efectúa dicha perturbación original. Tarifa et al. (2002) modelaron la perturbación original por medio de tres parámetros de la falla (Figura 1): el tiempo de activación ta, la magnitud M, y el tiempo de desarrollo td. El tiempo de activación es aquel en el cual la falla ocurre. La magnitud indica la máxima magnitud del cambio que sufrirá el parámetro o variable inicialmente perturbado. El tiempo de desarrollo indica el tiempo entre la activación (donde la magnitud del cambio es nulo) hasta que la falla se desarrolla totalmente (donde la magnitud del cambio alcanza su máximo valor).
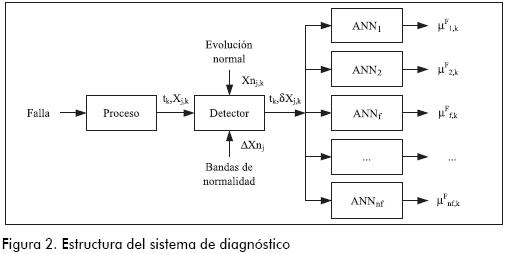
Debido a que cuando una falla ocurre en una planta química las variables afectadas evolucionan siguiendo trayectorias características, en la parte I se planteó que el estudio de estas trayectorias permite identificar la falla. Para lograr este fin, en el citado trabajo el sistema de diagnóstico adopta la estructura que se muestra en la Figura 2. En dicho sistema, cada Δt, el detector recibe del sistema de adquisición de datos el vector X que contiene los valores de las variables del proceso. Luego, compara estos valores con los valores normales Xn considerando una cierta tolerancia fijada por la banda de normalidad ΔXn. Como resultado de esta comparación, se obtiene el vector de desviaciones tipificadas δX. Este vector es enviado a un banco de ANN, el cual está conformado por una ANN por cada falla potencial de la planta; cada ANN está especializada únicamente en el reconocimiento de la falla que se le asignó. Las ANN analizan los datos provenientes del detector buscando síntomas o pruebas para sus respectivas fallas. El resultado de este análisis es el grado de certeza µF que soporta a cada falla, el cual es un número real entre 0 y 1. De esta forma, en un tiempo dado t, la certeza que reporta cada ANN indica el grado de concordancia entre la evolución observada de las variables con respecto a la evolución esperada para la correspondiente falla hasta ese momento. Un valor nulo significa que no existe concordancia alguna y, por lo tanto, no existen pruebas a favor de la falla correspondiente. Por el contrario, un valor igual a la unidad implica una concordancia total entre lo observado y lo esperado y, por lo tanto, todas las pruebas están a favor de la falla considerada. Valores intermedios significan respaldo intermedio para las fallas.
Modelado de fallas con flujos
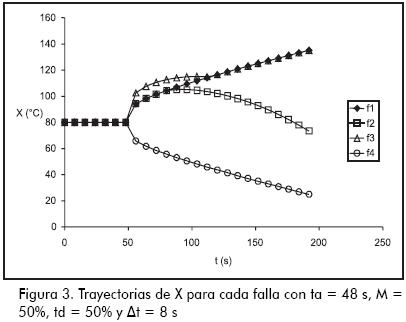
En este estudio la evolución de las variables de un proceso afectado por una falla será modelada utilizando flujos. Además, se considerará que el proceso tiene una única variable para supervisar. Esta última simplificación permite explicar con mayor claridad el trabajo realizado sin que por ello se vea afectado el valor de las conclusiones alcanzadas como queda comprobado en el trabajo de Tarifa et al. (2002). Entonces, consideremos un proceso que tenga una única variable medida, y que ésta es una temperatura. En condiciones normales, el proceso opera en estado estacionario manteniendo la temperatura en su valor normal Xn = 80°C. Considere, además, que existen cuatro fallas potenciales que amenazan al proceso, ellas son: f1, f2, f3 y f4. Cada vez que una de ellas afecte al proceso con un ta, M y td dados, la temperatura evolucionará con una trayectoria característica tal como lo muestra la Figura 3, la cual se obtuvo con M = 50%, td = 50% y Δt = 8 s; donde tanto la magnitud como el tiempo de desarrollo están expresados en porcentajes con respecto a los valores máximos que se considera pueden adoptar. Como puede apreciarse, la variable permanece en su valor normal hasta que ocurre una de las fallas en el tiempo de activación ta = 48 s. Tomando como referencia a la falla f1, la f2 es indistinguible en un principio, pero a partir de t = 88 s comienza diferenciarse. En cambio, f3 es en principio distinta, pero a partir de t = 112 s, se confunde con la falla de referencia. Finalmente, la f4 es en todo momento distinguible de f1.
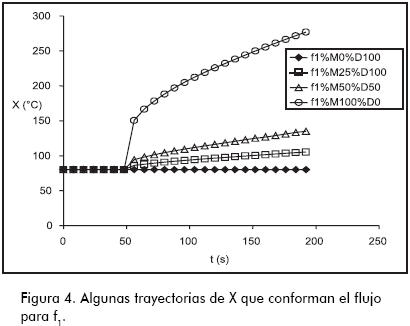
Debido a que existen infinitas combinaciones de ta, M y td, existen también infinitas trayectorias asociadas a cada falla; este conjunto infinito de trayectorias se denomina flujo. Cada falla tendrá asociado un flujo. La Figura 4 muestra algunas de las trayectorias que conforman el flujo para f1, y la Figura 5 hace lo mismo para f2; en ellas, el número que sigue a %M es la magnitud expresada en porcentaje, y el que sigue a %D es el tiempo de desarrollo expresado en porcentaje. El tiempo de activación es ta = 48 s.
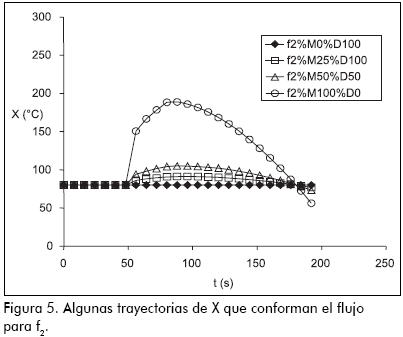
En la práctica los datos X obtenidos del proceso están afectados por ruido. La incertidumbre generada por él hace necesario que el sistema permita cierta variación alrededor del valor normal Xn, esta tolerancia está fijada por la banda de normalidad ΔXn; en el ejemplo se tomó ΔXn = 2°C.
Para este caso en particular, el problema del diagnóstico de fallas puede plantearse como: 1) Mientras X esté dentro de la banda de normalidad, no realizar acción alguna; 2) desde que se observe el primer valor anormal, determinar, por comparación con todas las trayectorias que conforman el flujo de cada falla, cuál es la que mejor explica la evolución observada. Esta tarea es mucho más compleja que la explicada en la parte I, donde se utilizaron trayectorias para modelar las evoluciones causadas por las fallas. En efecto, ahora debe compararse la trayectoria observada para X con las infinitas posibles que conforman el flujo de cada falla, de las cuales las Figura 4 y 5 develan sólo algunas de ellas, correspondientes a f1 y a f2, respectivamente. Esta enorme tarea es realizada automáticamente por el sistema aludido en la Figura 2; en las secciones siguientes se explica más detalladamente su funcionamiento.
El detector
Para el ejemplo bajo estudio, el detector transforma las trayectorias de la variable X en las trayectorias de la desviación tipificada δX. Para poder cumplir con su función, cada Δt el detector recibe del sistema de adquisición de datos el valor de X, siendo la muestra k tomada en el tiempo tk = kxΔt. Por otra parte, el detector también conoce el valor normal Xn, y lo utiliza para calcular la desviación cuantitativa ΔX = X - Xn. Calculada la desviación cuantitativa, el detector emplea la banda normal ΔXn para calcular la desviación tipificada como sigue:

La desviación tipificada es un número adimensional, y está escalada tomando como referencia la banda de normalidad de la variable.
El reloj del sistema de diagnóstico se pone en marcha en el momento en que se detecta el primer valor anormal, ese tiempo corresponde al to (tiempo de observación) del proceso y al tiempo cero del sistema de diagnóstico. La Figura 6 ofrece las trayectorias del vector δX correspondientes a las trayectorias X de la Figura 3. Por lo explicado anteriormente, dichas trayectorias nacen en el tiempo cero y con valores absolutos mayores o iguales a la unidad.
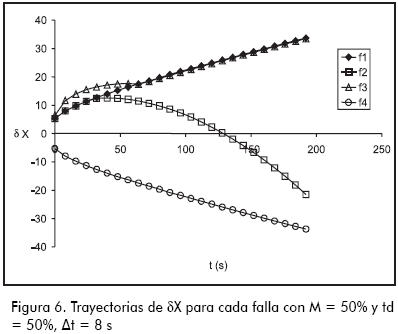
El sistema de diagnóstico
Para el caso particular del ejemplo bajo análisis, el sistema de diagnóstico propuesto por Tarifa et al. (2002) se simplifica como se explica a continuación. El grado de certeza µF, que soporta a la falla f en el tiempo tk, es definido como:
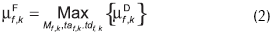
donde µD representa la certeza que soporta a la trayectoria definida por M, ta y td. De esta manera, la certeza de la falla es igual a la de la trayectoria, perteneciente al flujo asociado a ella que mejor explique la evolución de δX reportada por el detector. La certeza de una trayectoria se calcula de la siguiente forma:

donde µX representa la certeza que soporta a la variable X, y se calcula como:
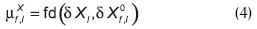
donde fd(δX, δX0) es la función de evaluación que se utiliza para evaluar la diferencia entre el valor observado δX, originado por una falla desconocida, y el valor esperado δX0 para el caso en que la falla f sea la que está afectando al proceso; ambos valores se obtienen de la Figura 6. La citada función describe el grado de pertenencia a un conjunto borroso (Russell y Norvig, 1995), y se define de la siguiente forma:
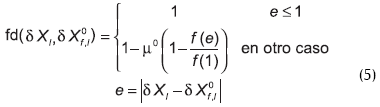
donde µ0 pertenece al intervalo [0, 1], y es utilizado para ajustar la severidad de la evaluación; a mayor valor, mayor severidad. En este trabajo se tomó µ0 = 1.
Si los valores de M, ta y td informados por el sistema de diagnóstico varían lentamente, dada la forma de las ecuaciones (2) y (3), la ecuación (3) puede ser rescrita de la siguiente manera recursiva:
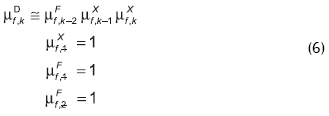
Por todo lo planteado, el procedimiento para realizar el diagnóstico es: 1) Recibir la muestra k de δX; 2) Para cada falla f, determinar M, ta y td que mejor explican lo observado por el detector – resolviendo el problema de optimización planteado por las ecuaciones de (2) a (6)-, estimar el correspondiente valor δX0 (por simulación o de una base de datos); 3) Para cada falla f, calcular µX utilizando la ecuación (4); 4) Para cada falla f, calcular µF utilizando las ecuaciones (2) y (6). Como resultado, se obtendrán las trayectorias de los µF para todas las fallas. Si se grafican estas trayectorias en función del tiempo de diagnóstico, se observará que todas las trayectorias se inician con valor unidad, pues no existe pruebas suficientes para descartar a ninguna falla; pero a medida que pasa el tiempo, los µF de las fallas que no son la causa del estado anormal observado, irán tendiendo a cero, mientras que el µF de la falla presente mantendrán su valor igual a uno.
El modelo de optimización planteado por las ecuaciones (2) a (6) presenta varios óptimos relativos, por lo cual fue necesario utilizar un método especial con el fin de encontrar el óptimo global. El método empleado en este trabajo fue el tunneling algorithm (Levy y Montalvo, 1985); para implementarlo se utilizó el utilitario MATLAB.
La Figura 7 presenta las trayectorias de las µF obtenidas al comparar las trayectorias δX de la Figura 6 con el flujo perteneciente a f1. Como puede apreciarse, cuando se ingresa la trayectoria originada por f1, µF se mantiene en 1, respaldando en todo momento dicha falla. En cambio, cuando se ingresa la trayectoria originada por f2, el sistema no descarta f1 debido a que las trayectorias que ambas fallas originan son similares hasta los 48 s. Sin embargo, a partir de los 56 s, el sistema descarta a la falla f1 disminuyendo µF. En comparación con lo analizado cuando se modeló la falla con trayectorias en la parte I, esta vez el sistema demora más en discriminar entre f1 y f2, y además presenta una notoria demora en discriminar entre f1 y f3. Esta degradación en el comportamiento del sistema de diagnóstico está ocasionada por la superposición de los flujos de las fallas, lo cual hace que muchas trayectorias causadas por distintas fallas sean similares, dificultando de esta manera la identificación de las mismas.
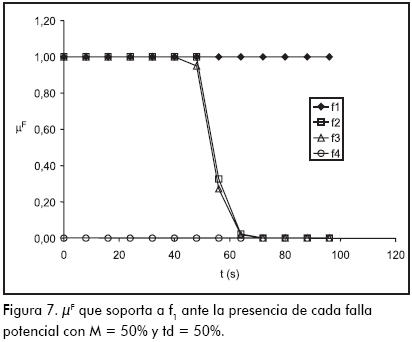
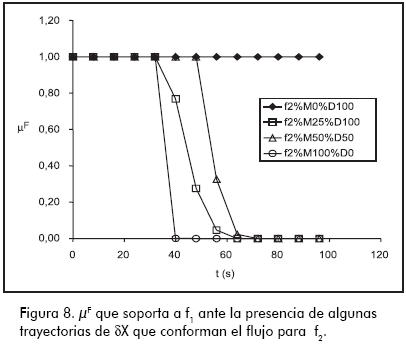
La Figura 8 registra las trayectorias del µF que soporta a f1 obtenidas al procesar algunas de las trayectorias δX que conforman el flujo de f2, las cuales están originadas en las trayectorias X de la Figura 5. Como puede verse, mientras más drástica y repentina sea la falla f2, más rápido el sistema de diagnóstico logra diferenciarla de f1.
ANN propuesta
Las ANN se caracterizan por su estructura y el método de entrenamiento (Russell y Norvig, 1995; Looney, 1997). La unidad fundamental de una ANN es la neurona. Las neuronas se agrupan en capas y de acuerdo a la forma cómo se agrupan y conectan, se tienen diferentes tipos de estructuras. En la parte I se recomendó tanto la estructura como el método de entrenamiento más adecuados para el reconocimiento de trayectorias en el marco del problema del diagnóstico de fallas. En el presente trabajo se amplió esa estructura propuesta para dar lugar a la estructura mostrada en la Figura 9, que es capaz de reconocer flujos. Esta nueva estructura proviene de una modificación de la conocida como red secuencial de Jordan (Jordan’s Sequential network; Lin y Lee, 1996), donde una retroalimentación de la salida µF es incorporada a la entrada a través de una neurona adicional que constituye la denominada capa de contexto, de tal forma que a la señal retroalimentada se le interpone un doble retardo (µF→[z-1] + [z-1]). Adicionalmente, el vector de entrada δX es incorporado a la red en forma directa y con un retardo de una muestra (δX→[z-1]). Todas estas modificaciones están justificadas por las ecuaciones (2) a (6)
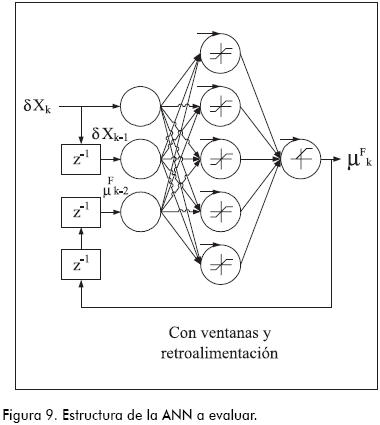
Una vez elegida la estructura, es necesario que la ANN aprenda a realizar la tarea asignada; esto se logra en la etapa de aprendizaje. Durante la misma, a la ANN se le exige salida igual a 1 cada vez que se le ingresa una trayectoria δX perteneciente al flujo de la falla correspondiente a la ANN (recuerde que existe una red por cada falla potencial); y cada vez que se le ingresan trayectorias δX pertenecientes a flujos de otras fallas, a la red se le exige que la salida sea igual a lo determinado por la ecuación (2).
La señal de excitación a de cada neurona está definida por la función de excitación, que en este trabajo se tomó como igual a la suma ponderada de todas las señales que llegan a la neurona:
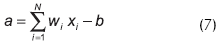
donde xi es la salida de la neurona i de la capa anterior formada por N neuronas, wi es el peso de la conexión entre dicha neurona y la que recibe la señal, y b es el bias de la neurona en consideración.
La señal de salida x de cada neurona está definida por la función de activación, que en este trabajo se tomó como igual a la función sigmoide bivaluada para las neuronas de la capa interna:
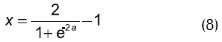
y como la función sigmoide positiva para la neurona de la capa de salida:

Resultados
Las pruebas efectuadas mostraron que la ANN pudo aprender a identificar correctamente todas las trayectorias que se utilizaron en el entrenamiento; por ejemplo, la ANN correspondiente a f1 pudo reproducir las trayectorias µF de los casos presentados en las figuras 7 y 8. En cuanto a la capacidad de generalizar de la ANN, la misma mostró un buen comportamiento cuando se le presentaron entradas con ruido, con excepción del caso mostrado en la Figura 10, donde la ANN correspondiente a f1 tiene problemas para identificar una trayectoria δX con ruido causada por dicha falla. En efecto, en lugar de mantener el valor de µF = 1 como debería, hacia el final produce algunas salidas menores que uno. Este problema está originado por la forma en que la ANN ve el flujo correspondiente a su falla.
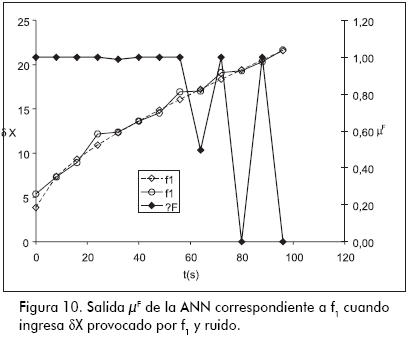
La Figura 11 –además de graficar las trayectorias correspondientes a f1, f2, f3 y f4 presentadas en la Figura 6– muestra la banda de tolerancia asignada a f1 (líneas verticales), dentro de la cual la ANN produce salidas µF > 0,95; como puede deducirse, esta banda se hace muy estrecha a partir de los 40 s, lo cual vuelve a la ANN demasiado sensible al ruido.
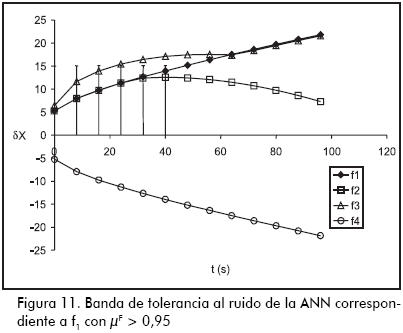
En pruebas adicionales, las ANN correspondientes a las fallas f2, f3 y f4, tuvieron el mismo buen desempeño que el descrito para la ANN correspondiente a la f1. Queda ahora perfeccionar el método de entrenamiento para que la ANN aumente su tolerancia inherente al ruido, lo cual puede lograrse incorporando trayectorias con ruido en la fase de entrenamiento, o considerando explícitamente las bandas de normalidad durante la citada fase.
Conclusiones
En la parte I se presentó un sistema de diagnóstico basado en ANN aplicándolo a un proceso que contaba con cuatro fallas posibles. Cada vez que una de ellas ocurría, la única variable medida del proceso evolucionaba siguiendo una trayectoria característica, y cada vez que se producía una misma falla, la variable evolucionaba siguiendo la misma trayectoria. En el presente trabajo se analizó el mismo proceso, pero esta vez se permitió que la variable pudiera seguir infinitas trayectorias siempre que ocurriera una misma falla. Esta modificación permitió desarrollar la teoría requerida para diseñar un sistema de diagnóstico de fallas más apropiado para la supervisión de procesos reales.
En esta investigación se definió como flujo al conjunto de infinitas trayectorias que una variable puede seguir en su evolución cuando el proceso es afectado por una falla dada, y se describió cómo es posible determinar por simulación los flujos asociados a cada falla de interés. Luego, se establecieron los principios para el diseño y entrenamiento de las ANN encargadas de realizar el diagnóstico de fallas por medio del reconocimiento de flujos. Para ello se formuló y resolvió un problema de optimización con múltiples óptimos relativos. Las ANN así construidas presentaron un buen comportamiento al aprender y al generalizar, convalidando así el procedimiento seguido. Queda, sin embargo, profundizar el estudio del efecto del ruido. Por último, el hecho de poder justificar teóricamente tanto la estructura como el método de entrenamiento de las ANN es un avance muy importante, ya que permite adaptarlas a nuevos procesos minimizando la cantidad de ensayos requeridos para alcanzar el funcionamiento óptimo del sistema de diagnóstico. En efecto, de todas las estructuras posibles, y de todos los métodos disponibles para el entrenamiento de las ANN, las variantes a estudiar quedaron reducidas al tipo de estructura contenida en la Figura 9 y al método de entrenamiento propuesto, quedando por definir únicamente la cantidad de neuronas, capas y retardos.
Agradecimientos
Los autores desean expresar su agradecimiento a la Universidad Nacional de Jujuy (UNJu, Argentina) y al Consejo Nacional de Investigaciones Científicas y Técnicas (Conicet, Argentina), por el apoyo brindado a esta investigación.
Nomenclatura
δX: vector de desviaciones tipificadas.
δX0: vector de desviaciones tipificadas esperadas.
µF: vector de certeza de fallas.
µD: vector de certeza de trayectorias.
µX: vector de certeza de variables medidas.
Δt: intervalo de muestreo.
ΔX: vector de desviaciones cuantitativas.
ΔXn: vector de bandas de normalidad.
a: señal de excitación en una neurona.
b: bias de una neurona.
f: fallas.
nf: cantidad de fallas potenciales.
t: tiempo de muestreo.
ta: tiempo de activación de una falla.
td: tiempo de desarrollo de una falla.
to: tiempo de observación del primer síntoma de una falla.
x: salida de la neurona.
w: vector de pesos de conexión en una ANN.
M: magnitud de una falla.
N: número de neuronas en la capa de una ANN.
X: vector de variables medidas.
Xn: vector de valores normales.
Bibliografía
Ferrer-Nadal, S., Yélamos-Ruiz, I., Graells, M. and Puigjaner, L., An integrated framework for on-line supervised optimization, Computers & Chemical Engineering, Vol. 31, Issues 5-6, 2007, pp. 401-409. [ Links ]
Levy, A.V. and Montalvo, A., The tunneling algorithm for the global minimization of functions., SIAM Journal on Scientific and Statistical Computing, Vol. 6, No. 1, 1985, pp. 15-29. [ Links ]
Lin, C.T. and Lee, C.S., Neural Fuzzy Systems, A Neuro-Fuzzy Synergism to Intelligent Systems., Prentice Hall, New York, 1996, pp. 346-349. [ Links ]
Looney, C.G., Pattern Recognition Using Neural Networks: Theory and Algorithms for Engineers and Scientists., Oxford University Press, New York, 1997. [ Links ]
Power, Y. and Bahri, P.A., A two-step supervisory fault diagnosis framework., Computers & Chemical Engineering, Vol. 28, Issue 11, 2004, pp. 2131-2140. [ Links ]
Russell, S.J. and Norvig, P., Artificial Intelligence - A Modern approach., Prentice Hall, New Jersey, 1995. [ Links ]
Srinivasan, R., Wang, C., Ho, W.K. and Lim, K.W., Neural network systems for multi-dimensional temporal pattern classification., Computers & Chemical Engineering, Vol. 29, Issue 5, 2005a, pp. 965-981. [ Links ]
Srinivasan, R., Wang, C., Ho, W.K., Lim, K.W., Context-based recognition of process states using neural networks., Chemical Engineering Science, Vol. 60, Issue 4, 2005b, pp. 935-949. [ Links ]
Tarifa, E.E. y Martínez, S.L., Diagnóstico de fallas con redes neuronales. Parte I: Reconocimiento de trayectorias., Ing. Investig., Vol 27, No. 1, abril, 2007, pp. 68-76. [ Links ]
Tarifa, E.E., Humana, D., Franco, S., Martínez, S., Nuñez, A., and Scenna, N., Fault diagnosis for a MSF using neural networks., Desalination, 152, 2002, pp. 215-222. [ Links ]














