Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.27 no.2 Bogotá May/Aug. 2007
Máximo Alejandro Roa1, Camilo Villegas2 y Diego Alexander Garzón-Alvarado3
1 Ingeniero mecánico. M. Sc., en Automatización industrial. DEA, en Ingeniería de sistemas y automática. Candidato a Ph. D., en Ingeniería. Investigador, Grupo de Plataformas Robóticas UNROBOT, Universidad Nacional de Colombia. Profesor asistente, Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia, Bogotá. maroag@unal.edu.co
2 Ingeniero mecánico, Universidad Nacional de Colombia. Investigador, Grupo de Plataformas Robóticas UNROBOT, Universidad Nacional de Colombia. camilovi@hotmail.com
3 Ingeniero mecánico. M. Sc., en Ingeniería de materiales y procesos de manufactura. M. Sc., en Ingeniería mecánica. Candidato a Ph. D.., en Ingeniería. Profesor asistente, Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia, Bogotá. dagarzona@unal.edu.co
RESUMEN
Los caminadores bípedos pasivos pueden lograr una caminata estable descendiendo por un plano inclinado solamente bajo la influencia de la atracción gravitacional. Este artículo presenta el modelamiento de un caminador bípedo pasivo de tres grados de libertad, buscando la relación entre las características de la caminata, las propiedades físicas del robot y la inclinación del plano. Se incluyen las ecuaciones del modelo dinámico adimensional propuesto para estudiar el caminador, se describen el proceso de implementación y modelamiento y los principales resultados obtenidos. Se analizan también los límites en los parámetros del robot que permiten obtener ciclos límites estables, ya que aparecen bifurcaciones dobles periódicas que aparentemente son naturales en la caminata pasiva. Finalmente, se hallan resultados interesantes cuando se compara la caminata natural pasiva con la locomoción bípeda humana.
Palabras clave: caminata pasiva, caminador pasivo con rodilla, marcha humana.
ABSTRACT
Passive dynamic walkers can achieve a steady gait down an inclined plane simply by the influence of gravity. This article presents the modelling of a 3 DOF passive bipedal walker, searching for a relationship between gait characteristics, the robot’s physical properties and the slope of the plane. The proposed adimensional dynamical model’s equations are also given, implementing and modelling the dynamics is described and the main results are presented. Limits on robotic parameters leading to establishing stable limit cycles are also analysed as periodic doubling bifurcations appear to be natural in passive gait. Interesting results arose when comparing natural passive walking with human bipedal locomotion.
Keywords: passive gait, kneed passive walker, human gait.
Recibido: diciembre 7 de 2006
Aceptado: junio 28 de 2007
Introducción
Se ha demostrado mediante simulaciones numéricas y físicas que ciertos mecanismos pueden lograr la caminata bípeda sobre planos inclinados de muy poca pendiente, sin actuadores ni sistemas de control, sólo bajo la influencia de la atracción gravitacional (McGeer, 1990). Estos sistemas pasivos pueden crear patrones de caminata estable; dichos movimientos son naturales y óptimos energéticamente y ser usados como inspiración para mejores diseños mecánicos y para estrategias de control en máquinas caminadoras activas.
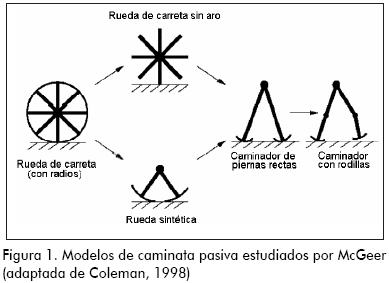
McGeer (1990) estableció diferentes modelos pasivos simples (Figura 1):
- Rueda en 2D sin aro: simula las colisiones del pie y el comportamiento de péndulo invertido en la caminata, pero no las oscilaciones de la pierna.
- Rueda "sintética" en 2D: dos piernas largas articuladas en la cadera con pies curvos de radio igual a la longitud de la pierna, simulando las oscilaciones de la pierna y el comportamiento de péndulo invertido pero no las colisiones del pie.
- Caminador de piernas rectas en 2D: usa un radio del pie menor a la longitud de la pierna.
- Caminador con rodillas: considera un caminador con pies curvos y con piernas que poseen la articulación de la rodilla.
En diversos trabajos se han realizado simulaciones numéricas extensivas sobre algunos de estos modelos para entender las características dinámicas de la caminata pasiva. Goswami et al. (1996b) presentan el modelamiento extenso de la caminata pasiva con dos grados de libertad, esto es, del caminador con piernas rectas, que exhibe la denominada caminata tipo compás; tal modelamiento se lleva a cabo seleccionando como números adimensionales las relaciones de masas y de longitudes. García et al. (1998) brindan el modelo más simple de caminata, un doble péndulo con una masa puntual en la cadera y dos masas puntuales más pequeñas en los pies. Se han desarrollado estudios previos sobre el caminador pasivo con rodillas (Yamakita y Asano, 2001) aunque no estudiado en profundidad las implicaciones dinámicas del modelo. Este artículo ofrece el proceso de simulación mediante un nuevo modelo matemático adimensional y resume los resultados preliminares del estudio de estabilidad en el caminador con rodilla, o caminador de tres grados de libertad. Se deduce la existencia de relaciones entre los parámetros de masa y longitud del robot que condicionan la obtención de ciclos límites estables. Estas relaciones permiten una comparación con la locomoción bípeda humana, dando así un soporte matemático intuitivo a algunas hipótesis empíricas empleadas en el análisis de la marcha humana. De esta forma se contribuye al trabajo conjunto de los grupos de investigación en biomecánica y del Grupo de Plataformas Robóticas de la Facultad de Ingeniería en la Universidad Nacional de Colombia, en donde se ha venido desarrollando en los últimos años un importante trabajo de investigación en el campo del desarrollo de prótesis de pierna y robots bípedos (Ramírez et al., 2005; Roa et al., 2005).
El artículo está organizado de la siguiente forma: la sección 2 introduce el modelo dinámico para el caminador pasivo con rodilla y el proceso de normalización de parámetros; la 3 presenta el comportamiento dinámico de un ciclo típico de caminata pasiva y la 4 sintetiza los principales resultados obtenidos en el proceso de simulación.
Modelo dinámico del caminador con rodillas
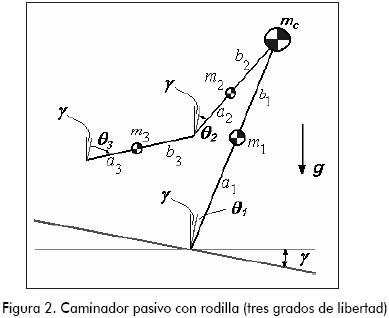
El caminador con rodillas (Figura 2) está compuesto por tres eslabones: la pierna de apoyo (1), el muslo (2) y la pantorrilla (3), y cuatro masas puntuales, ya que cada eslabón tiene una masa concentrada (m1, m2 y m3) más una masa extra en la cadera (mc). Los pies del robot son puntuales y no tienen masa. Las proporciones geométricas del caminador están dadas por las distancias distal (a) y proximal (b) a la masa puntual en cada uno de los eslabones. θ denota los ángulos de los eslabones con respecto a la vertical, y γ es el ángulo de inclinación del plano.
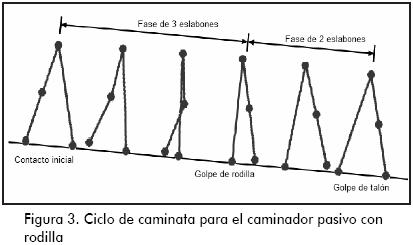
La Figura 3 muestra el diagrama de un ciclo típico de caminata pasiva. El ciclo empieza con ambos pies en el suelo. La pierna en balanceo (muslo y pantorrilla) comienza a oscilar libremente hasta que los dos eslabones se alinean; este evento se denomina golpe de rodilla. Después del golpe de rodilla, el muslo y la pantorrilla se mueven como un solo eslabón (previniendo una hiperextensión en la rodilla); se inicia así la fase de dos eslabones, en donde el robot se comporta como un caminador con caminata tipo compás hasta que la pierna en balanceo toca el suelo, en un evento denominado golpe de talón. En este punto, las piernas en balanceo y en apoyo intercambian sus papeles, y se origina un nuevo ciclo.
Las ecuaciones dinámicas para el modelo en la fase de tres eslabones (incluyendo el golpe de rodilla) se adquieren mediante dinámicas newtoniana o lagrangiana, y han sido indicadas previamente por Yamakita y Asano (2001), mientras que Goswami et al. (1996a) reseñan en detalle el modelo dinámico y la condición de golpe de talón para la fase de dos eslabones. La forma matricial general del modelo dinámico es
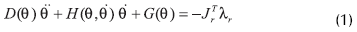
siendo D(θ) la matriz de términos inerciales, H(θ,θ) la matriz con los términos centrípeto y de Coriolis y G(θ) el vector de efectos gravitacionales. El término que incluye a la variable λr en la ecuación diferencial (1) es una restricción artificial introducida para representar las consecuencias dinámicas del golpe de rodilla, generada a partir de la condición θ2=θ3 en la fase de dos eslabones. Así, el mismo modelo dinámico puede ser usado para la fase de tres eslabones (entre el contacto inicial y el golpe de rodilla) y la de dos eslabones (entre el golpe de rodilla y el de talón). Las ecuaciones de transición para el golpe de talón se logran mediante consideraciones de conservación de momentum angular y tienen la forma general

Los detalles completos de la obtención del modelo dinámico se encuentran en (Roa, 2004). Para simplificar la simulación numérica del modelo, las ecuaciones dinámicas y de transición se normalizan usando los siguientes parámetros adimensionales:
Relaciones de masa:
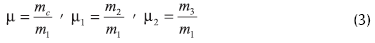
Relaciones de longitud:
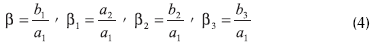
Sin embargo, no todos estos números son independientes; debido a la simetría del caminador se tienen las siguientes restricciones:
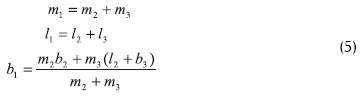
Así, el modelo dinámico normalizado es
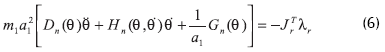
mientras que la condición de golpe de talón normalizada es

El modelo está completamente descrito mediante el conjunto de ecuaciones diferenciales no lineales (6), junto a las ecuaciones normalizadas del golpe de talón (7). El anexo contiene todas las expresiones del modelo dinámico y de las condiciones de transición adimensionales.
Comportamiento dinámico de un ciclo de caminata típico
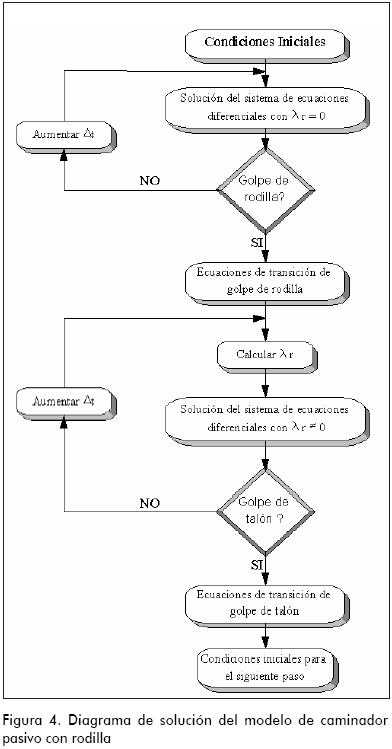
El modelo dinámico del caminador pasivo con tres grados de libertad se implementó en Matlab usando una rutina de integración Runge Kutta de cuarto orden, con un error numérico de 10-6. El código implementado resuelve el sistema equivalente de ecuaciones de primer orden para la dinámica de la fase de balanceo. Se verifica el evento de golpe de rodilla (θ2=θ3), y cuando sucede, se empieza a calcular λr (λr es cero antes del golpe de rodilla), y así se incluye el efecto de bloqueo de la rodilla en el modelo dinámico. El sistema se resuelve hasta el golpe de talón; en este punto, se aplican las ecuaciones de transición en el golpe de talón y se da inicio a un nuevo ciclo de caminata. La Figura 4 esquematiza el proceso de simulación del modelo.
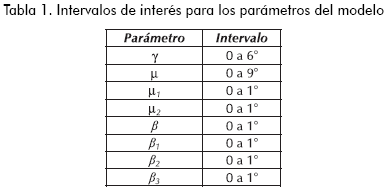
En un ciclo límite estable las variables de las articulaciones (desplazamiento y velocidad) siguen una trayectoria cíclica. Tal trayectoria puede encontrarse con condiciones iniciales apropiadas al comienzo de un paso. Las características de la caminata (velocidad, tiempo y longitud del paso) dependen de la geometría y de las propiedades inerciales del robot y de la inclinación del plano. En la Tabla 1 se presentan los intervalos de interés seleccionados para los números adimensionales del modelo; las ecuaciones se resolvieron repetidamente hasta encontrar los ciclos límites estables para cada conjunto particular de parámetros del caminador.
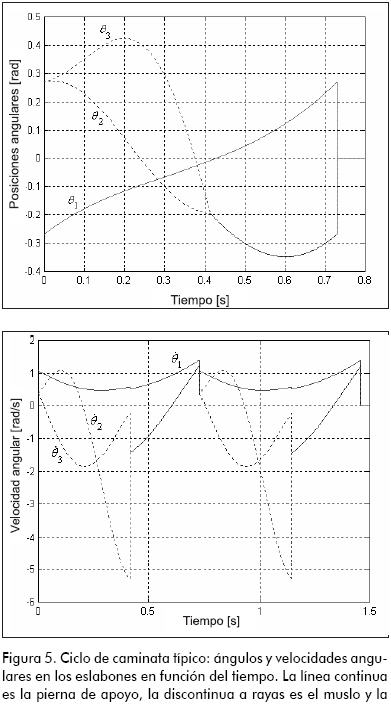
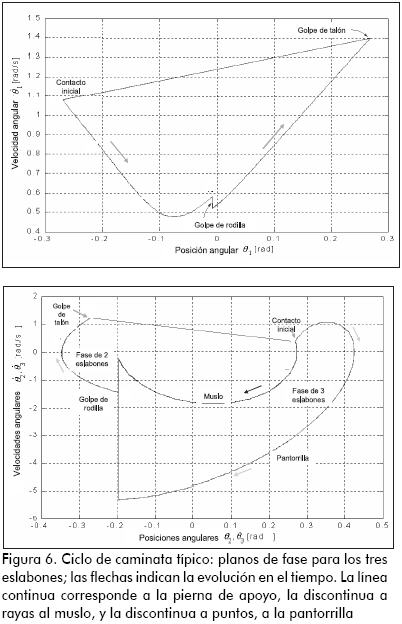
Los resultados de cada modelo particular incluyen la progresión en el tiempo del ángulo y la velocidad para cada eslabón, y el plano de fases para cada eslabón, como se muestra en las figuras 5 y 6. Este ejemplo usa los mismos valores numéricos empleados por Yamakita y Asano (2001), esto es, m2=3,5 kg, m3=1,5 kg, mc=10 kg, a2=0,15 m, b2=0,35 m, a3=0,35 m, b3=0,25 m, g=9,81 m/s2, γ=0,05 rad (2.865°). Los planos de fase muestran claramente los saltos discretos ocurridos en los eventos de golpe de rodilla y de talón, causados por la disipación de energía en tales eventos. El muslo y la pantorrilla se balancean libremente en la fase de tres eslabones, hasta que ocurre el golpe de rodilla; allí, los dos eslabones se bloquean y una fuerza de restricción (representada por λr) previene una hiperextensión en la rodilla. En este momento comienza la fase de dos eslabones, que va hasta el golpe de talón, momento en el que hay un intercambio del papel de las dos piernas: la pierna en balanceo se vuelve la de apoyo, y viceversa.
Estabilidad y bifurcaciones
La simulación numérica extensiva y las herramientas y el análisis de la dinámica no lineal permiten dilucidar el comportamiento dinámico del caminador pasivo, y establecen algunos límites interesantes para la obtención de un ciclo límite periódico. Un paso de la caminata puede ser pensado como un operador 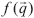 , una función de "paso", tomando como entradas el vector de estado
, una función de "paso", tomando como entradas el vector de estado 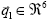 (ángulos y velocidades angulares) y dando como resultado el nuevo vector de estado
(ángulos y velocidades angulares) y dando como resultado el nuevo vector de estado 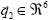 después del golpe de talón:
después del golpe de talón:

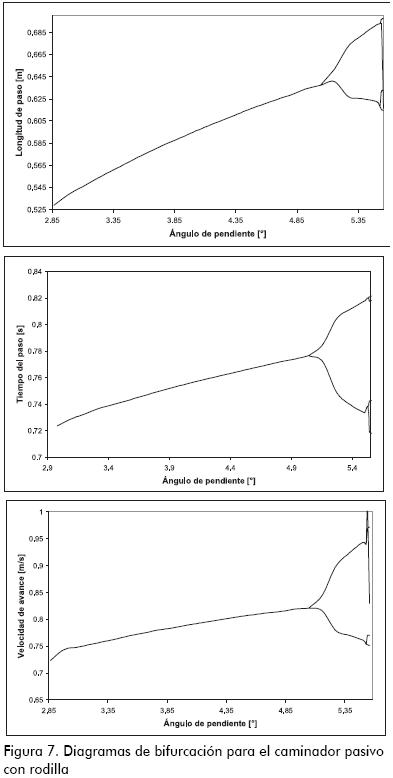
De esta forma, la función de paso es un mapa de Poincaré, y la dinámica del caminador pasivo puede ser analizada mediante el estudio de la función f. Un ciclo límite simple (caminata de periodo 1), si existe, corresponde a un vector de estado 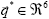 que se genera a sí mismo después de un paso, esto es,
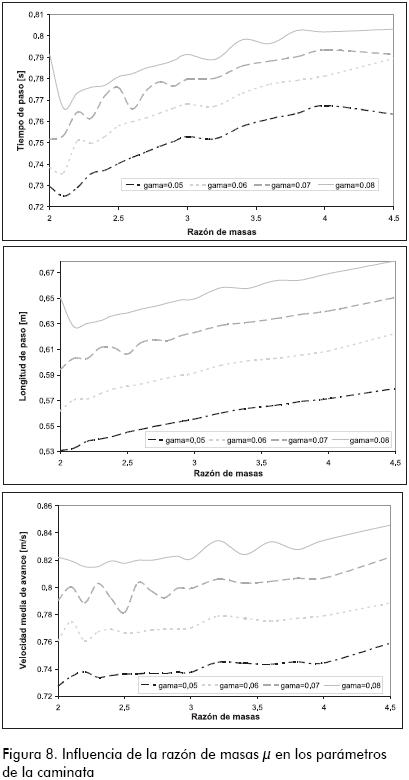
que se genera a sí mismo después de un paso, esto es, 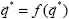 . Tal vector se denomina un punto fijo de la función f. Un ciclo límite estable de periodo dos genera el vector de estado original después de dos pasos, y así sucesivamente. La estabilidad para cada ciclo límite se verifica mediante los valores propios del jacobiano de la función de paso, siguiendo el procedimiento presentado por García (1999).
. Tal vector se denomina un punto fijo de la función f. Un ciclo límite estable de periodo dos genera el vector de estado original después de dos pasos, y así sucesivamente. La estabilidad para cada ciclo límite se verifica mediante los valores propios del jacobiano de la función de paso, siguiendo el procedimiento presentado por García (1999).
Bifurcaciones
El modelo dinámico despliega una cascada de bifurcaciones dobles periódicas, como se verifica también para el de caminata tipo compás (García et al., 1998). La Figura 7 muestra este comportamiento para el modelo con los mismos valores numéricos usados en el ejemplo anterior; las gráficas enseñan ciclos límite de periodos 1, 2, 4 y 8 en las caminatas periódicas para el comportamiento del tiempo de paso, longitud de paso y velocidad de progresión como función del ángulo de pendiente. A medida que el ángulo se incrementa, la caminata se vuelve caótica (tal comportamiento no se muestra en la figura). Es interesante notar que aunque el caminador es totalmente simétrico, se pueden lograr caminatas asimétricas de forma natural, de forma semejante al comportamiento de cojeo, sugiriendo que probablemente este es un comportamiento posible en los humanos debido a la dinámica natural implícita en el mecanismo de caminata.
Influencia de la razón de masas µ
La Figura 8 muestra la influencia del parámetro adimensional µ, la razón de masas entre la cadera y la pierna de apoyo, sobre el tiempo y la longitud de un paso y en la velocidad de progresión del caminador, para diferentes valores del ángulo de pendiente.
Los ciclos límites estables se pueden conseguir si se observan las siguientes restricciones (obtenidas mediante la simulación) sobre la distribución de masa:
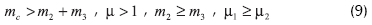
La Tabla 2 contiene los datos antropométricos de masa y longitud para la pierna de un cuerpo humano; este será el punto de referencia para comparar los resultados obtenidos con el modelo de caminata pasiva con tres grados de libertad y para inferir algunas implicaciones biomecánicas. Los datos se basan en la síntesis de trabajos clásicos de antropometría presentados por Winter (1979).
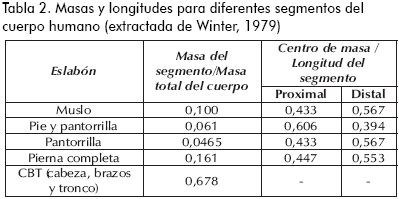
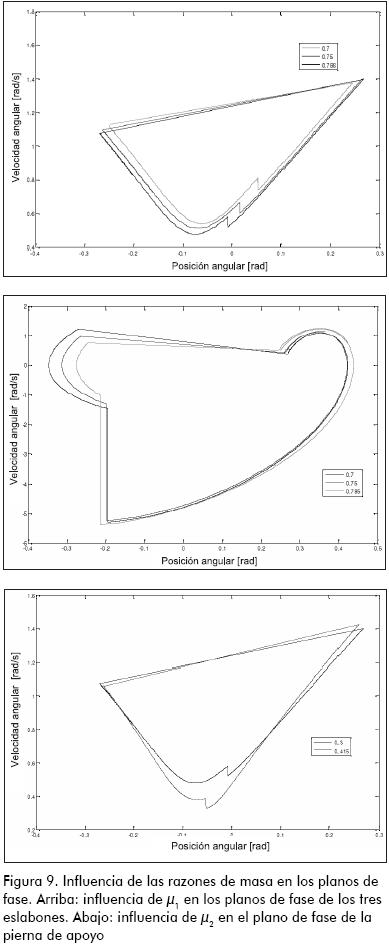
Nótese que la pierna completa hace el 16% del total de la masa corporal. De acuerdo a los límites dados por (9), la masa del muslo no debe ser mayor que la de la pantorrilla. Para realizar una comparación con el cuerpo humano, el pie y la pantorrilla se toman como un solo eslabón, que proporciona el 6,1% de la masa total del cuerpo humano, mientras que solamente el muslo tiene una masa equivalente al 10% de la corporal. Además, la del CBT (cabeza, brazos y tronco) debe considerarse como una masa concentrada en la cadera (mc). De nuevo, el cuerpo humano cumple con los límites establecidos en (9) entre la masa de la cadera y de la pierna. La Figura 9 señala la influencia de las otras dos razones de masa en los planos de fase de los ciclos límites estables.
Influencia de la razón de longitudes
Empíricamente se han obtenido restricciones adicionales sobre las longitudes de los eslabones del modelo para obtener ciclos límites estables, así:
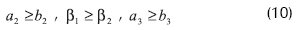
Esto significa que la distancia distal al centro de masas debe ser mayor que la proximal en todos los eslabones; en el cuerpo humano esta relación se cumple cuando se consideran el muslo, la pantorrilla y la pierna completa como eslabones, pero no cuando se consideran la pantorrilla y el pie como eslabón 3 en el modelo con rodillas. Tal diferencia surge porque el modelo aquí considerado no incluye la existencia de pies (que son puntuales y sin masa en el modelo).
Implicaciones biomecánicas
Goswami et al. (1996b) plantearon algunas relaciones en los parámetros de caminata entre dos modelos con razones de masa y longitud similares en la caminata tipo compás. Por ejemplo, las características de esta son idénticas para dos modelos con la misma relación de masas µ. Además, las características de la caminata para un caminador con razón de longitudes β=b1'/a1' pueden ser comparadas con las de otro caminador con la misma proporción siguiendo las relaciones presentadas en la Tabla 3, que hacen uso del escalar ka=a1/a1'.

Como resultado interesante, se ha verificado que las mismas relaciones pueden ser aplicadas al caso del caminador pasivo con rodillas. Si dos robots pasivos con rodillas tienen iguales proporciones de masa (esto es, equivalentes números de masa adimensionales) los robots tienen exactamente el mismo comportamiento en la caminata. Además, las relaciones resumidas en la Tabla 3 se mantienen para el caminador con rodillas; las variaciones en la longitud del eslabón 1 manteniendo idéntica la proporción con respecto a un modelo de referencia afecta a todos los parámetros de caminata por un factor de escala ka, excepto por el ángulo de progresión ante el tiempo, que no se afecta en absoluto. Este comportamiento dinámico del modelo está relacionado directamente con una de las hipótesis que soportan el análisis de la caminata humana: que toda persona, sin importar su altura, y en consecuencia su longitud de piernas (considerando un biotipo normal, esto es, una persona con proporciones antropométricas normales), describe la misma trayectoria de ángulos para cada eslabón en el ciclo de caminata. Esta hipótesis ha sido reconocida y empleada por años en el análisis de la marcha humana a partir de resultados experimentales, pero hasta ahora no existía un soporte matemático para esta afirmación; el caminador pasivo con rodillas lo proporciona a dicha hipótesis.
Conclusiones
El modelamiento numérico del caminador pasivo con tres grados de libertad fue desarrollado mediante un nuevo modelo dinámico que emplea diferentes números adimensionales para considerar las proporciones de masa y longitud del caminador. En el estudio numérico de la estabilidad en los ciclos límite para el caminador pasivo se han obtenido diferentes restricciones en los números adimensionales. Es interesante observar que el cuerpo humano cumple las mismas restricciones obtenidas en el modelo de caminata pasiva con tres grados de libertad, que fueron logradas solamente mediante la dinámica del modelo. Los resultados obtenidos para el caminador pasivo con rodilla proporcionan un soporte matemático a dos hipótesis muy utilizadas en el análisis biomecánico de la marcha humana. En primer lugar, dos personas con la misma proporción de masas presentan similar comportamiento general de caminata. En segundo término, todas las personas que cumplen con las proporciones antropométricas normales describen la misma trayectoria de ángulo para cada eslabón en el ciclo de caminata.
Bibliografía
Coleman, M., A stability study of a three-dimensional passive-dynamic model of human gait., Tesis presentada a Cornell University, para optar al titulo de Ph. D., 1998. [ Links ]
García, M., Stability, scaling and chaos in passive – dynamic gait models., Tesis presentada a Cornell University, para optar al titulo de Ph. D., 1999. [ Links ]
García, M., Chatterjee, A., Ruina, A. and Coleman, M., The simplest walking model: stability, complexity and scaling., ASME J. Biomechanical Engineering, Vol.120, No.2, 1998, pp. 281-288. [ Links ]
Goswami, A., Espiau, B. y Keramane, A. Limit cycles and their stability in a passive bipedal gait., Proc. Int. Conf. Robotics and Automation – ICRA, 1996a. [ Links ]
Goswami, A., Thuilot, B. and Espiau, B. Compass – like biped robot. Part I: stability and bifurcation of passive gaits, Research Report, INRIA (Institut Nacional de Recherche en Informatique et en Automatique), 1996b. [ Links ]
McGeer, T., Passive dynamic walking, Int. J. of Robotic Research., Vol. 9, No.2, 1990, pp. 62 – 82. [ Links ]
Ramírez, A., Garzón, D., Roa M. and Cortés, C. Test on Patient of Damper Device for Lower Limb Prosthetic., Gait & Posture, Vol.22, Sup.1, 2005, pp. S48. [ Links ]
Roa, M. Modelamiento y simulación de la caminata bípeda., Tesis presentada a la Universidad Nacional de Colombia, para optar al título de Maestría en Automatización Industrial, 2004. [ Links ]
Roa, M., Ramírez, R. y Garzón, D., Development of Biped Robots at the National University of Colombia, Proc. 8th Int. Conf. on Climbing and Walking Robots – CLAWAR, 2005. [ Links ]
Winter, D. Biomechanics of human movement., John Wiley & Sons, 1979. [ Links ]
Yamakita, M. y Asano, F., Extended passive velocity field control with variable velocity fields for a kneed biped, Advanced Robotics., Vol. 115, No.2, 2001, pp. 139 – 168. [ Links ]
Anexo
Expresiones completas del modelo dinámico adimensional del caminador pasivo con tres grados de libertad.
Modelo dinámico
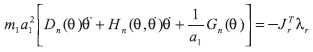
Matriz de términos inerciales:
Matriz con términos centrípetos y de coriolis:
Vector con efectos gravitacionales:
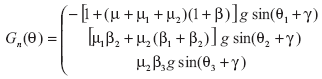
Restricción artificial en el golpe de rodilla:
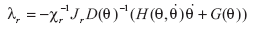
con
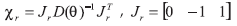
Condición de golpe de talón
Se activa cuando θ1-+θ3-=0.
Ecuación de transición:
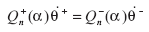
con
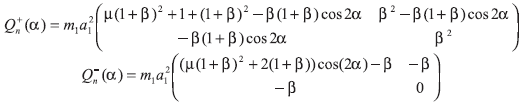
En esta ecuación,