Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería e Investigación
versão impressa ISSN 0120-5609
Ing. Investig. v.27 n.2 Bogotá maio/ago. 2007
Alexander Gómez Cassab1 y Juan Manuel Lizarazo Marriaga2
1 Ing. Civil, Universidad de Cartagena, Colombia. M. Sc., en estructuras, Universidad Nacional de Colombia, Bogotá. Investigador, grupo de investigación en estructuras y materiales GIES. aogomezc@unal.edu.co
2 Ingeniero civil. Especialista y M.Sc., en estructuras, Universidad Nacional de Colombia. Estudios sobre construcción y materiales, Instituto de Ciencias de la Construcción Eduardo Torroja, Madrid, España. Research student, Coventry University, Coventry, Reino Unido. Profesor, Departamento de Ingeniería Civil y Agrícola, Universidad Nacional de Colombia, Bogotá. Investigador, grupo de investigación en estructuras y materiales GIES. jmlizarazom@unal.edu.co
RESUMEN
Este artículo presenta los resultados analíticos y experimentales de una investigación realizada por el Grupo de Investigación GIES sobre la influencia de la no linealidad de material sobre las deflexiones inmediatas de vigas de concreto reforzado. Bajo condiciones reales y diferentes situaciones de carga fueron ensayadas seis vigas de dicho material. El comportamiento teórico de las vigas fue simulado mediante el modelo no lineal de material del programa comercial de elementos finitos Ansys®. La comparación de los resultados del modelo no lineal de Ansys®, las recomendaciones del código de construcción ACI 318, y los ensayos experimentales, mostraron que el comportamiento estructural de una viga simplemente apoyada está fuertemente influenciado por la no linealidad de material.
Palabras clave: vigas, concreto reforzado, no linealidad de material, deflexiones inmediatas.
ABSTRACT
This paper presents an analytical and experimental research programme’s results regarding material nonlinearity’s influence on reinforced concrete beams’ immediate deflections. Six full-size laboratory beams were tested under different type of loads in the experimental programme. The ANSYS finite element software nonlinear material model was used for simulating the beams’ analytical behaviour. Comparing ANSYS nonlinear material model results, ACI 318 equations and the results of the tests made revealed that a beam’s structural behaviour is strongly influenced by material nonlinearity.
Keywords: beam, reinforced concrete, material nonlinearity, immediate deflection.
Recibido: noviembre 24 de 2006
Aceptado: junio 7 de 2007
Introducción
El concreto se considera un material frágil, presenta una buena resistencia a la compresión, mientras que su resistencia a la tracción es mínima. Normalmente los esfuerzos máximos a tensión que soporta son muy bajos, por lo que para condiciones de diseño se suelen despreciar, y su resistencia a la tracción es suministrada por las barras de acero que sirven como refuerzo. La interacción entre estos dos materiales (concreto y acero) permite tener un material compuesto con el cual se ha construido gran parte de la infraestructura mundial.
Las estructuras de concreto reforzado son ampliamente usadas en una variedad de situaciones y aplicaciones; estas, son diseñadas siguiendo metodologías elásticas o procedimientos de rotura simplificados y basados en datos experimentales. En los primeros se usan conceptos de la teoría de la elasticidad, que actualmente se encuentran vigentes en los reglamentos de diseño, pero en los que se hace poco énfasis. De la misma forma, los procedimientos para la evaluación de desplazamientos y deflexiones se basan en conceptos elásticos. Las segundas metodologías de diseño se basan en datos y consideraciones experimentales; el ACI (American Concrete Institute), por ejemplo, adopta un esfuerzo de compresión uniforme en el concreto, el cual se asume distribuido sobre un área limitada por los bordes de la sección y por una línea paralela al eje neutro.
Aunque las metodologías experimentales son adecuadas para el diseño convencional de elementos de concreto reforzado, la aparición de los computadores y el desarrollo de la técnica de simulación numérica conocida como método de los elementos finitos ha permitido el desarrollo y aplicación de teorías no lineales en una forma mucho más amplia.
El desarrollo del método de los elementos finitos en sus inicios se dio a partir de los trabajos conjuntos que hicieron matemáticos, físicos e ingenieros sobre aproximación de funciones en la década de los cincuenta y del desarrollo de las primeras computadoras. En esencia, la solución de un problema se establece mediante un grupo de operaciones matriciales realizadas por un computador.
El comportamiento de un elemento de concreto reforzado obedece a la interacción de los diferentes elementos que lo componen y al tipo de solicitación a la que está sometido. Debido a la complejidad de la naturaleza compuesta del material, en los últimos años se ha intensificado la investigación en la obtención de modelos que predigan el comportamiento no lineal de las estructuras de concreto reforzado, siendo un tema que demanda mucha investigación y requiere enlazar los adelantos teóricos y experimentales realizados, con la práctica común. Aunque actualmente existen grandes avances en modelos para materiales que incluyen conceptos de plasticidad, teoría de daño y mecánica de la fractura, entre otros, un modelo constitutivo único y exacto que defina el comportamiento del concreto reforzado aún está por desarrollarse.
Aunque desde hace ya varias décadas la teoría y concepción analítica de los modelos no lineales y de plasticidad fue desarrollada, únicamente en los últimos años ha sido posible su aplicación en la simulación de estructuras de concreto reforzado, esto debido al desarrollo actual de los computadores personales.
Con el fin de estudiar la influencia de la no linealidad de material en las deflexiones inmediatas de vigas simplemente apoyadas, en la presente investigación se estudiaron cuatro condiciones de carga, las cuales representan las situaciones más comunes en cualquier diseño estructural.
El método empleado para validar los resultados de la simulación con elementos finitos consistió en comparar los datos obtenidos experimentalmente con los arrojados por el modelo analítico; para tal fin, se construyeron seis vigas a escala real, correspondientes a los dos primeros casos mostrados en la Figura 1.
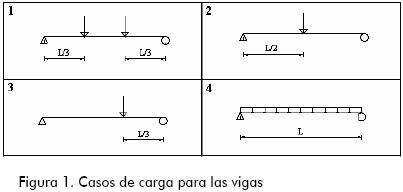
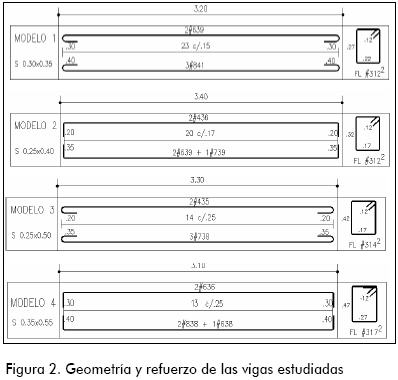
Para los casos uno y dos se ensayaron tres vigas por cada uno, esto con el propósito de efectuar tres repeticiones y evitar así el sesgo inherente del ensayo. En la Figura 2 se registra el detallado del acero de refuerzo usado en las vigas estudiadas. Así mismo, el análisis estructural de las vigas se hizo mediante el programa de elementos finitos Ansys®, el cual provee un elemento sólido tridimensional que es capaz de fisurarse en tensión y aplastarse en compresión.
Descripción de los ensayos
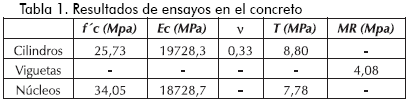
El concreto utilizado en las vigas fue diseñado para una resistencia nominal de 21 MPa, fue suministrado por una planta premezcladora. Al momento de la fundida de las vigas se elaboraron cilindros y viguetas para verificar sus propiedades. De la misma forma, una vez ensayadas las vigas se extrajeron núcleos con el fin de corroborar los datos obtenidos en los ensayos sobre cilindros. En la Tabla 1 se indican los resultados de los ensayos.
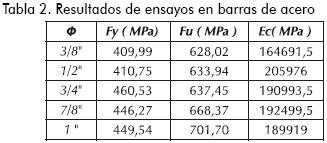
El refuerzo utilizado fue acero corrugado con un esfuerzo de fluencia nominal de 420 Mpa. Los resultados de los ensayos a tracción se registran en la Tabla 2.
El montaje de los ensayos para la aplicación de la carga vertical en los tercios y en el centro de los elementos (casos 1 y 2) se muestra en las fotos de la Figura 3. Los ensayos se llevaron a cabo en los laboratorios de la Universidad Nacional de Colombia, sede Bogotá.

Para cada una de las vigas ensayadas se colocaron deformímetros mecánicos con una precisión de 0,01 mm, los cuales se localizaron en el centro y en los cuartos de los elementos tal y como se aprecia en la Figura 4.

En todos los ensayos se presentó una zona de falla por aplastamiento del concreto en la zona de aplicación de carga. En las fotos de la Figura 5 se aprecia el estado de la falla de las vigas ensayadas.

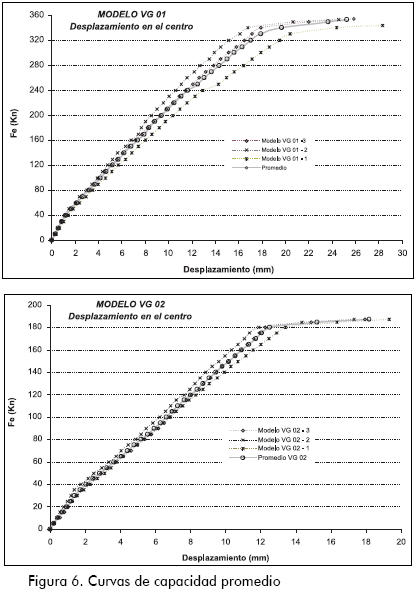
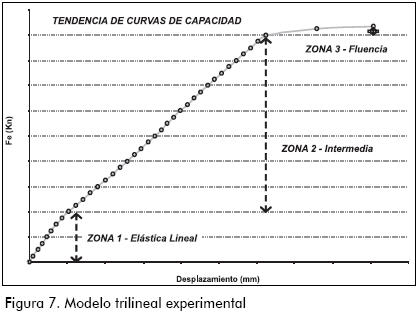
En la Figura 6 se exhiben los resultados promedios de las curvas de capacidad (fuerza–desplazamiento), medidas en el centro de la luz para los casos ensayados. En el eje horizontal está a deflexión medida en milímetros, mientras que en el eje vertical, la carga aplicada en KN. En la Figura 7 está contenido de manera general el comportamiento idealizado de una viga de concreto reforzado sometida a cualquier condición de carga.
Modelos analíticos
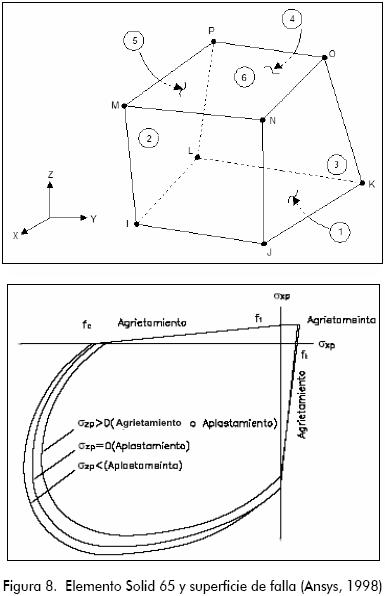
Como ya se mencionó, las vigas fueron simuladas mediante el programa de elementos finitos Ansys®, el cual provee un elemento sólido isoparamétrico tridimensional, Solid 65 (Ansys, 2004), capaz de fisurarse en tensión y aplastarse en compresión. El elemento está definido por ocho nodos con tres grados de libertad cada uno: traslación en todas sus direcciones. El aspecto más importante del Solid 65 es la capacidad de simular las propiedades de no linealidad de material, es capaz de fisurarse, sufrir aplastamiento y deformación plástica. La superficie de falla para esfuerzos de compresión está basada en el modelo constitutivo para el comportamiento triaxial del concreto propuesto por William y Warnke (William y Warnke, 1975). La falla en tensión consiste en el criterio del máximo esfuerzo de tensión. En la Figura 8 se despliegan las características del elemento Solid 65.
El acero de refuerzo fue introducido dentro del modelo computacional de dos maneras. Las barras principales o longitudinales al eje de la viga fueron simuladas como elementos tipo cercha de dos nodos y tres grados de libertad por nodo. Igualmente, los estribos fueron modelados como parte integral del Solid 65; este elemento permite tener en cuenta el acero que sirve como confinamiento mediante una cuantía volumétrica.
Con el objeto de tener en cuenta el fenómeno de adherencia entre el concreto y el acero, se introdujo en la simulación el elemento finito Combin39. Este es unidireccional, con capacidad no lineal, bajo una curva de fuerza de desplazamiento. Para él se utilizó el modelo de adherencia propuesto por el Eurocódigo CEB/FIP (Model Code 90), el cual define una curva esfuerzo cortante contra deslizamiento, las variables τ, s1, s2 y s3 dependen principalmente de la resistencia a compresión del concreto, de las condiciones del confinamiento y del corrugado de la varilla. En la Figura 9 se detallan las características del modelo de adherencia utilizado.
Una variable muy importante en un análisis de elementos finitos es la discretización del modelo; la selección del número y forma de los elementos en que es dividida la estructura está directamente relacionada con la calidad de los resultados (Bathe, 1996). Por ser un procedimiento numérico la convergencia de los resultados se logra usando un adecuado número de elementos, esto se obtiene cuando un incremento en el número de elementos produce un efecto negativo en los resultados.
Para obtener la discretización óptima de los modelos propuestos se efectuó un análisis de sensibilidad en el que se calcularon los desplazamientos en el centro de la luz para una carga determinada. Variando el número de elementos puede observarse el comportamiento de la densidad de la malla. En la Figura 10 se registra el análisis de sensibilidad llevado a cabo para cada modelo.
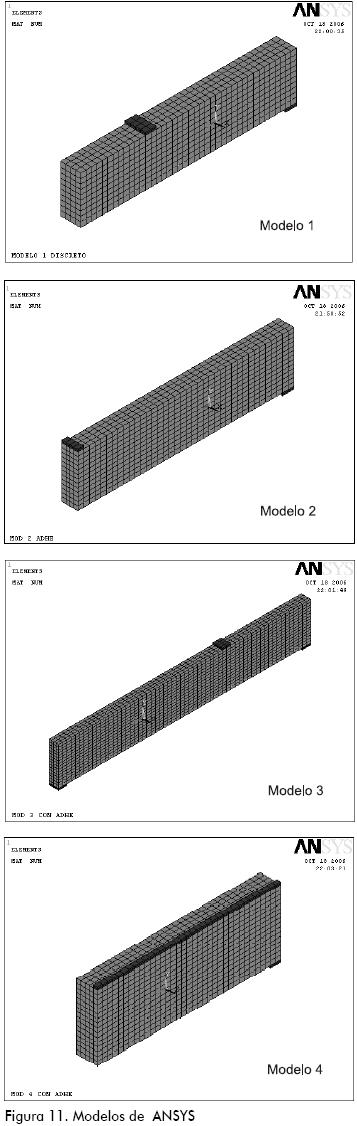
Aprovechando las condiciones de simetría de las vigas estudiadas, para los modelos 1, 2 y 4 se simuló un cuarto de la viga por presentarse simetría tanto en carga como en geometría, mientras que para el 3 se simuló la mitad longitudinal por hallarse únicamente simetría geométrica. Esta aproximación redujo notablemente el tiempo de cálculo computacional. En la Figura 11 se presentan los modelos discretizados de elementos finitos utilizados en los análisis.
La Figura 12 se enseña las curvas de capacidad (fuerza aplicada - deflexión) para los resultados experimentales, las simulaciones de elementos finitos y las recomendaciones analíticas de deflexión en vigas de los códigos ACI 318 y NSR 98 (AIS 1997). El comportamiento del modelo de elementos finitos no se ajusta en su totalidad al promedio experimental, esta diferencia es esperada y se debe básicamente a dos tipos de errores; el primero contiene las propiedades paramétricas del material, es decir, los valores de los datos de entrada que se necesitan para definir un elemento determinado; estos valores son obtenidos por medio de ensayos experimentales realizados a muestras que se consideran representativas, por tanto, conllevan un error implícito. El segundo tipo de error contiene factores numéricos tales como las técnicas de solución usadas para resolver las ecuaciones no lineales, la densidad de la malla, el número y tamaño de incrementos, el máximo número de iteraciones en cada incremento, el criterio de convergencia, el tipo de elemento utilizado en el análisis, el número de puntos de Gauss por elemento, la simulación de soportes y cargas aplicadas, entre otros.
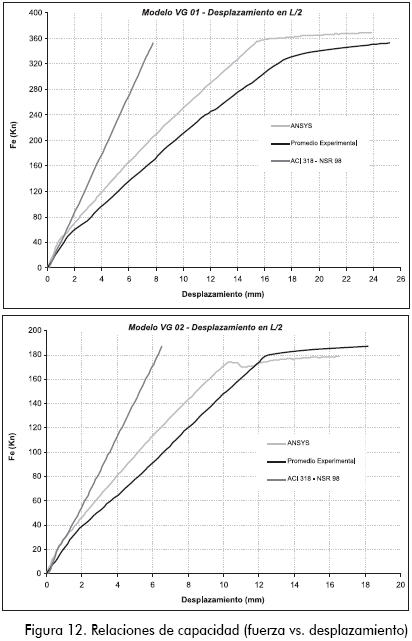
Análisis de resultados
En las curvas de capacidad obtenidas experimentalmente claramente se evidenció la presencia de tres zonas definidas por cambios internos en el elemento; la primera zona corresponde al comportamiento elástico del material en donde el concreto aún no ha presentado degradación de rigidez por fisuración interna, esta primera zona llega hasta aproximadamente un 20% de la última carga obtenida del elemento; la segunda región empieza en el inicio de la fisuración interna del concreto y termina donde se observa el inicio de la fluencia en el acero de refuerzo, en esta zona es notoria la pérdida de rigidez ya que la pendiente de la curva es mucho más acostada, comportamiento debido a la fisuración en el concreto y a la no linealidad del material. La tendencia se mantiene hasta aproximadamente un 95% de la carga de falla; la tercera zona corresponde a la fluencia del acero de refuerzo, en donde se presentan grandes desplazamientos sin un aumento considerable de la carga aplicada.
Con el objetivo de proyectar el modelo trilineal experimental en los casos 3 y 4, a los cuales no se les realizaron ensayos experimentales, se promediaron los porcentajes de error obtenidos para el MEF en el centro del elemento y se graficó la tendencia del comportamiento, como se puede observar en la Figura 13.
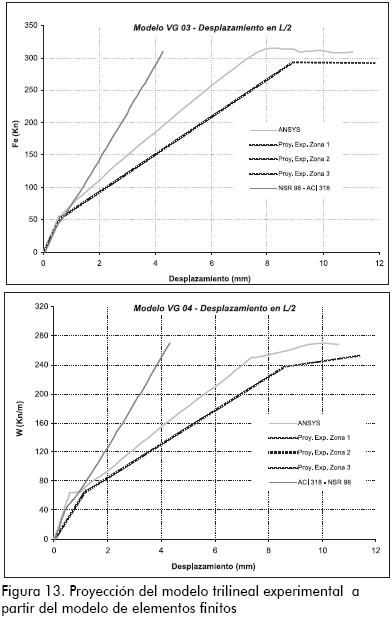
Con los datos de deflexiones obtenidos experimentalmente en los modelos 1 y 2, y con las proyecciones del comportamiento experimental logradas a partir de las curvas del modelo de elementos finitos para los modelos 3 y 4, se procedió a calcular las curvas de capacidad en función del porcentaje de la última carga y del último desplazamiento elástico, definiendo el comportamiento trilineal mencionado.
De igual manera, se establecieron las curvas de capacidad de los modelos analíticos elásticos lineales definidos en los reglamentos NSR–98/ACI 318 en función del porcentaje de la carga última y del desplazamiento último elástico. En la Figura 14 se presenta la gráfica de las curvas promedio de cada caso, por medio de las cuales se evaluó la efectividad de los modelos lineales encontrados en los códigos de diseño utilizados en la actualidad.
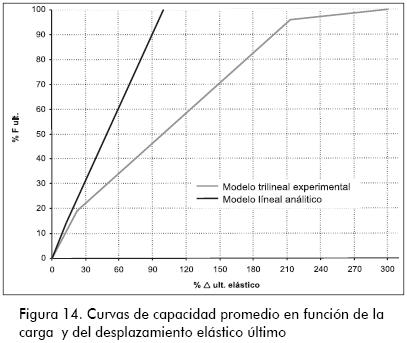
Hoy en día, en la mayoría de los códigos de diseño de concreto reforzado se especifica la necesidad de mayorar las cargas de diseño por medio de los llamados coeficientes de carga, los cuales son factores de seguridad con respecto a las exteriores; la norma NSR 98 los define como coeficientes que tienen en cuenta las desviaciones inevitables de las cargas reales con respecto a las cargas nominales y las incertidumbres que se tienen en el análisis estructural al transformar las cargas en efectos internos de los elementos; los porcentajes de mayoración que define la norma colombiana de diseño NSR-98 para cargas verticales corresponden a un 40% en el caso de cargas muertas y del 70% en el caso de cargas vivas (1,4 D + 1,7 L), otros porcentajes de mayoración que logran considerar los efectos de la retracción del fraguado y fluencia lenta son del 60% para cargas muertas y el 100% para cargas vivas (1.6 D + 2.0 L) (Segura 2002).
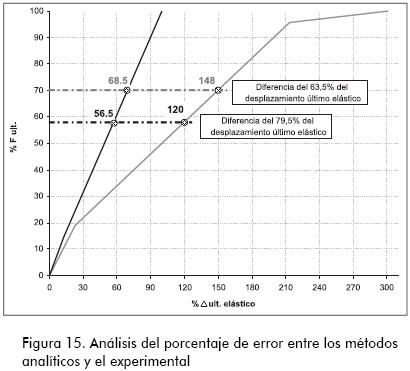
En estructuras convencionales, es decir, aquellas en que la carga viva no excede del 40% de la carga muerta, se pueden utilizar factores de mayoración del 70% para ambos tipos de carga (1,7 D + 1,7 L) (Segura, 2002). De acuerdo a lo anterior y de manera general, se podría decir que los elementos diseñados con cargas mayoradas trabajarán la mayor parte de su vida útil ante cargas gravitacionales entre el 58% y el 70% de la carga teórica de falla; con estos datos se puede realizar un análisis en condiciones de servicio sobre qué tan cercanos se encuentran los métodos analíticos elásticos para el cálculo de deflexiones (recomendaciones de los códigos), del modelo trilineal experimental encontrado en esta investigación. En la Figura 15 se muestran las diferencias en el desplazamiento obtenido mediante el método analítico propuesto por el ACI 318 y el modelo trilineal experimental.
Conclusiones
Las curvas de capacidad de los modelos obtenidos por el análisis de elementos finitos presentaron un comportamiento más rígido que las encontradas experimentalmente, es decir, para el mismo nivel de carga mostraron una deformación menor.
Los máximos porcentajes de error relativo logrados entre los modelos por elementos finitos y los experimentales corresponden al 17,5% para los desplazamientos en el centro del elemento y del 25,44% en los cuartos de la viga. Se puede afirmar entonces, teniendo en cuenta las diferentes fuentes de error del proceso experimental, que los modelos no lineales de elementos finitos tienen un grado de exactitud aceptable.
La zona lineal elástica encontrada en el modelo trilineal experimental llega hasta aproximadamente un 20% de la carga última. Se considera, por tanto, que el comportamiento lineal elástico de una viga de concreto reforzado únicamente se cumple en esta zona.
Teniendo en cuenta los coeficientes de carga utilizados normalmente en el diseño estructural, se encontró que los elementos diseñados para condiciones de servicio con cargas mayoradas trabajan la mayor parte de su vida útil ante cargas gravitacionales entre el 58% y el 70% de la carga teórica de falla.
Las diferencias halladas en el análisis comparativo entre los modelos analíticos elásticos usados normalmente y los datos del modelo experimental, se encuentran entre el 63,5% y el 79,5% del desplazamiento elástico para la carga de falla teórica en cargas de servicio.
Mediante el análisis con elementos finitos realizado, utilizando modelos constitutivos nolineales para concreto y acero, y considerando la pérdida de adherencia entre ambos, se obtuvieron mayores deflexiones a las calculadas con los modelos analíticos tradicionales (recomendaciones de los códigos ACI 318 / NSR-98), evidenciándose la fuerte influencia de la no linealidad en el cálculo de deflexiones inmediatas.
Bibliografía
ANSYS, Inc., ANSYS, INC. Theory reference, SAS IP, 2004. [ Links ]
Willam, W. J. and Warnke, E.P., Constituve model for the triaxial behavior of concrete., Proceedings, International Association for Bridge and Structural Engineering, Vol. 19, ISMES, Bergamo, Italy, 1975, pp. 174, 1975. [ Links ]
CEB-FIP MODEL CODE, 1990. [ Links ]
Bathe, K. J., Finite element procedures., Prentice-Hall, Inc., Upper Saddle River, New Jersey, 1996. [ Links ]
ACI 318-03., American Concrete Institute., Building code requirements for reinforced concrete, 2003. [ Links ]
NSR 98., Normas Colombianas de Diseño y Construcción Sismo Resistente, Asociación Colombiana de Ingeniería Sísmica, 3R Editores, Segunda Edición, Colombia, 2001. [ Links ]
Segura-Franco, J., Estructuras de concreto I., Universidad Nacional de Colombia, Quinta Edición, Colombia, 2002. [ Links ]














