Guillermo González-Vargas¹ y Felipe González Aristizábal²

¹ Ingeniero industrial, Universidad Nacional de Colombia. M. Sc., Ingeniería Industrial, Universidad de los Andes, Colombia. Aspirante a M. Sc., en Administración, Universidad Nacional de Colombia. gagonzalesvar@unal.edu.co
² Ingeniero industrial, Universidad Nacional de Colombia. M. Sc., Ingeniería Industrial, Universidad de los Andes, Colombia. felipe.aristizabal@bbva.com.co

RESUMEN

En este artículo se presenta una metaheurística híbrida denominada Genetic Clustering and Tabu Routing, con la cual se soluciona un problema de ruteo de vehículos a través de la metodología de dos fases: clusterizar primero – rutear después. Los resultados son comparados con los obtenidos al aplicar las técnicas metaheurística y heurística, presentadas en la parte 2 de esta serie de artículos, encontrando mejoras promedio del 23% y 9.1% respectivamente.

Palabras clave: ruteo de vehículos, algoritmo genético, búsqueda tabú.

ABSTRACT

This paper presents hybrid meta-heuristics called Genetic Clustering and Tabu Routing for solving a vehicle routing problem using two phases methodology: first clustering and then routing. The results are compared with those obtained using meta-heuristics and heuristic techniques presented in previous papers. Genetic clustering and Tabu routing average results were 23% and 9.1% better, respectively.

Keywords: vehicle routing problem, genetic algorithm, tabu search.

Recibido: abril 18 de2006
Aceptado: septiembre 20 de 2006

Introducción

Este, es el tercer artículo de una serie que se inició dos números atrás en esta misma revista (González-Vargas y González, 2006, 2007) y que se ha encargado de abordar el Problema de ruteo de vehículos (VRP), en el marco de la decisión de localización de una empresa manufacturera que tiene como objetivo minimizar la distancia total a recorrer para abastecer a todos sus clientes.

En este artículo se encuentra la descripción de una metaheurística hibrida diseñada para resolver el problema de ruteo en dos fases: primero clusterizar y luego rutear, la técnica propuesta por los autores ha sido denominada Genetic Clustering and Tabu Routing, e intenta responder a la necesidad de lograr una correcta asignación de nodos por vehículo para facilitar de esta forma, el ruteo y por ende alcanzar una baja distancia total a recorrer, tal como se concluyó en el artículo anterior.

Teniendo en cuenta la importancia que representa la metaheurística de Búsqueda Tabú en este artículo y dado que esta temática no había sido expuesta hasta el momento en esta serie de artículos, los autores realizan en las siguientes líneas, una breve descripción de la misma, para posteriormente presentar al lector el algoritmo híbrido desarrollado, exponiendo los operadores utilizados, los experimentos realizados y los resultados obtenidos. El artículo culmina con la presentación de algunas conclusiones y la propuesta de algunos trabajos futuros que pueden ser desarrollados a partir del trabajo presentado.

Una breve introducción a la búsqueda tabú

La búsqueda tabú (Tabu search: TS) es una extensión de los métodos clásicos de búsqueda local, y según Gendreau (2003) es la técnica más efectiva para afrontar problemas combinatorios difíciles. Esta metaheurística fue desarrollada en 1986 por Fred Glover como alternativa para superar los principales problemas a los que se enfrentaban los algoritmos de búsqueda clásicos: el ciclaje, que se evita al implementar la memoria en el algoritmo, y el estancamiento en óptimos locales lo que se supera gracias a la aceptación de soluciones no mejorantes. Según Skorin-Kapov (1990), un desarrollo similar al de Glover, el denominado steepest ascent/mildest descent fue logrado de manera independiente por Hansen en 1986, sin embargo la diferencia básica radica, según Gendrau (2003) en que TS no es una heurística en sí misma, sino una metaheurística que se encarga de guiar y controlar heurísticas internas.

En la terminología de la búsqueda Tabú se incluyen diferentes términos que vale la pena tener en cuenta para lograr entender el funcionamiento de esta metaheurística. Un vecindario en TS, es un subconjunto del espacio total de posibles soluciones y se consigue al aplicar una transformación sencilla a la solución actual, la estructura del vecindario se define al decidir que transformación se realizará cada vez para encontrar un nuevo vecino. Una “movida” tabú es un movimiento que reversa el efecto de una transformación reciente, por ejemplo si en la iteración n se intercambiaron las posiciones k y l de una solución, en la iteración n+1 el intercambio de las posiciones k y l será considerado una movida tabú, ya que llevaría al algoritmo a una solución recientemente explorada. Un término asociado al anterior es la lista tabú, que es la memoria del algoritmo y se encarga de almacenar las movidas recientes para evitar que éstas se repitan. Las listas tabú estándar son listas circulares de longitud fija (Gendreau, 2003), sin embargo, estas no siempre previenen el ciclaje por tanto, en algunas ocasiones, es útil emplear tamaños de lista variable (ver Skarin-Kapov, 1990). Vale la pena mencionar que TS permite utilizar una movida tabú si ésta presenta una mejora frente a la mejor solución obtenida hasta el momento por el algoritmo. Esta revocación a las órdenes de la lista tabú se produce gracias al criterio de aspiración de la técnica y pretende evitar el descarte de buenas soluciones.

Metaheurìstica híbrida: genetic clustering & tabu routing

Según los resultados obtenidos en el segundo artículo de esta serie, la calidad de las soluciones obtenidas en el problema de ruteo del que trata este artículo, mejora de manera sustancial al utilizar dos fases para resolverlo: primero realizar una correcta agrupación de clientes en clusters para posteriormente proceder a realizar la asignación de rutas dentro de cada agrupación. Teniendo en cuenta lo anterior y dado que la técnica de clusterizar primero y rutear después fue aplicada a través de heurísticas con las que se obtuvo resultados altamente variables y dependientes de la aleatoriedad presente en su implementación, se decidió diseñar una nueva metodología que permitiera explotar los beneficios de la clusterización previa al ruteo de vehículos pero con la inclusión de metaheurísticas de tal manera que los resultados obtenidos fueran fruto de una evolución “inteligente” y controlada de las soluciones.

Con el propósito de aprovechar las bondades de las metaheurísticas multiarranque en cuanto a diversificación de la búsqueda se refiere, al mismo tiempo que los beneficios en intensificación que ofrecen las metaheurísticas de vecindario, se construyó lo que los autores denominan Genetic Clustering and Tabu Routing, metaheurística híbrida que consiste en la utilización de un algoritmo genético (metaheurística multiarranque) para construir clusters y búsqueda tabú (metaheurística multiarranque) para construir las rutas dentro de cada cluster. En términos generales el Genetic Clustering and Tabu Routing es un algoritmo genético que pretende encontrar clusters en los que se requieran pequeñas distancias a recorrer para satisfacer a los clientes, algoritmo en el cual se utiliza una búsqueda tabú para calcular el valor de la función objetivo de cada solución.

La estructura del algoritmo propuesto en este caso, es similar al algoritmo genético implementado en el artículo anterior. Las estrategias de cruce y mutación son las mismas, sin embargo funcionalmente los dos algoritmos son muy diferentes. Las disimilitudes tienen su base en la representación de las soluciones, la técnica de reparación utilizada y la metodología de evaluación de los individuos. El pseudocódigo con el que se describe el denominado Genetic Clustering and Tabu Routing es el que sigue (los operadores son los usados en C++):

Este algoritmo se implementa utilizando los operadores que se describen a continuación.

Codificación de individuos

Los individuos que evolucionan con el algoritmo genético se representan a través de un cromosoma de 52 genes, cada uno de los cuales corresponde a uno de los nodos que deben ser visitados. Teniendo en cuenta que el propósito del algoritmo genético es realizar una clusterización, lo que se asigna a cada gen es un vehículo, de tal manera que sea posible agrupar los nodos según el vehículo que los atenderá. Desde este punto de vista, cada uno de los genes que componen el cromosoma debe contener el número del vehículo encargado de satisfacer la demanda del nodo al que corresponde el gen. La Figura 1, ilustra la representación de los individuos utilizados en el algoritmo genético.

Estrategia de reparación

En Genetic Clustering and Tabu Routing un cromosoma puede ser infactible debido a que la demanda de productos en los nodos asignados a un vehículo es superior a su capacidad, en este caso el algoritmo se encarga de realizar una reparación del cromosoma mediante la aplicación de la siguiente subrutina:

Otras consideraciones

Las demás estrategias y operadores son iguales a los utilizados en el algoritmo genético propuesto en el artículo anterior: la población inicial se genera aleatoriamente, la ordenación de la población en cada generación se realiza de manera ascendente según la distancia total a recorrer de modo que la solución con valor de la función objetivo más baja ocupa el primer lugar mientras aquella con mayor valor toma la última posición, y se utilizan las estrategias elitista para la selección de padres, cruce uniforme para la combinación de individuos y el intercambio de dos posiciones para la mutación. Por último vale la pena mencionar que el algoritmo finaliza cuando se alcanzan un determinado número de generaciones.

Cálculo de fitness (evaluación del individuo)

El cálculo del valor de la función objetivo para cada individuo en Genetic Clustering and Tabu Routing requiere de la ejecución de un procedimiento en el que en primera instancia se construye una codificación nueva que permite dar solución al problema de ruteo, para posteriormente realizar una búsqueda tabú con la cual se intenta alcanzar la mejor ruta posible dentro de cada cluster y con base en esto valorar el individuo entregado por el algoritmo genético.

La búsqueda tabú se realiza solo para clusters compuestos por más de 2 nodos, ya que en caso contrario la distancia a recorrer no es variable, el costo total de la solución se obtiene de la suma de los costos o distancias recorridas por cada vehículo para completar su recorrido. El cálculo del fitness del Genetic Clustering and Tabu Routing se puede ilustrar mediante el siguiente pseudoscódigo:

Representación de la solución de ruteo

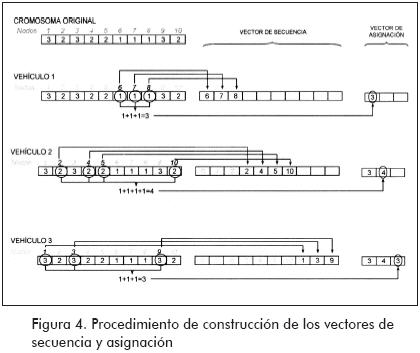
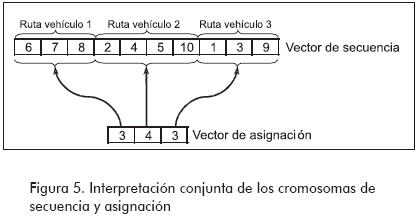
El algoritmo genético entrega al procedimiento de cálculo de fitness un vector de 52 posiciones en el que se señala qué vehículo visita cada nodo, o en otras palabras, a qué cluster pertenece cada nodo. Sin embargo esta información no ilustra la configuración de la ruta a seguir dentro de cada uno de los clusters y por ende, no es posible establecer el valor del individuo. Por esta razón es necesario construir una representación que describa la secuencia en la que serán atendidos los nodos por parte de cada uno de los vehículos. Para esto los autores proponen la construcción de dos vectores: el vector de ruteo, de 52 componentes con los cuales se indica la secuencia de viaje de los vehículos y el vector de asignación, de 6 componentes que indica la cantidad de nodos asignados a cada vehículo, o bien que componen cada cluster.

El vector de ruteo (Figura 2), es similar al utilizado para codificar las soluciones del algoritmo genético del artículo anterior, ya que en cada uno de sus componentes se ubica un nodo y el orden en el que estos aparecen en el vector representa la secuencia de la ruta. En el vector de asignación (Figura 3), los valores contenidos en cada una de sus posiciones indican la cantidad de nodos que visita cada uno de los vehículos y por lo tanto delimitan el componente del vector de ruteo en el que inician y terminan las rutas los diferentes vehículos. Por ejemplo, si el primer componente del vector de asignación contiene el valor cinco (5) entonces los primeros cinco nodos del vector de ruteo pertenecen al primer cluster por lo tanto la ruta va desde el origen hasta el nodo del primer componente pasando de manera secuencial por todos los nodos hasta llegar al quinto componente del vector, donde se finaliza la ruta y por tanto se regresa al origen, el siguiente cluster iniciará entonces en el nodo del sexto componte del vector de ruteo. Es claro que la suma de los valores de los componentes del vector de asignación siempre debe ser igual a la cantidad total de nodos a visitar (52).

Los vectores de ruteo y asignación, se construyen antes de empezar la búsqueda tabú según como lo describe el siguiente pseudocódigo:

El anterior pseudocódigo se encarga de convertir el cromosoma entregado por el algoritmo genético en una solución al problema de ruteo, secuenciando de manera lexicográfica todos los nodos ha ser visitados por cada vehículo. Un ejemplo del procedimiento de construcción de los vectores de secuencia y asignación se ilustra en la Figura 4, y su interpretación en la Figura 5, en este caso se utilizan diez nodos y 3 vehículos.

Búsqueda tabú

Una vez se construyen los vectores de secuencia y asignación el algoritmo cuenta con una solución inicial desde la cual es posible efectuar la búsqueda tabú. El propósito de ésta es encontrar una ruta de bajo costo (distancia total recorrida) para atender las demandas de los nodos que pertenecen a cada cluster. La búsqueda tabú implementada sigue el siguiente pseudocódigo:

La búsqueda tabú se inicia con la localización de las posiciones del vector de secuencia en las cuales se inicia y finaliza el recorrido del vehículo i, es decir, los límites del cluster, esto se realiza con ayuda del vector de asignación. Teniendo en cuenta lo anterior, el algoritmo se encarga de explorar mediante búsqueda local todos los vecinos de la solución actual, realizando todos los posibles intercambios entre pares de posiciones en el mismo cluster (esta estrategia es la misma utilizada en la búsqueda local expuesta en el artículo anterior). El algoritmo expuesto, se dedica entonces, a realizar búsquedas locales de manera iterativa a partir de diferentes soluciones, cada una de ellas escogida por ser la mejor solución (mejor vecino) encontrada a partir de una modificación de la anterior mediante una movida que no se encuentra en la lista Tabú (movida NO tabú), a menos que el mejor vecino, a pesar de encontrarse gracias a una movida tabú, mejore la solución actual, caso en el que se aceptaría utilizar una movida vetada por la lista Tabú (criterio de aspiración). En el algoritmo propuesto la lista tabú es de tamaño constante (ajustado por ensayo y error) y es actualizada iteración tras iteración excluyendo la movida más antigua e incluyendo la mas reciente. La condición de terminación de la búsqueda Tabú propuesta es la convergencia del resultado.

Implementación

El algoritmo programado en C++ fue ejecutado en una PC Pentium IV de 2.4 Ghz con 512 MB de RAM y 120 Gb de disco duro. En cada ejecución es responsabilidad del usuario ingresar los parámetros que rigen el algoritmo: tamaño de la población, el porcentaje de individuos que componen la “élite”, porcentaje de hijos generados por la “élite”, probabilidad de mutación, cantidad de generaciones a realizar y tamaño de lista tabú. Al igual que en el algoritmo genético del artículo anterior, es necesario ajustar los parámetros a través de la realización de diferentes experimentos de tal manera que se logre una evolución adecuada de las soluciones.

Experimentos y resultados

Para lograr un algoritmo que permita encontrar resultados satisfactorios al problema de ruteo de vehículos planteado, no basta con escribir el código que se ha expuesto hasta el momento. Es necesario además, encontrar un juego de parámetros que permita encontrar direcciones de mejora, a medida que el algoritmo avanza, lo cual resulta de una evolución “inteligente” y controlada del mismo.

En este artículo se presentan diferentes experimentos mediante los cuales se intentó encontrar un juego de parámetros que permitiera la mejor evolución posible de los resultados, característica que se midió a través de la comparación de medias mediante la prueba ANOVA, y para experimentos no diferenciados estadísticamente, se compararon los valores promedio, mínimo y desviación típica de los experimentos. Es importante notar que el Genetic Clustering and Tabu Routing requiere ajustar parámetros tanto para el algoritmo genético como para la búsqueda tabú. En este proceso se realizaron nueve experimentos en los que se ajustaron la cantidad de generaciones, el porcentaje de individuos de la “élite”, el porcentaje de hijos generados por la “élite”, la probabilidad de mutación y el tamaño de la población, como parámetros del algoritmo genético, y el tamaño de la lista para la búsqueda tabú (véase Tabla 1). Los nueve experimentos se aplicaron al ruteo a partir de las tres ciudades candidatas a convertirse en ubicación de la empresa, es decir, a los nodos 9, 28 y 49.

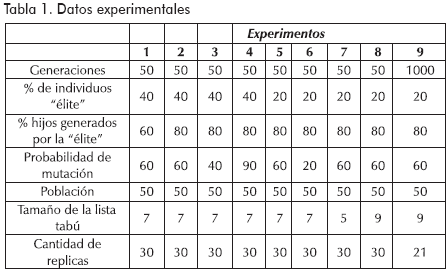
Los experimentos de la Tabla 1 se ejecutaron en tres etapas: en la primera de ellas se realizaron seis experimentos variando el porcentaje de individuos que pertenecen a la “élite”, el porcentaje de hijos generados por estos y la probabilidad de mutación; la siguiente etapa consistió en variar el tamaño de lista de la búsqueda tabú, para lo que se utilizó el juego de parámetros de mejor comportamiento de la primer etapa, con lo que se generó los experimentos 7 y 8; por último, la tercer etapa, constó de un solo experimento en el que se elevó la cantidad de generaciones del algoritmo genético con el juego de parámetros que hasta el momento hubiera presentado el mejor comportamiento. Los resultados obtenidos en los nueve experimentos para el ruteo a partir de cada uno de los tres nodos candidatos a convertirse en sede de la empresa se presenta en la Tabla 2.

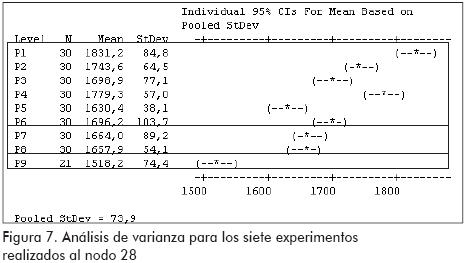
La comparación estadística de los resultados obtenidos se realizó mediante la prueba ANOVA para comparación de medias con el paquete informático MINITAB versión 14³. Los resultados de las pruebas efectuadas para los nodos 9, 28 y 49 se encuentran en las Figuras 6, 7 y 8 respectivamente. En estas Figuras se identifican los resultados de cada experimento con la misma numeración en que aparecen en las Tablas 1 y 2. En las Figuras 6, 7 y 8 se aprecia que el experimento 5 (P5) se destaca entre los resultados de la primera etapa (seis primeros experimentos), manteniendo una diferencia estadísticamente comprobable con todos los experimentos para el nodo 28 (Figura 7) y con los experimentos 1, 4 y 6 en los nodos 9 y 29 (Figuras 6 y 8), nodos en los que el experimento 5 presentó el valor mínimo. Por lo anterior, se decidió proseguir con la segunda etapa variando el tamaño de lista al juego de parámetros 5, al comparar los resultados obtenidos para los parámetros 5 con un tamaño de lista de 7 (P5), 5 (P7) y 9 (P8) se encontró que no existe ninguna diferencia significativa entre ellos, sin embargo se decidió llevar a la tercera etapa el juego de parámetros 8, es decir, el experimento en el que se usó un tamaño de lista igual a nueve, ya que en este caso se encontró el mínimo valor para los todos los nodos candidatos.

La tercera etapa de experimentación se realizó con una cantidad de generaciones 20 veces superior a la utilizada en los experimentos previos, esta modificación se llevo a cabo con el juego de parámetros identificado con el número 8. Los resultados obtenidos, estadísticamente inferiores a los anteriores, se deben a que el tiempo de evolución del algoritmo es mucho mayor al permitido en los experimentos previos.

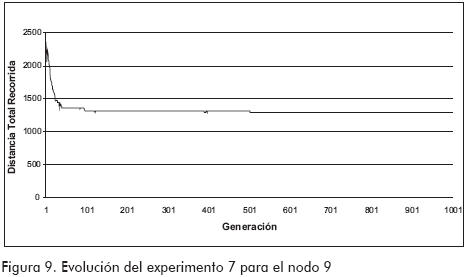
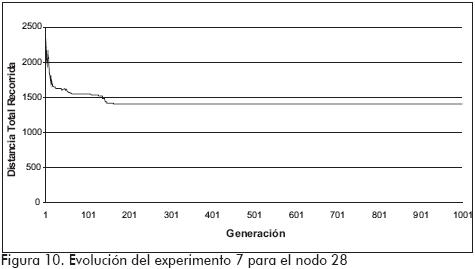
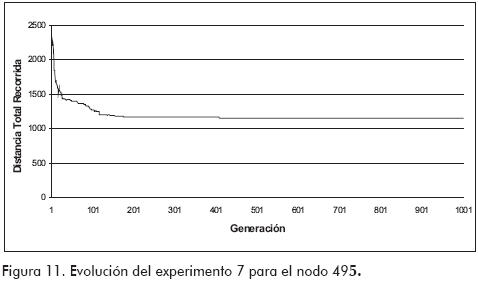
Con el noveno experimento se obtuvo el valor mínimo para cada nodo, es decir, la menor distancia total a recorrer desde los nodos 9, 28 y 49, la cual fue de 1286,5kms, 1399,6 kms y 1155,2kms respectivamente. La evolución de los resultados en la mejor réplica del juego de nueve experimentos desde los nodos 9, 28 y 49 es la que se ilustra en las Figuras 9, 10 y 11 respectivamente. En ellas se puede observar el rápido descenso en el valor de la distancia total a recorrer que se presenta durante las primeras 200 generaciones, momento desde el que se aprecia una convergencia del resultado, el cual se altera levemente durante las siguientes generaciones, alteración que puede ser fruto de alguna variación en los cromosomas debida a la aleatoriedad de la mutación.

Conclusiones

Mediante la aplicación del denominado Genetic Clustering and Tabu Routing se logra mejorar los resultados obtenidos a través del algoritmo genético en promedio en un 23%, con reducciones de 395,6 kms para recorridos desde el nodo 9, lo que equivale a una reducción del 23.5%; 439,6 kms para recorridos desde el nodo 26, es decir, una reducción del 23.9%; y una disminución de 337.3 kms en el recorrido desde el nodo 49, lo que a su vez equivale a un 22.6% menos de distancia.

Al comparar los resultados obtenidos con Genetic Clustering and Tabu Routing y la heurística aplicada en el artículo anterior, se encuentra que, para el ruteo a partir de los nodos 28 y 49, los resultados de la metaheurística híbrida presentan reducciones del 21% para el ruteo a partir del nodo 28 (372.5 kms) y del 8.5% a partir del nodo 49 (107.6 kms), las rutas encontradas para el nodo 9 presentan una menor distancia total a recorrer al aplicar la heurística, manteniéndose 2,1% por debajo del valor encontrado con Genetic Clustering and Tabu Routing, es decir, 27,9 kms por debajo del valor encontrado con la metaheurística híbrida.

Lo anterior pone en manifiesto que la calidad de las soluciones obtenidas a través de la heurística aplicada en el artículo anterior es altamente dependiente de la calidad de la clusterización efectuada mediante barrido, la cual eventualmente puede significar una asignación de nodos tal que cualquier ruteo, así se halle en un óptimo local, permita encontrar una distancia a recorrer bastante pequeña. En este caso específico, el barrido aplicado desde el nodo 9 encuentra en el área de influencia de la empresa, seis regiones en las cuales se facilitan las rutas de los vehículos y por tanto no se pudo encontrar ninguna solución mejor (desde este nodo). No obstante los resultados obtenidos a través de la aplicación del Genetic Clustering and Tabu Routing son altamente satisfactorios toda vez que permiten encontrar distancias totales relativamente bajas sin requerir ningún punto de partida específico, las mismas que superan en dos de los ruteos a las técnicas anteriormente aplicadas y en el otro caso solo se encuentra un 2% por encima del mejor valor hallado.

El Genetic Clustering and Tabu Routing propuesto, es susceptible de mejoras con las cuales se logre mejorar los resultados obtenidos. Esta mejoras pueden radicar en modificaciones en los operadores del algoritmo genético que dirigen la búsqueda de tal manera que la convergencia de los resultados se retrase un poco y por ende se explore una porción mayor del espacio de posibles soluciones. Así mismo, es posible mejorar el resultado final del algoritmo realizando una intensificación de la búsqueda sobre la solución encontrada, esto se puede llevar a acabo realizando inserción de nodos de un cluster a otro. Por otra parte se puede limitar el problema de ruteo realizando una correcta asignación de nodos a cada cluster a partir de técnicas más avanzadas de clusterización, con las cuales se pueda asegurar una asignación coherente y no fruto de la casualidad que proporciona el barrido. Todas estas observaciones se dejan abiertas al lector que desee profundizar en este tema y considere pertinente realizar desarrollos a partir de lo propuesto.

Bibliografia

Gendrau, M., An introduction to Tabu Search., En: Glover, F. & Kochenberger, G. (Eds.), Handbook of metaheuristics. Kluwer academic publisher, 2003.        [ Links ]

González-Vargas, G. y González, F., Metahurísticas aplicadas al ruteo de vehículos. Un caso de estudio. Parte 1: formulación del problema., Ing. Investig., Vol. 26, No. 3, 2006, pp. 149-156.        [ Links ]

González-Vargas, G. y González, F., Metahurísticas aplicadas al ruteo de vehículos. Un caso de estudio. Parte 2: algotritmo genético, comparación con una solución heurística., Ing. Investig., Vol. 27, No. 1, 2007, pp. 149-157.        [ Links ]

Skorin-Kapov, J., Tabu Search Applied to the quadratic assignment problem., Journal on computing, Vol 2, No. 1, 1990.        [ Links ]

3 MINITAB^® Release 14.13. 1972 - 2004 Minitab Inc. All rights reserved.