Zósimo Arévalo Velosa², Alexander V. Sinitsyn³, Octavio Alejandro Castañeda U.⁴, Miguel Hernando Camelo B.⁵

¹ Este trabajo es resultado del diplomado "Temas recientes y avanzados de la electrónica", organizado por el Grupo GMACON como parte de la estrategia de preparación de su personal y difusión del conocimiento.
² Ingeniero electrónico, Universidad Distrital Francisco José de Caldas, Colombia. M.Sc., Electrical Engineering, Pennsylvania State University. M.Sc., Ingeniería Electrónica, Universidad Central Marta Abreu de Las Villas, Cuba. Director, Programa Ingeniería Electrónica, Universidad de Ibagué. Investigador del Grupo en Materia Condensada-GMACON, Programa de Ingeniería electrónica, Facultad de Ingeniería, Universidad de Ibagué, Tolima, Colombia. zosimo.arevalo@unibague.edu.co
³ Ph.D. en Matemáticas. Profesor, Universidad Nacional de Colombia, Bogotá. Profesor del diplomado, en "Temas recientes y avanzados en electrónica", Universidad de Ibagué. Colombia. avsinitsyn@yahoo.com
⁴ Ingeniero electrónico, Universidad de Ibagué, Colombia. Investigador del Grupo en Materia Condensada-GMACON, Programa de Ingeniería electrónica, Facultad de Ingeniería, Universidad de Ibagué, Tolima, Colombia. alejandro_cu@hotmail.com
⁵ Ingeniero electrónico. Investigador del Grupo en Materia Condensada-GMACON, Programa de Ingeniería electrónica, Facultad de Ingeniería, Universidad de Ibagué, Tolima, Colombia. miguelhdo@hotmail.com

RESUMEN

Los dispositivos de alta energía son diseñados para que funcionen con campos eléctricos y magnéticos extremadamente altos. Debido a esto, dichos dispositivos presentan fenómenos y comportamientos no lineales, como el aislamiento magnético que altera el transporte de los electrones. La no linealidad ha obligado a analizar y revisar desde el punto de vista matemático las condiciones de frontera y las soluciones del problema. El objetivo de este trabajo es exponer el tema a un nivel que facilite su difusión entre la comunidad académica no familiarizada con el mismo. Para ello, el trabajo presenta una descripción de los fenómenos que se generan cuando hay campos eléctricos y magnéticos muy altos, tomando el caso de un diodo plano al vacío, así como las ecuaciones que modelan el fenómeno de aislamiento magnético; también demuestra la existencia de las soluciones y encuentra las positivas en base a los métodos de solución superior e inferior para problemas de valor de frontera, y proporciona algunos ejemplos de aplicación del fenómeno de aislamiento magnético.

Palabras clave: aislamiento magnético, flujo de potencia, flujo estacionario, condición de Child-Langmuir, diodo plano al vacío, sistema Vlasov-Maxwell, soluciones superiores e inferiores.

ABSTRACT

High energy devices are designed to work with extremely high electric and magnetic fields. As a consequence, these devices show non-linear phenomena and behaviour, such as magnetic insulation which alters electron trajectory. A mathematical analysis and review of magnetic insulation were carried out as a consequence of non-linearity to find frontier conditions and solutions to the problem. This paper was aimed at presenting the topic in a way which is easier for that part of the academic community which is unfamiliar with it to understand it. The paper gives a description of the phenomena developed by high electric and magnetic fields in a vacuum plane diode, some equations modelling the phenomenon, proves its existence and finds positive solutions based on upper and lower solutions for boundary limit problems and gives some practical applications.

Keywords: magnetic insulation, power flow, stationary flow, Child-Langmuir condition, plane vacuum diode, Vlasov-Maxwell solutions, upper and lower solutions.

Recibido: abril 19 de 2007
Aceptado: octubre 31 de 2007

Introducción

Un haz de electrones que se mueve en una región genera una corriente eléctrica, la que a su vez genera un campo magnético en un plano perpendicular al movimiento de los electrones. Si la corriente es muy grande la intensidad del campo magnético generado puede ser suficiente para alterar la trayectoria de los electrones, los cuales pueden no llegar a su destino, dando lugar al fenómeno de aislamiento magnético. Este fenómeno (magnetic wall) fue primero tratado por Sacharov y Tamm en 1961.

Los primeros dispositivos en los que se utilizaron haces de electrones para conducir corriente eléctrica fueron los diodos al vacío, que datan de finales del siglo XIX⁶. Para 1931 Langmuir y Compton realizaron estudios sobre la conducción en el diodo al vacío y establecieron la corriente de saturación. Para 1961 se reporta el fenómeno de asilamiento magnético cuando la corriente en el diodo se hace muy grande (Sinitsyn y Dulov, 2005). En 1995 se inició el estudio matemático del fenómeno de aislamiento por un grupo francés, del cual ha hecho parte uno de los autores (Sinitsyn).

El objetivo de este trabajo es exponer el tema a un nivel que facilite su difusión entre la comunidad académica no familiarizada con él. Se inicia con una descripción cualitativa del tema, que incluye la descripción física del fenómeno en un diodo plano al vacío, se continua con la aplicación de las herramientas físico-matemáticas utilizadas en el modelamiento del fenómeno, la prueba de existencia de soluciones, deducción de las soluciones positivas del sistema planteado, y se finaliza con la presentación de algunas aplicaciones. Más adelante se describe el diodo al vacío, la formación de la carga espacial (fenómeno Child-Langmuir) que limita la corriente máxima del diodo a un valor que depende del voltaje aplicado y la separación ánodo-cátodo. Se muestra la aparición del fenómeno del plasma. Se explica cómo la corriente cátodo-ánodo que se desplaza en el eje X produce un campo magnético en el plano YZ perpendicular al desplazamiento, que desvía el haz de electrones y puede provocar, a corrientes muy elevadas, que el haz no alcance el ánodo (fenómeno de aislamiento magnético, magnetic insulation). Posteriormente, se revisan las herramientas físico-matemáticas a utilizar y se efectúa el planteamiento matemático del problema, discutiendo la existencia de soluciones semitriviales a este problema y la existencia de soluciones completas al problema. Finalmente, se mencionan algunas de las aplicaciones actuales, como la propagación de pulsos electromagnéticos de alta potencia en líneas de transmisión al vacío y la producción de energía eléctrica en plantas termonucleares.

Funcionamiento del diodo al vacío, formación de la carga espacial, el plasma y aparición del aislamiento magnético

El diodo al vacío consiste de un filamento incandescente que calienta un elemento denominado cátodo, el cual, al alcanzar la temperatura suficiente, emite electrones que son atraídos por un potencial positivo (V_P) en otro elemento denominado ánodo, colocado a una distancia (L). Todo el sistema se encuentra en un recipiente al vacío para permitir el libre flujo de los electrones sin colisiones con otras partículas. En algunos casos el filamento actúa como filamento y cátodo al mismo tiempo. El filamento se lleva a una alta temperatura aplicándole un voltaje DC o AC. (Ver esquema conceptual, Figura 1).

Si la emisión de electrones desde el cátodo se mantiene baja, la distribución de potencial en el espacio placa-cátodo está representada por una línea recta que une los puntos correspondientes al potencial del cátodo V_K=0 y el potencial de la placa V_P. El voltaje aplicado entre ánodo y cátodo crea una intensidad de campo eléctrico E=V/L dirigido del ánodo al cátodo.

Los electrones son emitidos por el cátodo con velocidad de escape igual o mayor que cero (V_f>=0). Los electrones son atraídos por el potencial positivo de la placa (V_P), formándose una corriente eléctrica cuyo sentido positivo convencional es de ánodo a cátodo. Esa región de funcionamiento se conoce cono la región de emisión limitada.

Si no hay emisión en el cátodo, el diodo se comporta como un capacitor de placas planas paralelas con una diferencia de potencial (V_P) (Dulov y Sinitsyn, 2005).

Si el voltaje del filamento se incrementa, aumenta la temperatura y por ende la emisión de electrones. Cuando los electrones salen del cátodo con velocidad igual a cero (V_f=0) se incrementa su cantidad cerca del mismo y se produce, en el espacio interelectródico, una nube de electrones llamada carga espacial. Esta carga altera la distribución de potencial y produce un potencial negativo (-Vmín) cerca del cátodo, en donde se presenta su máxima densidad, a una distancia (x_mín) de céntimos a décimos de mm. Este potencial negativo hace que los electrones emitidos, con bajas velocidades, sean regresados al cátodo y el diodo no sobrepase una corriente límite, llamada de saturación, porque la corriente de Placa no aumenta con la emisión del cátodo.

En los diodos al vacío, especialmente los de alta energía, el transporte de los electrones exhibe varios fenómenos no lineales debidos a los altos voltajes aplicados y a las altas corrientes utilizadas. Uno de estos efectos es la saturación de corriente explicada. Langnuir y Compton (1931); investigaron este fenómeno y establecieron una formulación explícita para la corriente de saturación en los diodos planos y aproximaciones en los cilíndricos y esféricos. Child Langmuir encontraron que la corriente máxima, o de saturación, que puede fluir a través de un diodo al vacío, independiente de la forma como los electrones son extraídos desde el cátodo, es:

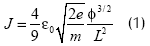
en donde: ε₀ es la permitividad del vacío, e y m son la carga y la masa del electrón, φ el potencial aplicado y L la longitud del diodo.

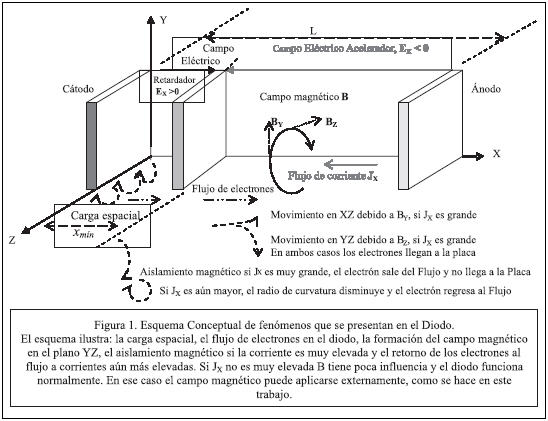
Cuando la emisión de electrones en el cátodo es muy alta, se forma un campo eléctrico retardante cerca del mismo (0 < x < x_min) contrario al campo acelerante dirigido desde este punto hacia la placa (x_min < x < x_L). Para vencer el campo retardante la energía cinética de los electrones que salen del cátodo debe ser mayor que la energía potencial producida por el voltaje 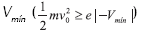. Así que, la velocidad inicial v₀ de los electrones que dejan el cátodo, debe exceder un valor determinado por |-V_min|, 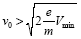. Si la velocidad del electrón está debajo de este valor, no podrá vencer la barrera de potencial, su velocidad bajará lentamente hasta parar, y el campo lo regresará al cátodo. La región del campo retardante (desde 0 hasta x_min) contiene no solamente los electrones que viajan hacia la placa, sino también aquellos que se regresan al cátodo. En la región de carga espacial se lleva a cabo el fenómeno del plasma.

A un voltaje de filamento constante se logra un equilibrio dinámico tal que el número de electrones que alcanzan la placa y el que es regresado al cátodo es igual al de electrones emitidos por el cátodo. Por lo tanto, la corriente de placa es menor que la emitida, o el cátodo produce más electrones de los que llegan al ánodo (Dulov y Sinitsyn, 2005).

Los electrones que superan el campo retardador de la región de carga espacial se dirigen hacia el ánodo formando una corriente de densidad J_X normal. El movimiento de cargas eléctricas produce corriente, la que a su turno, produce campos magnéticos en el plano perpendicular al movimiento de las mismas cuyo sentido se determina por la ley de la mano derecha. En este caso la corriente en sentido negativo de la X produce un campo magnético en el plano YZ, con componentes B_Y, B_Z.

Cuando una carga eléctrica (q) con velocidad (v) ingresa en un campo magnético (B), perpendicular a su trayectoria, experimenta una fuerza (F) dada por el producto vectorial F = qv x B conocido como la ley de Lorentz, y cambia su trayectoria a un movimiento circular. A medida que la densidad de corriente se incrementa, el campo magnético que se forma es mayor y el cambio de trayectoria es más pronunciado (el radio del movimiento de la partícula se hace menor). Esto trae como consecuencia que, a corrientes elevadas, el electrón se desvíe y no alcance la Placa; esta condición se conoce como el fenómeno de aislamiento magnético (magnetic insulation).

Si la corriente se incrementa por encima del valor al cual se produce el aislamiento magnético, el radio de la trayectoria se hace más pequeño y el electrón puede lograr nuevamente su trayectoria original. Si el ánodo se hace negativo con respecto al cátodo, los electrones son repelidos y la corriente inversa es casi cero (debido a la cola de la distribución maxwelliana de los electrones, que es mayor que cero).

Planteamiento matemático

El estudio del fenómeno de aislamiento magnético se lleva a cabo bajo el marco de validez de la física de plasma, que presenta tres descripciones: la aproximación como partículas sencillas, la teoría cinética y la descripción de fluidos. La descripción que se trabaja en este documento es la de la teoría cinética, cuyas bases se fundamentan en las ecuaciones de Klimontovich y Liouville, mediante las cuales se estudian las propiedades del plasma a un nivel de detalle microscópico, con el más alto grado de aproximación^{7 8}.

En base al nivel de detalle que se desea estudiar el sistema, la teoría cinética presenta tres alternativas: en un nivel de detalle alto se encuentran la ecuación de Klimontovich (Schram, 1991); en un nivel de detalle medio, las ecuaciones de Boltzmann, Vlasov y de deriva cinética [Krall and Trivelpiece]; y en un nivel de detalle bajo, de fluidos macroscópicos de partículas cargadas (Chen, 2005). En este documento se trabaja un nivel de detalle medio debido a que el nivel de detalle más alto proporciona demasiada información al punto de ser inservible.

A pesar de que la ecuación de Klimontovich, junto con las de Maxwell, proporcionan un análisis exacto de un sistema de plasma, este tipo de soluciones no son útiles por ser muy específicas, diciendo en qué puntos del espacio fásico se encuentra la partícula, y por lo tanto resulta mucho más útil obtener el valor promedio de la distribución de partículas. Por esta razón surgieron aproximaciones de la ecuación de Klimontovich, como por ejemplo, la ecuación de Vlasov, la cual trabaja con la función de distribución.

La ecuación de Vlasov es para sistemas no colisionales, es decir, el plasma en la que se aplica debe tener efectos colisionales muy pequeños o nulos, y es precisamente esta una de las características de las que goza el sistema de plasma del diodo plano al vacío que se estudia en este documento. Por lo tanto, la ecuación de la teoría cinética con la que se trabaja es la ecuación de Vlasov, a continuación:

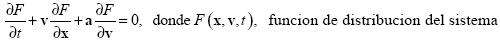
De los tres términos que conforman la anterior ecuación se descarta el primero, para el caso del diodo plano al vacío, ya que el sistema es invariante en el tiempo y por lo tanto la variación de la función de distribución con respecto al tiempo es nula.

Con respecto al último término de la ecuación de Vlasov es importante anotar que la aceleración es usualmente reemplazada por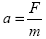

Donde F es la conocida fuerza de Lorentz, representada por F=q(V x B), en presencia de campos magnéticos únicamente; y en presencia de campos eléctricos y magnéticos, se representa por F=q(E + V x B).

Finalmente, la ecuación de Vlasov que se usará en este documento quedaría de la siguiente manera:

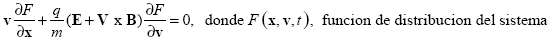
A manera de aclaración es importante mencionar que debido a que se desea estudiar las propiedades de un sistema de partículas con carga y masa puntual que pueden tener velocidades comparables con la de la velocidad de la luz, es necesario el uso de la siguiente ecuación relativista, que relaciona energía y masa.

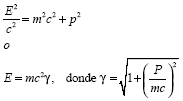
A continuación se estudiarán las propiedades del plasma de un diodo plano al vacío, para lo cual se considerará la siguiente descripción del sistema, tomado de Creedon (1975, 1977) [10, 11], Sinitsyn (2002) [12], Dulov y Sinitsyn (2005) y Dengond y Raviart (1991) [13]: el diodo plano al vacío está conformado por dos conductores perfectos (electrodos), que son el cátodo (X=0) y el ánodo (X=L). Se supone que son planos infinitos, paralelos a (Y, Z), como se aprecia en la Figura 2.

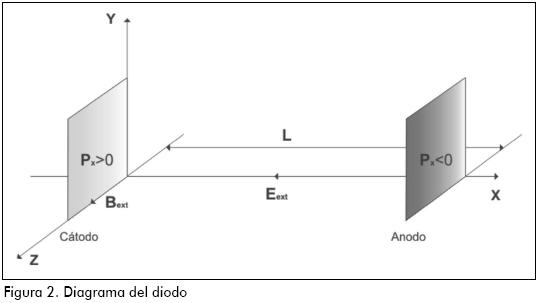
Cuando el diodo está polarizado directamente e produce un movimiento de electrones con carga -e y masa m, desde el cátodo hasta el ánodo, y se dice que el diodo está en conducción. Los electrones son sometidos a un campo electromagnético externo aplicado, el cual no actúa sobre la componente en z del momento de la partícula (P_z). Se considera que esta componente del momento de la partícula es nula, lo que conlleva a un confinamiento de electrones en el plano (X,Y), es decir, Z=0.

Finalmente, en este caso el campo eléctrico se coloca en X y el magnético se ubica solo en Z, como lo muestran las ecuaciones.

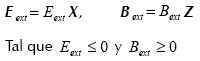
Debido a que el plasma es un sistema formado por partículas cargadas representadas por cargas y masas puntuales, el diodo plano al vacío es considerado como plasma y por consiguiente se utiliza la teoría cinética del plasma para estudiar detalladamente sus propiedades.

Para el problema planteado del diodo plano al vacío vamos a considerar que la función de distribución F no depende de las componentes en Y de las posiciones de las partículas del sistema y que además el flujo de partículas es estacionario y sin colisiones, lo que implica que debemos analizar el sistema con la ecuación de Vlasov no colisional. Esto indica que el sistema se representa mediante una distribución promedia en el espacio de las partículas del sistema, que son únicamente electrones.

La descripción del sistema se da por el modelo Vlasov-Maxwell, conformado por la ecuación de Vlasov no colisional y las ecuaciones de Maxwell.

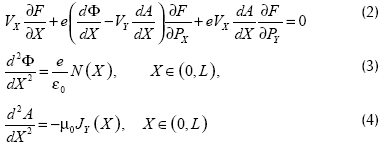
Las condiciones de frontera para la función de distribución son las siguientes:

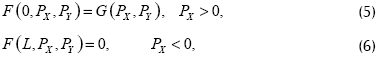
Las condiciones de frontera para el potencial electroestático Φ y el potencial magnético A, tanto en el ánodo como en el cátodo, son las siguientes:

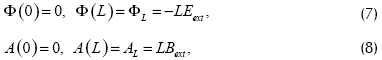
Si evaluamos las condiciones de frontera en el ánodo para Φ y A en el sistema de Maxwell obtenemos que la densidad de partículas N y la componente Y de la densidad de corriente J_Y son nulas (N=J_Y=0), debido a que los campos eléctricos y magnéticos son exactamente iguales a los externos que son constantes.

Debido a que las partículas que se estudian en este caso en particular viajan a una velocidad comparable con la de la luz, es necesario recordar de la mecánica relativista que la masa de una partícula libre (en este caso los electrones) se relaciona con su momento y energía a través de la siguiente ecuación:

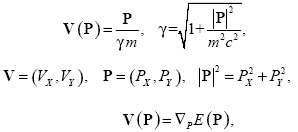
donde E es la energía cinética relativista y c es la velocidad de la luz.

Las cantidades macroscópicas del sistema Vlasov-Maxwell, como la densidad de partículas N y las componentes X y Y de la densidad de corriente J_x, J_y, son respectivamente dadas por las siguientes fórmulas:

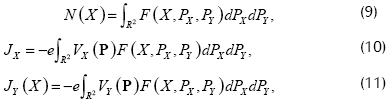
Aquí, ε₀ y µ₀ son, respectivamente, la permitividad y la permeabilidad en el vacío.

El modelo utilizado para el diodo plano al vacío descrito por la ecuación de Vlasov-Maxwell describe dos regímenes principales. Uno de ellos se presenta cuando un campo magnético fuerte es aplicado, provocando que los electrones no alcancen el ánodo y regresen al cátodo teniendo como consecuencia que la componente en X de la densidad de corriente J_x desaparezca, caso para el cual el sistema Vlasov-Maxwell se debe aplicar rigurosamente. El otro régimen se presenta cuando se aplica un campo magnético pero este no es lo bastante fuerte como para provocar que los electrones regresen al cátodo, de manera que J_x no desaparece y el modelo Vlasov-Maxwell puede ser aproximado a las tradicionales ecuaciones de Maxwell.

A continuación se da una definición de los momentos asociados con la función de distribución de la partícula en la frontera del cátodo.

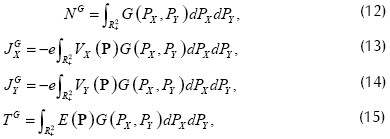
Donde R₊²={(P_X,P_Y)∈R², P_X>0}, (ver la Figura 1) y la velocidad de emisión termal es 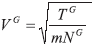. Las cantidades (12)-(15), respectivamente, definen la densidad de la partícula entrante, componentes X y Y de la densidad de corriente entrante y la densidad de energía cinética de la partícula entrante.

Para conseguir una mejor visión en el comportamiento del diodo se escribe el modelo (2)-(8) en variables adimensionales. Siguiendo a Degond y Raviart (1991, 1992), se introducen las siguientes unidades, en su orden para posición, velocidad, momento, potencial electroestático, vector potencial, densidad de partícula, corriente y función de distribución:

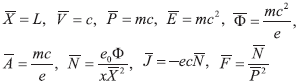
Y las correspondientes variables adimensionales

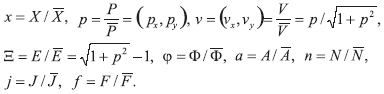
Supongamos que el diodo esté controlado en el régimen de Child-Langmuir. En tal situación, la velocidad térmica V_G es mucho más pequeña que la típica tendencia de velocidad supuesta de ser del orden de la velocidad de la luz c. Dejando 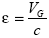, debemos asumir que

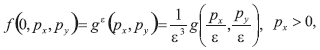
Donde es un contorno dado. El sistema adimensional se lee

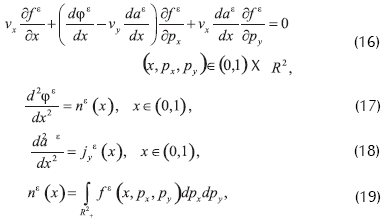
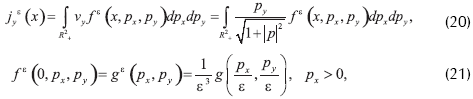
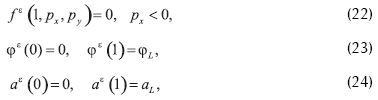
Para deducir el límite del modelo (I) a ε→0, se consideran las diversas invariantes del problema.

Las siguientes dos cantidades son constantes de movimiento:

Significando que sobre cada trayectoria del electrón (en el espacio de fase), las anteriores cantidades son constantes. Denotemos f,n,a,j,φ... el límite cuando ε tiende a cero f^ε,n^ε,.. puesto que en el límite ε=0 los electrones son inyectados con velocidad cero, ya que la energía del electrón W y el momento canónico P_yse desvanecen simultáneamente. En consecuencia,

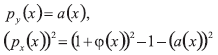
Y las siguientes identidades sostienen:

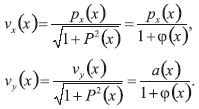
Ahora definíamos el potencial efectivo por:

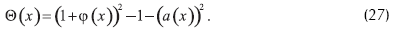
Los electrones no entran al diodo a menos que el potencial efectivo Θ sea no negativo en la cercanía del cátodo. Además, siempre tenemos Θ'(0)≥0. Dejando Θ_L ser el valor de Θ del ánodo.

Si Θ_L<0, los electrones no pueden alcanzar el ánodo x=1; estos son reflejados por la fuerza del campo magnético de regreso al cátodo y se dice que el diodo está magnéticamente aislado. Si Θ es no negativo, entonces todos los electrones alcanzan el ánodo y se dice que el diodo está sin aislamiento.

Para analizar el régimen “sin aislamiento”, asumimos que

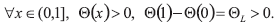
Esto último denota un retrato de fase (x,p_x) de trayectorias del electrón que tiene esa forma.

Desde que ningún electrón sea inyectado al ánodo, 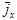se desvanece. Ahora:

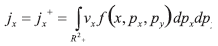
Y la función de distribución es la de una emisión de un rayo monocinético desde el cátodo x=0 con desvanecimiento de la velocidad inicial:

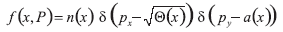
Por consiguiente,

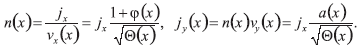
Insertando esta expresión dentro de las ecuaciones de Poisson y Ampere (3), (4) da

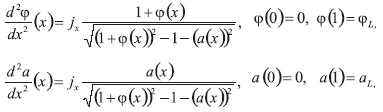
Los que se desconocen en el sistema (I) son el potencial electroestático φ, el potencial magnético a y la corriente j_x (esta no depende de x).

Existencia de soluciones semitriviales del problema

Permítasenos introducirlos en la definición de cono en un espacio Banach X:

Definición 1. Digamos que X es un espacio Banach. Un conjunto no vacío convexo P⊂X es llamado un cono, si este satisface las siguientes condiciones:

(i) x∈P, λ≥0 implica que λx∈P;

(ii) x∈P, -x∈P implica que x=Ο, donde Ο denota cero elementos de X. Aquí ≤ es el orden en X inducido por P,i.e., x≤y si y solo si y-x es un elemento de P.

Denotaremos [x,y] el orden del intervalo cerrado entre x y y,i.e.,

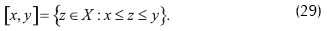
También asumiremos que el cono P es normal en X,i.e., los intervalos del orden son normalmente limitados.

En X

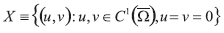
Introducimos la norma |U|x=|u|c¹+|v|c¹ y la norma |U|x=|u|_∞+|v|_∞ en C, donde U=(u,v) Aquí un cono P está dado por

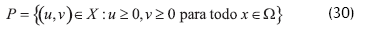
Así, si u≠0, v≠0 pertenecen a P, entonces -u,-v no pertenecen. Trabajaremos con espacios clásicos sobre intervalos :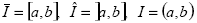

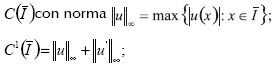
C_loc(I), la cual contiene todas las funciones que son local y absolutamente continuas en I. Introdujimos un espacio C_loc(I), porque el problema (I) es singular para φ=0. El orden ≤ en el cono P es entendido en el sentido débil, i.e., y se incrementará si a≤b, lo que implica que y(a)≤y(b), y y se decrementará si i>a≥b, lo que implica que y(a)≥y(b).

Teorema 1. (Walter [4]) (principio de comparación en el cono) permita 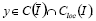. La función f está definida sobre I x R. Permita a f(x,y) incrementarse en función de y, entonces:

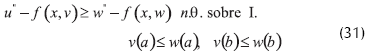
Implica

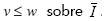
Comentario 1: Permita a f(x,y) decrementarse, luego el teorema 1 permanece sin cambios si ambas partes de (31) se multiplican por -1.

Para la conveniencia de definir una relación de ordenamiento en el cono P hacemos una transformación para el problema (I). Permitamos a F(φ,a) y G(φ,a) estar definidas por (I). Entonces a través de la transformación φ=-u el problema (I) se reduce a la forma

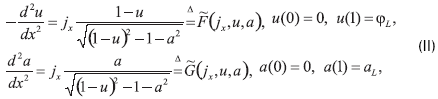
Notemos que todas las soluciones tanto del problema (I) como del problema (II) son simétricas con respecto a la transformación de signo para el potencial magnético a:(φ,a)=(φ,-a) o lo mismo que decir (u,a)=(u,-a). De esta manera, debemos buscar solamente soluciones positivas φ>a, a>0 en el cono Po únicamente negativas: φ<a, a<0. Gracias a la simetría del problema este es equivalente y no produce la extensión de los tipos de soluciones de signo definido del problema (I) (respecto del (II). Una vez más apreciemos que la introducción de potencial electroestático negativo en el problema (II) está conectada con la relación más conveniente entre el orden en el cono y la certeza de la función de Green para el operador -u'' que usamos abajo.

Definición 2. Un par [(φ₀,a₀),(φ₀,a₀)] es llamado

a) Solución sub-super del problema (I) relativa a P, si las siguientes condiciones se satisfacen

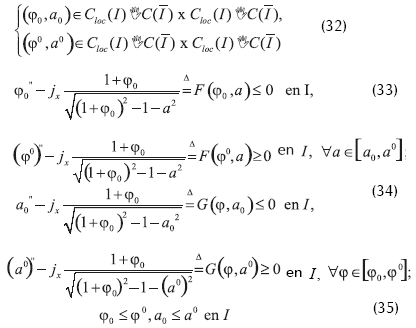
Y sobre la frontera

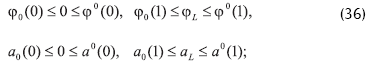
b) Solución sub-sub del problema (I) relativo a P, si la condición (5) se satisface y

Y sobre la frontera

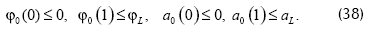
Comentario 2. En la definición 2, la expresión con la raíz cuadrada, tomamos por módulo |(1+φ)²-1-a²|.

Por analogía con (4.9), (4.10), introducimos la definición de solución super-super en el cono.

Definición 3. Las funciones Φ(x,x_ai,j_x),Φ₁(x,x_φj,j_x) podríamos llamarlas soluciones semitriviales del problema

(I) si Φ(x,x_ai,j_x) es una solución del problema de valor escalar de frontera

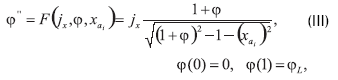
Y Φ₁(x,x_φj,j_x) es una solución del problema de valor escalar de frontera

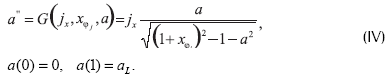
Aquí x_ai, i=1,2,3 y x_φj, i=1,2 son, respectivamente, los indicadores de las soluciones semitriviales, Φ(x,x_ai,j_x),Φ₁(x,x_φj,j_x) definidas de la siguiente forma:

De la definición 3. obtenemos los siguientes tipos de problemas de valores escalares de frontera para las soluciones (I) semitriviales (en el sentido de la definición 3) (resp. (II)):

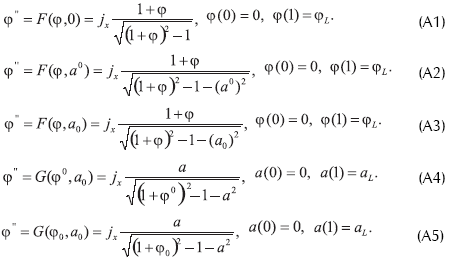
Debemos encontrar las soluciones a los problemas (A1)-(A3) con la condición

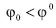
donde φ₀(x_a1),φ⁰(x_a2) son, en su orden las soluciones inferior y superior del problema (A1). La solución (φ,a) del problema (I) podría corresponder al intervalo

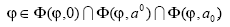
Por otra parte, el ordenamiento de soluciones superiores e inferiores de los problemas (A1)-(A3) está satisfecho:

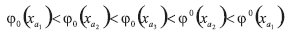
Buscaremos la solución de los problemas (A4)-(A5) con la condición

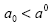
En este caso el siguiente ordenamiento de soluciones superiores e inferiores de los problemas (A4)-(A5)

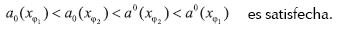
Vamos al estudio directo del problema (III) el cual incluye los casos (A1)-(A3).

Permítasenos considerar el problema (III) de valor de frontera con

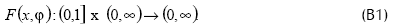
En la condición (B1) para F(x,φ) bajamos el índice a_i, considerando un caso de dependencia no lineal F de x.

Asumiremos que F es una función Caratheodory, i.e.,

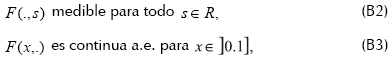
Y la siguiente condición se mantiene

Existe γ(x)∈L¹(]0,1]) y α∈R, 0<α<1 tal que

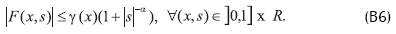
Estamos interesados en la solución clásica positiva de la ecuación (III), i.e., φ>0 en P para x∈]0,1] y φ∈C([0,1])∩C²(]0,1]). El problema (III) es singular, por lo tanto, la condición (B1) no se cumple sobre el intervalo φ∈(0,∞) y en esta conexión. Los bien conocidos teoremas (ver Aman [1]) sobre la existencia de soluciones superiores e inferiores en el cono P no funcionan. Esto sigue del teorema 3, ya que F en (III) se incrementa en φ, entonces φ<w para x∈]0,1] donde φ y w satisfacen la inecuación diferencial (31).

Teorema 2. Asumiendo las condiciones (B2)-(B6), allí existe una solución positiva φ∈C([0,1])∩C²(]0,1]) del problema (III) de valor de frontera.

Demostración. Concedamos φ>0 ser una solución del problema (III). Por el teorema 1 φ>w para x∈]0,1]. Tomamos ε>0 y consideramos la ecuación

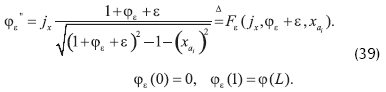
Permitamos a w y a φ ser las soluciones superior e inferior de la ecuación (39) (abajo, en la proposición 1 es mostrado tal que las soluciones realmente existen). Aquí el teorema sobre iteraciones monótonas da una existencia de soluciones clásicas φ_ε de la ecuación (39), la cual satisface w>φ_ε>φ para x∈]0,1] y es frontera en C. De esta manera F_ε(j_x,φ_ε+ε,x_ai) es frontera y allí existe un límite uniforme lim_ε→0φ_ε=φ. Esto sigue hasta lo ultimo, si 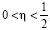entonces el lim_ε→0F_ε(j_x,φ_ε+ε,x_ai)=F(j_x,φ,x_ai) uniformemente sobre [η,1-η] y φ>0 para x∈⌊η,1-η⌋.

Ya que φ_L es convergente uniformemente en [0,1] entonces esto implica la existencia de lim_ε→0φ'_ε(η). Por consiguiente, existe lim_ε→0φ''_ε(η) sobre el subespacio compacto (0,1) y {φ'_ε} es uniformemente convergente sobre (0,1) para una función diferenciable φ' sobre [η,1-η]. Por último, φ es dos veces diferenciables sobre [η,1-η], φ''=F(j_x,φ,x_ai) y u∈C([0,1])∩C²(]0,1]) es una solución positiva al problema (III).

El teorema 2 es probado.

Comentario 3. El momento delicado en la prueba del teorema 2 está conectado con encontrar las soluciones inferior y superior al problema de perturbación (39). Como una solución inferior podemos tomar la solución de la ecuación (A₁) (solución semitrivial φ), entonces una solución superior será, por ejemplo, la solución máxima de la ecuación (A₁).

Aplicando de técnicas de iteración monótonas para la ecuación (III), dan la existencia de solución máxima 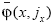tal que:

Proposición 4.1. Dejando 0<c≤j_x≤j_x^max. Entonces la ecuación (A₁)

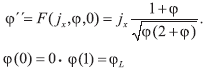
Como solución positiva inferior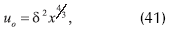

si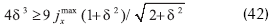

y una solución positiva superior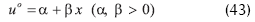

con

donde es definida desde (42)

Comentario 4. La raíz cuadrada es tomada como 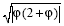en el caso de las soluciones negativas. Aquí u⁰=-εx es una solución superior, y u₀=-2+ε como solución inferior (0<ε<1). Acá la ecuación (A₁) tiene solución negativa sólo para 0<φ_L<-2 porque F(x,-2)=-∞.
Sigue de (42), (44) que el valor de la corriente es limitado por el valor de potencial electroestático sobre el ánodo φ_L.

El análisis de las soluciones superior e inferior (41), (43) exhibe que para δ²=φ_L>2 y α=β≤1 el intervalo en x entre las soluciones superior e inferior decrece, y para grandes valores del potencial φ_L el diodo entra en régimen .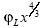

Proposición 2. Dejando 0<c≤j_x≤j_x^max. Entonces la ecuación (A₄)

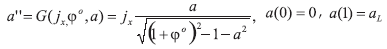
Con una solución inferior a₀=0 y solución superior a⁰=u⁰>0, las condiciones (42), (44) tienen una única solución a(x,j_x,c), la cual es positiva, además:

Demostración. La solución positiva del problema (A₄) es cóncava y se encuentra como una solución del problema inicial con a(0)=0, a'(0)=c, donde c es un parámetro de disparo. La solución a=a(x,j_x,c) es única y disminuyendo fuertemente en c porque la parte derecha de la ecuación diferencial está decreciendo en a. La menor solución no-negativa es f(x,j_x,0)=0 y para 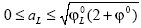ahí existe solamente una solución y soluciones no-positivas para otros valores a_L.

Comentario 5. EL problema (A₅) es considerado con analogía al problema (A₄), cambiando de una solución superior a⁰=u⁰ a una inferior a⁰=u₀ y .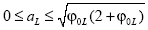

Continuando con la definición 2 y proposiciones 1, 2, las soluciones para los problemas (III), (IV) pueden ser escritas en la forma (Figura 3):

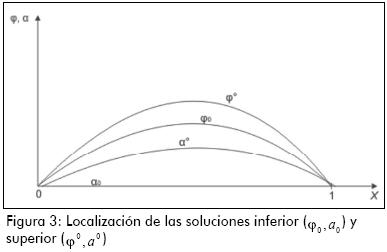
Inferior-inferior (φ₀,a₀):

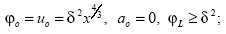
Superior-inferior (φ⁰,a₀):

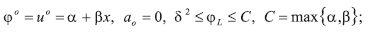
Inferior-superior (φ₀,a⁰):

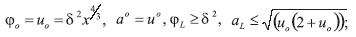
Superior-superior (φ⁰,a⁰):

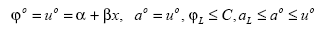
Existencia de las soluciones completas del problema

En la sección previa se demostró la existencia de soluciones semitriviales de soluciones de sistema (I). Aquí se muestra la existencia de soluciones completas para el sistema (I) usando el siguiente teorema McKenna-Walter.

Teorema 3. (McKenna, Walter, 1984). Se apropiaron las condiciones (B₁)-(B₆). Asumimos que allí existen los pares ordenados 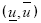- soluciones superior e inferior, i.e.,

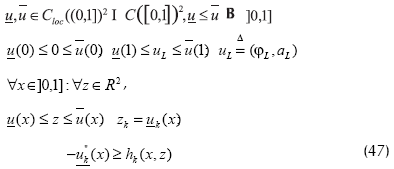
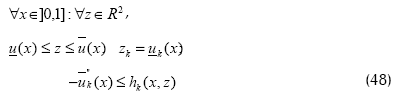
Para todo k∈{1,2}. Entonces existe una solución u∈C²((0,1])∩C((0,1])² del problema

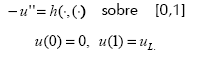
Para mantener el ordenamiento de las soluciones superior e inferior en el teorema 3 (en cono P) escribimos desigualdades diferenciales (47), (48) de la siguiente forma:

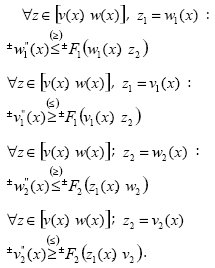
Observación 1. Sustituir signos con (+) o (-) en las desigualdades diferenciales está conectado con ajuste del signo y ordenando (≤) de inferior (superior) lociones del sistema (I) en la definición 2 y soluciones inferior (superior) en el teorema 3.

De la última relación obtenemos

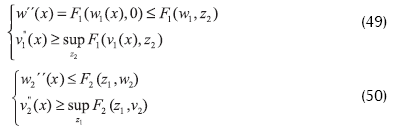
De la inecuación v₂''(x)≥sup_z1F₂(z₁,v₂) conseguimos estimaciones para el valor del campo magnético sobre el ánodo a_L

Tomando en cuenta de (45) y bajo la realización de la estimación (51) el diodo trabaja en régimen “sin aislamiento”, además el valor a_L está limitado por el valor del potencial electroestático sobre el ánodo φ_L con un valor critico φ_L=2. En el incremento del potencial magnético a_L el diodo transfiere en régimen “aislado” que conduce a un problema más complicado con frontera libre.

En consecuencia, tenemos los siguientes resultados principales de este documento.

Teorema 4. Asumiendo las condiciones (B2), (B3), (B6) y las inecuaciones (42), (45), (51), el problema (I) posee una solución positiva en el cono P tal que

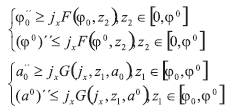
Donde 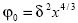es una solución inferior del problema (A1), φ⁰=α+βx(α,β>0) es una solución superior del problema (A1) con la condición φ_L≥δ²;a₀=0 es una solución inferior del problema (A4) con la condición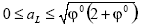

El teorema 4 podría ser usado para la construcción de soluciones mínimas y máximas de (I) sobre las bases del método de iteraciones monótonas en Heikkila (Degond y Raviart, 1991).

Aplicaciones

En la actualidad, algunas aplicaciones son:

1. El confinamiento magnético del plasma para fusión o fisión nuclear destinado a la producción de energía.

2. Las líneas transmisión, de alta eficiencia para formación y propagación de pulsos de alta potencia (miles de Terawatt), conocidas como líneas de transmisión aisladas magnéticamente (MITL, Magnetic Insulation Transsmision Line).

En esta sección se presenta una revisión de las aplicaciones del fenómeno de aislamiento magnético.

Fusión nuclear

La aplicación del aislamiento magnético en el área de la producción de energía por medio de reactores nucleares está dada de manera directa e indirecta.

En los reactores nucleares de confinamiento inercial se encuentran posibles aplicaciones de este fenómeno en la producción de pulsos de alta potencia que intervienen en el control de los rayos o haces de partículas, iones o fotones que se impactan en la micro cápsula para iniciar la ignición de la reacción de fusión (aplicación indirecta).

En reactores con confinamiento magnético, como son los casos de los Tokamaks y los Stellarators, la aplicación del aislamiento magnético es directa, permitiendo que el plasma este confinado y que no colisione con las paredes del contenedor.

La compresión y calentamiento de una micro cápsula (pellet) para las condiciones de ignición termonuclear por un haz de partículas y la producción de plasma de alta densidad de energía en laboratorios, requieren flujos de potencia de 100-1.000TW con una duración de 1 a 2x10^-8 segundos sobre un blanco de 1 cm de lado típicamente.

Para lograr estos flujos de potencia en tiempos muy cortos y con haces que puedan actuar sobre blancos muy pequeños se requiere utilizar dispositivos soportados por los conceptos del aislamiento magnético (Figura 4).

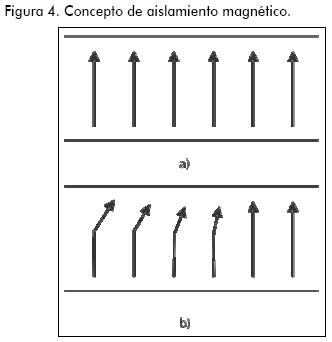
a) El flujo de cargas en la línea de transmisión en su estado no aislado va desde el cátodo al ánodo. b) Bajo la presencia de fuertes campos magnéticos, propios o externos, las cargas pueden no alcanzar el ánodo

Líneas de transmisión aisladas magnéticamente (MITL)

El aislamiento magnético provee la posibilidad de ondas electromagnéticas de muy alta potencia en líneas de transmisión al vacío ( 16]. A continuación se muestra el principio de las líneas de transmisión magnéticamente aisladas.

Las líneas de transmisión magnéticamente aisladas son típicamente usadas en los reactores nucleares porque son las encargadas de alimentar los diodos de iones o electrones que son bombardeados dentro de la cámara de fisión.

Es importante anotar que la relación del fenómeno de aislamiento magnético con la generación de pulsos de alta potencia permite la aplicación de estos fenómenos físicos en campos de la industria donde se usen descargas de pulsos de potencia, rayos de partículas cargadas, rayos X, ráfagas de neutrones, calentamiento de plasma, microondas, rayos láser, compresión de campos magnéticos, entre otros.

Conclusiones

Se ha hecho una presentación del fenómeno de aislamiento magnético a un nivel más asequible para la comunidad académica no relacionada con el tema., así como del desarrollo del modelamiento matemático del problema, realizado por otros investigadores, entre los cuales se encuentra uno de los autores; la demostración acerca de la existencia de soluciones matemáticas al problema, y algunas aplicaciones actuales del fenómeno del aislamiento electromagnético.

Basados en esta experiencia, se puede considerar la extensión del procedimiento a la explicación de otros temas, recientes y avanzados, como por ejemplo el plasma.

Este tipo de ejercicios se consideran necesario para la difusión de conocimiento reciente y avanzado entre la comunidad académica no relacionada con estos temas.

Bibliografía

Creedon, J. M., Relativistic Brillouin flow in the high diode., en J. Appl. Phys., Vol. 46, No. 7, 1975, pp. 2946-2955.        [ Links ]

Creedon, J. M., Magnetic cutoff in high-current diodes., en J. Appl. Phys., Vol. 48, No. 3, 1977, pp. 1070-1077.        [ Links ]

Degond, P.; Raviart, P. A., An asymptotic analysis for the one-dimensional Vlasov-Poisson system., en Asymptotic Anal. 4, 1991, pp.187-214.        [ Links ]

On a penalization of the Child-Langmuir emission condition for the one dimensional Vlasov-Poisson equation., en Asymptotic Anal. 6, 1992, pp. 1-27.        [ Links ]

Dulov, E. V.; Sinitsyn, A. V., A numerical modeling of the limit problem for the magnetically noninsulated diode., en Appl. Mathematics and Computation, Vol. 162, 2005, pp. 115-154.        [ Links ]

Chen, F. F., Introduction to Plasma Physics, Plenum, Cambridge University Press, 2005.        [ Links ]

Enciclopedia Wikipedia., disponible en:http://en.wikipedia.org/wiki/Vacuum_diode#History_of_development, consultado en Nov. de 2007.        [ Links ]

Krall, N. A., Trivelpiece, A. W., Principles of Plasma Physics, McGraw-Hill, Vlasov equation, 1973, p. 36.        [ Links ]

Langmuir, I.; Compton, K. T., Electrical discharges in Gases: Part II., Fundamental Phenomena in Electrical Discharges., en Rev. Mod. Phys., 3, 1931, pp. 191-257.        [ Links ]

McKenna, P. J.; Walter, W., On the multiplicity of the solution set of some nonlinear boundary value problems., en Nonlinear Anal; Theory Methods Appl. 8, 1984, pp. 893–907.        [ Links ]

Schram, P.P.J. M., Kinetic theory of gases and plasmas, Springer, 1991.        [ Links ]

Sinitsyn, A. V., Positive solutions of nonlinear singular boundary-value problem of magnetic insulation., Universidad Nacional de Colombia, Facultad de Ciencias, Departamento de Matemáticas, Reportes Internos, No. 84, 2002.        [ Links ]

Sinitsyn, A.V.; Dulov, E. V., Trabajos propuestos para el I semestre de 2005., Maestría en Matemática Aplicada., Universidad Nacional, Bogotá, http://www.unal.edu.co, consultada en febrero de 2007.        [ Links ]

http://europa.din.upm.es/plasmas/Tema7.4-Cineticav15.PDF        [ Links ]

http://europa.din.upm.es/plasmas/index.html        [ Links ]

http://pps.coe.kumamoto-u.ac.jp/streaming/PulsedPower/control/transmission1.htm        [ Links ]

6 En Wikipedia: http://en.wikipedia.org/wiki/Vacuum_diode#History_of_development, consultado nov. 2007.
7 http://europa.din.upm.es/plasmas/Tema7.4-Cineticav15.PDF
8 http://europa.din.upm.es/plasmas/index.html