Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.1 Bogotá Jan./Apr. 2008
Tomás Fernández Columbíe1, Isnel Rodríguez González2, Dayanis Alcántara Borges3 y Esther Fernández4
1 M.Sc., en Ciencias en Elecromecánica. Profesor, Departamento de Ingeniería Mecánica, Instituto Superior Minero Metalúrgico de Moa, Holguín, Cuba. tfernandez@ismm.edu.cu
2 Ingeniero mecánico. M.Sc., en Ciencias en Elecromecánica. Profesor, Departamento de Ingeniería Mecánica, Instituto Superior Minero Metalúrgico de Moa, Holguín, Cuba. irgonzalez@ismm.edu.cu
3 Ingeniero mecánico. Profesor, Departamento de Ingeniería Mecánica, Instituto Superior Minero Metalúrgico de Moa, Holguín, Cuba. dalcantara@ismm.edu.cu
4 T. M., Departamento de Ingeniería Mecánica, Instituto Superior Minero Metalúrgico de Moa, Holguín, Cuba. efguilarte@mecanica.ismm.edu.cu
RESUMEN
El trabajo muestra las técnicas empleadas en un diseño de experimento que permite evaluar el comportamiento de las variables independientes fuerza (P), desde 500 hasta 2500 N, número de revolución (n) mínimo 27, medio 54 y máximo 110 rev/min y avance (s), 0,075, 0, 125 y 0,25 mm/rev, para determinar el comportamiento de la variable dependiente dureza (H), cuando una probeta de acero AISI 1045 es sometida a tratamiento superficial por rodadura para crear un estado compresivo que lo deforme e incremente su resistencia al desgaste y la fatiga. Se realiza el procesamiento estadístico de las variables involucradas en el proceso donde se demuestra el incremento de la dureza desde 220 hasta 262 HV. Se empleó el método de microscopía óptica para analizar el efecto del endurecimiento por deformación, estableciendo el mecanismo de endurecimiento del acero por el deslizamiento de los granos en la red cristalina por el fenómeno de la acritud.
Palabras clave: deformación plástica, rodadura, variables, diseño de experimento, acritud, deslizamiento.
ABSTRACT
The work shows the techniques employees in an experiment design that allows to evaluate the behavior of the independent variables force (P), from 500 up to 2500 N, revolution number (n) minimum 27, half 54 and maximum 110 rev/min and advance (s), 0,075, 0, 125 and 0,25 mm/rev, to determine the behavior of the variable dependent hardness (H), when a steel test tube AISI 1045 are subjected to superficial treatment for rolling to create a compressive state that the unsightly thing and increase its resistance to abrasive wear and the fatigue. He/she is carried out the statistical prosecution of the variables involved in the process where the increment of the hardness is demonstrated from 220 up to 262 HV. The method of optic microscopy was used to analyze the effect of the hardening for deformation, establishing the mechanism of hardening of the steel for the slip of the grains in the crystalline net for the phenomenon of the acrimony.
Keywords: plastic deformation, rolling, variables, experiment design, acrimony, slip.Recibido: diciembre 10 de 2007
Aceptado: febrero 27 de 2008
Introducción
El proceso de deformación plástica superficial por rodillo simple es un método alternativo ventajoso respecto a los esquemas tecnológicos tradicionales empleados para aumentar la calidad de las superficies de las piezas, con mayor eficiencia técnico-económica y menor contaminación del medio ambiente. Existen diversos procedimientos para el empleo de la deformación plástica superficial como alternativa de endurecimiento de las piezas, siendo el rodilado o rodillado por rodillo simple o monorrodillo, un proceso muy empleado en la deformación plástica superficial. El mismo resulta sencillo, de fácil aplicación, y es posible emplearlo en una gran variedad de piezas y de metales.
Este trabajo tiene como objetivo fundamentar el procedimiento de endurecimiento del acero AISI 1045 cuando es sometido al proceso de deformación plástica superficial con rodillo simple, además se establecen técnicas del diseño de experimentales para evaluar el comportamiento de las variables que intervienen en el proceso y que permiten establecer a través del análisis microscópico el estado tensional de la red cristalina.
Uno de los aspectos a demostrar en el trabajo es la posibilidad de endurecimiento de piezas cilíndricas rotativas que requieren del endurecimiento de la capa superficial y reducir el empleo de métodos tradicionales de endurecimiento como son el temple y el revenido, los cuales son altos consumidores de energía eléctrica.
La deformación plástica superficial en frío es un método de endurecimiento de materiales que logra alta dureza, el aumento del grado de deformación está muy vinculado con la aparición del fenómeno de endurecimiento y a medida que el grado de deformación es mayor, son necesarias más tensiones para continuar deformando. Por tanto el aumento del grado de deformación en frío aumenta la resistencia del metal a la deformación (Álvarez, et al., 2004).
Se pudo determinar que en numerosos trabajos (Hasegawa, 2001; Mazein, 2001 y Skalki, 1995) se están desarrollando para tratar de modelar matemáticamente y simular a través de los métodos numéricos el comportamiento de los materiales en los procesos de deformación plástica superficial. Es común que en estos métodos se defina un criterio de plasticidad y un modelo de comportamiento del material.
El empleo de estos métodos se realiza para:
1. La adecuada selección de los parámetros de trabajo y de las respuestas
2. La predicción teórica del comportamiento del material durante el proceso
3. Controlar los procesos de deformación plástica superficial
En su trabajo Boada y Díaz (2003) consideran que, desde el punto de vista matemático, un modelo plástico queda perfectamente definido por varios elementos básicos, como son: criterio de plasticidad, ley de fluencia, ley de endurecimiento.
También se puede destacar que los modelos plásticos y elastoplásticos, a pesar de tomar en cuenta el fenómeno de la rotura del material, no resuelven de forma general e integral el fenómeno de modelación del estado tensional-deformacional en un punto de un material dado, porque desprecian, al igual que los modelos elásticos, la esencia de los fenómenos físicos reales (Odinzov, 1987).
Para estudiar el comportamiento de las cualidades superficiales de las piezas tratadas en la deformación plástica superficial por rodillo son muy útiles las técnicas de diseño de experimentos, que permiten darle solución y explicación científica efectiva y económica a los problemas objeto de análisis.
En la actualidad, el método de la simulación ha sido muy generalizado y constituye una potente herramienta de cálculo numérico capaz de resolver cualquier problema formulable de la matemática, la física y la mecánica; permitiendo simular y realizar una gran cantidad de análisis en componentes y estructuras complejos, difícilmente calculables por los métodos analíticos tradicionales.
Según Hernández (1997), la utilización del diseño de un modelo experimental se fundamenta, entre otros aspectos, en cuatro reglas básicas:
- Disminuir el número de corridas experimentales necesarias.
- Cambiar el valor de los factores de acuerdo con reglas.
- Utilizar en el procesamiento métodos matemáticos normalizados.
- Poseer una estrategia de trabajo por etapas.
Con la simulación se puede obtener la resolución numérica de las ecuaciones matemáticas que describen el fenómeno estudiado con el uso de un ordenador. Por lo tanto, se puede asumir que la simulación es tan exacta como tantas sean las ecuaciones de partida y la capacidad de los ordenadores para resolverlas, lo cual fija límites a su utilización (Ingham y Moreland, 1993).
Para optimizar procesos de fabricación, condiciones de reacción y métodos de análisis, entre otros, es necesario conocer qué variables influyen significativamente en el sistema y cómo afectan. A menudo esta información no está disponible y se genera experimentando. Primero se recogen en una lista todas las variables que podrían influir en la respuesta. A continuación, se realiza una serie de experimentos en los cuales se fijan las variables que no interesa modificar, se anota el valor de las que no se pueden controlar, y se varían las restantes. Finalmente, se obtiene la información comparando la variación de la respuesta entre experimentos (El Khabeery, 2003).
En lo referido al cálculo estructural, el método de simulación puede ser entendido como una generalización de estructuras al análisis de sistemas continuos. El principio del método consiste en la reducción del problema con infinitos grados de libertad, en un problema finito en el que intervenga un número finito de variables asociadas a ciertos puntos característicos del objeto.
Por el método de simulación, las incógnitas dejan de ser funciones matemáticas del problema cuando pasan a ser los valores de dichas funciones en un número infinito de puntos. Así pues, se supone que el comportamiento mecánico de cada parte o elemento en los que se subdivide el objeto queda definido por un número finito de parámetros asociados a los puntos que en dicho momento se unen al resto de los elementos de su entorno (Alfaro, 2001).
El elevado costo de la experimentación y las limitaciones de tiempo obligan a ejecutar sólo los experimentos imprescindibles. Y el método tradicional de variar un factor cada vez no suele ser la mejor opción. Puede implicar más experimentos de los necesarios y, a pesar de ello, proporcionar sólo información parcial. Por ejemplo, no mostrará si existe interacción entre factores (Braham, 1993).
Muchos de los modelos comunes son obtenidos de idealizaciones del estudio de los materiales, cuya composición es uniforme y reproducible, a tal grado que sus propiedades mecánicas son virtualmente las mismas que las obtenidas en laboratorios. Los parámetros que caracterizan estas ecuaciones se obtienen por ajustes de los datos experimentales a los modelos matemáticos, los cuales son seleccionados con alguna justificación teórica o empírica.
Las técnicas de diseño de experimentos se basan en estudiar simultáneamente los efectos de todos los factores de interés, son más eficaces y proporcionan mejores resultados con un menor costo.
Materiales y métodos
Diseño de experimento
Para la confirmación de la hipótesis se escogió un diseño de experimento factorial completo (Gutiérrez, De la Vara, 2003), con dos variables y tres niveles. Este método de planificación estadística de la investigación establece el número de ensayos (N) a realizar. Se realizará el tratamiento matemático de las variables involucradas en el proceso que después de un estudio preliminar se consideran como las más importantes, son las que aparecen reflejadas en la Tabla 1.
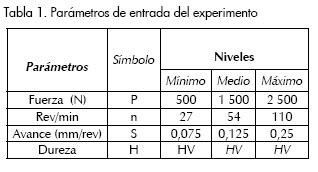
El número de experimentos cuando intervienen k factores con tres niveles cada uno (-1, y +1), se determina con un arreglo de la función exponencial: N = 3k
Donde:
N = Número de experimentos.
K = Número de factores.
En este caso, se analizará la influencia de dos factores, de aquí que K =2; luego, el número de experimento sería: N = 32, por lo que
N = 9 experimentos.
Determinación de los coeficientes de regresión.
La ecuación de regresión resultante tiene la forma siguiente.
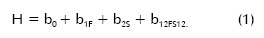
Donde:
P = Fuerza del rodillo sobre la probeta, MPa.
S = Avance, mm/rev
H = Dureza obtenida del ensayo, HRC.
Cálculo de la varianza
Después de calcular los coeficientes de regresión (b0, b1, b2, b12), se comienza el procesamiento estadístico de los resultados determinando la varianza de reproducibilidad (error) del experimento.
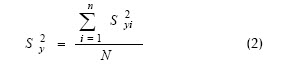
La significación de los coeficientes de regresión se comprueba por el criterio de t de Student para una probabilidad de un 95% o un intervalo de confianza de 0,05 y 15 grado de libertad (N-1). Posteriormente se calcula la varianza con adecuación al modelo:
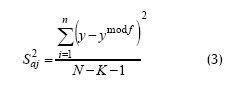
Donde:
N = j y K es el número de coeficientes significativos.
Se calcula el coeficiente de Fisher (FCál) y se compara con el Fisher tabulado (FTab) según los grados de libertad del numerador y del denominador:
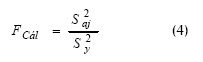
Si el FCál > FTab entonces la ecuación describe adecuadamente el campo de la experimentación.
Resultados y discusión
Con las datas obtenidas (los valores de las durezas de las réplicas a), se modeló el comportamiento de cada uno de estos coeficientes obtenidos de los ensayos de macrodureza respecto a las variables del proceso (P, S y H). Las expresiones matemáticas de dichos modelos se muestran en las ecuaciones 1, 2, 3 y 4.
Análisis de regresión para las variables involucradas
Los resultados experimentales fueron procesados por el análisis de regresión lineal.
La salida muestra los resultados del ajuste a un modelo de regresión lineal múltiple para describir la relación entre H y 3 variables independientes. La ecuación del modelo ajustado es:
H = 222,42 + 0,3127*n + 0,00333*P - 13,3333*S
Donde:
n = Número de revoluciones; rev/min.
P = Fuerza; N.
S = Avance; mm/rev
Según el modelo obtenido, la relación es estadísticamente significativa entre las variables para un nivel de confianza del 95%.
Análisis factorial completo
El diseño estadístico de experimentos contempla una amplia variedad de estrategias experimentales que son adecuadas para generar la información que se busca.
En la Tabla 2 se reflejan los resultados del análisis factorial completo para las variables involucradas en el proceso de experimentación. Se realizó para obtener un pequeño números de factores que expliquen la mayoría de la variabilidad en cada una de las cuatro variables.
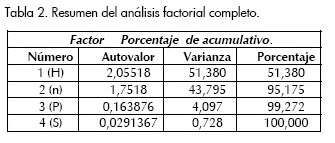
En este caso, al efectuar el análisis se extrajeron dos factores dado que los mismos son iguales a 1,0; juntas las variables explican el 96,3116% de la variabilidad en los datos obtenidos, asumiendo que toda la variabilidad en los datos es debida a factores comunes. Esto confirma el criterio de que lo determinante en las variaciones de la dureza del acero AISI 1045 son los factores n, S y P.
Comportamiento de la dureza
Análisis del comportamiento de la dureza en relación con la fuerza.
A partir de las bases de datos del experimento fue posible obtener las medias y los residuos de las variables fuerza y dureza. El gráfico de la Figura 1 relaciona el comportamiento de la dureza en relación con la presión, para la que la ecuación del modelo se escribe como:
Dureza = 18, 109 Ln (x) +219,57
Con un coeficiente de correlación de:
R2 = 0,8825
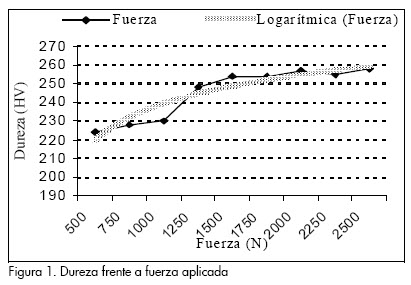
El intervalo de confianza para la diferencia entre las medias de las dos muestras demuestra que estadísticamente existe diferencia significativa para un nivel de confianza del 95,0%.
Los resultados expuestos demuestran que se mantiene la tendencia a incrementar la dureza en la medida en que aumenta la fuerza. Se confirma el incremento del tensionamiento de la red y el endurecimiento del material, puesto que el mismo ofrece mayor resistencia a la penetración una vez deformado plásticamente.
Además está condicionado por la aptitud del material para adquirir dureza por trabajo de deformación en frío. Se puede plantear que la variable P es significativa para lograr el endurecimiento de acero AISI 1045 mediante la deformación plástica superficial empleando rodillo simple.
Análisis del comportamiento de la dureza en relación con el avance
Se realiza una valoración de la influencia que ejerce el avance sobre la dureza se calculan varios estadígrafos y gráficos para cada muestra, con el fin de determinar si existen diferencias estadísticamente significativas entre muestras. En el gráfico de la Figura 2 se refleja el comportamiento de la dureza con relación al avance.
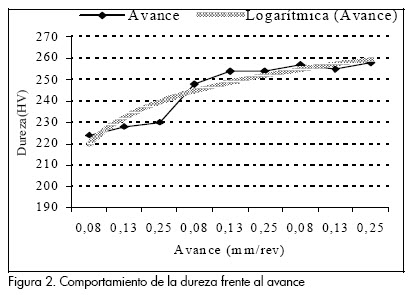
En el gráfico de la Figura 2 se relaciona el comportamiento de la dureza respecto al avance, se obtuvo la ecuación para el modelo de avance y dureza:
Y = 18, 109 Ln(x)+219,57
La correlación para este caso es de:
R2 = 0,8825
Al estimar el error del modelo experimental con el calculado existe diferencia estadísticamente significativa entre las medias de las dos muestras para un nivel de confianza del 95,0%.
El parámetro avance trae consigo un aumento del tensionamiento de la red en las muestras deformadas del acero ferrito-perlítico AISI 1045. Este aumento es consecuencia directa del trabajo de deformación en frío provocado por la acción de las cargas de rodadura y obedece a la reducción en las distancias interplanares del metal tensionado. Se puede establecer que el parámetro denominado avance (S) es significativo para lograr el endurecimiento del mismo mediante la deformación plástica superficial empleando un rodillo como elemento deformante.
Error del experimento.
Es necesario definir si el efecto de la variable en estudio es significativo, con lo cual se procede a separar los efectos principales de los de interacción de dos o más variables, empleando los niveles de significancia de las variables, que mediante el cálculo del error permite determinar cuál será la desviación permisible, siempre y cuando su valor sea el doble del error. La Figura 3 muestra el comportamiento de las curvas al plotear cada una de las variables teniendo en cuenta sus niveles.
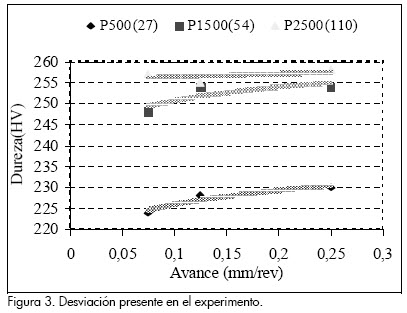
Para estudiar el efecto del rodillo, se graficaron por separado las diferentes fuerzas, números de revoluciones y avance a la que fueron sometidas las probetas, de acuerdo con la matriz del diseño del experimento descrito en la Tabla 1.
Se observa que en el acero AISI 1045 hay tendencia al incremento de la dureza en la medida en que se incrementa el valor de las variables, existe marcada diferencia entre la curva de 500 N, con respecto a las curvas de 1 500 N y 2 500 N, aunque estas dos tienden a igualarse, es con mayor fuerza que el material alcanza mayor capacidad de endurecimiento.
Se realizó el procedimiento del resumen de análisis entre las variables para encontrar las combinaciones lineales y determinar el error del experimento.
Al plotear las curvas se demuestra que existe diferencia estadísticamente significativa entre las medias de las muestras, para un nivel de confianza del 95%.
Análisis microestructural
Para la observación de la microestructura de la probeta patrón, la cual se empleará para la comparación de las micrografías obtenidas, se empleó un microscopio óptico binocular, este está dotado con un portaobjetos giratorio e iluminador vertical Watson. La observación se realiza empleando distintas combinaciones de objetivo y ocular para obtener las imágenes más precisas. Las probetas se montan en un dispositivo con plastilina que permite una nivelación adecuada. Para procesar la información se utilizó una cámara fotográfica digital.
El ataque químico se realizó con el objetivo de resaltar la estructura obtenida después de realizado el pulido, para observar la estructura metalográfica formada después de la deformación del material bajo carga por rodadura (ASTM E-262-Practice A). Para este ataque químico se utilizó nital al 4%.
Análisis metalográfico
El análisis metalográfico consistió en la observación e identificación de las características de la estructura metalográfica en probetas de acero AISI 1045.
Se efectuó la micrografía de todas las probetas antes de aplicar la carga (Figura 4) y posterior a esta. Se analizará el comportamiento en correspondencia con el diseño del experimento, desde el valor mínimo hasta el máximo.
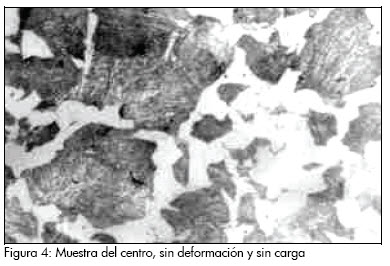
Al comenzar el proceso (Figura 5), en nivel mínimo con valor de la fuerza de 500N, 27 rev/min y avance de 0,25 mm/rev, se observa la deformación de la red cristalina del material con el alargamiento de los granos.
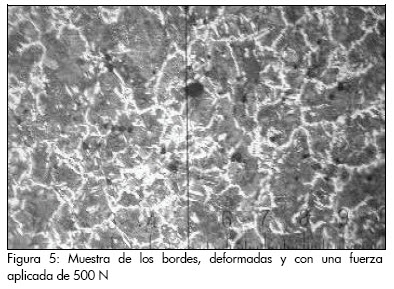
En el nivel intermedio, en iguales condiciones de operación pero aplicando una fuerza de 1500 N, 54 rev/min y avance de 0,125 mm/rev, se observa mayor agrupación de los granos en la red cristalina, producto del deslizamiento (ver Figura 6).
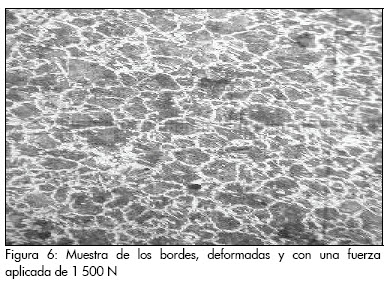
El máximo nivel con valor de la fuerza de 2 500 N, 110 rev/min y avance de 0,125 mm/rev. (Figura 7), se caracteriza por una mayor compactación de los granos, lo cual se produce como resultado del incremento de los valores de las variables n, S y P.
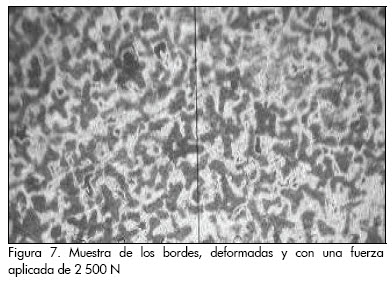
En las probetas sometidas a deformación podemos observar una estructura bifásica de ferrita-perlita, lo que demuestra que el endurecimiento del acero AISI 1045 por rodadura ocurre por el fenómeno de las dislocaciones y no por el cambio de fase. Los límites de los granos se hacen más finos en la medida en que se va incrementando la fuerza que se introduce a través de la herramienta de deformar, se observa el deslizamiento en los granos.
Después de someter a las probetas a la acción de cargas por rodadura, se notan vestigios de deformación plástica, con bloques de la estructura en mosaico divididos en pequeñas proporciones y una deformación clara de la red cristalina, típico del fenómeno de la acritud. Las micrografías mostradas con un aumento del microscopio (500x) corresponden a los diferentes niveles a las que fueron deformadas.
Como se aprecia, la capacidad de endurecimiento (H) tiene un comportamiento creciente en la misma medida en que se incrementan los valores de las variables del proceso de experimentación (n, S, y P), al incrementar las tensiones de compresión surge un estado tensional que deforma el acero, incrementando su dureza final; de esta forma se reducen los niveles de desgaste, mejorando el comportamiento del material en correspondencia con el mecanismo de endurecimiento.
Conclusiones
1. Se establecen las regularidades del comportamiento mecánico y funcional del acero AISI 1045 endurecido mediante la deformación plástica superficial por rodadura. Los modelos experimentales describen la interacción entre las mismas y cumplen satisfactoriamente todas las pruebas estadísticas para su validación.
2. Los parámetros de deformación (n, P, S) constituyen factores principales para el trabajo de endurecimiento de metales, y ellos pueden ser considerados a partir de las variables del proceso experimental: número de revoluciones del husillo, fuerza y avance (cada una de ellas evaluadas en tres niveles), mediante la utilización de un diseño factorial de planificación de experimentos que ofrece la posibilidad de estimar la incidencia de dichas variables en el comportamiento mecánico y funcional del acero AISI 1045.
3. La capacidad de endurecimiento (H) tiene un comportamiento creciente en la misma medida en que se incrementan los valores de las variables del proceso de experimentación (n, S, y P); este resultado se corresponde con que, al incrementar las tensiones de compresión, surge un estado tensional que lo deforma, incrementando su dureza final, de esta forma se reducen los niveles de desgaste mejorando el comportamiento del material en correspondencia con el mecanismo de endurecimiento.
4. Los resultados del análisis metalográfico revelan en las muestras deformadas de acero AISI 1045 una estructura de ferrita-perlítica antes y después del tratamiento con rodadura. No se detectó la presencia de aparición de nuevas fases por el trabajo de compresión dinámica. Se comprobó la reducción del tamaño del grano.
Bibliografía
Alfaro, W., Simulación de procesos. En: http://www.monografías.com/trabajos/. 2001. [ Links ]
Alvarez, E. N, Lancestremere, J, Mareglia, J. C, Barr, J. Fundamentos de la trafilación. Tecnología Mecánica II. Universidad de Buenos Aires. Facultad de Ingeniería, 2004. . [ Links ]
Boada, O., Díaz, S., Campos, Y. Estudio del estado físico-mecánico de superficies tratadas por deformación plástica superficial, Revista Ingeniería Mecánica, Instituto Superior Politécnico José Antonio Echevarria (ISPJAE), Volumen 6, No. 2, Mayo-Agosto 2003, Pág. 53-58, Cuba. ISSN1029-516X. [ Links ]
Braham, S., Frelat, J., Modelling of crankshaft roller burnishing, Monograph in First International Conference on Computer Methods and Experimental Measurements for Surface Treatment Effects, 1993, Page 255, Computational Mechanics Publisher Southampton, England. [ Links ]
El-Khabeery, M.M. Influence of orthogonal burnishing parameters on surface characteristics for various materials, Journal of Materials Processing Technology, Volume 132, Issue 1-3, January 2003, Pages 82-89, The Netherlands. [ Links ]
Gutierrez, F. y R. De la Vara. (2003). Análisis y Diseño de Experimentos, Mc Garw Hill, 1a ed, 237-264. C. México. México. [ Links ]
Ingham, T. y E. Moreland: The Influence of Time-dependent Plasticity on elastic-plastic fracture toughness. En: ASTM STP 803, Vol. I. 1983. [ Links ]
Hasegawa, S., The road to smoother surfaces, Manufacturing Engineering, Volume 126, No. 2, February 2001, Pages 70, 72, 74, 76, 78, USA. [ Links ]
Hernández, S. Metodología de la Investigación. Editorial McGraw-Hil. México. 1997. [ Links ]
Mazein, P.G. Prusakov, D.V., Tchunin, A.V. Modelling the residual stresses and deformation during a surface plastic deformation operations, Proceeding of the Chelyabinsk Scientific Center, Issue #1, (10). January-March 2001, Russia. [ Links ]
Odintsov, L.G. Fortalecimiento y acabado de las piezas mediante la deformación plástica superficial, Editorial CM, 1987. Pág 385-422, URSS. [ Links ]
Skalski, K., Morawski, A., Przybylski, W., Analysis of contact elastic-plastic strains during the process of burnishing, International Journal of Mechanical Sciences, Volume 37, Nº 5, May 1995, Pages 461-472, UK. [ Links ]














