Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.1 Bogotá Jan./Apr. 2008
Héctor Andrés López Ospina1 y Mauricio Restrepo López2
1 Matemático, Universidad Nacional de Colombia. M.Sc., en Matemática Aplicada, Universidad Nacional de Colombia. Matemático-Universidad Nacional de Colombia. Profesor, Facultad de Ingeniería, Universidad de la Sabana, Colombia. hector.lopez1@unisabana.edu.co
2 Magíster, en Matemáticas, Universidad Nacional de Colombia. Profesor, Facultad de ingeniería, Universidad de La Sabana, Colombia. mauricio.restrepo@unisabana.edu.co
RESUMEN
El presente trabajo tiene como objetivo presentar los conceptos básicos de la programación lineal flexible o programación lineal con restricciones difusas. Dado que la literatura presenta dicha metodología para restricciones de desigualdad, se formula una metodología para restricciones de igualdad y de caja. Se muestra cómo un problema de este tipo equivale a uno de optimización paramétrica. Finalmente, se presentan dos ejemplos ilustrativos en los cuales se muestra la ventaja de la metodología al mejorar la solución óptima y, por otro lado, la obtención de una región factible en problemas con espacio de soluciones vacío.
Palabras clave: conjuntos difusos, programación lineal, optimización paramétrica.
ABSTRACT
The present work shows the basic concepts of the flexible linear programming or linear programming with fuzzy constrains. In the literature is often to find this methodology for inequality constrains, this works shows a methodology for box and equality constrains. Additionally, it presents the equivalence between this type of problems with parametric optimization. Finally two examples are presented to show the advantage for using this methodology.
Keywords: Fuzzy sets, linear programming, parametric optimization.
Recibido: septiembre 12 de 2007
Aceptado: febrero 29 de 2008
Introducción
En muchos modelos de optimización, la solución obtenida puede no ser satisfactoria para quien toma decisiones, y por eso se hace necesario generar nuevos modelos, con el objetivo de alcanzar las diversas metas trazadas. Esto se puede lograr aumentando la capacidad de producción o inventario de algún artículo o producto, incrementando o disminuyendo la demanda, elevando la capacidad de carga o transporte, entre otros. Por otro lado, cuando se realiza la modelación matemática en el sector industrial por medio de optimización, debido a la cantidad de parámetros y restricciones, en muchos casos no es posible encontrar una solución factible. Por lo expuesto anteriormente, se presenta una metodología de optimización flexible u optimización con restricciones difusas que permite dar solución a dichos problemas a través de la flexibilización de las restricciones. Para tal efecto, se hace la descripción de un método usual de optimización difusa que convierte el problema original en un modelo de optimización paramétrica. En la mayoría de la literatura se describe dicha técnica para restricciones de desigualdad (Cárdenas y Verdegay, 1999; Jaroslav, 2001). El presente documento también propone una formulación para restricciones de igualdad y restricciones de caja para las variables de decisión. Las restricciones de igualdad son muy importantes en modelos de programación lineal como transporte y planeación de la producción, donde se debe cumplir con una demanda determinada (Taha, 2004), problemas de inversión y mezcla de productos (Winston, 2005), distribución de bienes, flujo máximo, problema del agente viajero, entre otros, donde es necesario modelar ecuaciones de balance (Taha, 2004; Winston, 2005). Las restricciones de caja son muy comunes en todos los modelos reales de optimización. Por ejemplo, capacidad máxima y mínima de inventario, producción y transporte. En problemas de inversiones es natural tener una restricción de cantidad mínima y máxima de inversión en cada una de las opciones. En los modelos de flujo máximo siempre se debe suponer que entre los arcos existe una capacidad máxima y mínima de flujo, entre otros (Winston, 2005). En la sección (1) se presentan algunos preliminares. La sección (2) describe la metodología para encontrar la solución de problemas de optimización lineal flexible, y finalmente, la sección (3) presenta algunos ejemplos ilustrativos de la teoría desarrollada.
Preliminares
Representación de un problema de optimización
Todo modelo de optimización lineal se puede escribir de la forma:
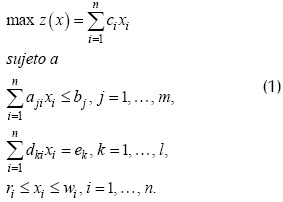
donde x = (x1,...,xn)  Rn definen las variables de decisión. En este problema se tienen restricciones de desigualdad y l restricciones de igualdad. Además, ri y rw son restricciones de caja para cada una de las variables. Por notación se dirá que la región factible es
Rn definen las variables de decisión. En este problema se tienen restricciones de desigualdad y l restricciones de igualdad. Además, ri y rw son restricciones de caja para cada una de las variables. Por notación se dirá que la región factible es
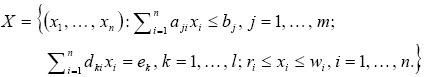
El problema (1) se escribe en forma matricial como:
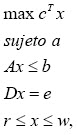
donde: A  Rmxn, D
Rmxn, D  Rlxn, c
Rlxn, c  Rn, b
Rn, b  Rm, e
Rm, e  Rl y r,w
Rl y r,w  Rn . Además, la región factible se escribe:
Rn . Además, la región factible se escribe:
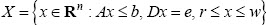
La idea fundamental es flexibilizar las restricciones en este tipo de problemas mediante conjuntos difusos.
Conjuntos difusos y λ-cortes
Definición 1 (Buckley y Esfandiar, 2002) Sea Y  R un conjunto no vacío. Un subconjunto difuso de es una función µ : Y → [0, 1].
R un conjunto no vacío. Un subconjunto difuso de es una función µ : Y → [0, 1].
El valor de en la función, µ expresa una medida o grado para el cual y está en Y. Si µ(y) = 1 entonces y  Y. Por otro lado, si µ(y) = 0 se puede afirmar que y
Y. Por otro lado, si µ(y) = 0 se puede afirmar que y  Y. En el caso que 0 < µ(y) < 1, dicho valor proporciona el grado o porcentaje de pertenencia de y en Y. µ(x) recibe el nombre de función de pertenencia.
Y. En el caso que 0 < µ(y) < 1, dicho valor proporciona el grado o porcentaje de pertenencia de y en Y. µ(x) recibe el nombre de función de pertenencia.
Definición 2 (Buckley y Esfandiar, 2002) Sea µ un subconjunto difuso de Y y 0 < λ ≤ 1, se define un λ-corte como:
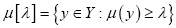
En el caso que λ=0, se tiene que µ[λ]=Y.
Definición 3 (Buckley y Esfandiar, 2002) Intersección entre conjuntos difusos: Dados µi, i,..., n conjuntos difusos de Y, se define la intersección como
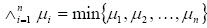
Definición 4 (Buckley y Esfandiar, 2002) Unión entre conjuntos difusos: Dados µi, i,..., n conjuntos difusos de Y, se define la unión como
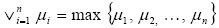
Los conjuntos difusos permiten modelar la flexibilidad de las restricciones.
Programación lineal flexible
Un problema de programación lineal flexible o con restricciones difusas se escribe de la forma:
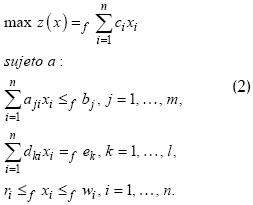
La notación =f y ≤f indica que existe cierto grado de flexibilidad en las restricciones. Es decir, se permiten algunas violaciones o incumplimiento sobre las mismas. Una de las maneras de resolver y atacar este tipo de problemas es por medio de conjuntos difusos (Cárdenas y Verdegay, 1999; Jaroslav, 2001).
Para realizar un análisis del modelo (2) se estudia cada tipo de restricción flexible de forma separada.
Función objetivo flexible
Esta sección está basada en lo expresado por por Jaroslav (2001). Cuando la función objetivo es flexible o difusa, se supone que existe un valor de aspiración para la función objetivo. Dicho valor se notará d0  R. Es decir, se espera encontrar un x*
R. Es decir, se espera encontrar un x*  tal que z(x*) ≥ d0. En muchos casos no es posible encontrar un punto factible que satisfaga esta condició, por lo cual se permite que la función objetivo pueda alcanzar valores menores a d0. Para esto, se fija un valor p0 que define el grado mínimo de cumplimiento o pertenencia al nivel de aspiración. De esta forma, si z(x) ≤ d0- p0, se dice que tiene un grado de cumplimiento de 0. Si z(x) ≥ d0, el grado de cumplimiento o nivel de pertenencia es 1. Además, si d0- p0 ≤ entonces el grado o porcentaje de cumplimiento está dado por
tal que z(x*) ≥ d0. En muchos casos no es posible encontrar un punto factible que satisfaga esta condició, por lo cual se permite que la función objetivo pueda alcanzar valores menores a d0. Para esto, se fija un valor p0 que define el grado mínimo de cumplimiento o pertenencia al nivel de aspiración. De esta forma, si z(x) ≤ d0- p0, se dice que tiene un grado de cumplimiento de 0. Si z(x) ≥ d0, el grado de cumplimiento o nivel de pertenencia es 1. Además, si d0- p0 ≤ entonces el grado o porcentaje de cumplimiento está dado por 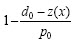 . Lo descrito anteriormente se puede expresar por medio de la siguiente función de pertenencia trapezoidal para la función objetivo z:
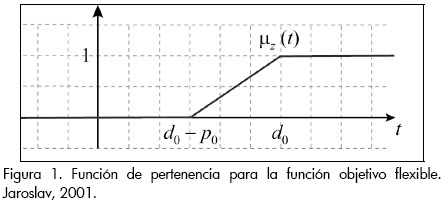
. Lo descrito anteriormente se puede expresar por medio de la siguiente función de pertenencia trapezoidal para la función objetivo z:
Gráficamente, 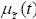 se describe de la siguiente manera:
se describe de la siguiente manera:
Luego, el problema (1) con función objetivo flexible es equivalente a
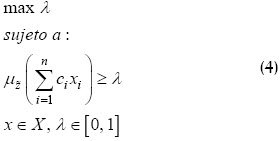
Como puede verse en Jaroslav (2001), el problema (4) es equivalente al siguiente problema de optimización paramétrica
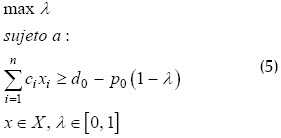
cuya solución óptima (λ*, x*) se considera la solución del problema (1) con función objetivo flexible.
Restricciones de desigualdad flexibles
Esta parte está basada en Cárdenas y Verdegay (1999) y Jaroslav (2001). Para cada una de las restricciones de desigualdad se definen las siguientes funciones de pertenencia:
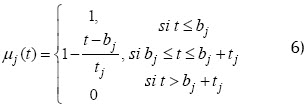
Gráficamente, la función de pertenencia es:
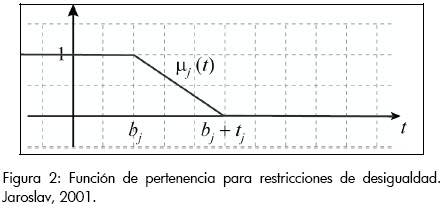
En este caso, dado un x = (x1, x2,...,xn)  Rn y
Rn y 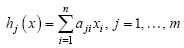 , entonces
, entonces
- Si hj(x) ≤ bj se dice que x tiene un grado de cumplimiento o pertenencia en la j-ésima restricción de 1, µj (hj(x)) = 1.
- Si hj(x) ≥ bj + tj, x tiene un grado de cumplimiento o pertenencia en la j-ésima restricción de 0, µj (hj(x)) = 0.
- Si bj ≤ hj(x) ≤ bj + tj entonces x satisface 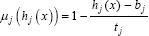 . Dicho valor define el grado o porcentaje de pertenencia.
. Dicho valor define el grado o porcentaje de pertenencia.
Restricciones de igualdad y de caja
El aporte fundamental de este trabajo está centrado en la inclusión de una metodología difusa que involucra restricciones de igualdad y de caja.
Para cada una de las restricciones de igualdad se definen las siguientes funciones de pertenencia triangular, que permiten un porcentaje de incumplimiento tanto por déficit o por exceso:
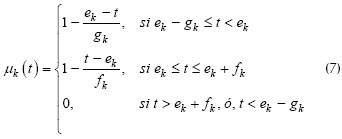
La representación gráfica de µk(t) se muestra en la Figura 3.
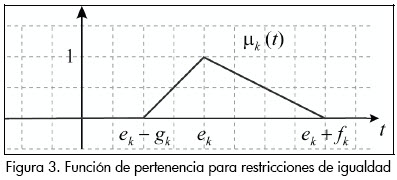
En este caso, dado un x = (x1, x2,...,xn)  Rn y entonces
Rn y entonces 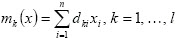
- Si mk(x) ≥ ek + fk o mk(x) ≤ ek - gk se dice que tiene un grado de cumplimiento o pertenencia a la k-ésima restricción de igualdad de 0, µk (mk(x)) = 0.
- Si ek ≤ mk(x) ≥ ek + fk, x tiene un grado de cumplimiento o pertenencia a la k-ésima restricción de 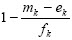 .
.
De forma análoga se hace el análisis si ek - gk(x) ≤ t + ek.
Por otro lado, cada restricción de caja ri ≤ xi(x) ≤ wi se puede definir de forma flexible por medio de la función de pertenencia trapezoidal:
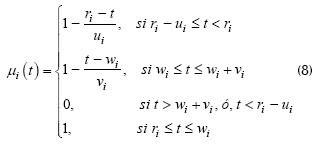
La representación gráfica de µi(x) se muestra en la Figura 4.
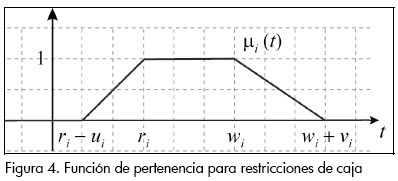
Es decir, si t = xi entonces:
- Si xi satisface las restricciones ri ≤ xi ≤ wi entonces su grado de pertenencia es 1, (µi(xi)) = 0.
- Si xi > xi + vi o xi ≤ ri - ui entonces su grado de cumplimiento de la i-ésima restricción es 0, (µi(xi)) = 1.
- Si wi ≤ xi ≤ wi + vi entonces se tiene un grado de pertenencia de 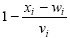 .
.
- Si ri - ui ≤ xi < ri entonces 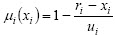 .
.
Problema de optimización paramétrica equivalente
Por medio de la intersección de las funciones de pertenencia (3), (6), (7) y (8), aplicadas a cada tipo de restricción, la solución del problema de optimización lineal (2) es:
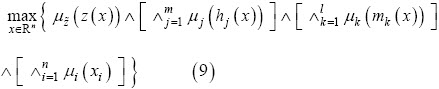
Por la definición de  , (9) es equivalente al siguiente problema maximin:
, (9) es equivalente al siguiente problema maximin:
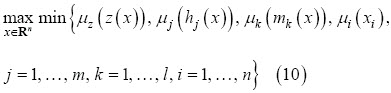
Haciendo
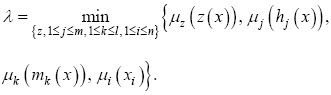
(10) se puede escribir como un problema de programación lineal,
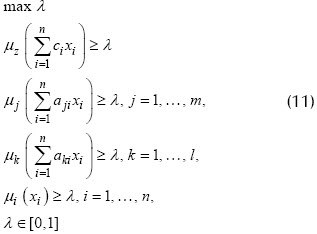
donde 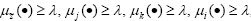 son λ-cortes de cada una de las funciones de pertenencia. Dicho problema quiere alcanzar el nivel más alto de cumplimiento o pertenencia a cada una de las restricciones. El modelo anterior es equivalente al siguiente problema de optimización paramétrica:
son λ-cortes de cada una de las funciones de pertenencia. Dicho problema quiere alcanzar el nivel más alto de cumplimiento o pertenencia a cada una de las restricciones. El modelo anterior es equivalente al siguiente problema de optimización paramétrica:
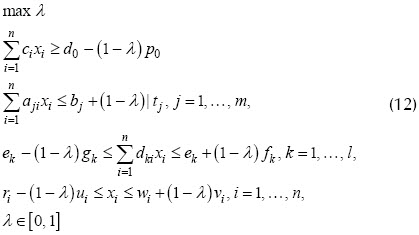
Matricialmente, (12) se expresa de la siguiente manera:
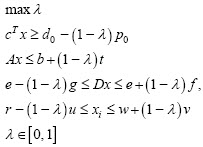
Existen métodos numéricos propios de optimización paramétrica que pueden ser aplicados para encontrar la solución de (12), y además es posible utilizar técnicas propias de optimización lineal relajando el espacio factible.
Ejemplos
Ejemplo 3.1 Producción para utilidad máxima: Un fabricante de juguetes prepara un programa de producción para dos tipos de juguetes, muñecas y soldados, con base en la información concerniente a sus tiempos de producción dados en la siguiente tabla:

Para la operación de la máquina A se dispone de 70 horas; para la máquina B 40 horas; para la máquina C 90 horas. Las utilidades en cada muñeca y cada soldado son $4 y $6, respectivamente. El modelo matemático de optimización que representa dicha situación es:
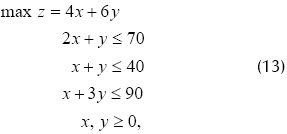
donde x es el número de muñecas a fabricar y el número de soldados.
Por medio del paquete de optimización LINDO se obtiene la siguiente solución óptima: z* = 210, x* = 15, y* = 25. Gráficamente, (13) se expresa como se muestra en la Figura 5.

Supongamos que el fabricante desea obtener utilidades de $300 o como mínimo $260. Para esto es posible ampliar el número de horas para cada una de las máquinas de la siguiente forma: Máquina A, hasta 80 horas (es decir, 10 horas extras); máquina B, hasta 70 horas (30 horas extras). Máquina C, hasta 120 horas (30 horas extras). De esta forma, el modelo de programación flexible se escribe:
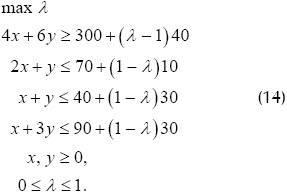
Se trata de encontrar el mejor que satisfaga la utilidad deseada con los mínimos recursos en horas adicionales. Una aproximación gráfica de (14) es la que se presenta en la Figura 6.
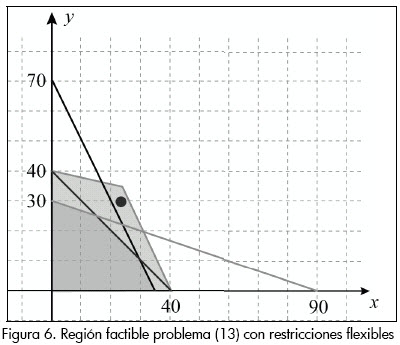
Además, con la relajación del espacio factible a R3 se obtiene la solución λ = 0,25, x = 24, y = 29. El factor de cumplimiento o satisfacción para cada restricción es:
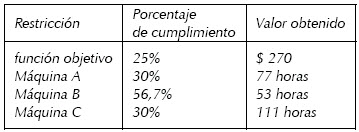
En todos los casos, es necesario utilizar horas extras. Aunque el número de horas extras de la máquina A: 7 horas (70% de las horas adicionales) es menor que el número de horas para la máquina B: 13 horas (43,3% de las horas adicionales), el porcentaje o nivel de cumplimiento de la restricción de dicha máquina es mayor puesto que utilizó un menor porcentaje del recurso adicional. En la función objetivo se logra un porcentaje de cumplimiento del 25% sobre la meta de $300 tomando un valor de $270, pero se incrementó en un total de $60, sobre la solución original.
Ejemplo 3.2 Región factible vacía: Una compañía de encuestas telefónicas ha sido contratada para llevar a cabo una encuesta sobre hábitos televisivos entre las familias de las zonas rurales y urbanas de una ciudad determinada. El cliente ha determinado que se deben entrevistar 150 familias, entre ellas mínimo 30 deben ser de zonas rurales y máximo 60. De las familias de la zona urbana se deben entrevistar como mínimo 40 y máximo 100. Por este servicio, la empresa recibe $6.000 por cada entrevista a familias de la zona rural y $5.000 por cada entrevista a las familias de zona urbana. Por la experiencia obtenida anteriormente, se determina que la compañía realizará un gasto de $2.500 por cada llamada a las zonas rurales y $2.000 a zonas urbanas y sólo se dispone de $320.000 para realizar dichas llamadas. En este problema el objetivo es maximizar las ganancias.
Las variables de decisión son:
- x : número de llamadas a familias de zonas rurales
- y : número de llamadas a familias de zonas urbanas
El modelo matemático que representa dicha situación es
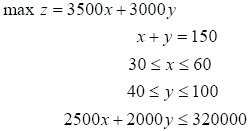
Este problema no tiene solución factible, por lo cual se hace necesario que algunas restricciones tengan algún nivel de flexibilidad (restricciones difusas). Para esto el cliente permite que el número de entrevistados pueda estar entre 140 y 155. Además, que el máximo número de familias a entrevistar de la zona rural sea 65. No se hacen modificaciones en el resto de las restricciones. Es importante notar que en este caso, la función objetivo no se convierte en flexible. Por lo cual el problema con restricciones difusas se puede ver como un problema de optimización con dos objetivos:
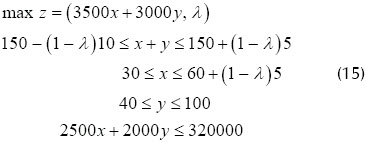
La región factible para el problema (15) se puede describir gráficamente como se muestra en la Figura 7.
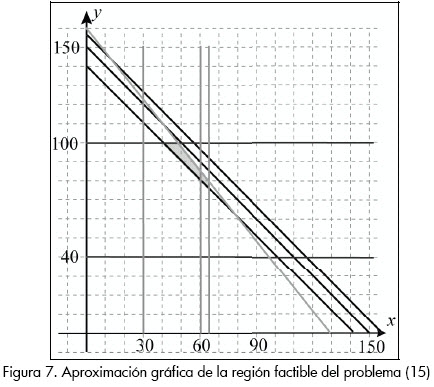
Utilizando el método de la ε - restricciones de programación multiobjetivo descrito en Smith et al. (2000), (15) se puede escribir como:
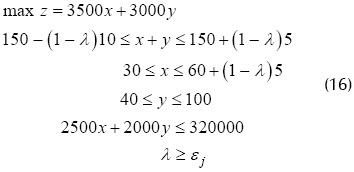
donde la variación paramétrica de εj genera la frontera de Pareto. En la siguiente tabla se describen las soluciones obtenidas
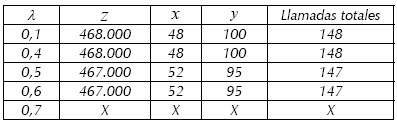
A partir de λ= 0,7 no se obtienen puntos factibles. Es decir, el máximo valor de pertenencia obtenido en la intersección de todas las restricciones es 0,6.
Conclusiones
La programación lineal flexible es una herramienta de programación difusa que sirve para resolver problemas de optimización, donde la solución óptima no es satisfactoria para el tomador de decisiones o la gran cantidad de restricciones y limitaciones no genera puntos factibles. La metodología que incluye las restricciones de igualdad y de caja difusas permitió mejorar soluciones óptimas y encontrar soluciones factibles en problemas con espacio factible vacío. Además, este desarrollo permite abarcar problemas más generales de programación lineal. Sería interesante aplicar esta técnica en modelos donde el valor de los parámetros correspondientes al lado derecho de cada una de las restricciones sea incierto o difuso.
Por otro lado, dependiendo de la aplicación se puede explorar la utilización de funciones de pertenencia de tipo no lineal como lo desarrollado en Taha (2004). Además, es posible comparar los resultados obtenidos por medio de programación lineal flexible con modelos de programación por metas Smith et al. (2000). Aunque el desarrollo matemático es distinto, se puede notar que la filosofía es muy parecida.
Bibliografía
Buckley, J., Esfandiar E. An introduction to fuzzy logic and fuzzy sets., Heidelberg: Physica-Verlag, 2002. [ Links ]
Cárdenas, J., Verdegay, J., Modelos de optimización con datos imprecisos Servicio de Publicaciones., Universidad de Murcia, 1999. [ Links ]
Jaroslav, R., Soft Computing: Overview and Recent Developments in Fuzzy Optimization., Ostravská univerzita. Listopad, 2001. [ Links ]
Smith, R., Jaramillo, P., Poveda, G., Mesa, O., Dyner, I., Valencia, D., Decisiones con múltiples objetivos e incertidumbre., Facultad de Minas Universidad Nacional de Colombia, Sede Medellín, 2 Edición, 2000. [ Links ]
Taha, H., Investigación de Operaciones., Séptima edición, Editorial Pearson, 2004. [ Links ]
Vasant, P., Optimization in product mix problem using fuzzy linear programming., Department of Mathematics, American degree Program, Nilai International College. Malasia, 2004. [ Links ]
Winston, W., Investigación de Operaciones: Aplicaciones y algoritmos., Séptima edición, Editorial Thomson, 2005 [ Links ]














