Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.2 Bogotá May/Aug. 2008
Ibsen Chivatá Cárdenas1
1 Ingeniero civil. Universidad Nacional de Colombia. Magíster, Medio Ambiente y Desarrollo, Universidad Nacional de Colombia. Instituto de investigaciones sobre incertidumbre, INCER, Manizales, Colombia. ibsen_13@yahoo.es
RESUMEN
En este artículo se muestra el uso de métodos no paramétricos y de probabilidades imprecisas en el desarrollo de un modelo de precipitaciones. Se acude a estas herramientas debido a que no se dispone de información representativa y homogénea. En la zona, la información hidrológica sobre las precipitaciones es escasa y además las series hidrológicas existentes no son uniformes ni continuas. Se construyó un modelo distribuido de excedencias de precipitación y en su elaboración se acudió a las denominadas cajas de probabilidad, a distribuciones de probabilidad multinomiales y a la estimación de intervalos de confianza. La modelación no paramétrica se elaboró a partir de estas dos últimas herramientas, logrando una amigable propuesta de computación. El modelo permite observar los altos contenidos de incertidumbre que suelen presentarse al estudiar los patrones de lluvia en el área. La incertidumbre copa todo el dominio de valores de probabilidad y muestra las altas limitaciones de información, con lo que se concluye que una estimación puntual de probabilidades conduce a significativos errores. Se extrae información relevante como que el umbral de lluvia máxima diaria de 70 mm puede ser superado al menos una vez cada tres años, y las magnitudes de incertidumbre que afectan las estimaciones de parámetros hidrológicos. Las conclusiones de esta investigación determinan que la modelación no paramétrica y la estimación de probabilidades imprecisas no sólo representan una alternativa para la modelación hidrológica, sino que quizás sea un procedimiento obligado; su potencial radica en el tratamiento de información escasa y constituye una estrategia de modelación robusta en condiciones de no estacionalidad estocástica.
Palabras clave: incertidumbre, modelación no paramétrica, probabilidades imprecisas, distribuciones de probabilidad multinomiales..
ABSTRACT
This article presents a rainfall model constructed by applying non-parametric modelling and imprecise probabilities; these tools were used because there was not enough homogeneous information in the study area. The areas hydrological information regarding rainfall was scarce and existing hydrological time series were not uniform. A distributed extended rainfall model was constructed from so-called probability boxes (p-boxes), multinomial probability distribution and confidence intervals (a friendly algorithm was constructed for non-parametric modelling by combining the last two tools). This model confirmed the high level of uncertainty involved in local rainfall modelling. Uncertainty encompassed the whole range (domain) of probability values thereby showing the severe limitations on information, leading to the conclusion that a detailed estimation of probability would lead to significant error. Nevertheless, relevant information was extracted; it was estimated that maximum daily rainfall threshold (70 mm) would be surpassed at least once every three years and the magnitude of uncertainty affecting hydrological parameter estimation. This papers conclusions may be of interest to non-parametric modellers and decisions-makers as such modelling and imprecise probability represents an alternative for hydrological variable assessment and maybe an obligatory procedure in the future. Its potential lies in treating scarce information and represents a robust modelling strategy for non-seasonal stochastic modelling conditions.
Keywords: uncertainty, non-parametric modelling, imprecise probability, multinomial probability distribution.
Recibido: enero 31 de 2008
Aceptado: julio 1 de 2008
Introducción
La incertidumbre es tratada tradicionalmente con las herramientas de la teoría de la probabilidad; sin embargo, restricciones epistemológicas, temporales e inclusive financieras, impiden obtener en la mayoría de los casos la información necesaria y suficiente sobre las variables de un fenómeno, para aplicar con rigor la teoría y para que ésta ofrezca resultados confiables y útiles para la toma de decisiones. De otro lado, aun cuando la teoría de la probabilidad, en condiciones de suficiente información, puede modelar adecuadamente la ocurrencia del cambio estacionario (heterogeneidad, aleatoriedad), pueden encontrarse toda una serie de escollos en situaciones de limitada información y de volatilidad estocástica (Bogardi y Duckstein, 2003). Las dificultades se incrementan cuando se presentan incertidumbres como las debidas a la ambigüedad y conflicto de la información que sirve de evidencia para la construcción de modelos, como puede darse, por ejemplo, en un programa ampliado de muestreo sobre una variable (examen a varias muestras o diferente calidad de las mismas). Pero, han surgido desde las teorías y herramientas para tratar la incertidumbre, técnicas que ponen en juego varias posibilidades con el propósito de tratar con incertidumbres como las que se denotan. Entre ellas podrían referirse: el análisis de intervalos, la teoría de las probabilidades imprecisas, la modelación no paramétrica, la simulación numérica, la teoría de los conjuntos difusos, la teoría de los conjuntos rough, la teoría de la posibilidad, la teoría de los números inciertos, las estructuras o funciones de creencia, los números cloud, e hibridaciones de las anteriores, entre otras.
En este artículo pretende mostrarse la aplicación de una modelación no paramétrica a través de funciones multinomiales de probabilidad, la estimación de intervalos y modelos de probabilidades imprecisas para el desarrollo de un modelo de precipitaciones, en un caso donde la información hidrológica disponible es escasa y no homogénea. Las condiciones de baja representatividad, confiabilidad y homogeneidad son frecuentes en el desarrollo de estudios y modelos en Colombia, por lo que se espera que la propuesta que se desarrolla sea de alto impacto a nivel nacional.
La modelación estadística no paramétrica se refiere a aquella modelación que prescinde de modelos estándares de probabilidad, como por ejemplo, la distribución normal. En los modelos imprecisos de probabilidad, el objetivo es que el modelo probabilista mismo revele información sobre su imprecisión y las incertidumbres mismas del fenómeno modelado. El objetivo final es el de que la toma de decisiones sea más adecuada porque los modelos desarrollados informan adicionalmente sobre las incertidumbres del modelo y del fenómeno, y además, se permita tratar o manejar de manera sistemática y adecuada la incertidumbre.
De acuerdo con los resultados y conclusiones que se registran en este artículo, se determina que la modelación no paramétrica y la estimación de probabilidades imprecisas y en general el tratamiento de la incertidumbre en una modelación hidrológica, no sólo representan alternativas para el desarrollo de modelos sino que quizás sean procedimientos ineludibles: la importancia de estos métodos y sus conceptos radica en la manipulación de información escasa, lo cual se logra de manera altamente coherente y constituyen estrategias de modelación robusta y confiable en situaciones de no estacionalidad estocástica. En el contexto de investigación nacional y aun en el internacional, todavía no se reconoce la importancia debida a estas propuestas.
El texto está estructurado en la siguiente forma: primero se identifican y describen los conceptos básicos de las probabilidades imprecisas, las distribuciones multinomiales de probabilidad y la estimación de intervalos de probabilidad; en una segunda parte se muestran detalles de la construcción del modelo, y finalmente, se registran los resultados y conclusiones.
Algunas herramientas de modelación de incertidumbre
Es necesario identificar algunas de las situaciones de incertidumbre que rodean la estimación de variables hidrológicas. La estadística probabilista posee algunas herramientas para tratar la incertidumbre: en el caso de la estimación de excedencias puede acudirse a la estimación de intervalos de confianza. Esta última es una forma directa de revelar información sobre la incertidumbre de una estimación en cuanto a que la estimación se refiere a un conjunto de posibles valores acotados por dos valores posibles y extremos. La amplitud de dicho intervalo depende del número de elementos que componen la muestra, es decir, de la representatividad de la información analizada, de la dispersión de los datos y del modelo de probabilidad que se emplea o se considera en las estimaciones.
Se destaca que las técnicas convencionales de modelación exigen la adopción de un modelo de probabilidad, situación que es vista por Almond (1995), Bogardi, (2006), Ferson y Hajagos (2004), Borgman (2004), entre otros, como una debilidad en las modelaciones, ya que en una situación dada puede: no haber suficientes datos que evidencien inicialmente comportamientos aleatorios, o que permitan finalmente identificar su comportamiento paramétrico, o que indiquen su ajuste a modelos estandarizados. También es posible que se intenten modelar fenómenos con regímenes no estacionarios, lo cual dificulta la adopción de un modelo único de probabilidad. Han aparecido técnicas de modelación, como la no paramétrica y otras (Borgman, 2004), que facilitan tratar estos escollos. Dentro de la modelación no paramétrica podría referenciarse también el uso de distribuciones multinomiales. Estas se construyen de acuerdo con los datos de una determinada muestra, de tal forma que no se tiene que asumir un modelo estándar de probabilidad. Puede referenciarse también el método de las cajas de probabilidad, que se identifica como una combinación de la teoría de la probabilidad y el análisis de intervalos: la incertidumbre se expresa a través de dos distribuciones de probabilidad acumuladas de borde que definen o delimitan todo un conjunto de modelos de probabilidad; de esta forma los fenómenos no paramétricos y no estacionarios pueden ser analizados por un conjunto o familias de modelos.
De lo anterior pueden denotarse inicialmente dos condiciones de incertidumbre habitualmente presentes: la ausencia de datos representativos y el problema de adoptar modelos de probabilidad estándar, lo que en su conjunto es referido como incertidumbre epistemológica (Bogardi y Duckstein, 2003). Debe anotarse adicionalmente otra forma de incertidumbre epistemológica y es la que corresponde a la ocurrencia de ambigüedad entre piezas o paquetes de información a partir de las cuales se construyen los modelos de probabilidad: en un programa de muestreo ampliado, es decir de varias muestras, pueden resultar varios patrones aleatorios, cuya incidencia debe ser considerada en la estimación de la incertidumbre y en la toma de decisiones.
De este modo, es posible plantear que las herramientas que se describen a continuación permiten tratar en parte las incertidumbres identificadas, lo cual será objeto de revisión en la construcción del modelo de distribución de excedencias de lluvia propuesto.
Distribuciones multinomiales de probabilidad
Si un vector de probabilidades p = (p1, p2,...., pk) caracteriza una distribución de probabilidad desconocida de una variable X en el vector de clases o grados de libertad Ω = {ω1, ω2,..., ωk} donde cada pi = px({ωk}) > 0 es la probabilidad de ocurrencia de la clase i y con la condición de que Σpi = 1, y si igualmente, el vector n = (n1, n2,....,nk) es una distribución de eventos relacionados a un vector de clases Ω en donde ni denota el número de observaciones que se asignan a la clase ωl y en la cual nk denota el número de observaciones para cada ωk en una muestra aleatoria de tamaño N; en general una variable X puede ser representada mediante una distribución multinomial, si se hace equivaler el vector de probabilidades p al vector de frecuencias observadas f = (f1, f2,..., fk), estimando cada fk como fk= ni/N. Con lo anterior se asume, entonces, que f es el vector que define las propiedades de la población (Masson y Denoeux, 2006).
Lo que se propone en este papel, y siendo consonantes con las ideas de Masson y Denoeux (2006), es que si X es una variable aleatoria hidrológica se considera factible que se represente mediante una función de probabilidad del tipo multinomial como la que se describe. En la Figura 1 se representan esquemáticamente una distribución multinomial y sus parámetros.
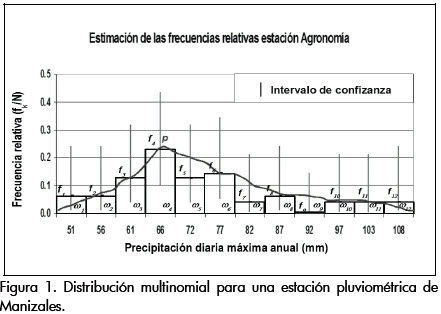
Intervalos de confianza
En la inferencia estadística se producen estimaciones de parámetros o estadísticas, como la media, la desviación estándar o una proporción de una población, a partir de las propiedades de muestras o subconjuntos de una población. Los intervalos, conjuntos de valores acotados por un par de valores extremos, son empleados en la inferencia para estimar parámetros de una población mediante intervalos de confianza definidos en un nivel de confianza 1-α. Dichos conjuntos definen los valores más esperados que se pueden estimar de un parámetro estadístico, ya que se pueden obtener diferentes valores de una estadística cuando se hacen estimaciones de diferentes muestras. Así, 1-α es la probabilidad de que el valor del parámetro se halle dentro del intervalo de estimación. A diferencia de una estimación puntual (de un único valor) de una estadística, los intervalos de confianza indican los contenidos de incertidumbre que se tienen en su estimación de acuerdo con el número de evidencias o tamaño de la muestra y su dispersión o variabilidad. De este modo un intervalo de confianza Ψ, puede definirse como:
Donde E es una estadística o parámetro de una población, ε_ ψ ε← son el valor extremo inferior y el valor extremo superior respectivamente que acotan el conjunto de valores posibles o más esperados ε para estimar E a un nivel de confianza 1-α
En este trabajo, los intervalos de confianza permitirán definir la incertidumbre en la estimación de las frecuencias relativas o proporciones de las distribuciones multinomiales.
Cajas de probabilidad (probability boxes)
De acuerdo con Ferson et al. (2003), si X es una variable aleatoria que se distribuye en Ω pueden obtenerse un par de funciones de distribución acumuladas F¯ y F_, tal que F: R → [ 0, 1] y que F_ (x) ≤ F¯(x) para todo x ∈ R. El intervalo [F_ y F¯], conocido como caja de probabilidad de una distribución F, es definido por un conjunto de funciones no decrecientes tal que F_ (x) ≤ F(x) ≤ F¯(x) y representa a un conjunto de funciones de probabilidad no bien conocidas F, excepto por las funciones F_ (x) y F¯ (x). F_ (x) es la función límite inferior del conjunto de funciones F(x) y así mismo F_(x) es la función límite superior del conjunto de funciones F(x), con la condición de que:
La Figura 2 muestra una caja de probabilidad.
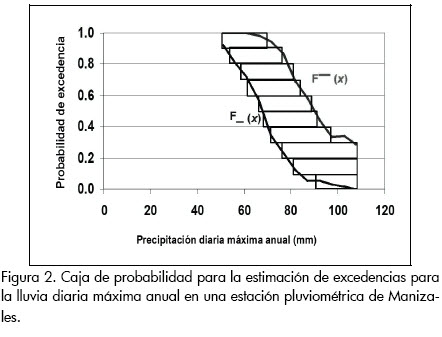
Como se menciona antes, la técnica de las cajas de probabilidad puede identificarse como una combinación de la teoría de la probabilidad y el análisis de intervalos: la incertidumbre se expresa a través de dos distribuciones de probabilidad acumuladas de borde que definen todo un conjunto de modelos de probabilidad. De otra forma, puede definirse un vector P de probabilidades asociado a un conjunto de variables expresadas en intervalos.
Siguiendo esta última idea, puede igualmente establecerse:
Si F(x) es una función de distribución acumulada en la que ∀ x ∈ R y donde F(x) es un función f(x,P), donde P = (P1, P2,...., Pn) es un vector de parámetros que definen la probabilidad acumulada para cada x, puede especificarse que cada Pi en P sea un intervalo cerrado [Pi_, Pi¯] y en conjunto establezcan a F_ (x) y F¯ (x).
El cómputo de F_ (x) y F¯ (x) debe no sólo considerar la incertidumbre debida a la estimación de las frecuencias relativas de la distribución multinomial, según el número de evidencias disponibles y los grados de libertad, sino la precisión misma de la distribución. Una determinada distribución discreta, como las que se pueden definir muestralmente, está asociada a un parámetro de precisión δ que define la extensión uniforme de las clases o grados de libertad ωk de la distribución. La medición de incertidumbre referida a una precisión δ se estima tradicionalmente como ν = ±δ /2, pero siendo que este caso específico se refiere a una distribución discreta (es decir, de precisión irreductible) de probabilidad asociada a una variable X, el módulo de incertidumbre ν debe ser igual al índice de precisión de la distribución δ y por lo tanto ν= ±δ En este caso, adaptando a Hall y Lawry (2004), se define un modelo simple y aproximado de cajas de probabilidad si se establece un intervalo [xi-1, xi+1] tal que F¯(xi) = Pi+1 y F_ (xi) = Pi-1, cuando F(xi) = Pi, donde xi-1= xi-δ y xi+1 = xi+δ. Lo anterior se describe esquemáticamente en la Figura 3. En los escritos de Williamson y Downs (1990) se hallan otros algoritmos para la estimación de las funciones de probabilidad de borde. Los detalles y refinamientos de la estimación de cajas de probabilidad pueden ser consultados en Ferson et al. (2003), Ferson y Hajagos (2004) y Hall y Lawry (2004).
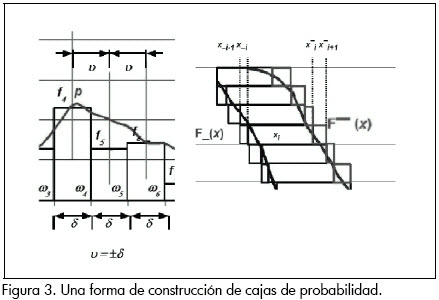
En este trabajo las cajas de probabilidad serán empleadas para representar la incertidumbre debida a la precisión de los modelos multinomiales de probabilidad.
Desarrollo del modelo de distribución de excedencias
El modelo de lluvias a desarrollar corresponde a un modelo de excedencias de lluvias diarias máximas anuales. Esta labor se dificulta porque la zona de estudio cuenta con una red pluviométrica densa pero joven, lo que quiere decir que las series históricas de registros de lluvias son cortas. Esto implica que la estimación de dichas probabilidades de excedencia no es posible ni funcional dentro del rigor estadístico, si se tienen en cuenta, entre otras, las recomendaciones de Remeneiras (1974) y Nam et al. (2005). Remeneiras (1974) señala que se requieren series históricas de registros de lluvias de una longitud superior a 20 años, mientras que Nam et al. (2005) sugieren que las series históricas deben ser de dos veces el período de retorno sobre el cual se estiman las probabilidades de excedencia. Estos requisitos no es posible suplirlos en todas las estaciones de la zona de estudio. Puede agregarse al problema la situación de que las series históricas de registros de lluvias no son uniformes y continuas, lo que obliga a emplear métodos de homogeneización de series.
Modelación
A partir de los registros de precipitaciones correspondientes a series históricas de 19 estaciones en el área de influencia de la zona de estudio (Figura 4) y con las herramientas descritas, es posible construir un modelo aproximado de probabilidaddes de excedencia. Se cuenta con series continuas y discontinuas de datos de entre seis y cuarenta y siete años. Datos más específicos de las estaciones pueden encontrarse en el documento de Chivatá (2007).
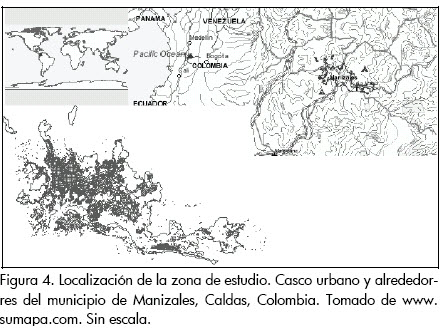
Se procedió a realizar la estimación de una distribución multinomial, para cada estación pluviométrica en la zona, dicho procedimiento se efectuó mediante el cálculo de intervalos, con un nivel de confianza del 95% para cada grado de libertad ωk en la distribución. Para tal efecto se empleó el algoritmo de Goodman (1965) presentado en Masson y Denoeux (2006), que se describe en el Cuadro 1. El algoritmo sugerido para estimar la función acumulada de probabilidad fue desarrollado por el autor de este artículo.
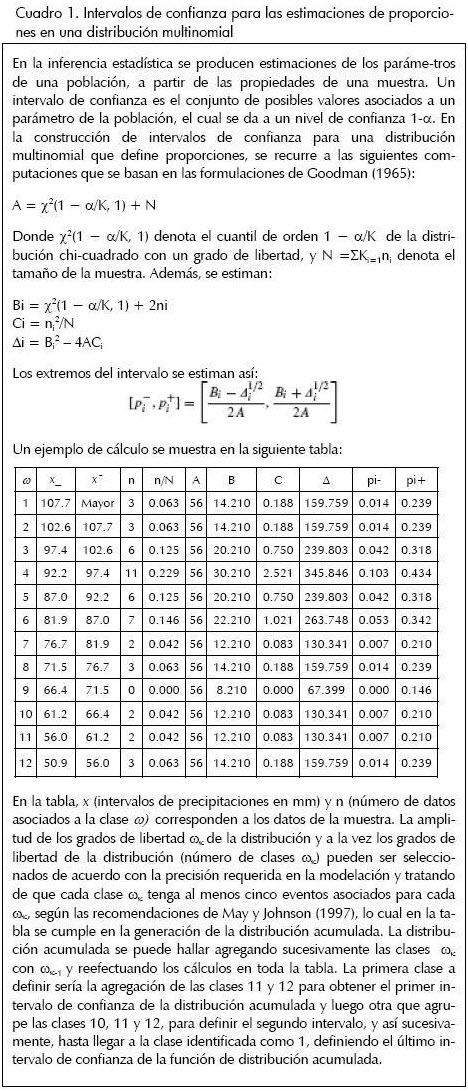
Con el algoritmo presentado en el Cuadro 1 se obtuvieron, para cada una de las estaciones, distribuciones multinomiales y de frecuencia acumulada como las que se muestran en las Figuras 5 y 6.
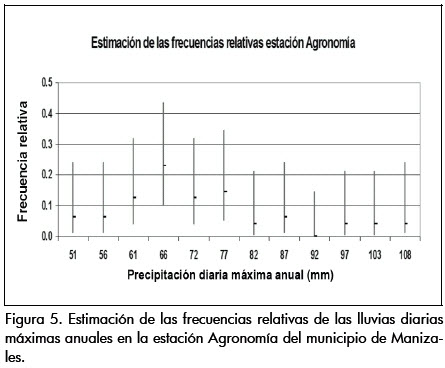
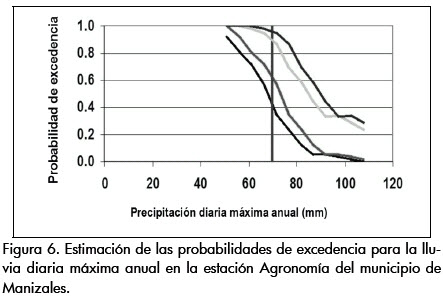
En las Figuras 5 y 6 se aprecia la incertidumbre relativa a la disponibilidad de datos. En la figura 5 existen ciertas clases en las cuales la extensión del intervalo de confianza asociado es mayor que la de otras clases, y ello se debe a que el número de eventos asociado a tal clase es reducido en comparación con las demás. De esta forma la distribución multinomial no sólo es una fiel representación de los datos de una muestra sino que también provee información sobre la incertidumbre debida a la disponibilidad de los mismos. Los intervalos de confianza estimados corresponden a la estimación más probable, creíble o esperada, de las probabilidades asociadas a un determinado grado de libertad o clase ωk en la distribución.
A partir de la generación de las distribuciones acumuladas pueden desarrollarse las cajas de probabilidad correspondientes. El propósito es incorporar la incertidumbre derivada de la ambigüedad de las piezas de información que sirven de evidencia para generar los modelos de probabilidad. En otras palabras, debe integrarse mayor incertidumbre para considerar los efectos de un muestreo reducido. Para tal efecto se estiman los intervalos [xi-1, xi+1], tal que F¯ (xi) = Pi+1 y F_( xi+1) = Pi, cuando F(xi) = Pi, donde xi-1= xi-δ y xi+1 = xi+δ, de acuerdo con lo precisado en anteriormente.
En la Figura 6, las curvas extremas definen F_ (x) y F¯(x). Estas curvas podrían identificarse con los escenarios menos creíbles, en cuanto representan los valores extremos que se pueden derivar de los datos disponibles y de la precisión de la distribución. Podrá notarse que dichas funciones de probabilidad de borde van a depender de la precisión definida para la distribución multinomial, es decir, de la amplitud δ de los grados de libertad ωk. Se deberá efectuar un estudio muy riguroso de las necesidades de precisión de la información en la toma de decisiones, pero también observar las restricciones que se registraron para el desarrollo de la función de frecuencia relativa multinomial, en cuanto al número de eventos asociados a cada grado de libertad o clase ωk, lo cual depende de la disponibilidad de información: la generación de intervalos de confianza está sujeta a las restricciones de un número mínimo de grados de libertad y de eventos asociados a cada clase ωk, lo cual incide en la definición de la resolución o precisión de las distribuciones cuyo parámetro índice es el factor δ, que a su vez define la precisión de las cajas de probabilidad ν.
Una vez computado cada juego de distribuciones en cada estación, se generó un modelo espacial continuo, para los datos de excedencia para un umbral de 70 mm. Se empleó para tal efecto el método comúnmente conocido de interpolación de distancia inversa, método que se considera apropiado dadas las condiciones de incertidumbre. En este procedimiento se empleó el sistema de información geográfica ILWIS 3.4 Open.
Resultados
Los siguientes son los mapas de distribución de las probabilidades de excedencia obtenidos (Figuras 7 a 10), para los puntos: a, que corresponde a la probabilidad mínima anual de una lluvia de exceder el umbral de 70 mm (umbral seleccionado a partir del cual se generan deslizamientos), en el escenario menos creíble a = P70= F_(70); b, correspondiente al extremo inferior del intervalo de confianza muestral para el conjunto de escenarios más esperado; c, es el extremo superior del conjunto de escenarios más esperado, y d, que corresponde a la probabilidad máxima anual de una lluvia de exceder el umbral de 70 mm, en el escenario menos creíble, es decir, d = P70= F¯(70).
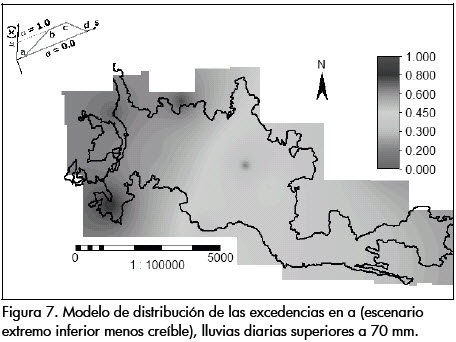
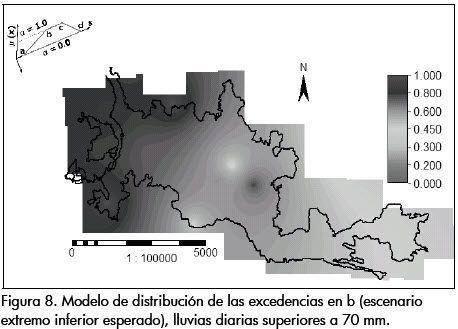
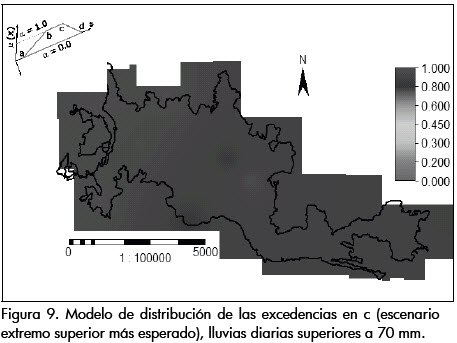
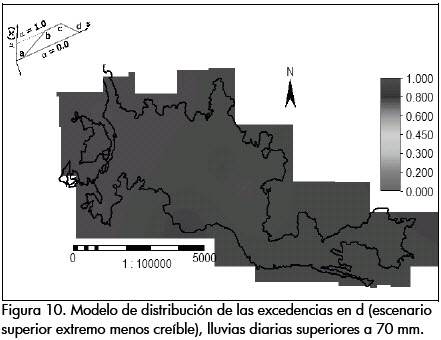
En las Figuras 7 a 10 se muestran los escenarios extremos de los posibles modelos de distribución de las probabilidades de excedencias para lluvias diarias anuales que superan el umbral de 70 mm. Se observan probabilidades de excedencia anuales superiores a 0.30 en los escenarios más creíbles.
Discusión y conclusiones
Se obtuvo un modelo distribuido de excedencias de lluvia, el cual permite establecer en cada punto del territorio de estudio la probabilidad de exceder cierto nivel de lluvias y los posibles valores de ella de acuerdo con las incertidumbres asociadas que se derivan del tamaño de las muestras, es decir, de la longitud de las series y de la falta de uniformidad y continuidad de las mismas. El modelo desarrollado permite observar los altos contenidos de incertidumbre que suceden al modelar los patrones de lluvia en la zona. La magnitud de la incertidumbre copa todo el dominio de valores de probabilidad posibles y muestra irremediablemente las altas limitaciones de información. Puede evidenciarse a la vez que una estimación puntual de las probabilidades con la información disponible puede inducir a graves errores. La información está definida por todo un conjunto de escenarios creíbles y menos creíbles, lo que permite a un determinado modelador o tomador de decisiones orientar su curso de acción en el tiempo y el territorio.
Se puede extraer información relevante del conjunto de escenarios más creíbles: se denota, por ejemplo, que el umbral de lluvia máxima diaria de 70 mm puede ser superado al menos una vez cada tres años, en toda la extensión de estudio. De igual manera, se muestra la restricción de confiar en estimaciones estadísticas de excedencias de precipitación puntuales, sin miramiento a las incertidumbres planteadas.
También se denota que la distribución de excedencias es heterogénea, observándose un patrón que indica que al occidente del territorio, las probabilidades de excedencia son mayores en todos los escenarios.
El conjunto de modelos mostrados corresponde a representaciones que sólo se derivan de los datos disponibles; se prescindió en un alto grado de asumir suposiciones, como la de asignar un modelo de probabilidad estándar, lo que puede entenderse como una mejor aproximación y una estrategia para el tratamiento de la incertidumbre, con lo que podría esperarse una mejor descripción del comportamiento de las lluvias en Manizales, a sabiendas de que el régimen de lluvias exhibe ya comportamientos no estacionarios.
Se espera haber presentado una alternativa amigable para la modelación no paramétrica y el uso de cajas de probabilidad en la estimación de modelos de excedencia de datos hidrológicos; el desarrollo de estos instrumentos cuenta ya en el contexto internacional con amplias sofisticaciones que pueden dificultar su adopción en el ámbito colombiano. Considerando lo anterior, el autor prefirió hacer uso de elementos sencillos como las distribuciones multinomiales y la estimación de intervalos de confianza, conceptos básicos de la estadística, para efectuar la modelación no paramétrica, y de las cajas de probabilidad, las cuales se consideran herramientas sencillas y de fácil aplicación dentro del conjunto de las teorías de la incertidumbre mencionadas.
De otro lado, la estimación de probabilidades imprecisas no sólo representa una alternativa para la estimación de variables hidrológicas, sino quizás un paso obligado. Su potencial radica en el manejo de información escasa, en la que se extrae la mayor información para la toma de decisiones, y como una estrategia de modelación robusta en situaciones de no estacionalidad estocástica: los modeladores esperan ansiosamente poder definir con rigor estadístico los procesos estocásticos, una vez se completen las condiciones de representatividad requeridas de las series históricas. No obstante los comportamientos no estacionarios de procesos hidrológicos y las dificultades epistemológicas, paradójica y potencialmente pueden restringir el uso de las series largas para efectuar pronósticos confiables. Por lo anterior, la estimación de probabilidades inciertas, como la que se ha propuesto, resulta ser una herramienta indispensable aun cuando se cuente con información representativa estadísticamente.
Nomenclatura
p = (p1, p2,...., pk): vector de probabilidades que caracteriza una distribución de probabilidad de una variable X, donde cada pi = px({ωk}) > 0 es la probabilidad de ocurrencia de una clase ωk y con la condición de que Σpi = 1.
Ω {ω1, ω2,..., ωk}: vector de clases o grados de libertad de una distribución de probabilidad de una variable X.
n = (n1, n2,....,nk): vector de una distribución de frecuencias multinomial, en la cual nk denota el número de observaciones para cada ωk en una muestra aleatoria de tamaño N.
f = (f1, f2,..., fk): vector de frecuencias observadas donde fk= ni/N, f es el vector que se hace equivaler al vector de probabilidades p de una distribución de probabilidad.
X: variable aleatoria hidrológica.
1-α nivel de confianza en una estimación de un intervalo en el cual se estima una estadística, o la probabilidad de que el valor del parámetro se halle dentro del intervalo de estimación.
Ψ: intervalo de confianza igual al conjunto definido por {ε| p( ε_ ≤ E ≤ ε¯) = 1-α}, donde E es una estadística o parámetro de una población, ε_ y ε¯ son el valor extremo inferior y el valor extremo superior respectivamente que acotan el conjunto de valores posibles o más esperados ε para estimar E a un nivel de confianza 1-α.
P: función de distribución acumulada de probabilidad de una variable X. P = (P1, P2,...., Pn) es un vector de parámetros que definen la probabilidad acumulada para cada xn.
F(x): función discreta de una distribución acumulada de probabilidad de una variable X.
F¯ (x): función límite superior del conjunto de funciones F(x), F¯ (x) = 1 – P (X > x).
F_(x): función límite inferior del conjunto de funciones F(x), F_(x) = P (X ≤ x).
[Pi_, Pi¯]: intervalo cerrado que define la probabilidad acumulada de xi, en P.
δ: precisión o resolución de una distribución de frecuencias. Define la extensión uniforme de las clases o grados de libertad ωi dela distribución.
ν medición de incertidumbre que se relaciona con δ.
[xi-1, xi+1]: intervalo de variables tal que xi-1= xi-δ y xi+1 = xi+δ, y que F¯ (xi) = Pi+1 y F_ ( xi+1) = Pi, cuando F(xi) = Pi,
a: corresponde a la probabilidad mínima anual de una lluvia de exceder el umbral de 70 mm, en el escenario menos creíble a = P70= F_ (70).
b: corresponde al extremo inferior del intervalo de confianza muestral de la probabilidad anual de una lluvia de exceder el umbral de 70 mm, para el conjunto de escenarios más esperado.
c: corresponde al extremo superior de la probabilidad anual de una lluvia de exceder el umbral de 70 mm, del conjunto de escenarios más esperado.
d: corresponde a la probabilidad máxima anual de una lluvia de exceder el umbral de 70 mm, en el escenario menos creíble, es decir, d = P70= F¯ (70).
Bibliografía
Almond, R. G., Discussion: Fuzzy Logic: Better Science? Or Better Engineering?, Technometrics, Vol. 37, No. 3, Disponible en http://links.jstor.org, 1995. [ Links ]
Bogardi, I., Duckstein, L., The Fuzzy Logic Paradigm of Risk Analysis., Conference Proceeding Risk-Based Decision making in Water Resources X, Reston: American Society of Civil Engineers, 2003. [ Links ]
Bogardi, I., Coping with uncertainties in flood management., Transboundary Floods: Reducing Risks Through Flood Management, The Netherlands: Springer, 2006. [ Links ]
Borgman, L., New Nonparametric Methods in Risk Analysis Based on Resampling Techniques and Empirical Simulation, Proceedings of the International Conference., Civil Engineering in the Oceans VI. Baltimore, Maryland, USA: ASCE, 2004. [ Links ]
Chivatá, I., Contribuciones para el tratamiento de la incertidumbre en la estimación de la amenaza por fenómenos de remoción en masa, Tesis, Maestría en Medio Ambiente y Desarrollo, Manizales: Universidad Nacional de Colombia., 2007. [ Links ]
Ferson, S., Kreinovich, V., Ginzburg, L., Myers, D. S., Sentz K., Constructing Probability Boxes and Dempster-Shafer Structures., Reporte SAND2002-4015. Disponible en www.sandia.gov/epistemic/Reports/SAND2002-4015.pdf, 2003. [ Links ]
Ferson, S., Hajagos, J. G., Arithmetic with uncertain numbers: rigorous and (often) best possible answers, Reliability Engineering and System Safety, Vol. 85, Elsevier Science Ltd. B.V., 2004. [ Links ]
Goodman, L. A., On simultaneous confidence intervals for multinomial proportions, Technometrics, Vol. 7, No. 2, Disponible en http://links.jstor.org, 1965. [ Links ]
Hall, J. W., Lawry, J., Generation, combination and extension of random set approximations to coherent lower and upper probabilities., Reliability Engineering and System Safety, Vol.85, Elsevier Science Ltd. B.V., 2004. [ Links ]
Masson, M. H., Denoeux, T., Inferring a possibility distribution from empirical data, Fuzzy sets and systems, Vol.157, Amsterdam: Elsevier Science Ltd. B.V., 2006. [ Links ]
May, W. L., Johnson, W. D., A SAS macro for constructing simultaneous confidence intervals for multinomial proportions., Comput. Methods Programs Biomed, Vol. 53, 1997. [ Links ]
Nam, W-S., Shin, H -J., Heo, J-H, Kim. K – D., Regional Rainfall Frequency Analysis Based on Generalized Logistic Model., Memorias de World Water and Environmental Resources Congress 2005, Anchorage-Alaska: Raymond Walton, 2005. [ Links ]
Remeneiras, G., Tratado de hidrología aplicada, Barcelona: Editores técnicos asociados. S.A., 1974. [ Links ]
Williamson, R. C., Downs, T., Probabilistic arithmetic I: numerical methods for calculating convolutions and dependency bounds., International Journal of Approximate Reasoning, Vol.4, No.2, 1990. [ Links ]














