Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.2 Bogotá May/Aug. 2008
Cecilia E. Sandoval Ruiz1, Katerine C. Velazco S.2 y José Gregorio Díaz P.3
1 Ingeniera electricista y Magíster en Ingeniería Eléctrica, Universidad de Carabobo, Venezuela. Magíster, en Ingeniería Eléctrica. Miembro del Programa de Promoción al Investigador (PPI), estudios del Doctorado en Ingeniería Eléctrica. Profesora, Universidad Nacional Experimental de las Fuerzas Armadas – UNEFA, Venezuela. cecisandova@yahoo.com
2 Ingeniera electricista, Universidad de Carabobo, Venezuela. katerinevelazco@hotmail.com
3 Ingeniero electricista, Universidad de Carabobo, Venezuela. Magíster, en Ingeniería Eléctrica. Profesor, Universidad de Carabobo, Venezuela j_g_diazp@hotmail.com
RESUMEN
Este trabajo tiene como enfoque el estudio de la optimización de los parámetros de control de la velocidad variable y el control del par de tensado del producto a través de control de corriente de los motores de corriente continua que forman parte del sistema dinámico –en una línea de producción de papel– realizando un diseño de los controladores basados en los criterios de valor absoluto y el criterio óptimo simétrico. Para ello se plantearon como objetivos la definición del modelo matemático que representa el sistema de accionamiento eléctrico para el control de la velocidad y par de los motores DC del sistema de enrollado de papel, el diseño de un algoritmo de control ajustando los parámetros necesarios y la simulación del sistema de accionamiento eléctrico. En este sentido, la metodología seguida consistió en realizar una investigación documental y un estudio de campo para definir el modelo y establecer los parámetros a simular, presentándose como un proyecto analítico y descriptivo. Los resultados obtenidos permiten observar la eficiencia de los controladores diseñados y del sistema de accionamientos en general, para el cual las variables velocidad y corriente siguen la señal de referencia, permitiendo concluir que los criterios seleccionados para el diseño del control han sido apropiados, y representando un aporte en el desarrollo de aplicaciones de control de sistemas dinámicos para accionamientos eléctricos.
Palabras clave: control óptimo, criterio calor absoluto, óptimo simétrico, motores DC.
ABSTRACT
This work was aimed at optimising control parameters for variable speed control and post-tensioning torque by controlling the current of DC motors forming part of a dynamic system (in a paper-making production line) by designing controllers based on absolute value and optimal symmetry criteria. A mathematical model representing an electric drive system for controlling DC motor speed and torque in a paper-rolling system was defined, a control algorithm adjusting the parameters was designed and an electric drive system simulated. The methodology consisted of a literature search and a field study for defining the model and establishing the parameters to be simulated, thereby presenting an analytical and descriptive project. The results led to observing the efficiency of the controllers so designed and the overall drive system for which speed and current (power) continue being the reference signal, leading to the conclusion that the criteria selected for control design were suitable and representing an input in developing applications for monitoring dynamic electric drive systems.
Keywords: optimal control, absolute value criteria, symmetric optimum, DC motor.
Recibido: febrero 23 de 2008
Aceptado: junio 27 de 2008
Introducción
La dinámica que caracteriza el proceso de una línea de producción de papel tiene un nivel de complejidad tal, que ha centrado la atención de investigadores en la materia (Asea, s/ f). A través de la investigación se pudo notar que en la mayoría de las industrias papeleras aún mantienen implementados los accionamientos neumáticos tradicionales.
En la presente investigación se estudian los criterios de optimización de parámetros para la automatización de un proceso a través de accionamientos eléctricos, en el cual se controla velocidad y tensión mecánica de una lámina de papel, a través de tres motores DC, el método seleccionado para el control de los motores será el de control óptimo aplicado a sistemas dinámicos.
La búsqueda de soluciones radica en mejorar el diseño, lograr predecir el comportamiento ante las limitaciones que presenta el aumento o disminución de la velocidad y del par de los motores sobre el tensado del papel, a fin de obtener las condiciones óptimas para el mejor funcionamiento del accionamiento, por lo que se desarrolla un modelo matemático que represente detalladamente el comportamiento del sistema.
El problema de la aplicación de control óptimo se reduce a identificar los parámetros del proceso a optimizar de acuerdo con el modelo matemático de cada etapa modelada, y obtener a través de estos los coeficientes para el diseño de los controladores (Sandoval y Velazco, 2002). Bajo en esta premisa se efectúo el desarrollo teórico necesario para el diseño del control óptimo del proceso de una planta rebobinadora de papel (donde los parámetros de la carga son variables).
Por medio de la optimización paramétrica pueden determinarse los parámetros más apropiados para un sistema de control, lo que asegura que el sistema satisface todos los requisitos con respecto a los índices estáticos y dinámicos de desempeño que caracterizan su comportamiento.
Basados en la documentación presentada en Szklarski y otros, donde se exhibe un desarrollo teórico de control óptimo, se aplicaron los criterios óptimos de valor absoluto y simétrico para el diseño de los controladores del sistema de accionamiento de la planta rebobinadora de papel; se establecieron los modelos de la carga, los componentes del sistema de accionamiento, a partir de los cuales se obtuvieron los parámetros de los controladores; y finalmente se realizó la simulación en Matlab/Simulink para verificar la efectividad del diseño del control automático del sistema dinámico particular de esta aplicación.
En el diseño de los controladores se comienza por el lazo más profundo y más rápido (lazo de corriente) y luego el exterior y más lento (lazo de velocidad).
La razón para proceder del lazo interno al externo en el proceso de diseño es que se resuelven las ganancias y constantes de tiempo de solo un controlador a la vez, en lugar de resolver las ganancias y constantes de tiempo de todos los controladores simultáneamente. No sólo es lógico, también tiene una implicación práctica. Nótese que no todo accionamiento de motores requiere control de velocidad, pero sí puede controlarse el par del motor, como es el caso de una aplicación de control de tracción, en donde el lazo de corriente es esencial y existe sin tener en cuenta si el de velocidad va a ser cerrado.
Adicionalmente, la actuación del lazo exterior es dependiente del interno; por consiguiente, la afinación del lazo interno tiene que preceder en el diseño y luego calibrarse el lazo externo. De esa manera, la dinámica del lazo interno puede simplificarse y el impacto de su actuación en el lazo externo podría minimizarse (Szklarski, 1996).
Este trabajo plantea la simulación y verificación de la respuesta de las señales de velocidad y corriente que maneja el par de tensado de la rebobinadora, en el sistema de accionamiento de la planta rebobinadora de papel, a fin de establecer su efectividad y aplicabilidad en procesos de esta índole a nivel industrial.
Para ilustrar los objetivos logrados se desarrolla el presente artículo en una sección de desarrollo teórico-matemático, seguida de una descripción detallada del diseño, análisis de los resultados de la simulación y conclusiones derivadas del uso de control óptimo para el sistema de accionamiento.
Optimización paramétrica y control óptimo
Para escoger los parámetros de un sistema de control deben usarse índices de calidad íntegro-diferencial; es, en otras palabras, un criterio de optimización (Szklarski, 1996). Estos índices deben relacionarse con todas las propiedades del sistema.
Los problemas de control óptimo consisten en determinar la estrategia de control para cada sistema y cuál satisface mejor sus objetivos, entendiendo como tales los valores de un cierto criterio óptimo (índice de calidad o función objetiva). Un sistema que logra un control óptimo se llama sistema óptimo.
Este método de control se aplica en procesos dinámicos, es decir, este es idóneo en el diseño del accionamiento eléctrico de un sistema dinámico como el de la rebobinadora de papel, ya que en régimen de operación se tienen parámetros variables del proceso (inercia de las bobinas de carga). Para obtener la optimización de los parámetros usualmente se escoge una de las formas del criterio de la integral, bien sea integral del error al cuadrado, integral del error e integral del valor absoluto del error (Krishnan, 2001). En aquellos sistemas donde la señal de salida y la regulación del error presentan oscilación en el transitorio, se aplica el criterio de la integral del error al cuadrado. Los sistemas optimizados con respecto a este índice de calidad se caracterizan por presentar oscilaciones, pero puede obtenerse un menor overshoot. Basándose en este índice de calidad se deriva el criterio óptimo del valor absoluto y simétrico.
Finalmente, el control óptimo se debe determinar como una función de un vector de estado y tiempo que permitan su aplicación en un sistema del lazo cerrado, a este se le conoce como síntesis de un control óptimo o síntesis de un sistema de control óptimo (Krishnan, 2001). En la presencia de perturbaciones estos problemas presentan mayor dificultad.
Criterio óptimo del valor absoluto
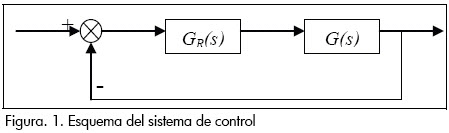
El criterio óptimo del valor absoluto surge durante el proceso de diseñar las características de fase y de amplitud (que determinan la función de transferencia) para un sistema de control de lazo cerrado. Podemos considerar un sistema de control elemental como el mostrado en la Figura 1. El paso directo del sistema consiste en un controlador de función de transferencia GR(s) y un sistema controlado de función de transferencia G(s).
Para el sistema de lazo abierto la función de transferencia del circuito principal es:
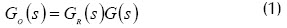
Por consiguiente, la función de transferencia GC(s) de lazo cerrado es:

Como la función de transferencia GO(s) es el punto de interés se asume que:
GO(s) contiene un elemento integrador.
Para un rango de frecuencias del valor absoluto, la respuesta de frecuencia de la función de transferencia satisface la condición:

Queda sobreentendido en la asunción anterior, que el valor absoluto de la función de transferencia del sistema de lazo cerrado es aproximadamente igual a uno en un rango de frecuencia:

El rango (0, wg], en el que la condición satisface el rango de frecuencias y el sistema de control tiene propiedades de no poseer inercia, este requisito se logra cuando la función GB(s) cumple las condiciones de Whiteley:
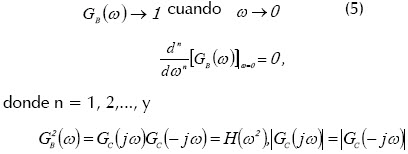
De esta manera, para ω=0, todas las derivadas impares de GB(s) son iguales a cero; sólo las derivadas pares con respecto a w pueden ser consideradas. Estas derivadas dependen de los parámetros del sistema de control. La condición (5) también puede aplicarse para la función G2B(w), y por consiguiente se cumple (6):
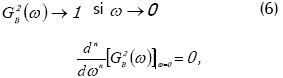
Donde n = 1,2,... La relación (5) da el criterio óptimo de valor absoluto según el cual el sistema puede ser optimizado.
Dado un sistema de lazo abierto cuya función de transferencia es:
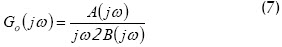
Lo cual implica que la función de transferencia que corresponde al sistema de lazo cerrado es:
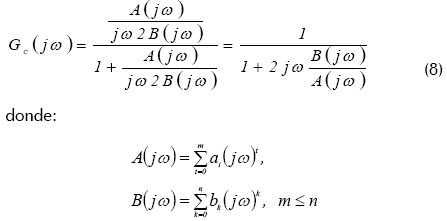
La función G2B(s) tiene la forma (9):
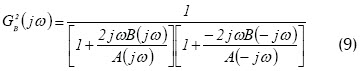
La condición (5) y (6) se satisface si el denominador es igual a uno, donde se mantiene que:
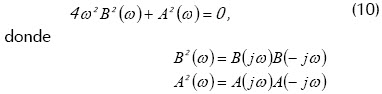
De la condición anterior podemos determinar los parámetros de un controlador tipo básico: P, PI o PID
El sistema controlado puede ser descrito por la función de transferencia:
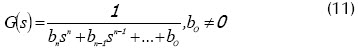
y el controlador es descrito en forma teórica por la ecuación:
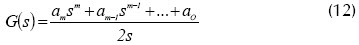
Diseño del controlador basado en el criterio óptimo del valor absoluto
Para el diseño del controlador basado en el desarrollo teórico del criterio óptimo del valor absoluto, se realizó la modelación del sistema (Sandoval y Velazco, 2002). El lazo de control de corriente (primer lazo de control a optimizar) se utiliza para limitar el valor de la corriente máxima admisible y la proporción de cambio de corriente al valor máximo admisible.
La función de transferencia del circuito principal del sistema tiene la forma:
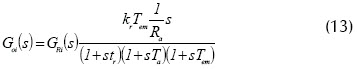
Luego la función de transferencia tiene la forma (14):
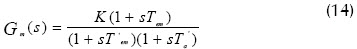
Un sistema que es óptimo según el criterio óptimo del valor absoluto con respecto a la señal del mando no es, en general, óptimo con respecto a perturbaciones del par. Por consiguiente, en cada caso tenemos que decidir el objetivo de la optimización: el arranque óptimo de un sistema sin carga o conducta óptima bajo perturbaciones del par. La decisión depende de la frecuencia de arranque del sistema y de la frecuencia de los cambios de carga. Normalmente, se perfecciona el sistema con respecto a perturbaciones (principalmente las del par de carga) usando el criterio óptimo simétrico, y con respecto al control de señales usando el criterio mínimo del valor absoluto.
Si la señal de salida de un motor bajo una señal escalón a la entrada no oscila, por ejemplo si la condición Tem >> 4Ta se satisface, entonces el diagrama de bloques del motor puede representarse como una cascada de dos elementos del primer orden. Entonces, el denominador de la función de transferencia de voltaje-corriente del motor tiene la forma:
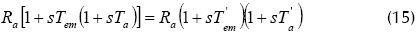
Criterio óptimo simétrico
En esta sección se considerará un caso donde el sistema de regulación es de tipo integrativo. Aquí no es posible compensar la constante de tiempo dominante, en régimen permanente debido a que esto puede causar inestabilidad en el sistema de regulación.
En efecto, se asumirá que el sistema estudiado consiste en una parte integral y una parte no periódica de primer orden y que seleccionaremos un controlador PI (Szklarski, 1996). La función de transferencia del sistema en este caso corresponde con:
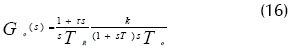

La función de transferencia del sistema en lazo cerrado está dada por:
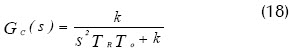
Entonces los componentes libres de la ecuación de movimiento está dada:

Dado por la expresión:
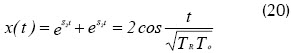
La cual describe los armónicos de las oscilaciones libres. Ahora tenemos que el sistema bajo consideración debe ser optimizado usando otro método.
La optimización de acuerdo al criterio del valor absoluto es conveniente en sistemas que se caracterizan por ser significativamente amortiguados y por desiguales valores del error en régimen permanente con respecto al control y a las señales de perturbación (Szklarski, 1996).
Considerando ahora el segundo criterio propuesto por Kessler, El criterio óptimo simétrico:
Dado el sistema controlado cuya función de transferencia G(s) ha sido caracterizado por N constantes de tiempo grandes Tv (v=1, 2,...N) y M constantes de tiempo pequeñas el tµ (µ= 1.2....,M). Donde cada constante de tiempo grande es significativamente mayor que la suma de las constantes de tiempo pequeñas.
Entonces la función de transferencia puede representarse por:
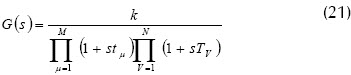
Ignorando el producto de constantes de tiempo pequeñas, obtenemos:
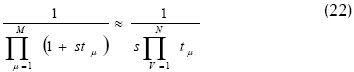
Al asumir que el regulador escogido para el sistema (en estudio) es descrito por la siguiente función de transferencia
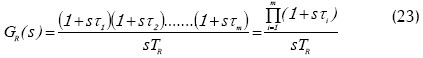
donde para tµ muy pequeños, obtenemos:
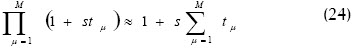
Y la función de transferencia del sistema se reduce a
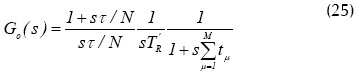
Consecuentemente, la función de transferencia de lazo cerrado del sistema viene dada por
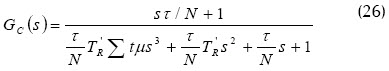
Diseño del controlador basado en el criterio óptimo simétrico
Despejando el valor de la constante de tiempo del sistema –de control del convertidor TR– de la condición expuesta en el desarrollo teórico del método de optimización simétrico (Sandoval y Velazco, 2002), obtenemos:
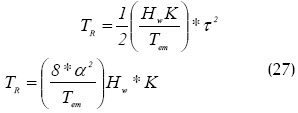
La parte real de los polos es negativa, y no hay ningún polo repetido en el origen, por lo que el sistema será asintóticamente estable. Entonces, en el diseño óptimo simétrico la estabilidad del sistema se garantiza.
El método óptimo simétrico elimina muy rápidamente los efectos debidos a las perturbaciones, comparado con otras técnicas óptimas empleadas en sistemas prácticos, tales como la lineal o de valor absoluto óptimo. Esta aproximación indica uno de los posibles métodos para sintetizar al controlador de velocidad.
La opción más acertada de aproximación se basa en las constantes físicas del motor, del convertidor y el transductor; las ganancias, y los retrasos de tiempos.
La función de transferencia del sistema en lazo cerrado es:
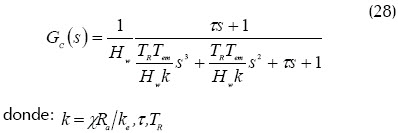
donde:
Los cuales son los parámetros del controlador PI, cuya función de transferencia está dada por: 1 + sτ/sTR
La función de transferencia puede ser representada por 1/kωG'c(s), donde se escogieron los parámetros τ y Tr del controlador según el criterio óptimo simétrico.
Resultados de la implementación de los controladores diseñados a través de control óptimo
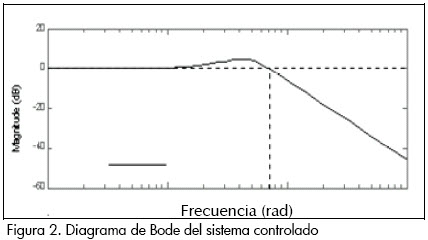
La respuesta del controlador en el sistema dinámico cumplió con las condiciones establecidas para el diseño, lo que demuestra la efectividad del control automático diseñado; el diagrama de Bode es el mostrado en la Figura 2, donde se muestra el valor de la frecuencia característica del sistema optimizado, el cual corresponde a 0.7088 rad/seg.
En las simulaciones realizadas se encontró que las señales controladas siguen a las respectivas referencias de modo satisfactorio, cumpliendo las condiciones del proceso de velocidad tangencial constante y par de tensado igual en todos los puntos del sistema, para preservar las condiciones de la lámina de producto (en este caso papel).
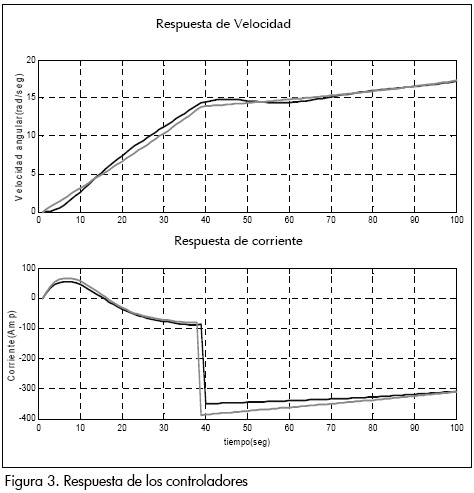
En la Figura 3 se muestra el comportamiento de los controladores de velocidad angular (rad/seg) para una de las etapas del sistema, al mismo tiempo se observa el comportamiento de la corriente del motor de accionamiento de la bobina, el cual corresponde al lazo interno de control diseñado en la sección anterior. Como se puede ver la respuesta de la señal controlada es satisfactoria, demostrando que los criterios seleccionados optimizan el sistema de accionamiento eléctrico diseñado.
Conclusión
A partir de los modelos planteados del proceso de embobinado de papel (Sandoval y Velazco, 2002) que sirvieron como base para el establecimiento de las características y parámetros en la modelación del sistema, a la hora de seleccionar el método idóneo para el diseño y cálculo de los parámetros de los controladores de velocidad y tensión mecánica se escogió el de control óptimo, para lo cual se realizó este estudio de carácter teórico sobre las bases y criterios del método de control y a través de las cuales se optimizó el proceso, empleando un modelo linealizado del sistema.
Se realizó el enfoque particular al proceso de la línea de producción de papel, donde previa modelación (Sandoval y Velazco, 2002) se sustituyen los parámetros del proceso y se efectúa el diseño óptimo de los controladores.
Se obtuvieron los resultados esperados de acuerdo a la respuesta en frecuencia y velocidad teóricos (Krishnan, 2001), (Y. Hou, s/f), con lo que se obtuvo un control satisfactorio de las variables de velocidad y tensión mecánica sobre el papel.
Es de hacer notar que se trabajó con tres motores, accionados automáticamente, haciendo uso de seis controladores; de acuerdo a las características de cada variable a controlar, se tomó el criterio óptimo apropiado, según las características de la variable a controlar: criterio óptimo de valor absoluto para variables rápidas, donde se requiere gran exactitud; criterio óptimo simétrico en variables lentas; donde no se puede compensar la constante de tiempo dominante, se diseña para los parámetros promedios del sistema de modo que el controlador responda de manera simétrica en el entorno de los valores de diseño.
Como una herramienta adicional para la simulación de sistemas dinámicos con características de carga variable, como el caso tratado en esta investigación, se realizó un programa para el cálculo de los valores de los controladores del proceso, basados en control óptimo, lo cual representa una alternativa versátil para los procesos de embobinado de material, al mismo tiempo se creó la interfase gráfica que permite simular estos sistemas de manera directa, con los parámetros específicos del sistema de interés.
Bibliografía
ASEA Industry., Drive systems for winders supercalanders and coatin machines., AP 41-103 E, Edition 1. [ Links ]
ASEA Industry., Speed-Controlled drive system with DC motor., ASEA DRIVES A 07-7001 E, Edition 1 [ Links ]
Hou, Y., Gao, Z., Jiang, F., Boulter, B. T., Active Disturbance Rejection Control for Web Tension Regulation Department of Electrical and Computer Engineering Cleveland State University., Cleveland Ohio, 44115. [ Links ]
Krishnan. R., Electric motor drives., Prentice Hall, 2001. [ Links ]
Sandoval, C., Velazco, K., Simulación en ambiente Matlab/ Simulink del control automático de velocidad y par de tensado de una planta rebobinadora de papel., Revista Ingeniería UC, Vol.9, No. 2. Dic. 2002, pp. 42-47. [ Links ]
Szklarski, L, Jaracz, K, Y., Horodecki, A, Electric drive system dynamics., 1996. [ Links ]














