Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.2 Bogotá May/Aug. 2008
Juan Carlos Osorio Gómez1, Oscar Eduardo Castrillón Montenegro2, Juliana Andrea Toro Cardona3 y Juan Pablo Orejuela Cabrera4
1 Ingeniero industrial, Especialista en Logística y Magíster en Ingeniería, Universidad del Valle, Colombia. Profesor Asistente, Escuela de Ingeniería Industrial y Estadística, Universidad del Valle, josorio@pino.univalle.edu.co, juancarosorio@yahoo.es
2 Ingeniero industrial, Universidad del Valle, Colombia. oscastrillon@gmail.com
3 Ingeniera industrial, Universidad del Valle, Colombia. Ingeniera de Mejoramiento, Industrias Kraft. ing.julianatoro@gmail.com
4 Ingeniero industrial, Especialista en Logística y Magíster en Ingeniería, Universidad del Valle, Colombia. Profesor Auxiliar, Escuela de Ingeniería Industrial y Estadística, Universidad del Valle, Colombia. juanp77@pino.univalle.edu.co
RESUMEN
La planificación y control de la producción es reconocida como un problema complejo dentro de las organizaciones. El enfoque jerárquico para la planificación y control de la producción es una aproximación a este problema, que se caracteriza por su capacidad de disminuir la complejidad y lograr buenas soluciones con economías de tiempo y requerimientos computacionales. En este artículo se presenta una propuesta jerárquica para resolver el problema de programación de la producción en una configuración productiva del tipo job shop flexible, incluyendo interrupciones y tiempos de alistamiento dependientes de la secuencia. La solución propuesta, sin llegar a ser óptima, dada la clasificación NP-hard del problema referido, es una buena solución tal como se demuestra en su validación, en la cual se resuelve un problema de 6 trabajos en 6 máquinas con 13 operaciones, obteniéndose un valor de makespan de 183.67, que comparado con el valor de 214 obtenido mediante un reconocido software para scheduling, mostró ser una buena solución.
Palabras clave: planificación jerárquica, programación de producción, interrupciones, tiempos de alistamiento dependientes de la secuencia, máquinas paralelas.
ABSTRACT
Production planning and control are complex problems for manufacturing organisations. Hierarchical production planning and control is one way to address the problem as it can reduce its complexity and reach good solutions in reasonable computational time. This paper presents a hierarchical approach to resolving production programming in a flexible job shop configuration; this problem includes preemption and sequence-dependent setup times. Although non-optimal (as expected), good solutions were obtained as shown in the validation of the method.
Keywords: hierarchical planning, production programming, preemption, sequence-dependent setup time, parallel machines.
Recibido: enero 31 de 2008
Aceptado: julio 1 de 2008
Introducción
Tradicionalmente se ha considerado que la gestión de las operaciones está enfocada en el logro de objetivos aparentemente en conflicto tales como la satisfacción de los clientes, el control de los inventarios y la utilización de los recursos, lo que ha llevado al desarrollo de técnicas que permitan obtener una planificación y programación de las actividades de producción.
Una de estas técnicas es el denominado enfoque jerárquico para la planificación de la producción. Este considera el problema de la planificación descomponiéndolo en subproblemas interrelacionados de manera tal que al resolver estos se obtiene la solución al problema original, buscando disminuir la complejidad de su manejo y ganar velocidad de procesamiento, junto con menores exigencias desde el punto de vista computacional, que si se abordara el problema total.
Existen también diferentes sistemas de producción de acuerdo con el flujo de los productos o los procesos. Entre ellos se pueden mencionar: sistemas continuos y sistemas intermitentes de fabricación, entre los últimos podemos encontrar los sistemas flow shop o fabricación en línea y los job shop, o taller de tareas. Dichos sistemas son considerados altamente complejos para la programación de las operaciones que se llevan a cabo en ellos. Esta complejidad es objeto de permanente estudio por parte de expertos tanto desde el punto de vista académico como práctico.
Entre los sistemas job shop existe el denominado job shop flexible, el cual tiene como característica adicional que las diferentes operaciones pueden ser procesadas en cualquier máquina de un conjunto de ellas existente en el taller (problema de máquinas paralelas).
A continuación se presenta una discusión inicial sobre la planificación jerárquica, señalando los principales trabajos publicados al respecto. Igualmente, se define el problema del job shop flexible, y particularmente se trata lo relacionado con su programación. Finalmente se presenta una propuesta original sobre cómo abordar este problema desde la planificación jerárquica, incluyendo en él la posibilidad de interrupciones en las operaciones y la existencia de tiempos de alistamiento dependientes de la secuencia de la programación.
La planificación jerárquica de la producción
El problema de la planificación de la producción reviste un carácter complejo dada la cantidad de elementos que involucra y las múltiples interrelaciones existentes entre ellos; esto ha hecho que en torno a la solución del mismo hayan sido desarrollados gran cantidad de trabajos. Entre otros se cuentan algunos derivados de la práctica, son de carácter eminentemente académico, y como un punto intermedio surge una corriente relativamente nueva con un grado de desarrollo importante en los últimos años y que se apoya en una visión jerárquica del sistema objeto de trabajo. Tal aproximación, denominada planificación jerárquica de la producción (Hierarchical Production Planning), reconoce en el sistema de gestión de la producción diversos niveles u horizontes con problemas de decisión particulares, con un manejo agregado del tiempo y de los datos de las diversas entidades identificables, y con la exigencia fundamental de lograr sinergia entre las diferentes decisiones que se toman en el sistema (Motoa y otros, 2007).
Los primeros trabajos que abordaron el problema de la planificación de la producción desde la perspectiva jerárquica son los desarrollados por Hax y Meal (Hax y Meal, 1975). Después se presentaron otros que los complementaban, especialmente en lo referente a la agregación y desagregación y al ambiente de manufactura específico (Bitran y Hax, 1977; Bitran y otros, 1981; Bitran y otros, 1982); pero alrededor de la conceptualización y el sustento teórico del enfoque solamente aparecen investigaciones serias al respecto cuando Schneeweiss (Schneeweiss, 1995) presenta una estructura sólida y coherente de los modelos jerárquicos en las organizaciones, llevando su enfoque al contexto de los modelos de toma decisiones distribuidas y a los modelos de soporte a la toma de las mismas.
En un trabajo posterior, Schneeweiss (Schneeweiss, 2003) desarrolla de manera más amplia los elementos del sistema jerárquico, presentando una propuesta frente a uno de los aspectos más importantes, la anticipación, la cual es considerada como uno de los principales conceptos que define el fenómeno de la jerarquía, y de la que pueden distinguirse cuatro tipos: anticipación perfecta, perfecta aproximada, implícita y la no reactiva.
Dentro de las aplicaciones en sistemas de producción más recientes se pueden comentar las presentadas en (Karumanasseri y Abourizk, 2002;, Respicio y otros, 2002; Tisher y Carrión, 2003; Tsubone y otros, 2002; Yan, 2003; Yan y otros,2004). Todos estos trabajos son aplicados en ambientes reales de manufactura y sustentados especialmente por la modelación matemática.
Los ambientes job shop y el problema del job shop flexible
En el problema específico del job shop se tiene que hay un conjunto de trabajos y otro de máquinas. Cada trabajo consiste en una secuencia de operaciones, las cuales se realizan en una de las máquinas durante un tiempo definido (tiempo de procesamiento). Cada máquina lleva a cabo solamente una operación a la vez. Un programa entonces, consiste en definir los tiempos de inicio y fin de las actividades con sus respectivos recursos, de manera que el problema es encontrar el programa que satisfaga el criterio establecido, el cual generalmente está asociado con la terminación de las operaciones de todos los trabajos en el menor tiempo posible. Los criterios más comunes mediante los cuales se valoran los objetivos de utilizar de la mejor manera posible los recursos y prestarle el mejor servicio al cliente en la programación de un job shop incluyen minimizar los valores máximo y medio del tiempo de flujo, del tiempo de finalización (makespan), del retraso (lateness), y de la tardanza (tardiness) y minimizar el número de trabajos retrasados (Domínguez Machuca y otros, 1995). Si estos no se consideran con igual importancia, puede encontrarse un valor ponderado aplicando un factor de ponderación propio para cada uno (Jain y Meeran, 1998).
La dimensionalidad del problema del job shop viene dada por n x m, siendo n el número de trabajos y m el número de máquinas, de tal manera que se tienen al menos (n!)m posibles soluciones, generándose una explosión combinatoria al crecer n y m. El crecimiento exponencial del número de posibles soluciones hace que este problema sea reconocido como NP – hard (Sipper y Bulfin, 1998). La completa enumeración de todas estas posibilidades para identificar el programa óptimo no es práctico y supremamente demandante de recursos de computación.
Por su parte, el problema del job shop flexible (Flexible job shop scheduling Problem – FJSSP) es considerado como una variante del problema del job shop original, aunque tratado en la literatura de una manera mucho menor, siendo más complejo que el del job shop debido a la necesidad de asignar las operaciones a las máquinas (Sotskov y Shakhlevich, 1995).
Generalmente se consideran dos pasos para la solución del FJSSP: primero, asignar las tareas a los recursos, y después, secuenciarlas de acuerdo con la asignación realizada en el primer paso, lo que algunos autores han denominado equivocadamente modelos jerárquicos (Brandimarte y Calderini, 1995, Xia y Wu, 2005). Este enfoque debe entenderse como un modelo de planificación por niveles, que resultaría jerárquico sólo en la medida en que contemplase algún tipo de agregación. Así como está planteado, en el primer nivel se hace la asignación de tareas a máquinas, y en el segundo, se secuencian las tareas en cada máquina. También existen trabajos donde se busca resolver el problema de asignación y secuenciación en un solo paso. A estos modelos suele llamárseles monolíticos, y se caracterizan fundamentalmente por incluir modelación matemática de gran complejidad no sólo en su formulación, sino principalmente en su solución (Kacem y otros, 2002; Kacem, 2003; Rigao y otros, 2004;, Zribi y otros, 2004;, Ho y Tay, 2005; Torabi y otros, 2005; Tanev y otros, 2004).
Respecto a los enfoques presentados como jerárquicos, podría decirse que existe registro sobre un trabajo que utiliza el jerárquico para la solución de un job shop que aunque no es presentado como flexible, claramente lo es (Bradley y otros, 1977). El problema en concreto considera un job shop naval, donde es necesario tanto la definición de los recursos de manufactura (maquinaria y personas), como el secuenciamiento de las ordenes. Los autores plantean dos niveles para la solución: uno agregado en que definen un plan agregado de producción que determina las necesidades de recursos (asignación de maquinaria y personas a las tareas) y después, con el resultado del plan agregado van al nivel inferior y mediante un modelo de simulación resuelven el problema del scheduling. Aunque este trabajo no es referenciado en los artículos actuales sobre el job shop flexible, es indudable que se trata de un antecedente importante para resolver este problema y realmente, uno de los pocos que se plantea un enfoque que se puede denominar jerárquico.
Modelo para la planificación jerárquica de la producción en un job shop flexible
El modelo busca resolver el problema mediante la definición de dos niveles, cada uno de los cuales tiene asociados diferentes problemas de toma de decisiones. Antes de presentarlos, se configura el job shop flexible considerado para el modelo.
Configuración del job shop flexible
En el modelo propuesto se consideran M máquinas (I = 1, 2, ..., M) y N trabajos (J = 1, 2, ..., N). Ahora, en el nivel superior se conforman L centros de trabajo (R = 1, 2, ..., L), cada uno conformado por m máquinas (i = 1, 2, ..., m) de tal manera que m  M. A cada centro L se le asignan n trabajos (j = 1, 2, ..., n) siendo n
M. A cada centro L se le asignan n trabajos (j = 1, 2, ..., n) siendo n  N. Cada trabajo j implica k operaciones ( o = 1, 2, ..., k) y cada operación o trabajo j tienen definido un tiempo de procesamiento en la máquina i, poji.
N. Cada trabajo j implica k operaciones ( o = 1, 2, ..., k) y cada operación o trabajo j tienen definido un tiempo de procesamiento en la máquina i, poji.
En este problema, además, se tienen las siguientes consideraciones (Castrillón y Toro, 2008):
-Todos los trabajos están disponibles para iniciar su proceso en t = 0. (fecha de liberación)
-Todas las máquinas se encuentran listas para su operación en t = 0. (Disponibilidad)
-Se considera que los tiempos de alistamiento son dependientes de la secuencia.
-Se permite la interrupción de los trabajos en las máquinas, es decir, que se puede interrumpir el proceso sin haber terminado en una máquina y pasar a otra, al reiniciar sólo se requerirá el tiempo faltante para terminar la operación (migración).
-Existe recirculación en el job shop, es decir, que un trabajo puede visitar una máquina en más de una ocasión, permitiéndose inclusive que todas las operaciones de un trabajo sean procesadas en una sola máquina.
-Una máquina no podrá procesar más de una operación al tiempo. Hasta tanto una operación no haya terminado su procesamiento o haya sido interrumpida, la máquina en la cual se esté realizando dicha operación no se podrá considerar disponible para ningún otro trabajo.
-Todos los trabajos tienen la misma prioridad dentro del sistema (el valor del peso w es igual para cada uno de ellos).
-Todas las máquinas pueden realizar todas las operaciones (flexibilidad total).
-Las máquinas que conforman el job son idénticas (paralelas), luego, los tiempos de procesamiento de las operaciones son los mismos indistintamente de la máquina en la que se lleven a cabo.
-Los tiempos de procesamiento de las operaciones son conocidos y determinísticos.
-El tiempo total de procesamiento para un trabajo j es la suma del tiempo de proceso de cada una de las operaciones que lo componen más los alistamientos.
-No se consideran tiempos de transporte para los trabajos entre una y otra máquina.
-Un trabajo solamente se considerará terminado en el momento en que sus operaciones hayan sido procesadas completamente.
La solución final consistirá en un programa detallado de producción en el cual se incluyan las operaciones que deben realizarse, especificando dónde se procesan (en qué máquinas), la existencia de interrupciones (qué tanto se procesa la operación en la máquina) y cuándo se hacen (en qué momento inician y finalizan esos procesamientos, es decir, la secuencia de trabajo), de manera que el taller tenga un grado de desempeño conveniente para un criterio específico, que en este caso será el makespan.
El problema del nivel superior
En este nivel, el problema es solamente el de la asignación de los procesos a los centros de trabajo, de manera que se minimicen los tiempos de ejecución, pero se busca también que los centros estén balanceados, esto es, que no se recargue uno solo, puesto que si esto llega a suceder, el makespan, o máximo tiempo de terminación de los trabajos, tendería a incrementarse, puesto que el centro mayor cargado sería el que determine el último tiempo de terminación; por lo tanto, lo que se debe buscar es que todos los centros tengan una carga similar y de esa manera, el tiempo de terminación de cada uno sea equivalente, para lograr un mejor valor de makespan (Osorio y Motoa, 2007).
La agregación
El modelo propuesto presenta dos tipos de agregación: el de las operaciones en trabajos y el de las máquinas en centros de trabajo.
Agregación de las operaciones en trabajos
En este sentido, se considera un trabajo con un tiempo de procesamiento equivalente a la suma de los tiempos de procesamiento de todas las operaciones que lo componen, sin contar tiempos de alistamiento o paradas en el proceso.
Agregación de máquinas en centros de trabajo
En el caso del problema que se está abordando, en el cual las máquinas son idénticas y existe flexibilidad total de operación, la agregación de las máquinas en centros puede hacerse sencillamente formando grupos de máquinas de tal forma que los centros queden tan balanceados como sea posible en cuanto al número de máquinas que los conforman y respetando las limitaciones que se presentan en el nivel inferior.
El modelo para la asignación
Para resolver el problema del nivel agregado se ha planteado un modelo de programación lineal que logra la asignación óptima de los trabajos a los centros, minimizando el tiempo total de terminación y balanceando la utilización de los mismos.
En el modelo se define una variable Z equivalente al makespan, de tal manera que
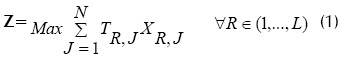
Donde TRJ son los tiempos de procesamiento del trabajo J en el centro R y XRJ es una variable binaria mediante la cual se define si el trabajo J se procesa o no en el centro R, y se busca el valor mínimo de Z mediante el siguiente modelo de programación lineal:

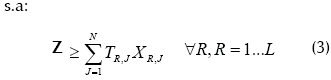
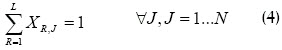

En (1) se tiene la definición del makespan, o sea, el máximo tiempo de terminación de los trabajos. Y se ha definido (2) para buscar el valor mínimo mediante un modelo de programación lineal. Las restricciones presentadas en (3) garantizan un balance de los centros de trabajo, y las de (4), que todos los trabajos sean asignados a un solo centro.
Es un modelo que genera L+N restricciones y (L*N)+1 variables, donde L es el número de centros de trabajo creados en la agregación y N el número de trabajos que deben ser programados. Es una cantidad considerablemente menor que si se abordase el problema sin agregar, y esta reducción de variables y restricciones favorece el tiempo de solución del modelo. El resultado de este, entonces, es la asignación de los trabajos a los centros, convirtiéndose en una instrucción directa para el nivel detallado.
El problema del nivel detallado
En el nivel inferior o detallado se realiza inicialmente la desagregación de los centros de trabajo en máquinas y de los trabajos en operaciones. Una vez se efectúa esta desagregación, se tienen L subproblemas similares, en los cuales debe resolverse la asignación de las operaciones que conforman los trabajos (en el nivel superior), a las máquinas que conforman el centro, y una vez resuelta la asignación, se procede a realizar el secuenciamiento de dichas operaciones en las máquinas.
El problema de asignación y secuenciación
Para este caso en particular en el que los tiempos de alistamiento son dependientes de la secuencia y se permiten los preemptions, el problema de asignación en cada centro consiste, entonces, en determinar en qué máquina serán procesadas las secciones o partes en las que pueden ser divididas las operaciones que conforman un trabajo; esta asignación es tomada como información de entrada para un modelo matemático que busca encontrar la mejor secuencia en cada máquina de tal forma que se minimice el makespan teniendo en cuenta los tiempos de alistamiento.
Para resolver este caso se va a adoptar la misma metodología utilizada por Tahar (Tahar y otros, 2006), quienes proponen, primero, reducir el problema de cada centro de trabajo a uno en el que se tiene un único recurso (single machine scheduling problem - SMSP) y transformarlo en otro tipo del viajero de negocios (TSP), teniendo en cuenta los setups dependientes de la secuencia; posteriormente se resuelve este problema y la secuencia resultante es dividida entre el número de máquinas que conforman el centro de trabajo; tal procedimiento da como resultado la asignación de secciones o partes de operaciones a las máquinas y luego, por medio de un modelo de programación lineal, se optimizan los tamaños de las mismas buscando minimizar el makespan, modelo se presenta a continuación:
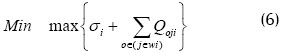
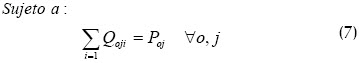
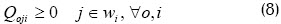
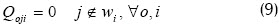
Las restricciones en (7) aseguran que la operación o del trabajo j tenga efectivamente un tiempo de procesamiento poj. Las restricciones (8) y (9) indican que el valor Qoji (tamaño de las secciones, es decir, la cantidad de la operación o del trabajo j que se realiza en la máquina i) puede ser positivo o igual a cero en el caso de que el trabajo j no haya sido asignado a la máquina i, y el valor σ es el tiempo de alistamiento total en la máquina i.
La función objetivo (6) no es lineal, pero puede linealizarse introduciendo una nueva variable C que denote el makespan. Seguidamente se muestra el modelo resultante:

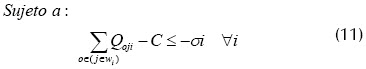

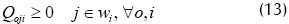
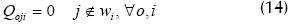
Con la nueva función objetivo (10) se garantiza el cálculo del makespan para cada máquina, incluyendo tiempos de procesamiento de las operaciones pertenecientes a los trabajos, siendo wi el conjunto de trabajos asignados a la máquina i, tiempos de alistamiento y preemptions.
Para resolver el problema se propone una adaptación al algoritmo desarrollado por Tahar (Tahar y otros, 2006). Mientras que el algoritmo original trata con trabajos, en este caso se va a tratar al nivel de operaciones. Este algoritmo debe correrse para cada uno de los centros de trabajo, como sigue:
Paso 1: Hallar el makespan C* resolviendo el problema como si se tratara de una sola máquina. El mismo puede ser reducido a un TSP y resuelto a través de un método apropiado para ello.
Paso 2: Dividir el scheduling obtenido en el paso 1 en M partes iguales. Las secciones procesadas en el intervalo de tiempo [(i-1)C* / M,iC(1) / M] son asignadas a la máquina i, siendo wi el conjunto de trabajos a ser programados en la máquina i.
Paso 3: Volver a resolver el problema del scheduling para cada máquina con los trabajos asignados a la misma como un TSP, esto se hace para encontrar la mejor secuencia en cada máquina, siendo σi los tiempos totales de alistamiento en la máquina i.
Paso 4: Resolver el modelo definido en (10) a (14) teniendo en cuenta sólo las operaciones programadas en cada conjunto wi.
El modelo del último paso tiene solución óptima sólo para problemas que no sobrepasan un total de 7 operaciones y 3 máquinas en cada centro, esto debido al gran número de variables y restricciones resultantes (Tahar y otros, 2006).
Debido a que el problema que se enfrenta en los pasos 1 y 3 del algoritmo anterior es de optimización combinatoria, se decidió dar solución al mismo por medio de un algoritmo de búsqueda tabú, con el que se pretende encontrar la mejor secuencia haciendo cambios por pares de operaciones; los pasos del algoritmo general se presentan en (Glover y Laguna, 1998).
Aplicación del modelo propuesto
Para la aplicación del modelo y validación de los resultados se crearon las instancias y se resolvieron mediante el uso del software de programación Lekin5, a efectos de comparar los resultados obtenidos.
En la Tabla 1 se muestra la información concerniente a los tiempos de procesamiento de las operaciones que conforman cada uno de los trabajos; como las máquinas son idénticas, los tiempos son los mismos en cualquiera de ellas. En la Tabla 2, se presentan los tiempos de alistamiento dependientes de la secuencia.
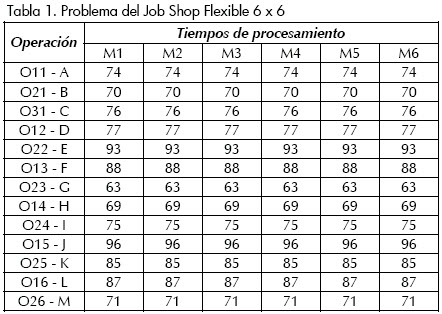
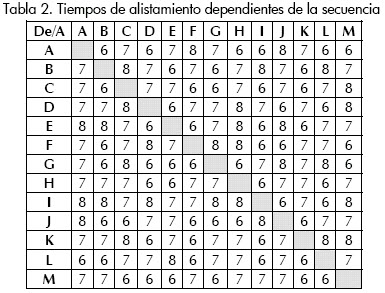
Los datos corresponden a un problema que consiste en 6 trabajos que deben programarse en 6 máquinas idénticas considerando flexibilidad total, es decir, que todos los trabajos pueden procesarse en cualquiera de ellas.
Al resolver el problema con Lekin el mejor valor encontrado para el makespan (heurística de cuello de botella móvil) fue igual a 214 u.t, esta solución se presenta en la Figura 1.
Al resolver dicho problema con el modelo planteado, se obtuvieron los siguientes resultados para la asignación de los trabajos (solución del nivel superior):
Con este resultado como entrada, se resuelve el nivel inferior, obteniéndose la solución que se aprecia en las Figuras 2 y 3, donde se evidencia que el mínimo makespan para el sistema fue de 183.67 u.t para el centro de trabajo 1 y de 180 u.t para el centro de trabajo 2.
Se ha demostrado, entonces, que el modelo funciona, y que si bien no se está hablando de una solución óptima, sí se logra una buena solución comparada con la que se obtiene por medio de un reconocido software de scheduling y con una inversión de tiempo y capacidad de procesamiento menor a las grandes y sofisticadas metaheurísticas o modelos monolíticos desarrollados en otras investigaciones.
Conclusiones y propuestas para futuros trabajos
Con respecto al enfoque jerárquico, se puede concluir, primero, que funcionó para resolver el problema del job shop flexible, lo cual es realmente significativo, más si se observa que en la literatura existente no se había planteado hasta el momento un enfoque realmente jerárquico como el propuesto, es decir, que incluyera agregación de la información en el nivel superior con respecto al inferior.
Otro elemento relevante es la efectividad del modelo al descomponer el problema en subproblemas que debido, a su tamaño, son más fáciles de resolver con métodos menos exigentes en cuanto a tiempo y requerimientos computacionales, lo cual sugiere mayor facilidad para implementación práctica.
Con respecto a la agregación, también es importante destacar la sensibilidad del modelo frente a la misma (especialmente la de las máquinas en centros), ya que aun utilizando el mismo procedimiento para agregar, en el momento que cambie una máquina de un centro a otro el resultado puede sufrir cambios importantes, por ello debe experimentarse más al respecto, de manera que se logren resultados más cercanos al óptimo mediante el refinamiento del modelo de agregación.
Una de las características particulares del modelo es la posibilidad del particionamiento de lotes; las diferentes pruebas llevadas a cabo muestran que esta condición ofrece la ventaja de hallar un perfecto balance de carga entre los centros de trabajo y las máquinas que los conforman.
Vale destacar la labor que realiza el algoritmo de búsqueda tabú, que a través del uso de estructuras de memoria logra escapar de los óptimos locales, en los que se puede caer al "moverse" de una solución a otra por el espacio de soluciones, permitiendo así obtener una secuencia de producción factible y cercana al óptimo.
A pesar de la limitante que presenta la metodología propuesta, de garantizar su solución sólo para problemas con hasta 3 máquinas y 7 operaciones, la sinergia lograda con la estructura jerárquica permite que el modelo se replique para varios centros respetando esta limitación, lo que permite que se trabaje con problemas de gran tamaño.
La estructura utilizada para abordar el problema convierte al modelo desarrollado en uno de carácter general que puede adaptarse a diferentes condiciones, convirtiéndose en una buena herramienta de solución para problemas en ambien1tes de job shop flexible.
El enfoque utilizado para resolver el problema se convierte en una base de comparación para futuras investigaciones en el tema.
5 Flexible job shop scheduling system - herramienta para resolución de problemas de scheduling.
Bibliografía
Bitran, G. R., Hax, A.C., On the design of hierarchical production planning systems., Decision Sciences, Vol. 8, No. 1, 1977, pp. 28-55. [ Links ]
Bitran, G., Hass, E., Hax, A., Hierarchical production planning: a single stage system., Operations Research, Vol. 29 No. 4, 1981, pp 717-743. [ Links ]
Bitran, G., Hass, E., Hax, A., Hierarchical production planning: a two stage system., Operations Research, Vol. 30 , No. 2, 1982, pp 232-251. [ Links ]
Bradley, S. P., Hax, A. C., Magnanti, T. L., Applied Mathematical Programming Addison-Wesley., 1977. [ Links ]
Brandimarte, P., Calderini, M., A hierarchical bicriterion approach to integrated process plan selection and job shop scheduling.,. International Journal of Production Research, Vol. 33 No. 1, 1995, pp 161-181. [ Links ]
Castrillón, O., Toro, J., Modelo para la programación de la producción en ambientes job shop bajo un enfoque jerárquico., Trabajo de grado presentado en la Universidad del Valle –Cali, Para optar al titulo de ingeniero industrial, 2008. [ Links ]
Domínguez Machuca, J. A., Álvarez Gil, M. J., Domínguez Machuca, M. A., González, S. G., Ruiz Jiménez, A., Dirección de operaciones-Aspectos estratégicos en la producción y los servicios., McGraw Hill, España, 1995. [ Links ]
Glover, F., Laguna, M., Tabu Search., Kluwer Academic Publishers, Estados Unidos, 1998. [ Links ]
Hax, A., Meal, H., Hierarchical integration of production planning and scheduling., Working paper, Massachusetts Institute of Technology, 1975. [ Links ]
Ho, N. B., Tay, J. C., Evolving dispatching rules for solving the flexible job shop problem., Working paper, School of computer engineering, Nanyang Technological University, Singapore, 2005. [ Links ]
Jain, A. S., Meeran, S., A state of the art review of job shop scheduling techniques., Workin paper, Department of applied physics, electronic and mechanical engineering. University of Dundee, Dundee, Scotland, 1998. [ Links ]
Kacem, I., Hammadi, S., Borne, P.., Pareto optimality approach for flexible job shop scheduling problems: hybridization of evolutionary algorithms and fuzzy logic., Mathematics and computers in simulation, Vol. 60, No. 3-5, 2002, pp. 245 – 276. [ Links ]
Kacem, I., Scheduling flexible job shops: a worst case analysis an evolutionary algorithm., International Journal of Computational Intelligence and Applications, Vol. 3 No. 4, 2003, pp. 437 – 452. [ Links ]
Karumanasseri, G. y S. Abourizk. Decision support system for scheduling steel fabrication projects, Journal of Construction Engineering and Management, 2002. 128 (5), pp 392-399. [ Links ]
Motoa, G, Osorio, J. C., Orejuela, J. P., Planificación Jerárquica de la Producción (Hierarchical Production Planning). El estado del arte y presentación de experiencias., Revista Heurística No 14. 2007. pp. 35-50. [ Links ]
Osorio, J. C., Motoa, G., Planificación jerárquica de la producción en un job shop flexible., Revista Facultad de Ingeniería, Universidad de Antioquia, No 44, Junio de 2008, pp.158- 171. [ Links ]
Respicio, A., Captivo, M. E., Rodríguez, A. J., A DSS for Production Planning and Scheduling in the Paper Industry., DSI Age-2002, International Conference on Decision Making and Decision Support in the Internet Age, University College Cork, Cork, Ireland, 2002, pp 298-308. [ Links ]
Rigao, C., Amaral, V., Laguna, M., Tardiness minimization in a flexible job shop: a tabu search approach., Journal of Intelligent Manufacturing, Vol. 15, No. 1, 2004, pp. 103–115. [ Links ]
Schneeweiss, C., Hierarchical structures in organizations: A conceptual framework., European Journal of Operational Research, Vol. 86, No. 1, 1995, pp 4-31. [ Links ]
Schneeweiss, C., Distributed decision making – a unified approach., European Journal of Operational Research, Vol. 150, No. 2, 2003, pp. 237-252. [ Links ]
Sipper, D., Bulfin Jr., R. L., Planeación y control de la producción., MacGraw Hill, México, 1998. [ Links ]
Sotskov, Y. N., Shakhlevich, N V., NP-hardness of shop-scheduling problems with three jobs., Discrete Applied Mathematics, Vol. 59, No. 3, 1995, pp. 237 – 266. [ Links ]
Tahar, D. N., Yalaoui, F., Chu, Ch., Amodeo, L., A linear programming approach for identical parallel machine scheduling with job splitting and sequence-dependent setup times., International journal of production economics, Vol.99, 2006, pp 63-73. [ Links ]
Tanev, I., Takashi, U., Yoshiharu, M., Hybrid evolutionary algorithm base real World flexible job shop scheduling problem: application service provider approach., Applied soft computing, Vol. 5, No. 1, 2004, pp. 87 – 100. [ Links ]
Tisher, I., Carrión, A., La planificación jerárquica y su aplicación a la cosecha de la caña de azúcar., Ingeniería y Competitividad, Vol. 4, No. 2, 2003, pp. 42-52. [ Links ]
Torabi, S. A, Karimi, B., Fatemi Ghomi, S. M. T., The common cycle economic lot scheduling in flexible job shops: The finite horizon case., International Journal of Production Economics, Vol. 97, No. 1, pp. 52-65. [ Links ]
Tsubone, H., Ishikawa, Y., Yamamoto, H., Production planning system for a combination of make to stock and make to order products., International Journal of Production Research, Vol. 40, No. 18, 2002, pp. 4835-4851. [ Links ]
Xia, W., Wu, Z., An effective hybrid optimization approach for multi objective flexible job shop scheduling problems., Computers Industrial engineering, Vol. 48, No. 2, 2005, pp. 409 – 425. [ Links ]
Yan, H-S., Practical solution approaches to solve a hierarchical stochastic production planning problem in a flexible automated workshop in China., IIE Transaction, Vol. 35, No. 2, 2003, pp. 113-115. [ Links ]
Yan, H.S, Zhang, X. D., Jiang, M., Hierarchical production planning with demand constraints., Computers and Industrial Engineering, Vol. 46, No. 3, 2004, pp.533-551. [ Links ]
Zribi, N., Kacem, I., E. Elkamel, A., Hierarchical Optimization For The Flexible Job-Shops Scheduling Problem., 11th IFAC Symposium on Information Control Problems in Manufacturing (Incom04), Brasil, 2004. [ Links ]














