Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.28 no.3 Bogotá Sep./Dec. 2008
Luis Patiño1, Yordy González2, Antonio Carmona3, José Valero4 y Henry Espinoza5
1 Ingeniero mecánico. Especialista y M.Sc. Profesor, Departamento de Mecánica, Universidad de Oriente, Venezuela. Investigador, Centro de Termofluidodinámica y Mantenimiento. lapatinoc@cantv.net
2 Ingeniero mecánico. Especialista. Profesor, Departamento de Mecánica de la Universidad de Oriente, Venezuela. Investigador, Centro de Termofluidodinámica y Mantenimiento. ygonzalez@anz.udo.edu.ve
3 Ingeniero mecánico. Investigador, Centro de Termofluidodinámica y Mantenimiento, Venezuela.
4 Ingeniero mecánico. Investigador, Centro de Termofluidodinámica y Mantenimiento, Venezuela.
5 Ingeniero mecánico. Dr. Profesor, Departamento de Mecánica de la Universidad de Oriente, Venezuela. Investigador, Centro de Termofluidodinámica y Mantenimiento. hespinoza@cantv.net
RESUMEN
Se presenta una metodología teórico-experimental para determinar los coeficientes intersticiales de transferencia de calor promedio en el flujo radial de agua a través de un lecho de empaque de polietileno donde el fluido no está en equilibrio térmico con la fase sólida. Los coeficientes de transferencia de calor se obtienen a través del Single Blow Transient Method combinando los resultados experimentales en un banco de ensayo con las soluciones numéricas del modelo matemático. El sistema de ecuaciones diferenciales parciales generado en el modelo matemático es resuelto a través de una metodología numérica basada en el método de volúmenes finitos. Las pruebas experimentales y las soluciones numéricas se realizaron para diferentes valores de velocidad superficial del fluido a la entrada del lecho y para diversos valores de porosidad del medio, obteniéndose que los números de Nusselt aumentan al incrementarse el número de Reynolds, y de igual manera, también aumentan al disminuir la porosidad del medio, observándose valores de Nusselt hasta de 2,8 para una porosidad de 0,375 y un número de Reynolds de 650.
Palabras clave: convección, transferencia de calor, medios porosos.
ABSTRACT
A numerical-experimental methodology was used for determining interstitial heat transfer coefficients in water flowing through porous media where it was not in heat balance with the solid phase. Heat transfer coefficients were obtained through the single blow transient test method, combining experimental test equipment results with a mathematical models numerical solution. The partial differential equation system produced by the mathematical model was resolved by a numerical finite volume method-based methodology. Experimental tests and numerical solutions were satisfactorily carried out for different values from the fluids surface speed from the entrance to the bed and for different porosity values, finding that Nusselt numbers increased when Reynolds numbers also increased and that Nusselt numbers increased when porosity decreased. A 650 Reynolds number and 0.375 porosity gave a Nusselt number of up to 2.8.
Keywords: convection, heat transfer, porous media.
Recibido: abril 22 de 2008
Aceptado: octubre 27 de 2008
Introducción
Un medio poroso provee una gran dispersión térmica y un área de contacto fluido–sólido mucho más grande que el área de transferencia de calor de un fluido en un conducto continuo, lo que trae como consecuencia que la transferencia de calor sea también más elevada. Durante muchos años se han venido desarrollando investigaciones en esta área, en vista de las innumerables aplicaciones industriales que tiene. Entre estas se pueden citar la ingeniería de yacimientos de agua (acuíferos), de petróleo y de gas, los procesos de separación (como por ejemplo la adsorción), diseño de reactores químicos, sistemas geofísicos y geotérmicos, entre otros.
En el flujo de fluidos no isotérmicos a través de medios porosos se tiene un número importante de publicaciones recientes tanto en el área de modelado teórico como trabajos experimentales; entre estas se pueden citar las siguientes: en el modelado teórico de fenómenos de transporte en medios porosos se presenta el trabajo de Vafai et al., 1981. Ellos usaron un modelo no darciano para estudiar los efectos inerciales y de las fronteras en medios porosos. El estudio de la convección forzada en medios porosos con los efectos de flujo inercial, dispersión térmica, porosidad variable y fricción de Brinkman se presentan en los trabajos de Vafai et al., 1985; Berkerman et al., 1987; Cheng et al., 1987.
Hwang et al., 1994; y Hwang et al., 1995, encontraron que los valores de los coeficientes fílmicos de transferencia de calor entre el sólido y la fase fluida puede afectar en gran proporción la transferencia de calor en canales porosos de alta conductividad. Wu et al., 1998; estudiaron la transferencia de calor en canales porosos usando el Single Blow Transient Method (Alazmi et al., 2000) combinado con un modelo térmico no equilibrado de dos ecuaciones y concluyeron que los parámetros que más afectan a la transferencia de calor son el número de Reynolds y la porosidad del medio.
En un trabajo publicado por Hwang et al., 1994, y Hwang et al., 1995; se presenta una metodología numérico-experimental para determinar los coeficientes intersticiales de transferencia de calor de un sistema poroso constituido por aire como fluido y una esponja de aluminio como medio. En este trabajo los autores determinan estos coeficientes de transferencia de calor con ayuda del Single Blow Transient Method (Alazmi et al., 2000) combinando los resultados experimentales provenientes de un banco de ensayo con la solución numérica de un modelo matemático constituido por dos ecuaciones diferenciales parciales. En estas investigaciones la dirección predominante del flujo del fluido es la axial. Recientemente se presentan los trabajos de Patiño y Espinoza (2004) y Patiño et al. (2006); en ambos trabajos se presentan los cálculos de coeficientes intersticiales de transferencia de calor en medios porosos constituidos por una matriz de acero, diferenciándose en que en el primero de estos trabajos el flujo predominante es axial y en el segundo predomina el flujo radial.
En este trabajo se presenta una metodología teórico-experimental para determinar los coeficientes fílmicos de transferencia de calor promedio en el flujo de fluidos (agua) a través de medios porosos donde el fluido no está en equilibrio térmico con la fase sólida, y la dirección predominante en el flujo del fluido es la radial. Los coeficientes de convección de calor se obtienen a través del método transitorio de golpe simple (Single-Blow Transient Methods), utilizado en Liang et al., 1975, combinando los resultados experimentales que se obtienen en un banco de ensayo con las soluciones numéricas del modelo matemático propuesto. El modelo matemático está constituido por las ecuaciones de conservación de masa, cantidad de movimiento y energía para la fase fluida y la ecuación de conservación de la energía para la fase sólida (lecho de empaque), todas expresadas en coordenadas cilíndricas axisimétricas. La solución numérica de estas ecuaciones se obtiene a través del método de los volúmenes finitos, determinando de esta manera el perfil de velocidades, la distribución de presiones y la distribución de temperaturas transitorias en la fase fluida y la distribución de temperaturas transitorias en la fase sólida. Finalmente, se presentan los resultados de los cálculos del número de Nusselt en función del número de Reynolds y de la porosidad de la matriz sólida. Es importante destacar que la metodología empleada en este trabajo para la determinación de los coeficientes de transferencia de calor es la misma usada por Wu et al., 1998; Hwang et al., 1994, Hwang et al., 1995, Patiño y Espinoza, 2004 y Patiño et al., 2006.
Equipo y procedimiento experimental
Equipo experimental
La Figura 1 muestra una representación esquemática del equipo utilizado para realizar las pruebas experimentales. El mismo consta fundamentalmente de cuatro partes, que se describen a continuación:
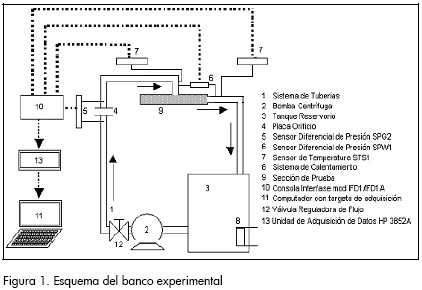
Sistema de bombeo y transporte de líquido: está constituido por una bomba centrífuga de ½ HP que transporta el agua por medio de un sistema de tuberías de acero de ¾ de diámetro desde un tanque de almacenamiento hasta otro receptor, pasando a través de la sección de pruebas. El fluido en el tanque de almacenamiento es calentado hasta una temperatura deseada por medio de un par de resistencias eléctricas de 1.200 vatios.
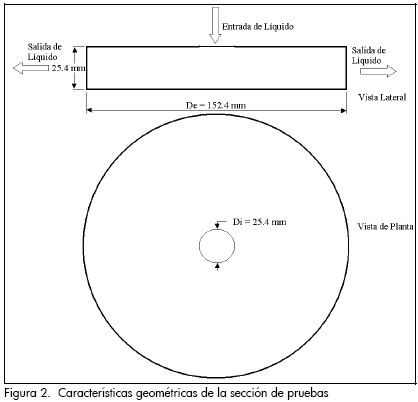
Sección de pruebas: en esta sección se simula el flujo radial del fluido y sus características geométricas se muestran en la Figura 2. Está fabricada en acero al carbono y conectada al sistema de tuberías por intermedio de bridas. Esta sección se encuentra aislada térmicamente. Es importante destacar que en su interior se encuentra colocado el medio poroso.
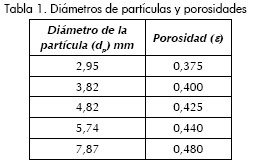
Medio poroso: para modelar el medio poroso se utilizaron esferas de polietileno de densidad 960 Kg/m3, conductividad térmica 0,33 W/mK y calor específicico 2.100 J/KgK. La porosidad del medio fue evaluada utilizando la expresión Φ = (vt –vs)/vt. En esta expresión vt es el volumen total de la sección de pruebas y vs el volumen ocupado por el sólido. La estrategia planteada para generar medios porosos con diferentes porosidades fue utilizar diferentes diámetros de partículas esféricas. Por ejemplo, para generar un medio poroso de porosidad igual a 0,375 sólo se utilizaron, en la sección de pruebas, esferas de 2.95 mm de diámetro, para generar un medio poroso de porosidad igual a 0,40, sólo se utilizaron esferas de 3,82 mm de diámetro, y así con el resto de las porosidades. La Tabla 1 muestra los diámetros de las esferas usadas y las correspondientes porosidades generadas con dichos diámetros.
Sistema de adquisición de datos: está constituido por dos sensores diferenciales de presión y dos sensores de temperatura. Los sensores de presión están ubicados en la placa orificio (cuya función es determinar el flujo másico), y el otro en la entrada y salida de la sección de pruebas. Los sensores de temperaturas están ubicados justamente en la entrada y la salida de la sección de pruebas. Todos estos medidores son de la marca Armfield y están interconectados a una unidad de adquisición de datos (HP3852A). Los datos adquiridos son configurados y leídos por un computador PC gracias a un programa computacional de adquisición. Las diferentes mediciones tomadas por los sensores fueron realizadas con una frecuencia de 20 muestras por segundo por cada sensor.
Procedimiento experimental
Se encienden las resistencias eléctricas en el tanque de almacenamiento de agua y se lleva el agua hasta la temperatura deseada. Luego se enciende el sistema de bombeo y con la válvula de compuerta se regula el caudal al valor deseado. El flujo se monitorea por la pantalla del microcomputador gracias al sistema de adquisición de datos. Una vez colocado el material poroso en la sección de pruebas (Figura 1) se hace pasar el flujo a través de ella y se miden los valores de temperatura del fluido antes y después de la sección de pruebas. Una vez que el tanque de suministro de agua alcance su nivel inferior, tanto las resistencias eléctricas como la bomba hidráulica deben ser desenergizadas a través del cambio de posición de sus interruptores. El sistema de adquisición termina su operación automáticamente. De esta manera se obtienen los perfiles transitorio-experimentales de temperaturas en el fluido. Los experimentos se realizaron tomando variaciones de la velocidad del fluido a la entrada de la sección de pruebas y variando también la porosidad del medio. Se efectuaron cincuenta corridas experimentales; diez corridas, con diferentes flujos volumétricos (números de Reynolds) para cada porosidad
Modelo matemático del proceso
El problema en estudio consiste en la determinación de los coeficientes fílmicos de transferencia de calor promedio en el flujo de fluidos (agua) a través de un lecho de empaque, donde el fluido no está en equilibrio térmico con la fase sólida. En esta sección se indica la formulación matemática que permite modelar la convección de calor transitoria en el flujo de fluidos a través de medios porosos. Todos los detalles referentes a la deducción de la presente formulación matemática se encuentran en la investigación desarrollada por Patiño (2003).
Ecuaciones gobernantes
Tomando como fluido en estudio, agua en estado líquido transportándose a través de la sección de pruebas (medio poroso), suponiendo que el líquido es incompresible y newtoniano donde las propiedades tales como densidad (ρ), viscosidad absoluta (μ), conductividad térmica (k) y calor específico (Cp) permanecen constantes. Considerando que la matriz sólida está constituida por esferas de polietileno, y que es isotrópica, homogénea e indeformable, cuyas propiedades tales como porosidad (ε), permeabilidad (K), densidad (ρs), conductividad térmica (ks) y calor específico (Cs) son constantes, las ecuaciones de variación en coordenadas cilíndricas y régimen transitorio pueden expresarse como:
Ecuación de continuidad:
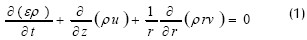
donde u es la velocidad del fluido en la dirección axial (z), v es la velocidad del fluido en la dirección radial (r) y t es el tiempo
Ecuación de cantidad de movimiento en la dirección axial:
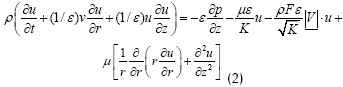
donde p es la presión del fluido; V es el vector velocidad del fluido; F es el coeficiente inercial y también se le denomina el término de Forchheimer (Bear, 1976); y K es la permeabilidad del medio.
Ecuación de cantidad de movimiento en la dirección radial:
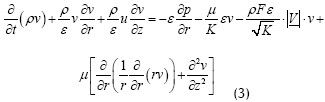
Ecuación de la energía de la fase líquida:
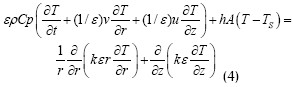
donde es la temperatura en la fase líquida; Ts es la temperatura en la fase sólida; h es el coeficiente intersticial de convección de calor; y A es el área superficial de transferencia de calor.
Ecuación de la energía de la fase sólida:
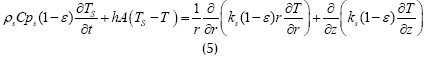
Es importante indicar que la permeabilidad del medio y el coeficiente inercial son calculados a través de las ecuaciones (6) (Hunt, 1988). En las ecuaciones (6) dp representa el diámetro promedio de la partícula que conforma el medio poroso.
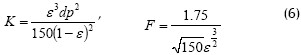
Condiciones del problema
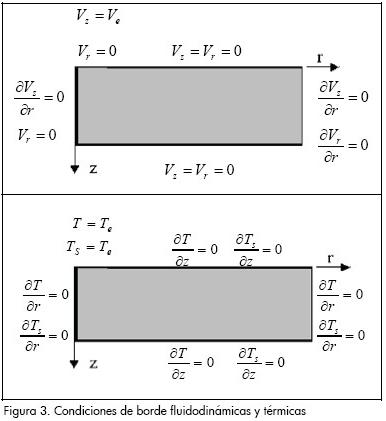
Las condiciones iniciales son velocidades radiales y axiales nulas, y temperaturas homogéneas para las fases líquidas y sólidas (Ti). Las condiciones de borde asociadas al problema se aprecian en la Figura 3.
Solución del modelo matemático
Para la resolución de este modelo se empleó una metodología numérica. Las ecuaciones diferenciales con sus respectivas condiciones de borde e iniciales descritas en el modelo matemático fueron resueltas a través del código comercial CFX versión 4.3, el cual basa la solución en el método de los volúmenes finitos utilizando una discretización estructurada coincidente con las fronteras (Hunt, 1988). Para todas las simulaciones los flujos convectivos y difusivos en las interfaces de los volúmenes se calculan a través del esquema de interpolación híbrido y el procedimiento de acoplamiento presión–velocidad, en las ecuaciones de movimiento, el utilizado fue el Simple (Patankar, 1787). El régimen transitorio fue implementado a través de un esquema totalmente implícito, y el criterio de convergencia fue establecido tomando el máximo residuo en la ecuación de continuidad. Se desarrollaron dos subrutinas en el lenguaje de programación Fortran, una para incluir las condiciones de borde en la entrada del dominio variable en el tiempo y la otra para anexar el término fuente en la ecuación de la energía en las fases fluida y sólida. La temperatura inicial en cada simulación dependió de los resultados experimentales obtenidos, y de manera general se indica que están en un rango entre 25 °C y 35 °C. Se realizaron dos estudios: uno de malla, y otro del tamaño del intervalo de tiempo, de esta manera el dominio simulado fue la sección de prueba y para ello fue dividido con una malla de 80 volúmenes en la dirección radial y 24 volúmenes en la dirección axial, lo cual generó una discretización de 1.920 volúmenes finitos. El periodo de tiempo máximo en las simulaciones fue de aproximadamente 90 segundos, y el intervalo de tiempo utilizado fue de 0,1 segundos.
Determinación de los coeficientes intersticiales de transferencia de calor
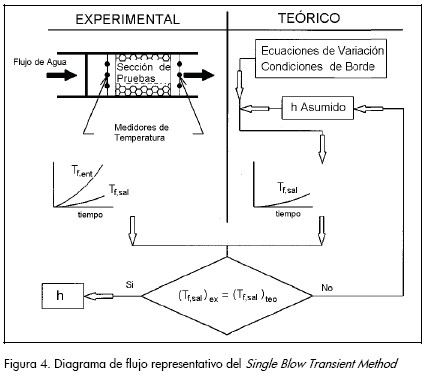
Para determinar los coeficientes intersticiales de convección de calor h para cada una de las corridas experimentales se utilizó el Single Blow Transient Method desarrollado por Liang et al., 1975. Este método requiere solamente la curva de respuesta transitoria de las temperaturas promedio a la entrada y a la salida de la sección de pruebas, y consiste en suponer un valor inicial del coeficiente de convección de calor, determinar la distribución de temperatura del fluido a la salida de la sección analizada a través del modelo teórico y luego comparar esta curva obtenida teóricamente con la respuesta transitoria determinada experimentalmente. Si la curva teórica coincide con la curva experimental, entonces el coeficiente de convección supuesto es el correcto; si no es así, se debe suponer otro coeficiente de convección y repetir el proceso hasta que las dos soluciones sean iguales (típicamente con una desviación menor a 0.001). Este proceso se repite hasta obtener seis casos en que se cumpla el error. El coeficiente h será el promedio aritmético de los coeficientes h para los seis casos. La Figura 4 muestra un flujograma descriptivo del Single Blow Transient Method.
Análisis de resultados
Como fue mencionado, para determinar los coeficientes de transferencia de calor se efectuaron cincuenta simulaciones numéricas que modelan el intercambio de energía térmica entre el fluido y el medio poroso descrito en esta investigación. Por razones de limitación de espacio sólo se presentan las curvas de respuesta de temperatura para algunas de las simulaciones.
En la Figura 5 se presentan los perfiles de temperaturas del fluido a la entrada y a la salida de la sección de pruebas obtenidos experimentalmente, y se comparan con el perfil transitorio del fluido a la salida de la sección determinado teóricamente a través del modelo numérico y del Single Blow Transient Method. Adicionalmente, en ellas se presenta el valor del coeficiente de convección de calor determinado en dichas pruebas. En forma general se aprecia que existe una muy buena aproximación entre los resultados experimentales y los teóricos, con un error máximo del 0,1 %.
En la Figura 6 se observan los perfiles transitorios de temperaturas del fluido y de la matriz sólida para tres posiciones radiales del dominio estudiado y para tres valores de porosidades 0,40, 0,425 y 0,44, respectivamente. Se nota que, a medida que transcurre el tiempo, la temperatura de cualquier punto en la dirección del flujo (radial) va en ascenso. La presencia del medio poroso en el camino del fluido va a generar una disminución en la temperatura del fluido, la cual es absorbida por la matriz porosa.
A pesar de que el sólido está inicialmente a una temperatura uniforme, este aumenta su temperatura debido al intercambio térmico con la fase fluida. A medida que transcurre el tiempo la temperatura del sólido se incrementa para cualquier posición; sin embargo, esta temperatura va en descenso cuando se incrementa la coordenada radial. Si el fluido se enfría cuando se desplaza en la dirección del movimiento, entonces el sólido que está en contacto con él también presentará disminución en su temperatura. Estas Figuras evidencian la ausencia del equilibrio térmico entre las dos fases y muestran que, a medida que aumenta la porosidad del medio esta diferencia de temperaturas entre fluido y sólido se incrementa, demostrando que, a medida que aumenta la porosidad, la transferencia de calor entre estas dos fases disminuye.
En la Figura 7 se muestran los perfiles de temperaturas del fluido y del sólido en función de la posición y para dos instantes de tiempo (1 y 20 s).

Para todos los casos se aprecia que la temperatura de la fase fluida es de magnitud mayor que la de la fase sólida, demostrando la ausencia de equilibrio térmico entre las fases.
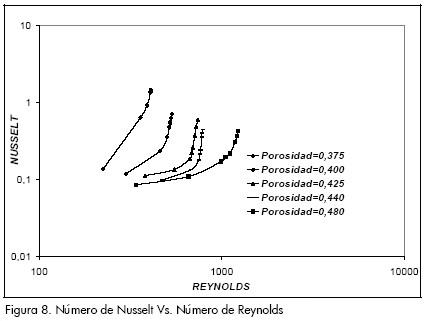
En la Figura 8 se presentan los valores de los números de Nusselt Vs. el número de Reynolds para los cinco valores de porosidad estudiados en esta investigación. Es importante destacar que el número de Nusselt utilizado está basado en una longitud característica igual al diámetro de la partícula que constituye el medio poroso, Nu = hdp/kf, donde h es el coeficiente fílmico o intersticial de transferencia de calor y dp es el diámetro de las partículas. En esta Figura se aprecia claramente que el coeficiente de transferencia de calor h es una variable dependiente tanto de la porosidad del medio, como del número de Reynolds. A medida que aumenta la porosidad del medio, el número de Nusselt disminuye, y a medida que aumenta el número de Reynolds, el número de Nusselt también lo hace.
Conclusiones
Para poder realizar análisis o diseños de lechos de empaque es de vital importancia conocer la dependencia de los coeficientes de convección de calor o números de Nusselt (Nu) con el número de Reynolds (Re) y la porosidad del lecho de empaque. El principal objetivo de este trabajo es estudiar precisamente esta correspondencia en el caso particular de agua y una matriz sólida de polietileno. Exceptuando este trabajo de investigación, hasta la fecha no se han reportados bibliográficamente investigaciones que muestren las variaciones del Nu con el Re y la porosidad del medio para esta pareja de fluido y sólido. Entre las principales conclusiones arrojadas en este trabajo se tienen:
Las mediciones experimentales de temperatura del fluido en la entrada y en la salida de la sección de pruebas presentaron valores físicamente congruentes, ya que en todo instante de tiempo se registraron magnitudes más elevadas de temperatura en la entrada, evidenciándose la absorción de energía térmica por parte del medio poroso.
Se ha presentado el desarrollo de un modelo matemático y la solución de un problema de convección de calor transitoria en un medio poroso tomando en consideración un dominio axisimétrico y el uso de las velocidades axiales y radiales del fluido para el cálculo del transporte de energía.
Los perfiles de temperaturas de las fases fluida y sólida dependen de la posición radial y axial y, adicionalmente, también del tiempo.
Se evidenció la no existencia del equilibrio térmico entre las fases fluida y sólida. Concordando con el comportamiento típico del transporte de un fluido a través de un medio poroso, se evidencia que la caída de presión del fluido aumenta al aumentar el número de Reynolds y al disminuir la porosidad. Adicionalmente los resultados mostrados indican que el perfil de temperatura de la fase fluida es parabólico en la dirección radial en todo instante de tiempo.
Desde el punto de vista metodológico, el método Single Blow Transient, conjuntamente con el modelo teórico propuesto, representan una técnica efectiva para la determinación de los coeficientes de transferencia de calor en el flujo de fluidos a través de medios porosos. El Single Blow Transient combina los resultados experimentales obtenidos en laboratorio con los resultados numéricos logrados teóricamente a través de la solución del modelo matemático planteado.
Se ha demostrado que el número de Nusselt, y por ende, el coeficiente intersticial de transferencia de calor, en el flujo de fluidos a través de medios porosos, dependen tanto del número de Reynolds como de la porosidad del medio. A medida que aumenta el número de Reynolds, el número de Nusselt aumenta, y al aumentar la porosidad del medio, el número de Nusselt disminuye.
Es importante señalar que trabajos similares a este pueden desarrollarse pero tomando en consideración variaciones en la relación conductividad térmica de la fase fluida a conductividad térmica de la fase sólida, y de esta manera poder conformar correlaciones empíricas que muestren la correspondencia de los coeficientes de transmisión de calor en términos de esta relación de conductividades térmicas y del número de Reynolds y la porosidad del lecho de empaque.
Bibliografía
Alazmi, B., Vafai, K., Analysis of Variants Within the Porous Media Transport models., ASME Journal of Heat Transfer, Vol. 122, 2000, pp. 303-325. [ Links ]
Bear, J., Dynamics of Fluids in Porous Media., American Elsevier Publishing Company, NY, 1976. [ Links ]
Beckerman, C., Viskanta, R., Forced Convection Boundary Layer Flow and Heat Transfer Along a Flate Plate Embedded in a Porous Media., Int. J. Heat Mass Transfer, Vol. 30, No. 7, 1987, pp. 1547-1551. [ Links ]
Cheng, P., Zhu, H., Effects of Radial Thermal Dispersion on Fully Developed Forced Convection in Cylindrical Packed Bed., Int. J. Heat Mass Transfer, Vol. 30, 1987, pp. 2373-2383. [ Links ]
Hunt, L., Tien, C., Non Darcian convectión in cilyndrical pocked beds., Trans-Asme J. Heat Transfer, 1988, pp. 110-378. [ Links ]
Hwang, G. J., Chao, C. H., Heat Transfer measurent and Analytical for sintered Porous Channells., ASME Journal of Heat Transfer, Vol. 116, 1994, pp. 456-464. [ Links ]
Hwang, G.J., Wu, Cc Y Chao, C.H. Investigation of Non-Darcian Forced Convection in an asymmetrically Heated Sintered Porous Channel. ASME Journal of Heat Transfer, vol. 117, 1995, pp. 725-732. [ Links ]
Hwang, J.J., Hwang, G.J., Yeh, R.H Y Chao, C.H. Measurement of Intertitial Convective Heat Transfer and Frictional Drag for Flow Across Metal Foams. ASME Journal of Heat Transfer, vol. 124, 2002, pp. 1-10 [ Links ]
Liang, C., Yang, W., Modified Single-Blow Technique for Performance Evaluation on heat Transfer Surfaces., ASME Journal of Heat Transfer, Vol. 96, 1975, pp. 16-21. [ Links ]
Patankar, S., Spalding, D., A Calculation Procedure for Heat, Mass and Momentum Transfer in Three-Dimensional Parabolic Flows., Int. Journal of Heat and Mass Transfer, Vol. 15, 1972, pp. 1787-1806. [ Links ]
Patiño, L., Análisis Teórico – Experimental de la Convección de Calor Transitoria en el Flujo de Fluidos a través de Medios Porosos., Tesis presentada para optar al título de Magister Scientiarum en Ingeniería Mecánica Mención Ciencias, Universidad de Oriente, Escuela de Ingeniería y Ciencias Aplicadas, Puerto La Cruz - Venezuela, 2003, pp. 133. [ Links ]
Patiño, L., Espinoza, H., Convección de Calor Intersticial en el Flujo de Fluidos a través de Medios Porosos., Revista Ingeniería Hidráulica en México, Morelos, México, Vol. XIX, No. 2, 2004. [ Links ]
Patiño, L., Carvajal, D., Maza, J., Figueroa, R., Espinoza, H., Convección de Calor Transitoria en el Flujo Radial a través de un Lecho de Empaque Metálico., Revista Ingeniería Química, Uruguay, No. 29, Julio, 2006. [ Links ]
Vafai, K., Tien, C. L., Boundary and Inertia Effects on Flow and Heat Transferin Porous Media., Int. J. Heat Mass Transfer, Vol. 24, No. 6, 1981, pp. 195-203. [ Links ]
Vafai, K., Alkire, R., Tien, C. L., An Experimental Investigations of Heat Transfer in Variable Porosity Media., ASME Journal of Heat Transfer, Vol. 107, 1985, pp. 642-647. [ Links ]
Wu, Cc., Hwang, G. J., Flow and Heat Transfer Characteristics Inside Packed and Fluidized Beds., ASME Journal of Heat Transfer, Vol. 120, 1998, pp. 667-673. [ Links ]














