Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería e Investigación
versão impressa ISSN 0120-5609
Ing. Investig. v.28 n.3 Bogotá Set./dez. 2008
Alejandro García Zamora1 y Maritzabel Molina Herrera2
1 Ingeniero civil, Universidad Nacional de Colombia. M.Sc., en Estructuras, Universidad Nacional de Colombia. fagarciaz@unal.edu.co
2 Ingeniera civil. M.Sc., en Ingeniería, Estructuras, Universidad Nacional de Colombia. Estudiante de doctorado, Análisis estructural, Universidad Politécnica de Cataluña, España. Universidad Nacional de Colombia, Bogotá. mmolinah@unal.edu.co
RESUMEN
En el presente artículo, partiendo de un análisis teórico-experimental, se determinan y caracterizan los parámetros de diseño que rigen el comportamiento de las vigas compuestas de perfiles de acero y losa de concreto empleando conectores de cortante tipo tornillo, dado que para esta clase de conector no existe un estudio específico de su comportamiento, además en la actualidad su diseño no está definido en las NSR-98, aunque es uno de los tipos de conectores más empleados en la construcción de secciones compuestas en Colombia. El análisis se desarrolló con base en los resultados de 36 ensayos experimentales a escala, para dos resistencias de concreto (fc), 21MPa y 28MPa, cada resistencia de concreto con tres diámetros de tornillos, Ø1/2, Ø5/8 y Ø3/4, con dos tipos de separaciones de 0,10 m y de 0,30 m. En esta investigación se estudian, entre otros efectos, el deslizamiento producido tanto por la degradación del concreto como por las deformaciones en el perfil de acero y en los conectores, para ello se emplean formulaciones que involucran diversas variables como el deslizamiento y la separación de los conectores. Así mismo, en el estudio se plantea una metodología de diseño de vigas en sección compuesta con conectores de cortante tipo tornillo, donde se propone una formulación para el cálculo de la resistencia de los conectores de cortante, con la cual se obtienen resistencias de los conectores del orden del 62% de las planteadas para los espigos cuando la separación es de 0,10 m y 13% mayores para las separaciones de 0,30 m, en los parámetros elásticos donde se obtienen inercias efectivas del orden de 62% de las teóricas y en de resistencia a flexión de las vigas compuestas, las cuales mostraron una sobrerresistencia promedio del 23% mayor de los valores nominales de la normatividad actual.
Palabras clave: vigas compuestas, deslizamiento, deformación, conectores de cortante, acción parcial.
ABSTRACT
This paper reports using theoretical-experimental analysis for obtaining and characterising the design parameters governing steel and concrete slab composite beams behaviour using shear connector screws. Currently no research has been found about such behaviour and Colombian seismic-resistant regulations (NSR-98) have not yet defined such design; these types of connectors are most used in constructing composite sections in Colombia. The results of 36 experimental scale tests for 21MPa and 28MPa concrete strengths were taken for the analysis; each concrete strength had three screw diameters (Ø1/2 ", Ø5/8 " and Ø3/4 ") with 0.10m and 0.30m separations. This research also studied other effects such as slip caused by steel and connector profile deformation or deformation due to concrete degradation. Formulations were thus used which included connector slip and separation. The article sets out a methodology for designing composite beams using shear connector screws. It also proposes a formulation for calculating connector shear strength, thereby obtaining almost 62% stud connector resistance when separation was 0.10m and an extra 13% for 0.30m separations in elastic parameters where 62% of theoretical effective inertia was obtained and 23% more composite beam average bending strength was found than that required by current regulations.
Keywords: composite beams, slip, deformation, shear connectors, partial interaction.
Recibido: febrero 1 de 2008
Aceptado: octubre 27 de 2008
Introducción
El análisis de las vigas de sección compuesta, en la práctica, se realiza partiendo de las propiedades de la sección transformada de la viga y de la resistencia obtenida al considerar la plastificación total; estos elementos no involucran el deslizamiento entre la losa y el perfil como resultado de las deformaciones inherentes los conectores de cortante, la losa de concreto y el perfil de acero. El cálculo de la resistencia de los conectores, del módulo de sección de la viga, de la inercia efectiva y del momento resistente en las NSR-98, no involucra el efecto del deslizamiento presentado en la interfase de los materiales y la separación de los conectores, sin embargo, estas variables deben ser estudiadas para determinar su influencia en el comportamiento de las vigas de sección compuesta. Estos efectos han sido estudiados en las investigaciones llevadas a cabo por Oehlers y Sved (1995), las cuales, al fundamentarse sobre condiciones generales, permiten usarse con el objeto de establecer el comportamiento de las vigas de sección compuesta y de los conectores de cortante tipo tornillo.
Las condiciones reales en las cuales interactúan la losa de concreto, el perfil de acero y los conectores de cortante, hacen que se presenten diferencias en las propiedades mecánicas de las vigas. La variación entre las fuerzas resistentes y las aplicadas en los conectores a lo largo del eje longitudinal de las vigas compuestas no se tienen en cuenta en los análisis validados por las normas actualmente vigentes (AISC-LRFD (American Institute of Steel Construction, 2005), NSR-98 (Asociación Colombiana de Ingeniería Sísmica, 1998)), al considerar las vigas compuestas como monolíticas y extrapolar las propiedades mecánicas de esta condición a los casos en los que el comportamiento no es de acción total, como sucede en las vigas parcialmente compuestas. La metodología que se desarrolló en la investigación se encamina al planteamiento de una formulación que relacione los parámetros estudiados y que permita predecir aproximadamente el comportamiento real de los conectores de cortante tipo tornillo en vigas de sección compuesta con losa de concreto y perfil de alma llena en acero teniendo como contexto, de una parte, que no existe una normatividad con un lineamiento para determinar su diseño, y por otra, que este tipo de conectores es comúnmente empleado en la construcción de secciones compuestas en nuestro país.
Estudio analítico de las vigas compuestas
La metodología analítica que se aplica en la investigación se basa en los estudios realizados en la última década por Nie y Cai (2003), en lo que respecta al comportamiento elástico de las secciones compuestas, y por Burnet y Oehlers (2001) en lo concerniente con el comportamiento inelástico. Para los dos rangos los estudios parten de la condición general de acción parcial y son aplicables para la acción total (acción parcial de 100%) como un caso particular de la acción parcial. Los estudios citados tienen como punto de partida las investigaciones efectuadas por Oehlers y Sved (1995), las cuales se centran en la capacidad de deslizamiento de las secciones compuestas en función de su geometría y de sus materiales.
Rango elástico de las vigas
Para una viga de sección compuesta, simplemente apoyada con ejes coordenados en el centro de la luz y distribución uniforme de conectores de cortante, como se muestra en al Figura 1, se realiza equilibrio de una porción de viga teniendo en cuenta el deslizamiento entre la losa y el perfil, y la hipótesis de que las secciones planas permanecen planas.
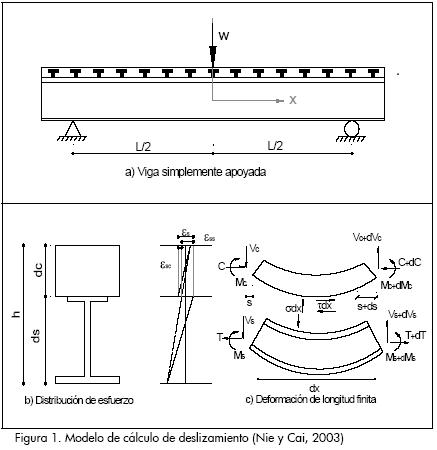
Empleando la compatibilidad de curvatura de la losa y el perfil se plantea la ecuación 1 (Nie y Cai, 2003) que describe la segunda derivada de la ecuación que relaciona el desplazamiento entre la losa y el perfil para las condiciones de geometría y de cargas expuestas en la Figura 1.

Teniendo la dependencia entre la curvatura y el giro, se relaciona la deformación por deslizamiento con la carga aplicada y se calculan en el sistema los incrementos de la curvatura, del giro y de la deflexión producidos por el deslizamiento, como se indica en la ecuación 2.
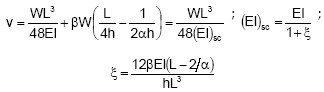
Rango plástico de las vigas
La evaluación del momento último en una viga de sección compuesta debe realizarse en el rango inelástico, condición en la que se identifican dos tipos de comportamiento: uno, correspondiente a la porción longitudinal de la losa de concreto y del perfil de acero que están trabajando en el rango elástico, y otro, donde el concreto se encuentra fisurado y el perfil de acero está en fluencia por tracción, como se muestra en la Figura 2.
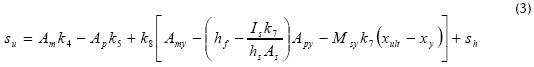
Burnet y Oehlers (2001) plantean una extensa formulación analítica para calcular el deslizamiento último entre la losa de concreto y el perfil de acero que está en función de la fractura de los conectores, de la fisuración del concreto, de la fluencia del acero y de la formación de rotulas plásticas. La expresión a la que llegan Burnet y Oehlers (2001) se presenta en la ecuación 3.
Partiendo de la ecuación 3 se plantea la ecuación 4, que consiste en una expresión cúbica en función de la fuerza sobre los conectores.
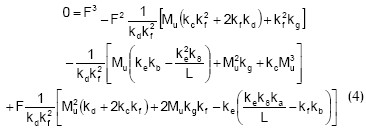
Desarrollo experimental
Descripción de las probetas
Las vigas construidas para los ensayos se componen de tres elementos: el perfil de acero, la losa de concreto y los conectores de acero tipo tornillo; estos componentes están caracterizados por su geometría y las propiedades mecánicas de los materiales, entre las que se encuentran los parámetros de diseño como el esfuerzo de fluencia en el perfil, la resistencia a la compresión en el concreto y el esfuerzo de rotura en los tornillos. El perfil IPE 200 empleado para las vigas compuestas se seleccionó considerando que la resistencia al corte del perfil fuera mayor a la resistencia a flexión de la sección compuesta para el tipo de carga aplicada. En la Figura 3 se muestra la configuración de las probetas.
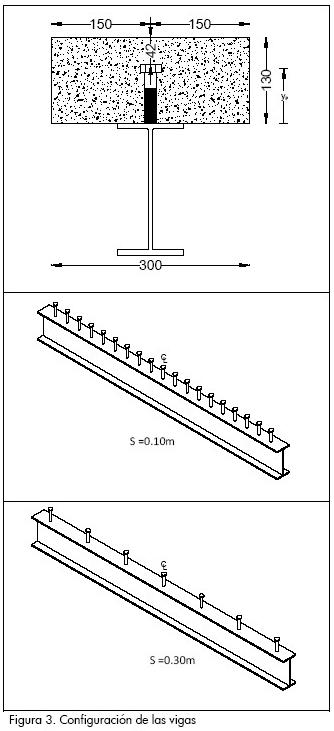
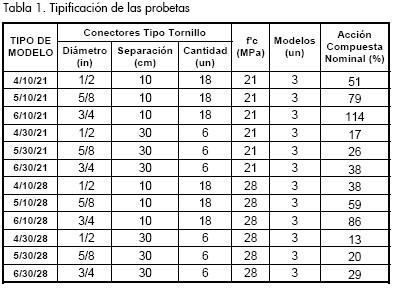
Se realizaron 36 ensayos sobre vigas compuestas para dos resistencias de concreto (fc), 21 MPa y 28 MPa, 18 probetas respectivamente, cada resistencia de concreto con tres diámetros de tornillos: Ø1/2, Ø5/8 y Ø3/4, y para cada diámetro dos separaciones de 0,10 m y de 0,30 m.
La denominación de cada tipo de probeta se expresa con el formato A/B/C; por ejemplo, la nomenclatura 5/30/21 indica que la viga tiene conectores de Ø5/8, espaciados cada 30 cm, y una losa de concreto con fc=21 MPa.
Materiales
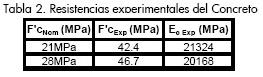
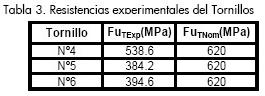
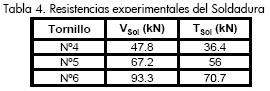
Las Tablas 2 a 4 muestran las resistencias experimentales de los materiales empleados.
Cargas nominales
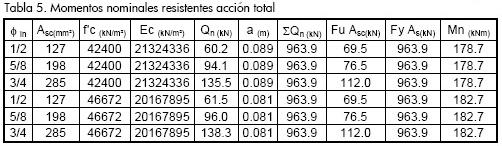
Con base en los resultados de las pruebas efectuadas al concreto, la soldadura, el perfil metálico y los conectores, se estableció el momento plástico para cada una de las configuraciones de modelos (García, 2008). En la Tabla 5 se resume la información de cargas nominales calculadas.
Descripción del ensayo
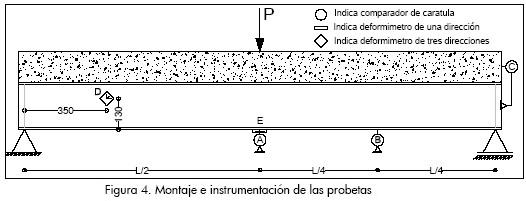
Las vigas compuestas se ensayaron con apoyos de primer género en sus extremos y una carga estática puntual en el centro de la luz. El tipo de carga y su ubicación se estableció con el fin de tener un cortante constante a lo largo de la viga para conseguir un flujo de cortante también constante entre la losa de concreto y el perfil del acero, generando así una solicitación aproximadamente igual en todos los conectores de cada probeta. En la Figura 4 se presenta el montaje de la viga y la instrumentación empleada.
Descripción de resultados
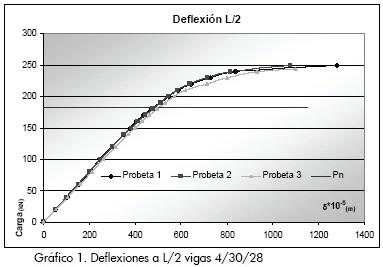
Las probetas ensayadas en su totalidad se llevaron hasta la falla, condición que se consideró cuando la viga presentó un gradiente positivo para la deflexión a L/2 bajo carga sostenida. El trabajo en el rango plástico de la sección compuesta y la fluencia del perfil de acero se desarrollo en todas las probetas indicando que para todos los grados de acción compuesta se presenta un comportamiento inelástico. En los Gráficos 1 y 2 se observa la forma como se evidenció la plastificación en las deflexiones y las deformaciones; la línea correspondiente a Pn corresponde a la carga puntual a L/2 que genera el momento nominal de la viga compuesta.
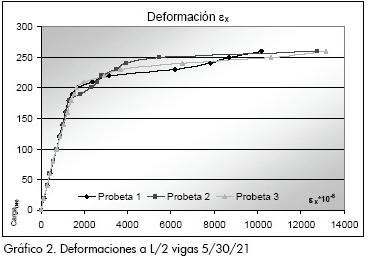
En general las losas de concreto presentaron tres tipos de falla, como se muestra a continuación:

-Tipo 1 (T1), caracterizada por una fisura longitudinal desde un extremo de la viga hasta el centro de la luz junto con una fisura transversal a lo largo del centro de la luz.
-Tipo 2 (T2) definida por sólo una fisura transversal a lo largo de todo el centro de la luz.
-Tipo 3 (T3) identificada por sólo una fisura longitudinal desde un extremo de la viga hasta el centro de la luz.
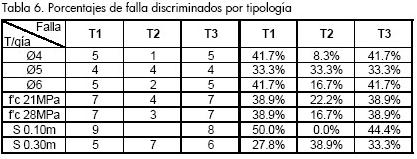
En la Tabla 6 se presentan los porcentajes de falla discriminados por tipo, evidenciando con ello la influencia del diámetro, del material y de la separación en el tipo de falla, cabe destacar lo siguiente:
-Diámetro: se observa que para las configuraciones con diámetros de Ø1/2 y Ø3/4, el mayor porcentaje de falla corresponde a los tipos 1 y 3, y para el diámetro de Ø5/8 los porcentajes son iguales para los tres tipos de falla. Las proporciones en los tipos de falla indican que el variar el diámetro no influye considerablemente.
-Concreto: los porcentajes de falla para los dos concretos son iguales, esto señala que la variación en la resistencia del concreto no influye en el tipo de falla.
-Separación: las probetas con separación de conectores cada 0,30 m presentaron mayor porcentaje para la falla tipo 2, lo que puede establecer que para esta separación en la mayoría de casos, las zonas de aferencia de los conectores no se interceptaron. En contraste con la separación de 0,10 m ninguna probeta tuvo falla del tipo 2, se concluye que las zonas de aferencia siempre se superpusieron. Se observa así la relevancia que tiene el espaciamiento de los tornillos, ya que esta variable limita si las zonas de aferencia de los conectores se intersectan o no, y por ende, si se presenta una falla de tipos 1 ó 3 en el caso de que se traslapen las zonas de aferencia, o de tipo 2 al no superponerse.
Análisis experimental
La evaluación experimental se realiza estudiando los resultados de los ensayos en los rangos elástico y plástico, con el fin de analizar para cada tipo de comportamiento la influencia de las propiedades mecánicas y características de configuración en las vigas.
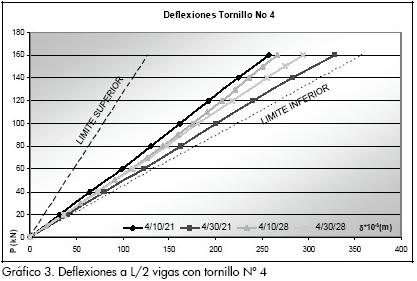
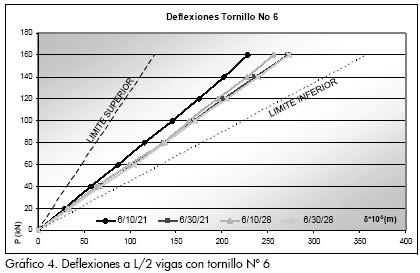
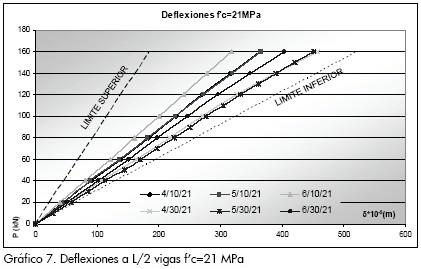
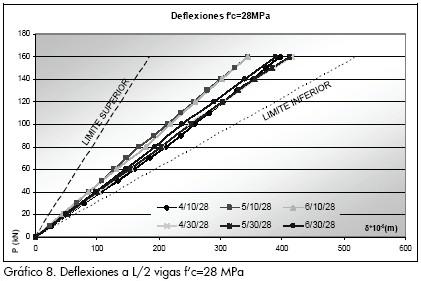
Los gráficos de carga contra deflexiones que se muestran a continuación corresponden al comportamiento elástico promedio de las diferentes configuraciones. En estas se presentan dos límites que corresponden a la región factible de inercia efectiva:
-El límite superior se define por la inercia máxima calculada a través de la sección transformada correspondiente a la acción total de la sección en la cual teóricamente no debe presentarse deslizamiento entre el acero y el concreto.
-El límite inferior está dado por la inercia mínima, calculada como la suma aritmética de la inercia del perfil y la losa transformada por el acero, condición para la cual el deslizamiento no está restringido dado que se considera que no hay adherencia entre los dos materiales.
Diámetro del conector
Con los Gráficos 3 y 4 se encontró que la mayor rigidez es la que corresponde a la menor separación de conectores (0,10 m), como consecuencia de la mayor restricción al deslizamiento entre la losa y el perfil que tiene esta configuración. Se evidencia en los gráficos que el tipo de concreto influye en la rigidez de las vigas al identificarse la diferencia de pendientes entre las configuraciones con el mismo espaciamiento y diferente concreto, de igual forma que la separación de los conectores incide en la rigidez de las vigas.
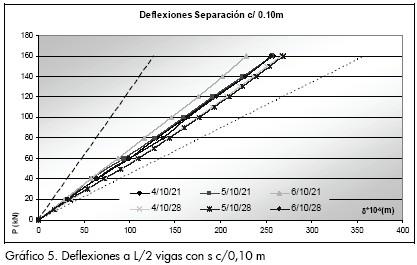
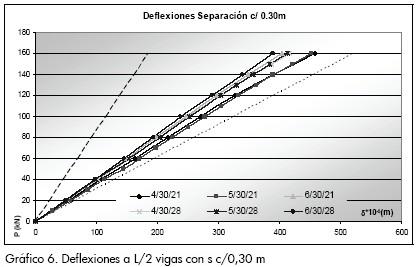
Separación del conector
En los Gráficos 5 y 6 se presenta los correspondientes a todas las configuraciones para las separaciones de 0,10 m y 0,30 m respectivamente. Los modelos con la más alta rigidez corresponden a los conectores con mayor diámetro y al concreto con superior módulo de elasticidad, la configuración de más baja rigidez se relaciona con el diámetro más pequeño y el concreto de menor módulo de elasticidad.
Resistencia de la losa del concreto
El Gráfico 7, correspondiente al concreto de resistencia nominal de 21 MPa, muestra que la mayor rigidez corresponde a los conectores espaciados 0,10 m y que las probetas con conectores de Ø3/4 tienen rigidez superior a las de los conectores de Ø5/8 y Ø1/2. En el Gráfico 8 para 28 MPa se encontró que el cambio de rigidez en las vigas al variar los conectores no es significativo, lo que indica que al aumentar la resistencia del concreto el comportamiento de la viga está controlado en mayor proporción por las propiedades de la losa que por el diámetro y separación del conector.
Inercia y resistencia máxima
Los Gráficos 9 y 10 presentan una recta diagonal correspondiente a la deflexión teórica empleando la inercia efectiva y con una línea horizontal se señala el límite superior del momento efectivo, valores calculados con las fórmulas propuestas por AISC. Se halló que para todos los modelos ensayados la resistencia obtenida es superior a la encontrada teóricamente, en particular se tiene que el momento nominal propuesto en la NSR-98 se alcanza en todos los ensayos para cargas dentro del rango elástico de la viga. Los resultados experimentales están mostrando que al diseñar a flexión las vigas de sección compuesta, se está despreciando la resistencia aportada en el rango plástico de la viga en la sección compuesta; también se identifica que en la zona elástica la rigidez teórica representada por la pendiente de la curva de inercia efectiva siempre muestra un mayor valor que la obtenida experimentalmente.
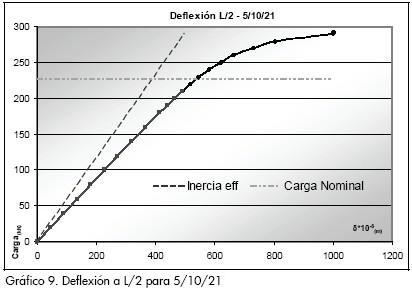
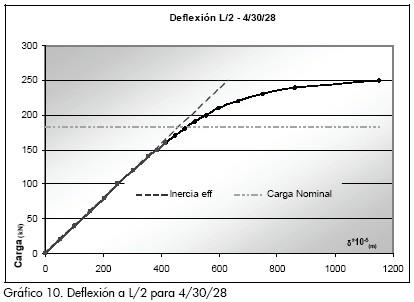
Deslizamiento
El deslizamiento entre la losa de concreto y el perfil de acero se midió en uno de los extremos de las probetas, teniendo presente que para una viga simplemente apoyada con carga simétrica el deslizamiento es nulo en el centro de la luz y aumenta hasta llegar a su valor máximo en los extremos. Los Gráficos 11 a 14 presentan las curvas de carga de deslizamiento, identificando una relación potencial para todos los modelos. El gráfico correspondiente a separaciones c/0,30 m tiene curvas suavizadas frente a la dispersión observada en el deslizamiento para separaciones c/0,10 m.
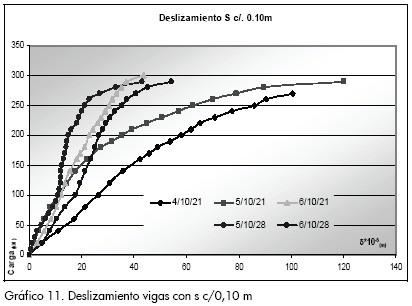
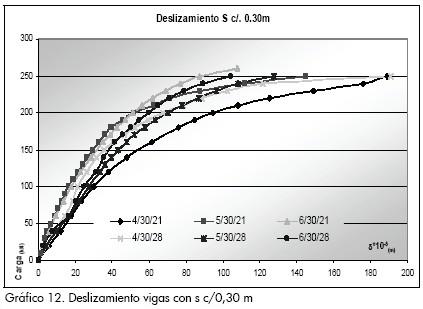
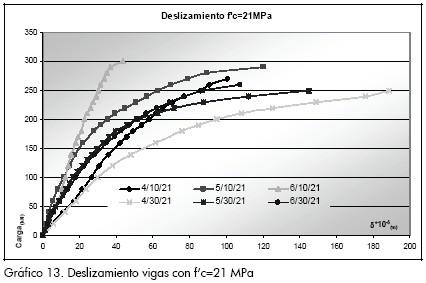
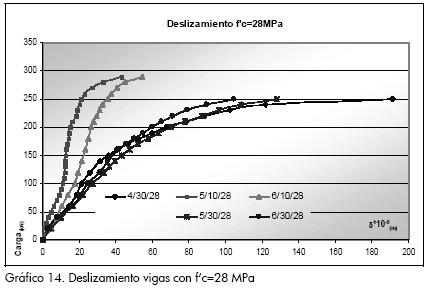
Los Gráficos 13 y 14 muestran que el deslizamiento también aumenta al incrementarse el espaciamiento entre los conectores y que para una misma carga y una misma separación las vigas con conectores de mayor diámetro presentan menor deslizamiento, en comparación con las vigas que poseen conectores con menor diámetro.
Análisis de resultados
El análisis matemático considerado en el presente estudio describe el comportamiento en los rangos elástico y plástico de las vigas de sección compuesta. Su formulación analítica se usa para definir la carga máxima impuesta en los conectores, correspondiente al momento último resistido por las vigas ensayadas y al cálculo de la inercia efectiva en el rango elástico de las mismas.
Deslizamiento
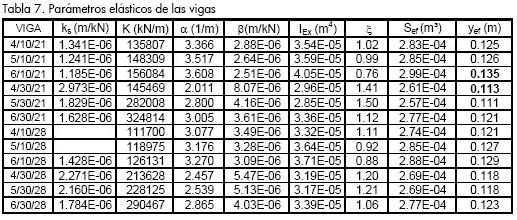
En la Tabla 7 se recopilan los resultados de los parámetros elásticos para todas las vigas. Sobre estos valores se realizó el análisis del comportamiento de las vigas en el rango elástico y el planteamiento de la metodología para su estudio junto con las fórmulas propuestas.
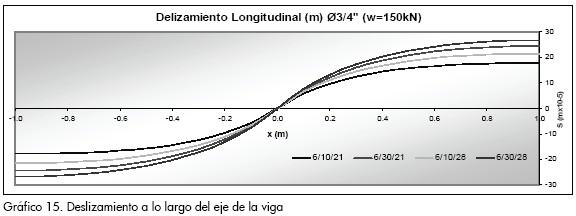
El Gráfico 15 muestra el deslizamiento longitudinal que se presenta en la interfase de la placa y el perfil para los modelos con tornillos de Ø3/4, y se determinó aplicando los parámetros calculados en la Tabla 8, en la ecuación 1.
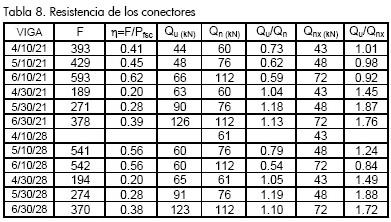
Fuerza en los conectores
Con la ecuación 4 se calculó la fuerza desarrollada en los conectores, correspondiente a la carga de falla en las vigas; esta fuerza se asumió como una distribución uniforme al no poder conocer la fuerza en cada conector, y por lo tanto se divide por el número de conectores instalados entre el apoyo de la viga y el centro de la luz para obtener la máxima carga aplicada en un solo conector. En la Tabla 8 se presentan las resistencias nominales de los conectores calculadas conforme a la normatividad y a las expresiones planteadas por Hurtado et al. (2008). Los resultados de Q se compararon con las cargas experimentales sobre los conectores, con el fin de encontrar la relación que permita obtener la carga máxima de los conectores en función del espaciamiento y sus propiedades mecánicas.
Partiendo de la relación 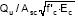 que se despliega en la Tabla 9 se observa que el factor encontrado es aproximadamente igual a la raíz cuadrada de la separación entre los conectores, tendencia general para todas las probetas. Basados en este resultado se propone como válida la ecuación 5 para el cálculo de la resistencia del conector de cortante tipo tornillo.
que se despliega en la Tabla 9 se observa que el factor encontrado es aproximadamente igual a la raíz cuadrada de la separación entre los conectores, tendencia general para todas las probetas. Basados en este resultado se propone como válida la ecuación 5 para el cálculo de la resistencia del conector de cortante tipo tornillo.
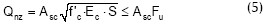
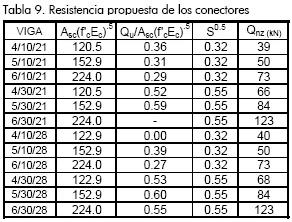
La ecuación es aplicable para separaciones dentro del rango en estudio y debe validarse para valores fuera de este, definiendo, de una parte, un límite superior que evite la pérdida de capacidad en la viga debido a la degradación de la losa de concreto ocasionada por el excesivo deslizamiento y que a la vez genera mayores deflexiones, y de otra, un límite inferior para controlar la intersección de las zonas de aferencia, con el propósito de no reducir la acción de los conectores. La definición de estos límites está fuera del alcance del presente artículo.
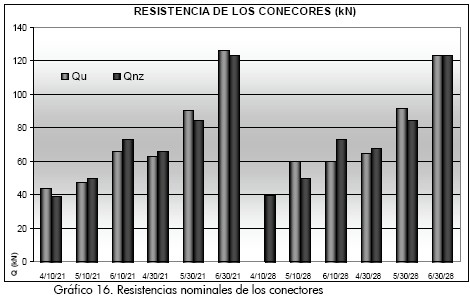
En el Gráfico 16 se comparan las resistencias experimentales de los conectores y las nominales calculadas con la ecuación 5.
Inercia efectiva
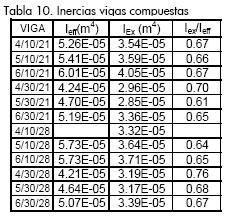
La inercia efectiva se determinó encontrando la relación entre la inercia experimental y la teórica calculada con AISC. Calculando la inercia efectiva con los valores experimentales de grado de acción compuesta se obtiene aproximadamente la misma diferencia porcentual para todos los grados de acción con respecto a la inercia experimental. Los valores de inercia se indican en la Tabla 10.
Partiendo de las relaciones encontradas en la Tabla 11 y teniendo presente que para la inercia efectiva no se tiene en cuenta el coeficiente de 0,75 en su cálculo con el fin de obtener un factor general, se plantea la siguiente expresión para determinar la inercia efectiva:
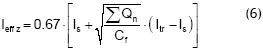
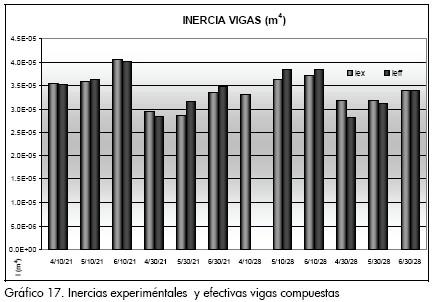
En el Gráfico 17 se muestra la comparación entre las inercias experimentales y las nominales calculadas con la ecuación 6. La expresión propuesta se hace aplicable para cualquier grado de acción compuesta y es general para separación dentro del rango en estudio, debido a que el factor es aplicable para las dos separaciones y a diferentes grados de acción compuesta.
Momento resistente
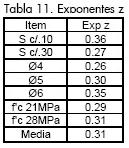
Partiendo de la base de que la expresión para encontrar el momento resistente no debe ser lineal debido a que las vigas fallan en el rango plástico y que esta debe ser función del grado de acción compuesta, se plantea la ecuación 7, que toma como referencia el momento nominal para acción compuesta total y para la cual se calculan diferentes coeficientes z agrupando las resistencias de las vigas para una misma separación, un mismo diámetro de conector y una misma resistencia del concreto. Los coeficientes encontrados se presentan en la Tabla 11.
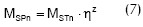
En la Tabla 12 se observa que los exponentes tienden al valor medio de 0,31, identificando que prácticamente hay una variación poco apreciable de este coeficiente cuando se cambia de resistencia del concreto, y que por el contrario, esta variación es relevante cuando se varían el diámetro de conector o el espaciamiento. Se propone que los coeficientes a usar para el cálculo de los momentos nominales sean los determinados en función del espaciamiento, teniendo en cuenta que la formulación elástica ha planteado como la variable más relevante el espaciamiento de los conectores.
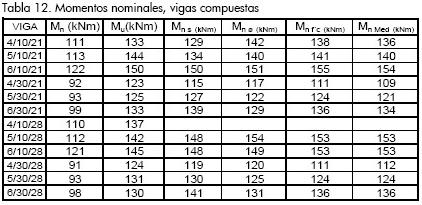
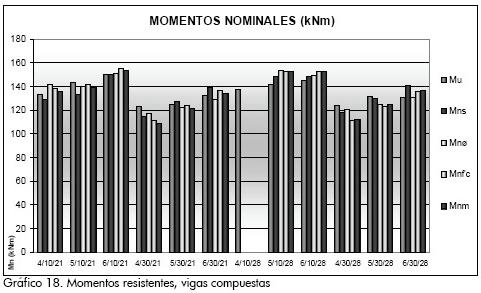
La Tabla 12 presenta los valores de momento calculados para los diferentes exponentes de la Tabla 11, los cuales se comparan en el Gráfico 18. Se puede apreciar que los valores correspondientes a los coeficientes de espaciamiento son los que más se aproximan a los momentos experimentales.
Metodología de diseño
Partiendo del análisis anterior, se propone la siguiente metodología para aplicar en el diseño de los conectores de cortante y en el cálculo de la resistencia a flexión de las vigas de sección compuesta con conectores de cortante tipo tornillo grado dos (2).
1. Partiendo de un momento último que debe ser resistido por la sección compuesta y de una geometría base de la losa de concreto y del perfil de acero, así como de los materiales de los mismos, se calcula el momento resistente para acción total de la geometría seleccionada aplicando las fórmulas: (a) – eje neutro plástico en la losa de concreto, (b) – eje neutro en la aleta a compresión del perfil, o (c) – eje neutro plástico en el alma del perfil. Estas ecuaciones son válidas para perfiles de aletas iguales.
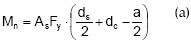
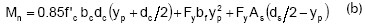
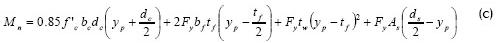
2. Conociendo el momento resistente de la geometría seleccionada se calcula el grado de acción compuesta requerido en función del momento nominal y el mayorado, partiendo de la ecuación (d) en caso de requerir un momento igual al nominal se debe tomar un grado de acción igual a 1.
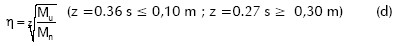
Los exponentes presentados en la ecuación (d) deben interpolarse de forma lineal para separaciones entre 0,10 m y 0,30 m.
3. Con el grado de acción compuesta necesario se calcula la fuerza que requiere resistir los conectores de cortante a partir de la ecuación (f).

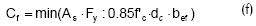
4. Se selecciona una geometría y distribución de conectores cuya cantidad y resistencia aporte la fuerza necesaria calculada en (f). El cálculo de la resistencia de los conectores se realiza con la ecuación (f), que es función de la separación seleccionada.
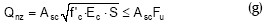
5. La resistencia de la soldadura aplicada debe superar la resistencia del conector. Esta se calcula con las ecuaciones (h) e (i).
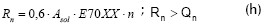
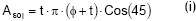
6. La estimación de la inercia efectiva para efectos de determinar las deflexiones por cargas de servicio y el módulo de sección para calcular los esfuerzos en el rango elástico en el perfil se definen con las ecuaciones (j) y (k) respectivamente.
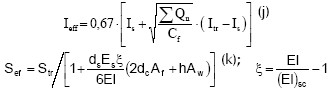
7. Se calculan las deflexiones por cargas de servicio empleando la inercia encontrada con la ecuación (j). Los valores de deflexión deben cumplir con una adecuada condición de servicio de la estructura y por ello la norma en el ítem F.2.12.3.1 las limita. En el caso de que se soporten cielos rasos en pañete la deflexión máxima por carga viva debe ser de 1/360 de la luz.
Conclusiones
La formulación planteada en la presente investigación para el cálculo de la inercia efectiva y el módulo elástico efectivo de la viga con sección compuesta proporciona valores menores respecto a los dados por la normatividad. Adicionalmente las expresiones propuestas son aplicables para cualquier porcentaje de acción compuesta, contrario a la formulación vigente, la cual indica que el cálculo de la inercia efectiva no es aplicable para porcentajes de acción compuesta menores al 0,25.
Los ensayos mostraron momentos resistentes que se ubicaron en todos los casos en el rango plástico de las vigas con valores superiores a las resistencias teóricas, indicando así que para porcentajes de acción compuesta de hasta 0,20 las vigas presentan fluencia y trabajan en el rango plástico. Se concluye que es necesario plantear una separación mínima en la normatividad para los tornillos debido a que la separación planteada para los espigos no permitió en los ensayos el desarrollo de toda la capacidad de los conectores.
Las expresiones analíticas expuestas en el segundo ítem del documento son de uso general para cualquier tipo de carga, configuración de conectores, dimensiones de la losa de concreto, geometría del perfil de acero, propiedades mecánicas y resistencia de los materiales empleados, debido a que las formulaciones están en función de las variables mencionadas y particularmente la aplicación de la formulación en el presente estudio se realizó para una viga simplemente apoyada con carga puntual en el centro de la luz, distribución uniforme de conectores y un perfil de aletas iguales. Así mismo, el desarrollo de las expresiones teóricas planteadas para las consideraciones generales mencionadas, son analíticamente válidas.
Al aplicar la metodología de diseño propuesta para tornillos se obtienen resultados aproximados al comportamiento observado en los ensayos, teniendo presente que la normativa no tiene expresiones específicas para este tipo de conectores. Se deben de tener en cuenta para la aplicación de la metodología las bases de la formulación, como es el rango de separación de los conectores y la resistencia de los concretos empleada, cantidad de constantes que deben ser reducidas desarrollando investigaciones que tengan en cuenta mayor número de variables.
Nomenclatura
a : Espesor
Ac : Área transversal de la losa.
Asc : Área transversal del conector.
C : Fuerza de compresión en la losa.
Es : Módulo de elasticidad del acero.
EI : Rigidez sección transformada.
Ec : Módulo del concreto.
(EI)sc : Rigidez efectiva de la sección.
EcExp : Módulo experimental del concreto.
fc : Resistencia del concreto.
F : Carga máxima sobre el conjunto de conectores
FcNom : Resistencia nominal del concreto.
FuT : Esfuerzo último a tensión.
FcExp : Resistencia experimental del concreto.
Fu : Esfuerzo de rotura del conector.
Fy : Esfuerzo de fluencia del acero.
hc : Centroide de la losa.
hs : Centroide del perfil.
hf : Distancia entre los centroides.
Ic : Inercia de la losa de concreto.
Iex : Inercia experimental.
Ieff : Inercia efectiva para acción parcial NSR 98.
Ieff z : Inercia efectiva para acción parcial GZ 2007.
k : Rigidez sistema conector losa.
 : Espaciamiento de los conectores.
: Espaciamiento de los conectores.
L : Luz libre de la viga.
Mn : Momento nominal para acción total NSR 98.
Mu : Momento último experimental.
Mn s : Momento nominal controlado por separación.
Mn ø : Momento nominal controlado por Ø.
Mnfc : Momento nominal controlado por fc.
Mn M : Momento nominal para factor medio.
Mc : Momento actuante en la losa.
Ms : Momento actuante en el perfil.
MSPn : Momento nominal viga parcialmente compuesta.
MSTn : Momento nominal viga totalmente compuesta.
Pfsc : Carga sobre los conectores acción total.
Qn : Resistencia nominal espigo NSR 98.
Qnx : Resistencia nominal de un conector XH.
Qu : Resistencia última experimental conector.
S : Deslizamiento elástico
TSol : Carga máxima aplicada para tensión.
T : Carga máxima aplicada para tensión.
V : Deflexión en la viga compuesta.
VSol : Carga máxima aplicada para cortante.
Vc : Fuerza de cortante en la losa.
Vs : Fuerza de cortante en el perfil.
W : Carga puntual aplicada a la viga.
yp : Eje plástico .
z : Exponente de porcentaje de acción.
α : Parámetro α de deslizamiento
β : Parámetro β de deslizamiento.
εcb : Deformación inferior de la losa.
εst : Deformación superior del perfil.
εs : Deformación entre losa-perfil.
φ : Curvatura elástica de la viga.
η : Porcentaje de acción compuesta.
τ : Cortante en la interfase losa perfil.
σ : Fuerza axial en la interfase.
Nota: Las unidades están en Sistema Internacional
Bibliografía
American Institute of Steel Construction., Load & Resistance Factor Desing., AISC, Chicago, 1999. [ Links ]
American Institute of Steel Construction., INC. Seismic Provisions for Structural Steel Buildings., Chicago, 2005. [ Links ]
Asociación Colombiana de Ingeniería Sísmica., Normas Colombianas de Diseño y Construcción Sismo Resistente., NSR-98, Bogotá, 1998. [ Links ]
Burnet, M. J., Oehlers, D. J., Fracture of Mechanical Shear Connectors in Composite Beams., MECH. STRUCT. & MACH, 29(1), 2001, pp 1-41. [ Links ]
García, A., Comportamiento de vigas de sección compuesta con perfiles de acero laminado y losa de concreto empleando conectores de cortante tipo tornillo grado dos (2)., tesis presentada Universidad Nacional de Colombia – Sede Bogotá, para optar al grado de Magister en Estructuras Colombia, 2008. [ Links ]
Hurtado, X. F., Molina, M., Linero, D. L., Comportamiento de conectores de cortante tipo tornillo de resistencia grado dos para un sistema de sección compuesta, Ingeniería e Investigación, Vol. 28 No. 2, abril, 2008, pp. 4-14. [ Links ]
Nie, J. G., Cai, C. S., Steel–Concrete Composite Beams Considering Shear Slip Effects., Journal of Structural Engineering, Vol. 129, No. 4, April 1, 2003. pp 495-506. [ Links ]
Oehlers, D. J, Sved, G., Composite Beams with Limited-Slip-Capacity Shear Connector., Journal of Structural Engineering, Vol. 121, No. 6, June, 1995. pp 932-938. [ Links ]
Otras referencias bibiliográficas
American Concrete Institute., Building Code Requeriments for Structural Concrete (ACI 318-2005) Farmington Hills., MI, USA, 2005. [ Links ]
American Institute of Steel Construction., INC. Manual of Steel Construction, New York, 1970. [ Links ]
Baird, D. C., Experimentación – Introducción a la Teoría de Mediciones y al Diseño de Experimentos., México, Prentice Hall, 1991. [ Links ]
Chandrupatla, T. R. Belegundu, A. D. Introducción al estudio del Elemento Finito en Ingeniería., México, Prentice Hall, 1999. [ Links ]
Gere, J., Timoshenko, S., Mecánica de Materiales., Ed. Thomson Editores, Mexico, 1998. [ Links ]
McCorman, J., Diseño de Estructuras de Acero., Método LRFD, Ed. Alfaomega, México, 1991. [ Links ]
McCorman, J., Diseño de Estructuras de Acero., Método ASD, Ed. Alfaomega, México, 1999. [ Links ]
Rankovic, S., Drenic, D., Static Strength of the Shear Connectors in Steel-Concrete Composite Beams., Regulations and Research Analysis, Architecture and Civil Engineering, Vol. 2, No 4, 2002, pp. 251–259. [ Links ]
Salmon, Ch., Johnson, J., Steel Structures, Desing and Behavior., Prentice Hall, USA, 1994. [ Links ]














