Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.29 no.1 Bogotá Jan./Apr. 2009
Diana Jimena López Mesa1, Guillermo Alberto Camacho Muñoz2, Jaime Oscar Díaz Chávez3, Carlos Alberto Gaviria López4 y Gilberto Bolaños Pantoja5
1 Ingeniera en automática industrial. Estudiante, M.Sc., en Automática, Universidad del Cauca, Colombia. Docente de cátedra, Universidad del Cauca, Colombia. djlopez@unicauca.edu.co
2 Ingeniero en automática industrial, Universidad del Cauca, Colombia. Investigador, grupo de Automática Industrial (AI), Universidad del Cauca, Colombia. gacamacho@unicauca.edu.co
3 Ingeniero en Electrónica y Telecomunicaciones, Universidad del Cauca, Colombia. M.Sc., en Control Automático. Candidato a Ph.D., Universidad Marta Abreu de Santa Clara, Cuba. Profesor titular, Departamento de Electrónica Instrumentación y Control, Facultad de Ingeniería Electrónica y Telecomunicaciones, Universidad del Cauca, Colombia. jadiaz@unicauca.edu.co
4 Ingeniero en Electrónica y Telecomunicaciones. Especialista, en Informática industrial, Universidad del Cauca, Colombia. Ph.D., en Automatización Avanzada y Robótica, Universidad Politécnica de Cataluña, España. Profesor titular, Departamento de Electrónica Instrumentación y Control, Facultad de Ingeniería Electrónica y Telecomunicaciones, Universidad del Cauca, Colombia. cgaviria@unicauca.edu.co
5 Licenciado en Matemáticas y Física, Universidad de Nariño, Colombia. Ph.D., en Ciencias Físicas, Universidad del Valle, Colombia. Profesor titular, Departamento de Física, Facultad de Ciencias Naturales, Exactas y de la Educación, Universidad del Cauca, Colombia. Director, grupo de Física de bajas temperaturas (FISBATEM), Universidad del Cauca, Colombia. Investigador, Centro de Excelencia de Nuevos Materiales (CENM), Universidad del Valle, Colombia. gbolanos@unicauca.edu.co
RESUMEN
Este artículo presenta el diseño y validación de un nuevo algoritmo de modulación por ancho de pulso (PWM) híbrido que supera el desempeño armónico de varios algoritmos de modulación empleados en procesos de conversión de potencia en accionamientos eléctricos AC. A partir del análisis armónico de los algoritmos PWM más comunes en la literatura, se establece una metodología para diseñar un esquema de modulación híbrido que ofrece un desempeño armónico superior; este desempeño es verificado teórica y experimentalmente utilizando el factor de distorsión armónica total FDIST y el índice de distorsión armónica de corriente VWTHD.
Palabras clave: accionamientos eléctricos AC, análisis armónico, flujo armónico del estator, inversores, modulación por ancho de pulso (PWM), PWM de vectores espaciales (SV-PWM).
ABSTRACT
This paper presents a novel hybrid modulation algorithm which improves the harmonic performance of eight of the most common pulse width modulation (PWM) algorithms for voltage source inverters (VSI) in the electric drive field. From harmonic analysis of these eight algorithms, a methodology was established for designing a hybrid modulation scheme offering superior harmonic performance. The algorithm so designed was validated theoretically by calculating the total harmonic distortion factor FDIST and experimentally by measuring the weighted total harmonic distortion factor VWTHD.
Keywords: AC electric drive, harmonic analysis, stator flux ripple, inverter, pulse width modulation (PWM), space vector PWM (SV-PWM).
Recibido: mayo 19 de 2008
Aceptado: marzo 9 de 2009
Introducción
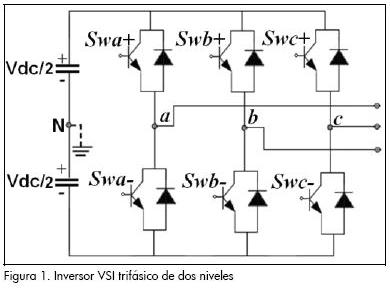
Los accionamientos eléctricos de baja y mediana potencia se construyen con base en inversores VSI (Voltage Source Inverter) trifásicos de dos niveles, como el presentado en la Figura 1 (Murphy et ál., 1998). Mediante conmutación continua de los interruptores de potencia de este esquema, se generan señales seno de amplitud y frecuencia variable. La secuencia de conmutación se origina a partir de un proceso de modulación PWM.
Las señales generadas por el inversor son pulsos de ancho variable donde el valor medio de cada pulso corresponde al valor que toma la señal seno de referencia en el tiempo, como se observa en la Figura 2a).
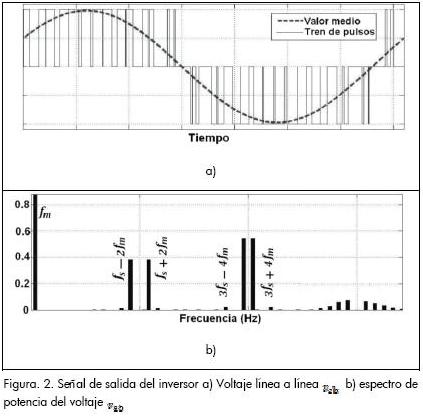
El voltaje línea a línea a la salida de los inversores PWM presenta un espectro de frecuencias con componentes de distorsión armónica en los múltiplos enteros de la frecuencia fundamental (fm), alrededor de la frecuencia de conmutación (fs ) y sus múltiplos enteros (Figura 2b).
La relación fs / fm se conoce como índice de frecuencias (N). En accionamientos de baja y mediana potencia se emplean altos índices de frecuencia, por tanto los voltajes armónicos se ubican en altas frecuencias, donde no afectan el comportamiento funcional del sistema. Sin embargo, estos armónicos provocan efectos indeseables en la máquina (Murphy et ál., 1998), como incremento de pérdidas, sobrecalentamientos, vibraciones, generación de pares parásitos y reducción del par útil (Van der Broeck y Skudelny, 1988; Rodriguez, 2005). En consecuencia, analizar el desempeño armónico de alternativas de modulación PWM es un factor decisivo en el campo de accionamientos eléctricos, especialmente en aplicaciones que no usen filtros pasivos o activos en la carga.
Para medir el desempeño armónico se define el índice de distorsión armónica de corriente (VWTHD ):
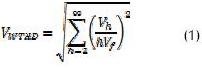
donde Vf y Vh son valores RMS de la componente fundamental y el h-ésimo armónico de la señal línea a línea Vab, respectivamente. Su obtención implica el cálculo de magnitud de las componentes armónicas de la señal de voltaje línea a línea (Figura 2b) mediante métodos de análisis en frecuencia (Holmes y Lipo, 2003; Holmes y McGrath, 2003).
Un índice alternativo para medir el desempeño armónico es el factor de distorsión armónica total (FDIST ), el cual se basa en la definición del rizado de flujo del estator y resulta útil en la evaluación de es-quemas de modulación basados en vectores espaciales (SV-PWM) (Narayanan y Ranganathan, 2005), (Narayanan et ál., 2006).
Recientemente se ha reportado la superioridad armónica del algoritmo de particiones simétricas (SY-SVPWM, Symmetrical-Space Vector PWM) en un amplio rango de operación en zona lineal (82%) (Camacho y López, 2008). En este trabajo se describe el diseño de un nuevo algoritmo híbrido que supera este rango. Inicialmente se presentan los fundamentos de la modulación SV-PWM, describiendo la obtención de ocho algoritmos de modulación co-munes en la literatura. Se evalúa el desempeño armónico mediante el cálculo del factor FDIST y se observa una oportunidad de mejora a partir de los resultados obtenidos. El aporte central de este trabajo es un algoritmo que mejora los índices de desempeño armó-nico respecto de los ocho algoritmos descritos previamente. El desempeño de este nuevo algoritmo es verificado teóricamente mediante cálculo del FDIST y experimentalmente mediante medición del VWTHD.
Fundamentos de la modulación PWM
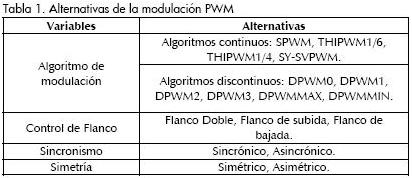
La modulación PWM presenta dos enfoques: la modulación basada en portadora (CB-PWM) y la modulación basada en vectores espaciales (SV-PWM) (Wells, 2006; Hava, 1998). Las diferentes alternativas dentro de estos enfoques se presentan en la Tabla 1 (Camacho y López, 2008). Esta investigación se concentra en el análisis de los esquemas de modulación sincrónicos, asimétricos y de control de flanco doble debido a la superioridad en el desempeño armónico reportada en Holmes y Lipo, 2003; Murphy et ál., 1998; Wells, 2006.
CB-PWM modula el ancho de pulsos comparando la amplitud entre una señal de alta frecuencia denominada portadora y una señal de baja frecuencia llamada moduladora. Este enfoque resulta útil en exposiciones teóricas por su conceptualización simple; sin embargo, en el momento de la implementación presenta desventajas frente a SV-PWM, como el incremento en el procesamiento debido a las comparaciones simultáneas que precisan los esquemas de modulación trifásicos y la disminución en el rango de flexibilidad, ya que en CB-PWM no existe contraparte para todas las alternativas de modulación SV-PWM (Narayanan et ál., 2006).
El enfoque SV-PWM es complejo en conceptualización pero presenta ventajas en el desempeño armónico, rangos de modulación y eficiencia de señales moduladas. Por esta razón, SV-PWM tiene gran aplicación en accionamientos eléctricos (Murphy et ál., 1998; Narayanan, 1999).
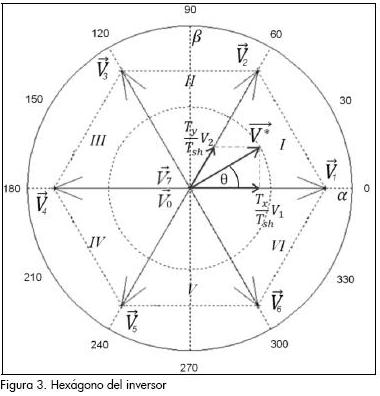
SV-PWM sintetiza un vector espacial de voltaje de referencia 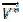 en el plano αβ mediante aplicación instantánea de los posibles estados en un VSI. Los ocho vectores espaciales de voltaje posibles en un inversor VSI trifásico de dos niveles se clasifican en vectores activos (V1 – V6) y vectores cero (V0 y V7). Como se muestra en la Figura 3, estos vectores dividen el plano αβ en seis sectores, (I- VI), formando los ejes de un hexágono, en donde los vectores activos poseen igual magnitud y están desfasados mutuamente 60°, por tanto pueden ser expresados mediante (2):
en el plano αβ mediante aplicación instantánea de los posibles estados en un VSI. Los ocho vectores espaciales de voltaje posibles en un inversor VSI trifásico de dos niveles se clasifican en vectores activos (V1 – V6) y vectores cero (V0 y V7). Como se muestra en la Figura 3, estos vectores dividen el plano αβ en seis sectores, (I- VI), formando los ejes de un hexágono, en donde los vectores activos poseen igual magnitud y están desfasados mutuamente 60°, por tanto pueden ser expresados mediante (2):
para 
donde Vdc es el voltaje del bus DC y k es un sector del hexágono.
Cualquier vector de referencia 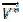 dentro de los límites de un sector del hexágono se sintetiza por descomposición en sus componentes respecto a los vectores que forman el sector (Vx ,VY) y los vectores cero (V0 y V7). El desarrollo de esta síntesis se encuentra descrito detalladamente en Narayanan, 1999; Hava, 1998. Con respecto a los vectores que forman el sector, las expresiones son:
dentro de los límites de un sector del hexágono se sintetiza por descomposición en sus componentes respecto a los vectores que forman el sector (Vx ,VY) y los vectores cero (V0 y V7). El desarrollo de esta síntesis se encuentra descrito detalladamente en Narayanan, 1999; Hava, 1998. Con respecto a los vectores que forman el sector, las expresiones son:
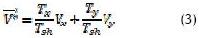
Donde Tsh corresponde a medio ciclo de conmutación y Tx ,Ty son los tiempos de activación de los vectores adyacentes al vector de referencia 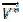 . Los tiempos Tx ,Ty se calculan a partir de (4), donde k es el sector de ubicación del vector referencia (k+1=1 para k=6 ) y M es el índice de modulación.
. Los tiempos Tx ,Ty se calculan a partir de (4), donde k es el sector de ubicación del vector referencia (k+1=1 para k=6 ) y M es el índice de modulación.
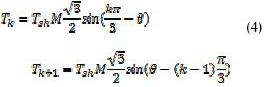
El tiempo de activación de los vectores cero (Tz) se obtiene por: Tz = Tsh.- Tx – Ty. .El resultante debe ser dividido entre los tiempos de activación de los vectores cero (T0 y T7). Esta división permite diversas alternativas que determinan el desempeño de la modulación PWM. Dichas alternativas pueden ser representadas mediante (5):
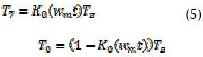
Donde K0(wmt) es el distribuidor de estados cero (1≥K0(wmt )≥0) (Zhou y Wang, 2002).
En consecuencia, la elección de permite modificar características de desempeño en la modulación como: contenido armónico, pérdidas por conmutación y rango de operación lineal. Las alternativas más comunes en la selección de se resumen en la Tabla 2; cada una se asocia a un algoritmo de modulación PWM en particular.
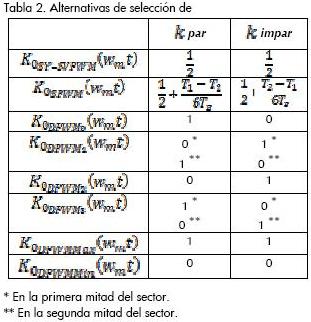
La secuencia de conmutación generada a partir de distintas selecciones de K0, durante un ciclo de conmutación dentro del sector se muestra en la Figura 4.
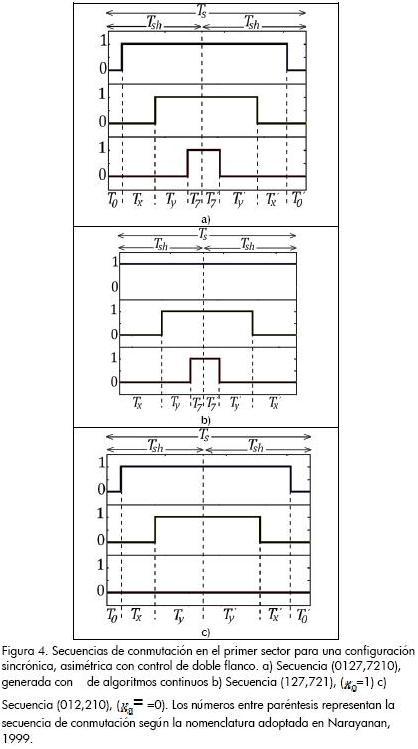
Análisis armónico mediante aplicación del FDIST
El análisis por factor de distorsión armónica total FDIST, válido para esquemas PWM alimentando cargas inductivas, emplea la representación vectorial de las señales trifásicas del inversor para formular tres índices que caracterizan el desempeño armónico del modulador en tres contextos: por ciclo de conmutación (vector de flujo armónico del estator 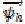 ), por sector (valor medio del vector de flujo armónico del estator F2ABCD) y por ciclo de fundamental (FDIST) (Narayanan y Ranganathan, 2005).
), por sector (valor medio del vector de flujo armónico del estator F2ABCD) y por ciclo de fundamental (FDIST) (Narayanan y Ranganathan, 2005).
Valor medio del vector de flujo armónico del estator
El desarrollo del vector de flujo armónico del estator ( 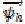 ) presentado con detalle en Narayanan y Ranganathan, 2005, se basa en la existencia de un vector de error implícito en la síntesis del vector referencia. Mediante integración de este error dentro de Tsh se calculan las componentes d (Ψd ) y q (Ψq ) de en función de las componentes abreviadas del vector error (Q0, Q1, Q2, Q7, y D). Como resultado se obtienen trayectorias de alrededor del origen del plano
) presentado con detalle en Narayanan y Ranganathan, 2005, se basa en la existencia de un vector de error implícito en la síntesis del vector referencia. Mediante integración de este error dentro de Tsh se calculan las componentes d (Ψd ) y q (Ψq ) de en función de las componentes abreviadas del vector error (Q0, Q1, Q2, Q7, y D). Como resultado se obtienen trayectorias de alrededor del origen del plano 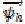 . Estas trayectorias caracterizan a cada algoritmo PWM para cada índice de modulación M y ángulo θ del vector de referencia sintetizado. El valor medio del vector de flujo armónico del estator (F2ABCD ) se calcula como el valor RMS del vector , dentro de Tsh, como se presenta en (6).
. Estas trayectorias caracterizan a cada algoritmo PWM para cada índice de modulación M y ángulo θ del vector de referencia sintetizado. El valor medio del vector de flujo armónico del estator (F2ABCD ) se calcula como el valor RMS del vector , dentro de Tsh, como se presenta en (6).
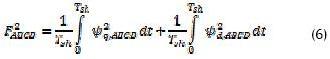
La solución de (6) para las secuencias de conmutación que emplean los algoritmos PWM más comunes se presenta en la Tabla 3, donde ABCD representa la secuencia de conmutación (Narayanan y Ranganathan, 2005). Mediante F2ABCD es posible asignar un valor a cada trayectoria del vector y generar curvas de desempeño armónico a lo largo de los 60° del primer sector o superficies, al considerar diversos índices de modulación M. Este trabajo reporta por primera vez un análisis gráfico de tales superficies.

La evolución del índice F2ABCD para algoritmos continuos SPWM y SY-SVPWM se presenta en la Figura 5.
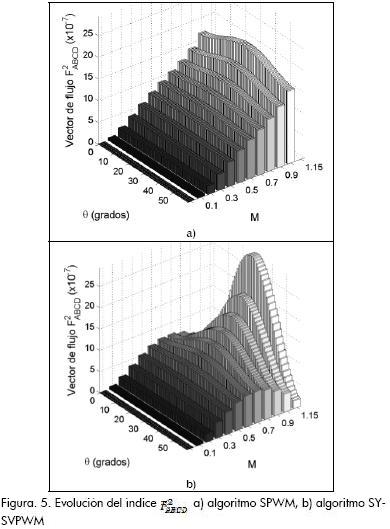
Para SPWM (Figura 5a) el índice F2ABCD es poco dependiente del ángulo de referencia θ hasta aproximadamente M=0.7. Por encima de M=0.7, alcanza la máxima amplitud del vector de F2ABCD alrededor de θ= 30.
En el algoritmo SY-SVPWM (Figura 5b) la dependencia respecto al ángulo θ se acentúa mientras el índice de modulación crece; para M= 1.15 el vector F2ABCD alcanza la máxima amplitud en θ=30°, mientras que en θ=0 y θ=60° la amplitud se reduce significativamente.
Los dos moduladores continuos presentan simetría alrededor de θ=30°, siendo comparativamente mayor la exhibida por SY-SVPWM dada la partición simétrica de estados cero de este algoritmo.
La evolución de los moduladores discontinuos se muestra en la Figura 6. La tendencia descrita por los seis algoritmos discontinuos puede ser agrupada en cuatro superficies debido al uso del mismo partidor de estado cero de algunos algoritmos DPWM dentro del primer sector, es el caso del DPWM0 y DPWMMIN o DPWM2 y DPWMMAX (Camacho y López, 2008).
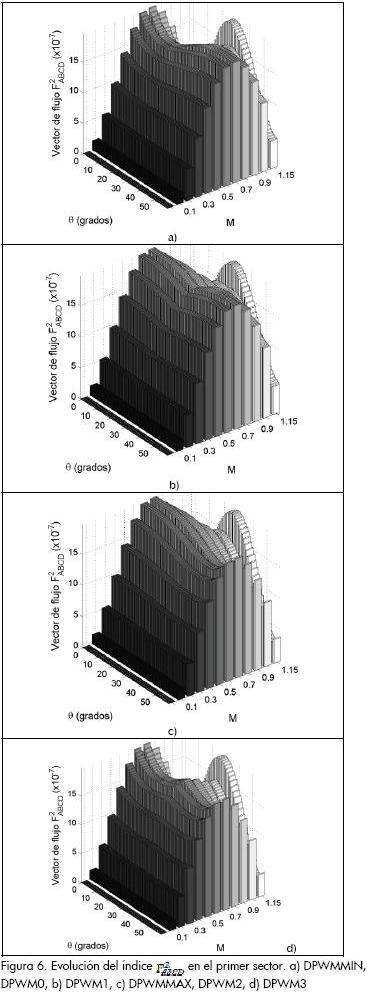
En general, para los algoritmos discontinuos las superficies del vector F2ABCD dependen de θ; sin embargo, dicha dependencia provoca una distribución de amplitudes del vector F2ABCD diferente a la ilustrada en algoritmos continuos. Como característica común de los moduladores discontinuos se observa una tendencia hacia la misma distribución de superficie en M= 1.15, distribución que presenta amplitudes menores a las ilustradas por los algoritmos continuos.
Comparando la superficie de las Figuras 5b y Figura 6, se aprecia superioridad del algoritmo SY-SVPWM en rangos bajos de M; no obstante, en alta modulación el desempeño de los algoritmos discontinuos se incrementa y en algunos puntos llega a superar a SY-SVPWM.
Factor de distorsión armónica total (FDIST)
El factor de distorsión armónica total se calcula como el valor RMS del rizado de flujo a lo largo del primer sector, como se muestra en (7).

Para realizar curvas de desempeño armónico (M,FDIST ) a lo largo del primer sector, se evaluó el índice FDIST para cada algoritmo de modulación PWM en la Tabla 1. La evaluación se hizo para N=24 (baja resolución) y N=360 (alta resolución). Los resultados se muestran en la Figura 7, donde se nota una relación inversamente proporcional entre la amplitud del índice y el índice de modulación debida al incremento de la componente fundamental como consecuencia del incremento en el índice de modulación (ecuación 7).
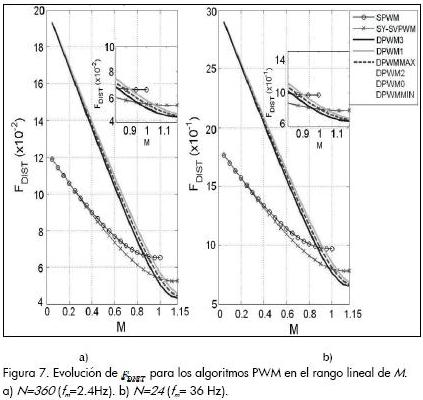
De las Figuras 7a y 7b, se deduce que la amplitud del índice FDIST es inversamente proporcional a la relación de frecuencias N y que existe una relación constante entre los desempeños armónicos de los algoritmos de modulación. Esta relación marca la superioridad de los algoritmos de modulación continuos sobre los discontinuos para índices de modulación menores a 0.9, siendo comparativamente superior el SY-SVPWM. Para índices de modulación mayores a 0.9, el desempeño armónico de los algoritmos discontinuos mejora superando al SY-SVPWM.
El análisis comparativo del factor FDIST indica que no existe un algoritmo PWM de desempeño armónico superior a lo largo del rango lineal de M; sin embargo, en pequeñas regiones de M existen algoritmos superiores. Aunque las tendencias presentadas en la Figura 7 se lograron analizando el sector I, las conclusiones dadas son válidas para todo el ciclo fundamental debido al comportamiento simétrico de los algoritmos de modulación en análisis (Camacho y López, 2008).
Diseño del algoritmo híbrido
La superioridad local de algunos algoritmos PWM brinda una alternativa para mejorar el desempeño armónico en la salida de un inversor VSI trifásico de dos niveles. Esta alternativa es la implementación de un esquema de modulación híbrido capaz de seleccionar en línea el algoritmo de modulación de menor distorsión armónica en cada punto de operación. El esquema propuesto utiliza el índice F2ABCD para seleccionar los algoritmos que conforman la solución híbrida. Este consiste en cuatro etapas:
Etapa 1: Determinar las superficies F2ABCD de cada uno de los algoritmos PWM que harán parte de la solución híbrida, para el sector I (Figuras 4 y 5).
Etapa 2: Encontrar la superficie F2ABCD de menor amplitud en cada punto de operación. Se compararon las superficies en las Figuras 4 y 5 y se seleccionaron las menores amplitudes. La superficie resultante se muestra en la Figura 8, ésta contiene las amplitudes mínimas del índice F2ABCD dentro del primer sector.
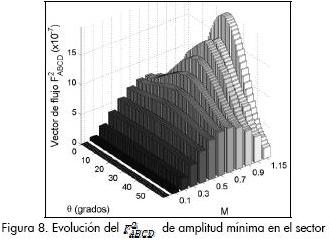
Etapa 3: Identificar los algoritmos PWM que conforman la superficie mínima encontrada. El resultado de esta búsqueda es la partición que se muestra en la Figura 9, donde se indican los algoritmos PWM que conforman la solución híbrida y los puntos de transición dentro del sector I.
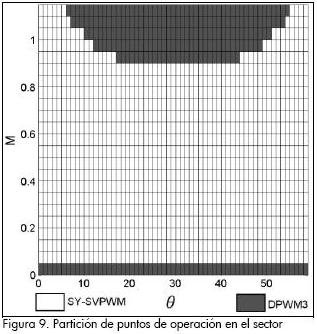
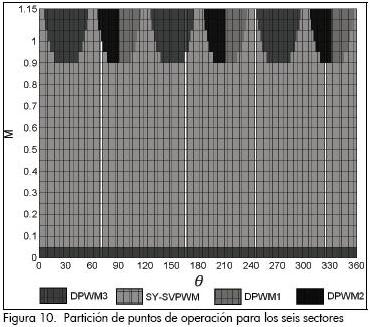
Etapa 4: Completar la partición para el ciclo fundamental. Debido a la simetría presentada por el hexágono del inversor (Figura 3), fue posible generalizar los resultados del sector I, y encontrar la partición ilustrada en la Figura 9 válida para el ciclo fundamental. Esta partición se caracteriza por presentar una simetría de 120° y emplear en el rango de modulación [0.05 < M < 0.95] el algoritmo SY-SVPWM y en alta modulación una combinación de algoritmos continuos y discontinuos dependiente de la orientación del vector referencia. Los algoritmos discontinuos PWM que constituyen la solución híbrida son: DPWM3, DPWM2 y DPWM1.
Es importante anotar que la distribución encontrada es independiente del índice N, estableciendo una ventaja en la implementación de aplicaciones que impliquen frecuencias fundamentales variables.
Validación del algoritmo diseñado
Los puntos de operación seleccionados para la validación del algoritmo híbrido se conformaron respecto de dos variables: el índice de modulación M variando entre 0.05 y 1.15 en pasos de 0,05, y el índice de frecuencias N con valores 24 y 360. La validación se realizó teóricamente mediante el cálculo del factor de distorsión armónica total FDIST y experimentalmente mediante la medición del índice de distorsión armónica de corriente VWTHD.
Validación teórica
Mediante aplicación de la ecuación (7) sobre las amplitudes del factor F2ABCD presentadas en la Figura 8 se obtuvieron las tendencias en la Figura 11. En ellas se corrobora el buen desempeño armónico teórico de la estrategia híbrida. Como se esperaba a partir de la distribución en la Figura 10, para M< 0.95 la estrategia híbrida sigue la evolución del algoritmo SY-SVPWM y en alta modulación mejora el desempeño armónico de los algoritmos continuos y discontinuos.
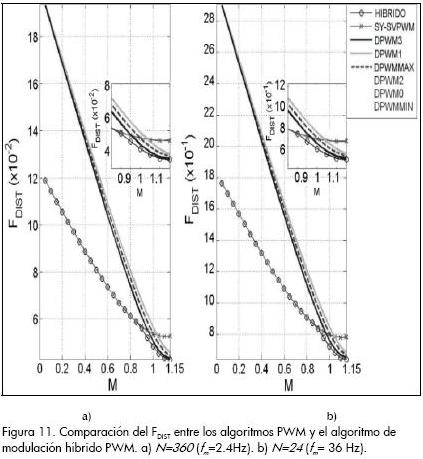
Validación experimental
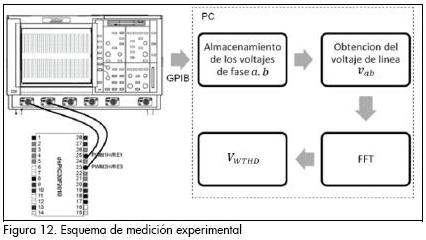
El algoritmo de modulación híbrido se implementó sobre un procesador digital de señales dsPIC30F2010 de Microchip®. El indicador de desempeño armónico adoptado fue el VWTHD, debido a la facilidad de su obtención en un entorno experimental. La validación se realizó con base en el algoritmo SY-SVPWM puesto que en (Camacho y López, 2008) se verifica que su desempeño armónico es superior al de los algoritmos discontinuos en la mayor parte del rango de operación. La obtención del VWTHD se hizo en dos etapas, inicialmente se muestrearon y almacenaron los pulsos de salida del modulador en sus niveles lógicos (0 a 5V) empleando el osciloscopio digital Lecroy 9310CM, y posteriormente mediante aplicación del algoritmo FFT (Fast Fourier Transform) (Matlab, 2007) se calculó la magnitud de las componentes armónicas y el índice VWTHD (Figura 12). Los errores de medición respecto a resultados de simulación fueron de 19,74% para N=360 y 5,21% para N=24 (Camacho y López, 2008).
Los resultados se resumen en la Figura 13. Nótese que el rango de variación de M se limita entre 0.9 y 1.15 puesto que la solución híbrida planteada difiere del SY-SVPWM a partir de M=0,95. Las tendencias obtenidas verifican que el algoritmo híbrido propuesto despliega mejor desempeño armónico dentro de todo el rango de operación lineal, superando al algoritmo SY-SVPWM y por ende a los algoritmos discontinuos. Esta mejora es más notable para un índice de frecuencias N=24, lo que evidencia su aplicabilidad en accionamientos eléctricos de alta potencia que precisan de bajas frecuencias de conmutación.
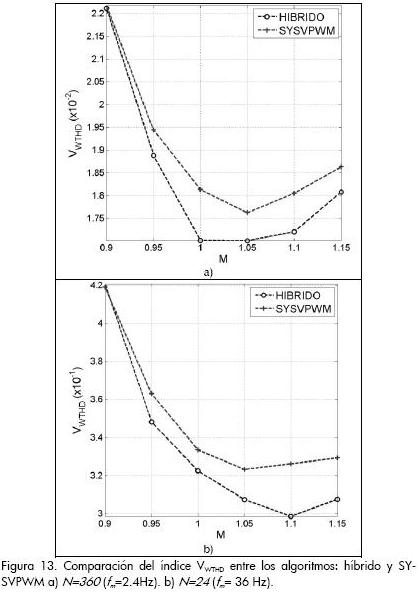
Este nuevo algoritmo de modulación PWM de desempeño armónico superior se propone llamar: Hybrid Discontinuous Pulse Width Modulation – HDPWM.
Conclusiones
En este trabajo se presenta el diseño y validación de un algoritmo PWM híbrido que supera el desempeño armónico de algoritmos de modulación comunes en procesos de conversión de potencia en accionamientos eléctricos AC. El algoritmo fue diseñado comparando los desempeños armónicos de varios algoritmos de modulación PWM caracterizados por la evolución del rizado del vector de flujo del estator. El algoritmo híbrido resultante fue validado teóricamente calculando el factor de distorsión armónica FDIST y experimentalmente midiendo el índice de distorsión armónica de corriente VWTHD. Los resultados son acordes con las predicciones teóricas y confirman la superioridad del algoritmo diseñado.
Adicionalmente, se presentó una metodología de selección de algoritmos PWM para mejorar desempeño armónico a la salida del inversor. Esta metodología fue aplicada para el inversor VSI trifásico de dos niveles, pero puede ser utilizada en otras topologías inversoras.
Nomenclatura
D Componente del eje d del vector de error generado al aplicar el vector activo V1.
fm Frecuencia fundamental
fs Frecuencia de conmutación.
FDIST Factor de distorisión armónica total
F2ABCD Valor medio del vector de flujo armónico del estator ( 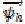 )
)
h índice armónico respecto al componente fundamental
k Indicador del sector del hexágono del inversor
K0 Partidor de estado cero
M Índice de modulación
N Índice de frecuencias
Qo Componente del eje q del vector de error generado al aplicar el vector cero V0.
Q1 Componente del eje q del vector de error generado al aplicar el vector activo V1.
Q2 Componente del eje q del vector de error generado al aplicar el vector activo V2.
Q7 Componente del eje q del vector de error generado al aplicar el vector cero V7.
t Tiempo
Tx Tiempo de activación del vector activo Vx
Ty Tiempo de activación del vector activo Vy
Tsh Medio periodo de conmutación
Tz Tiempo de activación de los vectores cero.
To Tiempo de activación del vector cero V0.
T7 Tiempo de activación del vector cero V7.
Tk Tiempo de activación del vector activo Vk.
Tk+1 Tiempo de activación del vector activo Vk+1.
vab Voltaje de línea a línea entre las fases a y b en la salida del inversor.
Vh Magnitud del h-ésimo armónico de la señal vab
Vf Magnitud del componente fundamental de la señal Vdc
VWTHD Índice de distorsión armónica total
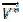 Vector espacial de referencia
Vector espacial de referencia
V0,V1,V2
V4,V5,V6 Vectores espaciales del hexágono del inversor.
Vdc Voltaje del bus DC del inversor
wm Frecuencia angular fundamental
θ Orientación del vector especial de referencia 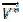
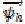 Vector especial de flujo armónico del estator
Vector especial de flujo armónico del estator 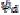 Componente del eje d de
Componente del eje d de 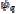 Componente del eje q de
Componente del eje q de 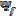 Flujo armónico fundamental.
Flujo armónico fundamental.
I II III IV V VI Sectores del hexágono del inversor
Bibliografía
Camacho, G., López, D., Evaluación experimental del contenido armónico en los algoritmos de modulacion PWM de inversores trifásicos., Tesis presentada a la Universidad del Cauca, para optar al titulo de Ingenieros en Automática Industrial, 2008. [ Links ]
Hava, A., Carrier Based PWM-VSI Drives in the overmodulation region., Tesis presentada a la Universidad de Wisconsin, para optar al grado de Doctor en Filosofía, 1998. [ Links ]
Holmes, D., Lipo, T., Pulse Width Modulation for Power Converters: Principles and Practice., Mohamed E. El Hawary (ed). Wiley -IEEE Press Series on Power Engineering, Vol. 1, 2003. [ Links ]
Holmes, G., McGrath, B., Opportunities for Harmonic Cancellation with Carrier Based PWM for Two-Level and Multi-Level Cascaded Inverters., Department of Electrical and Computer Systems Engineering, Monash University Australia, 2003. [ Links ]
Matlab., Software de análisis numérico., MathWorks Matlab Inc., 2007. [ Links ]
Murphy, J., Egan, M., Moynihan J., Theoretical spectra of space-vector-modulated waveforms., IEE Proceedings on line., No 19981564, Vol. 145, 1998, pp. 17-24. [ Links ]
Narayanan, G., Synchronised Pulsewidth Modulation Strategies based on Space Vector Approach for Induction Motor Drives., Tesis presentada al Instituto de Ciencia de la India, para optar por el grado de Doctor en Fiosofía, 1999. [ Links ]
Narayanan, G., Krishnamurthy, H., Di Zhao., Ayyanar, R., Advanced Bus-Clamping PWM Techniques Based on Space Vector Approach., IEEE Transaction on Power electronics, Vol. 21, No. 4, 2006, pp. 974-984. [ Links ]
Narayanan, G., Ranganathan, T., Analytical Evaluation of Harmonic Distortion in PWM AC Drives Using the Notion of Stator Flux Ripple., IEEE Transactions on power electronics, Vol. 20, 2005, pp. 466-474. [ Links ]
Rodriquez, P., Aportaciones a los acondicionadores activos de corriente en derivación para redes trifásicas de cuatro hilos., Tesis presentada a la Universidad politécnica de Catalunya, para optar por el grado de Doctor, 2005. [ Links ]
Van Der Broeck, H., Skudelny, H., Analytical analysis of the harmonic effects of a PWM AC drive., IEEE Transaction on Power electronics, Vol. 3, 1988, pp. 216-223. [ Links ]
Wells, J., Generalized selective harmonic control., Tesis presentada a la Universidad de Illinois, para optar por el grado de Doctor en Filosofia, 2006. [ Links ]
Zhou, K., Wang, D., Relationship between space-vector modulation and three-phase carrier-based PWM: A comprehensive analysis., IEEE transactions on Industrial Electronics, Vol. 49, 2002, pp. 186-196. [ Links ]














