Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.29 no.2 Bogotá May/Aug. 2009
Adriana Patricia Lobato Polo1, Rafael Humberto Ruiz Coral2, Julián Armando Quiróga Sepúlveda3 y Adolfo León Recio Vélez4
1 Ingeniera electrónica, Pontificia Universidad Javeriana, Colombia. Estudiante, Maestría, Informationstechnik, Hochschule Mannheim, Alemania. aplpolo@yahoo.com
2 Ingeniero electrónico, Pontificia Universidad Javeriana, Colombia. Estudiante, Maestría, Informationstechnik, Hochschule Mannheim, Alemania. ruiz.rafa@yahoo.com
3 Ingeniero electrónico, Universidad Nacional de Colombia, Manizales. M.Sc., en Ingeniería Electrónica, Universidad de los Andes, Colombia. Profesor asistente, Departamento de Ingeniería Electrónica, Pontifica Universidad Javeriana, Colombia. quiroga.j@javeriana.edu.co
4 Ingeniero electrónico, Pontificia Universidad Javeriana, Colombia. M.Sc, The Ohio State University, Columbus, OH, Estados Unidos. Estudiante Ph.D., Virginia Polytechnic Institute and State University, Estados Unidos. recio@vt.edu
RESUMEN
Muestreo compresivo es una rama emergente del procesamiento de señales, basada en el hecho de que un número pequeño de proyecciones lineales no adaptativas sobre una señal compresible contiene suficiente información para reconstruirla y procesarla. En este artículo se presentan los resultados obtenidos al evaluar cinco matrices de medición para la realización de muestreo compresivo en un sistema que utiliza el algoritmo orthogonal matching pursuit (OMP), para la recuperación de la señal original. Las matrices de medición están implicadas tanto en el proceso de muestreo–compresión de la señal, como en la reconstrucción de la misma. Dentro de este grupo de matrices estudiadas se destacó la matriz Hadamard aleatoria, con la cual es posible obtener el menor porcentaje de error en la recuperación de la señal. Adicionalmente se presenta una metodología para la evaluación de estas matrices, que permita posteriores análisis de la idoneidad de estas para aplicaciones específicas.
Palabras clave: muestreo compresivo, algoritmo orthogonal matching pursuit, matriz de medición.
ABSTRACT
Compressive sensing is an emergent field of signal processing which states that a small number of non-adaptive linear projections on a compressible signal contain enough information to reconstruct and process it. This paper presents the results of evaluating five measurement matrices for applying them to compressive sensing in a system using orthogonal matching pursuit (OMP) to reconstruct the original signal. The measurement matrices were those implicated in compressive sensing as well as in reconstructing the signal. The Hadamard-random matrix stood out within this group of matrices because the lowest percentage of error in signal recovery was obtained with it. This paper also presents a methodology for evaluating these matrices, allowing subsequent analysis of their suitability for specific applications.
Keywords: compressed sensing, orthogonal matching pursuit, measurement matrix.
Recibido: septiembre 29 de 2008
Aceptado: junio 1 de 2009
Introducción
Muestreo compresivo (MC) es un enfoque alternativo y optimizado al principio planteado por el teorema de Shanon/Nyquist, el cual permite, potencialmente, el desarrollo de aplicaciones a nivel de hardware y software menos costosas. Utilizando el principio de MC es posible realizar dos procesos de forma simultánea en la adquisición de la información: sensar y comprimir. La tecnología convencional, en contraste, realiza un proceso de muestreo seguido por uno de compresión.
Una señal dispersa o sparse es aquella que sólo presenta pocos valores distintos de cero en el dominio del tiempo o en algún otro dominio. El número de valores no nulos de una señal dispersa se conoce como su nivel de dispersión o sparcity. Muchas señales tienen representaciones dispersas en cierto espacio. Una señal perteneciente a un espacio vectorial tiene una representación dispersa si esta puede ser expresada como una combinación lineal de pocos vectores de una base de dicho espacio. Por ejemplo, las señales formadas por componentes armónicas son dispersas en bases de Fourier, y las suaves a trozos tienen representaciones wavelets con estructuras dispersas (Baraniuk, 2007; La y Do, 2006; Wakin y otros, 2006).
La matriz de medición o diccionario permite capturar información de una señal dispersa dada y es utilizada por el algoritmo OMP para la recuperación de dicha señal una vez ha sido comprimida. El hecho de que la matriz de medición presente un pequeño número de filas (vectores de medición) tiene ventajas como mayor compresión de la información y menor tiempo de procesamiento. Por tal motivo, en este artículo se presenta el estudio de diferentes clases de matrices de medición, con el fin de encontrar aquellas que permiten obtener una recuperación adecuada de la señal utilizando un menor número de vectores de medición.
En la sección muestreo-compresión de señales se presentan algunos conceptos básicos necesarios para la teoría de MC. En la sección recuperación de señales dispersas se define el problema de recuperación de una señal que ha sido comprimida bajo el principio de MC y se presenta OMP como solución a dicho problema.
En la sección herramientas de evaluación se detalla la metodología y las herramientas empleadas para la evaluación de las matrices. Posteriormente se exhiben las matrices de medición propuestas. Los resultados más relevantes se detallan en la sección resultados y análisis. En la sección trabajos relacionados se hace una breve comparación con trabajos precedentes. Finalmente, se presentan algunas conclusiones del trabajo realizado.
Muestreo – compresión de señales
Muestreo compresivo
Según el principio de muestreo compresivo, una señal discreta con una representación dispersa en cierta base puede ser recuperada a partir de un número pequeño de proyecciones lineales de dicha señal sobre una base arbitraria (Kirolos y otros, 2007).
MC sugiere una nueva forma de adquirir la información que necesita ser convertida de análoga a digital, debido a que los procesos de muestreo y compresión de la señal se realizan simultáneamente (Candes, 2006). Cuando se pretende aplicar el teorema de Shannon/Nyquist a sistemas de radiofrecuencia de amplio ancho de banda se presentan limitaciones de hardware para la implementación de una etapa análogo-digital de alta precisión y alta velocidad. Haciendo uso del principio de MC no sería necesario que todas estas muestras pasaran por dicho conversor, sino sólo un pequeño número de observaciones de la señal, lo que reduciría los requerimientos de velocidad del conversor.
Compresión – muestreo de la señal
Sea s  Rd una señal discreta real de longitud d, representada como un vector columna de d posiciones (1),
Rd una señal discreta real de longitud d, representada como un vector columna de d posiciones (1),
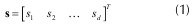
Sea Φ = [φ1 φ2 ... φd], con φi  RN para i = 1,2,...,d. La matriz Φ es un elemento de RNxd y se conoce como matriz de medición. Sus columnas, los vectores φi, se denominan átomos, los cuales tienen norma unitaria. Cada una de las N filas de Φ se conoce como vector de medición. El proceso de muestreo-compresión consiste en la obtención del vector ν como la combinación lineal de átomos de Φ dada por:
RN para i = 1,2,...,d. La matriz Φ es un elemento de RNxd y se conoce como matriz de medición. Sus columnas, los vectores φi, se denominan átomos, los cuales tienen norma unitaria. Cada una de las N filas de Φ se conoce como vector de medición. El proceso de muestreo-compresión consiste en la obtención del vector ν como la combinación lineal de átomos de Φ dada por:
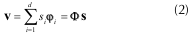
donde si es el i-ésimo elemento de s.
El vector columna ν  RN se conoce como vector de observación. Este contiene información importante acerca de la señal s.
RN se conoce como vector de observación. Este contiene información importante acerca de la señal s.
El tamaño del vector ν resultante, depende de N. A continuación analizamos dos casos de interés; en el primero de ellos, si N = d, no existe propiamente compresión de los datos, pues ν  RN, es decir, la señal original y el vector tienen la misma longitud. En el segundo caso, si N < d, la dimensión del vector V es menor a la dimensión de y por tanto existe compresión de la información. Se puede demostrar que bajo ciertas condiciones de y de la información contenida en puede ser suficiente para recuperar de forma aproximada la señal s.
RN, es decir, la señal original y el vector tienen la misma longitud. En el segundo caso, si N < d, la dimensión del vector V es menor a la dimensión de y por tanto existe compresión de la información. Se puede demostrar que bajo ciertas condiciones de y de la información contenida en puede ser suficiente para recuperar de forma aproximada la señal s.
Si s es una señal m-dispersa, es decir, solamente m de sus elementos son distintos de cero, la ecuación (2) equivale a una combinación lineal de sólo m átomos de Φ, es decir 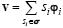 donde
donde 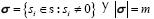 .
.
Recuperación de señales dispersas
Una vez se ha realizado la combinación lineal de átomos de Φ, el objetivo es recuperar la señal original s a partir del vector de observación ν. La recuperación difiere en complejidad dependiendo de N a continuación se analizan los dos casos mencionados en la sección anterior.
Para el primer caso, si N = d y los átomos de Φ constituyen un conjunto ortonormal (elementos mutuamente ortogonales y con norma unitaria), la señal S puede ser recuperada como:

donde la notación 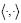 indica el producto interno en el espacio Rd.
indica el producto interno en el espacio Rd.
En este caso la representación del vector ν sobre los átomos de Φ permite recuperar de forma unívoca la señal s.
Para el segundo caso y el de mayor interés, en el cual N < d, los átomos de Φ no forman un conjunto linealmente independiente y por lo tanto tampoco un conjunto ortogonal. Por tal motivo, la recuperación de la señal no puede ser realizada descomponiendo el vector como un conjunto de proyecciones sobre los átomos de Φ.
Uno de los métodos para recuperar la señal s a partir del vector ν (Tropp, 2004), consiste en encontrar la señal 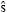 que minimiza la energía del error entre ν y la combinación lineal de átomos de Φ utilizando
que minimiza la energía del error entre ν y la combinación lineal de átomos de Φ utilizando 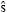 , es decir, resolver el problema de optimización:
, es decir, resolver el problema de optimización:

donde 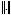 es la norma euclidiana en RN, definida como la raíz del producto interno y
es la norma euclidiana en RN, definida como la raíz del producto interno y 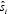 , para i = 1,2,...,d, corresponde al i-ésimo valor de
, para i = 1,2,...,d, corresponde al i-ésimo valor de 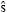 .
.
Si la señal s es m-dispersa se deben identificar los m átomos de Φ que participan en la combinación lineal para formar ν. En este caso se debe encontrar la señal 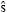 m dispersa que minimiza la ecuación (3).
m dispersa que minimiza la ecuación (3).
El éxito de la compresión y recuperación de la señal S depende del balance existente entre los siguientes tres factores:
1. La relación N/d que determina el grado de compresión de la información.
2. La matriz Φ.
3. El nivel de dispersión de la señal s.
Una solución al problema de optimización (3) es el algoritmo orthogonal matching pursuit (OMP).
Proceso iterativo
OMP es un algoritmo que en cada iteración selecciona la opción óptima a nivel local, dentro de un conjunto de posibles soluciones, esperando encontrar al final la solución óptima global.
El propósito de OMP es realizar una aproximación del vector V por medio de la selección y combinación de un conjunto de átomos de Φ que minimizan (3) en cada iteración.
La aproximación de ν se construye mediante un proceso iterativo, para lo cual el algoritmo selecciona en cada paso el átomo de Φ mejor correlacionado con el residuo de la señal (Mallat y Zhang, 1993), el cual está definido como la diferencia entre ν y su aproximación parcial, y se denota con la letra r.
Para indicar la iteración correspondiente se utiliza el subíndice t.
Al comienzo del proceso iterativo (t = 0), el residuo r0 es igual al vector ν. Seguidamente, se busca la máxima proyección de r0 sobre el conjunto de átomos de la matriz de medición.
Debido a que cada uno de los átomos se encuentra normalizado, el átomo que presenta la mayor proyección es encontrado como
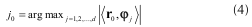

En (4) se determina la posición j0 del átomo que proporciona el mayor producto interno, el cual se conoce como átomo escogido φjo. El producto interno máximo dado por φjo y rjo se almacena en la variable λ0.
Posteriormente se procede a calcular el nuevo residuo r1 como la diferencia entre el residuo anterior y la proyección de este sobre el átomo seleccionado:
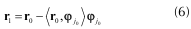
Claramente φjo es ortogonal a r1, por lo tanto:
Para minimizar la norma del nuevo residuo (error) 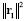 , el algoritmo OMP escoge el átomo φjo que maximiza
, el algoritmo OMP escoge el átomo φjo que maximiza 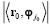 .
.
Este procedimiento se repite hasta seleccionar m-átomos de Φ. Con el fin de evitar la selección repetida, el átomo escogido en la iteración t, φjt, se ortogonaliza con los átomos escogidos en iteraciones pasadas y que han sido previamente ortogonalizados. Para dicho fin se utiliza el procedimiento de Gram-Schmidt, de acuerdo a
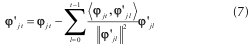
donde φ'jo es la versión ortogonalizada del átomo escogido en la iteración t.
Con el átomo φ'jo se calcula el vector residuo de la iteración t (8).
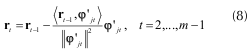
En otras palabras, la actualización del residuo consiste en suprimir del residuo actual la proyección que tiene este sobre el átomo escogido ortogonalizado (9).

Sean J y Λ los conjuntos que almacenan para cada iteración las posiciones de los átomos escogidos y los máximos productos internos, respectivamente, es decir:
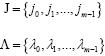
En cada una de las iteraciones se adjuntan elementos al conjunto J y Λ como en (4) y (5).
La señal s se reconstruye al final de las iteraciones como en (10), en donde se observa que la amplitud está dada por los elementos del conjunto Λ cuyas posiciones en el vector 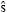 están determinadas por los elementos del conjunto J. Es decir, la posición j en
están determinadas por los elementos del conjunto J. Es decir, la posición j en 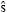 contiene la amplitud λi.
contiene la amplitud λi.

Herramientas de evaluación
Se realizó una rutina utilizando MATLAB® con la que se obtuvieron los resultados presentados a continuación. El algoritmo se ejecutó con 1.000 señales aleatorias para cada número de vectores de medición N. Las características de la señal son:
-Vector de 256 posiciones.
-Amplitud uniformemente distribuida en el intervalo de enteros [-10,10].
-Niveles de dispersión: 4, 12, 20, 28, 36, que corresponden a los mismos niveles de dispersión empleados en el artículo de Tropp y Gilbert (2005).
-Las posiciones no nulas de la señal están uniformemente distri-buidas en el intervalo de enteros [1,256].
El error de aproximación (e), es una medida de la exactitud entre la señal recuperada y la señal original, y se define como 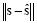 (Tropp, 2004).
(Tropp, 2004).
Definamos el porcentaje de recuperación (PR) de la señal como:
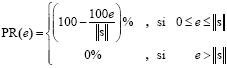
El e y PR brindan información importante sobre el desempeño del algoritmo, sin embargo utilizamos el segundo tipo de medición, pues este es independiente de la norma de s. Un PR de 100% implica un error cero, mientras un PR de 0% implica un error mayor o igual a 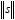 .
.
A continuación se explican las clases de gráficas extraídas de la ejecución del algoritmo OMP para las diferentes matrices de medición:
-Con base en los valores del porcentaje de recuperación de las señales en función de N, se obtuvieron gráficas estadísticas e histogramas tridimensionales.
-Función acumulativa de coherencia.
La función acumulativa de coherencia (FAC) se calcula como la máxima suma absoluta de los productos internos entre un átomo determinado con n otros átomos (Tropp, 2004), de acuerdo a
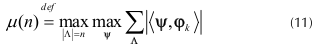
donde φk es un átomo determinado y Ψ es cualquier conjunto de átomos de cardinalidad n, que no contiene a φk, escogidos de la matriz de medición Φ.
La FAC permite tener una visión de la correlación entre todos los átomos de la matriz de medición. En general, entre más despacio crezca la FAC, mejor van a ser los resultados en la recuperación de señales.
Matrices de medición propuestas
La matriz aleatoria gaussiana, como su nombre lo indica, contiene números aleatorios con distribución gaussiana, con media cero y desviación estándar unitaria.
Para la matriz Bernoulli se implementó un caso particular de esta distribución, conocida con el nombre de distribución de Rademacher.
Una secuencia pseudo aleatoria (PN) se genera por medio de un registro de corrimiento de n Flip-flops y un circuito lógico (sumador módulo 2), interconectados para formar un circuito de realimentación con múltiples lazos. La secuencia depende de la semilla (valores iniciales en los Flip-flops) y del polinomio generador (determina las conexiones de los Flip-flops con el bloque de lógica). La secuencia PN implementada fue de máxima longitud y valores de unos y menos unos.
La matriz Hadamard de 2x2 es:
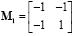
La matriz de Hadamard de puede ser construida recursivamente:
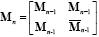
La matriz Hadamard aleatoria se construyó a partir de la matriz Hadamard desordenando sus filas con distribución aleatoria uniforme.
La matriz sinusoidal se construyó de la siguiente manera:
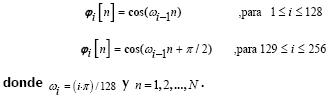
Resultados y análisis
Las gráficas estadísticas realizadas para las matrices Bernoulli, gaussiana y pseudo aleatoria arrojaron resultados muy similares, por consiguiente se analizan conjuntamente en esta sección y se referirá de ahora en adelante a estas como matrices BGP.
Estadísticas del PR
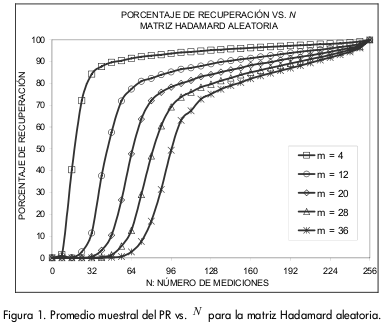
En la 0 se ilustra el PR para la matriz Hadamard aleatoria. Esta matriz arrojó las curvas más cercanas al 100% y aquellas con mayor pendiente para el menor número de vectores de medición N.
Cuando el número de vectores de medición es pequeño el PR es cercano a cero. A medida que se incrementa N la curva del PR crece, presentando un punto de pendiente máxima Nmax[m], donde m es el nivel de dispersión de la señal; por ejemplo, Nmax[4]=16. A partir de Nmax[m] la pendiente de la curva del PR comienza a disminuir. Se encontró que Nmax[m] coincide con porcentajes de recuperación en el rango del 25% al 75%. Para cada matriz el número de vectores de medición es dividido en tres zonas de acuerdo el desempeño del algoritmo:
-Zona de destrucción: para la cual el algoritmo en promedio presenta un PR menor al 25%.
-Zona de transición: para la cual el algoritmo presenta un PR promedio entre 25% y 75%.
-Zona de recuperación: para la cual el algoritmo presenta un PR promedio superior al 75%.
Las matrices BGP logran un porcentaje de recuperación superior al 80%, para todos los niveles de dispersión, excepto para , con el cual se alcanza un 78%, en el mejor de los casos.
En cuanto a la matriz sinusoidal se tiene que para los niveles de dispersión de estudio, excepto para m = 4, el algoritmo OMP requiere muchos vectores de medición para conseguir una buena recuperación de la señal.
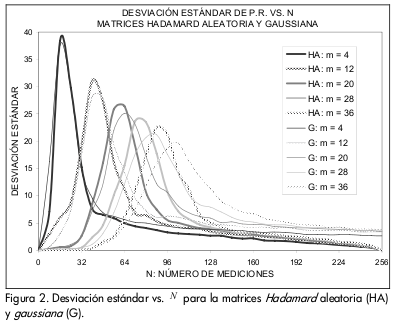
En la 0 se ilustran las gráficas de desviación estándar del PR. En la zona de destrucción se obtiene una mala recuperación para la mayoría de señales, por lo cual se presenta una baja desviación. En la zona de transición el promedio del PR mejora; sin embargo, este presenta una alta varianza que alcanza su máximo en Nmax[m], por lo que no se tiene certeza del desempeño del algoritmo. Para señales con pequeños valores de dispersión se presentan campanas de desviación angostas y con picos pronunciados, mientras que para señales con un nivel de dispersión más alto se obtienen resultados con una varianza menor, pero repartida sobre un conjunto más amplio de vectores de medición. La varianza en la zona de recuperación es una función monótonamente decreciente.
En la 0 se observa que las curvas de la matriz Hadamard aleatoria decaen más rápidamente que las matrices BGP. También se aprecia que las campanas de la matriz Hadamard aleatoria son más angostas, lo que indica que la incertidumbre en la recuperación se concentra en un número menor de vectores de medición.
Para una mejor visualización de cómo se distribuyen los PR para los diferentes valores de N se ilustra en la 0 un histograma tridimensional de los resultados obtenidos.
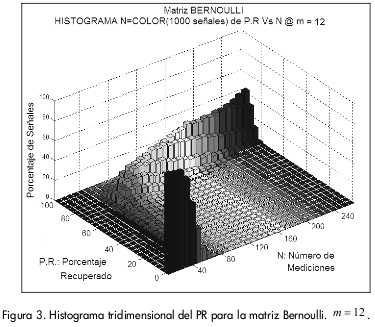
Se realizaron las siguientes observaciones:
-A medida que aumenta N las barras son más altas y la prominencia que forman se adelgaza, lo que ilustra que la desviación estándar de los porcentajes de recuperación disminuye con el aumento de N.
Se puede observar que en la zona de transición las barras son extremadamente bajas y dispersas, lo que indica que en esta zona no se tiene certeza de la recuperación la señal.
Análisis de la función acumulativa de coherencia (FAC)
En la 0 se compara la función acumulativa de coherencia para las matrices Hadamard aleatoria y sinusoidal. Para valores altos de m, la matriz sinusoidal tiene un crecimiento incluso más lento que la matriz Hadamard aleatoria. Sin embargo, se puede detallar en la gráfica que para valores pequeños de m, las pendientes de las curvas para las matrices sinusoidales son mucho mayores que las de las matrices Hadamard aleatoria.
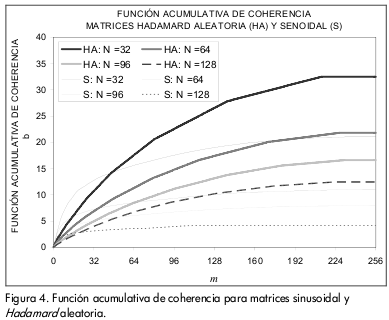
La matriz Hadamard también presenta un marcado crecimiento en la pendiente de cada una de sus curvas para valores pequeños de m. Lo anterior indica que existen productos internos muy altos, los cuales son perjudiciales para la exactitud de la recuperación de la señal.
Análisis de la correlación entre átomos
La importancia de inspeccionar la correlación entre los átomos en una matriz de medición se ilustra en el siguiente ejemplo. Suponga un conjunto ortogonal de átomos, entonces el producto interno entre el átomo φ1 y el vector de observación ν (valor del residuo en la primera iteración) es encontrado como
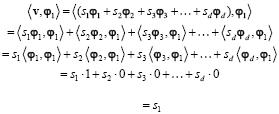
que corresponde al valor de la señal en la primera posición. Si los átomos no conforman un conjunto ortogonal se presentan productos internos diferentes de cero, los cuales, si se encuentran asociados con valores de s diferentes de cero, contribuyen a una recuperación inexacta en la amplitud de la señal.
Por tal motivo, la exactitud en la amplitud de la señal recuperada depende de:
-Grado de correlación entre átomos: Corresponde a la magnitud del producto interno entre los átomos. Entre más parecidos sean los átomos de la matriz de medición (producto interno cercano a uno), las contribuciones indeseadas que generan los productos internos tendrán mayor peso.
-Nivel de dispersión: A medida que este nivel aumenta, la amplitud del impulso buscado se ve afectada (aumentada o disminuida) por un mayor número de contribuciones indeseadas.
Obtención del número de vectores de medición
En esta sección se comparan directamente las matrices de medición con base en los resultados obtenidos del algoritmo OMP. La Figura 5 permite encontrar el mínimo número de vectores de medición N requerido para alcanzar la zona de recuperación, con un nivel de dispersión dado, para cada una de las matrices de medición propuestas.
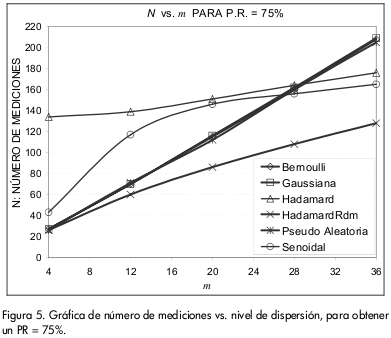
La mejor curva es aquella que utilice el menor N para obtener un PR igual a 75%. Naturalmente, si se escoge un N mayor al indicado en la Figura 5, el PR será mayor. Se observa que la matriz Hadamard aleatoria supera a todas las demás, ya que su curva está por debajo de las otras para todos los niveles de dispersión.
Existen puntos de interés en las gráficas de la Figura 5 que corresponden a las intersecciones de las diferentes curvas. Estos puntos establecen para qué intervalos en el nivel de dispersión una matriz de medición se desempeña mejor que otra. De esta manera, comparando las curvas de las matrices sinusoidal, con las de las matrices BGP, se encontró que para valores de m entre 4 y 27 las matrices BGP son mejor opción, mientras que para el intervalo de m comprendido entre 27 y 36 la matriz sinusoidal las supera. Análogamente, se observa una situación similar con la matriz Hadamard en el punto de intersección m = 28.
Así como la matriz Hadamard aleatoria superó las expectativas, también se encontró que la matriz Hadamard es la de menor PR en el intervalo de dispersión entre 4 y 28.
Trabajos relacionados
En diversos trabajos se han introducido variados arreglos de matrices y metodologías para evaluarlas. En este trabajo se presenta una comparación directa de las matrices, donde se emplearon dos tipos de herramientas de evaluación diferentes, en el sentido de que un grupo de estas son mediciones estadísticas de los esultados que arroja el algoritmo OMP al emplear cada una de las matrices, mientras que la otra herramienta utilizada efectúa mediciones directamente sobre las matrices de medición.
Haciendo referencia a las mediciones estadísticas, se encuentra que en el artículo de Tropp y Gilbert (2005), los resultados de la evaluación de las matrices Benoulli y gaussiana con el algoritmo OMP muestran un comportamiento casi idéntico en la recuperación de la señal, lo cual está en concordancia con los resultados obtenidos en este trabajo. Las diferencias entre ambos trabajos radican en que en Tropp y Gilbert (2005) se define el porcentaje de señales recuperadas a partir de la recuperación exacta de cada una de las señales, y en el caso de este trabajo se definió una medida (porcentaje de recuperación) que evalúa la recuperación a partir de la norma euclidiana del error.
En el presente trabajo se efectuaron estas mediciones para un grupo de seis matrices. Adicionalmente, se introducen los histogramas tridimensionales como herramienta de análisis.
Del conjunto de matrices evaluadas, la matriz Hadamard aleatoria, propuesta en este trabajo, es aquella con la que se obtienen los mejores resultados al recuperar señales dispersas utilizando el algoritmo OMP.
Conclusiones
Se encontró la matriz que a partir del menor número de vectores de medición logró la recuperación más adecuada de la señal. Esta es la matriz Hadamard aleatoria, la cual es la mejor opción dentro del conjunto de matrices estudiadas, para ser implementada con el algoritmo OMP.
Pese a que la matriz pseudo aleatoria no arrojó los mejores resultados, esta presenta una ventaja muy importante: su fácil generación. A partir de una semilla inicial se puede construir siempre la misma secuencia de números aleatorios y por tanto reconstruir idénticamente la matriz. Esto último puede ser aplicado en sistemas de criptografía en los cuales se encripta la información del mensaje por medio del vector de observación y en el receptor se desencripta el mensaje utilizando el algoritmo OMP. Naturalmente los únicos que conocen la semilla y el polinomio generador son el sistema transmisor y el receptor, mas no los escuchas que pueda tener el canal.
Se encontró que las matrices BGP presentan comportamientos casi idénticos al ser implementadas como matrices de medición en el algoritmo OMP.
En la compresión de los datos utilizando muestreo compresivo existe pérdida de la información que se ve reflejada en el porcentaje de error al recuperar la señal. Dependiendo de la aplicación se deben definir los niveles para una recuperación aceptable de los datos y a partir de estos determinar el nivel de compresión de los mismos.
Bibliografía
Baraniuk, R., Compressive Sensing [Lecture Notes]., IEEE Signal Processing Magazine, Vol. 24, 2007, pp. 118-121. [ Links ]
Candes, E., Compressive sampling., Proceedings of the International Congress of Mathematicians, 2006. [ Links ]
Kirolos, S., Laska, J., Wakin, M., Duarte, M., Baron, D., Ragheb, T., Massoud Y., Baraniuk, R., Analog-to-Information Conversion via Random Demodulation., 2007. [ Links ]
La, C., Do, M., Tree-based Orthogonal Matching Pursuit Algorithm for Signal Reconstruction., IEEE International Conference on Image Processing, 2006, pp. 1277-1280. [ Links ]
Mallat, S., Zhang, Z., Matching Pursuit with Time Frequency Dictionaries., IEEE Transactions in Signal Processing, 1993. [ Links ]
Tropp, J., Greed is Good: Algorithmic Results for Sparse Approximation., IEEE Trans. Inform. Theory, Vol. 50, 2004, pp. 2231-2241. [ Links ]
Tropp, J., Gilbert, A., Signal Recovery from Random Measurements via Orthogonal Matching Pursuit., 2005. [ Links ]
Wakin, M., Laska, J., Duarte, M., Baron, D., Baraniuk, R., Sarvotham, S., Takhar, D., Kelly, K., An Architecture for compressive imaging., IEEE International Conference on Image Processing, 2006, pp. 1273-1276. [ Links ]














