Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.29 no.3 Bogotá Sept./Dec. 2009
Lina Morales Laguado1 , Harold Chamorro2 y Jairo Soriano3
1 Ingeniera electrónica, Universidad Distrital Francisco José de Caldas, Colombia. Grupo Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, LAMIC, Universidad Distrital Francisco José de Caldas, Colombia. linam_26@hotmail.com.
2 Ingeniero electrónico, Universidad Distrital Francisco José de Caldas, Colombia. Grupo Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, LAMIC, Universidad Distrital Francisco José de Caldas, Colombia. hr.chamo@ieee.org.
3 Ingeniero químico, Universidad Nacional de Colombia. Ingeniero electrónico y M.Sc., en Ingeniería Industrial, Universidad Distrital Francisco José de Caldas, Colombia. Grupo Laboratorio de Automática, Microelectrónica e Inteligencia Computacional, LAMIC, Universidad Distrital Francisco José de Caldas, Colombia. jjsorianom@unal.edu.co.
RESUMEN
Este trabajo propone el análisis y diseño de dos estrategias de control para un conversor CC-CC reductor de corriente permanente. Tal tipo de dispositivos de electrónica de potencia convierten una tensión continua a otra de menor magnitud y cuyas características de no linealidad son evidenciadas. Se presentan entonces, dos técnicas de control no lineal, la primera propuesta es un control óptimo PI (error proporcional e integral del error) convencional, basado en la minimización del criterio ITSE (integral del cuadrado del error ponderado en el tiempo). Para ello se obtiene un modelo de la planta en un punto de operación. La segunda propuesta es un control difuso cuyos conjuntos de entrada y salida son también definidos minimizando el criterio ITSE en el sistema general, y estableciendo como entradas el error proporcional y la integral del error. A continuación se realiza una variación de la carga para establecer la eficiencia del sistema con los dos controladores mencionados. Se debe tener en cuenta que este tipo de sistemas no debe presentar sobretensiones considerables, ya que puede ocasionar daño en él. En este sentido, los parámetros encontrados en el diseño de los dos controladores corresponden a una metodología analítica y descriptiva. Los resultados obtenidos en simulación, y estableciendo como figura de mérito el índice de desempeño mencionado (ITSE) y el consumo de potencia, muestra que la respuesta del sistema para el control difuso presenta un mayor consumo de potencia que el control óptimo, mientras que el ITSE obtenido es mayor para el control óptimo que para el difuso. Se concluye que la exploración de este tipo de conversores, utilizando técnicas de control no lineal y minimizando los diferentes índices de desempeño, es aplicable.
Palabras clave: control difuso, control PI, conversor reductor, criterio ITSE, potencia.
ABSTRACT
This document proposes analysing and designing two control strategies for permanent current DC-DC buck converter. These kinds of electronic devices convert a constant-voltage to a lower constant-voltage (nonlinearity characteristics being demonstrated). Two nonlinear control techniques are shown. The first is a conventional optimal proportional error and integral error (PI) controller based on minimising integral of time per squared errors (ITSE) criteria. A model of the plant at an operation point was thus obtained. The second one was fuzzy control where input and output sets were also defined by minimising ITSE criteria in the overall system and establishing inputs such as proportional error and integral error. Load was then varied to establish the system's efficiency with both the aforementioned controllers. It must be borne in mind that such systems should not present supervoltage since this can cause damage. The parameters found in designing both controllers thus corresponded to analytical and descriptive methodology. Simulation results, the performance index mentioned above (ITSE) and power consumption showed that the system's response for the fuzzy control drew more power consumption than the optimal controller; otherwise, obtained ITSE was larger for the optimal control than the fuzzy control. It is concluded that exploring these types of converter is applicable when using nonlinear control techniques and minimising the different performance indices.
Keywords: fuzzy control, PI control, buck converter, ITSE criterion, power.
Recibido: octubre 22 de 2008
Aceptado: octubre 15 de 2009
Introducción
Los conversores CC-CC son elementos importantes en el campo de la electrónica de potencia, que convierten una tensión de Salida en una magnitud mayor o menor a la entrada. Un ejemplo de lo anterior es el conversor lineal, que corresponde al circuito más sencillo entre los diversos tipos de conversores (Hart, 2001). Pero la baja eficiencia de este conversor es una desventaja importante debido a la pérdida de potencia en el transistor. Una alternativa más eficiente al regulador lineal es el conversor conmutado, en el cual el transistor funciona como un interruptor electrónico, al estar completamente activado o completamente desactivado (Hart, 2001; Rashid, 2000). Esto permite que la potencia absorbida por la carga sea casi la totalidad de la potencia del sistema, y la potencia absorbida en el transistor sea casi nula.
Los conversores CC-CC que son conmutados se caracterizan por su comportamiento no lineal (Chamorro et al., 2008a; Díaz y Soriano, 2007; Chamorro et al., 2008b; Hart, 2001; Rashid, 2000). La conmutación es en alta frecuencia, por lo que se presenta una ventaja debido a que se reduce el tamaño y costo de sus componentes, pero presenta una desventaja en el funcionamiento en corte y saturación del transistor ya que éste no es ideal, generando pérdidas de potencia disminuyendo su eficiencia.
El conversor reductor es un dispositivo conmutado seguido de un filtro pasabajo conformado con una bobina y un condensador para obtener una salida de tensión continua pura. Al modificar alguno de sus principales parámetros (carga, el ciclo útil de conmutación, la bobina o la frecuencia de conmutación del transistor), ocasiona un cambio en las ecuaciones diferenciales que describen el comportamiento del sistema. Dado que dicho comportamiento es no lineal, diseñar y plantear un controlador adecuado es de gran importancia.
En este documento se utiliza un conversor reductor cuyas diferentes soluciones presentadas para su análisis realizan aproximaciones al modelo real del conversor. Se utiliza el modelo LTI (modelo lineal invariante en el tiempo) para diseñar los tipos de control planteados en este documento. El diseño de un controlador clásico o uno inteligente, pretende llevar a cabo la regulación de voltaje en la carga de este conversor. Primero se muestra un diseño de control óptimo minimizando el índice de desempeño ITSE, seguido de una nueva técnica no tradicional, catalogada dentro de la inteligencia computacional como lo es el control difuso, minimizando también el índice de desempeño ITSE. Finalmente se presentan los resultados cuantitativos evaluando los índices de desempeño definidos.
Sistema a controlar
El sistema a controlar es un convertidor CC-CC reductor, esto es, el interruptor seguido de un filtro pasa-bajo LC. El circuito correspondiente se muestra en la Figura 1.
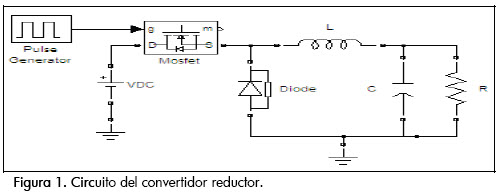
El modelo matemático del conversor depende no sólo de los componentes de su estructura, sino también de la configuración que adquiere el circuito al cambiar de estado de conmutación. Por esto, cada estado de conmutación es representado por un modelo diferente. Para obtener el modelo matemático general del sistema (1) se considera que la corriente sobre la bobina es permanente (Hart, 2001; Rashid, 2000).

Donde, Vo es la tensión de salida, D es el ciclo útil y Vs es la tensión de la fuente.
Filtro pasa-bajo:
El análisis del filtro pasa-bajo consiste en obtener la función de transferencia de éste usando la transformada de Laplace (2). La función de transferencia correspondiente al filtro pasa-bajo del conversor CC-CC reductor se expresa en (3).
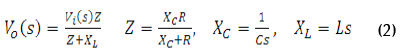
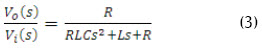
Donde, Vo es la tensión de salida, Vi la tensión de la fuente, R la resistencia, L la bobina, C la capacitancia, Xc y XL corresponden a las impedancias de la bobina y del capacitor, y Z es el paralelo entre la resistencia y el capacitor.
Otra representación matemática del sistema alternativo a la ecuación (3) y que incluye la conmutación del sistema es utilizar un modelo LTI obtenido por promediado del espacio de estados en el apéndice B de Hart (2001). Aquí se realiza un análisis en lazo cerrado y en lazo abierto representando el sistema mediante variables de estado. El promediado de estados es un método general para describir un circuito que cambia a lo largo de un periodo de conmutación (Hart, 2001). En dicho método se hace un análisis de pequeña señal y régimen permanente, por lo que es una aproximación adecuada de la función de transferencia que representa al conversor reductor en estado estacionario.
Se obtiene el modelo LTI en Hart (2001) para entrada VS., pero para efectos de este documento se efectúa un cambio de tal manera que la entrada al sistema sea el ciclo útil de conmutación D (4). La salida del conversor reductor se obtiene en (Hart, 2001). La función de transferencia del sistema puede hallarse del modelo LTI en (5), donde Vc es la tensión en el capacitor, iL la corriente en la bobina, rc la resistencia del capacitor y Vs corresponde a la tensión de la fuente.
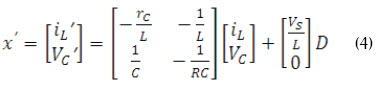
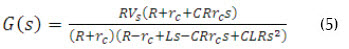
Teniendo en cuenta que se busca un diseño del sistema con corriente continua en la bobina y a partir de la planta con parámetros ya establecidos, para poder diseñar los dos tipos de control planteados en el documento el punto de operación para el convertidor CC-CC reductor se da en (6), donde f corresponde a la frecuencia de operación.
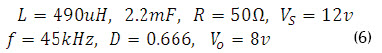
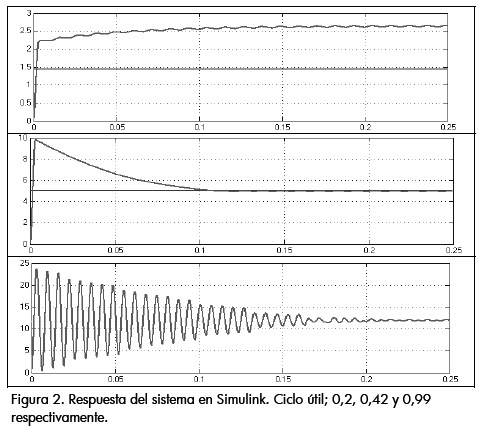
Utilizando Simulink® se puede observar la respuesta del conversor reductor al cambio de entrada D en el rango de valores de 0,12 a 1, rango que asegura que la corriente de la bobina será continua. En la figura 2 se evidencia el comportamiento no lineal del sistema para diversos ciclos útiles, junto con su valor de referencia.
Controlador PI óptimo
Selección del controlador
La manera como los controladores determinan una acción de control para mantener la referencia es mediante el error obtenido por realimentación. Para un controlador PI (proporcional-integral), el aporte del controlador proporcional genera un error de estado estacionario, el cual será eliminado por el aporte integral del controlador PI, ayudando no solo a esto, sino haciendo la respuesta del sistema aún más rápida (Beccuti et al., 2005; Chen, 1993).
El control óptimo es una técnica matemática para minimizar un criterio determinado en sistemas que evolucionan en el tiempo y que son susceptibles de ser influenciados por fuerzas externas (Chen, 1993). Se basa en llegar a la configuración del controlador desde la respuesta del sistema en general; es decir, primero se encuentra la función de transferencia general del sistema para encontrar después el compensador requerido.
Para este documento se eligió el índice de desempeño o criterio integral del cuadrado del error ponderado en el tiempo (ITSE) debido a que éste no sólo tiene en cuenta la minimización del error sino el tiempo de establecimiento del sistema (Chen, 1993). El índice de desempeño ITSE presenta más ponderación para errores grandes, los cuales se presentan generalmente en la respuesta transitoria, y menor ponderación para errores pequeños.
Diseño del modelo óptimo
Teniendo en cuenta el modelo LTI obtenido en (5), siendo una aproximación apropiada para describir el comportamiento del conversor reductor (Hart, 2001) y utilizando el punto de operación determinado en (6), se lleva a cabo la discretización del modelo empleando el método de Euler (Zak, 2003) con un periodo de muestreo de 0.1ms para el diseño del control óptimo PI del sistema mediante la herramienta computacional Solver® de EXCEL®, minimizando el índice de desempeño ITSE en el sistema. La función de transferencia del controlador PI se muestra en (7).
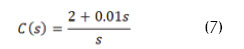
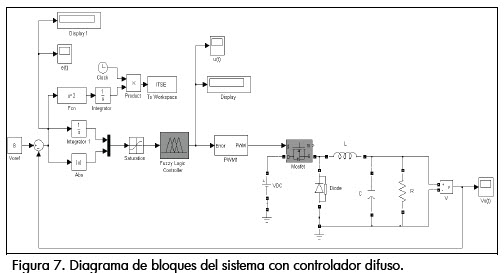
En la figura 3 se muestra el diagrama de bloques del sistema junto con el controlador PI óptimo.
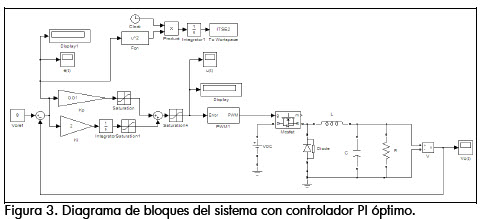
Resultados en simulación
Utilizando Simulink® se puede apreciar la respuesta del sistema para distintas cargas, así:
El control óptimo tiene una buena respuesta cuando los parámetros de la planta son los utilizados para el diseño del controlador a utilizar. Se puede ver en la figura 4 que al variar la carga, el control óptimo no responde de la mejor manera, ya que este control no fue diseñado para dichos puntos de operación y para mejorarlos habría que volver a calcular un nuevo controlador. Esto es una desventaja debido a que los elementos del dispositivo y en general los parámetros del conversor no son ideales y tendrán valores inexactos, o en su defecto, cambiarán debido a perturbaciones externas.
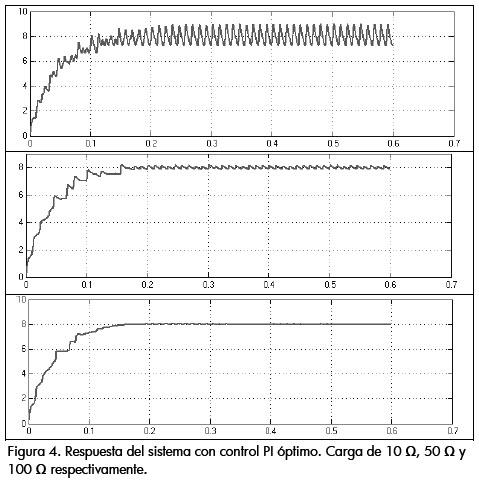
En la figura 4 se expresa el resultado del sistema variando la carga. Allí se nota que a mayor carga el comportamiento del sistema será mucho mejor debido a que requerirá menor potencia y por ende, menor energía para llegar a la referencia deseada. Sin embargo es de notar que la respuesta del sistema con carga de 50 Ω, que corresponde al punto de operación, exhibe un buen comportamiento, teniendo en cuenta que la carga es muy pequeña, esto se puede demostrar comparándolo con el comportamiento en lazo abierto del sistema (figura 2, ciclo útil 0,62). A partir del comportamiento mostrado utilizando los parámetros del controlador PI óptimo obtenidos se puede concluir que dicho controlador (7) es una buena alternativa debido a que variando la carga presenta una respuesta tolerable para el sistema, mejorando no sólo el tiempo de establecimiento sino la energía requerida para estabilizar en la referencia deseada.
Controlador difuso
Características del controlador
En la actualidad se han realizado muchos estudios y aplicaciones de la lógica difusa que han llevado a un rápido progreso de esta teoría, proporcionando una alternativa para enfrentar situaciones del mundo real, complejas y dinámicas (Chamorro y Trujillo, 2009). Así mismo, el control difuso posee una gran aplicabilidad en sistemas no lineales (Díaz y Soriano, 2007; Mendel, 1995; Mendel, 2001; Wang, 1997). Dada la no linealidad del conversor reductor, esta técnica puede ser utilizada, ya que permite simplificar el diseño del controlador del sistema general. La lógica difusa se basa en un algoritmo capaz de convertir una estrategia de control lingüístico descrita mediante reglas de la forma Si – Entonces, que por obvias razones resulta ser más sencilla que los modelos matemáticos, convirtiéndola en una estrategia de control automático que responda con mayor inteligencia a imprevistos y efectos externos al que pueda estar sometida la planta (Mendel, 1995; Mendel, 2001; Wang, 1997).
El control difuso utiliza el conocimiento de un experto en vez de ecuaciones diferenciales que describan la planta (Mendel, 1995; Mendel, 2001; Wang, 1997). Así se espera entonces que la máquina de control se base en dicho conocimiento empírico para tomar acciones en el sistema sin conocer de antemano el modelo de la planta a controlar. Esto es una ventaja, ya en muchas ocasiones conocer el modelo matemático de la planta no resulta posible.
Universos de discurso de entrada y salida
Se definen como variables de entrada el error y la integral del error. La variable de salida corresponderá al ciclo útil de acción en el convertidor reductor. A cada variable de entrada y de salida se le asocian términos lingüísticos o conjuntos difusos (antecedentes y consecuentes). Para el antecedente y consecuentes del control se proponen conjuntos difusos tipos gamma, L y triangular, debido a que estos tipos de conjuntos permiten facilidad de implementación, minimización en su cálculo y cobertura del universo de discurso. Se tiene en cuenta que para establecer los parámetros de los conjuntos difusos se utiliza la herramienta computacional Solver® de EXCEL®, minimizando el índice de desempeño ITSE en el sistema.
Los límites del universo de discurso de la entrada integral del error son -5v y 5v, y los de la entrada error son 0v y 5v, que son valores prácticos a la hora de implementar en dispositivos como FPGA's o microcontroladores. Los límites del universo de discurso de la Salida toman valores de 0,12 y 1 para el ciclo útil asegurando corriente continúa en la bobina. Es de notar que se debe hacer un ajuste de las señales de entrada al controlador para valores superiores e inferiores a los establecidos utilizando saturadores. Esto no representa mayor problema, pues si se observa de la manera como se definieron los conjuntos difusos extremos (figura 5), aquellos valores tendrán la misma pertenencia que para valores de entrada de -5v o 5v.
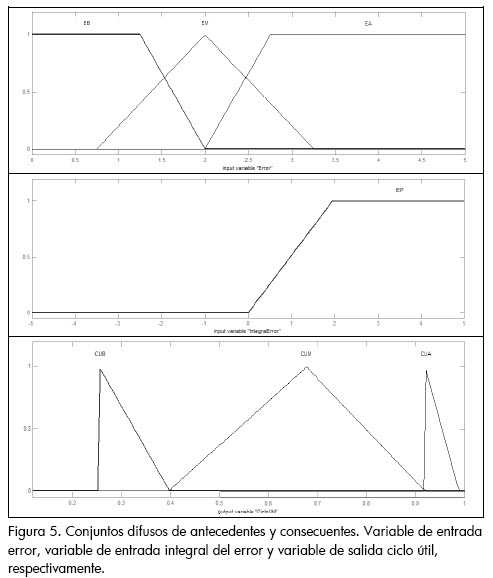
Los conjuntos difusos correspondientes a cada variable son denominados EB (error bajo), EM (error medio), EA (error alto) para la variable de entrada error, e IEP (integral del error positivo) para la variable de entrada integral del error. Por último, CUB (ciclo útil bajo), CUM (ciclo útil medio) y CUA (ciclo útil alto). A continuación se muestran los conjuntos difusos de las variables de entrada y salida del controlador:
Fusificador
El fusificador se encarga de otorgar a la entrada el valor de pertenencia Μ(x) respectivo a cada uno de los conjuntos difusos establecidos. Para el sistema planteado en el documento se utiliza el ToolBox Fuzzy Logic de la herramienta computacional MATLAB®, pues facilita la consecución de las funciones de pertenecía permitiendo la elección de varios tipos de ellas, como por ejemplo, trapezoidal, gamma, L, triangular, sigmoidea, entre otras. MATLAB® maneja como fusificador la función Singleton (valores puntuales).
Inferencia difusa
La herramienta computacional MATLAB® permite elegir entre la inferencia difusa tipo Mamdani y tipo Sugeno. Para efectos de este documento se utiliza la inferencia difusa tipo Mamdani por su simplicidad y por ser una de las más adecuadas y comunes en aplicaciones de sistemas de control con lógica difusa (Chamorro y Trujillo, 2009; Díaz y Soriano, 2007). Así mismo, se utiliza el método min para los operadores T-norma y el método máx para los operadores S-norma. La implicación utiliza el método min.
Base de reglas difusas
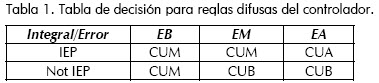
A partir del análisis del comportamiento de la planta se definen seis reglas difusas de tipo Si-Entonces (Tabla 1), teniendo en cuenta todos los estados posibles del conversor, facilidad de implementación y menor gasto computacional.
Defusificador
En un trabajo previo para el control difuso de un conversor reductor-elevador; se sugiere como método adecuado de defusificación el centroide (Lin y Hua, 1993). Se utiliza este método para el conversor propuesto, permitiendo un costo computacional bajo.
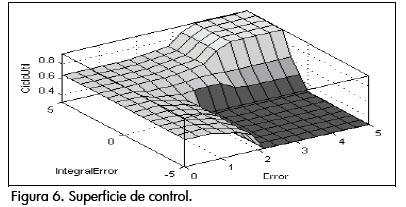
Superficie de control
La superficie de control describe el comportamiento del controlador para el intervalo de entrada (error y la integral del error) en el que opera el conversor. La superficie de control para el conversor reductor propuesto se muestra en la figura 6 y se obtuvo del ToolBox Fuzzy Logic de MATLAB®.
Resultados en simulación
Utilizando Simulink® se puede observar la respuesta del sistema para diferentes cargas (ver figura 8).
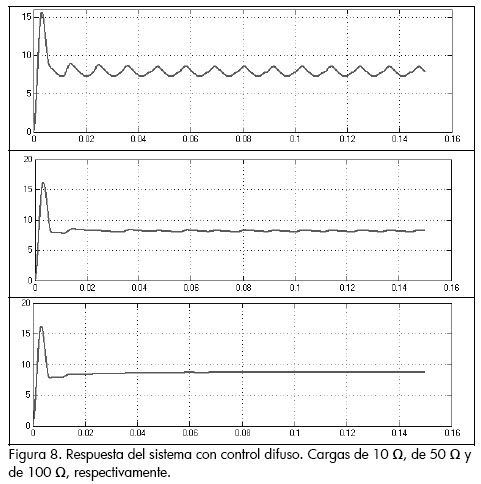
El control difuso tiene una buena respuesta, asegurando el punto de operación determinado en (6), pues posee un tiempo de establecimiento corto en comparación con el de lazo abierto. Se puede apreciar en la figura 8 que al variar la carga el sistema no responde de la mejor manera debido a que el tiempo de establecimiento no es igual. Además, de la misma manera que en el control óptimo, a medida que se aumenta la carga el comportamiento del sistema será mucho mejor por cuanto se reducen las oscilaciones, requiriendo menor potencia y por ende menor energía para llegar a la referencia deseada. Sin embargo, a diferencia del control óptimo, se presenta un sobrepico aproximado del 100%, lo que implica una sobretensión, generando un consumo de energía alto para la fuente de alimentación, además de sobrecarga en el sistema (Bose, 2002; Rashid, 2000). Es de notar que este pico tiene un tiempo de 60 ms aproximadamente; no obstante, puede producir daños o desgaste de los elementos que constituyen la planta.
Debido a que los conjuntos difusos fueron propuestos de acuerdo a un punto de operación, al cambiar la carga se modificara éste también, ocasionando que el comportamiento del sistema no sea el esperado. El desempeño del sistema con carga de 50 Ω (punto de operación) presenta la mejor respuesta pues tiene menor error de estado estacionario en comparación con la respuesta obtenida con carga de 100 Ω y menor oscilación en comparación con la respuesta obtenida con carga de 10 Ω.
En un control difuso se puede ver la dependencia directa que tiene el comportamiento del sistema con respecto a los conjuntos difusos con los cuales se diseña el controlador. Es de notar que a mayor cantidad de reglas difusas establecidas se abarca y se hace una mejor distribución del universo de discurso, mejorando la respuesta del sistema al variar parámetros de la planta como lo es la carga del sistema.
Resultados obtenidos
Los dos tipos de control analizados en el documento presentan ciertas ventajas uno con respecto al otro. El control óptimo muestra una respuesta con menor consumo de potencia (Figura 9) y en la tabla 2 se despliega la integral bajo la curva de potencia. Al variar la carga la respuesta con el control óptimo es muy similar a la obtenida en el punto de operación.
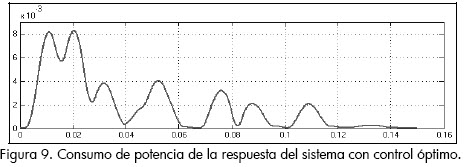
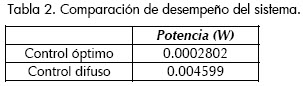
En la figura 9 se aprecian varios picos que representan el consumo de potencia de la respuesta del sistema. Se debe tener en cuenta que la escala de potencia esta en milivatios.
Con el control difuso, por el contrario, se presenta inicialmente un sobrepico a cambio de menor tiempo en su establecimiento (que equivale a una respuesta más rápida del sistema). Adicionalmente, para cargas diferentes a las del punto de operación, la respuesta empieza a mostrar errores de estado estacionario. A diferencia de la respuesta obtenida con control óptimo, el consumo de potencia es más alto. En la figura 10 se observa el consumo debido al sobre-pico mencionado. Es de aclarar que, a pesar de que en la figura se presenta sólo un pico, el consumo de potencia es mayor que el de la figura 9.
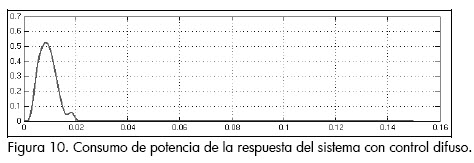
En la siguiente tabla se indican los valores de consumo de potencia de las respuestas de los dos controles diseñados.
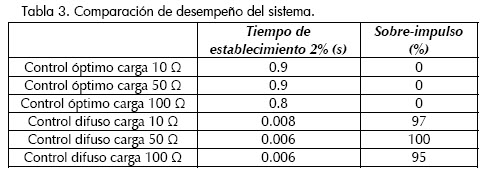
Las características de tiempo de establecimiento y sobreimpulso de las respuestas de los sistemas con los dos controladores diseñados se exponen en la tabla 3. Se observa que la respuesta con el control difuso exhibe menor tiempo de establecimiento pero con sobreimpulso, en contraste con la respuesta del control óptimo, cuyo tiempo de establecimiento es mayor pero sin sobreimpulso.
La figura de mérito determinada en este documento es el índice de desempeño ITSE. Los resultados obtenidos se ofrecen a continuación:
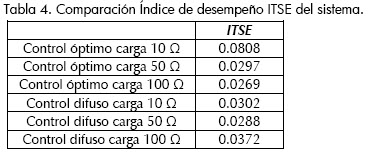
Al minimizar el índice de desempeño ITSE se obtiene para el punto de operación determinado (6) y con menor carga, un menor valor para el sistema con control difuso. En el punto de operación el ITSE es similar para las dos topologías de control utilizadas.
Conclusiones
La capacidad del control difuso para aplicarse a plantas no lineales con características como lo son las de un conversor reductor, se evidenció. Se demuestra en este documento que para variaciones de la carga en el conversor, la respuesta del sistema con los dos controladores es satisfactoria, mostrando un error de estado estacionario y tiempo de establecimiento tolerables. Teniendo en cuenta que el índice de desempeño propuesto para los controladores fue el ITSE, se minimiza la energía requerida por el sistema y la salida converge a lo deseado.
En trabajos futuros se propone explorar el uso de técnicas de control y el manejo de otros índices de desempeño para el control de conversores reductor debido a que han sido poco tratados académicamente. Las técnicas de control propuestas pueden ser utilizadas en otro tipo de conversor CC-CC, tales como los CUK y SEPIC, los cuales presentan características similares de no línealidad.
Bibliografía
Beccuti, A., Papafotiou, G., Morari, M., Optimal Control of the Boost DC-DC Converter Decision and Control., European Control Conference, 2005. [ Links ]
Bose, B., Modern Power Electronics and AC Drivers., Prentice Hall, 2002. [ Links ]
Chamorro, H. R., Morales, L., Soriano, J. J., Díaz, N., Control Óptimo para un Conversor Buck Boost., EPIM 2008. [ Links ]
Chamorro, H. R., Trujillo, C. L., Switching Losses Analysis of a DC Link Fuzzy Logic Controller Scheme Applied to a VSC., NAPS 2009. [ Links ]
Chamorro, H. R., Linares, D., Iregui, S., Soto, I., Diseño e implementación de un control optimo para un conversor DC – DC., II SIFAE & CE, 2008. [ Links ]
Chen, C., Analog and Digital Control System Design: Transfer- Function, State-Space, and Algebraic Methods., Saunders College, 1993, pp. 551. [ Links ]
Diaz, N., Soriano, J., Study of two Control Strategies based in Fuzzy Logic and Artificial Neural Network compared with an Optimal Control strategy applied to a Buck Converter., NAFIPS 2007. [ Links ]
Hart, D., Electrónica de Potencia., Pearson, 2001, pp. 201. [ Links ]
Lin, B., Hua, C., Buck/Boost Converter Control with Fuzzy Logic Approach., IECON 1993. [ Links ]
Mendel, J., Fuzzy Logic Systems for Engineering: A tutorial., Proceedings of IEEE, Vol. 83, No. 3, Marzo, 1995. [ Links ]
Mendel, J., Uncertain Rule based Fuzzy Logic System., Prentice Hall, New York, 2001. [ Links ]
Rashid, H., Electrónica de Potencia: Circuitos, Dispositivos y Aplicaciones., Academic Press, 2000. [ Links ]
Wang, L., A course in Fuzzy Systems and Control., Prentice Hall, 1997, pp. 1-59. [ Links ]
Zak, S., Systems and Control., Oxford University Press, 2003, pp. 62. [ Links ]














