Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.29 no.3 Bogotá Sept./Dec. 2009
Genaro Daza-Santacoloma1 , Julio Fernando Suárez-Cifuentes2 y Germán Castellanos-Domínguez3
1 Ingeniero electrónico, M.Sc., en Automatización Industrial y ©Ph.D., en Ingeniería Automática, Universidad Nacional de Colombia, Manizales. Miembro, Grupo de Control y Procesamiento Digital de Señales, Universidad Nacional de Colombia, Manizales. gdazas@unal.edu.co
2 Estadístico, Universidad Nacional de Colombia. M.Sc., en Estadística Matemática, Centro Iberoamericano de Enseñanza Estadística - CIENES-OEA, Chile. Profesor, Departamento de Matemáticas y Estadística y Miembro, Grupo de Control y Procesamiento Digital de Señales, Universidad Nacional de Colombia, Manizales. jfsuarezc@unal.edu.co
3 Ingeniero de sistemas radiotécnicos y Ph.D., en Dispositvos y Sistemas de Proceso, Universidad Técnica de Moscú de Comunicaciones e Informática, Rusia. Profesor, Departamento de Ingeniería Eléctrica, Electrónica y Computación y Líder, Grupo de Control y Procesamiento Digital de Señales, Universidad Nacional de Colombia, Manizales.cgcastellanosd@unal.edu.co
RESUMEN
Se presenta una metodología para el preproceso de características generadas a partir de registros electrónicos de bioseñales, particularmente se experimenta con señales de voz en la detección automática de patologías. La metodología de proceso propuesta se limita a tres fases: detección de datos atípicos, verificación de normalidad y transformación de distribuciones. La metodología conlleva al mejoramiento en la detección de las patologías de voz, además de reducir la complejidad computacional de los algoritmos de clasificación. El desempeño del clasificador indica un aumento superior a 15 puntos porcentuales en la detección de disfonías al emplear la metodología.
Palabras clave: preproceso, datos atípicos, normalidad, Box-Cox, reconocimiento de patrones, clasificación, patologías de voz.
ABSTRACT
A methodology for biosignal data preprocessing is presented. Experiments were mainly carried out with voice signals for automatically detecting pathologies. The proposed methodology was structured on 3 elements: outlier detection, normality verification and distribution transformation. It improved classification performance if basic assumptions about data structure were met. This entailed a more accurate detection of voice pathologies and it reduced the computational complexity of classification algorithms. Classification performance improved by 15%.
Keywords: preprocessing, outlier, normality, Box-Cox, pattern recognition, classification, voice pathology.
Recibido: octubre 5 de 2008
Aceptado: noviembre 3 de 2009
Introducción
Los sistemas de análisis de datos y de reconocimiento de patrones están frecuentemente afectados por los efectos que pueden acarrear mediciones erróneas o distorsión de la información medida. Sin embargo, múltiples procesos de verificación de la calidad y de la representatividad de dichas mediciones se realizan para ajustar los datos de análisis de forma objetiva. Además, seleccionar correctamente el volumen de la muestra y aplicar una apropiada metodología de registro, son factores igualmente importantes en la obtención de mediciones adecuadas. El preproceso de datos tiene como objetivo la disminución de la influencia, y en lo posible, la eliminación de los errores de medida ocasionados por fallas sistemáticas u ocasionales durante el registro de las señales. El preproceso permite ejercer control sobre la homogeneidad de las propiedades estadísticas de las diferentes características del fenómeno aleatorio (Daza-Santacoloma et al., 2007). Convencionalmente, el preproceso de los datos puede dividirse, por lo menos, en tres etapas básicas: remoción de valores atípicos, verificación de normalidad y transformación de distribuciones.
La etapa de remoción de valores atípicos es imprescindible. La consecuencia directa de la inclusión de observaciones atípicas dentro de los datos de análisis es la distorsión de las estimaciones de los valores de aleatoriedad, por ejemplo de las medias y desviaciones típicas, construyendo falsas relaciones entre los datos (Peña y Prieto, 2001). La verificación de normalidad consiste en corroborar que la función de densidad de probabilidad de las variables corresponda con una distribución normal, esto es necesario porque muchos análisis posteriores de los datos se realizan bajo este supuesto. Cuando la hipótesis de normalidad de los datos no se cumple, es preferible aplicar una transformación sobre ellos que permita que dicha hipótesis sí se verifique. Con el fin de evidenciar los beneficios del preproceso aplicado a sistemas de reconocimiento de patrones en bioseñales se presenta un ejemplo de reconocimiento automático de patologías de voz y sus mejoras al aplicar cada una de las etapas de preproceso señaladas. Se puede apreciar cómo la precisión final del sistema de reconocimiento es contundentemente mayor.
Este artículo tiene la siguiente estructura: corta descripción de un sistema básico de reconocimiento de patrones, descripción de las tres etapas del preproceso de los datos, en la tercera sección se plantea el marco experimental y se especifican las pruebas realizadas, finalmente se discuten los resultados y presentan las conclusiones.
Reconocimiento de patrones y preproceso de datos
Sistema de reconocimiento de patrones
Usualmente un sistema de reconocimiento de patrones se describe en concordancia con el diagrama que se aprecia en la figura 1. En una primera etapa, a partir del objeto (observación) se extraen mediciones (señales capturadas por medio de sensores) que se deben revisar y adecuar a fin de reducir o descartar problemas derivados del ruido o falla en los instrumentos de medida. A partir de las señales capturadas y adecuadas, se inicia la generación de características, que permite construir valores representativos que revelen o permitan descubrir algún tipo de patrón en los objetos que se analizan. Una vez construido el conjunto de características es necesario realizar el preproceso, con el fin de disminuir la influencia de los errores de registro sobre los datos caracterizados. Posteriormente, es posible hacer adaptaciones y transformaciones de dicho conjunto, de tal manera que se resalte el patrón subyacente en los objetos por medio de técnicas de selección o extracción de características. Finalmente, en la etapa de clasificación, es donde se hace una asociación del objeto a un tipo de clase (Daza-Santacoloma et al., 2007). La clasificación requiere ser validada y afinada, a fin de obtener un sistema con capacidad de generalización y precisión de respuesta.

Remoción de valores atípicos
Los valores atípicos son entendidos como observaciones que parecen haber sido generadas por distribuciones diferentes a las del resto de los datos, y pueden conllevar drásticos efectos sobre el análisis a realizar a partir de las observaciones (Peña y Prieto, 2001), (Peña y Guttman, 1993). La estimación de cualquier característica a partir de bioseñales es muy sensible a factores tales como las condiciones de toma y registro electrónico (ruido de fondo, perturbaciones del hardware, hora de adquisición de las muestras, estado emocional, etc.). Cuando las condiciones de registro son adversas, suelen aparecer observaciones con valores de medida que claramente no corresponden con la estructura de aleatoriedad asumida; este tipo de observaciones se conocen como datos atípicos. Existen múltiples formas de detectar datos atípicos. A continuación se presentan dos formas frecuentemente empleadas en esta labor.
Con base en intervalos de confianza
Sea ξ la característica a la que le corresponde un vector de observaciones 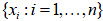 . La remoción de valores atípicos consiste, en este caso, en definir los intervalos de confianza para la estimación de una variable, y luego establecer un criterio de eliminación de observaciones. Si la distribución de una variable se considera gaussiana, el intervalo de confianza de las estimaciones de la media y la varianza de dicha característica, para un nivel de significación , están dados por:
. La remoción de valores atípicos consiste, en este caso, en definir los intervalos de confianza para la estimación de una variable, y luego establecer un criterio de eliminación de observaciones. Si la distribución de una variable se considera gaussiana, el intervalo de confianza de las estimaciones de la media y la varianza de dicha característica, para un nivel de significación , están dados por:

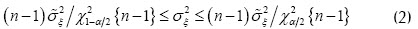
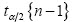 es la cuantilla de nivel
es la cuantilla de nivel 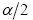 de la distribución t-Student con
de la distribución t-Student con 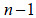 grados de libertad y
grados de libertad y 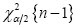 es la cuantilla de nivel
es la cuantilla de nivel 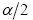 de la distribución
de la distribución 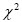 con
con 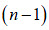 grados de libertad.
grados de libertad.
Cuando el volumen de la muestra es relativamente pequeño, 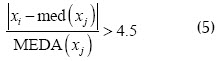 , se puede emplear el método del cálculo del valor de la desviación máxima respecto a la estimación de la media. Considerando solamente (1) se tiene que:
, se puede emplear el método del cálculo del valor de la desviación máxima respecto a la estimación de la media. Considerando solamente (1) se tiene que:
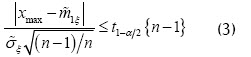
siendo 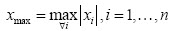 . Si para una observación se tiene un valor dado
. Si para una observación se tiene un valor dado 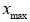 , la desigualdad (3) no se cumple, entonces este valor se remueve. Sobre la muestra acortada de volumen
, la desigualdad (3) no se cumple, entonces este valor se remueve. Sobre la muestra acortada de volumen 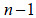 se vuelve a realizar el procedimiento con el siguiente valor encontrado de
se vuelve a realizar el procedimiento con el siguiente valor encontrado de 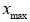 . El procedimiento se repite hasta obtener la muestra con volumen n - m , siendo la cantidad de valores anómalos extraídos. El término
. El procedimiento se repite hasta obtener la muestra con volumen n - m , siendo la cantidad de valores anómalos extraídos. El término 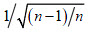 corresponde al coeficiente de corrección en la estimación sesgada de la varianza.
corresponde al coeficiente de corrección en la estimación sesgada de la varianza.
Si el volumen de la muestra es  , y teniendo en cuenta el valor crítico, límite del intervalo en (3), expresado en función del valor crítico de la distribución t-Student
, y teniendo en cuenta el valor crítico, límite del intervalo en (3), expresado en función del valor crítico de la distribución t-Student 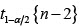 , se presenta la desigualdad (Lvovsky, 1988):
, se presenta la desigualdad (Lvovsky, 1988):
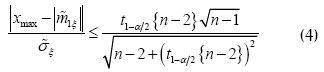
con base en la cual se toma la decisión de eliminar o no el valor que se analiza, según los siguientes tres criterios:
1. Si 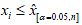 , no se remueve.
, no se remueve.
2. Si 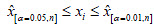 , se remueve sólo si se existe una condición adicional.
, se remueve sólo si se existe una condición adicional.
3. Si 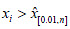 , se remueve
, se remueve
El procedimiento descrito para la detección y remoción de valores atípicos se efectúa por cada una de las características del vector inicial 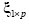 . Además, si durante el registro de una señal perteneciente a un paciente dado ocurre un error sistemático de medición es de esperar que para esta observación aparezcan
. Además, si durante el registro de una señal perteneciente a un paciente dado ocurre un error sistemático de medición es de esperar que para esta observación aparezcan 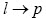 valores atípicos. En este caso, se toma un número máximo de coincidencias
valores atípicos. En este caso, se toma un número máximo de coincidencias 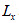 , a partir del cual se juzga que se debe eliminar el registro de observación correspondiente al paciente m . Por otra parte, si para una característica, que se asume con distribución normal, más de
, a partir del cual se juzga que se debe eliminar el registro de observación correspondiente al paciente m . Por otra parte, si para una característica, que se asume con distribución normal, más de 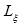 valores son identificados como atípicos, es posible tomar la decisión de remover dicha característica del conjunto completo de variables.
valores son identificados como atípicos, es posible tomar la decisión de remover dicha característica del conjunto completo de variables.
Basado en el cálculo de la mediana
Cuando existe más de un dato atípico en la muestra, es posible que se presenten efectos de enmascaramiento, en el cual observaciones atípicas similares se ocultan entre sí. Sea x la matriz original de datos de dimensión n x p , donde las filas corresponden a las observaciones y las columnas a las variables; además, se denota por 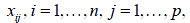 al elemento genérico de esta matriz. Una regla para la detección de valores atípicos de forma univariada está dada por señalar como datos atípicos aquellos que cumplan la siguiente condición,
al elemento genérico de esta matriz. Una regla para la detección de valores atípicos de forma univariada está dada por señalar como datos atípicos aquellos que cumplan la siguiente condición,
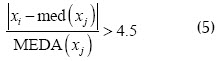
donde 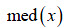 es la mediana de las observaciones, y
es la mediana de las observaciones, y 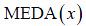 es la mediana de las desviaciones absolutas con respecto a la mediana.
es la mediana de las desviaciones absolutas con respecto a la mediana.
Verificación de normalidad
Con el fin de juzgar si la estructura de los datos es gaussiana, múltiples pruebas de hipótesis y procedimientos gráficos han sido propuestos. Las técnicas pueden ser univariadas o multivariadas (Montgomery y Runger, 2003). En este trabajo se presentan algunas formas convencionales para verificación de normalidad univariada.
La verificación de normalidad por medio del procedimiento de prueba de hipótesis se resume en las siguientes etapas:
1. Se formulan las hipótesis H0 y H1 y se fija el nivel de significación α , cuyo valor depende del conocimiento que se tenga sobre la validez de las hipótesis; a mayor certeza, menor valor de significación se puede dar.
2. Se selecciona el criterio estadístico para la verificación de H0 , cuya estadística 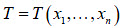 es función de las observaciones xj que tienen distribución conocida
es función de las observaciones xj que tienen distribución conocida 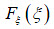 . El intervalo crítico w se halla del subconjunto del espacio de observaciones ξ , tal que se cumpla
. El intervalo crítico w se halla del subconjunto del espacio de observaciones ξ , tal que se cumpla
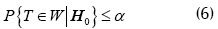
De acuerdo a la hipótesis alternativa, que puede tomar una de las formas: a) 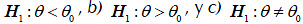 el intervalo crítico, expresado a través de los valores de la estadística , puede tomar una de las siguientes formas (Petrovich y Davidovich, 1989): a)
el intervalo crítico, expresado a través de los valores de la estadística , puede tomar una de las siguientes formas (Petrovich y Davidovich, 1989): a)  o , siendo
o , siendo  las cuantillas de la distribución conocida, escogidas de tal manera que al cumplirse H0 se cumple una de las relaciones:
las cuantillas de la distribución conocida, escogidas de tal manera que al cumplirse H0 se cumple una de las relaciones: 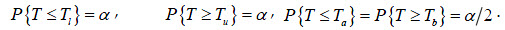 .
.
3. Si la estadística T , calculada de las observaciones, tiene un valor que no pertenece al intervalo crítico, esto es,  , entonces la hipótesis H0 se acepta, en caso contrario se rechaza.
, entonces la hipótesis H0 se acepta, en caso contrario se rechaza.
Los diversos criterios de verificación de hipótesis sobre la pertenencia de un conjunto de datos observados 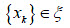 a una distribución dada
a una distribución dada 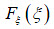 o criterio de concordancia, están basados en la selección de una medida determinada de diferenciación entre las distribuciones empírica y teórica (Thode, 2002).
o criterio de concordancia, están basados en la selección de una medida determinada de diferenciación entre las distribuciones empírica y teórica (Thode, 2002).
Criterio de Kolmogorov-Smirnov. La estadística para este criterio es el máximo valor de desviación entre la distribución observada (empírica) de la distribución pronosticada por la hipótesis :
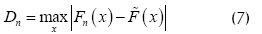
El cálculo de T se lleva a cabo de la siguiente manera:
-Construcción de la serie variacional 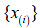 a partir de la observación
a partir de la observación 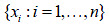 .
.
-Cálculo de la función empírica de distribución.
-Cálculo de 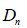
-Los parámetros de la distribución normal, se estiman de la observación. La estadística del criterio se asume 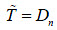 para valores
para valores 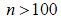 . Para valores
. Para valores 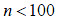 es conveniente realizar ajustes en la estadística (Petrovich y Davidovich, 1989).
es conveniente realizar ajustes en la estadística (Petrovich y Davidovich, 1989).
-Cálculo del valor crítico 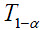 de acuerdo a la expresión:
de acuerdo a la expresión:
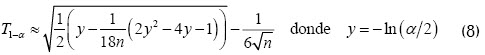
-Cálculo p de empleando la distribución de la estadística 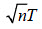 .
.
Transformación de distribuciones
Cuando la prueba de verificación de la distribución da como resultado el rechazo de la hipótesis de normalidad, entonces se deben tomar las medidas para transformar la observación, de tal manera que pueda aceptarse la hipótesis sobre la normalidad de los datos (Teugels y Vanroelen, 2004). Después de realizar la transformación se debe aplicar de nuevo la prueba de verificación de normalidad, y tomar aquella transformación que permita aceptar la hipótesis de normalidad, o bien, aquella que más se aproxime. En la práctica, la familia de transformaciones más utilizada para resolver los problemas de falta de normalidad y de heterocedasticidad es la familia de Box-Cox, mediante la cual se transforma la variable x , cu-yos valores muestrales se suponen positivos, en caso contrario se suma una cantidad fija kx tal que x + kx , la transformación consiste en:
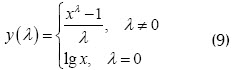
El valor se puede estimar por criterio de máxima verosimilitud, así, para diferentes valores de se realiza la transformación
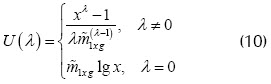
siendo la media geométrica de la variable .
La transformación de variables con distribuciones no normales es frecuente en procesos de análisis de datos, y se realiza principalmente con el fin de obtener mayor interpretación del proceso. Sin embargo, en el caso especial del reconocimiento de patrones existen problemas para desarrollar esta etapa del preproceso. Debido a que la etapa de verificación de normalidad de las características se lleva a cabo de forma separada para cada una de las clases, es muy posible que se encuentren diferentes transformaciones de la misma variable, para cada una de las clases, mientras se busca una distribución normal. Esta situación dificulta la clasificación de una muestra nueva, de la cual no se tiene conocimiento acerca de su pertenencia de clase, porque no se sabría cuál de las transformaciones encontradas aplicar.
Marco experimental
Base de datos
La base de datos pertenece a la Universidad de Las Palmas, Gran Canaria, y contiene grabaciones de audio de 160 individuos (hombres y mujeres), 80 pacientes sin anomalías de voz y 80 pacientes con disfonía. La grabación de voz ha sido realizada en una habitación de un centro hospitalario. El contenido de las grabaciones corresponde a la fonación de la vocal /a/ del idioma español, de forma sostenida y no susurrada. El formato de grabación es audiodigital, con una frecuencia de muestreo de 22.050 Hz y resolución de 16 bits. La caracterización de las señales se llevó a cabo con base en 4 dominios que se emplean frecuentemente en el procesamiento de señales de voz: dominio temporal, dominio espectral, dominio cepstral y dominio del modelo inverso. En este sentido, sobre la vocal son calculadas 144 características.
Pruebas de preproceso
Las pruebas de preproceso consisten en: 1) identificación de variables que contienen datos no convergentes (cuando la variable no se puede medir para cierto individuo o cuando el resultado de su medida fue ∞), 2) identificación de datos atípicos, y 3) verificación de gaussividad univariada. El esquema de preproceso seguido es el siguiente:
1. Revisar los valores al interior de cada una de las variables para detectar la presencia de datos no convergentes, datos iguales a 8, o datos faltantes. En caso de detectar este tipo de datos, la variable no se borra directamente, sino que debe analizarse la cantidad de observaciones con las que se cuenta, y determinar si es preferible eliminar la observación o la variable. Cabe anotar que no se recomienda eliminar observaciones cuando la cantidad inicial de observaciones es relativamente baja, debido que ello conllevaría a estimaciones con menor nivel de significancia. En particular, se opta por eliminar las variables y no reducir el número de observaciones.
2. Detección de datos atípicos. Aquellas observaciones que parecen tener un comportamiento diferente a las demás de una misma clase en análisis, son eliminadas. Al igual que para el caso anterior, debe tenerse cuidado con retirar observaciones de la base de datos, porque es posible que la muestra resultante no posea suficientes observaciones para trabajar con estimadores estadísticos. En particular, se prefiere identificar las variables que poseen más de un 10% de datos atípicos y descartar dicha variable; este proceso se lleva a cabo de forma univariada con base en intervalos de confianza y en el análisis de la mediana de las desviaciones absolutas.
3. Verificación de gaussividad univariada. Busca comprobar que las variables para cada una de las clases posean distribución normal. Se eliminan sobre todas las clases, las variables que no presentan distribución normal en cualquiera de las clases. Se lleva a cabo por medio de la prueba de Kolmogorov-Smirnov.
Clasificación y evaluación
Como algoritmos de decisión entre voces patológicas y normales se emplean dos clasificadores: uno basado en decisión bayesiana sobre distribuciones gaussianas y el otro es el clasificador de vecinos más cercanos (k-NN) (Duda y Hart, 2000), (Webb, 2002), particularmente las pruebas se realizan fijando k = 3.
Con el objetivo de evaluar el desempeño de cada una de las etapas de preproceso, los conjuntos de variables son clasificados antes y después de cada una de estas etapas, y se comparan medidas de discriminancia y confiabilidad obtenidas de los resultados de clasificación. Como medida de discriminancia se emplea la tasa de aciertos en validación, y como medida de confiabilidad se considera el intervalo de confianza para la tasa de aciertos de validación. Para la estimación de los errores de validación se usa la estrategia de validación cruzada leave-M-out (Webb, 2002), la cual consiste en generar conjuntos que corresponden a particiones aleatorias del conjunto de observaciones en pares de entrenamiento-validación donde se retienen observaciones para validar (se entrena con N-M observaciones). En este trabajo (80 por clase) se construyen conjuntos disyuntos de (8 por clase) muestras de validación.
Resultados y discusión
Se considera el conjunto total de 144 variables como el conjunto inicial a ser procesado. La primera prueba es identificar aquellas variables que contienen datos no convergentes; dichas variables son eliminadas del conjunto inicial de características, esto conlleva a reducir el conjunto inicial de variables a un subconjunto nombrado Conjunto 1. Se continúa con la identificación de datos atípicos a partir del Conjunto 1; en este caso en particular, debido al número reducido de observaciones con que se cuenta, no se eliminan las observaciones identificadas como atípicas, sino que se buscan y eliminan las variables que poseen más de un 10% de valores atípicos. Puesto que se emplean dos técnicas diferentes, el subconjunto de variables resultante luego de esta segunda etapa de preproceso se nombra como Conjunto 2a cuando se utilizan intervalos de confianza y Conjunto 2b cuando se emplea análisis de la mediana de las desviaciones absolutas. Finalmente, la etapa de preproceso termina con la verificación univariada de distribución normal. Esta prueba se desarrolla a partir de los Conjuntos 2a y 2b de variables, con base en la prueba de Kolmogorov-Smirnov, con un nivel de significancia . La prueba de normalidad se realiza para cada una de las clases, aquellas variables que no posean distribución normal se eliminan de todas las clases; y el conjunto resultante de variables no eliminadas será Conjunto 3a ó 3b, según corresponda.

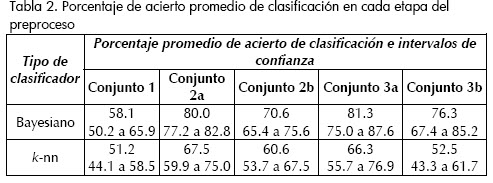
Una vez terminado el preproceso de los datos, se aplican dos tipos de técnicas de clasificación sobre cada uno de los conjuntos de variables identificados anteriormente. Con el procedimiento de clasificación se determina la efectividad del preproceso.
Conclusiones
En este artículo se presenta un esquema de preproceso de datos como etapa esencial en los sistemas de reconocimiento automatizado de patrones. Se comprobó la eficacia de la metodología de preproceso propuesta por medio de análisis experimental en la detección de patologías de voz. Un adecuado preproceso de los datos para el entrenamiento de sistemas de apoyo al diagnóstico médico contribuye con el incremento del acierto y la confiabilidad de los resultados, lo cual contribuye socialmente mejorando la calidad de vida de los pacientes que son sometidos a procesos diagnósticos modernos, no invasivos, de alta precisión y confianza.
Sin embargo, aunque se ha planteado una metodología básica de preproceso, es necesario aclarar que sus resultados son absolutamente dependientes de la técnica particular que se utilice en cada una de las etapas de dicho preproceso. Por ende, el rendimiento del preproceso puede variar sustancialmente al modificar alguna de las técnicas. Debe tenerse presente que aunque las técnicas que emplean umbrales heurísticos tienen, en general, una implementación algorítmica más simple, sus resultados son menos generales, y al emplear bases de datos u observaciones diferentes puede ser necesario recalcular las cotas empíricas. De los experimentos es evidente que el preproceso fue altamente efectivo cuando se emplea clasificador bayesiano para funciones de densidad de probabilidad gaussianas, esto se debe a que la mayoría de técnicas presentadas en el preproceso están diseñadas sobre la presunción de gaussividad. Sin embargo, cuando se empleó el clasificador de vecinos más cercanos, los resultados del preproceso no mejoraron de manera importante el acierto de clasificación, esto se debe a que el clasificador k-nn es enteramente no paramétrico, no depende de la función de densidad de probabilidad de los datos. Con base en lo anterior, se propone como trabajo futuro plantear una metodología de preproceso de datos en casos no paramétricos o cuando la presunción de gaussividad sea falsa.
Agradecimientos
Agradecemos a la Universidad de Las Palmas de Gran Canaria, por su colaboración y préstamo de la base de datos. A la Universidad Nacional de Colombia, a través del proyecto, "Identificación de posturas labiales en pacientes con labio o paladar hendido corregido", y a Colciencias por una beca para estudios de doctorado, convocatoria 2007.
Bibliografía
Daza-Santacoloma, G., Sánchez-Giraldo, L. G., Suárez-Cifuentes, J. F., Selección de características orientada a sistemas de reconocimiento de granos maduros de café., Scientia et Technica, Vol. 35, 2007, pp. 139-144. [ Links ]
Daza-Santacoloma, G., Soto-Mejía J., Castellanos-Domínguez, C. G., Reducción de dimensión para el reconocimiento automático de patrones sobre bioseñales., Scientia et Technica, Vol. 37, 2007, pp. 163-168. [ Links ]
Duda, R. O., Hart, P. E., Stork, D. G., Pattern Classification., 2nd ed., Wiley, 2000. [ Links ]
Thode, H. C. Jr., Testing for normality, Statistics: textbooks and monographs., Vol 164, Marcel Dekker Inc., 2002. [ Links ]
Lvovsky, E., Statistichekije metody postrojenija empiricheskij formul., Vysschaja Shkola, Moskva, 1988. [ Links ]
Montgomery, D. C., Runger, G. C., Applied Statistics and Probability for Engineers., John Wiley and Sons, Inc., 2003. [ Links ]
Peña, D., Guttman, I., Comparing probabilistic methods for outlier detection in linear models., Biometrika, Vol. 80, No. 3, 1993, pp. 603-610. [ Links ]
Peña, D., Prieto, F. J., Multivariate Outlier Detection and Robust Covariance Matrix Estimation., Technometrics, Vol. 43, No 3, 2001, pp. 286-310. [ Links ]
Petrovich, M. L., Davidovich, M. I., Statistichoskoe Otsenivanije I proverka Gipotez na EBM., Financy i Statistika, Moskva, 1989. [ Links ]
Teugels, J. L., Vanroelen, G., Box-Cox Transformations and Heavy-tailed Distributions., Journal of Applied Probability, Vol. 41, 2004, pp.213-227. [ Links ]
Webb, A. R., Statistical Pattern Recognition., 2nd ed., Wiley, 2002. [ Links ]














