Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.1 Bogotá Apr. 2010
Julián Carrillo León1 y Sergio M. Alcocer 2
1 Ingeniero civil. M.Sc., en Ingeniería Estructural. Profesor asistente, Universidad Militar Nueva Granada, UMNG, Colombia. Candidato a Ph.D., en Ingeniería, Universidad Nacional Autónoma de México - UNAM, México.wcarrillo@umng.edu.co 2Ingeniero civil. M.Sc. y Ph.D., en Ingeniería Estructural. Investigador, Instituto de Ingeniería, Universidad Nacional Autónoma de México - UNAM, México. salcocerm@i.unam.mx
RESUMEN
El método de puntales y tensores (P-T) es una herramienta práctica para el diseño sísmico de elementos de concreto reforzado. Con el propósito de evaluar el método de P-T propuesto en el reglamento vigente ACI-318 se llevó a cabo una investigación experimental y analítica con muros de concreto de baja altura. En el programa experimental se incluyeron cuatro especímenes diseñados para fallar por cortante, los cuales se ensayaron dinámicamente en mesa vibradora. Las variables estudiadas fueron el tipo de concreto (peso normal y celular), la cuantía de acero (0,125 y 0,25%) y el tipo de refuerzo a cortante en el alma de los muros (barras corrugadas y malla de alambre soldado). Las propiedades de los muros fueron típicas de viviendas mexicanas de baja altura. Cuando se comparó la resistencia calculada con la resistencia medida se encontró que el método de puntales y tensores del reglamento ACI-318 hace una estimación adecuada de la capacidad a cortante de los muros estudiados. Sin embargo, el modo de falla a cortante del muro, la velocidad de aplicación de carga, el número de ciclos y la energía disipada acumulada, pueden afectar significativamente la degradación de resistencia de muros de concreto reforzado de baja altura.
Palabras clave: muros de concreto, modelo de puntales y tensores, concreto celular, ensayos en mesa vibradora, degradación de resistencia a cortante, velocidad de aplicación de carga.
ABSTRACT
The strut-and-tie method (S-T) is a practical tool for the seismic design of reinforced concrete elements. Experimental and analytical research with low-rise concrete walls was carried out for assessing the S-T method proposed by the current ACI-318 building code. Four specimens designed to fail during shear and shaking table tests were included in the experimental programme. The variables studied consisted of the type of concrete (normal and cellular weight), the amount of steel web (0.125% and 0.25%) and the type of web reinforcement against shear (corrugated bars and welded wire mesh). Wall properties were typical of low-rise housing in Mexico. When the calculated shear strength was compared with the measured one it was found that the S-T method proposed by the ACI-318 building code suitably estimated the shear capacity of the models being studied. However, the walls shear failure mode, loading rate, the number of cycles and the cumulative energy dissipated would noticeably affect the degradation in strength of low-rise, reinforced concrete walls.
Keywords: concrete wall, strut-and-tie model, cellular concrete, shaking table test, shear strength degradation, loading rate.
Recibido: enero 30 de 2009 Aceptado: febrero 22 de 2010
Introducción
A partir del método de puntales y tensores es posible representar la forma como se transmite la carga a través de un miembro mediante un sistema de fuerzas estático que consiste básicamente en tres elementos: puntales, tensores y nudos. En el apéndice A del reglamento ACI‑318 (2008) se proporcionan los lineamientos para el diseño de elementos de concreto reforzado utilizando los resultados de un modelo de puntales y tensores. Con el propósito de evaluar la aplicación de la metodología para el diseño sísmico de muros de concreto de baja altura se llevó a cabo una investigación experimental y analítica en el Instituto de Ingeniería de la UNAM, con el patrocinio del Grupo Cemex. Las variables incluidas en la investigación fueron el tipo de concreto (peso normal y celular), la cuantía de acero (0,125 y 0,25%) y el tipo de refuerzo a cortante en el alma de los muros (barras corrugadas y malla de alambre sol-dado). En general, las propiedades de los muros fueron típicas de viviendas de baja altura en México.
En la literatura actual la mayoría de los estudios orientados a evaluar y validar metodologías de análisis y diseño se basan en resultados experimentales de ensayos cuasi estáticos (monótonos y cíclicos). En esta investigación la evaluación se realiza por medio de la comparación entre las resistencias a cortante probables y medidas en cuatro muros de concreto de baja altura, ensayados bajo excitaciones sísmicas reproducidas por una mesa vibradora. Las resistencias probables se calcularon a partir de modelos de puntales y tensores establecidos a partir de la geometría, la configuración del refuerzo y el flujo de fuerzas esperado durante el ensayo de los especímenes. Las resistencias medidas se consideran representativas de acciones sísmicas reales, ya que en los ensayos dinámicos se tienen en cuenta de forma directa los efectos de la velocidad de aplicación de carga, el número de ciclos y la energía disipada acumulada.
Programa experimental
El prototipo tridimensional corresponde a una vivienda de dos ni-veles con muros de concreto de 100 mm de espesor, 2.400 mm de altura y resistencia nominal a la compresión (fc) igual a 14,7 MPa (150 kgf/cm2). Dentro del programa experimental se construyeron modelos de muros aislados, los cuales se ensayaron bajo carga lateral cíclica reversible (Sánchez, 2010; Flores et ál., 2007). La altura y el espesor de dichos muros fueron iguales a 2.400 mm y 100 mm, respectivamente. Para estudiar el comportamiento de los especímenes frente a acciones sísmicas más representativas se construyeron modelos similares y se ensayaron dinámicamente en mesa vibradora. A continuación se describen las características de dichos especímenes.
Geometría y refuerzo
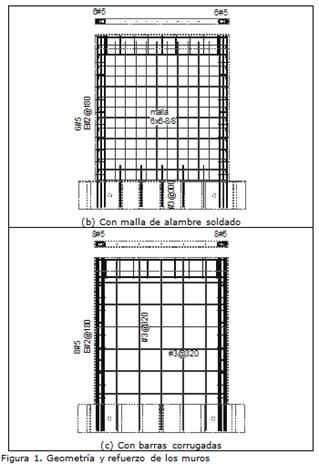
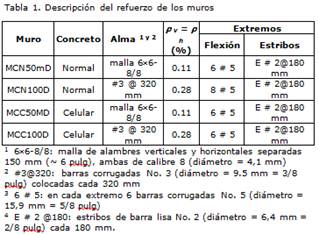
Con el propósito de que las solicitaciones y fuerzas encontradas durante el ensayo no superaran las características de la mesa vibradora y el comportamiento observado durante el ensayo fuera lo más aproximado posible al comportamiento real del prototipo, los especímenes fueron construidos y ensayados con una relación de escala igual a 1:1.25 (80% del tamaño real). Teniendo en cuenta las características de la estructura y el factor de escala geométrica levemente reducida se utilizaron los factores de escala del modelo de similitud simple (Tomazevic y Velechovsky, 1992). En este tipo de similitud los modelos se construyen con los mismos materiales que el prototipo, es decir, no se alteran las propiedades de los materiales, sólo las dimensiones de los modelos. La geometría y la configuración del refuerzo de los modelos se muestran en la Figura 1 y las características del refuerzo se presentan en la Tabla 1. La cuantía nominal de refuerzo a cortante en el alma de los muros MCN100D y MCN100D corresponde a la mínima estipulada en el reglamento ACI-318 (2008). En estos dos muros se utilizaron barras corrugadas. Los muros MCN50mD y MCC50mD fueron reforzados con el 50% de la cuantía mínima de refuerzo a cortante y se utilizó malla de alambre soldado.
Demanda sísmica
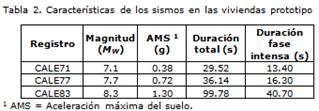
Para estudiar el comportamiento de los muros bajo diferentes estados límite, desde el inicio del agrietamiento hasta el colapso, los especímenes se sometieron a tres niveles de amenaza sísmica. Un evento ocurrido en la zona de subducción del Pacífico mexicano (Mw = 7,1) se utilizó para representar la demanda sísmica en el estado límite elástico. El sismo fue registrado en la estación Caleta de Campos, el 11 de enero de 1997 (Santoyo et ál., 2005). Este registro se consideró como función de Green para simular eventos de mayor severidad, es decir, con mayor intensidad y duración (Or-daz et ál., 1995). Para los estados límite de resistencia y último sesimularon numéricamente dos sismos con magnitud Mw igual a 7,7 y 8,3, respectivamente. En la Tabla 2 se ofrecen las características principales de los registros correspondientes al prototipo de vivienda. En los ensayos de los modelos los registros se afectaron con los factores de escala para la aceleración y el tiempo y se realizaron incrementando la intensidad de forma progresiva hasta alcanzar el estado final de daño. Esto se hizo utilizando el valor de la aceleración máxima como el factor de referencia en cada registro.
Características dinámicas
Con el fin de comparar adecuadamente la respuesta experimental (modelo) con la respuesta real (prototipo), los especímenes de ensayo se diseñaron para representar el comportamiento de los muros ubicados en el primer nivel de una vivienda de uso residencial. Así, fue necesario que los especímenes conservaran las características dinámicas que tendrían al hacer parte del prototipo. De acuerdo con los resultados de modelos analíticos elásticos (realiza-dos con las metodologías de la columna ancha y de elementos finitos) y de pruebas de vibración ambiental, el periodo fundamental de este tipo de estructuras es de aproximadamente 0,12 s (Carrillo, 2009). Por lo tanto, teniendo en cuenta el factor de escala para el periodo (1,25), los muros aislados se diseñaron para que, de acuerdo con su rigidez elástica y su masa, su periodo fundamental al inicio de los ensayos fuera aproximadamente de 0,10 s (0,12 s / 1,25). De esta manera, el peso dinámico (masa gravedad) adicionado a los especímenes construidos con concreto normal y celular fue igual a 234 kN y 207 kN, respectivamente.
Dispositivo de ensayo
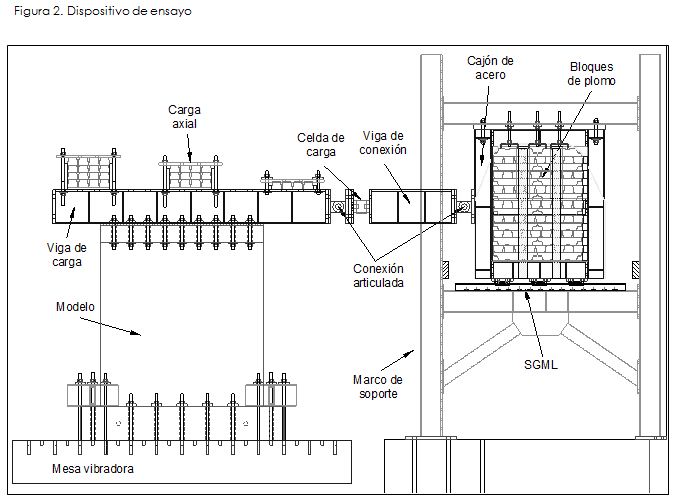
Cuando la masa adicional se ubica directamente sobre los modelos se aumenta significativamente el peso sobre la plataforma de la mesa y, por lo tanto, se hace más complejo y difícil el control de los movimientos. Para utilizar la capacidad total de la mesa vibra-dora sólo para el espécimen, disminuir los ruidos en las señales y, al mismo tiempo, disminuir el riesgo asociado con ubicar la masa directamente sobre el modelo, se diseñó un sistema de carga inercial para almacenar la masa y transmitir las fuerzas inerciales a los modelos. El dispositivo se desliza horizontalmente sobre una estructura de soporte fija localizada fuera de la mesa vibradora (Carrillo y Alcocer, 2010b). La masa adicional (bloques de plomo), se almacenó en un cajón de acero que se apoya sobre una guía de movimiento lineal (SGML) con muy baja fricción. El SGML está conformado básicamente por un riel de acero maquinado de alta precisión y un carro de deslizamiento. De acuerdo con los parámetros de diseño del programa experimental (cantidad de masa y valores máximos esperados de aceleración, velocidad y desplazamiento), se utilizaron dos rieles y seis carros de deslizamiento (tres en cada riel). La conexión entre el cajón de almacenamiento y el espécimen consiste en una viga de conexión articulada en sus extremos (rótulas con giro libre en el plano) y una viga de carga sujeta al extremo superior del espécimen. Para medir la fuerza parcial que actúa sobre el espécimen durante el ensayo, se ubicó una celda entre las vigas de conexión y de carga (Figura 2).
En el extremo superior de los modelos se aplicó un esfuerzo de compresión axial igual a 0,25 MPa, el cual es equivalente al peso del nivel superior de la vivienda de dos niveles. Para determinar este valor se utilizaron modelos analíticos de elementos finitos (Carrillo, 2009). La carga axial equivalente se mantuvo constante durante los ensayos y se representó por el peso de las vigas de carga y de conexión y por bloques de plomo atornillados a la viga de carga (Figura 2). Aunque los bloques tienen una configuración de carga triangular, el peso de las vigas de carga y de conexión genera un esfuerzo axial uniforme sobre la sección transversal de los muros.
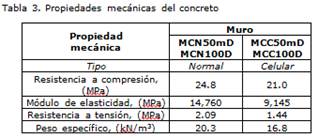
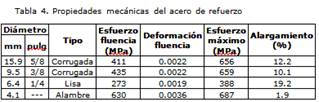
Propiedades mecánicas de los materiales
En la tablas 3 y 4 se despliegan los valores promedio de las propiedades mecánicas del concreto y del acero de refuerzo, respectiva-mente. Para el concreto estas propiedades se obtuvieron en una fecha cercana al ensayo de los modelos.
Predicción de la capacidad de resistencia
El modelo de puntales y tensores es una representación discreta de un campo de esfuerzos obtenido a partir de las fuerzas aplicadas y de las condiciones de apoyo. Este modelo representa la forma como se transmite la carga a través de un miembro de concreto mediante un sistema de fuerzas estático que consiste básicamente de tres elementos: puntales, tensores y nudos (Alcocer y Uribe, 2008). En la literatura actual existen varias metodologías que utilizan el modelo de puntales y tensores para calcular la resistencia máxima a cortante de muros de concreto de baja altura (Siao, 1994; Hwang et ál., 2001, entre otras). Como recomendación de análisis y diseño, en el apéndice A del reglamento ACI-318 (2008) se pro-ponen los requisitos para estimar la capacidad de resistencia de elementos de concreto. En dicho reglamento el diseño de puntales, tensores y zonas nodales está basado en la siguiente expresión:

donde Fn y Fu son la resistencia nominal y la fuerza de diseño actuando en un puntal, tensor o en una cara de una zona nodal; y f es el factor de reducción de resistencia para todos los elementos de la armadura, que es igual a 0,75. A continuación se presentan los parámetros de diseño establecidos para predecir la resistencia a cortante de los modelos a partir de la recomendación del ACI-318 (2008).
Modelo geométrico de puntales y tensores
En la Figura 3 a se muestra el modelo de puntales y tensores adoptado para calcular la capacidad de resistencia de los modelos. La carga vertical y horizontal se aplicó de acuerdo con la configuración del ensayo de los modelos. Debido a que se utilizaron tanto las dimensiones reales de los muros como las propiedades probables de los materiales, en los cálculos no se incluyó el factor de reducción de resistencia estipulado en el reglamento.
La geometría del modelo depende básicamente de las dimensiones del apoyo en compresión (nudo 6). De acuerdo con la configuración geométrica y de refuerzo, y de las cargas aplicadas en el modelo, se observa que los elementos críticos son los puntales 4, 8 y 7, los tensores 1, 3 y 5, y el nudo 6. A partir de la geometría del nudo 6 se calcularon las dimensiones de los elementos que actúan en dicho nudo (Figura 3 b). Para conocer la fuerza axial sobre cada uno de elementos, generada por una configuración de carga axial unitaria N y por una fuerza horizontal unitaria V, se elaboró un modelo matemático de análisis. Ya que no se conocen las fuerzas en los elementos producidas por la carga lateral (V), la cual es la fuerza que se desea estimar, el proceso es iterativo hasta encontrar la fuerza máxima lateral que resisten los elementos del modelo de puntales y tensores (Carrillo, 2010).
Puntales y zonas nodales
La verificación de la resistencia probable de los puntales y zonas nodales se hace a partir de la comparación entre el área disponible en el puntal o el nudo, con el área requerida. Debido a que el espesor del muro (tw) y de los apoyos es el mismo, la verificación se realizó comparando el ancho provisto (wprov) con el ancho requerido en el puntal (wreq-p) o el nudo (wreq-n) (Reineck, 2002). Por lo tanto, el ancho requerido en puntales y zonas nodales se calculó utilizando las ecuaciones (2) y (3), respectivamente.
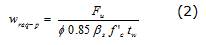
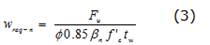
donde ßs y bn son factores que tienen en cuenta el efecto del agrietamiento en la resistencia del puntal y el anclaje de los estribos en la resistencia de la zona nodal, respectivamente. También es necesario revisar el acero de refuerzo (Avf-req) necesario para resistir la fuerza horizontal resultante transferida por el mecanismo de cortante por fricción (Rh). Para ello, se utilizó la ecuación (2).
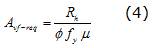
donde fy es el esfuerzo de fluencia del acero que resiste el cortante por fricción y m es el coeficiente de fricción, igual a 0.6l; l es un factor que refleja las propiedades mecánicas reducidas del concreto ligero (l = 1,0 para concreto normal y l = 0,75 para concreto ligero). De acuerdo con resultados experimentales, Carrillo (2010) recomienda no utilizar el factor de reducción, l, para el tipo de los concretos celulares aquí utilizados.
Tensores
La verificación del acero requerido en los tensores, As req, se calculó de acuerdo con la ecuación (3).

Curvas de histéresis experimentales
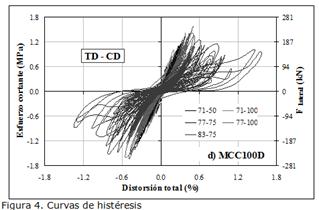
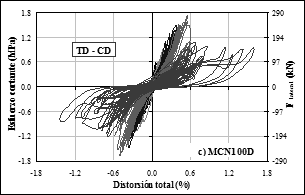
En la Figura 4 se muestran las curvas de histéresis medidas en los modelos, en términos de esfuerzo cortante (o fuerza lateral) y distorsión, junto con el modo de falla observado (TD = tensión diagonal, CD = compresión diagonal, TD-CD = combinado). La fuerza lateral se calculó a partir de las mediciones de la celda de carga y de la fuerza inercial adicional entre la celda de carga y el espécimen (Figura 2). El esfuerzo cortante se obtuvo al dividir la fuerza lateral entre el área real de la sección del muro (espesor longitud). La capacidad de despla-zamiento se ofrece en términos de distorsión total, es decir, el des-plazamiento medido a nivel de la losa superior normalizado por la altura correspondiente. Carrillo y Alcocer (2008) presentan la eva-luación detallada del comportamiento de los modelos.
Comparación de resistencias analíticas y experimentales
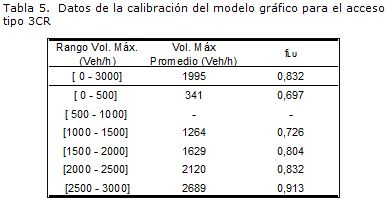
En la Tabla 5 se registran los modos de falla y las resistencias probables a cortante calculadas con el método de puntales y tensores (VACI), utilizando la geometría real de los modelos y las propiedades mecánicas probables de los materiales. De acuerdo con la recomendación de Carrillo (2010), en la predicción de la resistencia no se incluyó el factor de reducción para los concretos ligeros (l= 1,0). La tabla también contiene los modos de falla observados y las resistencias máximas a cortante medidas durante los ensayos en mesa vibradora de los modelos (Vensaye). Así mismo, se presenta la relación entre las resistencias calculadas y medidas (VACI / Vensaye). Como se ve en la Tabla 5, el promedio de la relación entre las resistencias calculadas y medidas es igual a 0,97, o sea que las resistencias calculadas son, en promedio, muy cercanas pero menores que las resistencias medidas. Aparentemente el modelo de puntales y tensores sobreestima la capacidad de resistencia de los muros donde se observó un modo de falla combinado de tensión y compresión diagonal. Sin embargo, aunque en los cuatro modelos el número de ciclos aplicados antes de alcanzar la resistencia fue, en general, comparable, la degradación de resistencia depende del modo de falla observado (Carrillo y Alcocer, 2010a). Por lo tanto, si el número de ciclos antes de alcanzar la resistencia hubiese sido menor, la resistencia máxima de los modelos podría haber sido mayor. Estos efectos no se tienen en cuenta en la mayoría de los modelos de predicción de resistencia disponibles.
En cuanto a la comparación con otras metodologías, Carrillo (2010) reporta que las ecuaciones propuestas en el capítulo 11 (requisitos generales) y en el capítulo 21 (requisitos para diseño sísmico) del cuerpo principal del reglamento ACI-318 sobrestiman la capacidad de resistencia a cortante de los muros estudiados. Por ejemplo, para las ecuaciones del capítulo 11 y del capítulo 21 del ACI-318 (l = 1.0), la relación entre las resistencias calculadas y medidas fue igual a 1,14 y 1,28, respectivamente; es decir, las resistencias calculadas fueron mayores que las medidas. De forma similar, Gulec et ál. (2008) realizaron la comparación de resistencias calculadas y medidas para una extensa base de datos de muros que cumplían con las cuantías mínimas del ACI-318 y reportaron valores iguales a 1,00 y 1,26 para las ecuaciones de los capítulos 11 y 21 del ACI-318, respectivamente. Sin embargo, sólo el 3% de los especímenes de la base de datos se ensayaron dinámicamente en mesa vibradora. Si se tienen en cuenta los efectos de degradación de resistencia que se presentan en ensayos dinámicos, en los cuales el efecto de la velocidad de aplicación de carga y el número de ciclos juegan un papel importante (Carrillo y Alcocer, 2010a), las relaciones entre las resistencias calculadas y medidas reportadas por Gulec et ál. (2008) podrían aumentar y ser semejantes a las reportadas por Carrillo (2010).
Conclusiones
Basados en los resultados experimentales y analíticos de los especímenes estudiados, es posible concluir que para fines de diseño práctico el modelo de puntales y tensores predice adecuadamente la resistencia a cortante de muros de concreto de baja altura sometidos a acciones sísmicas de cortante. Sin embargo, los parámetros de la respuesta (rigidez, resistencia, disipación de energía) dependen de la velocidad de aplicación de carga (tasa de deformación), el mecanismo de resistencia involucrado en el modo de falla (aplastamiento del concreto o fluencia del acero), el número de ciclos, la disipación de energía acumulada y, por supuesto, de la interacción entre ellos. Por lo tanto, aunque la mayoría de los estudios disponibles en la literatura destinados a validar metodologías de diseño utilizan resultados de ensayos cuasi estáticos (monóto-nos o cíclicos), los resultados se deben validar con métodos experi-mentales en los cuales la forma de aplicación de carga se relacione de forma directa con las demandas sísmicas reales que impone un evento sísmico a una estructura.

Agradecimientos
Los autores desean expresar su agradecimiento al Grupo Cemex (México) por el apoyo financiero del proyecto, y al personal de los Laboratorios de la Mesa Vibradora y de Estructuras y Materiales del Instituto de Ingeniería de la UNAM por su valiosa participación en la etapa experimental de la investigación.
Nomenclatura
As-req: acero de refuerzo requerido en un tensor, mm2 Avf -eq: acero de refuerzo requerido para resistir la fuerza de cortante por fricción, mm2 fc: resistencia nominal a la compresión del concreto, MPa fy: esfuerzo de fluencia del acero de refuerzo requerido en el tensor o del acero de cortante por fricción, MPa Flateral: fuerza lateral medida durante el ensayo de los modelos, kN Fn y Fn: resistencia nominal y fuerza de diseño que actúa en un puntal, en un tensor o en una zona nodal, kN Mw: magnitud de momento sísmico N: fuerza axial unitaria en el modelo de puntales y tensores Rh: fuerza horizontal de cortante por fricción en la zona nodal, kN V: fuerza cortante unitaria en el modelo de puntales y tensores VACI: resistencia probable a cortante calculada con el método de puntales y tensores del ACI-318, kN Vensaye: resistencia a cortante medida en los ensayos de los modelos, kN tw: espesor del muro, mm wprov: ancho provisto en un puntal o en una cara de una zona nodal, mm wreq-n: ancho requerido en una cara de una zona nodal, mm wreq-p: ancho requerido en un puntal, mm f: factor de reducción de resistencia para todos los elementos de la armadura bn: factor que tiene en cuenta el anclaje de los estribos en la resistencia efectiva a la compresión del concreto de la zona nodal bs: factor que tiene en cuenta el efecto del agrietamiento y el refuerzo de confinamiento en la resistencia efectiva a la compresión del concreto en el puntal l: factor que refleja las propiedades mecánicas reducidas del concreto ligero rh y rv: cuantías de refuerzo a cortante paralela y perpendicular a la fuerza cortante de diseñoBibliografía
Alcocer, S., Uribe, C., Monolithic and cyclic behavior of deep beams designed using strut-and-tie models., ACI Structural Journal, Vol. 105, No. 3, 2008, pp. 327-337. [ Links ]
American Concrete Institute - ACI., Building code requirements for structural concrete (ACI 318-08) and commentary (ACI 318R-08)., Farmington Hills, MI, USA, 2008. [ Links ]
Carrillo, J., Evaluación del comportamiento a cortante de muros de concreto por medio de ensayes dinámicos., Tesis doctoral, Universidad Nacional Autónoma de México, 2010. [ Links ]
Carrillo, J., Estimación de los periodos naturales de vibración de viviendas de baja altura con muros de concreto., Revista Ciencia e Ingeniería Neogranadadina, Vol. 19, No. 1, 2009, pp. 39-54. [ Links ]
Carrillo, J., Alcocer, S., Shaking table test of RC shear walls with openings., 9th US National and 10th Canadian Conference on Earthquake Engineering, Toronto, Canadá, 2010a, Art. 072. [ Links ]
Carrillo, J., Alcocer, S., Improved external device for a masscarrying sliding system for shaking table testing., Journal of Earthquake Engineering and Structural Dynamics, 2010b. [ Links ]
Carrillo, J., Alcocer, S., Shaking table test of low-rise concrete walls for housing., 14th World Conference on Earthquake Engineering, Beijing, China, 2008, Art. 12-01-0011. [ Links ]
Flores, L., Alcocer, S., Carrillo, J., Sánchez, A., Uribe, R., Ponce, A., Ensaye de muros de concreto con diferente relación de aspecto y bajas cuantías de refuerzo para uso en vivienda., XVI Congreso Nacional de Ingeniería Sísmica, Ixtapa-Zihuatanejo, [ Links ]
Guerrero, México, 2007, Tema XI, Art. 2. Gulec, C., Whittaker, A., Stojadinovic, B., Shear strength of squat rectangular reinforced concrete walls., ACI Structural Journal, Vol. 105, No. 4, 2008, pp. 488-497. [ Links ]
Hwang, S., Fang, W., Lee, H., Yu, H., Analytical model for predicting shear strength of squat walls., Journal of Structural Engineering - ASCE, Vol. 127, No. 1, 2001, pp. 43-50. [ Links ]
Ordaz, M., Arboleda, J., Singh, S., A Scheme of random summation of an empirical Green´ s function to estimate ground motions from future large earthquakes., Bulletin of the Seismological Society of America, Vol. 85, No. 6, 1995, pp. 1635-1647. [ Links ]
Reineck, K., Examples for the design of structural concrete with strut-and-tie models., Publicación SP-208, American Concrete Institute, Detroit, 2002, pp. 244. [ Links ]
Sánchez, A., Comportamiento sísmico de viviendas construidas con muros de concreto., Tesis doctoral, Universidad Nacional Autónoma de México, 2010. [ Links ]
Santoyo, M., Singh, S., Mikumo, T., Source process and stress change associated with the 11 January, 1997 (Mw = 7.1) Michoacán - Mexico - inslab earthquake., Geofísica internacional, Vol. 44, No. 4, 2005, pp. 317-330. [ Links ]
Siao, W., Shear strength of short reinforced concrete walls, corbels and deep beams., ACI Structural Journal, Vol. 91, No. 2, 1994, pp. 123-132. [ Links ]
Tomazevic, M., Velechovsky, T., Some aspects of testing smallscale masonry building model on simple earthquake simulator., Journal of Earthquake Engineering and structural Dynamics, Vol. 21, No. 11, 1992, pp. 945-963. [ Links ]














