Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería e Investigación
Print version ISSN 0120-5609
Ing. Investig. vol.30 no.1 Bogotá Apr. 2010
Germán González Silva1 , Antônio Carlos Luz Lisboa2 y Héctor José Ciro Velasquéz3
1 Ingeniero químico, Universidad Nacional de Colombia, Manizales, M.Sc., en Ingeniería Química, Universidade Estadual de Campinas, São Paulo, Brasil. Estudiante, doctorado, Departamento de Termofluidodinámica, Universidade Estadual de Campinas UNICAMP, São Paulo, Brasil. germangsilva@gmail.com 2 Ingeniero químico. M.Sc., en Ingeniería Química, Universidad Federal do Rio de Janeiro, Brasil. PhD., en Ingeniería Química, University of British Columbia, Canadá. Profesor, Departamento de Engenharia Quimica, Universidade Estadual de Campinas, UNICAMP, São Paulo, Brasil. lisboa@feq.unicamp.br 3 Ingeniero agrícola, Universidad Nacional de Colombia, Medellín. M.Sc., Mechanical Engineering, University of Puerto Rico-Mayaguez Campus, Puerto Rico. Ph.D., Engenharia de Alimentos, Universidade Estadual de Campinas, Brasil. Profesor Asociado. Departamento. de Ingeniería Agrícola y Alimentos, Universidad Nacional de Colombia, Medellín. hjciro@unal.edu.co, jciro@unal.edu.co
RESUMEN
En este trabajo se estudió el comportamiento fluidodinámico de un reactor de lecho fluidizado tipo Downer, adaptando un modelo matemático de conservación. El modelo matemático está basado en las propiedades y características físicas del sólido y del fluido, utilizando una aproximación CBA (Cluster-Based Approach). La comparación entre los resultados numéricos del modelo y los datos experimentales encontrados en la literatura indicaron que el modelo puede predecir los datos experimentales satisfactoriamente. Las simulación matemática estableció que dentro del reactor Downer existen tres regiones fluidodinámicas activas, caracterizadas por un flujo acelerado, desacelerado y completamente desarrollado, y que esta última región disminuye a medida que se incrementa la velocidad superficial del gas manteniendo el flujo de sólidos por unidad de área constante.
Palabras clave: reactor Downer, fluidización, simulación numérica.
ABSTRACT
The fluid dynamics of a downer reactor were numerically resolved by adapting a mathematical conservation model. The mathematical model was based on the solid and fluid properties and physical characteristics using a cluster-based approach (CBA). Comparing the numerical results to the experimental data found in the literature indicated that the mathematical model could satisfactorily predict the experimental data. The mathematical simulation determined that there were three fluid dynamic areas in the downer reactor which were characterised by accelerated, slowed -down and fully-developed flow. The fully developed flow area in the downer decreased with increased gas surface speed keeping solid flux constant.
Keywords: downer reactor, fluidisation, numeric simulation.
Recibido: febrero 03 de 2009 Aceptado: febrero 19 de 2010
Introducción
Convencionalmente se han utilizado en muchos procesos industriales reactores de lecho fluidizado circulante (CFB por sus siglas en inglés) en los que el gas y los sólidos fluyen ascendentemente (Riser) en cocorriente y contra la gravedad (Grace, 1990; Bi et ál., 1995; Lim et ál., 1995; Berruti et ál., 1995). Aunque estos reacto-res sean ventajosos sobre reactores tradicionales como los de lecho fluidizado burbujeante, tienen limitaciones para procesos de corto tiempo de reacción. En los reactores Riser existe una distribución no uniforme de los tiempos de residencia para sólidos. Además, por su hidrodinámica se forman distribuciones de concentración de sólidos en la dirección radial, provocando diferentes tiempos de contacto entre las fases gaseosa y sólida. Por ejemplo, en reacciones de pirólisis, en las que el contacto íntimo entre las fases es esencial bajo condiciones de tiempo controladas, el retromezclado da lugar a un sobrecraqueo y a una reducción en la selectividad de productos deseados (Kraemer, 1990; Chen, 2003).
En respuesta a las desventajas observadas en el reactor Riser, se desarrolló un nuevo tipo de reactor gas-sólido (Downer) en el cual el gas y los sólidos fluyen en forma descendente en cocorriente (Niccum et ál., 1985; Gross y Ramaje, 1983). Este tipo de reactor ha sido objeto de gran interés e investigación durante los últimos 10 años y se proyecta como una de las tecnologías más prometedoras en el futuro cercano para los procesos de lecho fluidizado circulante o CFB (Kim et ál., 2001; Deng et ál., 2002; Alvarez et ál., 2004; Brust et ál., 2004; Grace et ál., 2006; Chen et ál., 2006; Cheng et ál., 2008; Wu et ál., 2008).
El reactor Downer tiene una distribución de tiempos de residencia más uniforme que el Riser, su desempeño es semejante al de un reactor de flujo pistón, y posee una estructura de flujo más uniforme que cualquier otro reactor de lecho fluidizado gas-sólido. Además tiene tiempos de residencia muy cortos, beneficiando reacciones donde los productos intermedios sean los deseados. El uniforme y corto tiempo de contacto evita las reacciones secundarias indeseadas; se estima el tiempo de reacción en milisegundos a segundos, lo que resulta importante en sistemas de desactivación rápida (Zhu et ál., 1995; Zhu et ál., 1999; Talman, 1999; Cao et ál., 2000; Luo et ál., 2001; Liu et ál., 2001; Song et ál., 2005; Grace et ál., 2006; Cheng et ál., 2008). En general, debido a su gran potencial como reactor multifásico, en la literatura se encuentra dos aplicaciones potenciales para este tipo de reactor: la primera es la conversión rápida de feedstock pesados a gasolina y otros derivados como el propileno (Cheng et ál., 2008; Pinho et ál., 2002), la segunda aplicación es la pirólisis de materiales sólidos donde las reacciones se realizan a altas temperaturas y los gases intermedios son los productos deseados, tal como en los procesos de gasificación de carbón, biomasa o residuos sólidos (Kim et ál., 2001; Jiao, 1998). Un ejemplo más es la pirolisis de carbón en plasma de hidrógeno, que abre un camino para la producción de acetileno, siendo ésta una nueva ruta para sintetizar productos químicos utilizando carbón limpio (Cheng et ál., 2008).
Estudios realizados por Pinho et ál., (2002) en un unidades de craqueamento catalítico Downer y Riser, concluyeron que se alcanza en el reactor Downer un aumento de 2% en peso de GLP (gas licuado de petróleo), generando una rentabilidad específica de 6,7 US$/t de carga, en comparación con el reactor Riser, posiblemente debido a la baja selectividad del Downer hacia el coque.
Dada la creciente potencial aplicación industrial de los reactores tipo Downer, se requiere una comprensión cuantitativa de la fluidodinámica para propósitos de escalamiento, diseño y optimización. El objetivo de este estudioes el de presentar un modelo matemático aplicable al análisis fluidodinámico de sistemas particulados en flujo descendente y su validación experimental.
Metodología
Modelamiento y simulación numérica
Según Ho (2003), se han propuesto en la literatura dos clases de modelos para describir el funcionamiento de reactores de lecho fluidizado: uno está basado en una aproximación seudo homogénea, y el otro plantea la existencia de dos fases.
El enfoque seudo homogéneo propone la existencia de una fase utilizando modelos convencionales del flujo multifase para los reactores de lecho fluidizado tales como modelos de flujo ideales, modelos de dispersión, modelos de distribución de tiempos de residencia y modelos de distribución de tiempos de contacto (Kunii y Levenspiel, 1991). El enfoque de dos fases, sin embargo, considera que los reactores de lecho fluidizado consisten en por lo menos dos fases, una burbuja y una emulsión, o una fase gaseosa y una fase sólida (Gidaspow, 1994) y propone una ecuación gobernante para cada fase que describe la transferencia de masa entre las dos fases.
Los modelos fluidodinámicos para lechos fluidizados tipo Riser han tenido gran atención (Kunii y Levenspiel, 1991; Berruti et ál., 1995; Ho, 2003). Para el reactor tipo Downer los modelos son bastante escasos; el primer modelo predictivo para reactores Downer fue presentado por Bolkan-Kenny et ál., (1994), donde se comparó el proceso FCC para los reactores Downer y Riser por medio de un modelo fluidodinámico unidimensional utilizando una aproximación basada en una partícula individual (Particle Based Approach, PBA). El autor utilizó un reactor comercial de 35 m de altura y 1 m de diámetro adoptado para el Riser y el Downer, encontrando grandes ventajas del reactor Downer sobre el reactor Riser, siendo el gran inconveniente del Riser la poca uniformidad radial y la recirculación de sólidos (backmixing).
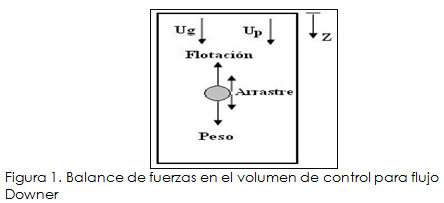
El modelo fluidodinámico Downer presentado en este trabajo se basa en un balance de fuerzas sobre un aglomerado de partículas o clusters de forma esférica y diámetro constante (Figura 1). Este tipo de balance se conoce con el nombre de aproximación basada en cluster (Cluster-Based Approach., CBA).
Balance de momento para una partícula
Realizando un balance de fuerzas y aplicando la segunda ley de Newton sobre un aglomerado de partículas o clusteres, en la corriente descendiente, y asumiendo éstos con geometría esférica, se tiene
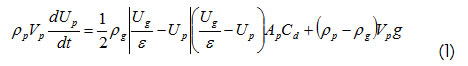
Usando la igualdad:
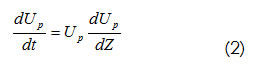
Reemplazando la ecuación 2 en la ecuación 1, el balance de momento resulta:
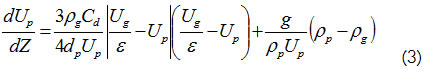
Ésta es la ecuación que describe el perfil de velocidades de partícula a través de la altura del reactor Downer.
Balance de masa
El balance de masa se utiliza para el cálculo de la porosidad (ε) o la proporción de sólidos en el Downer (1-ε):
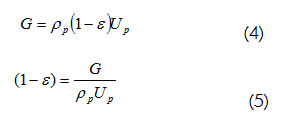
Donde G es la densidad de flujo másico de solidos por unidad de área (kg/s m2).
Se considera la velocidad de los sólidos igual a la velocidad del cluster, esto significa que todas las partículas se mueven como los aglomerados. En el alimentador, a la entrada del Downer las partículas son fluidizadas; por consiguiente, para resolver la ecuación 1 la condición inicial debe ser la de mínima fluidización. De la ecuación 5 se tiene:
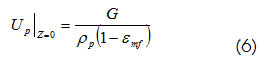
donde εmf es la porosidad en la condición de mínima fluidización.
Balance de momento para suspensión gas-sólido
El gradiente de presión está compuesto por tres componentes: la cabeza estática de presión y los factores debido a la aceleración y fricción de las partículas.

donde:
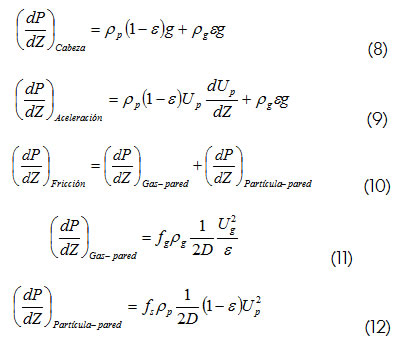
Para el cálculo del coeficiente de descarga (Cd) se utiliza la métodología de cálculo de Mostoufi y Chaouki (1999), donde el coeficiente de descarga estándar se multiplica por un factor de corrección (f) el cual es función de la porosidad del lecho.

donde:
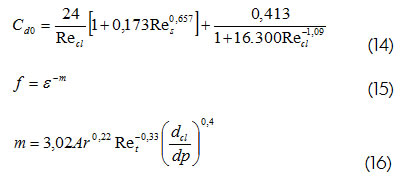
Ar y Ret son el número de Arquímedes y el número de Reynolds terminal (calculado a la velocidad terminal de la partícula), respec-tivamente.
Para el cálculo de la velocidad terminal (Uter) se utiliza el método presentado por Kunii y Levenspiel (1991):
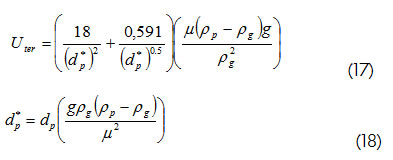
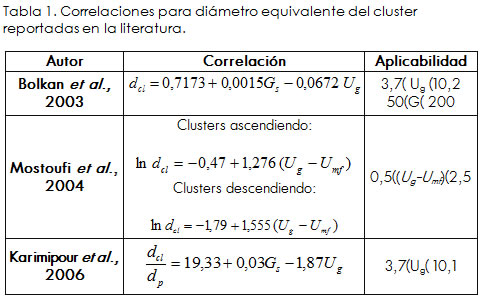
Existen diferentes correlaciones empíricas para estimar el coeficiente de fricción de sólidos (fs). Capes y Nakamura (1973) correlacionaron el factor de fricción como una función de la porosidad y la velocidad de los sólidos. Ratnayake (2005) y Chen et ál., (2006) presentan la correlación de Konno y Saito, donde el factor de fricción es función de la velocidad de sólidos (Us) y el diámetro de la columna (Dd):
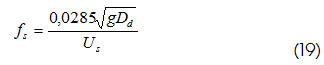
Para estimar el factor de fricción del gas (fg), se utiliza la ecuación de Blasius (Fox, 2003):
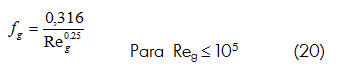
En el presente modelo el sistema se discretiza y se resuelven simultáneamente las ecuaciones diferenciales utilizando el método de Runge-Kutta-Fehlberg. Este algoritmo supervisa la estimación del error de la integración y reduce o aumenta el tamaño del paso de la integración para que el error esté siempre debajo de un umbral especificado. El valor predefinido de esta tolerancia es 10-6. El código del programa fue desarrollado completamente en Visual Fortran.
Análisis de resultados
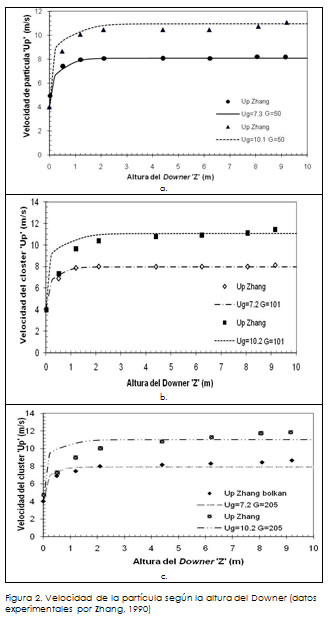
Para la validación del modelo implementado se utilizaron los datos y las condiciones experimentales reportadas por Zhang (1999, 2000). El autor realizó los experimentos en un reactor Downer de 10 m de longitud, 0,1 m de diámetro interno, utilizando partículas de catalizador FCC con diámetro medio de Sauter de 67 μm y densidad de partícula de 1.500 Kg/m3.
La Figura 2 muestra los perfiles de velocidad de sólidos a lo largo del reactor Downer. Se observa que las partículas inicialmente tienen una zona de aceleración y luego llegan a un estado estable (velocidad terminal de la partícula en un fluido). Las partículas continúan acelerando una vez que ellos entran en el Downer hasta alcanzar una velocidad constante. El valor de esta velocidad de la partícula totalmente desarrollada excede la del gas real debido a los efectos de la gravedad.
La variación de la proporción de sólidos (1-e) a lo largo del reactor Downer se indica en la Figura 3. Básicamente, al aumentar la velocidad superficial del gas, la concentración de sólidos en la región de flujo desarrollado disminuye. La concentración de sólidos en la región desarrollada no cambia de forma notoria al aumentar la densidad de sólidos, manteniendo la velocidad superficial del gas.
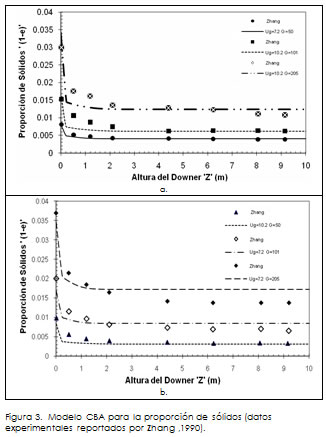
Los resultados también revelan que al incrementar la velocidad de gas manteniendo la densidad de flujo másico de sólidos constante, la zona de flujo en régimen desarrollado se reduce.
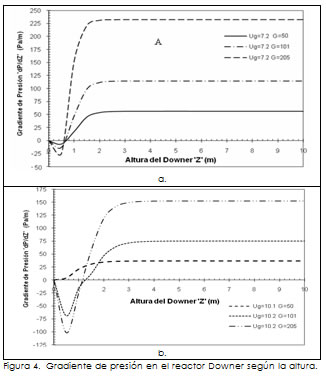
El gradiente de presión está formado por tres componentes, como lo señala la expresión matemática (8). La cabeza estática causa un aumento en la presión a lo largo del Downer, por lo tanto, las pérdidas son debidas a la aceleración y fricción de las partículas.
La existencia de un gradiente negativo a la entrada del Downer posiblemente es provocada por la aceleración rápida de las partículas (Figura 4). Cuando las partículas desaceleran, la cabeza estática de presión se vuelve predominante y el gradiente se hace positivo hasta que alcanza el estado de flujo desarrollado, en esta región el gradiente es constante. Además, la caída de presión cerca a la entrada del Downer y en la región de flujo en régimen desarrollado, aumenta al incrementar la densidad de flujo másico, manteniendo la velocidad del gas constante.
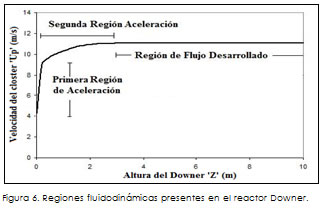
Cuando la velocidad del gas aumenta manteniendo la densidad de flujo másico constante, se disminuye la caída de presión en la región de flujo desarrollado, pero se incrementa en la región de aceleración (entrada del Downer), como lo presenta la Figura 6.
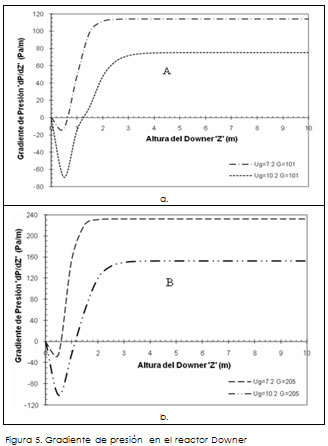
Los perfiles fluidodinámicos del sistema Downer (Up, ε, P) están formados por dos regiones bien definidas (figura 6):
-La región de aceleración, la cual está dividida en dos partes: una donde las partículas aceleran rápidamente, y la otra, donde la ace-leración se hace más lenta hasta llegar al estado de velocidad constante.
-La región de flujo desarrollado, donde la velocidad, la fracción de sólidos y la presión permanecen constantes
Los resultados también muestran que al incrementar la velocidad de gas manteniendo la densidad de flujo másico de sólidos constante, la zona de flujo desarrollada se reduce.
Conclusiones
De acuerdo a la validación experimental, el modelo matemático presentado describe adecuadamente la fluidodinámica de sistemas particulados en un reactor Downer: velocidad de partícula, caída de presión y proporción de sólidos.
Del modelo se distinguen tres regiones en el reactor:
-Región de primera aceleración, con una longitud reducida en el reactor Downer.
-Región de segunda aceleración, caracterizada porque las partículas comienzan a desacelerar y su longitud es un poco mayor a la región de primera aceleración.
-La región de flujo desarrollado, donde las partículas alcanzan una velocidad constante dentro del reactor Downer, con una longitud mucho mayor a las dos anteriores, lo que obliga a que el reactor debe ser lo suficientemente largo para que las partículas alcancen este estado.
Nomenclatura
A = Área transversal, m2
Ap = Área proyectada de la partícula en el volumen de control, m2
Ar= Número de Arquímedes (dpρg(ρp- ρg)g/μ2)
Cd = Coeficiente de descarga, adimensional
dcl = Diámetro de cluster, m
dp = Diámetro de partícula, m
Dd = Diámetro del reactor, m
fg=Factor de fricción del gas, adimensional
fs=Factor de fricción del sólido, adimensional
G = Densidad de flujo másico, kg/(s m2)
HD = Altura del Downer, m
P = Presión, Pa
Recl = Número de Reynolds terminal del cluster (dcl Up ρg/ μg)
Ret = Número de Reynolds terminal del cluster (dcl Ut ρg/ μg)
Up = Velocidad del cluster, m/s
Ug = Velocidad del gas, m/s
Uter = Velocidad terminal, m/s
Z = Coordenada axial, m
ε = Porosidad, adimensional
μ = Viscosidade, kg/(m s)
ρi = Masa específica de fase i, kg/m3
Bibliografía
Aenor Alvarez, P. I., Vega R., Blasco, R., Downer fluidized bed reactors: an application to drying operations, Proceedings of the 14th international drying symposium, 2004, pp. 656-663. [ Links ]
Berruti, F., Chaouki, J., Godfroy, L., Pugsley, T.S., Patience, G.S., hydrodynamics of circulating fluidized bed risers: a review, Can. J. Chem. Eng., Vol.73, No. 5, 1995, pp.579-602. [ Links ]
Bi, H. T., Grace, J. R., Flow regime diagrams for gas-solid fluidization and upward transport, Int. J. Multiphase Flow, Vol. 21, No.6, 1995, pp.1229-1236. [ Links ]
Bolkan Y. G., Pugsley, T. S., Berruti, F., Computer simulation of the performance of fluid catalytic cracking risers and downers, Ind. Eng. Chem. Res., Vol.33, No.12, 1994, pp. 3043-3052. [ Links ]
Bolkan, Y., Berruti, F., Zhu, J., Milne, M., Modeling circulating fluidized bed downers, Powder Technology, Vol.132, No.2-3, 2003, pp.85- 100. [ Links ]
Brust H., Wirth K. E., Residence time behavior of gas in a downer reactor, Ind. Eng. Chem. Res., Vol. 43, No.18, 2004, pp.5796-5801. [ Links ]
Cao, C., Weinstein, J., Characterization of downflowing high velocity fluidized beds, AIChE Journal, Vol. 46, No.3, 2000, pp.515-522. [ Links ]
Capes, C., Nakamura, K., Vertical pneumatic conveying: An Experimental study with particles in the intermediate and turbulent flow regimes, Can. J. Chem. Eng., Vol.51, No. 1, 1973, pp.31-38. [ Links ]
Chen, Y., Handbook of fluidization and fluid-particle systems, Marcel Dekker, 2003, pp.379-396. [ Links ]
Chen, H., Li, H., Tan, S., Mechanism of achieving a dense downer: Modeling and validation, Ind. Eng. Chem. Res., Vol. 45, No.10, 2006, pp.3488-3495. [ Links ]
Cheng, Y., Wu, C., Zhu, J., Wei, F., Jin Y., downer reactor: From fundamental study to industrial application, Powder Technology, Vol. 183, No.3, 2008, pp.364-384. [ Links ]
Deng, R., Wei, F., Jin, Y., Zhang, Q., Jin, Y., Experimental study of the deep catalytic cracking process in a Downer reactor, Ind. Eng. Chem. Res., Vol.41,No.24, 2002, pp.6015-6019. [ Links ]
Fox, R. W., McDonald, A. T., Pritchard, P. J., Introduction to fluid mechanics, Wiley & Sons: New York, 2003. [ Links ]
Grace, J.R., High velocity fluidized bed reactors. Chem. Eng. Sci., Vol. 45, No.8, 1990, pp.1953-1966. [ Links ]
Grace, J.R., Leckner B., Zhu, J., Cheng, J., Multiphase flow handbook, CRC Press Taylor & Francis Group, 2006. [ Links ]
Gross, B., Ramage, M. P, FCC reactor with a downflow reactor Riser. U.S. Patent 4385985, 1983. [ Links ]
Jiao, S. Y., Zhu, J. X., Bergougnou, M. A., Ikura, M., Stanciulescu. M., Investigation and modelling of the thermal cracking of waste plastics derived oil in a Downer reactor, Trans Icheme, Vol.76, No.4, 1998, pp. 319-331. [ Links ]
Ho, T. C., Handbook of fluidization and fluid-particle systems. Marcel Dekker, Nueva York, 2003, pp.239-256. [ Links ]
Karimipour, S., Mostoufi, N., Sotudeh, G. R., Modeling the hydrodynamics of downers by the cluster based approach, Ind. Eng. Chem. Res., Vol.45, No.21, 2006, pp.7204-7209. [ Links ]
Gidaspow, D., Multiphase flow and fluidization, Academic Press, Nueva York, 1994. [ Links ]
Kim,Y. J., Lee, S. H., Kim, S. D., Coal gasification characteristics in a Downer reactor Source, Fuel, Vol. 80, No.13, 2001, pp.1915-1922. [ Links ]
Kraemer, D., Modelling catalitic cracking in novel riser simulator, tesis presentada a la Universidad de Western Ontario, para optar al grado de Doctor of Philosophy, 1990. [ Links ]
Kunii, D. E., Levenspiel, O., Fluidization engineering, John Wiley&Sons, New York, 1991. [ Links ]
Lim, K. S., Zhu, J. X., Grace, J.R., Hydrodynamics of gas-solid fluidization, Int. J. Multiphase flow Vol.21,No.1, 1995, pp.141-193. [ Links ]
Liu, W., Luo, K., Zhu J., Beeckmans, J., Characterization of highdensity gas-solids downward fluidized flow, Powder Technology Vol.115, No.1, 2001, pp.27-35. [ Links ]
Luo, K.B., Liu, W. D., Zhu, J.X., Beeckmans, J. M., Characterization of gas upward-solids downward counter-current fluidized flow, Powder Technology, Vol.115, No.1, 2001, pp.36-44. [ Links ]
Mostoufi, N., Chaouki, J., Prediction of effective drag coefficient in fluidized beds, Chem. Eng. Sci., Vol.54, No.7,1999, pp.851-858. [ Links ]
Mostoufi, N., Chaouki, J., Flow structure of the solids in gas-solid fluidized beds, Chemical Engineering Science, Vol. 59, No. 20, 2004. pp.4217-4227 [ Links ]
Niccum, P.K., Bunn, D.P., Catalytic cracking system, US Patent 4514285, 1985. [ Links ]
Pinho, A., Furtado, J., Silva, M., Kenzo, W., Downflow - O FCC do Futuro. Bol. téc.PETROBRAS, Rio de Janeiro, 45, 16-20, jan./mar. 2002. [ Links ]
Ratnayake, C., A Comprehensive scaling up technique for pneumatic transport systems, tesis presentada a la Universidad de Telemark, Noruega, para optar al grado de Doctor of Philosophy, 2005. [ Links ]
Song, X., Bi, X. T., Bolkan, Y., Hydrodynamics of high-density downer reactors using a novel solids feeder, International Journal of Chemical Reactor Engineering, Vol. 3,2005, pp.1054-1062. [ Links ]
Talman, J. A., Geier, J. A., Reh, R., Development of a downer reactor for fluid catalytic cracking, Chem. Eng. Sci., Vol. 54, No.13-14, 1999, pp. 2123-2130. [ Links ]
Wu, C., Cheng, Y., Jin, Y., Modeling the hydrodynamics in a coupled high-density downer-to-Riser reactor, Powder Technology, Vol. 181, No.3, No.2008, pp. 255-265. [ Links ]
Zhang, H., Zhu, J. X., Hydrodynamics in down flow fluidized beds II: Particle velocity and solids flux profiles, Chem. Eng. Sci., Vol. 55, No. 19, 2000, pp. 4367-4377. [ Links ]
Zhang J., Zhu Y., Tian Y., Xie K., Effect of injecting inert particles on coking prohibition and particle velocity uniformization in downer reactors, Chin. J. Chem. Eng., Vol.15, No. 1, 2007, pp.17-23. [ Links ]
Zhu, J. X., Yu, Z.Q., Jin, Y., Grace, J. R., Issangya, A., Cocurrent Downflow circulating fluidized bed (downer) reactors: A state of the art review, The Canadian Journal of Chemical Engineering, Vol.73, No.5, 1995, pp.662-677. [ Links ]
Zhu, J. X., Ma, Y., Zhang, H., Gas-solids contact efficiency in the entrance region of a co-Current downflow fluidized bed (downer), Trans IChemE, Vol.77, No.2, 1999, pp.151-158. [ Links ]














